Mouvements périodiques d'une corde vibrante en présence d'un obstacle rectiligne

HAL Id: hal-01527104

https://hal.archives-ouvertes.fr/hal-01527104

Submitted on 23 May 2017

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Distributed under a Creative Commons Attribution| 4.0 International License

Mouvements périodiques d’une corde vibrante en

présence d’un obstacle rectiligne

Henri Cabannes

To cite this version:

Henri Cabannes. Mouvements périodiques d’une corde vibrante en présence d’un obstacle rectiligne.

Zeitschrift für Angewandte Mathematik und Physik, Springer Verlag, 1980, 31 (4), pp.473-482.

�10.1007/BF01590858�. �hal-01527104�

Journal de Math~matiques el de Physique appliqubes (ZAMP)

Vol. 31, 1980 Birkh/iuser Verlag Basel

Mouvements p6riodiques d'une corde vibrante

en pr6sence d'un obstacle rectiligne

P a r Henri Cabannes, Laboratoire de M6canique Theorique associ6 au C.N.R.S., Universit6 Pierre et Marie Curie, Paris, France

1. Introduction

Si l'~tude des mouvements des cordes vibrantes est un probl~me fort ancien, l'6tude des m o u v e m e n t s en pr6sence d ' u n obstacle sur lequel la corde peut rebondir a 6t6 6tudi6 seulement dans les derni6res armies. L. Amerio et G. Prouse [1] ont consid6r6 te cas d ' u n obstacle rectiligne et ont d~montr6 l'existence globale de la solution; M. Schatzmann [2] a 6tendu ce r6sultat au cas d ' u n obstacle concave. C. Reder [-3] a 6tudi~ des m o u v e m e n t s en pr6sence d'obstacles ponctuels; C. Citrini et B. d ' A c u n t o [-4] ont envisag6 le cas de deux cordes vibrantes qui peuvent se heurter au cours de leur mouvement.

Lorsque la corde, suppos6e de longueur finie, est fix6e ~ ses deux extr6mit6s, le m o u v e m e n t , en l'absence d'obstacle, est p6riodique. En pr6sence d ' u n obstacle fixe donne, le caract6re pdriodique ou non du m o u v e m e n t d6pend des conditions initiales ; l'6tude g6ndrale de cette question est un probl6me ouvert qui est tr6s compliqu& L'objet de cet article est l'6tude de ce probl6me darts des conditions suffisamment simples p o u r que sa solution soit possible. La corde ne peut se d6placer que dans un plan, et l'obstacle qu'elle peut heurter est une droite fixe parall61e au segment quijoint les extr6mit6s de la corde. A l'instant initial, la corde est au repos, plac6e suivant une certaine courbe ; nous d6montrons que, suivant le choix de cette courbe, le m o u v e m e n t est p6riodique ou non, et, dans le cas d ' u n m o u v e m e n t p~riodique, nous calculons la p6riode. La d6monstration est faite d ' a b o r d dans le cas o/1 la position initiale de la corde est une sinuso~de; elle est ensuite ~tendfie/~ des cas plus g6n~raux par deux m6thodes. Une des m6thodes est une d6monstration directe, c o m m e dans le cas de la sinuso~de, l'autre m6thode utilise un certain changement de variable. Dans un prochain article, nous traiterons un probl6me analogue, lorsque l'obstacle est ponctuel, plac6 au milieu du segment quijoint les extr6mit6s de la corde. La diff6rence essentielle entre deux cas est que, pour un obstacle ponctuel, Ie contact de la corde et de l'obstacle persiste pendant un temps born6, en g6n6ral non nul, tandis que, sur un obstacle rectiligne, la corde rebondit instantan6ment.

474 Henri Cabannes Z A M P

2. l~quations du probl~me

N o u s consid6rons une corde qui peut vibrer dans un plan x - u ; le f r o t t e m e n t et la p e s a n t e u r sont n6glig6s. L a corde est fix~e/t ses deux extr6mit~s (x = + 2 l , u = 0); dans sa position d'6quilibre elle est situ6e sur l'axe des abscisses (u = 0). Lorsqu'elle est 6cart6e de cette position, l ' o r d o n n 6 e de ses points est une fonction u(x, t) Solution de l'6quation [1], fi laquelle il y a lieu d ' a j o u t e r les conditions aux limites [2] et les conditions initiales [3]. (~2b/ ~2 u - - - = 0 (1) Ot 2 Ox 2 u ( + 1, t) = 0

u(x,

0) = ~(x) ~(+~) = 0 ~ t ( x , o) = fl(x) fl(+_-~) = O. (2) (3)

Le p r o b l 6 m e [ 1 ] - [ 3 ] est le p r o b l 6 m e de l'oscillation libre de la c o r d e ; nous d6signerons p a r w(x, t) sa solution ; celle-ci est p & i o d i q u e en t, de p6riodique 2. N o u s s u p p o s o n s m a i n t e n a n t que la corde soit astreinte ~ rester au-dessus d ' u n obstacle d ' 6 q u a t i o n u = ~0(x) sur lequel elle peut r e b o n d i r suivant les lois de la r6flexion sp6culaire. P o u r r6soudre ce n o u v e a u p r o b l b m e , il convient d ' a j o u t e r aux relations [ 1 ] - [ 3 ] , les relations suivantes:

u(x, t) >i q)(x) (4)

3 U ( x , t + ) = au

& - ~ (x, t - ) p o u r u(x, t) = q0(x). (5)

N o u s 6tudierons l'existence et les propri6t~s des solutions p~riodiques du pro- bl6me [ 1 ] - [ 5 ] , dans le cas off l'obstacle est une droite fixe u = - 1, et lorsque la corde est initialement au repos dans la position u(x, O)= 1/h cos 7cx. O n peut toujours r e m p l a c e r u p a r uh, ce qui r e v i e n t / t consid6rer que la position initiale est toujours la m~me, tandis que l'obstacle a p o u r o r d o n n 6 e - h. O n dolt d o n c r6soudre le p r o b l 6 m e

[ 1 ] - [ 5 ] , avec:

au

u(x, 0) = ~(x) = cos ~x ~ (x, 0) = / 3 ( x ) = 0 (6)

u(x, t) >>. - h (0 <<. h <<. 1). (7)

D a n s les deux cas limites on obtient :

p o u r h = 1 u(x, t) = w(x, t) = cos 7cx. cos ~t

p o u r h = 0 u(x, t) = Iw(x, t)l = cos 7cx. Icos ~t[. (8) Ces m o u v e m e n t s sont p6riodiques en t, de p6riode 2 et 1 respectivement. En dehors de

Vol. 31, 1980 M o u v e m e n t s p 6 r i o d i q u e s d ' u n e c o r d e v i b r a n t e 475 wl w-v=- \ v=l w

[

o5

F i g u r e 1 -0.5 0 . %

ces deux cas limites la solution peut ~tre construite de p r o c h e en proche, c o m m e cela est indiqu6 dans 1-1] p a r exemple. Aussi longtemps que l'obstacle n ' a pas 6t6 heurt6, le m o u v e m e n t de la corde est l'oscillation libre u = w; cette solution est valable j u s q u ' h la premi6re ligne d'influence, qui c o m p r e n d un arc A A ' n o n caract6ristique d6fini par

cos ~ x . c o s ~t = - h , ~-x t ~ 1 (9)

et deux arcs caract6ristiques A C et A ' C ' .

Cette ligne est repr6sent6e sur la figure 1; les points A et A' ont p o u r c o o r d o n n 6 e s + XA et t A = 1 --

IxAI

avec cos ~zx A = x f h ; la partie caract6ristique est constitut6e p a r les tangentes A C et A ' C ' ~ l'arc A A ' , tangentes issues des points A et A'

x - - t = 2 x A - 1

476 H e n r i C a b a n n e s Z A M P sur A'C' x + t = 1 - 2 x A cos rc(x + t) = 2h - 1. Au-del~t d e la p r e m i 6 r e ligne d ' i n f l u e n c e , le m o u v e m e n t d e la c o r d e s ' e x p r i m e u n i q u e m e n t en f o n c t i o n de la s o l u t i o n libre w(x, t) et de la s o l u t i o n a d j o i n t e v(x, t) = sin ~ x - s i n 1ft. (10)

Sur les c a r a c t 6 r i s t i q u e s parall611es/i AC la s o m m e w + v = cos ~r(x - t) d e m e u r e c o n s t a n t e ; sur les c a r a c t 6 r i s t i q u e s parall61es /~ A'C' la diff6rence w - v = cos ~(x + t) d e m e u r e c o n s t a n t e . Les c a r a c t 6 r i s t i q u e s a u t r e s que AC et A'C' issues des p o i n t s A e t A ' se c o u p e n t sur l ' a x e des t e m p s a u p o i n t B 1 , d ' o r d o n n 6 e 1, et apr6s r6flexions suecessives s u r les d r o i t e s x = + 89 elles se r e c o u p e n t aux p o i n t s B2, B 3, 9 . .

d ' o r d o n n 6 e s enti6res. Sur ces c a r a c t 6 r i s t i q u e s , issues des p o i n t s B, o n a + v = ( - 1 ) " si elles s o n t parall61es g AC

- v ( - 1 ) n si elles s o n t parall61es/t A'C'

on d 6 m o n t r e ce r6sultat en p a r t a n t des v a l e u r s en A et A', et en r e m a r q u a n t que sur les d r o i t e s x = _+89 w s ' a n n u l e . En o u t r e la travers6e de la deuxi6me ligne d ' i n f t u e n c e et des s u i v a n t e s n ' a l t 6 r e p a s l a s o m m e w + v (sur l ' u n e des families d e c a r a c - t6ristiques) ou la diff6rence w - v (sur l ' a u t r e famille de c a r a c t 6 r i s t i q u e s ) . En effet, d ' u n c6t6 de la caractfiristique x - t = - 2 p a r e x e m p l e , o n a u = k + w, de l ' a u t r e c6t6, u = k ' - v, et, a u - d e l ~ de la ligne d ' i n f l u e n c e , u = - k - w - 2h et u = - k ' + v - 2h; d o n c , a v a n t et apr6s la ligne d ' i n f l u e n c e , w - v = k ' - k.

Les c a r a c t 6 r i s t i q u e s AC et A'C' se r~fl6chissent sur les d r o i t e s x = + 89 et sur les lignes d ' i n f l u e n c e , et se r e c o u p e n t sur l ' a x e des t e m p s a u x p o i n t s D 1, D2 . . . L a d ~ t e r m i n a t i o n de la f o n c t i o n u(x, t) d a n s les diverses r6gions d6finies p a r ces c a r a c - t6ristiques est une suite de p r o b l 6 m e s de C a u c h y et de G o u r s a t . D a n s la r6gion AA'BI, on a u = - w + const., de f a g o n / t satisfaire sur AA' la loi de r~flexion ( c h a n g e m e n t de signe de la vitesse); la c o n s t a n t e v a u t - 2 h , p u i s q u e sur AA', on d o i t a v o i r ~ la fois u = - h et w = - h . Sur la c a r a c t + r i s t i q u e AC, on a v + w = c o s ~ ( x - t ) =

1 - 2h, d ' o f i la s o l u t i o n d a n s le r e c t a n g l e ABa C . . . : u = 1 - 2h - v; o n calcule ainsi la

s o l u t i o n p a r t o u t . D a n s les r6gions travers6es p a r les d r o i t e s x = _+89 u = _+w et p a r suite d a n s les r6gions a b o u t i s s a n t a u x p o i n t s D i e t situ6es de p a r t et d ' a u t r e de l ' a x e des t e m p s on a u = 1 + v, d o n c a u x p o i n t s D~: u(0, t) = 1. D a n s les r6gions a b o u t i s s a n t aux p o i n t s D~ et travers6es p a r l ' a x e des t e m p s o n a u = + w + c o n s t a n t e .

Le m o u v e m e n t d u milieu de la c o r d e est doric d6fini p a r une suite de f o n c t i o n s de la f o r m e

u(0, t) = k. + ( - ) " w ( 0 , t);

le c h a n g e m e n t de c o n s t a n t e k , se fait a u x p o i n t s B,. qui c o r r e s p o n d e n t aux v a l e u r s entihres d u t e m p s , si b i e n q u ' e n ces p o i n t s le sens de v a r i a t i o n de la f o n c t i o n u(0, t) ne c h a n g e p a s ; il se fait aussi sur les lignes d ' i n f l u e n c e qui c o r r e s p o n d e n t aux

Vol. 31, 1980 Mouvements p6riodiques d'une corde vibrante u(Ot) 1 - Wo ~ ':',., " m ~ 0 .'~

h

\/;

wo=w(O,t)=cos ~t Figure 2

Mouvement du milieu de la corde

- ' ~ + k 6 .':s W 0

477

rencontres de la corde avec l'obstacle, soit p o u r u(0, t) = - h e n ces points la vitesse change de signe. I! se fait enfin aux points D i en lesquels on a u(0, t ) = 1, et en lesquels la vitesse change 6galement de signe. Ce m o u v e m e n t est repr6sent6 sur la figure 2. Les constantes k, se d6terminent de proche en proche. Le m o u v e m e n t du milieu de la corde peut ainsi atre ddtermin6 sans qu'il soit n6cessaire de connaitre le m o u v e m e n t de toute la corde.

3. Mouvements p~riodiques: cas de la sinusoide

Lorsque le m o u v e m e n t de la corde est p6riodique il en est de m~me du m o u v e m e n t du milieu; r6ciproquement si la fonction u(0, t) est p6riodique, la fonction

u(x, t)

est p6riodique en t avec la m~me p6riode. Ce r6sultat est une cons6quence du fait que la d6termination du m o u v e m e n t de la c o r d e / t partir de la fonction

u(O, t)

est une suite de probl6mes de Cauchy et de Goursat. Ces remarques nous permettent d'6noncer le th6or6me suivant :

Th~or~me. Si le n o m b r e h est irrationnel, le m o u v e m e n t de la corde n'est pas p~riodique; si ce n o m b r e est le quotient de deux entiers: h =

p/q, le

mouvement est p6riodique de p6riode T = p + q.

On peut d6montrer ce r6sultat en d6finissant un proc6d6 de construction globale de la fonction u(0, t). Dans ce but, on introduit d ' a b o r d la fonction v?(t) et la suite t,, d6finies par les formules

~ ( t ) = - 2 n + ( - ) n c o s T r t p o u r n ~ < t ~ < n + 1 (11) W(tm) = 1 -- m(1 + h) p o u r m = 1,2 . . . . (12) la fonction u?(t), repr6sent6e sur la figure 3, est m o n o t o n e d6croissante; donc la suite tmest une suite croissante. Les

vaieurs

enti6res de t,, :tm = N c o r r e s p o n d e n t aux valeurs

478

Henri Cabannes

ZAMP

u(09

I / i

,,...-"

,...,." .f

-2 84

-2h-~(t)

t4 i -2-3h

~ - 3 - 4 h

Figure 3

i " ~ , ( t ) Mouvement du milieu de la corde

du second m e m b r e 6gales 5` 1 - 2 N ; la valeur de h est alors rationnelle, 6gale 5` ( 2 N / m ) - 1.

A partir de la fonction ~(t), on obtient le m o u v e m e n t du milieu de la corde par les f o r m u l e s :

u(0, t) = ~(t) + 2m(1 + h) p o u r tZm ~ t <~ tzm+ 1

(13)

u(0, t ) = - ~ ( t ) - 2 h - 2 m ( 1 + h ) p o u r t2m+ 1 ~ < t ~ t 2 , , + 2 .

Ainsi, p o u r que le m o u v e m e n t soit p6riodique, il faut et il suffit qu'il existe un entier m tel que 1 - m(1 + h) soft 6gal 5, un entier n6gatif i m p a i r 1 - 2 N ; la p6riode T e s t alors 6gale 5. la valeur c o r r e s p o n d a n t e de tin, soit T = N. Si h est irrationnel, une telle 6ventualit6 est impossible, et le m o u v e m e n t n'est pas p6riodique. Si h e s t rationnel, 6gal 5, p/q (p et q entiers), la condition est satisfaite p o u r m = 2q si bien que la p6riode a p o u r valeur

T = p + q. (14)

4. Mouvements p~riodiques: cas g~n~ral

Les r6sultats de la section pr~c~dente p e u v e n t ~tre & e n d u s au cas oO la corde est initialement au repos dans une position u(x, O) = ~(x), lorsque la fonction ~(x) est paire, croissante p o u r x n~gatif, d o n c d6croissante p o u r x positif, et telle que ~(89 = 89 Le r~sultat peut ~tre o b t e n u p a r deux m 6 t h o d e s diff~rentes.

Vol. 31, 1980 Mouvements p6riodiques d'une corde vibrante 479

a) mdthode directe

Supposant la fonction c~(x) deux fois continfiment d6rivable, il est possible de reprendre t o u s l e s raisonnements de la section 3. P o u r cela on prolonge la fonction ~(x) sur tout l'axe r6el, par antisym&rie par r a p p o r t a l'une quelconque des extr6mit6s de la corde x = _+1 et ensuite par p&iodicit6 de p6riode 2"

~(1 - x) = - c ~ ( x ) (15)

e(x + 2) e(x). On pose ensuite:

w(x,

t) = l{c~(x + t) + c~(x - t)} (16)

v(x,

t) = l{ct(x - t) - c~(x + t)}. (17)

La fonction

w(x, t)

repr6sente l'oscillation libre; la fonction

v(x, t)

est la solution adjointe. N o u s supposerons e(0) = 1, ce qui est toujours possible. La premi&e ligne d'influence,

w(x, t ) = - h , ]dt/dx[

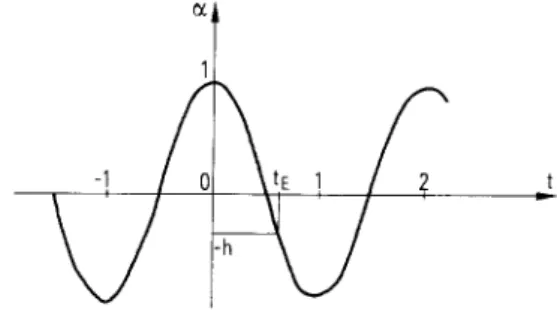
~< 1 (cf. [1]) coupe l'axe des temps au point E d ' o r d o n n & tE, tel que c~(tE) = - h figures 4 et 5. C o m m e h est compris entre 0 et 1, t E positif est compris entre 89 et 1. Puisque

w(x, t)

est constant sur la partie charac- t6ristique

A'EA

de la ligne d'influence, on a sur cette pattie t = r(x) et

dr a'(~) + a'(t/)

dx

- e'(q) - ct'(~) (18)

d2-c 0{"(~)0{'2(?/) -{- ~"(?/)0{'2(~)

d x 2 - -

4

{c((rl)

-- CZ'(~)} 3 ( 1 9 )

La fonction z(x) est paire, d o n c la d6riv~e premi&e impaire et la d6riv& seconde paire.

P o u r 0 ~ < { ~ < l o n a ~'(~)~<0 P o u r - l ~ < t / ~ 0 o n a a'(t/)~>0.

Ainsi dans la r~gion ( ~ ) du plan x - t, d6finie par - 1 ~ q ~ 0 ~ ~ ~< 1, les d~riv~es

d~/dx

et

d2z/dx 2

ont le signe du d 6 n o m i n a t e u r des fractions qui figurent aux seconds m e m b r e s des formules (18) et (19) respectivement. Sur l'arc

EA,

on a puisque ~(~,) + c~(~/) = - h , figure 4, ~'(t/) > - ~ ' ( ~ ) , d o n c d'apr6s (18)

Figure 4 Fonction ~(t)

1

480 Henri C a b a n n e s Z A M P 1" C'

l

-0.5 t 0 0.5 x Figure 5 & 0 ~ dxx ~< 1. (20)

Le point A, en lequel &/dx = 1, est situ6 sur la caract~ristique ~ = 1 ; en ce point a ~ ( d ) = 1 , et c o m m e w = - 2 h , ~ ( q ) = 1 - 2h. O n en d6duit les expressions de l'ellongation u(x, t) c o m m e dans la section pr6c6dente; en particulier les valeurs indiqu6es sur la figure 1, sont encore valable, & c o n d i t i o n de consid6rer que les fonctions v et w sont d6finies par les expressions (16) et (17). La figure 2 est 6galement valable avec Wo = w(0, t) = ~(t), ainsi que la figure 3 avec

u ? ( t ) = - 2 n + (-)"c~(t) p o u r n ~ < t ~ < n + l (21) u?(tm) = 1 - m(1 + h) p o u r m -- 1, 2 . . . (22) O n en d+duit que p o u r h = p/q (p et q entiers) le m o u v e m e n t est p6riodique de p6riode T = p + q.

Si la position de la corde est affine par m o r c e a u x (corde pinc+e) on a

~(x) = 1 - 21xl (23)

v~(t) = 1 - 2t (24)

et le m o u v e m e n t est p6riodique quel que soit h (compris entre 0 et 1) de p & i o d e T = l + h .

b) M~thode du changement de variable

U n e seconde m6thode, dite du c h a n g e m e n t de variable, permet /t partir d ' u n e fonction u(x, t) repr6sentant un m o u v e m e n t de la corde en pr6sence d ' u n obstacle u(x) = - h , d ' e n obtenir une infinit6 d ' a u t r e s d 6 p e n d a n t d ' u n e fonction arbitraire et

Vol. 31, 1980 Mouvements p6riodiques d'une corde vibrante 481 repr6sentant des mouvements de la corde en pr6sence du m6me obstacle. Dans ce but, on consid6re le changement de variable d6fini par la fonction

X = F(x)

(25)

F d6signant une fonction impaire, croissante, d6rivable, v6rifiant les formules F(89 -- 89

F(x + n) = F(x) + n. n

entier. (26)

Th6or~me. Si

u(X, T)

repr6sente le mouvement de la corde en pr6sence de l'obstacle

u(X) = - h ,

et correspondant aux conditions initiales paires

u(X, O) = ~(X),

(Ou/OT)

(X, 0) = fl(X), alors le mouvement de la corde en pr6sence du m~me obstacle,

partir des conditions initiales (27) est d6fini par la formule (28)

~(x, 0) = ~{r(x)), ~ (x, 0) =

fl{r(x)} .F'(x)

(27)

{F(x + t) + F ( x - t) F(x + t ) - F ( x - - O}

(28)

~(x, t) = u

2

'

2

"

Pour d6montrer ce th6or+me on consid6re les identit~s"

~

•u F'(x + t) - F'(x - t)

Ou F'(x + t) + F'(x - t)

~t ~X 2 + 0T 2 (29)

Zu'~

02~0t

2

Ox 2~2ff- F'(x + t ) ' F ' ( x - ,){0?~uz

0 t 2 j . (30) La relation (30) prouve que la fonction a(x, t) v6rifie l'6quation des ondes; la relation (29) prouve que cette fonction v6rifie sur l'obstacle ~ = - h , la condition de r6flexion

~a (x, t +) = c~a

~ t

- ~ (x, t ).

(31)

En effet si ~ = - h , on a aussi

u(X, T) = - h ,

donc ~ u ( X , T + ) = ~u

OT

- o T ( X , T - )

et

Ou

dT Ou

(32)

OX

dX •T

ce qui prouve que les deux d6riv6es partielles

Ou/•X, Ou/OT

changent de signe, donc d'apr6s la formule (29), il en est de marne pour la d6riv6e

O~/Ot.

Ce qui d6montre le th6or6me.

Les formules (26) et (28) indiquent que si le mouvement d6fini par la fonction

482 Henri Cabannes ZAMP ~7(x, t) est p 6 r i o d i q u e a v e c la m ~ m e p h r i o d e . D a n s le c a s off la c o r d e est i n i t i a l e m e n t a u r e p o s d a n s la p o s i t i o n u ( x , 0) = 1 - 2lxl, u n c a l c u l d i r e c t m o n t r e q u e le m o u v e m e n t est p 6 r i o d i q u e de p h r i o d e 1 + h ( p o u r h c o r n p r i s e n t r e 0 et 1). Si h est r a t i o n n e l 6 g a l p / q , le m o u v e m e n t p o s s h d e la p h r i o d e e n t i & e p + q, p 6 r i o d e q u i se c o n s e r v e d o n e p a r c h a n g e m e n t de v a r i a b l e . O n r e t r o u v e a i n s i le r 4 s u l t a t de la s e c t i o n 4a et le r 6 s u l t a t d e la s e c t i o n 3 q u i e n est u n cas p a r t i c u l i e r . 5. Conclusion

Les p r o b l e m e s pos6s p a r les m o u v e m e n t s d ' u n e c o r d e v i b r a n t e e n p r 6 s e n c e d ' u n o b s t a c l e c o n c e r n e n t e s s e n t i e l l e r n e n t l ' e x i s t e n c e des s o l u t i o n s et l ' 6 t u d e d e leur p 6 r i o d i c i t 6 6 v e n t u e l l e . E n ce q u i c o n c e r n e l ' e x i s t e n c e , celle-ci a 6t6 d 6 m o n t r 6 e p o u r des o b s t a c l e s r e c t i l i g n e s o u c o n c a v e s ; le cas des o b s t a c l e s c o n v e x e s reste h t r a i t e r . L ' 6 t u d e d u c a r a c t 6 r e p e r i o d i q u e o u n o n p 6 r i o d i q u e d u m o u v e m e n t est d6j/t a v a n c 6 e p o u r u n o b s t a c l e p o n c t u e l ; le cas des o b s t a c l e s n o n p o n c t u e l s s e m b l e p l u s difficile et le p r 6 s e n t t r a v a i l est u n e c o n t r i b u t i o n / l cette 6 t u d e .

Bibliographie

[1] L. AMEglO et PROUSE, Study of the Motion of a String Vibrating against an Obstacle. Rend. Matematica 8, 563-585 (1975).

[2] M. SCHATZMANN, An Hyperbolic Problem of Second Order with Unilateral Constraints: the Vibrating

String with a Concave Obstacle, Pnbl. Universit~ Paris VI, n ~ 78 031.

[3] C. REDER, F.tude qualitative d'un problkme hyperbolique avec contrainte unilatdraIe, Th6se de 36 cycle, Universit6 de Bordeaux (1979).

[4] C. CITRINt et B. D'ACuNTO, Sur le choc de deux cordes. Compt. Rend. Acad. Sc. Paris, 289, A, 5-7 (1979).

R6sum6

Une corde fix~e ~t ses deux extr~mit~s peut vibrer dans un plan en pr6sence d'un obstacle rectiligne, fixe, parall61e au segment qui joint ses extr6mit6s. La corde peut rebondir sur l'obstacle. La corde est initialement au repos, plac6e suivant une certaine courbe. On d6montre que, suivant la choix de cette courbe, le mouvement est p6riodique ou non, et, lorsque le mouvement est p6riodique, on calcule la p6riode.

Abstract

A string fixed at both ends oscillates in a plane in which there is a fixed straight line segment, parallel to the line joining the ends of the string. The string can rebound from the solid segment. The string is initially at rest, with prescribed shape. We prove that depending on the prescribed initial form of the string the motion is either periodic or aperiodic, and in the former case we compute the period. (Regu: 11 janvier 1980)