Université Ibn Tofail Faculté des Sciences Département d’Informatique Kénitra MASTER MRI
Programmation Logique
et Intelligence Artificielle
A. EL HARRAJ 2016-2017Partie I
Introduction au Prolog ... 1 Introduction ... 2 Principe ... 3 1. Les faits ... 3 2. Les questions ... 5 3. Les règles ... 7 4. Prédicats et clauses ... 9 5. Mécanisme de résolution ... 10 Données en Prolog ... 13 1. Constantes ... 13 2. Variables ... 13 3. Structures ... 14 Opérateurs ... 15 Unification ... 17 Arithmétique ... 19 Listes ... 20 1. Définition ... 202. Opérations sur les listes ... 21
La coupure (cut) ... 25
1. Principe ... 25
2. La négation comme échec ... 29
Prédicats prédéfinis ... 31
1. Chargement, débogage et compilation des programmes ... 31
2. Les prédicats d'entrée/sortie ... 31
3. Contrôle de la base de connaissance ... 32
4. Tests sur le type d'un terme ... 35
5. Unification et comparaison des termes ... 36
6. Construction et décomposition des termes ... 37
7. Prédicats de contrôle ... 38
Introduction
Prolog comme son nom l'indique est un langage de la programmation logique.
La programmation logique est un paradigme de programmation qui définit une application comme un ensemble de faits et de règles logiques. Cet ensemble est ensuite exploité par un moteur d'inférence pour répondre à des questions ou des requêtes.
Contrairement aux autres paradigmes de programmation telles que la programmation impérative, fonctionnelle ou la programmation orientée objet, où les programmes sont des suites d'instructions qui précisent comment résoudre un problème, la programmation logique est considérée comme une programmation déclarative puisque les programmes y sont constitués par des informations décrivant le problème à résoudre lui-même.
Le moteur d'inférence est un programme qui diffère d'un interpréteur ou d'un compilateur du fait qu'il ne traite pas des instructions, mais utilise les informations contenues dans le code du programme pour répondre à des questions.
Le Prolog est né aux besoins de pouvoir traiter la langue naturelle par ordinateur (Alain Colmerauer et Robert A. Kowalski - 1970), mais son utilisation s'est étendue vers d'autres domaines :
− Intelligence artificielle (Systèmes experts, …)
− Résolution symbolique des équations, Logique et mathématiques. − Bases de données relationnelles.
− Compilation.
− Preuve des programmes.
Il existe différentes implémentations du Prolog: − SWI Prolog (www.swi-prolog.org) − GNU Prolog (http://gnu-prolog.inria.fr) − Sicstus Prolog (www.sics.se/sicstus)
Dans cette partie du cours nous utiliserons SWI-Prolog et nous baserons essentiellement sur le livre de référence :
Ivan Bratko : Prolog Programming for the Artificial Intelligence. 3rd Ed., Addison-Wesley
Principe
• La programmation en Prolog consiste donc à décrire les entités (ou les objets) d'un problème donné et les relations entre ces objets, et établir les règles qui les gèrent.
• Ainsi, dans un programme : − On spécifie les faits. − On déclare les règles. Et pour exécuter ce programme :
− On pose des questions.
1. Les faits
• Les faits sont les hypothèses du problème posé qu'on suppose vraies. Ils décrivent les relations et les propriétés des objets de ce problème. L'ensemble des faits constitue ce qu'on appelle une base de connaissance.
• En Prolog, chaque fait est représenté par une clause. Une clause est constituée par un identificateur de la relation correspondante au fait représenté, suivi entre parenthèses de la liste ordonnée des objets en question et terminée par un point.
Par exemple, les faits suivants: Cloé aime le chocolat. Paul est un parent de Marc. Paul est un parent de Cloé. Socrate est une personne. Cloé est une femme.
Le train de ligne numéro 12 relie Rabat et Fès. Ali est un étudiant en master d'informatique.
L'étudiant Ali a eu 16 en java et s'est classé premier. 0! = 1.
peuvent être représentés en Prolog par les clauses suivantes : aime(cleo,chocolat). parent(paul,marc). parent(paul,cloe). personne(socrate). femme(cloe). train(train_ligne,12,rabat,fes). etudiant(ali,master,informatique). etudiant(ali,java,16,1). factoriel(0,1).
• Les noms des relations et des objets (ou entités) utilisés doivent commencer par une lettre minuscule.
• Si une relation à un seul argument, alors il s'agit d'une propriété (personne, femme).
• Plusieurs clauses peuvent correspondre à une même relation (parent). Ainsi une relation est définie par l'ensemble des clauses correspondantes décrites dans le programme.
• D'autre part, on peut utiliser le même nom pour designer deux relations différentes à condition qu'elles ne possèdent pas le même nombre d'arguments.
Dans l'exemple, on a défini deux relations avec le même identificateur 'etudiant'. Ces deux relations sont différentes, du fait qu'elles n'ont pas le même nombre d'arguments.
Exemple 1 :
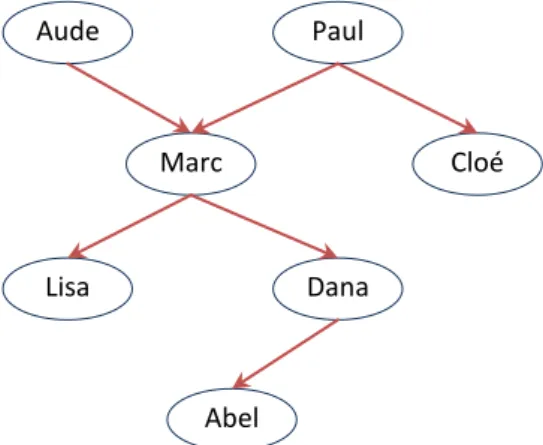
On se propose d'écrire un programme qui décrit les faits contenus dans l'arbre généalogique suivant :
où la flèche représente "parent de".
Pour ce, on choisit l'identificateur "parent" pour représenter la relation de parenté, et "feminin" et "masculin" pour représenter les informations relatives aux sexes des personnes cités, on obtient le programme suivant :
/*
fichier : famille_1.pl */
/* Clauses décrivant la relation 'parent' */ % parent(X,Y) : X est un parent de Y
parent(paul,cloe). parent(paul,marc). parent(aude,marc). parent(marc,lisa). parent(marc,dana). parent(dana,abel).
/* Clauses décrivant la propriété feminin */ feminin(aude).
feminin(cloe). feminin(lisa). feminin(dana).
/* Clauses décrivant la propriété masculin */ masculin(paul).
masculin(marc). masculin(abel).
Remarque
− L'extension d'un programme source en Prolog est 'pl'. :
− Les commentaires s’écrivent entre /* et */ et % est utilisé pour les commentaires de fin de ligne.
Figure I.1 : Arbre généalogique
Aude Paul
Marc Cloé
Lisa Dana
2. Les questions
• Pour exécuter un programme, on le charge dans l'interpréteur du Prolog et on pose des questions. • Pour charger un programme source dans l'interpréteur du Prolog on utilise la procédure :
consult(nom_programme).
2.1. Questions simples
• Une question simple, dit aussi but, peut être une simple demande sur la véracité d'une relation entre objets contenue dans la base de connaissance.
• Pour poser une question simple, il suffit d'écrire la question en la formulant comme une clause à l'invité de l'interpréteur du Prolog qui est '?-'.
Par exemple, pour poser la question :
est-ce que Marc est un parent de Lisa. on l'écrit en Prolog, comme suit :
?- parent(marc,lisa).
Prolog va comparer la question posée avec les clauses de la base de connaissances chargée.
La réponse du Prolog sera 'true' ou 'false', selon l'existence ou non de ce qu'on a écrit est vrai ou faux par rapport à la base de connaissances.
Exemple
2.2. Questions avec variables
:
On charge le programme famille_1.pl, et on pose les questions suivantes : % est-ce que Marc est un parent de Lisa.
?- parent(marc,lisa). true.
% est-ce que Cloé est un parent de Dana. ?- parent(cloe,dana).
false.
% est-ce que Paul est le père de Marc. ?- pere(paul,marc).
ERROR: toplevel: Undefined procedure: pere/2 (DWIM could not correct goal)
La dernière question, génère une erreur, puisqu'aucune relation 'pere' n'est définie dans le programme.
• Pour pouvoir poser des questions qui permettent de trouver des informations sur la base de connaissances qui sont plus qu’une simple demande sur la véracité d’un seul fait, Prolog permet l’utilisation des variables. Ici, Les variables prennent le sens d'indéterminées ou d'inconnues. Par exemple, si on veut connaitre :
Qui sont les enfants de Paul ?
cités dans la base de connaissances du programme famille_1.pl, on formule premièrement la question comme suit :
X est un enfant de Paul si Paul est un parent de X. La question à poser serait donc :
?- parent(paul,X).
Ce qui donne dans l’interpréteur de Prolog :
?- parent(paul,X). X = cloe █
Après la première réponse, Prolog attend une entrée de l’utilisateur qui lui permettra de savoir s’il continu à chercher les autres réponses ou arrêter la recherche :
− Un point virgule, lui permet de continuer − Un point, lui demandera de s’arrêter
?- parent(paul,X). X = cloe ;
X = marc.
• En Prolog, le point virgule signifie 'OU'. Ainsi, Prolog nous informe que la question posée est vraie si :
X=cloe OU X= marc
• Pour répondre à cette question, Prolog essai de trouver parmi les clauses du programme, celles qui peuvent être égales à la question posée. Il commence par comparer terme à terme (y compris le nom de la relation) en commençant par le début du fichier programme. Si l'égalité est possible en substituant la variable libre par une donnée alors cette dernière sera retournée en tant que réponse. On parle alors d'unification : Prolog tente, au fait, d'unifier (de rendre égales) la question et les clauses décrites dans le programme.
Autre exemple :
% Qui sont les femmes citées dans famille_1.pl ? ?- feminin(X). X = aude ; X = cloe ; X = lisa ; X = dana. Notez que :
− Les identificateurs de variables doivent commencer par une lettre majuscule. − La portée de la variable se limite à l’énoncé.
2.3. Questions composées
• D'une manière générale, une question peut être composée de plusieurs buts simples ou avec des variables. La composition peut se faire avec la conjonction ET (représentée par une virgule) et/ou avec la conjonction OU représentée par un point virgule.
Par exemple, si on veut connaitre : Qui est le père de Dana ? notre formulation serait :
X est le père de Dana Si X est un parent de Dana
ET
X est de sexe masculin. La question à poser serait donc :
parent(X,dana), masculin(X).
Ce qui donne dans l’interpréteur de Prolog :
?- parent(X,dana), masculin(X). X = marc.
Pour répondre à cette question, Prolog commence par unifier le premier but : parent(X,dana)
avec les clauses du programme.
Si l'unification réussit pour le premier, alors il sauvegarde la position, substitue les variables libres par les données correspondantes réalisant l'unification :
X=marc dans le but, ce qui donne :
parent(marc,dana),masculin(marc) le premier étant vrai, alors il est retiré de la liste et le nouveau but devient :
masculin(marc) et passe à l'unification du nouveau second but.
Ce nouveau but ne contient pas de variable, il est soit vrai soit faux, dans les deux cas de figure, à la fin de l'unification de ce second but, il retourne à la position sauvegardée lors de l'unification du premier but pour continuer la recherche.
Autre exemple :
% Qui sont les filles de Paul ? ?- parent(paul,X), feminin(X). X = cloe.
3. Les règles
3.1. Définition
• Les règles sont des relations qui sont établies à partir d’autres relations existantes. Leur utilisation permet d’ajouter des faits qui peuvent être déduites d’autres faits.
Dans l’exemple famille_1.pl, la relation 'père de' peut être déduite des relations 'parent' et 'masculin'. Ainsi, il est inutile d'ajouter tous les faits décrivant cette relation, il suffit de définir une règle qui permet de la définir.
En effet, la règle qui permet de définir la relation 'pere' est :
Pour tout X,Y parent(X,Y) ET masculin(X) ⇒ pere(X,Y) La clause correspondante en Prolog s'écrit comme suit :
pere(X,Y) :- parent(X,Y), masculin(X).
• L'écriture se fait dans l'ordre inverse. Ainsi, le symbole ':-' représente '⇐' et la virgule représente la conjonction ET.
On peut ajouter d'autres règles, à notre programme, par exemple les relations mere, enfant, grand_parent, etc.
/* fichier : famille_2.pl */
/*---FAITS ---*/ ...
/*--- REGLES ---*/ % R1 : pere(X,Y) -> X est le père de Y
pere(X,Y) :-
parent(X,Y), masculin(X).
% R2 : mere(X,Y) -> X est la mere de Y mere(X,Y) :-
parent(X,Y), feminin(X).
% R3 : enfant(X,Y) : X est un enfant de Y enfant(X,Y) :- parent(Y,X).
% R4 : grand_parent(X,Z) ; X est un grand_parent de Z grand_parent(X,Z) :-
parent(X,Y), parent(Y,Z).
− La relation 'enfant' est l'inverse de la relation parent, ce qui donne :
enfant(X,Y) :- parent(Y,X).
− La relation 'grand_parent' découle de l'assertion suivante :
𝑋𝑋 𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑔𝑔𝑔𝑔𝑔𝑔𝑢𝑢𝑔𝑔 𝑝𝑝𝑔𝑔𝑔𝑔𝑒𝑒𝑢𝑢𝑒𝑒 𝑔𝑔𝑒𝑒 𝑍𝑍 SI 𝑖𝑖𝑖𝑖 𝑒𝑒𝑒𝑒𝑖𝑖𝑒𝑒𝑒𝑒𝑒𝑒 𝑌𝑌 𝑒𝑒𝑒𝑒𝑖𝑖𝑡𝑡𝑢𝑢𝑒𝑒 �𝑋𝑋 𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑝𝑝𝑔𝑔𝑔𝑔𝑒𝑒𝑢𝑢𝑒𝑒 𝑔𝑔𝑒𝑒 𝑌𝑌ET 𝑌𝑌 𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑝𝑝𝑔𝑔𝑔𝑔𝑒𝑒𝑢𝑢𝑒𝑒 𝑔𝑔𝑒𝑒 𝑍𝑍
soit :
∀ 𝑋𝑋, 𝑍𝑍 [∃ 𝑌𝑌 ∶ 𝑝𝑝𝑔𝑔𝑔𝑔𝑒𝑒𝑢𝑢𝑒𝑒(𝑋𝑋, 𝑌𝑌) ET 𝑝𝑝𝑔𝑔𝑔𝑔𝑒𝑒𝑢𝑢𝑒𝑒(𝑌𝑌, 𝑍𝑍)] ⟹ 𝑔𝑔𝑔𝑔𝑔𝑔𝑢𝑢𝑔𝑔_𝑝𝑝𝑔𝑔𝑔𝑔𝑒𝑒𝑢𝑢𝑒𝑒(𝑋𝑋, 𝑍𝑍)
qui se traduit en Prolog par :
grand_parent(X,Z) :- parent(X,Y), parent(Y,Z).
3.2. Règles récursives
• Prolog accepte d'écrire des règles sous une forme récursive. Par exemple la règle 'descendant', qui permet de trouver tous les descendants d'une personne, peut être formulée comme suit :
𝑋𝑋 𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑔𝑔𝑒𝑒𝑒𝑒𝑑𝑑𝑒𝑒𝑢𝑢𝑔𝑔𝑔𝑔𝑢𝑢𝑒𝑒 𝑔𝑔𝑒𝑒 𝑍𝑍 Si �𝑋𝑋 𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑒𝑒𝑢𝑢𝑒𝑒𝑔𝑔𝑢𝑢𝑒𝑒 𝑔𝑔𝑒𝑒 𝑍𝑍OU 𝑋𝑋 𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑔𝑔𝑒𝑒𝑒𝑒𝑑𝑑𝑒𝑒𝑢𝑢𝑔𝑔𝑔𝑔𝑢𝑢𝑒𝑒 𝑔𝑔′𝑢𝑢𝑢𝑢 𝑒𝑒𝑢𝑢𝑒𝑒𝑔𝑔𝑢𝑢𝑒𝑒 𝑔𝑔𝑒𝑒 𝑍𝑍 Autrement dit : 𝑋𝑋 𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑔𝑔𝑒𝑒𝑒𝑒𝑑𝑑𝑒𝑒𝑢𝑢𝑔𝑔𝑔𝑔𝑢𝑢𝑒𝑒 𝑔𝑔𝑒𝑒 𝑍𝑍 Si ⎩ ⎪ ⎨ ⎪ ⎧𝑍𝑍 𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑝𝑝𝑔𝑔𝑔𝑔𝑒𝑒𝑢𝑢𝑒𝑒 𝑔𝑔𝑒𝑒 𝑋𝑋 OU ∃𝑌𝑌 𝑒𝑒𝑒𝑒𝑖𝑖 𝑡𝑡𝑢𝑢𝑒𝑒 ∶ �𝑍𝑍 𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑝𝑝𝑔𝑔𝑔𝑔𝑒𝑒𝑢𝑢𝑒𝑒 𝑔𝑔𝑒𝑒 𝑌𝑌ET 𝑋𝑋 𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑔𝑔𝑒𝑒𝑒𝑒𝑑𝑑𝑒𝑒𝑢𝑢𝑔𝑔𝑔𝑔𝑢𝑢𝑒𝑒 𝑔𝑔𝑒𝑒 𝑌𝑌
Ce qui donne en Prolog :
descendant(X,Z) :- parent(Z,X);
parent(Z,Y), descendant(X,Y).
ET (représenté par une virgule) et prioritaire sur le OU (représenté par un point virgule).
• Le moteur d'inférence de Prolog utilise le 'OU' entre les clauses d'un programme. En effet, un but (ou question) est réalisé s'il est unifiable avec l'une au moins des clauses du programme. D'autre part, la consultation des clauses se fait dans l'ordre de début du fichier programme jusqu'à la fin si nécessaire. Ceci, nous permet d'écrire la règle 'descendant' en 2 clauses comme suit :
descendant(X,Z) :- parent(Z,X). descendant(X,Z) :-
parent(Z,Y), descendant(X,Y).
Cette présentation est la plus couramment utilisée en Prolog. Elle rend le code beaucoup plus lisible.
4. Prédicats et clauses
• Les relations, les propriétés et les règles décrites en Prolog sont au fait des prédicats, puisque pour une liste d'arguments donnés, elles sont soient vraies, soient fausses.
• Dans certains manuels, on utilise parfois le mot 'procédure' pour désigner une règle.
• Un prédicat (ou procédure) est caractérisé par un identificateur dit foncteur et le nombre d'argument dit arité, et il est référencé par foncteur/arité (parent/2, feminin/1,…).
• Un prédicat est définit par l'ensemble des clauses dont l'en-tête est constitué du nom du prédicat suivi entre parenthèses d'un nombre d'arguments égale à l'arité du prédicat.
• Deux prédicats différents peuvent avoir le même nom, mais dans ce cas ils ne devront pas avoir la même arité.
• En Prolog, une clause est formée de 2 parties : l'en-tête (head) et le corps (body), sous la forme : en_tete :- corps.
où le corps est une suite de buts séparés par des virgules représentants la conjonction ET. − Les faits sont des clauses sans corps.
− Les questions sont des clauses sans en-tête.
− Les règles sont des clauses avec un en-tête et un corps non vide.
• Il n'est pas nécessaire de regrouper les clauses définissant un prédicat, mais il est préférable de le faire pour assurer la lisibilité du programme.
Par ailleurs, Dans un programme, l'ordre des clauses ne change pas le sens déclaratif du programme et il peut changer le sens procédural, autrement dit, la définition d'une relation ou d'une règle est donnée par le contenu des ses clauses indépendamment de leur ordre, mais l'utilisation de cette relation (ou de cette règle) par Prolog dépend de l'ordre des clauses dans le programme :
Par exemple, les deux formulations suivantes de 'descendant' :
descendant_1(X,Z) :- parent(Z,X). descendant_1(X,Z) :- parent(Z,Y), descendant_1(X,Y). et descendant_2(X,Z) :- descendant_2(X,Y), parent(Z,Y). descendant_2(X,Z) :- parent(Z,X).
ont le même sens logique, et définissent bien la relation 'descendant', mais le mécanisme de résolution du Prolog ne les traite pas de la même manière.
5. Mécanisme de résolution
• Une question est une suite de un ou plusieurs buts et répondre à une question revient à satisfaire ces buts.
• Satisfaire un but, c'est démontrer que ce but découle logiquement des faits et règles définis dans le programme.
• Pour satisfaire un but simple, Prolog cherche du haut vers le bas (dans l'ordre) dans le fichier programme une clause qui peut s'unifier avec le but, autrement dit :
− Il cherche une clause dont le foncteur est le même que celui du but.
− Puis il compare les arguments, en substituant éventuellement les variables par les objets pour lesquels le but pourrait être satisfait.
− Si le but est satisfait, alors sa réponse serait 'true' (En cas où la question comporte des variables, Prolog affiche les objets utilisés lors de la substitution pour satisfaire le but et attend l'ordre de continuer ou d'arrêter la recherche d'autres objets pouvant satisfaire le but).
− Si aucune clause ne permet de satisfaire le but, alors la véracité du but ne peut être démontrée et la réponse du Prolog serait 'false'.
• Si une question est composée par plusieurs buts avec la conjonction ET (représentée par une virgule), alors Prolog tente de satisfaire les buts un par un de gauche à droite.
− Si un but est satisfait, alors il est retiré de la liste après avoir remplacé dans les autres buts les variables par les objets correspondants qui permettent de satisfaire ce but.
− Si un but échoue, alors Prolog retourne en arrière en rétablissant les buts originaux et tente de trouver une autre alternative, jusqu'à ce que toutes les possibilités soient consultées. − Si Prolog ne peut démontrer la véracité des buts, alors sa réponse sera 'false'.
Prenons, par exemple le test de la règle 'descendant' définie dans (famille_3.pl)
/* fichier : famille_3.pl */ % parent(X,Y) : X est un parent de Y parent(paul,cloe). parent(paul,marc). parent(aude,marc). parent(marc,lisa). parent(marc,dana). parent(dana,abel). ...
% R5 : descendant(X,Z) : X est un descendant de Z % R5_a descendant(X,Z) :- parent(Z,X). % R5_b descendant(X,Z) :- parent(Z,Y), descendant(X,Y). Et posons la question : ?- descendant(dana,paul).
Le but principal à satisfaire est :
1. Prolog cherche la première clause correspondante au but (celle dont l'en-tête correspond au but). Il trouve la clause :
descendant(X,Z) :- parent(Z,X). (R5_a)
1.1. Il l'applique (R5_a) en substituant les variables X et Z par 'dana' et 'paul', le nouveau but devient :
parent(paul, dana) (B1)
1.2. Il cherche à satisfaire ce nouveau but, donc à chercher les clauses correspondantes. Puisqu'aucune clause ne s'unifie avec ce but, alors le but échoue.
Puisque le but échoue, Prolog revient au premier but (B0).
2. Prolog cherche alors une autre clause correspondante à (B0). Il trouve (R5_b).
descendant(X,Z) :- parent(Z,Y), descendant(X,Y). (R5_b)
Il applique la règle (R5_b) (de la même manière que dans l'étape 1.1), en substituant les variables. Ce qui donne un nouveau but :
parent(paul, Y), descendant(dana,Y) (B2)
Ce dernier but étant composé de 2 buts, Prolog tente alors de les satisfaire dans l'ordre :
parent(paul, Y) (B2_1)
descendant(dana,Y) (B2_2)
2.1. la première clause dans le fichier qui correspond à (B2_1) est :
parent(paul, cloe)
Pour satisfaire (B2_1), l'unification force l'instanciation de Y par 'cloe' dans (B2).
parent(paul, cloe), descendant(dana,cloe)
La première partie de ce but est satisfaite, donc le nouveau but de vient :
descendant(dana,cloe) (B3)
2.1.1. La première clause correspondante à (B3) est (R5_a), Prolog l'applique et le nouveau but devient :
parent(cloe,dana) (B3')
Or aucune clause ne correspond à ce but,
(B3') échoue, et Prolog revient en arrière et cherche une autre alternative pour satisfaire (B3). 2.1.2. La deuxième clause correspondante à (B3) est (R5_b), en l'appliquant on obtient le
nouveau but :
parent(cloe,Y), descendant(dana,Y) (B3")
Or la première partie de ce but échoue, du fait qu'aucune clause d'en-tête 'parent' ne correspond à ce but.
Donc (B3") échoue, et par suite (B3) échoue.
Par suite, Prolog revient à (B2) et cherche une autre alternative pour satisfaire (B2_1). 2.2. La deuxième clause correspondante à (B2_1) est :
parent(paul, marc)
Ce qui donne après substitution des variables comme dans 2.1, un nouveau but :
descendant(dana,marc) (B4)
La règle (R5_a) est applicable, puisqu'elle correspond au but, ce qui donne un nouveau but :
Ce dernier but étant satisfait, puisqu'il correspond à une clause du programme.
Le but (B4') est donc atteint, il s'ensuit alors que (B4) est aussi atteint, de même pour (B2) et (B0). Puisque nous avons :
(B4') ⇒ (B4) ⇒ (B2) ⇒ (B0)
• Ce mécanisme de résolution est représenté par un arbre dit arbre de résolution, où les nœuds sont les buts à satisfaire et les arcs correspondent à l'application des différents clauses qui transforme un but vers un autre.
• Le but du nœud racine est satisfait si au moins un nœud est libellé par 'Yes'.
• Durant la recherche, Prolog entre dans toutes le branches et si une branche échoue, Prolog retourne en arrière : on dit que Prolog effectue un 'backtrack'.
Figure I.2 : Mécanisme de résolution descendant(dana,paul) parent(paul,dana) No parent(paul,Y) descendant(dana,Y) descendant(dana,cloe) descendant(dana,marc) parent(cloe,Y) descendant(Y,dana) No parent(cloe,dana) No Yes parent(marc,dana) parent(paul,cloe)
Y = cloe parent(paul,marc) Y = marc
R5_b
R5_a
X = dana
Z = paul X = dana Z = paul
R5_b
R5_a R5_a
X = dana
Données en Prolog
• La programmation en Prolog suit le principe de la programmation déclarative. Par ailleurs, il n'effectue aucune différence entre les données du programme et le programme lui-même.
• La syntaxe du Prolog est relativement simple, il ne se base que sur la notion de 'terme'.
Ainsi, les clauses d'un programme qui représentent un fait, une règle, une question (ou contenant des données) sont constituées de termes.
• Un terme est soit un terme simple ou un terme composé :
− Un terme simple : qui est une constante ou une variable.
− Un terme composé ou structure : formé par un foncteur et des arguments qui sont aussi des termes
1. Constantes
• Une constante est un atome ou un nombre.
1.1. Nombres
• Un nombre est un entier ou un réel :
25, -110, 9.1, 0.1e+03, …
1.2. Atome
• On appelle atome l'une des données suivantes :
− Une chaine de caractères contenant des caractères alphanumériques et le trait de soulignement '_' et commençant par une lettre minuscule :
parent, grand_parent, henri4, …
− Une chaine formée par des caractères spéciaux :
+, >, =, :-, …
− Une chaine de caractères entre apostrophes :
'Grand parent', 'Henri IV', …
2. Variables
• L'identificateur d'une variable est une chaine de caractères formée par des alphanumériques et le tiret de soulignement :
X, Qui, U_01, _, _Var, _var, __
On appelle variable isolée (ou 'singleton variable'), toute variable qui apparait une seule fois dans une clause. Une telle variable peut être remplacée par un tiret de soulignement '_', dit variable anonyme.
Prenons par exemple, le prédicat 'a_un_enfant', défini par :
𝑋𝑋 𝑔𝑔 𝑢𝑢𝑢𝑢 𝑒𝑒𝑢𝑢𝑒𝑒𝑔𝑔𝑢𝑢𝑒𝑒 SI ∃ 𝑌𝑌 ∶ 𝑋𝑋 𝑒𝑒𝑒𝑒𝑒𝑒 𝑢𝑢𝑢𝑢 𝑝𝑝𝑔𝑔𝑔𝑔𝑒𝑒𝑢𝑢𝑒𝑒 𝑔𝑔𝑒𝑒 𝑌𝑌 ce qui donne en Prolog :
a_un_enfant(X) :- parent(X,Y).
Dans cette clause, la valeur de Y n'a aucune importance, il est par suite inutile de la nommée. En Prolog on remplace de telle variable par la variable anonyme '_', ce qui donne :
a_un_enfant(X) :- parent(X,_).
qq_a_un_enfant :- parent(X,Y).
les deux variables sont isolées, on peut l'écrire alors comme :
qq_a_un_enfant :- parent(_,_).
Notez que cette relation est différente de :
qq_a_un_enfant :- parent(X,X).
• Dans SWI-Prolog, une erreur est signalée si une variable isolée n'est pas marquée. Pour marquer une variable isolée, on utilise à sa place la variable anonyme, ou on lui donne un nom qui commence par 2 tirets de soulignement '__' ou un tiret suivi d'une lettre majuscule, par exemple :
__var ou _Var
• L'utilisation de la variable anonyme dans une question, évite de faire apparaitre les valeurs correspondantes dans la réponse du Prolog :
?- parent(X,_).
affichera les X qui sont parents sans afficher leurs enfants.
• Notons que la portée d'une variable est une clause et que celle d'un atome est tout le programme.
3. Structures
• Une structure ou terme composé est constituée par :
− un atome dit aussi foncteur, qui permet d'identifier la structure − liste ordonnée de termes qui sont les arguments.
sous la forme :
nom_foncteur(arg1, arg2, …) • Le nombre d'arguments est dit l'arité de la structure.
• Les structures définissent au fait une relation entre les arguments dont le nom est le foncteur. Exemple
• Une structure est généralement représentée par un arbre, dont la racine est le foncteur et les branches sont les arguments.
: date(1,1,2015). point(a1,a2).
segement(point(1,2),point(1,3)). etudiant(nom,prenom,date(j,m,a),cne).
• Rappelons enfin que toute clause en Prolog est formée de termes : Comme déjà cité, toute clause est de la forme :
Figure I.3 : Arbre d'une structure etudiant
prenom
nom date cne
en-tete :- corps − L'en-tête est un terme
− ':-' est un atome
− Le corps est une suite de termes séparés par des virgules.
Opérateurs
• En Prolog, un opérateur est un atome, et une opération est un prédicat dont le foncteur est l'opérateur :
% a+b est équivalent à +(a,b) ?- X = +(2,3).
X = 2+3.
• Par suite, toute expression est un terme qui est évalué suivant : − L'ordre de priorité des opérateurs ou précédence des opérateurs. − Le type des opérateurs : binaire, unaire préfixé ou unaire postfixé. − L'associativité des opérateurs : gauche, droite ou aucune.
Par exemple, en SWI-Prolog :
+ est un opérateur binaire associatif à gauche :
2+3+5 ⟺ +(2+3, 5) ⟺ +(+(2,3), 5)
* est prioritaire sur + :
2*a+b*c ⟺ +(2*a, b*c) ⟺ +(*(2,a), *(b,c))
• En Prolog, on peut définir de nouveaux opérateurs ou redéfinir les opérateurs prédéfinis. Pour ce on utilise la directive op/3 :
:- op(Précédence, Type, Nom) − Nom : est un atome représentant le nom de l'opérateur.
− Précédence : est un entier, compris entre 1 et 1200, qui détermine l'ordre de priorité d'un opérateur. La précédence la plus petite donne la priorité la plus élevée. Ainsi, la précédence 1 donne la plus haute priorité et la précédence 1200 donne la plus basse priorité.
− Type : détermine si un opérateur est infixé, préfixé ou suffixé ainsi que l'associativité de l'opérateur.
Le tableau suivant énumère les valeurs que peut prendre l'argument Type :
Type Spécification
fx Préfixé, non associatif
xf Postfixé, non associatif fy Préfixé, associatif yf Postfixé, associatif yfx Infixé, associatif à gauche
xfy Infixé, associatif à droite
xfx Infixé, non associatif
Autrement dit, le type de l'opérateur est donné par trois caractères 'f', 'x' et 'y', avec : − Le caractère 'f' détermine la position de l'opérateur.
− 'x' représente un argument dont la précédence est strictement inférieure à celle de l'opérateur.
− 'y' représente un argument dont la précédence est inférieure ou égale à celle de l'opérateur. Sachant que :
− Si un argument est un objet simple ou entre parenthèse alors sa précédence est 0. − Si un argument est une structure alors sa précédence est celle du foncteur principal. Exemple de quelques opérateurs prédéfinis en SWI-Prolog.
1200 xfx :- 1100 xfy ; | 1000 xfy ,
200 fy + - \
Exemple
− 'aime' (verbe) : qui relie deux objets, le premier est un objet simple (nom) et le deuxième est un objet composé (contenant 'et', des articles et des noms).
:
Définir les opérateurs nécessaires pour pouvoir écrire les clauses suivantes : salim aime les voyages et la lecture.
samir aime le chocolat et les gateaux. fahd aime la lecture et le cinema.
Ces clauses ont la même forme, ils contiennent les atomes suivants :
− la conjonction 'et' : qui relie deux objets contenant des articles et des noms. − les articles (le, la, les) : applicables à un seul objet.
− des noms (salim, voyages, …).
On en déduit que les relations définies dans ces clauses sont
aime/2, et/2, le/1, la/1, les/1
et que les articles sont prioritaires sur la conjonction 'et', et que cette dernière est prioritaire sur la relation 'aime'.
Ainsi on peut écrire ces clauses comme suit : aime(salim, et( les(voyages), la(lecture) )). aime(samir, et( le(chocolat), les(gateaux))). aime(fahd, et( la(lecture) , le(cinema) )).
Les opérateurs à définir sont donc : aime, et, le, la, les.
− l'opérateur 'aime' est un opérateur binaire non associatif, puisqu'on ne peut pas écrire :
X aime A aime B
donc son type est xfx, et en lui donnant par exemple la précédence 500, sa définition sera : :- op(500, xfx, aime).
− l'opérateur 'et' est binaire associatif. on lui donnera le type xfy et la précédence 400, puisqu'il est prioritaire sur l'opérateur 'aime'.
:- op(400, xfy, et).
− Les opérateurs 'le', 'la' et 'les' sont des opérateurs unaires préfixés non associatifs (le le A : n'a aucun sens), ils sont donc de type fx, on leur donne la précédence 300, puisqu'ils sont prioritaires sur l'opérateur 'et'.
:- op(300, fx, la). :- op(300, fx, le). :- op(300, fx, les).
Le programme complet est : (operateur.pl)
:- op(500, xfx, aime). :- op(400, xfy, et). :- op(300, fx, la). :- op(300, fx, le). :- op(300, fx, les).
samir aime le chocolat et les gateaux. fahd aime la lecture et le cinema.
En chargeant ce programme, on peut poser les questions suivantes : ?- salim aime Quoi.
Quoi = les voyages et la lecture. ?- Qui aime Quoi.
Qui = salim,
Quoi = les voyages et la lecture ; Qui = samir,
Quoi = le chocolat et les gateaux ; Qui = fahd,
Quoi = la lecture et le cinema. ?- Qui aime le chocolat.
false.
Unification
• Dans son mécanisme de résolution Prolog utilise le principe d'unification : Unifier deux termes consiste à les rendre égaux.
• L'unification de deux termes ne peut se faire que s'il y a une correspondance entre ces termes (matching). Il faut donc que :
− Les deux termes soient identiques. ou
− Les variables dans les deux termes peuvent être substituées par des objets de telle sorte que les deux termes deviennent identiques.
• Prolog utilise l'opérateur '=' pour l'unification. Ainsi, si S et T sont deux termes :
S'il y a correspondance entre S et T, alors S = T est satisfait et unifie S et T. Sinon S = T échoue.
Exemple
• Plus précisément, si S et T sont deux termes, alors :
% exemple d'unification qui réussit
?- date(Jour,10,An) = date(5, Mois, 2015). Jour = 5
An = 2015 Mois = 10
% exemple d'unification qui échoue. ?- date(X) = date(5, 10, 2015). False.
i. Si S et T sont des constantes, alors S=T réussit si et seulement si S et T sont identiques : ?- a = a.
true. ?- a = b. false.
ii. Si S est une variable libre (non instanciée) et T est autre qu'une variable libre, alors S=T réussit et S est substituée par T.
?- T = a, S = T. T = S, S = a.
?- date(J,10,2015) = S. S = date(J, 10, 2015).
iii. Si S et T sont tous les deux des variables libres, alors S=T réussit et S et T feront référence au même objet dans la suite.
?- X = Y, X = a. X = Y, Y = a.
iv. Si S et T sont des structures, alors S=T réussit si et seulement si :
a. S et T ont le même foncteur principal et le même nombre d'arguments.
b. Les arguments s'unifient l'un avec l'autre dans l'ordre (de gauche vers la droite). ?- date(An, Mois, Jour, Heure)= date(2015, 10, 5).
false.
?- date(An, Mois, Jour, Heure)= date(2015, 10, 5, heure(9,0,0)). An = 2015, Mois = 10, Jour = 5, Heure = heure(9, 0, 0). ?- date(1,2,2015)=date(X,X,2015). false. Exemple :
Quelle est la réponse du Prolog à la question suivante : ?- f(g(X,A,h(X,b)),Z) = f(g(A,b,Z),Y).
Les deux termes ont le même foncteur principal : f/2.
L'unification sera satisfaite si et seulement si les 2 unifications suivantes sont satisfaites dans l'ordre :
g(X,A,h(X,b)) = g(A,b,Z) Z = Y
Les termes de la première unification ont le même foncteur g/3, alors elle est équivalente à :
X = A A = b, h(X,b) = Z
Dans X = A, les deux termes sont des variables libres, l'unification réussit et X et A feront référence au même objet, dans la suite.
Dans A = b, la variable A sera substituée par b, et donc X sera aussi substituée par b.
Dans h(X,b) = Z, X sera premièrement remplacée par b, ce qui donne h(b,b) = Z. Z est une variable libre donc elle sera substituée par h(b,b).
Pour la dernière unification Z = Y, Z sera remplacée par h(b,b) et par suite Y qui est une variable libre sera substituée par h(b,b).
En conclusion, l'unification des deux termes réussit et réalise les substitutions suivantes:
A ← b, X ← b, Z ← h(b,b) et Y ← h(b,b)
Sous l'interpréteur du Prolog, on obtient : ?- f(g(X,A,h(X,b)),Z) = f(g(A,b,Z),Y). X = A, A = b,
Arithmétique
• Les expressions arithmétiques en Prolog sont construites à partir de nombres, de variables et d'opérateurs arithmétiques et y sont considérées comme des structures.
• Les opérateurs de calcul prédéfinis en Prolog sont :
500 yfx + addition
500 yfx - soustraction
400 yfx * multiplication
400 yfx / division
400 yfx // division entire
400 yfx mod modulo
200 xfy ^ puissance
• L'unification en Prolog ne prend pas en charge l'évaluation des expressions, ainsi : ?- 2 + 5 = 7.
false.
Ici, les deux termes ne peuvent s'unifier, puisque le premier est une structure et le deuxième est une constante.
• Pour forcer Prolog à calculer une expression, il faut utiliser le prédicat is/2 : ?- X is 2+5. X = 7. ?- X = 3, Y is X ^ X. X = 3, Y = 27. Exemple
− Si N = 0 alors M = 1 donc : fact(0,1)
: Calcul du factoriel Pour définir la relation :
fact(N,M)
où M est le factoriel de N et N est un entier positif. On a :
− Si N > 0, alors M est N *M1 où M1 est le factoriel de N1 et N1 est N-1. donc : N1 is N-1, fact(N1,M1), M is N*M1 ce qui donne : fact(0,1). fact(N,M) :- N > 0, N1 is N-1, fact(N1,M1), M is N*M1.
• Prolog définit aussi des opérateurs de comparaisons pour pouvoir comparer les valeurs des expressions arithmétiques. Les opérateurs de comparaisons prédéfinis en Prolog sont tous de type
xfx et de précédence 700 :
X =:= Y Vrai si X et Y ont la même valeur
X =/= Y Vrai si X et Y sont différents
X < Y Vrai si X est inférieur strictement à Y
X =< Y Vrai si X est inférieur ou égal à Y
X > Y Vrai si X est supérieur strictement à Y
• Les opérateurs de comparaison forcent l'évaluation des expressions. ?- 2+5 =:= 7. true. Exemple − Si X >= Y alors Max = X. : (extremum_1.pl) Pour définir la relation
max(X, Y, Max)
où Max est le maximum de X et Y. Nous avons : − Si X < Y alors Max = Y. d'où : max(X, Y, X):- X >= Y. max(X, Y, Y):- X < Y. ?- max(25,10,M). M = 25 .
Listes
1. Définition
• Une liste en Prolog est une suite ordonnée de données entre crochets et séparées par des virgules. Ces données peuvent être des constantes (atomes ou nombres) ou des termes composés, par exemple :
[a,b,c,X,1,parent(f,g)]
est une liste qui contient des constantes, une variable et un terme composé. • Comme toute autre donnée en Prolog, une liste est aussi un terme, qui est :
− soit la liste vide qui est représentée par [].
− soit une structure composée, dont le foncteur principale est '.' (le point), avec deux arguments :
le premier argument est le premier élément de la liste dit tête (head) le deuxième argument est la liste formée par le reste dit queue (tail). • Ainsi, toute liste non vide est de la forme :
.(T,Q)
où T est une donnée et Q est une liste.
• En Prolog on peut utiliser : Exemple ?- L =.(a,.(b,.(c,[]))). L = [a,b,c]. [T|Q] au lieu de .(T,Q) Ainsi : ?- L = [a|[b,c]). L = [a,b,c]. % ou
?- L = [a,b|[c]]. L = [a, b, c]. % ou ?- L = [a,b,c|[]]. L = [a, b, c]. Remarque
2. Opérations sur les listes
:Le constructeur de listes [|] est le plus utilisé. Dans certaines implémentations du Prolog (comme SWI-Prolog) l'opérateur '.' (point) n'est plus utilisé comme constructeur de listes, son utilisation est réservé pour d'autres fins, surtout pour qualifier les champs d'une structure.
• Les implémentations du Prolog offrent plusieurs prédicats sur les listes, notamment l'appartenance, la concaténation, le tri,… On trouve ceux qui sont prédéfinis et chargés au début et ceux qui sont définis dans des modules à part (comme le module lists en SWI-Prolog).
• D'autre part, le fait que les listes sont des structures permet de définir aisément des prédicats de manipulations des listes.
2.1. L'unification des listes
Elle suit la même règle générale de l'unification en Prolog. ?- [A,2,C] = [1,B,3]. A = 1, C = 3, B = 2. ?- [a,b,c] = [T1,T2|R]. T1 = a, T2 = b, R = [c]. ?- [X]=[1,2]. false.
2.2. Constructeur d'une liste
cons(X,R,[X|R]). ?- cons(a,[b,c],L). L = [a, b, c].
2.3. Extraction du premier et du reste d'une liste
% Extraction du premier élément de la liste premier([Premier|_],Premier).
% Extraction du reste de la liste reste([_|Reste], Reste).
?- premier([a,b,c],X). X = a.
?- reste([a,b,c], R). R = [b, c].
• Le prédicat cons/3 peut être utilisé pour extraire le premier ou le reste de la liste : ?- cons(X, _, [a,b,c]).
X = a.
R = [b, c].
2.4. Longueur d'une liste
Pour définir le prédicat :
longueur(L,N)
qui permet de trouver le nombre d'éléments N de la liste L, il suffit de remarquer que : − Si L = [] alors N = 0.
− Si L = [T|R] alors N est 1 + Nr où Nr est la longueur de la liste R. Ce qui donne : longueur([],0). longueur([_|R], N) :- longueur(R,Nr), N is Nr + 1. ?- longueur([a,b,c|[d]], N). N = 4.
• Le prédicat correspondant prédéfini est length/2.
2.5. Appartenance
Pour que X soit un membre de la liste L, il suffit que l'une des conditions suivantes soit satisfaite : − X est le premier de la liste L.
− X est un membre du reste de la liste. Autrement dit :
L = [X|_] ou (L=[_|Reste] et X est un membre de Reste) Si nous appelons ce prédicat 'membre', sa définition serait :
membre(X,[X|_]). membre(X,[_|Reste]) :- membre(X,Reste). ?- membre(b,[a,b,c]). true . ?- membre(1,[a,b,c]). false. ?- membre(X,[a,b,c]). X = a ; X = b ; X = c ; false.
• En SWI-Prolog, ce prédicat est prédéfini avec memberchk/2.
2.6. Concaténation
Considérons la relation :
conc(L1, L2, L)
qui est vraie si L est composée par les éléments de L1 suivis par ceux de L2. Pour définir cette relation, nous considérons les cas de L1 :
− Si L1 est vide alors L est égal à L2
− Si L1=[X|R1] alors L=[X|R] où R est la concaténation de R1 et L2. ce qui donne :
conc([], L, L).
conc(R1,L2,R). ?- conc([a,b,c],[1,2,3],L). L = [a, b, c, 1, 2, 3].
• Cette relation peut réaliser plus que la concaténation de deux listes, par exemple : i. Décomposition d'une liste :
?- conc(L1,L2,[a,b,c]). L1 = [], L2 = [a, b, c] ; L1 = [a], L2 = [b, c] ; L1 = [a, b], L2 = [c] ; L1 = [a, b, c], L2 = [] ; false.
On peut, ainsi définir un prédicat qui permet de connaitre si S est une sous liste de L :
sous_liste(S,L) :- conc(L1, L3, L), conc(S, L2, L3).
En effet S est une sous liste de L si L peut être décomposée en trois listes L1, S et L2 (notez qu'il s'agit d'une sous-liste et non d'un sous-ensemble, autrement dit l'ordre des éléments est pris en compte).
ii. Chercher un motif dans la liste : % chercher les mois avant et après mai
?- Mois = [jan,fev,mars,avr,mai,juin,jul,ao,sep,oct,nov,dec], | conc(Avant,[mai|Apres],Mois).
Mois = [jan, fev, mars, avr, mai, juin, jul, ao, sep|...], Avant = [jan, fev, mars, avr],
Apres = [juin, jul, ao, sep, oct, nov, dec] ; false.
iii. Chercher le prédécesseur (ou le successeur) immédiat d'un élément : ?- Mois = [jan,fev,mars,avr,mai,juin,jul,ao,sep,oct,nov,dec],
| conc(_,[Avant,mai,Apres|_],Mois).
Mois = [jan, fev, mars, avr, mai, juin, jul, ao, sep|...], Avant = avr,
Apres = juin ; false.
iv. Chercher un élément de la liste.
Du fait que, X est un élément de la liste L si et seulement si L est la concaténation d'une liste L1 et d'une liste L2 dont la tête est X, on peut définir la relation membre/2 en utilisant conc/3 :
membre1(X,L) :-
conc(_, [X|_], L). ?- membre1(b,[a,b,c]). true .
2.7. Ajout et suppression d'un élément de la liste
• La relation qui permet d'ajouter un élément au début de la liste est évidente :
ajout(X,L, [X|L]). ?- ajout(a,[b,c],L).
L = [a, b, c].
• Pour supprimer un élément X d'une liste L, on considère les cas suivants : − Si L = [X|R] alors le résultat de la suppression est R.
− Si L = [Y|R], avec Y = X , alors le résultat de la suppression est [Y|R1] où R1 est R privé de
X. Ce qui donne : suppr(X,[X|R],R). suppr(X,[Y|R],[Y|R1]):- suppr(X,R,R1). ?- suppr(b, [a,b,c], L). L = [a, c] .
suppr/3 peut être utilisée dans le sens inverse pour ajouter un élément. ?- suppr(a, L, [1,2,3]). L = [a, 1, 2, 3] ; L = [1, a, 2, 3] ; L = [1, 2, a, 3] ; L = [1, 2, 3, a] ; false.
Nous remarquons, que Prolog nous donne toutes les possibilités d'insertion.
On peut, ainsi, définir le prédicat insert/3, qui permet d'insérer un élément n'importe où dans une liste.
% insert(X, L, L1) : insert X dans L pour obtenir L1 insert(X, L, L1) :- suppr(X, L1, L).
Du fait que suppr(X, L, L1) échoue si X n'est pas un élément de L, on peut utiliser cette relation pour définir une autre version de du prédicat membre/3.
membre2(X, L) :- suppr(X, L, _).
2.8. Les chaines de caractères
• Les chaines de caractères sont traitées en Prolog comme des listes d'entiers contenant les codes ASCII des caractères.
?- T="abc". T = [97, 98, 99]. Remarque :
En SWI-Prolog 7.2.0, les chaines de caractères forment un type à part nommé string, et ne sont pas considérées comme des listes. Cependant, on peut revenir à la configuration traditionnelle en exécutant le but suivant :
La coupure (cut)
1. Principe
• Prolog effectue un retour en arrière (backtracking) si nécessaire pour satisfaire un but. Pour éviter le backtracking, qui dans certain cas n'est pas nécessaire, on utilise le cut (la coupure).
Exemple :
Considérons la relation f(X,Y) définie par les trois règles suivantes : R1 : Si X < 3 alors Y = 0.
R2 : Si 3 =< X et X < 6 alors Y = 2. R3 : Si 6 =< X alors Y =4.
Ce qui donne en Prolog :
/* fichier : cut_1.pl */ % relation f(X,Y)
f(X,0) :- X < 3. % R1
f(X,2) :- 3 =< X, X < 6. % R2
f(X,4) :- 6 =< X. % R3
Et considérons le but suivant : ?- f(1,Y), Y > 2.
false.
Evidemment ce but échoue, puisque la seule valeur possible pour Y pour satisfaire f(1,Y) est 0 qui n'est pas supérieur à 2. Mais, en Prolog si une règle échoue alors il cherche les autres possibilités, qui sont dans notre cas inutiles.
L'arbre de résolution dans ce cas est donnée par :
La trace de l'exécution de ce but en Prolog donne : [trace] ?- f(1,Y), Y > 2.
Call: (8) f(1, _G1556) ? creep % applique R1 Call: (9) 1<3 ? creep
Exit: (9) 1<3 ? creep
Exit: (8) f(1, 0) ? creep % instancie Y par 0 Call: (8) 0>2 ? creep % test du 2ème but
Fail: (8) 0>2 ? creep % echec
Redo: (8) f(1, _G1556) ? creep % applique R2 Call: (9) 3=<1 ? creep
Fail: (9) 3=<1 ? creep
Redo: (8) f(1, _G1556) ? creep % applique R3 Call: (9) 6=<1 ? creep
Figure I.4 : Procédé de la coupure
f(1,Y), Y > 2 1 < 3, 0 > 2 No 3 =< 1, 1 < 6, 2 > 2 No 6 =< 1, 4 > 2 No X ← 1 Y ← 0 R1 R2 R3 X ← 1 Y ← 0 X ← 1 Y ← 0 0 > 2
Fail: (9) 6=<1 ? creep
Fail: (8) f(1, _G1556) ? creep false.
Ici, Prolog applique les règles R2 et R3, qui sont inutiles.
Pour éviter que Prolog teste les autres règles applicables, on utilise un pseudo but représenté par un point d'exclamation '!', qui l'informe qu'il doit arrêter la recherche des autres alternatives même si l'un des sous buts suivants échoue.
Notre programme devient :
/* fichier : cut_2.pl */
f(X,0) :- X < 3, !. % R1
f(X,2) :- 3 =< X, X < 6. % R2
f(X,4) :- 6 =< X. % R3
En chargeant ce programme, la trace de la réponse du Prolog au même but donne : [trace] ?- f(1,Y), Y > 2. Call: (8) f(1, _G1556) ? creep Call: (9) 1<3 ? creep Exit: (9) 1<3 ? creep Exit: (8) f(1, 0) ? creep Call: (8) 0>2 ? creep Fail: (8) 0>2 ? creep false.
Ici, Prolog n'applique pas les autres règles R1 et R2, qui sont unifiables avec le but f(1,Y).
De même, on remarque que si la règle R2 échoue alors il est inutile d'appliquer la règle R3. On introduit donc un 'cut' au niveau de la règle R2, ce qui donne :
/* fichier : cut_3.pl */ % relation f(X,Y)
f(X,0) :- X < 3, !. % R1
f(X,2) :- 3 =< X, X < 6, !. % R2
f(X,4) :- 6 =< X. % R3
En fin, remarquons que certains tests dans notre programme sont inutiles. En effet, pour certaines valeurs de X, le programme teste si X < 3 puis teste si 3 =< X, par exemple :
[trace] ?- f(7,Y).
Call: (7) f(7, _G2574) ? creep Call: (8) 7<3 ? creep
Fail: (8) 7<3 ? creep
Redo: (7) f(7, _G2574) ? creep
Call: (8) 3=<7 ? creep % test inutile Exit: (8) 3=<7 ? creep
Call: (8) 7<6 ? creep Fail: (8) 7<6 ? creep
Redo: (7) f(7, _G2574) ? creep
Call: (8) 6=<7 ? creep % test inutile Exit: (8) 6=<7 ? creep
Exit: (7) f(7, 4) ? creep Y = 4.
Ici, le but '7<3' échoue, alors le but '3=<7' réussi et donc il est inutile de le tester. De même, le but '7<6' échoue, ce qui le test '6=<7' inutile.
L'algorithme de la relation f est au fait donné par : Si (X < 3) Alors Y = 0 Sinon Si (X < 6) Alors Y = 2 Sinon Y = 4 FinSi FinSi
Ce qui permet d'écrire une version modifié du programme :
/* fichier : cut_4.pl */ f(X,0) :- X < 3, !. % R1 f(X,2) :- X < 6, !. % R2 f(_,4). % R3 [trace] ?- f(7,Y). Call: (7) f(7, _G3634) ? creep Call: (8) 7<3 ? creep Fail: (8) 7<3 ? creep Redo: (7) f(7, _G3634) ? creep Call: (8) 7<6 ? creep Fail: (8) 7<6 ? creep Redo: (7) f(7, _G3634) ? creep Exit: (7) f(7, 4) ? creep Y = 4.
• D'une manière générale, le fonctionnement du 'cut' est le suivant : Etant donné la régle :
H:- B1, B2, ...,Bn, !, C1,...,C Prolog essayera de satisfaire le but 'B
m Si cette règle est invoquée par un but G (qui correspond à H), alors :
1, B2, ..., Bn', en utilisant le
backtracking entre les Bk
Si le but 'B1, B2, ..., B. n
Si le but B
' échoue, Prolog cherchera une autre clause qui correspond à G.
1, B2, ..., Bn réussi, Prolog rencontre un cut (qu'il considère
satisfait), à partir de ce moment, Prolog essayera de satisfaire le but 'C1,
C2, ..., Cm', en utilisant le backtracking entre les Ck. Mais, ne cherchera
pas de trouver une autre alternative pour satisfaire G même si le but 'C1,
C2, ..., Cm
Lorsque Prolog rencontre une coupure, il oublie tous les sous buts qui sont à gauche (c'est-à-dire les B
' échoue. k
• D'autre part, le cut n'affecte que la règle où il est présent. Par exemple, si A, B, C,... sont des termes tels que :
dans notre exemple).
C :- P, Q, R, !, S, T, U. ...
A :- B, C, D. Alors :
− Le cut affecte l'exécution de C : le backtracking est possible pour P, Q, R, il est aussi possible pour S, T, U, mais n'est pas possible entre S et R.
− Le cut présent dans C n'affecte pas l'exécution de A : le backtracking est possible entre B, C et
Exemple : calcul des extremums
Dans extremum_1.pl (voir Arithmétique), les relations max1 et mini1 sont définies par :
% max1(X,Y,Max) : Max est le maximum de X et Y max1(X, Y, X):- X >= Y.
max1(X, Y, Y):- X < Y.
% min1(X,Y,Min) : Min est le minimum de X et Y min1(X, Y, X):- X =< Y.
min1(X, Y, Y):- X > Y.
Pour trouver le maximum par exemple de 3 et 5, Prolog effectuera des tests inutiles : [trace] ?- max(3,5,M).
Call: (7) max(3, 5, _G2755) ? creep Call: (8) 3>=5 ? creep
Fail: (8) 3>=5 ? creep
Redo: (7) max(3, 5, _G2755) ? creep
Call: (8) 3<5 ? creep % test inutile Exit: (8) 3<5 ? creep
Exit: (7) max(3, 5, 5) ? creep M = 5.
Et si pour éviter ce test inutile, on l'élimine, on obtient :
/* fichier : extremum_2.pl */ max2(X, Y, X):- X >= Y. max2(X, Y, Y).
min2(X, Y, X):- X =< Y. min2(X, Y, Y).
En testant ce programme avec max2(3,2), on trouve deux solutions : [trace] ?- max2(3,2,M).
Call: (7) max2(3, 2, _G3324) ? creep Call: (8) 3>=2 ? creep
Exit: (8) 3>=2 ? creep
Exit: (7) max2(3, 2, 3) ? creep M = 3 ;
Redo: (7) max2(3, 2, _G3324) ? creep % Prolog continue la recherche Exit: (7) max2(3, 2, 2) ? creep
M = 2.
Après avoir trouvé la première solution, Prolog tente de trouver d'autres alternatives pour satisfaire le but. Il applique donc la deuxième règle de max2 (puisqu'elle correspond au but) et trouve une autre solution.
Pour éviter ceci, on introduit une coupure au niveau de la règle 1 :
/* fichier : extremum_3.pl */ max2(X, Y, X):- X >= Y, !. max2(X, Y, Y). min2(X, Y, X):- X =< Y, !. min2(X, Y, Y). Ce qui donne : [trace] ?- max3(3,2,M).
Call: (7) max3(3, 2, _G3324) ? creep Call: (8) 3>=2 ? creep
Exit: (8) 3>=2 ? creep
Exit: (7) max3(3, 2, 3) ? creep M = 3.
Exemple
2. La négation comme échec
: membre d'une liste.La relation membre décrite dans la partie 'Opération sur les listes', qui teste l'appartenance d'un élément à une liste, ne s'arrête pas même s'il trouve l'élément cherché.
% membre(X,L) est vrai si X est membre de la liste L membre(X,[X|_]).
membre(X,[_|Reste]) :- membre(X,Reste).
En effet :
[trace] 9 ?- membre(2, [2,3,4,2,1]).
Call: (7) membre(2, [2, 3, 4, 2, 1]) ? creep Exit: (7) membre(2, [2, 3, 4, 2, 1]) ? creep
true ; % Devrait s'arrêter ici
Redo: (7) membre(2, [2, 3, 4, 2, 1]) ? creep Call: (8) membre(2, [3, 4, 2, 1]) ? creep Call: (9) membre(2, [4, 2, 1]) ? creep Call: (10) membre(2, [2, 1]) ? creep Exit: (10) membre(2, [2, 1]) ? creep Exit: (9) membre(2, [4, 2, 1]) ? creep Exit: (8) membre(2, [3, 4, 2, 1]) ? creep Exit: (7) membre(2, [2, 3, 4, 2, 1]) ? creep true ;
Redo: (10) membre(2, [2, 1]) ? creep Call: (11) membre(2, [1]) ? creep Call: (12) membre(2, []) ? creep Fail: (12) membre(2, []) ? creep Fail: (11) membre(2, [1]) ? creep Fail: (10) membre(2, [2, 1]) ? creep Fail: (9) membre(2, [4, 2, 1]) ? creep Fail: (8) membre(2, [3, 4, 2, 1]) ? creep Fail: (7) membre(2, [2, 3, 4, 2, 1]) ? creep false.
Nous devrons donc introduire une coupure au niveau de la première règle :
/* fichier : liste_2.pl */ membre3(X,[X|_]) :- !. membre(X,[_|Reste]) :- membre(X,Reste). Ce qui donne : [trace] ?- membre3(2, [2,3,4,2,1]).
Call: (7) membre3(2, [2, 3, 4, 2, 1]) ? creep Exit: (7) membre3(2, [2, 3, 4, 2, 1]) ? creep true.
• Pour formuler le fait suivant :
Sara aime tous les animaux sauf les serpents.
Si on écrit en Prolog :
aime(sara, X) :- animal(X).
la solution serait fausse, puisqu'il faut exclure les serpents.
Une des solutions, consiste à utiliser le but prédéfini 'fail', qui échoue toujours, de la manière suivante :
aime(sara, X) :- animal(X).
La première règle veut dire que :
Si le but serpent(X) réussi Alors
aime(sara, X) échoue (puisque fail échoue).
Ne chercher plus à satisfaire aime(sara, X) (puisqu'il y a une coupure). • Cette méthode, nous permet de définir la relation :
different(X,Y)
qui est satisfaite si X est différent de Y. En effet :
X est différent de Y si X = Y échoue. ce qui donne :
different(X,Y) :- X=Y, !, fail. different(X,Y).
qu'on peut écrire de la manière suivante :
different(X,Y) :- X=Y, !, fail ;
true.
où true est un terme prédéfini qui est toujours satisfait.
• La combinaison de cut et fail, permet aussi de formuler le prédicat not :
% not(P) est satisfait si P échoue not(P) :-
P, !, fail ;
true.
Ce prédicat est prédéfini, et il est aussi défini avec l'opérateur unaire \+ : not(P) et \+P sont équivalents.
• Le prédicat not peut être utilisé comme alternative dans les relations aime et different :
aime(sara,X) :- animal(X), not (serpent(X)).
different(X,Y) :- not (X = Y).
• En résumé, le cut nous permet de programmer des règles mutuellement exclusives :
Si (Condition) Alors P Sinon Q
et il permet aussi d'imposer à Prolog de ne pas chercher d'alternatives pour satisfaire un but. Cependant, avec le cut l'ordre des clauses est primordial :
Par exemple : p:- a, b. p:- c. ⇔ (a ET b) OU c ⇒ p En insérant le cut : p:- a, !, b. p:- c. ⇔ (a ET b) OU (NON(a) ET c) ⇒ p Et si on change l'ordre : p:- c. p:- a, !, b. ⇔ c OU (a ET b) ⇒ p
Prédicats prédéfinis
• Quelques prédicats sont prédéfinis dans le langage et permettent aux programmeurs d'utiliser des fonctionnalités standards, comme de l'évaluation numérique, les entrée/sortie, les fonctionnalités de l'interface graphique ou la communication avec le système d'exploitation.
Parmi ces prédicats prédéfinis, on trouve :
1. Chargement, débogage et compilation des programmes
• Pour charger un programme dans l'interpréteur du Prolog, on utilise le prédicat :consult(nom_programme).
Ce prédicat permet de charger tous les clauses du programme source passé en argument. Un deuxième appel à 'consult' permet de charger le deuxième programme et les clauses de ce dernier s'ajouteront aux premiers.
On peut charger plusieurs programmes à la fois
consult(prog1, prog2, …)
Une alternative à consult est l'utilisation d'une liste [...] :
[nom_programme]. % charge un programme [prog1, prog2, prog3]. % charge les 3 programmes
• Pour charger un module ou une librairie, on utilise use_module :
use_module(library(lists)). % charge le module lists
Ce prédicat peut être aussi remplacé par […].
[library(lists)] % charge le module lists
• La procédure include/1 permet d'inclure un fichier source dans un autre. • La procédure compile/1 permet de compiler un programme.
• Parmi les prédicats de contrôle de l'exécution on trouve :
trace notrace debugging nodebug spy nospy
2. Les prédicats d'entrée/sortie
• Pour les entrées/sorties, un programme en Prolog communique avec des flux (stream). Les flux d'entrée/sortie en Prolog sont des fichiers.
• Prolog utilise le mot clé user pour designer l'entrée et la sortie standards qui correspondent au clavier/écran (Dans certaines implémentation du Prolog on utilise les mots user_input et user_output).
• Durant l'exécution d'un thread seulement deux flux sont actifs : current_input et current_output. Au début ils correspondent à user. Pour modifier le flux courant on utilise les prédicats prédéfinis see et tell.
see(Fichier) Change le flux d'entrée vers Fichier
see(user) Change le flux d'entrée vers l'entrée standard tell(Fichier) Change le flux de sortie vers Fichier
tell(user) Change le flux de sortie vers la sortie standard
• Les prédicats :
seen et told
ferment respectivement le flux d'entrée et de sortie pour revenir aux flux standard user. • Les prédicats standards de lecture et d'écriture sont read/1 et write/1.
Exemple
• Prolog offre aussi d'autres prédicats d'entrée/sortie tels les prédicats de lecture/écriture de caractère ou de formatage, on trouve par exemple :
:
Exemple de saisie d'une valeur au clavier.
/*
Fichier : cube.pl
lit une valeur suivi d'un point et affiche son cube Pour arrêter le programme entrez : stop.
*/ cube :-
read(X), % lit une valeur
process(X). % exécute une procédure avec X process(stop) :- !. % stop pour arrêter le programme process(N) :-
C is N*N*N, % calcul le cube write(C), % affiche le résultat cube. % attend une autre entrée
put(C) Affiche le caractère dont le code ASCII est C
get0(C) Lit un caractère et instancie C par le code ASCII de ce caractère get(C) Lit un caractère imprimable (blanc non compris)
nl Retour à la ligne
tab(N) N espaces
3. Contrôle de la base de connaissance
• Un programme Prolog est au fait une base de connaissance, on peut par ailleurs, lui ajouter dynamiquement des clauses représentant des faits ou des règles :
asserta(Term)
Ajoute la clause représentée par le terme Term à la base de connaissance.
Term est inséré comme première règle ou premier fait du prédicat correspondant.
assert(Term) Equivalent à assertz. Prédicat obsolète. retract(Term) Supprime la clause Term.
• Dans certaines implémentations du Prolog, pour pouvoir ajouter ou supprimer une clause, il faut déclarer le prédicat correspondant comme dynamique par la directive :
:- dynamic pred1/arité1, pred2/arité2,….
Exemple
• Pour ajouter une règle, on doit la passer à assert comme un seul argument. Pour ce, si la règle contient il faut la mettre entre parenthèses.
:
Considérons le programme suivant :
/* fichier : meteo.pl */ % déclaration des prédicats dynamiques :- dynamic
soleil, pluie, brouillard. % Définition de certaines règles beau :- soleil, \+ pluie. bizzard :- soleil, pluie. mauvais :- pluie, brouillard. % temps actuel pluie. brouillard.
Pour ce programme, on peut changer les données du temps actuel, en ajoutant ou en retranchant dynamiquement l'un des prédicats soleil, pluie et brouillard.
?- beau. false. ?- mauvais. true. ?- retract(brouillard). true. ?- mauvais. false. ?- assert(soleil). true. ?- bizzard. true. Exemple :
Considérons le programme suivant :
/* fichier : plusrapide.pl */ % déclaration des prédicats dynamiques :- dynamic
rapide(lapin). lent(tortue). lent(escargot).
L'exécution du but suivant :
?- assertz((plusrapide(X,Y) :- rapide(X), lent(Y))). true.
permet d'ajouter la règle plusrapide/2 au programme. Remarquez que la règle est écrite entre parenthèses pour qu'elle soit considérée comme un seul argument.
On peut alors poser la question suivante : ?- plusrapide(A,B).
A = lapin, B = tortue ; A = lapin, B = escargot.
• retract est non-déterministe, une seule clause avec rectract peut effacer plusieurs clauses, par le procédé du backtracking.
Exemple
• Une application usuelle et efficace du prédicat assert est la sauvegarde des résultats intermédiaires en vue d'une utilisation ultérieure.
:
Avec l'exemple précédent : ?- retract(lent(X)).
X = tortue ; X = escargot.
supprime toutes les clauses correspondantes au prédicat 'lent'. En effet : ?- plusrapide(X,_).
false.
Exemple :
/* fichier : table_multi.pl */
% Sauvegarde de la table de multiplication maketable :- L = [0,1,2,3,4,5,6,7,8,9], member(X,L), member(Y,L), Z is X*Y, assertz(produit(X,Y,Z)), fail.
La procédure maketable permet de définir le prédicat produit comme un ensemble de faits. En effet, le prédicat fail, à la fin de la procédure assure avec le backtracking de parcourir toute la liste [0,1,2,3,4,5,6,7,8,9] pour X et pour Y et assertz ajoute à la base de connaissance le fait :
produit(X,Y,Z) où Z est le produit de X et Y. ?- maketable. false. ?- produit(X,Y,15). X = 3, Y = 5 ; X = 5, Y = 3.
4. Tests sur le type d'un terme
• Les termes sont de différents types : variable, constante, nombre, entier, … Les prédicats prédéfinis suivant permettent de tester le type d'un terme :
var/1 teste si l'argument est une variable non instanciée novar/1 teste si l'argument n'est pas une variable non instanciée atomic/1 teste si l'argument est une constante
atom/1 teste si l'argument est un atome number/1 teste si l'argument est un nombre integer/1 teste si l'argument est un entier float/1 teste si l'argument est un réel
compound/1 teste si l'argument est un terme composé ground/1 teste si l'argument est un terme sans variables
Exemple : ?- var(X). true. ?- X=5, var(X). false. Exemple
− Si L = [], alors N=0 pour tout A. :
On se propose de calculer le nombre d'un atome dans une liste. Pour ce, on définit le prédicat :
count(A,L,N)
qui est vrai si N est le nombre d'occurrences de l'atome A dans la liste L. L'algorithme de ce prédicat est donné par :
− Si L = [A|R] alors N=Nr+1 où Nr est le nombre d'occurrences de A dans R. − Si L = [X|R] avec X=A, alors N est le nombre d'occurrences de A dans R. Ce qui donne en Prolog :
/* fichier : count.pl */ count(_, [], 0). count(A, [A|R], N) :- !, count(A, R, Nr), N is Nr + 1. count(A, [_|R], N) :- count(A, R, N).
Des exemples de son application : 13 ?- count(a, [a,b,a,a], N). N = 3 ; false. 14 ?- count(a, [a,b,X,Y], N). X = Y, Y = a, N = 3 .
Dans la deuxième application de count, le résultat est erroné (on devrait avoir N=1). Ceci vient du fait que Prolog ait instancié X et Y par a puisqu'elles sont des variables libres.
Nous devrons donc nous assurer que pour comptabiliser un élément, il faut bien qu'il soit un atome égal à l'atome cherché. Soit :
/* fichier : count.pl -suite -*/ count1(_, [], 0). count1(A, [B|R], N) :- atom(B), A = B, !, count1(A, R, Nr), N is Nr + 1. count1(A, [_|R], N) :- count1(A, R, N). ?- count1(a, [a,b,X,Y], N). N = 1 .
5. Unification et comparaison des termes
• L'unification entre deux termes est réalisée soit implicitement par Prolog ou explicitement avec l'opérateur binaire =. L'opérateur \= est la négation de l'opérateur d'unification. Ainsi :
T1 = T2 Réussi si T1 et T2 sont unifiable
T1 \= T2 Réussi si T1 et T2 ne peuvent être unifiés équivalent à \+(T1=T2). 12 ?- f(a,b) = f(a,X).
X = b.
13 ?- f(a,b) \= f(a,X). false.
• Pour la comparaison de deux termes, on dispose en Prolog des opérateurs suivants : =:=
=\= comparaison des valeurs == \== comparaison littérale ?- 5 =\= 3. true. ?- f(a,b) == f(a,b). true. ?- f(a,b) == f(a,X). false.
• Prolog établi un ordre entre les différents types de termes de la manière suivante : Entre les termes de types différents l'ordre est :
Variables < Nombres < Atomes < Termes composés Les variables sont triées par adresse.
Les nombres entiers ou réels sont comparés par valeurs Les atomes sont comparés avec l'ordre alphabétique.
Pour les termes composés, on commence par comparer les arités, puis les foncteurs principaux par ordre alphabétique enfin on compare les arguments un par un en commençant par le plus à gauche.
• Pour tester cet ordre on utilise les opérateurs suivants : @< @=< @> @>=
?- f(a,h(b),d) @< f(c, h(b), a). true.
6. Construction et décomposition des termes
Parmi les prédicats prédéfinis qui permettent la décomposition et la construction des termes, on trouve :
functor/3 :
functor(T, F, A) Vrai si F est le foncteur principal du terme T d'arité A. ?- functor(t(f(X), X, 1), F, A). F = t, A = 3. ?- functor(T, f, 2). T = f(_G1460, _G1461). arg/3 :
arg(N, T, X) T est un terme, N est un entier entre 1 et l'arité du terme T. ce prédicat unifie X avec le Nième argument de T. ?- arg(2, f(X, t(a), t(b)), Y).
Y = t(a). ?- functor(D, date, 3), | arg(1, D, 29), | arg(2, D, june), | arg(3, D, 1982). D = date(29, june, 1982). =../3 :
T =.. L =.. est un opérateur nommé 'univ'. Vrai si L est la liste formée par le foncteur principal de T suivi de ses arguments ?- f(a,b,2) =.. L. L = [f, a, b, 2]. ?- a+b*c =.. L. L = [+, a, b*c]. ?- T =.. [f,a,b]. T = f(a, b). name/2 :
name(A, L) L est la liste des codes ASCII des caractères formant l'atome A. ?- name(rectangle,L).