Sur quelques inégalités intégrales et leurs applications

ةرازو

ميلعتلا

يلاعلا

ثحبلاو

يملعلا

BADJI MOKHTAR-ANNABA

UNIVERSITY

UNIVERSITE BADJI

MOKHTAR-ANNABA

ةعماج

يجاب

راتخم

-ةبانع

–

Année : 2018

Faculté des Sciences

Département de Mathématiques



THÈSE

Présentée en vue de l’obtention du diplôme de

Doctorat

Sur quelques inégalités intégrales et leurs applications

Option

:

Modélisation Mathématique, contrôle

optimal déterministe et stochastique

Par

Meziri Imen

DIRECTEUR DE THÈSE: Boukerrioua Khaled M.C.A U.B.M. ANNABA

CO-DIRECTEUR DE THÈSE: Laouar Abdelhamid

Prof. U.B.M. ANNABA

Devant le jury

PRESIDENT :

Guezane- Lakoud Assia

Prof.

U.B.M. ANNABA

EXAMINATEUR :

Frioui Assia

M.C.A

Univ. GUELMA

Remerciements

T

out d’abord, je tiens à remercier Dieu qui m’a donné force, et courage afin

d’élaborer ce mémoire.

J

’adresse mes vifs remerciements à mon directeur de thèse, Boukerrioua Khaled, Maître de conférences à l’université d’Annaba pour la confiance qu’il m’a accordé, son suivi attentif, ses conseils avisés et surtout sa disponibilité. Je lui suis reconnaissante de m’avoir fait bénéficier tout au long de ce travail de sa grande compétence, de sa rigueur intellectuelle, et de son efficacité certaine que je n’oublierai jamais.

J

e remercie aussi le co-directeur de thèse Monsieur Laouar Abdelhamid, Professeur à l’université d’Annaba pour son aide et son soutien.

M

es remerciements les plus chaleureux à Madame Guezane-Lakoud Assia, Professeur à l’université d’Annaba qui a accepté de présider le jury de cette thèse.

J

e remercie également, Madame frioui Assia, Maître de conférences à l’université de Guelma, Monsieur Khaldi Rabah, Professeur à l’université d’Annaba qui ont bien voulu accepter de faire partie du jury.

J

e ne saurais trouver les mots nécessaires pour exprimer ma profonde gratitude envers mes oncles Mahmoud, Mohamed, et Rabah pour leur réconfort moral et affectif prodigué sans relâche.

p

our tous mes ami(e)s qui m’ont toujours soutenue durant ces années d’études, je les en remercie sincèrement.

V

oici venir les derniers remerciements de ce mémoire et non pas des moindres, ils sont bien évidement adressés à mes très chers parents Akila et Salah qui font preuve d’un soutien inconditionnel, et à mes sœurs Ryma, Mouna, et Bouchra. Merci du fond du cœur d’avoir été et d’être toujours là pour moi.

Introduction 1

1 Preliminaires 3

1.1 Notions de base sur les echelles de temps . . . 3

1.1.1 Terminologie . . . 4

1.1.2 Operateurs de saut et classi cation des points . . . 4

1.1.3 Les sous-ensembles derives d'une echelle de temps . . . 6

1.1.4 Derivation sur les echelles de temps . . . 7

1.1.5 Integration sur les echelles de temps . . . 10

1.1.6 Fonction exponentielle . . . 12

1.2 Notions fondamentales de stabilite . . . 14

1.3 C0 semi-groupes et leurs generateurs . . . 16

1.4 Quelques inegalites importantes . . . 17

1.5 Equation di erentielle a retard . . . 18

2 Inegalites integrales de type Gronwall-Bellman-Bihari a retard 20 2.1 Quelques celebres inegalites integrales unidimensionnelles . . . 21

2.2 Quelques Generalisations des inegalites de type Gronwall-Bellman . . . 25

2.3 Nouvelles generalisations . . . 30

2.3.1 Inegalites a retard de type Gronwall-Bellman-Bihari . . . 30

3 Ra nements de quelques inegalites integrales de type Gamidov 48

3.1 Quelques celebres inegalites de type Gamidov . . . 49

3.2 Quelques generalisations . . . 51

3.3 Nouvelles extensions et generalisations . . . 54

3.3.1 Inegalites integrales de type Gronwall-Bellman-Gamidov . . . 54

3.3.2 Inegalites integrales de type Gronwall-Bellman-Bihari-Gamidov . . 63

3.3.3 Applications . . . 74

4 Stabilite de quelques systemes perturbes sur les echelles de temps par l'approche des inegalites integrales 77 4.1 Existence et unicite de la solution du probleme a valeur initiale perturbe . 79 4.2 Stabilite des solutions du probleme a valeur initiale perturbe . . . 83

4.2.1 Inegalites Integrales de Gronwall sur les echelles de temps . . . 83

4.2.2 Caracterisation de la h-stabilite via les inegalites integrales . . . 85

4.2.3 Applications . . . 90

Conclusion 93

Il est bien connu que la theorie des inegalites integrales joue un r^ole essentiel dans l'etude de l'analyse qualitative et quantitative du comportement des solutions d'equations di erentielles.

L'objectif de cette these est d'etablir, en premier lieu, de nouvelles inegalites a retard non lineaires de type Gronwall-Bellman-Bihari qui sont des extensions des resultats de [2].

En deuxieme lieu, nous avons etabli de nouvelles inegalites de type Gamidov aux echelles de temps.

En n, nous avons etudie la h-stabilite de certains systemes dynamiques non lineaires perturbes en utilisant quelques inegalites integrales aux echelles de temps.

Mots-cles: Echelles de temps; Inegalite de Gronwall; Inegalite de Bihari; Inegalite

Abstract

It is well known that the theory of integral inequalities plays a key role in the study of qualitative and quantitative analysis behaviour of the solutions of di erential equations.

The objective of this thesis is to establish, initially, new delay non-linear Gronwall-Bellman-Bihari type inequalities, which represent some extensions of the works from [2]. Next, we have established new generalizations of Gamidov type inequalities on time scales.

We conclude this thesis by studying the h-stability of some perturbed nonlinear dy-namical systems by using some integral inequalities on time scales.

Keywords: Time scales; Gronwall's inequality; Bihari's inequality; Gronwall-Bellman's

صـــــــخـــلم

نم

فورعملا

نأ

ةٌرظن

تانٌابتملا

ةٌلماكتلا

بعلت

ارود

اٌسٌئر

ًف

ةسارد

لٌلحتلا

ًعونلا

ًمكلاو

كولسل

لولح

ا

تلاداعمل

ةٌلضافتلا

.

ثٌح

أ

ن

فدهلا

نم

هذه

ةحورطلأا

ًف

ةٌادبلا

وه

ءاشنإ

تانٌابتم

ةدٌدج

رٌغ

ةٌطخ

عم

لا

رٌخأت

عونل

لاونرج"

-ناملاب

-يراهٌب

"

،

لاو

ت

ً

ت

لثم

ضعب

تادٌدمتلا

ل

لمعل

[

2

]

.

.

ةٌنمزلا

لسلاس

لا

ىلع

"فودماج"

عون نم تانٌابتمل

ةدٌدج

تامٌمعت

انئشنأ

،

اه

دعب

و

ًف

ةٌاهنلا

،

انمدختسا

ضعب

ةٌلماكتلا تانٌابتملا

ىلع

لا

لسلاس

ةٌنمزلا

ةساردل

رارقتسا

ضعب

ةمظنلأا

ةٌكٌمانٌدلا

رٌغ

ةٌطخلا

ةلاح ًف

دوجو

.بارطضا

:ةيحاتفملا تاملكلا

لا

لسلاس

ةٌنمزلا

،

تانٌابتم

لاونرج

تانٌابتم ،

يراهٌب

تانٌابتم ،

لاونرج

-ناملاب

،

تانٌابتم

فودماج

،

فصن

ةرمز

،

رارقتسلاا

.

Introduction

Les inegalites sont au coeur de l'analyse mathematique depuis des siecles et possedent

un r^ole eminent dans le developpement de toutes les branches des mathematiques

mod-ernes telles que la theorie des espaces de Hilbert, l'analyse numerique, l'analyse complexe, les probabilites et les statistiques.

En e et, cette importance semble avoir considerablement pris de l'ampleur pendant

le siecle dernier et la theorie des inegalites peut ^etre consideree comme une branche a

part et entiere des mathematiques modernes. En particulier, les inegalites integrales de divers types ont ete largement etudiees dans la plupart des sujets impliquant l'analyse mathematique. Au cours des dernieres annees, divers chercheurs ont obtenu des nom-breuses inegalites integrales utiles dans les diverses types des equations di erentielles et integrales, ou elles sont souvent la base des lemmes importants pour prouver des theoremes ou pour rapprocher les di erentes fonctions; citons en particulier, les inegalites de Pach-patte [55], Tricomi [65], Bainov et Simenov [7] et Dragomir [31].

Par ailleurs, la theorie des inegalites integrales a emerge comme sujet interessant et fasci-nant d'analyse avec un large eventail d'applications non seulement dans les mathematiques, mais egalement dans les domaines de la physique, de la technologie et des sciences bi-ologiques; la plus connue parmi ces inegalites est sans doute, celle de Gronwall [39].

L'objectif de cette these est d'etablir, dans un premier temps, de nouvelles generalisations des inegalites integrales de type Gronwall-Bellman a retard et celles de Gamidov-Bihari aux echelles de temps ainsi que leurs applications.

Dans un second temps, nous montrons l'utilite de quelques inegalites integrales aux echelles de temps pour l'etude de la h-stabilite de certains systemes perturbes.

Le premier chapitre, qui est plut^ot un glossaire, regroupe quelques notions de base introductives et necessaires a la comprehension de l'ensemble de cette these.

Le deuxieme chapitre concerne les inegalites de type Granwall-Bellman-Bihari, dans lequel nous presentons tout d'abord quelques resultats classiques, puis nous citerons quelques generalisations apparues ces dernieres annees. En n, nous presentons de nou-velles generalisations qui sont illustrees par quelques applications.

Les resultats obtenus sont soumis pour une eventuelle publication dans une revue inter-nationale.

Le troisieme chapitre est consacre a l'etude des inegalites integrales de type Gamidov. Nous allons citer brievement les resultats classiques obtenus de ce type d'inegalites ainsi que quelques generalisations obtenues par Pachpatte [59] et Kendre & Latpate [47], puis nous allons etablir des variantes des extensions et des ra nements des resultats obtenus par [47; 59], sur des echelles de temps quelconques. D'autres nouvelles inegalites de type Gamidov-Bihari sont demontrees.

Ces nouvelles inegalites ont contribue a l'etude d'une nouvelle classe d'equations integrales et di erentielles, et ont fait l'objet de la publication :

K. Boukerrioua, I. Meziri et T. Chiheb, Some re nements of certain Gamidov integral inequalties on time scales and applications. Kragujevac Journal of Mathematics.Vol 42, No. 1 (2018) , 131{152.

Le dernier chapitre est consacre a la caracterisation de la h-stabilite de quelques systemes perturbes, en montrant l'utilite de quelques inegalites integrales sur les echelles de temps. Nous allons alors montrer l'existence et l'unicite de la solution de certains systemes perturbes, ensuite nous donnons l'etude de la h-stabilite en utilisant les inegalites integrales. Ces nouveaux resultats ont ete soumis pour une eventuelle publication dans une revue internationale.

CHAPITRE

1

Preliminaires

Dans ce chapitre, nous allons aborder quelques notions de base necessaires pour introduire la theorie des echelles de temps. Aussi, nous rappelerons brievement quelques notions fondamentales et des de nitions relatives a la stabilite, les equations di erentielles a retard et aux semi-groupes. Nous citerons egalement quelques inegalites importantes qui seront utiles tout au long de ce travail. Pour plus de details, le lecteur pourra consulter [5; 15; 45].

1.1

Notions de base sur les echelles de temps

Le calcul des echelles de temps a ete initie par Stefane Hilger [44] dans sa these de doctorat en 1988 a n de mettre au point une nouvelle theorie qui peut uni er l'analyse discrete

et continue, ou il a de ni la notion de la -derivee. C'est a partir de cette de nition

qu'ont ete introduites les equations aux echelles de temps qui ont la m^eme forme qu'une

equation di erentielle ou presque, a titre d'exemple: une equation du premier ordre dont

la derivee (u0_{) est remplacee par la -derivee u .}

Nous verrons plus loin que si T = R, la -derivee equivaut a la derivee au sens classique et les equations aux echelles de temps deviennent des equations di erentielles. Si T = Z, les equations aux echelles de temps deviennent des equations aux di erences nies; d'ailleurs,

l'inter^et pour ce dernier type d'equations a connu un essor considerable au cours des

dernieres annees pour expliquer plusieurs phenomenes discrets notamment en economie, en psychologie, en genie et en informatique. Ainsi, la theorie des equations aux echelles de

temps vient, dans un premier temps, pour uni er les resultats realises dans le domaine des equations di erentielles et des equations aux di erences nies. Dans un deuxieme temps, elle permet l'etude des phenomenes se modelisant d'une facon qui fait appel simultanement au discret et au continu.

1.1.1

Terminologie

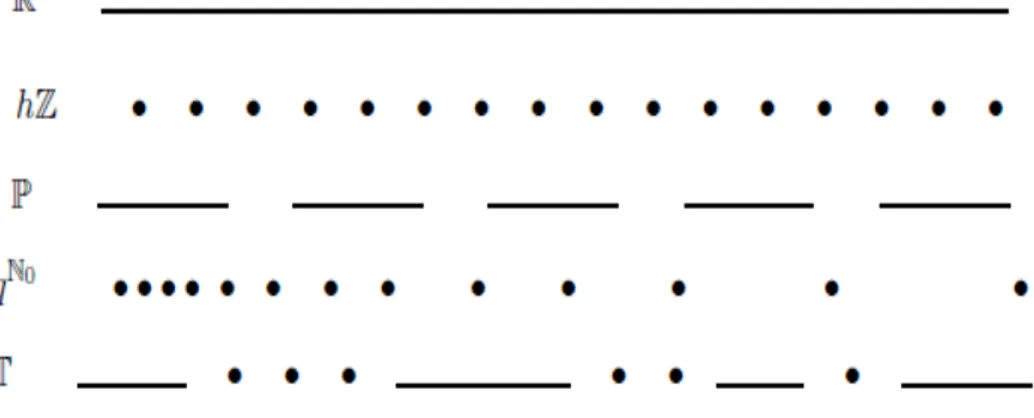
De nition 1.1.1 _{Une echelle de temps T est un sous ensemble ferme non vide de R.}

Exemple 1.1.1 _{Les ensembles R, Z}+, [ 1; 0]_{[ [1; 2], q}z _{= q}k _{: k}

2 Z; q > 1 [ f0g,

[0; 1]_{[ N et les ensembles de Cantor sont des echelles de temps.}

Exemple 1.1.2 _{Les ensembles Q, RnQ, C, (0; 1) ne sont pas des echelles de temps.}

Remarque 1.1.1 _{La topologie de T est induite par celle de R.}

Figure 1.1.1 : Quelques echelles de temps

1.1.2

Operateurs de saut et classi cation des points

De nition 1.1.2 _{Soit T une echelle de temps, pour t 2 T, l'operateur de saut avant}

: T ! T, est de ni comme suit :

1.1. Notions de base sur les echelles de temps

De nition 1.1.3 _{Soit T une echelle de temps, pour t 2 T, l'operateur de saut arriere}

: T ! T, est de ni comme suit :

(t) = sup_{fs 2 T : s < tg :} (1.2)

En utilisant les operateurs _{: T ! T et : T ! T, les points t dans une echelle de}

temps arbitraire T sont classes comme suit :

De nition 1.1.4 _{On dit que t est un point dense a droite de T (resp. un point dense a}

gauche de T), si (t) = t (resp. (t) = t).

De nition 1.1.5 On dit que t est un point dense s'il est simultanement dense a droite

et a gauche.

De nition 1.1.6 _{On dit que t est un point disperse a droite de T (resp. un point disperse}

a gauche de T), si (t) > t (resp. (t) < t).

De nition 1.1.7 t est dit point isole s'il est simultanement disperse a droite et a gauche.

Figure 1.1.2 : Classi cation des points

De nition 1.1.8 On appelle fonction de granulation la fonction de nie par

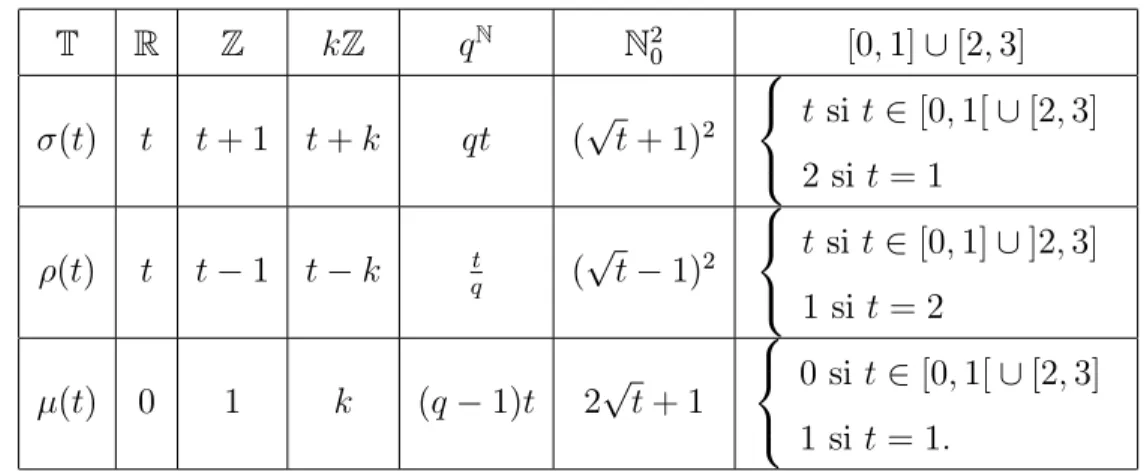
Nous illustrons les de nitions precedentes par quelques ensembles des echelles de temps ainsi que leurs carateristiques (operateurs de saut, fonction de granulation) indiquees dans le tableau ci-dessous

[Tab.1.1.1] Quelques echelles de temps et leurs carateristiques

T R Z kZ qN _N2 0 [0; 1][ [2; 3] (t) t t + 1 t + k qt (pt + 1)2 8 < : t si t_{2 [0; 1[ [ [2; 3]} 2 si t = 1 (t) t t 1 t k _qt (pt 1)2 8 < : t si t_{2 [0; 1] [ ]2; 3]} 1 si t = 2 (t) 0 1 k (q 1)t 2pt + 1 8 < : 0 si t_{2 [0; 1[ [ [2; 3]} 1 si t = 1:

1.1.3

Les sous-ensembles derives d'une echelle de temps

Soit m l'element maximum dans une echelle de temps T.

L'ensemble Tk represente dans la gure 1.1.3 est de ni comme suit : si le point m est

disperse a gauche alors, Tk

= T fmg, sinon Tk = T. Alternativement, Tk = 8 < :

T ] (sup T) ; sup T] si sup T < 1;

T si sup T = 1:

Figure 1.1.3 : Illustration de l'ensemble Tk

Notons que de chaque echelle de temps, nous pouvons extraire le sous ensemble suivant :

De nition 1.1.9 Pour deux points a; b_{2 T, l'intervalle d'echelle de temps est de ni par :}

1.1. Notions de base sur les echelles de temps

Remarque 1.1.2 Nous notons par [a; b]k= [a; b) = [a; (b)] dans le cas ou b est un point

disperse a gauche, sinon [a; b]k = [a; b].

Les resultats presentes dans les sous-sections suivantes sont tires des deux livres [15; 16].

1.1.4

Derivation sur les echelles de temps

Nous rappelons en premier temps, la de nition de la -derivee dite aussi la derivee au

sens de Hilger.

De nition 1.1.10 _{Soit la fonction f : T ! R, f est dite} -di erentiable en t_{2 T}k _s'il

existe un nombre f (t) tel que pour tout " > 0, il existe un voisinage U de t satisfaisant

[f ( (t)) f (s)] f (t) [ (t) s] "_{j (t)} s_{j ;}

pour tout s _{2 U. Si f est} -di erentiable en tout point t _{2 T}k_{, alors la fonction f :}

Tk

! R est dite la -derivee de f sur Tk_.

Le theoreme suivant donne plusieurs observations importantes sur la -derivee.

Theoreme 1.1.1 _{Soit f : T ! R une fonction et t 2 T}k_.

(i) Si f est -di erentiable en t, alors f est continue en t.

(ii) Si f est continue en t et si t est disperse a droite, alors f est -di erentiable en

t, de plus nous avons

f (t) = f ( (t)) f (t)

(t) : (1.4)

(iii) Si t est dense a droite, alors f est -di erentiable en t si et seulement si

lim s!t

f (t) f (s)

t s

existe et est nie. Dans ce cas nous avons f (t) = lim

s!t

f (t) f (s)

t s :

(i ) Si f est di erentiable en t, alors

Exemple 1.1.3 _{Considerons l'ensemble T =} p4

2n + 1; n_{2 N}0 avec N0 est l'ensemble

des entiers non negatifs, f (t) = t4_{, t}

2 T. Pour tout t; s_{2 T, t =}p4 2n + 1, s = p4 2l + 1, n = t4 1 2 , n; l 2 N0, nous avons (t) = infnp42l + 1 : p4 2l + 1 >p4 2n + 1o=p4 2n + 3 = p4t4_{+ 2:}

Par consequent, chaque point de T est disperse a droite. Nous notons que la fonction f(t) est continue sur T. Ainsi,

f (t) = f ( (t)) f (t) (t) t = 4_{(t) t}4 (t) t = 3(t) + t 2(t) + t2 (t) + t3 = p4 (t4 _{+ 2)}3_{+ t}2p4 t4_{+ 2 + t}p_t4_{+ 2 + t}3_{; t 2 T}k_: Remarque 1.1.3

Si T = R, alors d'apres (iii) du theoreme precedent la fonction f : R ! R est

-di erentiable en t_{2 R, si et seulement si} f (t) = lim t!s f (t) f (s) t s existe et de plus, f (t) = f0_(t).

Si T = Z, d'apres (ii) la fonction f : Z ! R est -di erentiable en t _{2 Z et nous}

aurons

f (t) = f ( (t)) f (t)

(t) t =

f (t + 1) f (t)

1 = f (t + 1) f (t) = f (t):

Le theoreme suivant etablit quelques identites de base pour calculer la -derivee.

Theoreme 1.1.2 _{Si f; g : T ! R sont} -di erentiables en t_{2 T}k_{, alors}

(i) f + g est -di erentiable en t, de plus

1.1. Notions de base sur les echelles de temps

(ii) ( f ) est -di erentiable en t pour tout _{2 R et nous avons}

( f ) (t) = f (t) :

(iii) f g est -di erentiables en t et nous avons

(f g) (t) = f (t) g (t) + f ( (t)) g (t) = f (t) g (t) + f (t) g ( (t)) :

(iv) Si f (t)f ( (t))_{6= 0, alors} 1

f est -di erentiable en t et nous avons

1

f (t) =

f (t) f (t)f ( (t)):

(v) Si g(t)g( (t))_{6= 0, alors} f

g est -di erentiable en t et nous avons

f

g (t) =

f (t) g (t) f (t) g (t)

g(t)g( (t)) :

Exemple 1.1.4 _{Soient f; g : T ! R deux fonctions de nies par f(t) = t}2_{; g(t) = t}3_et

soit la fonction h(t) = 1

t2, pour tout t2 T f0g. D'apres la regle de la di erentiation du

produit (voir (iii) du theoreme ci-dessus), nous obtenons

f (t) = tt + t (t) = t + (t) :

g (t) = t2t + (t2) (t) = t2+ t (t) + 2(t) ; pour tout t_{2 T}k:

En utilisant (iv) du theoreme ci-dessus, nous obtenons

h (t) = (t 2₎ (t (t))2 = t + (t) (t (t))2; t2 T k f0g :

Theoreme 1.1.3 _{Soit g : R ! R une fonction continue, g : T ! R est -di erentiable}

en Tk

et si f : R ! R est contin^ument di erentiable, alors il existe c 2 [t; (t)] satis-faisant

(f g) (t) = f0(g (c)) g (t) :

De nition 1.1.11 _{Une fonction f : T ! R est dite rd-continue si elle est continue en}

tout point dense a droite de T et si sa limite a gauche existe et est nie en tout point dense a gauche de T.

Remarque 1.1.4 L'ensemble de toutes les fonctions rd-continues est note par Crd ou

Crd(T).

Remarque 1.1.5 L'ensemble de toutes les fonctions -di erentiables et rd-continues est

note par C1

rdou Crd1 (T).

1.1.5

Integration sur les echelles de temps

De nition 1.1.12 _{La fonction F : T ! R, est dite primitive de f : T ! R, si elle}

veri e F (t) = f (t) pour tout t_{2 T}k_.

Exemple 1.1.5 _{Si T = N}2_{0et f : T ! R est une fonction de nie par f(t) = 1+2}1p

tlog

(pt+1)2

t ,

alors la fonction g(t) = log t est une primitive de f . En e et: (t) = pt + 1 2 et pour

tout t_{2 T}k_{, nous avons}

g (t) = log( (t)) log t (t) t = log ( p t + 1 2) log t p t + 1 2 t = 1 1 + 2ptlog p t + 1 2 t ! = f (t):

Theoreme 1.1.4 _{Toute fonction rd-continue f : T ! R, admet une primitive F :}

T ! R, et nous notons

Z r

s

f (t) t = F (r) F (s) pour tout r; s_{2 T.}

Theoreme 1.1.5 Si f _{2 C}rd(T) et t 2 Tk, nous avons :

Z (t)

t

1.1. Notions de base sur les echelles de temps

Theoreme 1.1.6 Soit a; b; c_{2 T; 2 R et f; g 2 C}rd(T) alors :

i) R_ab[f (t) + g (t)] t =R_abf (t) t +R_abg (t) t.

ii) R_ab( f (t)) t = R_abf (t) t.

iii) R_abf (t) t = R_baf (t) t.

iv) R_abf (t) t =R_acf (t) t +R_cbf (t) t.

v) R_aaf (t) t = 0.

vi) Si _{jf (t)j} g (t) sur [a; b]_T, alors R_abf (t) t R_abg (t) t.

Proposition 1.1.1

Pour T = R, nous avons :

Z b a f (t) t = Z b a f (t) dt: Pour T = Z, nous avons :

Z b a f (t) t = 8 > > > > > < > > > > > : b 1_P t=a f (t) si a < b 0 si a = b a 1_P t=b f (t) si a > b: Si [a; b] contient des points isoles alors :

Z b a f (t) t = 8 > > > > > < > > > > > : P t2[a;b[ (t) f (t) si a < b 0 si a = b P t2[b;a[ (t) f (t) si a > b:

Proposition 1.1.2 Les formules d'integration par partie sont :

Z b a f (t) g (t) t = [(f g) (t)]t=b_t=a Z b a f (t) g (t) t; Z b a f (t) g (t) t = [(f g) (t)]t=b_t=a Z b a f (t) g (t) t: Theoreme 1.1.7 Soit a _{2 T}k_{, b} 2 T et L : T Tk

! R, est continue en (t; t), pour

t _{2 T}k_{, t > a et L (t; :) est rd-continue sur [a; (t)], nous supposons que pour tout}

" > 0, _{9 U voisinage de t independant de 2 [a; (t)] tel que :}

ou f denote la derivee de f par rapport a la 1iere _{variable, alors nous avons :} g (t) = Z t a L (t; ) _{) g (t) =} Z t a L (t; ) + L ( (t) ; ) ; et h (t) = Z b t L (t; ) _{) h (t) =} Z b t L (t; ) L ( (t) ; ) :

1.1.6

Fonction exponentielle

De nition 1.1.13 Soit h > 0, l'ensemble des nombres complexes de Hilger est de ni

comme suit : Ch = z 2 C : z 6= _h1 .

De nition 1.1.14 _{Pour h > 0, on de nit l'ensemble Z}h = z 2 C : _h < Im(z) _h et

pour h = 0, on xe Z0 = C:

De nition 1.1.15 Pour h > 0, la transformation cylindrique _{h : C}h7 !Z h, est de nie

par :

h(z) =

1

hLog (1 + zh) ;

ou Log est le logarithme principal. Pour h = 0, nous aurons : ₀(z) = z pour tout z _{2 C.}

De nition 1.1.16 _{Soit p : T ! R, p est dite regressive si elle veri e}

1 + (t) p (t)_{6= 0; pour tout t 2 T}k:

Remarque 1.1.6 Pour tout t_{2 T}k_{, l'ensemble des fonctions regressives et rd-continues}

est note par _<:

De nition 1.1.17 L'ensemble de toutes les fonctions regressives positives est de ni par :

<+ = p_{2 < : 1 + (t) p (t) > 0, pour tout t 2 T}k : (1.6)

Theoreme 1.1.8 Nous supposons que p_{2 < et t}0 2 T un point xe, alors le probleme a

valeur initiale

y (t) = p (t) y (t) ; y (t0) = 1; (1.7)

1.1. Notions de base sur les echelles de temps

De nition 1.1.18 Soit p _{2 <, la fonction exponentielle est de nie comme solution du}

probleme (1:7) et nous avons y (t) = exp

Z t

t0

( )(p ( )) ; pour t; t0 2 T;

nous la notons souvent par ep(t; t0) = exp

Z t

t0

( )(p ( )) ; pour t; t0 2 T;

ou est la transformation cylindrique donnee par la de nition 1.1.15.

Proposition 1.1.3 Soit p; q_{2 < et t; t}0; s2 T, alors

e0(t; t0) 1 et ep(t; t) 1,

ep( (t) ; t0) = (1 + (t) p (t)) ep(t; t0), ep(t; t0) ep(t0; s) = ep(t; s),

ep(t; t0) = _ep(t01_;t),

ep(t; t0) eq(t; t0) = ep q(t; t0) ou (p q)(t) := p(t) + q(t) + (t) p (t) q(t), 8t 2 Tk.

Pour plus de details, le lecteur pourra consulter [15; 16].

Exemple 1.1.6 Soit p _{2 <, t; t}0 2 T et t > t0, si T = R, alors ep(t; t0) = exp Rt t0p ( ) d , si T = R et p(t) , alors ep(t; t0) = e (t t0), si T =Z, alors ep(t; t0) = =t 1_Q =t0 (1 + p ( )), si T =hZ, avec h > 0 et p(t) , alors ep(t; t0) = (1 + h) t _t0 h .

1.2

Notions fondamentales de stabilite

La stabilite est l'une des notions les plus utilisees pour etudier les comportements quali-tatifs des systemes di erentiels ainsi que les equations aux di erences.

La premiere etude de stabilite aux echelles de temps a ete realisee en 1892, par l'utilisation de la methode de Lyapunov.

Les de nitions de stabilite des systemes sur les echelles de temps sont obtenues avec une legere modi cation de leurs de nitions standard pour les equations di erentielles ordinaires. Hamza [42] et Dacunha [28] ont donne des caracterisations generalisees des di erents types de stabilite (stabilite uniforme, stabilite exponentielle, h-stabilite...) des solutions pour des systemes dynamiques aux echelles de temps.

Considerons l'equation dynamique de nie sur une echelle de temps T comme ci-dessous

x (t) = f (t; x) ; x (t0) = x0 2 X (1.9)

ou t; t0 2 T, x 2 X, f : T X ! X est rd-continue en t avec f(t; 0) = 0 et X est un

espace de Banach.

De nition 1.2.1 ([42]) L'equation (1:9) est dite exponentiellement stable s'il existe > 0

avec _{2 <}+ _{tel que pour tout t}

0 2 T, il existe = (t0) 1 tel que, toute solution

x (t) = x (t; t0; x0) de l'equation (1:9) satisfait kx (t) k kx0ke (t; t0), pour tout t t0,

t_{2 T.}

De nition 1.2.2 ([42]) L'equation (1:9) est dite uniformement exponentiellement stable

s'il existe > 0 avec _{2 <}+_{et il existe 1 independant de tout point initial t}

0 tel que,

toute solution x (t) = x (t; t0; x0) de l'equation (1:9) satisfait kx (t) k kx0ke (t; t0),

pour tout t t0, t2 T.

De nition 1.2.3 _{([42]) Soit h : T ! R une fonction positive et bornee. On dit que}

l'equation (1:9) est h-stable s'il existe une constante 1 telle que, toute solution

x (t) = x (t; t0; x0) de l'equation (1:9) satisfait

kx (t; t0; x0)k kx0kh (t) h (t0) 1

; t t0;

1.2. Notions fondamentales de stabilite

Remarque 1.2.1 Si nous prenons h(t) = e (t; 0) ou > 0 et _{2 <}+_{. La h-stabilite}

de l'equation (1:9) co•ncide avec la stabilite exponentielle uniforme.

Remarque 1.2.2 _{Si X = R}n

et f : T Rn

! Rn _{une fonction rd-continue en t ,}

localement Lipchitzienne en x, et regressive (i.e., la fonction id + (t)f (t; :) : Rn

! Rn

est inversible). Nous obtenons les implications suivantes :

h-stabilite =_{) stabilite exponentielle uniforme}

=_{) stabilite de Lipschitz uniforme}

=_{) stabilite uniforme.}

Pour plus de details sur les di erents types de stabilite, se referer a [25; 28; 42].

L'analyse de la stabilite des systemes lineaires non-autonomes peut ^etre completement

caracterisee en termes de la resolvante du systeme etudie. En e et, considerons le

probleme

x (t) = A(t)x(t); x(t0) = In; (1.10)

ou x_{2 R}n_{, t; t}

0 2 T et A : T7 !Rn n une matrice rd-continue, regressive, depend de t.

De nition 1.2.4 _{L'application A : T !M}n(R) est appelee regressive, si pour tout

t _{2 T la matrice carre I + (t)A de degre n} n est inversible, ou I est la matrice

identite.

La classe de toutes les fonctions regressives et rd-continues A de T vers Mn(R) est notee

par Crd<(T; Mn(R)).

De nition 1.2.5 Pour t0 2 T, la solution du probleme (1:10) s' appelle exponentielle de

la fonction matricielle, notee par _A(t; t0), ou A2 Crd<(T; Mn(R)).

En consequence, la fonction _A(t; t0) possede les deux proprietes suivantes :

A(t; t0) = A(t) A(t; t0); (1.11)

Cette fonction matricielle est appelee matrice de transition et notre hypothese sur A(t) montre que la matrice de transition existe et elle est unique.

Theoreme 1.2.1 Supposons r; s; t _{2 T et A; B 2 C}rd<(T; Mn(R)), alors la matrice de

transition possede les proprietes suivantes :

(i) _A(t; r) _A(r; s) = _A(t; s).

(ii) _A( (t); s) = (I + (t)A(t)) _A(t; s).

(iii) Si T = R et A est constante, alors A(t; s) = eA(t; s) = eA(t s).

(iv) Si T = hZ, avec h > 0 et A est constante, alors A(t; s) = (I + hA)

(t s)

h .

1.3

C

0

semi-groupes et leurs generateurs

De nition 1.3.1 Soit L (X) l'espace des operateurs lineaires bornes d'un espace de

Ba-nach X. On appelle C0 semi-groupe d'operateurs lineaires bornes dans X, une famille

fT (t) : t 2 Tg L (X) veri ant les proprietes suivantes :

1. T (t + s) = T (s) T (s) pour tout t; s_{2 T (la propriete du semi-groupe),}

2. T (0) = I, (I est l'operateur identite dans X),

3. lim_t!0+T (t) x = x pour tout x2 X,

ou l'echelle de temps T est un semi-groupe additif de R+.

Si de plus lim_t!0+kT (t) Ik = 0, alors T s'appelle un semi-groupe continu uniformement.

De nition 1.3.2 On dit qu'un operateur lineaire A est l'operateur generateur de T si

Ax = lim

s!0+

T ( (t)) x T (s) x

(t) s ; x2 D (A) ; (1.14)

ou le domaine D (A) de A est l'ensemble de tout x _{2 X pour lequel la limite ci-dessus}

existe uniformement en t.

La reference [43] donne plus de details sur les proprietes d'un C0 semi-groupe T et son

1.4. Quelques inegalites importantes

1.4

Quelques inegalites importantes

Dans cette section, nous donnons un petit rappel de quelques classes de fonctions ainsi que des inegalites utiles dans cette etude.

De nition 1.4.1 _{([29]) Soit g une fonction continue positive et croissante de nie sur R}+,

g est dite de classe _{S, si elle veri e}

1

ag(x) g(

x

a) pour tout x 0 et a 1:

De nition 1.4.2 _{([29]) Soit g une fonction continue et positive sur R}+, g est dite de

classe _{T , si elle veri e}

1

ag(x) g(

x

a) pour tout x 0 et a 1:

Lemme 1.4.1 ([46]) Supposons a 0; p q 0 et p_{6= 0, nous avons}

aqp q pk q p p _{a +}p q p k q p pour tout k > 0:

Lemme 1.4.2 ([7]) Soient b et f deux fonctions continues sur I = [ ; ] et soit une

fonction di erentiable sur I. Si les inegalites

0_{(t) b(t) (t) + f (t); t}

2 I

( ) 0;

sont satisfaites, alors

(t) 0exp 0 @ t Z b(s)ds 1 A + t Z f (s) exp 0 @ t Z s b( )d 1 A ds; t 2 I: Lemme 1.4.3 ([15]) (Comparaison) On suppose que x; b_{2 C}rd; a2 <+. Si x (t) a (t) x (t) + b (t) ; t t0; t2 Tk: Alors, x (t) x (t0) ea(t; t0) + Z t t0 ea(t; (s)) b (s) s; t t0; t2 Tk:

Lemme 1.4.4 ([11]) Soit p une fonction positive et rd-continue, nous avons les inegalites 1 + t Z t0 p( ) ep(t; t0) exp 0 @ t Z t0 p( ) 1 A ; pour tout t 2 T+ t0: ou T+t0 = ft; t0 2 T; t t0g.

Lemme 1.4.5 ([11]) Supposons que t0 2 T. Si U; ; # 2 Crd(T; R+) et est une fonction

delta-di erentiable sur T avec (t) 0. Si U satisfait

U (t) (t) +

Z t

t0

#(s)U (s) s; t_{2 T}k;

alors, nous avons

U (t) (t0)e#(t; t0) +

Z t

t0

(s)e#(t; (s)) s; t2 Tk:

Lemme 1.4.6 ([15]) (Inegalite de H•older)

Soient a; b_{2 T et f; g : [a; b] ! R deux fonctions rd-continues, nous avons}

Z b a jf(t)g(t)j t Z b a jf(t)j p t 1 p Z b a jg(t)j q t 1 q ; ou p > 1et q = _{p 1}p .

1.5

Equation di erentielle a retard

De nition 1.5.1 Une equation di erentielle a retard (EDR) est une equation di erentielle

ou la variable d'etat appara^t avec un argument retarde, autrement dit lorsque l'etat a un instant donne est une fonction de son passe. Cela peut s'exprimer comme suit :

u0(t) = f (t; u(t); u(t )); u(t)_{2 R;}

ou le retard > 0 est constant.

Exemple 1.5.1 ([27]) Considerons l'evolution d'une population animale ne tenant compte

que de la natalite et de la mortalite naturelle. En supposant que la mortalite est instan-tanee dans la population, par rapport a l'echelle de temps consideree (typiquement, la se-maine ou le mois), la description de l'evolution de cette population necessite de connaitre

1.5. Equation di erentielle a retard le nombre d'individus a l'instant t, que l'on peut noter N (t), mais egalement le nombre

d'individus a l'instant t , ou est la duree de gestation moyenne de la population.

On peut alors ecrire l'equation lineaire a retard discret suivante : d

dtN (t) = aN (t) + bN (t ); t > 0;

N (t) = (t); t_{2 [} ; 0] ;

ou a et b sont respectivement les taux de mortalite et de naissance de la population et

2

Inegalites integrales de type

Gronwall-Bellman-Bihari

a retard

Diverses inegalites integrales ont joue un r^ole important dans le developpement de la

theorie des equations integrales et plus generalement dans la theorie des equations di erentielles ordinaires, au point de vue existence et unicite des solutions et de la stabilite des points d'equilibres. Les inegalites integrales qui sont appliquees frequemment dans la litterature, sont les celebres inegalites de Gronwall-Bellman [9]. Leur premiere generalisation non

lineaire due au Bihari [14]. Des generalisations et des applications de l'inegalite de

Gronwall-Bellman ont ete obtenues par de nombreux auteurs ([2]; [8]; [18]; [29]; [33]; [35]; [36]; [48]; [56]).

Nous commencons ce chapitre en citant quelques inegalites integrales lineaires clas-siques de type Gronwall-Bellman en une dimension. Nous donnons par la suite quelques generalisations de ces inegalites intervenant dans les equations di erentielles ordinaires et a retard.

Nous concluons ensuite ce chapitre par donner des nouvelles generalisations des inegalites integrales de type Gronwall-Bellman a retard, illustrees par deux applications. Les

nou-2.1. Quelques celebres inegalites integrales unidimensionnelles veaux resultats obtenus ont ete soumis pour une eventuelle publication dans une revue internationale.

2.1

Quelques celebres inegalites integrales

unidimen-sionnelles

En 1919, Gronwall, a etabli une remarquable inegalite suscitant l'attention de plusieurs mathematiciens, dont l'enonce est le suivant :

Lemme 2.1.1 ([39]) Soit u une fonction continue sur I = [ ; + h] et a et b sont deux

constantes positives. Si l'_inegalite

0 u(t)

t Z

[bu(s) + a] ds; t_{2 I;}

est veri ee, alors

0 u(t) ah exp(bh); t_{2 I:}

En 1943, Bellman a demontre une inegalite similaire dans le cas, ou b est une fonction dependante de la variable t et elle porte le nom d'inegalite de type Gronwall-Bellman. Ce resultat a ete repris dans le theoreme suivant :

Theoreme 2.1.1 ([9]) Soient u et g deux fonctions continues et positives sur I = [ ; ]

et c une constante positive. Si l'_inegalite

u(t) c +

t Z

g(s)u(s)ds; t_{2 I;}

est veri ee, alors

u(t) c exp(

t Z

g(s)ds); t_{2 I:}

En 1956, Bihari a prouve une inegalite encore plus generale que celle de Gronwall-Bellman, dont l'intitule est :

Theoreme 2.1.2 _{([14]) Soient u, f deux fonctions continues positives sur R}+, w une

fonction croissante et continue sur R+, veri ant w(x) > 0 pour tout x > 0 et c une

constante positive. Si l'inegalite

u(t) c +

t Z t0

f (s)w(u(s))ds;

est satisfaite pour tout t 0, alors

u(t) G 1 0 @G(c) + t Z t0 f (s)ds 1 A pour tout 0 t T;

ou G est solution de l'equation integrale suivante

G(t) = t Z t0 1 w(s)ds; t > t0 > 0:

G 1 _{est la fonction inverse de G, T est choisi de telle sorte que}

( G(c) + t R t0 f (s)ds ) 2

Dom G 1 pour tout 0 t T .

Nous presentons maintenant une des inegalites la plus utile dans le developpement de la theorie des equations di erentielles. Cette derniere est prouve par Ou-Iang en 1957.

Theoreme 2.1.3 _{([71]) Soient u et g deux fonctions continues et positives sur R}+ et soit

u0 une constante positive, si l'inegalite

u2(t) u2₀+ 2

t Z

0

g(s)u(s)ds;

est satisfaite, alors

u(t) u0+

t Z

0

g(s)ds:

Remarque 2.1.1 L'inegalite de Ou-Iang (1957) a ete utilisee pour etablir la bornitude des solutions de certaines equations di erentielles de second ordre, elle a permis d'exploiter les proprietes des solutions des di erents types d'equations di erentielles non lineaires telles que l'existence globale, l'unicite, la stabilite.

2.1. Quelques celebres inegalites integrales unidimensionnelles En 1958, Bellman generalisa son propre Theoreme 2:1:1 comme suit :

Theoreme 2.1.4 ([10]) Soient u et g deux fonctions continues et positives sur I = [ ; ]

et soit n une fonction continue, positive et croissante de nie sur I. Si l'inegalite

u(t) n(t) +

t Z

g(s)u(s)ds; t_{2 I;}

est satisfaite, alors

u(t) n(t) exp(

t Z

g(s)ds); t_{2 I:}

En 1967, Chu and Metcalf ont etabli une variante de l'inegalite de Gronwall-Bellman dans le cas ou la fonction g dependra du parametre t ( i.e., g(s) = k(t; s)), dont l'enonce est le suivant :

Theoreme 2.1.5 ([26]) Soient u et f deux fonctions continues et positives sur I = [ ; ]

et k(t; s) une fonction continue et positive sur le triangle : s t . Si l'_inegalite

u(t) f (t) + t Z k(t; s)u(s)ds; t_{2 I;} alors, u(t) f (t) + t Z H(t; s)f (s)ds; t_{2 I;} ou H(t; s) = 1 X t=1 ki(t; s); (t; s)2 ;

est le noyau resolvant.

En 1969, Gollwitzer prouva une inegalite encore plus generale que celle de Bellman donnee par le theoreme suivant :

Theoreme 2.1.6 ([38]) Soient u; f; g et h des fonctions continues et positives sur I =

u(t) f (t) + g(t) t Z

h(s)u(s)ds; t_{2 I;}

est veri ee, alors

u(t) f (t) + g(t) t Z h(s)f (s) exp( t Z h( )g( )d )ds; t_{2 I:}

Gy•ori a, en 1971, etabli une variante de Theoreme 2:1:2.

Theoreme 2.1.7 ([40]) Soient u et deux fonctions continues et positives sur I = [t0;1)

et soient f; g et des fonctions di erentiables avec f positive, g positive et croissante et

positive et decroissante. Supposons que

u(t) f (t) + (t) t Z t0 (s)g(u(s))ds: Si f0(t) 1 g( (t)) 1 0; sur I ;

pour toute fonction continue et positive , alors

u(t) G 1 8 < :G(f (t0)) + t Z t0 [ (s) (s) + f0(s)] ds 9 = ;;

ou G est solution de l'equation integrale suivante

G(t) = t Z t0 1 g(s)ds; t > t0 > 0:

G 1 _{est la fonction inverse de G et}

( G(f (t0)) + t R t0 [ (s) (s) + f0_{(s)] ds} ) 2 Dom G 1_.

En 1987, Norbury et Stuart ont etabli une autre variante du Theoreme 2:1:5.

Theoreme 2.1.8 ([54])Soient u(t) et k(t; s) de nies comme dans le Theoreme 2:1:5

2.2. Quelques Generalisations des inegalites de type Gronwall-Bellman i) Si l'_inegalite u(t) c + t Z k(t; s)u(s)ds; t_{2 I}

est satisfaite pour toute constante c 0, alors

u(t) c exp 0 @ t Z k(t; s)ds 1 A ; t 2 I: ii) Soit n une fonction continue, positive et croissante sur I. Si

u(t) n(t) +

t Z

k(t; s)u(s)ds; t_{2 I}

est satisfaite, alors

u(t) n(t) exp 0 @ t Z k(t; s)ds 1 A ; t 2 I:

Dans la section suivante, nous allons presenter quelques generalisations apparues dans les revues mathematiques [2; 17; 35; 34; 56]. Ces generalisations sont utilisees comme un outil tres important dans l'etude de certaines nouvelles classes d'equations integrales et di erentielles.

Nous enoncons ces resultats, sans demonstrations.

2.2

Quelques Generalisations des inegalites de type

Gronwall-Bellman

Pachpatte [56] a etabli plusieurs generalisations de l'inegalite de Ou-Iang, donnee par le Theoreme 2:1:3. Nous citons les plus celebres.

Theoreme 2.2.1 ([56]) Soit u; a; b; g; h des fonctions continues, positives et de nies sur

R+. Si l'inegalite up(t) a(t) + b(t) t Z 0 [g(s)up(s) + h(s)u(s)] ds; t_{2 R}+;

est satisfaite pour p > 1 alors, u(t) 8 < :a(t) + b(t) t Z 0 (g(s)a(s) + h(s)ha(s)_p +p 1_p i exp 0 @ t Z s b( )hg( ) + h( )_p id 1 A ds 9 = ; 1 p :

Theoreme 2.2.2 ([56]) On suppose que les hypotheses du Theoreme 2:2:1 sont veri ees.

Soit c une fonction continue, croissante et positive sur R+, si l'inegalite

up(t) cp(t) + b(t)

t Z

0

[g(s)up(s) + h(s)u(s)] ds;

est satisfaite alors,

u(t) c(t) 8 < :1 + b(t) t Z 0 (g(s) + h(s)c(s)1 p exp 0 @ t Z s b( )hg( ) + h( )_p id 1 A ds 9 = ; 1 p :

Boukerrioua et Guezane-Lakoud [17] ont generalise le Theoreme 2:2:2, dont l'enonce est ci-dessous

Theoreme 2.2.3 ([17]) Sous les hypotheses du Theoreme 2:2:2 et supposons que la

fonc-tion a +

p r

b est croissante, si l'inegalite

up(t) a(t) + b(t)

t Z

0

[g(s)uq(s) + h(s)ur(s)] ds;

est satisfaite, alors

u(t) (a(t) + p r) 1 p 0 @1 (_pq 1) t Z 0 b(s)(g(s) + r_ph(s))(a(s) + p_r) q p 1_ds 1 A 1 p q ;

2.2. Quelques Generalisations des inegalites de type Gronwall-Bellman

dans le cas 0 < r < p < q et pour tout t < _p;q;r , ou

p;q;r = sup 8 < :t2 R+= ( q p 1) t Z 0 b(s)(g(s) + r ph(s))(a(s) + p r) q p 1_{ds 1} 9 = ;:

Dans tous ce qui suit, nous designons par C(R+; R+) l'ensemble de toutes les fonctions

continues sur R+ et par C1(R+; R+) l'ensemble des fonctions contin^ument derivables sur

R+.

El-Owaidy [35] a introduit les theoremes suivants :

Theoreme 2.2.4 ([35]) Soient u; g; f _{2 C(R}+; R+). Si l'inegalite

u (t) u0+ t Z 0 f (s) 2 4u(2 p)_{(s) +} s Z 0 g( )uq( )d 3 5 p ds; _{8t 2 R}+;

est satisfaite ou u0 > 0 et 0 < p 1; 0 q < 1, sont des constantes. Nous avons

u(t) u0+ t Z 0 f (s)k(s) exp 0 @p(2 p) s Z 0 f ( )d 1 A ds; 8t 2 R+; ou k(t) = 2 4u(1 q)(2 p) 0 + (1 q) t Z 0 g(s) exp 0 @ (1 q)(2 p) s Z 0 f ( )d 1 A ds 3 5 [ p (1 q)] ; _{8t 2 R}+:

Theoreme 2.2.5 _{([35]) Soit u une fonction positive, continue et a valeurs dans R, g;}

f _{2 C(R}+; R+) et n une fonction positive, monotone, croissante et continue sur R+ Si

u(t) n(t) + t Z 0 f (s) 2 4u(s) + s Z 0 g( )u( )d 3 5 p ds; _{8t 2 R}+;

est satisfaite, ou p est une constante telle que p_{2 (0; 1). Alors}

u(t) n(t) 2 41 + t Z 0 f (s)k0(s)n(p 1)(s) exp 0 @p(1 p) s Z 0 g( )d 1 A ds 3 5 ; 8t 2 R+; avec k0(t) = 2 41 + (1 q) t Z 0 f (s)n(p 1)(s) exp 0 @ (1 p) s Z 0 g( )d ds 1 A 3 5 [ p (1 p)] ; _{8t 2 R}+:

Nous nous sommes interesses a etudier certaines inegalites integrales non lineaires a

retard en changeant l'argument non retarde t par l'argument (t) qui exprime le retard.

Le theoreme suivant est etroitement lie a ce type des inegalites integrales.

Theoreme 2.2.6 (Lipovan [49]) Soient u; f _{2 C([t}0; T ); R+); 2 C1([t0; T ); [t0; T )) des

fonctions positives avec (t) t sur [t0; T ) et soit u0 une constante positive, alors

l'inegalite u(t) u0+ (t) Z (t0) f (s)u(s)ds; t0 < t < T; implique que u(t) u0exp 0 B @ (t) Z (t0) f (s)ds 1 C A ; t0 < t < T:

Recemment, de nombreux nouveaux resultats sur les inegalites non lineaires a retard

peuvent ^etre trouves. Nous referons entre autres le lecteur a [1 4; 23; 34; 49; 60; 63; 66

70].

Abdeldaim a elabore des generalisations des deux theoremes d'El-Owaidy (2:2:4 et 2:2:5).

Theoreme 2.2.7 ([2]) Soient u; g; f _{2 C(R}+; R+) et 2 C1(R+; R+) une fonction

crois-sante avec (t) _{t sur R}+. Si l'inegalite

u(t) u0+ Z (t) 0 f (s) u(2 p)(s) + Z s 0 g( )uq( ) d p ds; _{8t 2 R}+;

ou q; u0 > 0 et 0 < p 1 sont des constantes.

A: Si 0 q < 1 alors u(t) u0 + Z (t) 0 f (s)k1( 1(s)) exp p(2 p) Z s 0 f ( )d ds; _{8t 2 R}+; ou k1(t) = " u(1 q)(2 p)₀ + (1 q) Z (t) 0 g(s) exp (1 q)(2 p) Z s 0 f ( )d ds #[ p (1 q)] :

2.2. Quelques Generalisations des inegalites de type Gronwall-Bellman B: Si q > 1 alors u(t) u0+ up(2 p)0 Z (t) 0 f (s)k2( 1(s)) exp p(2 p) Z s 0 f ( )d ds; _{8t 2 R}+; ou k2(t) = " 1 (q 1)u(2 p)(q 1)₀ Z (t) 0 g(s) exp (2 p)(q 1) Z s 0 f ( )d ds #[ p (q 1)] ; pour tout t_{2 R}+, et 1 (q 1)u(2 p)(q 1)₀ Z (t) 0 g(s) exp (2 p)(q 1) Z s 0 f ( )d ds > 0; _{8t 2 R}+:

Theoreme 2.2.8 ([2]) Soient u; g; f _{2 C(R}+; R+), et n; 2 C1(R+; R+) avec n(t)

1; (0) = 0, et (t) _{t sur R}+. Si l'inegalite u(t) n(t) + Z (t) 0 f (s) u(s) + Z s 0 g( )u( )d p ds; _{8t 2 R}+;

est satisfaite avec p_{2 [0; 1). Alors, nous avons}

u(t) n(t) + Z (t) 0 k3( 1(s))f (s) exp p Z s 0 g( )d ds; _{8t 2 R}+; ou k3(t) = n(1 p)(0) + (1 p) Z t 0 [n0(s) + 0(s)f ( (s))] exp (1 p) Z s 0 g( )d ds p (1 p) : Un autre resultat prouve par Abdeldaim est le suivant :

Theoreme 2.2.9 ([2]) Soient u; f; h _{2 C(R}+; R+) et n; 2 C1(R+; R+) avec n(t) 1,

(0) = 0 et (t) t, _{8t 2 R}+. Si l'inegalite up(t) n(t) + Z t 0 f (s)up(s)ds + Z (t) 0 h(s)uq(s)ds; _{8t 2 R}+;

est satisfaite, ou p > q 0 sont des constantes. Alors, nous avons

u(t) k4(t) exp 1_p Z t 0 f (s)ds ; _{8t 2 R}+; ou k4(t) = np1(0) + p1 Z t 0 (n0(s)h( (s)) exp p1 Z s 0 f ( )d ds 1 p q ;

2.3

Nouvelles generalisations

2.3.1

Inegalites a retard de type Gronwall-Bellman-Bihari

L'objectif principal de ce chapitre est d'etablir des nouvelles inegalites integrales non

lineaires a retard qui peuvent ^etre utilisees comme outils pratiques pour etudier le

com-portement qualitatif de certaines equations di erentielles et integrales a retard.

Dans cette partie, nous allons enoncer et prouver quelques nouvelles inegalites integrales non lineaires a retard de type Gronwall-Bellman-Bihari, qui sont des generalisations des resultats obtenus par El-Owaidy [34; 35] et Abdeldaim [2].

Theoreme 2.3.1 Supposons que u; g; h; n_{2 C(R}+; R+) telle que n est une fonction

crois-sante. Soit _{2 C}1

(R+; R+) une fonction croissante, veri ant (t) t et (0) = 0. Soit

w : R+ ! R+une fonction di erentiable croissante sur ]0;1[ telle que sa derivee premiere

est continue et decroissante sur ]0;_{1[. Si l'inegalite}

up(t) n(t) + Z t 0 g(s)up(s)ds + Z (t) 0 h(s)w(uq(s))ds; (2.1)

est satisfaite, ou p q 0 et p_{6= 0. Alors}

u(t) n(t) + Z t 0 P1(s) exp Z t s Q1( )d ds 1 p ; _{8t 2 R}+; (2.2) ou P1(t) = g(t)n(t) + 0(t)h( (t))w _pqk q p p n(t) +p q p k q p ; Q1(t) = g(t) + q_pk q p p 0(t)h( (t))w0 q pk q p p n(t) + p q p k q p ; (2.3) pour tout t_{2 R}+.

Preuve. De nissons la fonction z(t) par :

z(t) = Z t 0 g(s)up(s) ds + (t) Z 0 h(s)w(uq(s))ds; (2.4)

ainsi, nous avons

2.3. Nouvelles generalisations

Derivons z(t) par rapport a t, et utilisons l'inegalite (2:5), nous obtenons

z0(t) g(t)(n(t) + z(t)) + 0(t)h( (t))w (n(t) + z(t))pq _{: (2.6)}

Appliquons le Lemme 1:4:1 a cette derniere, nous trouvons

z0(t) g(t)(n(t) + z(t)) + 0(t)h( (t))w q_pkqpp(n(t) + z(t)) + p q

p k

q

p ; (2.7)

par une simple application du Theoreme de la valeur moyenne a la fonction w, nous aurons, pour tout x1 > y1 > 0, il existe c2 ] y1; x1[ tel que,

w(x1) w(y1) = w0(c)(x1 y1) w0(y1)(x1 y1):

L'inegalite (2:7) peut ^etre reecrite sous la forme suivante :

z0(t) g(t)(n(t) + z(t)) + 0(t)h( (t))hw q_pkqpp_{n(t) +} p q p k q p + q_pkqpp_w0 q pk q p p _{n(t) +} p q p k q p _z(t) i ; ainsi, nous avons

z0(t) g(t)n(t) + 0(t)h( (t))w q_pkqpp_{n(t) +} p q p k q p _(2.8) +z(t)hg(t) +q_pkqpp 0_{(t)h( (t))w}0 q pk q p p _{n(t) +} p q p k q p i :

L'inegalite (2:8) peut ^etre exprimee de la maniere suivante :

z0(t) P1(t) + Q1(t)z(t);

ou P1(:) et Q1(:) sont donnees par (2:3).

Faisons appel au Lemme 1:4:2, l'inegalite ci-dessus donne z(t) Z t 0 P1(s) exp Z t s Q1( )d ds; 8t 2 I: (2.9)

Utilisons (2:5), nous obtenons l' inegalite desiree (2:2).

Remarque 2.3.1 Si nous prenons, w(t) = t, alors l'inegalite (2:1) donnee par le Theoreme

Corollaire 2.3.1 Sous les m^emes hypotheses du theoreme precedent. Si l'inegalite up(t) n(t) + Z t 0 g(s)up(s)ds + Z (t) 0 h(s) arctan(uq(s))ds;

est satisfaite, ou p q 0 et p_{6= 0. Alors}

u(t) n(t) + Z t 0 P1(s) exp Z t s Q1( )d ds 1 p ; ou, P1(t) = g(t)n(t) + 0(t)h( (t) arctan q_pk q p p n(t) + p q p k q p ; Q1(t) = g(t) + q_pk q p p 0(t)h( (t)) 0 B @ 1 1 + q_pkqpp_{n(t) +} p q p k q p 2 1 C A ; pour tout t_{2 R}+.

Theoreme 2.3.2 Supposons que u; g; h; n_{2 C(R}+; R+) telle que n est une fonction

crois-sante. Soit _{2 C}1_(R+; R+) une fonction croissante, veri ant (t) t et (0) = 0.

Soient w1; w2 : R+ ! R+ deux fonctions di erentiables croissantes sur ]0;1[ telles que

leurs derivees premieres sur ]0;_{1[ sont continues et decroissantes. Si l'inegalite}

up(t) n(t) + Z t 0 g(s)w1(up(s))ds + Z (t) 0 h(s)w2(uq(s))ds; 8t 2 R+; (2.10)

est satisfaite, sachant que p_{6= 0 et p} q 0. Alors

u(t) n(t) + Z t 0 P2(s) exp Z t s Q2( )d ds 1 p ; _{8t 2 R}+; (2.11) ou P2(t) = g(t)w1(n(t)) + 0(t)h( (t))w2 q_pk q p p n(t) + p q p k q p ; Q2(t) = g(t)w01(n(t)) + q pk q p p 0_{(t)h( (t))w}0 2 q pk q p p _{n(t) +} p q p k q p _; (2.12) pour tout t_{2 R}+.

Preuve. De nissons la fonction z(t) par :

z(t) = Z t 0 g(s)w1(up(s))ds + (t) Z 0 h(s)w2(uq(s))ds; (2.13)

2.3. Nouvelles generalisations

alors, nous avons

u(t) [n(t) + z(t)]1p_{; z(0) = 0: (2.14)}

et

z0(t) g(t)w1(up(t)) + 0(t)h( (t))w2(uq(t)):

Utilisons l'inegalite (2:14) et appliquons par la suite le Lemme 1:4:1, nous trouvons

z0(t) g(t)w1(n(t) + z(t)) + 0(t)h( (t))w2 q_pk q p p (n(t) + z(t)) + p q p k q p :

Par une simple application du Theoreme de la valeur moyenne aux fonctions w1 et w2;

nous obtenons z0_{(t) g(t) [w} 1(n(t)) + w01(n(t))z(t))] + 0(t)h( (t)) h w2 q_pk q p p _{n(t) +} p q p k q p ₊ q pk q p p _w0 2 q pk q p p _{n(t) +} p q p k q p _z(t) i ; (2.15) ainsi, z0_{(t) g(t)w} 1(n(t)) + 0(t)h( (t))w2 q_pk q p p n(t) +p q p k q p + z(t)hg(t)w0₁(n(t)) +_pqkqpp 0_{(t)h( (t))w}0 2 q pk q p p _{n(t) +} p q p k q p i ; (2.16)

on peut reecrire l'inegalite (2:16) sous la forme :

z0(t) P2(t) + Q2(t)z(t);

ou P2(:) et Q2(:) sont donnees par (2:12). Faisant appel au Lemme 1:4:2, l'inegalite

ci-dessus implique une estimation de z(t) comme suit : z(t) Z t 0 P2(s) exp Z t s Q2( )d ds 8t 2 R+: (2.17)

Utilisons l'inegalite (2:14), nous obtenons l'inegalite requise (2:11). Ce qui acheve la preuve.

Theoreme 2.3.3 Supposons que u; g; h; n_{2 C(R}+; R+) telle que n est une fonction

crois-sante. Soit _{2 C}1

(R+; R+) une fonction croissante, veri ant (t) t et (0) = 0. Etant

que leurs derivees premieres sont des fonctions continues et decroissantes sur ]0;_{1[. Si} l'inegalite up(t) n(t) + Z t 0 g(s)w1(uq(s))ds + Z (t) 0 h(s)w2(ur(s))ds; 8t 2 R+: (2.18)

est satisfaite, ou p_{6= 0, p} q 0 et p r 0. Alors

u(t) n(t) + Z t 0 P3(s) exp Z t s Q3( )d ds 1 p ; _{8t 2 R}+; (2.19) ou P3(t) = g(t)w1 q_pk q p p _{n(t) +} p q p k q p ₊ 0_{(t)h( (t)w} 2 _prk r p p _{n(t) +}p r p k r p _; Q3(t) = _pqk q p p g(t)w0 1 q pk q p p n(t) + p q p k q p + r pk r p p 0(t)h( (t))w0 2 r pk r p p n(t) + p r p k r p ; (2.20) pour tout t_{2 R}+.

Preuve. La preuve est similaire a celle du Theoreme 2:3:2.

Remarque 2.3.2 Si nous prenons w1(t) = t et w2(t) = t, q = p, alors l'inegalite (2:18)

donnee par le Theoreme 2:3:3 a ete etudiee par Abdeldaim dans le Theoreme 2:2:9.

Corollaire 2.3.2 Supposons que toutes les conditions du Theoreme 2:3:3 sont veri ees.

Si l'inegalite up(t) n(t) + Z t 0 g(s) arctan(uq(s))ds + Z (t) 0 h(s) log(1 + ur(s))ds; _{8t 2 R}+:

est satisfaite, ou p_{6= 0; p} q 0 et p r 0. Alors

u(t) n(t) + Z t 0 P3(s) exp Z t s Q3( )d ds 1 p ; _{8t 2 R}+; ou P3(t) = g(t) arctan _pqk q p p n(t) +p q p k q p + 0(t)h( (t)) log 1 + r pk r p p n(t) + p r p k r p ; Q3(t) = q_pk q p p g(t) 1 1 + q_pkqppn(t) + p q p k q p 2 + r pk r p p 0(t)h( (t)) 1 1 + r_pkrppn(t) + p r p k r p ; pour tout t_{2 R}+.

2.3. Nouvelles generalisations

Theoreme 2.3.4 Supposons que u; g; h; n_{2 C(R}+; R+) telle que n est une fonction

crois-sante. Soit _{2 C}1_(R+; R+) une fonction croissante, veri ant (t) t et (0) = 0.Soient

L; M 2 C R2 +; R+ satisfaisant 0 _{L (t; x) L (t; y)} M (t; y) (x y) ; pour t_{2 R}+ et x y 0; Si l'inegalite up(t) n(t) + Z t 0 g(s)up(s)ds + Z (t) 0 h(s)_{L(s; u}q(s))ds; (2.21)

est satisfaite, ou p_{6= 0, p} q 0. Alors

u(t) n(t) + Z t 0 P4(s) exp Z t s Q4( )d ds 1 p ; _{8t 2 R}+; (2.22) ou P4(t) = g(t) + q_pk q p p 0(t)h( (t))M (t);q pk q p p n(t) + p q p k q p ; Q4(t) = n(t)g(t) + 0(t)h( (t))L (t);q_pk q p p _{n(t) +} p q p k q p _; (2.23) pour tout t_{2 R}+.

Preuve. De nissons la fonction z(t) comme suit

z(t) = Z t 0 g(s)up(s) ds + (t) Z 0 h(s)_{L(s; u}q(s))ds; (2.24) ce qui entra^ne, u (t) [n(t) + z (t)]1p_{: (2.25)}

Derivons z (t), par rapport a t et utilisons l'inegalite (2:25), nous obtenons

z0(t) g(t)(n(t) + z (t)) + 0(t)h( (t))_{L ( (t); (n(t) + z (t))}qp_{): (2.26)}

Appliquons le Lemme 1:4:1 a cette derniere, nous trouvons

z0(t) g(t)(n(t) + z (t)) + 0(t)h( (t))_L (t);q_pkqpp(n(t) + z (t)) + p q p k q p ; (2.27) z0(t) g(t)(n(t) + z (t)) + 0(t)h( (t))h_L (t);q_pkqppn(t) + p q p k q p + q_pkqppz (t) M (t);q pk q p p n(t) + p q p k q p i : (2.28)

Ainsi, z0(t) n(t)g(t) + 0(t)h( (t))_L (t);q_pkqpp_{n(t) +} p q p k q p _(2.29) +hg(t) + q_pkqpp 0_{(t)h( (t))M (t);}q pk q p p _{n(t) +} p q p k q p i z(t):

Faisons appel au Lemme 1:4:2, l'inegalite (2:29) donne une estimation de z(t) de la forme suivante : z(t) Z t 0 P4(s) exp Z t s Q4( )d ds ; 8t 2 R+; (2.30)

ou P4(:) et Q4(:) sont donnees par (2:23). Le resultat souhaite decoule des deux inegalite

(2:25) et (2:30).

Remarque 2.3.3 Pour _{L (t; x) = x, l'inegalite (2:21) dans le Theoreme 2:3:4 a ete}

etudiee par Abdeldaim dans le Theoreme 2:2:9.

Theoreme 2.3.5 Soient u; f; g_{2 C(R}+; R+) et 2 C1(R+; R+) une fonction croissante

avec (t) t, (0) = 0 et _{L; M 2 C R}2_{+; R}+ satisfaisant 0 _{L (t; x) L (t; y)} M (t; y) (x y) ; pour t_{2 R}+ et x y 0; Si l'inegalite, u (t) u0+ Z (t) 0 f (s) u(2 p)(s) + Z s 0 g ( )_{L ( ; u}q( )) d p ds; (2.31)

est satisfaite, ou 0 < p 1, 0 q < 1. Alors

u (t) u0+ Z (t) 0 f (s) ₃ 1(s) exp p (2 p) Z s 0 P3( ) d ds; (2.32) ou 8 < : P5(t) = f (t) + _{2 p}q kq 1g (t) M (t; (1 q) kq) ; Q5(t) = h u(2 p)₀ +R₀ (t)g (t)_{L (t; (1} q) kq_{) exp (2 p)}Rs 0 P3( ) d ds ip ; (2.33) pour tout t_{2 R}+.

2.3. Nouvelles generalisations

Preuve. De nissons la fonction z(t) par

z(t) = u0+ Z (t) 0 f (s) u(2 p)(s) + Z s 0 g ( )_{L ( ; u}q( )) d p ; donc z (0) = u0 et u (t) z (t) : (2.34)

Derivons z (t), par rapport a t et utilisons l'inegalite (2:34), nous trouvons

z0(t) 0(t) f ( (t)) " z(2 p)(t) + Z (t) 0 g (s)_{L (s; z}q(s)) ds #p : (2.35) Posons v (t) = z(2 p)_{(t) +}R (t) 0 g (s)L (s; z

q_{(s)) ds, ainsi, nous avons v (0) = u}(2 p)

0 et

z0(t) 0(t) f ( (t)) vp(t) ; (2.36)

comme p 1_{) 2} p 1 et z(2 p)_{(t) v (t), nous obtenons}

z (t) v (t) : (2.37)

Derivons v (t) par rapport a t et utilisons les deux inegalites (2:36) et (2:37), nous trouvons

v0(t) (2 p) 0(t) f ( (t)) v (t) + 0(t) g ( (t))_{L ( (t) ; v}q(t)) : (2.38)

Posons q = m_n avec n > m 0; n_{6= 0 et appliquons le Lemme 1:4:1, nous avons}

vq(t) qkq 1v (t) + (1 q) kp; donc v0(t) (2 p) 0(t) f ( (t)) v (t) + 0(t) g ( (t)) _{L ( (t) ; (1} q) kq) + qkq 1M ( (t) ; (1 q) kq) v(t) ; v0(t) 0(t) g ( (t))_{L ( (t) ; (1} q) kq) + (2 p) 0(t) f ( (t)) + 0(t) g ( (t)) qkq 1M ( (t) ; (1 q) kq) v(t):

L'application du Lemme 1:4:2 a l'inegalite ci dessus, nous permet d'obtenir une estimation de v (t) comme suit v (t) exp (2 p) Z (t) 0 (f (s) + q 2 pk q 1_{g (s) M (s; (1 q) k}q_))ds ! " u(2 p)₀ + Z (t) 0 g (s)_{L (s; (1} q) kq) exp (2 p) Z s 0 (f ( ) + q 2 pk q 1_{g ( ) M ( ; (1 q) k}q_{))d ds} alors, vp(t) exp p (2 p) Z (t) 0 P5(s) ds ! Q5(t) ; (2.39)

avec P5(:) et Q5(:) sont donnees par (2:33).

La substitution de (2:39) dans (2:36) entra^ne

z0(t) 0(t) f ( (t)) Q5(t) exp p (2 p) Z (t) 0 P5(s) ds ! : Par consequent, z (t) u0+ Z (t) 0 f (s) Q5 1(s) exp p (2 p) Z s 0 P5( ) d ds:

Le resultat voulu decoule de l inegalite ci-dessus et l'inegalite (2:34). La preuve est ainsi achevee.

Remarque 2.3.4 Si _{L (t; x) = x, alors l'inegalite (2:31) donnee par le Theoreme 2:3:5 a}

ete discutee par Abdeldaim dans le [Theoreme 2:2:7 (A)].

Remarque 2.3.5 Notons que si_{L (t; x) = x et (t) = t, l'inegalite (2:31) donnee par le}

Theoreme 2:3:5 a ete aussi discutee par El-Owaidy dans le Theoreme 2:2:4.

Theoreme 2.3.6 Soient u; g; h_{2 C(R}+; R+) et 2 C1(R+; R+) une fonction croissante

avec (0) = 0; (t) t et u (t) u0+ Z (t) 0 g (s) up(s) ds+ Z (t) 0 g (s)_{L (s; u}q(s)) " u2 p(s) + Z (s) 0 h ( ) u ( ) d #p ds; (2.40)

2.3. Nouvelles generalisations

ou u0 > 0, 0 < p 1, 0 q < 1 sont des constantes et L; M 2 C R2+; R+ satisfaisant

0 L (t; x) L (t; y) M (t; y) (x y) ; pour t_{2 R}+ et x y 0;

alors, nous avons

u (t) K(t) exp_f Z (t) 0 (s)_gds; (2.41) ou (t) = pkp 1_{g (s) 1 +} q pk q p_{M (s; (1 q) k}q₎ p₍ 1_{(s)) ;} K(t) = u0+ R (t) 0 [g (s) (1 p) k p₊ L (s; (1 q) kq₎ p₍ 1_(s)) exp( R₀s ( )d )ds ; (2.42) (t) = expf R (t) 0 Q6(s) dsg C R₀ (t)P6(s) expf Rs 0 Q6( ) d g ds ; (2.43) et P6(t) = (2 p) qkq 1g (t) M (t; (1 q) kq) ; Q6(t) = (2 p) g (t)f1 + L (t; 1 q) kq)g + h (t) ; (2.44) avec R₀(t)P6(s) expf Rs 0 Q6( ) d g ds < C.

Preuve. De nissons la fonction z(t) par

z(t) = u0+ Z (t) 0 g (s) up(s) ds+ Z (t) 0 g (s)_{L (s; u}q(s)) " u2 p(s) + Z (s) 0 h ( ) u ( ) d #p ds;

alors nous avons z (0) = u0 et

u (t) z (t) : (2.45)

Derivons z (t), par rapport a t et utilisons (2:45), nous obtenons

z0(t) 0(t) g ( (t)) zp(t)+ 0(t) g ( (t))_{L ( (t) ; z}q(t)) " z2 p(t) + Z (t) 0 h (s) z (s) ds #p : (2.46)

Posons q = m_n avec n > m 0, n_{6= 0, ce qui donne}

donc z0(t) 0(t) g ( (t)) zp(t) + 0(t) g ( (t)) L ( (t) ; (1 q) kq) + qkq 1M ( (t) ; (1 q) kq) z (t) vp(t); (2.47) ou v (t) = z2 p(t) + Z (t) 0 h (s) z (s) ds; v (0) = u(2 p)₀ ; v(t) > 0; (2.48) z (t) z2 p(t) v (t) : (2.49)

Derivons v (t) par rapport a t, ensuite utilisons les inegalites (2:47) et (2:49), nous trouvons

v0(t) (2 p) 0(t) g ( (t)) vp(t) v1 p(t) + (2 p) 0(t) g ( (t)) L ( (t) ; (1 q) kq) + qkq 1M ( (t) ; (1 q) kq) v (t) vp(t) v1 p(t) + 0(t) h ( (t)) v (t) = (2 p) 0_{(t) g ( (t)) v (t) + (2 p)} 0_{(t) g ( (t)) v (t)} [_{L ( (t) ; (1} q) kq_{) + qk}q 1_{M ( (t) ; (1 q) k}q_{) v (t)] +} 0_{(t) h ( (t)) v (t)} = [(2 p) 0_{(t) g ( (t)) (1 +L( (t) ; (1 q) k}q_{)) +} 0_{(t) h ( (t))] v (t)} + [(2 p) 0_{(t) g ( (t))qk}q 1_{M ( (t) ; (1 q) k}q_{)] v}2_{(t) :} (2.50) Posons A(t) = (2 p) 0(t) g( (t))qkq 1M ( (t) ; (1 q) kq) ; (t) = (2 p) 0(t) g ( (t)) (1 +_{L ( (t) ; (1} q) kq)) + 0(t) h ( (t)) ;

par la suite, nous avons

v0(t) A (t) v2(t) + (t) v (t) ;

v 2(t) v0(t) A (t) + (t) v 1(t) ;

posons v 1(t) = y (t), ainsi nous obtenons

y0(t) A (t) + (t) y (t) ;

2.3. Nouvelles generalisations

Utilisons le Lemme 1:4:2, nous trouvons

y(t) u₀(2 p)exp_f Z t 0 (s)ds_g Z t 0 A(s)exp_f Z t s ( )d _gds = u_o(2 p)exp_f Z (t) 0 ((2 p) g (s)_{f1 + L (s; (1} q) kq)_{g + h (s)) dsg} (2 p) qkq 1 Z (t) 0 g (s) M (s; (1 q) kq) exp_f Z (t) s ((2 p) g ( )_{f1 + L ( ; (1} q) kq)_{g + h( ))d gds} = exp_f Z (t) 0 [(2 p) g (s) (1 +_{L (s; (1} q) kq)) + h (s)] ds_ghu₀(2 p) (2 p) qkq 1 Z (t) 0 g (s) M (s; (1 q) kq) exp_f Z s 0 [(2 p) g ( ) (1 +_{L ( ; (1} q) kq)) + h ( )] d _{gds ;} par consequent, y (t) exp Z (t) 0 Q6(s) ds ! fu0(2 p) Z (t) 0 P6(s) exp Z s 0 Q6( ) d dsg; (2.51)

ou P6(:) et Q6(:) sont donnees par (2:44).

y (t) u (2 p) 0 R (t) 0 P6(s) expf Rs 0 Q6( ) d g ds exp_fR₀ (t)Q6(s) dsg ; (2.52) donc, v (t) expf R (t) 0 Q6(s) dsg u₀(2 p) R₀(t)P6(s) expf Rs 0 Q6( ) d g ds : Prenons u₀(2 p)= C et Z (t) 0 P6(s) expf Z s 0 Q6( ) d g ds < C;

nous obtenons facilement v(t) (t), ou (t) est donnee par (2:43).

Utilisons l'inegalite (2:47), et prenons p = m_n avec n m > 0, n _{6= 0, nous aboutirons}

a

z0(t) 0(t) g ( (t)) [(1 p) kp+_{L ( (t) ; (1} q) kq) p(t)]

Appliquons une autre fois, le Lemme 1:4:2 sur cette derniere, nous pouvons donner une estimation de z (t) comme suit :

z (t) exp_f Z (t) 0 g (s) pkp 1+ qkq 1M (s; (1 q) kq) p 1(s) ds_g " u0 + Z (t) 0 g (s) (1 p) kp+_{L (s; (1} q) kq) p 1(s) exp_f Z s 0 g ( ) pkp 1+ qkq 1M ( ; (1 q) kq) p 1( ) d _{gds ;}

l'inegalite ci-dessus peut ^etre reformulee comme suit :

z (t) K(t) exp_f

Z (t)

0

(s)_gds; (2.53)

ou k(:) et (:) sont donnees par (2:42): L'inegalite (2:41) souhaitee decoule des deux inegalites (2:45) et (2:53). Ce qui acheve la preuve.

Theoreme 2.3.7 Supposons que u; g; h; n_{2 C(R}+; R+) telle que n est une fonction

crois-sante. Soit _{2 C}1

(R+; R+) une fonction croissante, veri ant (t) t et (0) = 0. Soit

une fonction croissante de classe_{T (voir De nition 1:4:2 page 17) telle que} 1_{(I) I}

et 1 _{1. Si l'inegalite suivante} (up(t)) np(t) + Z t 0 g(s)up(s)ds + Z (t) 0 h(s)uq(s)ds; _{8t 2 R}+; (2.54)

est satisfaite, ou p > q 0. Alors

u(t) " max(np(t); 1) 1 W 1(W (1) + Z t 0 g(s)ds + q_pkqpp ₊ p q p k q p Z (t) 0 h(s) ap q_(s)ds) !#1 p ; (2.55) avec W (1) + Z t 0 g(s)ds + _pqkqpp ₊p q p k q p Z (t) 0 h(s) ap q_(s)ds 2 Dom(W 1_); W 1 W (1) + Z t 0 g(s)ds + q_pkqpp + p q p k q p Z (t) 0 h(s) ap q_(s)ds ! 2 Dom( 1);

2.3. Nouvelles generalisations

Preuve. Posons ap_{(t) = max(n}p_{(t); 1). Ainsi l'inegalite (2:54) peut ^etre reecrite sous}

la forme suivante : (up_(t)) ap_(t) 1 + Z t 0 g(s) ap_(s)u p_{(s)ds +} Z (t) 0 h(s) ap_(s)u q_(s)ds; 8t 2 R+: (2.56) Prenons z(t) = u(t) a(t) : (2.57)

Comme la fonction est de classe _{T , nous aurons}

(zp(t)) 1 + Z t 0 g(s)zp(s)ds + Z (t) 0 h(s) ap q_(s)z q_(s)ds; 8t 2 R+: (2.58)

De nissons une fonction auxiliaire v(t) par

v(t) = 1 + Z t 0 g(s)zp(s)ds + Z (t) 0 h(s) ap q_(s)z q_{(s)ds; (2.59)}

utilisons l'inegalite-ci dessus (2:59) et les proprietes de la fonction , nous obtenons

z(t) 1(v(t))

1

p _{et v(0) = 1: (2.60)}

Substituons l'inegalite (2:60) dans l'inegalite (2:59), nous aurons

v(t) 1 + Z t 0 g(s) 1(v(s))ds + Z (t) 0 h(s) ap q_(s) 1_(v(s)) qp_{ds: (2.61)}

Derivons la fonction v (t) par rapport a t et appliquons le Lemme 1:4:1, nous trouvons v0(t) g(t) 1(v(t)) + 0(t)_aph( (t))q_{( (t))} q pk q p p 1(v(t)) + p q p k q p ; ainsi v0(t) 1_(v(t)) g(t) + 0(t) h( (t)) ap q_{( (t))} q pk q p p +p q p k q p : (2.62)

Integrons l'inegalite (2:62) de 0 a t, nous obtenons

W (v(t)) W (v(0)) + Z t 0 g(s)ds + q_pkqpp ₊p q p k q p Z (t) 0 h(s) ap q_(s)ds; donc v(t) W 1 W (1) + Z t 0 g(s)ds + _pqkqpp ₊p q p k q p Z (t) 0 h(s) ap q_(s)ds ! : (2.63)

Le resultat desire (2:55) decoule des inegalites (2:63), (2:60) et (2:57). La preuve est donc achevee.

Theoreme 2.3.8 Soient u; g; f _{2 C(R}+; R+) et 2 C1(R+; R+) une fonction croissante

avec (t) t, (0) = 0, _{L; m : R}+ R+ ! R+deux fonctions continues et : R+ ! R+

une fonction continue et strictement croissante veri ant (0) = 0;

et

0 _{L(t; x) L(t; y)} m(t; y) 1(x y); pour t_{2 R}+et x y 0; (2.64)

ou 1 est la fonction inverse de satisfaisant a la condition suivante

1 (xy) 1(x) 1(y): (2.65) Si l'inegalite up(t) n(t) + Z t 0 g (s)_{L (s; u}p(s)) ds + Z (t) 0 h (s)_{L (s; u}q(s)) ds ! ; (2.66)

est satisfaite, ou p > q 0. Alors

u (t) n(t) + Z t 0 P7(s) exp Z t s Q7( )d ds 1 p ; _{8t 2 R}+; (2.67) avec P7(t) =L(t; n(t))g(t) + 0(t) h ( (t))L (t) ;q_pk q p p _{n(t) +} p q p k q p _; Q7(t) = g(t)m(t; n(t)) + m( (t) ;q_pk q p p n(t) + p q p k q p) 1(q pk q p p ); (2.68) pour tout t_{2 R}+. Preuve. Soit z (t) =R₀tg (s)_{L (s; u}p_{(s)) ds +}R (t) 0 h (s)L (s; u

q_{(s)) ds, donc nous}

au-rons z (0) = 0 et

u (t) [n(t) + (z (t))]1p: (2.69)

Derivons z (t), par rapport a t, ensuite utilisons l'inegalite (2:69), ceci entra^ne

z0(t) g(t)_{L (t; n(t) + (z (t)) +} 0(t) h ( (t))_L (t) ; (n(t) + (z (t))qp _{; (2.70)}

utilisons (2:64) et le Lemme 1:4:1, nous obtenons

z0(t) g(t) _{L t; n(t)) + m(t; n(t))} 1( (z (t)

+ 0(t) h ( (t))_L (t) ;q_pkqpp(n(t) + (z (t)) + p q

p k

q