Good reduction of elliptic curves over imaginary quadratic fields

M

ASANARI

K

IDA

Good reduction of elliptic curves over imaginary

quadratic fields

Journal de Théorie des Nombres de Bordeaux, tome

13, n

o

_{1 (2001),}

p. 201-209

<http://www.numdam.org/item?id=JTNB_2001__13_1_201_0>

© Université Bordeaux 1, 2001, tous droits réservés.

L’accès aux archives de la revue « Journal de Théorie des Nombres de Bordeaux » (http://jtnb.cedram.org/) implique l’accord avec les condi-tions générales d’utilisation (http://www.numdam.org/conditions). Toute uti-lisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit conte-nir la présente mention de copyright.

Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques

Good

reduction of

_elliptic

curves over

imaginary

quadratic

fields

par MASANARI KIDA

RÉSUMÉ. Nous montrons que l’invariant

_{modulaire j}

d’une courbe

elliptique

définie sur un _corps

_{quadratique imaginaire}

_ayant

par-tout bonne réduction vérifie certaines

_{équations diophantiennes,}

sous réserve _que soient vérifiées certaines

hypothèses

relatives à

l’arithmétique

du _corps. En résolvant

_{explicitement}

ces

_equations

dans l’anneau des entiers du corps, nous _{montrons que} de telles

courbes n’existent pas sur certains _corps

quadratiques imaginaires.

Nos résultats

_{généralisent}

des résultats antérieurs de Setzer et

Stroeker.

ABSTRACT. We prove that the

j-invariant

of an

elliptic

curve

defined over an _imaginary

quadratic

number field

having good

re-duction

_everywhere

satisfies certain

_Diophantine

_equations under

some

hypothesis

on the arithmetic of the

quadratic

field.

By

solv-ing

the

_Diophantine

_equations

_explicitly

in the

_rings

of

_quadratic

integers, we show the non-existence of such

elliptic

curve for

cer-tain

imaginary quadratic

fields. This extends the results due to

Setzer and Stroeker.

Introduction

It is well-known that there is no

elliptic

curve

having good

reduction

everywhere

over the field

_Q

of rational numbers. This result is further

generalized

to certain

_quadratic

fields and some other fields

(see

[9]

and the

references

_there).

In this paper, we are

particularly

interested in the case of

_imaginary

quadratic

fields. For this _case, the

_following

nice result due to Setzer and Stroeker is known.

Theorem

_(Setzer

_[11,

Theorem

_5],

Stroeker

_{[16, (1.9) Theorem]).}

Let k be

an

imaginary quadratic

field. If

the class number

of k

is

_{prime to 6,}

then

there is no

elliptic

curve

defined

over k

having

good

reduction

_everywhere.

Manuscrit _reçu le 26 octobre 1999.

This research was _supported in part by Grant-in-Aid for _{Encouragement} of Young Scientists (No. 11740009), Ministry of Education, Science, Sports and _{Culture, Japan.}

Moreover,

Setzer

_gives

a criterion for the non-existence of

elliptic

curves

having good

reduction

_everywhere

_by

_using

certain Galois-theoretic proper-ties of the two division fields of the

_elliptic

curves

([11,

_p.

_249,

Proposition]).

The aim of this _{paper is} to prove the non-existence of such

elliptic

curves

under somewhat weaker

_assumptions

than Setzer and Stroeker’s in the above theorem. For that _purpose, we reduce the

problem

of

finding

such curves to

_solving

certain

_Diophantine

_equations

_(cf.

Theorem

₂₎

under

some

hypothesis. Solving

these

_Diophantine

_equations

explicitly,

we shall

show the

_following

theorem.

Theorem 1. There is no

elliptic

curve

_{having good}

reduction

_everywhere

over the

_{following four}

_imaginary

_quadratic

_fields:

The class numbers of these four fields are all 2. Therefore the non-existence of

_elliptic

curves

_{having good}

reduction

_everywhere

for these fields

does not follow from Setzer and Stroeker’s theorem above.

_Moreover,

Set-zer’s criterion cannot be

_applied

to these fields

_(cf.

_[11,

Theorem 4

_(a)]).

This _paper consists of three sections. In the first

_section,

we show that

the

_j-invariant

of an

_elliptic

curve over an

_imaginary

_quadratic

number field

having good

reduction

_everywhere

satisfies a set of

_Diophantine

_equations.

In the second

_section,

we

_explain

how to solve these

_Diophantine

_equations.

Some numerical

_examples

and the

_proof

of Theorem 1 are

_given

in the third section.

1.

_Diophantine

_equations

We shall _prove the

_following

theorem in this section. For the definition of the

_j-invariant

of an

elliptic

_curve, we refer to

_[1,

p. 364

(7.1)].

Theorem 2. Let k be an

_imaginary

_quadratic

field. Suppose

k

satisfies

the

following

assumptions:

(i)

The _{unit grouP}

_{of k}

consists

_of

_~1;

(ii)

The class number

_{of k}

is

_prime

to

_3;

(iii)

If the

class numbers

_{of k}

is divisible

_by

_2,

then _{ever y} ideal class

_of

order

2 contains an ideal c such that

c2

=

(r)

with _some rational

_integer

_r.

Then the

_{j-invariant j}

_of

an

elliptic

curve

defined

over k

having good

re-duction

_{everywhere satisfies}

the

_following

set

_{of Diophantine}

_equations

in

the

_ring

_of

_integers

_of

k:

Proof.

It is known that the

_{j-invariant j}

of an

_elliptic

curve

_having

_good

reduction

_everywhere

satisfies the

_following

conditions for every discrete

valuation v of the

_ring

of

_integers

of k

_{(see [2, (1.3)]):}

It follows from

_(2a)

_{that j}

is an

algebraic integer.

Furthermore, j

_generates

an ideal which is a cube

by

(2b):

(j)

=

63.

By

the

_assumption

_on the class

number of

_k,

the ideal b is

_principal,

_i.e.,

b =

(x).

Hence,

_we have

Here we used the

assumption

on the unit group. It is _{easy to} see that the

generator x

can be taken in the

_ring

of

algebraic

_integers

of k.

Now

_by

_(2c),

there exists an ideal a such that

Suppose

first that a in

(4)

is

principal,

_say a =

(y).

Then _we

_{get j}

-1728 =

±y 2

with _some

y E k. It is

_readily

seen from this

_equation

that _y is an

algebraic

integer.

Combining

this with

(3),

we obtain

:1::.y2

=

±~ 20131728.

Changing

the

_signs

of the

_variables,

we have

Ci : y2

= X3 ±

1728.

If a is not

_principal,

then the class of a is of order 2 in the ideal class

group. The class of a contains an ideal c such that

c2

=

(r)

with r E Z

_by

the third

_assumption.

This means that there

exists y

satisfying

a =

(y)c.

Hence it follows

a2

=

(y2)c2

=

(ry2).

Combining

this with

_(4),

we have

j -1728

=

~ry2.

This

implies

that

ry2

is _an

algebraic

integer.

Substituting

(3)

into this

_{equation and,}

if necessary,

changing

the

signs

of the

_variables,

we obtain

ry2

= x3 :1::.1728.

_{Multiplying by}

r3

then

_yields

(r2y)2

=

(rX)3 ±

1728r3.

Since

_(r2y)2

=

r3 .

ry2,

_{we see} that

r2y

is

integral. Replacing

(rx, r2y)

by

(x, y),

we have

C~.

We have thus

_proved

Theorem 2. D

Some remarks are in order. The first

assumption

in Theorem 2 is satisfied

if k is neither

_Q(B/2013l)

nor

~(~).

The class number of each field is one. Hence the non-existence for these two fields follows from Setzer and Stroeker’s theorem.

The

_resulting

_{Diophantine equations}

_Ct

in Theorem 2 define

_elliptic

curves over

Q. Thus,

to

_apply

the theorem to a

specific imaginary quadratic

field,

we have to determine the

integral

points

in the

ring

of

quadratic

integers

of an

elliptic

curve defined over

Q.

This is

actually

_possible

_by

the

method we will

_explain

in the next section.

2.

_{Integral points}

on an

elliptic

curve

Let k = be _an

imaginary

quadratic

field where m is a

curve

_given

_by

a short Weierstrass

_equation

with a,

b E Z. In this

_section,

we discuss how to find the

integral

points

of

E in

_7Gk.

First we consider the method of

computing

the Mordell-Weil _group

E(k).

We denote

_by

_E(-m)

the

_quadratic

twist of E

_{corresponding}

to the

quadratic

extension

_k/Q,

which is defined

_by

the

_equation

These two curves E and

E(-m)

are both defined

over Q

and are

_isomorphic

over k. An

explicit isomorphism

over k is

_given

by

By

this

_isomorphism,

we have c

_E(k).

Note that the

generator

Q of the Galois _group of the

quadratic

extension acts on

by

P ~ -P.

Hereafter,

for a

finitely generated

Abelian _group

A,

let

An

be the kernel

of the

_{multiplication-by-n}

_map and set

_A(2)

=

A/A2

-We now consider the

following

_map:

In the _map

_definition,

the addition is that of the _group law on E. Is is easy to see that the _map is a

homomorphism. By considering

the action

of _Q, it is verified that the intersection of and is a subset of

_E(~)2.

_Therefore,

the sum of the _groups on the left hand side is direct.

_Similarly,

it can be seen that the _map is

injective. Moreover,

the cokernel of _{cp is} killed

_by

the

_{multiplication-by-2}

_map.

_Indeed,

for _any

P E

_E(k)(2),

take E

E(Q)(2) C~(E(-m)(Q))(2),

then

we have

cp(P

+

_pu,

P -

_Pa)

= 2P.

Summing

up the above

arguments,

we can

_compute

E(k)

by

the

following

procedure.

Step

1

_Compute

the

_generators

of

_E(Q)

and

_{~((E(-~)(Q))(2)).}

For this _purpose, several

_{pseudo algorithms}

are known

(see [18])

and

they

are

implemented

in some number

theory packages

such as SIMATH

([6]).

Step

2 Determine whether the

_generators

found in the

_preceding

_step

and all

_possible

sums of them have a half

_point

(i.e.,

a

_point

Q

such

that P =

2Q

for _a

_given

P)

in

E(k)

or not. If there exists a half

point,

then

_compute

it and

_enlarge

the _group. This can be done

by

an

algorithm

due to

_Washington

_([17,

_Proposition

_4]).

_Repeat

this

Step

3 Fill _up the

_2-power

torsion

_points.

An

_explicit

_computation

of the division

_polynomials,

for

_example,

enables us to

_accomplish

it.

It should be

_emphasized

that we can

_compute

E(k)

because the curve

E is defined over

Q.

Computing

Mordell-Weil _groups over an

algebraic

number field

_larger

_{than Q}

is still difficult in

_general

_{(cf. [3]).}

Having

computed

the Mordell-Weil group, we now turn our attention to

computing

the

_integral

_points.

Let

_Pl,

_{P2, ... , P,}

be the

_generators

of

_E(k).

_Suppose

that P =

plP1

₊

P2 P2

+ ..-

_E(k)

is an

_integral

_point

with _{pl, P2, ... , ps} E Z.

Us-ing

Baker’s

_theory

for

_elliptic

_logarithms

_(cf.

_[5]),

Smart and

_Stephens

([14],

see also

[15,

Chapter

XIII])

give

a small

_computable

_upper bound for

jp2!? - "

Hence we are able to find all the

_integral

_points

in

E(k).

Here we make some remarks for a

_practical

_computation.

To use the

Smart-Stephens algorithm,

local minimal models of the curve E and the

canonical

_heights

and the

_{elliptic logarithms}

of the

_generators

of

_E(k)

are

required.

We

_implemented

the

_algorithms

_(Tate’s

_algorithm

_[13,

_Chapter

IV,

§9],

Silverman’s

_algorithm

_[12]

and

_Algorithm

7.4.8 in

_[1],

_{respectively)}

for

_computing

these invariants on KASH

([4]).

We refer to

_[10]

for more details.

Though Algorithm

7.4.8 in

_[1]

_only

describes how to

_compute

the

_elliptic

logarithm

of a

_point

in the real locus of an

elliptic

_curve, it is

enough

for our _purpose as the

_following

_proposition

shows.

Proposition.

(resp.

_{~~_~",~~}

be the

_elliptic

_logarithm

on E

(resp.

E(-m))

and A

_(resp.

the

_{corresponding}

_period

lattice. Then the

following

diagram is

commutative: 1

where the

_{map ai}

is

_{defined by}

_(5).

Proof.

Let _el, e2 and e3 be the roots of the

polynomial

where

_{b2, b4}

and

_b6

are the standard invariants of E

(for

the

_definitions,

see

[1,

p. 364

(7.1)]

for

example)

and

ei, e2

and

e’

the

corresponding

objects

for

_E(-m).

It is _{easy to} see that

they

are related

by

Hence we have

Noting

that the _{inverse map} of O

_(resp.

is

_given

_by

where

_{(resp. p(z;}

_A-m))

is the Weierstrass

_p-function

relative to

the lattice A

_{(resp. A-,),}

we have to show

The first half is obtained from the

_{following elementary}

calculations:

Differentiating

the both sides of the above obtained

_equation

_by

_z, we

have

/ ’Y B

This

_completes

the

_proof

of the

_proposition.

D

If P =

2Q

holds,

then it is

easy to see _agrees with

ether 2

7

(i

= 1 _or

2)

our

₊

w1,

where A = ₊

ZW2-

We _can

2 2 2 2 7

choose the correct one

by

computing

the p

function at these values.

Since the

_generators

of

_E(k)

_always

arise from the

_points

in or

E(-m) Q),

it is

_enough

to

_{compute $}

or for the

Q-rational points.

3.

_Examples

In this

_section,

we

apply

Theorem 2 to certain

specific imaginary

qua-dratic fields.

Among

61

_imaginary

_quadratic

₍₁

m

100,

m is

square-free),

the non-existence of an

elliptic

curve

having good

reduction is

proved

for the

_following

44 values of m

by

Setzer and Stroeker’s Theorem in the introduction and Setzer’s criterion

_([11,

Thereom

_4(a)]):

m = 1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 21, 22, 30, 33, 34, 39, 41, 42, 43, 46

47, 55, 57, 58, 62, 66, 67, 69, 70, 71, 73, 77, 78, 9, 82, 85, 86, 93, 94, 95, 97.

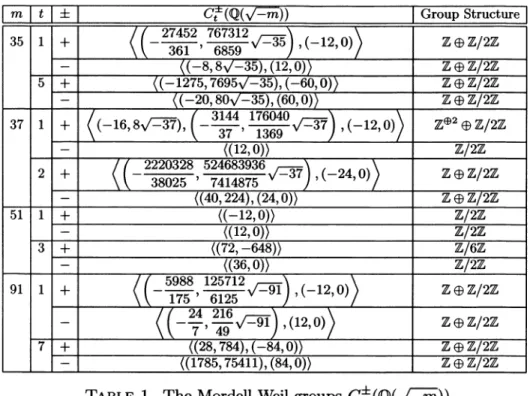
TABLE 1. The Mordell-Weil _groups

_C’

The bold-faced numbers

_corresponds

to the fields whose class numbers are

prime

to six.

In our

forthcoming

_paper

[8],

we show the non-existence for m = 74

by

a different method.

On the other

_hand,

the

_only

known

_examples

of

_elliptic

curves

_having

good

reduction

_everywhere

defined over an

imaginary quadratic

field of

small discriminant are the

_eight

curves

(up

to

_isomorphism)

defined over

~( -65)

found

_by

Setzer

_[11].

Among

the fifteen fields which

_remain,

the

_following

four fields

_satisfy

the

_assumptions

on the class number in Theorem 2 and

they

also

satisfy

the

third

_assumption

of the theorem on the existence of the rational

_integer

r.

Note that r is a rational

integer

that

necessarily

divides the discriminant

of the

_{quadratic field,}

since r satisfies

c2

= (r)

in 1~.

Although

there _may be

more than one r for one

field,

as for the Mordell-Weil _group

_computation,

and r2 be the r’s. In each case, m =

rlr2 holds. Then we have the

following

isomorphism

over

Q:

Similarly

we can show

Generally speaking,

the smaller r we

choose,

the faster the

_computation

is.

The Mordell-Weil _groups and the

_integral

_points

of the curves

Ct (k)

(t

=

1 or

r)

are

_compiled

in Table 1 and Table

_2,

_{respectively.}

By

Theorem

_2,

we have the candidates of the

_j-invariants

of

_elliptic

curves

having good

reduction

everywhere

as follows.

An

_algorithm

for

_computing

all the

_elliptic

curves

having good

reduction

everywhere

for a

_{given j-invariant}

is

_presented

in

[7].

_{Alternatively,}

we _may use the criterion of Comalada and Nart in

[2].

Their criterion tells us which

algebraic

integers

appear as the

_j-invariants

of

_elliptic

curves

having good

reduction

_{everywhere. By}

either of these

_methods,

it is shown that there is no

elliptic

curve

_{having good}

reduction

_{everywhere having}

the

_j-invariants

in the above list. We thus obtain Theorem 1.

References

[1] H. COHEN, A course in computational algebraic number theory. Springer-Verlag, Berlin,

1993.

[2] S. _COMALADA, E. NART, Modular invariant and good reduction _of elliptic curves. Math. Ann. 293 _(1992), no. _2, 331-342.

[3] J. E. CREMONA, P. SERF, Computing the rank of elliptic curves over real quadratic number

fields of class number 1. Math. _Comp. 68 _(1999), no. _227, 1187-1200.

[4] M. DABERKOW, C. FIEKER, J. KLUNERS, M. POHST, K. ROEGNER, M. _SCHÖRNIG, K. WILDANGER, KANT V4. J. Symbolic Comput. 24 _(1997), no. _{3-4, 267-283,}

Compu-tational algebra and number theory (London, 1993).

[5] S. DAVID, Minorations de hauteurs sur les variétés abéliennes. Bull. Soc. Math. France 121

(1993), no. _4, 509-544.

[6] C. HOLLINGER, P. SERF, SIMATH-a computer algebra system. Computational number

theory (Debrecen, 1989), de Gruyter, Berlin, 1991, pp. 331-342.

[7] M. KIDA, Computing elliptic curves _{having good} reduction everywhere over _{quadratic fields.} Preprint (1998).

[8] M. KIDA, Non-existence of elliptic curves _{having good} reduction _everywhere over certain quadratic fields. Preprint (1999).

[9] M. KIDA, Reduction _of elliptic curves over certain real _{quadratic fields.} Math. Comp. 68

(1999), no. _228, 1679-1685.

[10] M. _KIDA, TECC manual version 2.2. The University of Electro-Communications, November

1999.

[11] B. SETZER, Elliptic curves over _{complex quadratic fields.} Pacific J. Math. 74 _(1978), no. _1,

235-250.

[12] J.H. SILVERMAN, Computing heights on _elliptic curves. Math. Comp. 51 _(1988), no. _183,

339-358.

[13] J.H. SILVERMAN, Advanced topics in the arithmetic of elliptic curves. _{Springer-Verlag,} New

York, 1994.

[14] N.P. SMART, N.M. STEPHENS, Integral points on _elliptic curves over number _fields. Math.

Proc. Cambridge Philos. Soc. 122 _(1997), no. 1, 9-16.

[15] N.P. SMART, The algorithmic resolution of Diophantine equations. Cambridge University

Press, Cambridge, 1998.

[16] R.J. STROEKER, Reduction of elliptic curves over _{imaginary quadratic} number _fields. Pacific

J. Math. 108 _(1983), no. _2, 451-463.

[17] L.C. WASHINGTON, Class numbers _of the simplest cubic _fields. Math. _Comp. 48 _(1987),

no. _177, 371-384.

[18] H.G. ZIMMER, Basic algorithms for elliptic curves. Number _theory (Eger, 1996), de _Gruyter,

Berlin, 1998, pp. 541-595. Masanari KIDA

Department of Mathematics

The University of Electro-Communications

Chofu, Tokyo 182-8585

Japan