Réduction du bruit quantique de la lumière par une cavité bistable

HAL Id: tel-00011884

https://tel.archives-ouvertes.fr/tel-00011884

Submitted on 9 Mar 2006

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

To cite this version:

Laurent Hilico. Réduction du bruit quantique de la lumière par une cavité bistable. Physique Atom-ique [physics.atom-ph]. Université Pierre et Marie Curie - Paris VI, 1992. Français. �tel-00011884�

NORMALE

SUPERIEURE

Thèse

de doctorat de

l’Université Pierre

et

Marie

Curie. Paris VI

Spécialité : Physique Quantique

présentée

par

Laurent HILICO

Pour obtenir le titre de Docteur de l’université Pierre et Marie Curie

Sujet :

REDUCTION

DU

BRUIT

_QUANTIQUE

DE LA

LUMIERE

PAR

UNE

CAVITE

BISTABLE

Soutenue le 22

_Septembre

1992 devant le

_{jury composé}

de :

M. S. HAROCHE

_(Président)

M. A. DUCASSE Mme E. GIACOBINO M. P. GRANGIER M. L. LUGIATO M. C. SALOMON

Normale

_Supérieure

et de l’Université Pierre et Marie Curie. Je remercie

_Jacques

Dupont-Roc,

directeur du

laboratoire,

Bernard

_Cagnac

et Gilbert

_Grynberg

de m’avoir

accueilli à Jussieu.

Elisabeth Giacobino et Claude Fabre ont

_dirigé

ce travail. Je tiens à les remercier

pour le climat de

liberté,

de confiance et

_{d’intelligence qui règne}

dans le _groupe

d’optique quantique qu’ils dirigent,

et _{pour l’aide} efficace

_qu’ils

m’ont

_apportée

au

cours de ces trois années.

Je tiens aussi à remercier les autres membres _{du groupe :}

_{Serge Reynaud,}

Jean-Michel

_Courty

et Antoine Heidmann _{pour leurs} aides

_théoriques

et

_{expérimentales,}

ainsi que

Thierry

Debuisschert,

Jerome

Mertz,

Christian

_Richy

et Astrid Lambrecht.

Un

_grand

merci aux membres des autres _{groupes du}

_laboratoire,

et tout

particulièrement

à

_François

Biraben,

Michel Pinard et

_Philippe

Verkerk _{pour leur} aide

et leur

_{disponibilité}

lors de la mise en

_place

de

l’expérience,

à

Delphine

Grison et

Christophe

Salomon _{pour leur connaissance du}

_{piège magnéto-optique,}

et

_{à l’équipe}

de

Jean-Louis Oudar au CNET

_qui

m’a accueilli

_quelques

semaines.

Je remercie

_{également Serge}

_Haroche,

André

Ducasse,

Philippe Grangier, Luigi

Lugiato

et

_Christophe

Salomon

_qui

ont

_accepté

de

_participer

au

jury.

Enfin,

je

tiens à remercier le

_{personnel technique :}

Francis

_Tréhin,

_{Guy Flory,}

Jean

_Quilbeuf,

Marc

Thommé,

Bernard

_Rodriguez,

Ali

_Mezia,

Bernard

_Clergeaud,

Gérard Brener et Jean-Claude Bernard

_qui

assurent la

_logistique

des

_{expériences.}

Je

remercie aussi chaleureusement les secrétaires Marie-Noëlle Ollivier et Blandine Moutiers

_auxquelles

la

_frappe

et les corrections de ce mémoire doivent tout, ainsi que Mlle Gazan et M. Manceau

_qui

en ont assuré le

_tirage

et la reliure.

Ma bourse de thèse a été

_payée

_{par la DRET} et l’Ecole

_{polytechnique.}

Je remercie

ces deux institutions ainsi que Mme Guibert

_qui

a

géré

mon dossier. Ce travail de

Introduction...1

I. Bruit

_{quantique ...5}

1 Les fluctuations de la lumière ...5

a. Introduction ...5

b.

_{L’origine quantique...5}

c. Modèle de faisceau lumineux...6

d. Détection des fluctuations de la lumière...7

2 Cadre

_{théorique ...}

10

a. Position du

_problème...

10

b. Contrainte sur les commutateurs ... 11

c. Une solution : théorie entrée-sortie et linéarisation ... 11

d.

_Exemples

... 12

e. Relation entre la

_compression

des fluctuations et la stabilité du

système...

17

f. Lien avec les autres méthodes de calcul... 17

g. Conclusion ... 19

3

_Appendice

A : Notations ... 20

a. Vecteurs et matrices

_{d’opérateurs...}

20

b. Transformation de Fourier... 21

4

_Appendice

B :

_"champ

_{quasi-monomode" ... 21}

II. De l’effet Kerr idéal aux atomes ... 23

1 Introduction ... 23

2 Modèle de la cavité à effet Kerr ... 23

a. Les

_équations

d’évolution du

_champ

... 24

b. Discussion des _spectres de bruit... 27

c. Conditions sur la non-linéarité et

_{l’absorption}

... 30

d. Evaluation des

_{possibilités expérimentales}

... 31

3 Les limitations de ce modèle... 38

a. Effets des modes transverses... 39

b. Effet d’un _temps de

_réponse

de la non-linéarité... 40

c.

_Appendice

C-

_Couplage

entre modes

_gaussiens

... 42

4 Utilisation d’une non linéarité d’ordre 2 : l’OPO

_{dégénéré ... 46}

a.

_{L’oscillateur paramétrique}

_{optique dégénéré}

... 46

b. Etat stationnaire et

_analyse

linéaire de stabilité ... 47

c. Transformation des fluctuations ... 51

1 Introduction ... 59

2 Les

_{hypothèses du}

modèle ... 60

a.

_Hypothèses

sur les atomes et les

_champs

... 60

b.

_{Couplage atomes-champ ...60}

3 Relation entrée-sortie _pour le milieu

_{atomique... 60}

a.

_Equation

de

_{Heisenberg ... 61}

- b.

Réponse

linéaire... 63

c. Transformation

_canonique

des fluctuations du

_champ...65

d. Conservation des relations de commutation...65

4 Fluctuations

_quantiques

dans la bistabilité

_optique...67

a. Point de vue entrée-sortie ... 67

b. Article "Linear

_input-output

method for _quantum fluctuations in

_optical

bistability with

two level atoms" ... 68

c. Solutions stationnaires...96

d. Stabilité des solutions stationnaires ...99

e.

_Comparaison

avec d’autres théories standard... 101

5 Théorie

_générale

des fluctuations

_quantiques

dans la bistabilité

_optique...

102

a. Présentation de l’article ... 102

b.

_{Tiré à part de l’article ...}

104

c. Conclusions... 110

6 Ordres de

_grandeur...

110

a. Liens entre les

_{paramètres théoriques}

et

_{l’expérience ...}

110

b.

_Absorption

et non-linéarité... 111

c. Evaluation des

_paramètres

dans le cas du césium ... 112

d. Conclusion... 113

IV.

_Expérience

avec une cavité

_optique

contenant des atomes froids... 115

1

_Pourquoi

le césium dans un

_piège

_{magnéto-optique ?}

... 115

a. Les _avantages du césium froid... 115

b. Le césium est-il un atome à deux niveaux ? ... 116

2

_{Montage expérimental ...}

117

a.

_Principe

du

_{piège magnéto-optique}

... 117

b. Le _montage

_{expérimental,}

solutions

_techniques

retenues... 119

c.

_{Caractéristiques}

du

_piège...

126

3 Le

laser à atomes froids ...

128

c.

Conjugaison

de

_phase

dans les atomes froids... 133

d. Conclusions ... 134

4 Bistabilité

_optique

avec des atomes froids ... 134

a. Introduction ...134

b. La cavité

_optique

bistable ... 136

c. Bistabilité ... 138

d.

_Comparaison

avec la théorie des atomes à deux niveaux ... 150

5 Conclusion ... 155

V. Etude

_{expérimentale}

des fluctuations

_quantiques

dans la bistabilité

_optique...

157

1 Introduction ... 157

2 La détection des fluctuations de la lumière...158

a. Difficultés de la détection du bruit d’intensité de la lumière ... 158

b. Les autres sources de bruit

électronique ... 159

c. Utilisation d’un

_{amplificateur}

tension-tension... 160

d.

_{Amplificateur}

courant-tension... 162

e. Résultats... 165

f. Conclusions ... 168

3 Mesure du bruit d’intensité de la lumière réfléchie _{par la} cavité bistable ...169

a. Calibration du bruit

_quantique

standard...169

b. Résultats

_{expérimentaux préliminaires}

...171

c. Conclusions... 175

Conclusion...177

Les mesures en

_optique

sont

_parmi

les

_{plus précises}

_qu’on

sache réaliser. En

effet,

grâce

aux

lasers,

il est

_possible

d’obtenir des faisceaux lumineux continus d’intensité très stable et _ayant une

grande

longueur

de

_cohérence,

_permettant d’effectuer des mesures très

_sensibles,

_par

_absorption,

ou _par interférométrie.

_Cependant,

ces mesures ne sont

_jamais

_exemptes de bruit. Ce bruit ne

provient

pas seulement des

dispositifs électroniques

utilisés pour

amplifier

les

signaux

détectés,

mais

_provient

de la lumière elle-même.

_{L’électrodynamique}

_quantique

montre _{que le}

_champ

électrique

est décrit _par deux

_{opérateurs correspondant}

aux deux _composantes de

_quadrature

du

champ

électromagnétique

classique.

Ces deux

_opérateurs

ne commutent _pas et satisfont une

inégalité

de

_{Heisenberg :}

le

_produit

de leurs variances est

_supérieur

à une limite finie non nulle.

La

_conséquence

de la nature

_quantique

du

_{champ électromagnétique}

est

_qu’il

n’est _pas

_possible

de réaliser un état du

_champ

_{tel que le}

_{champ électrique}

soit

_parfaitement

_déterminé,

tout comme il n’est _pas

_possible

de connaître simultanément la

_position

et

_{l’impulsion}

d’une

_particule

matérielle. En

_revanche,

la

_souplesse

de la

_mécanique

_quantique

_permet

_d’imaginer

et de réaliser des états du

champ

où l’une des deux

_quadratures

est déterminée avec une

précision

meilleure _{que la limite}

quantique

standard,

et l’autre avec une

_précision

moins bonne. De tels états sont

_appelés

états

comprimés

du

_champ.

Les réferences suivantes sont des articles de revue consacrés aux

problèmes

de la réduction du bruit

_quantique

de la lumière

_{[Yamamoto 90]}

_{[Reynaud 92]}

_{[Houches 90,}

Kimble].

Le bruit de la lumière _peut

_{s’interpréter}

de

_plusieurs

manières. La

_première

utilise une

description corpusculaire

de la

lumière,

en termes de

_photons,

et attribue

_l’origine

du bruit d’intensité standard d’un faisceau lumineux à l’arrivée des

_photons

sur le

photodétecteur

à des instants aléatoires. La réduction du bruit d’intensité

_{s’interprète}

alors en termes de

_{réarrangement}

temporel

des

_photons.

Cette

_{interprétation}

a donné son nom au bruit d’intensité d’un faisceau lumineux : le bruit de

_grenaille

ou shot noise. Une autre

_{interprétation}

fructueuse du bruit de la

lumière consiste à la _{décrire par} un

_{champ classique}

_fluctuant,

_y

_compris

dans le cas où l’intensité

moyenne du

champ

est nulle

_{(fluctuations}

du

vide).

Les états

_comprimés

_peuvent avoir des

_{applications :}

_par

_exemple

un

_{champ comprimé}

en intensité _permet de mesurer des

_{signaux d’absorption plus}

faibles

_qu’avec

un

_champ

au shot

_noise,

et _{permet d’améliorer} le _rapport

_signal

sur bruit de la mesure. Ce

_procédé

est intéressant

_lorsqu’il

n’est pas

possible d’augmenter

ce _rapport

_signal

sur bruit en _augmentant l’intensité du faisceau ou le _temps de mesure, comme dans le cas de milieux très

dilués,

ou de milieux _ayant un seuil de

dommage

très bas. Un

_{champ comprimé}

en

_phase

trouvera des

_applications

dans les mesures

interférométriques

de très

_grande

_{sensibilité,}

comme _par

_exemple

la détection des ondes

gravitationnelles.

De nombreuses

_propositions

et

_depuis

_peu

_quelques

_{réalisations existent pour}

_générer

des

qui génèrent

un

champ

électromagnétique

dont les fluctuations d’une des _composantes de

quadrature

sont

_comprimées.

Par

_exemple,

il est

_possible

en alimentant une diode

_laser

de

_grand

rendement

_quantique

avec un courant _{très peu fluctuant filtré par} une résistance refroidie à la

température

de l’hélium

_liquide,

d’obtenir un faisceau laser dont les fluctuations d’intensité sont

comprimées

de

_près

de 90% sur une très

large

bande de

fréquence.

Il est aussi

_possible

de créer à

l’aide d’un oscillateur

_{paramétrique optique}

deux faisceaux laser

_jumeaux

dont les corrélations d’intensité sont _presque dix fois _{meilleures que la} limite

_quantique

standard. Ces corrélations ont

été utilisées _pour

_produire,

_par asservissement

_{électronique}

de l’intensité d’un des faisceaux

jumeaux

sur

_l’autre,

un faisceau dont le bruit d’intensité est réduit de 25% autour d’une

_fréquence

d’analyse

donnée.

La seconde idée consiste à transformer le

_champ

laser issu d’un laser

traditionnel,

dont le

bruit

_correspond

idéalement au bruit

quantique

standard,

en un

champ comprimé

à l’aide d’un

dispositif passif,

sans _pertes ni

gain

_{pour le}

champ.

Nous montrons au

chapitre

II,

_que l’utilisation d’un cavité non linéaire et bistable contenant un milieu Kerr

(c’est

à dire un milieu dont l’indice de

réfraction est

_{proportionnel}

à l’intensité

_qui

le

traverse)

est un

_{système passif susceptible}

de

comprimer

les fluctuations

_{lorsqu’elle}

est utilisée au

_voisinage

d’un

_point

tournant de la bistabilité. L’utilisation d’une non-linéarité non résonnante _permet

_{d’envisager}

des

applications

_{pour des} faisceaux d’intensité et de

_longueur

d’onde variées.

_Cependant,

l’étude des milieux non linéaires

disponibles

à ce

_jour

montre _{que les ordres de}

_grandeur

des non-linéarités d’ordre trois ne sont _pas

favorables à la réalisation

_{expérimentale}

d’un bistable réducteur de bruit. Nous sommes donc amenés à

_envisager

d’autres _types de non-linéarités

_plus

_fortes,

_provenant de mécanismes

physiques

variés,

qui

ne sont

_plus

_idéales,

et

_qui

_peuvent introduire du bruit sur le faisceau lumineux avec

_lequel

elles

_{interagissent.}

Nous montrons _{que la} non-linéarité la

_plus

_prometteuse est celle d’une assemblée d’atomes à deux niveaux immobiles excités au

voisinage

de résonance.

Le

_chapitre

III est consacré à l’étude détaillée des

_propriétés

de bruit de la lumière réfléchie

par une cavité

_optique

contenant des atomes à deux niveaux. Cette étude utilise un formalisme

entrée-sortie

_général

introduit au

chapitre

I,

_permettant de calculer la modification des fluctuations

du

_champ

_{par la}

_cavité,

et de _{tenir compte du bruit propre}

_apporté

_{par le} milieu non linéaire. Plus

précisémént,

nous montrons _{que les} fluctuations du

_champ

_rayonné

par les atomes _peuvent être

séparées

en deux contributions : un terme dû à la

_réponse

des atomes aux fluctuations du

_champ

incident,

et un terme lié à l’émission

_spontanée.

Nous montrons _{que, même} si la non-linéarité d’atomes à deux niveaux est différente de celle d’un effet _{Kerr pur}

(elle

est

_{résonnante),}

elle est un

excellent candidat _{pour la réduction du} bruit

_quantique

de la lumière en

_particulier

si on utilise une

cavité dont la

_largeur

en

fréquence

est

_grande

devant celle de la transition

_atomique.

Une telle non-linéarité a

_déja

été utilisée dans

_{plusieurs expériences}

en

_plaçant

des cavités

optiques

autour de

_{jets atomiques.}

Elle a

_permis

l’observation de réduction de

bruit,

mais cette

réduction reste inférieure aux

_prévisions

_théoriques

en

_particulier

à cause de l’effet

_Doppler

et de la

durée finie de l’intéraction entre les atomes et le _rayonnement

_(temps

de

_transit).

L’invention du

atomiques

a relancé l’intérêt des non-linéarités

_{atomiques quasi-résonnantes.}

C’est dans ce

contexte _que nous avons décidé la construction d’un

_{piège magnéto-optique}

contenant du césium autour

_duquel

nous avons

_placé

un résonateur

_optique

de finesse environ 50. L’étude de la

réduction du bruit de la lumière dans la bistabilité

_optique

_passe tout _{d’abord par} l’étude de la

bistabilité

_optique.

L’étude de notre résonateur non linéaire nous a

_permis

dans un

_premier

_temps d’observer la

_première

oscillation d’un laser à atomes froids

_qui

_pourrait

se révéler très intéressant

pour

l’optique quantique.

Par la suite nous avons étudié la bistabilité

_optique

_{pour des écarts à} résonance du

_champ

très

_variés,

et avons aussi observé les instabilités

_prévues

_{par la} théorie de la bistabilité

_optique

avec des atomes à deux niveaux. Nous avons déduit des courbes

expérimentales

les

_{caractéristiques}

de notre cavité non linéaire. La

_comparaison

avec le modèle

théorique

montre

que les

régimes qui

nous sont accessibles sont favorables à l’observation de la réduction de bruit

quantique.

Le

_chapitre

V détaille les méthodes _permettant de mesurer le bruit

quantique

de la lumière sur des intensités lumineuses faibles. _{Nous y proposons deux}

_systèmes

de

_{photodétection,}

dont l’un

très

_performant.

Nous

_présentons

ensuite les résultats

_{préliminaires}

_que nous avons obtenu et

1

Les fluctuations de la

lumière

a. Introduction

Le but de ce

chapitre

est de

_rappeler

brièvement

_l’origine

des fluctuations

_quantiques

de la lumière et

_d’indiquer

comment elles

_apparaissent

dans les diverses mesures couramment effectuées

en

_optique,

détection

d’intensité,

mesures

homodynes

ou

_{hétérodynes}

_(§1)

et nous

_précisons

à

cette occasion les notations utilisées dans ce mémoire.

Au

§2,

nous

_présentons

le cadre

_général

du formalisme _que nous

_employons,

fondé sur une méthode "d’entrée-sortie". A titre d’introduction aux

_{techniques qui}

_permettent de

manipuler

le

bruit

_quantique

nous donnons

_{quelques exemples}

de

systèmes

linéaires et non linéaires

simples,

et

nous établissons certaines

_{propriétés générales}

vérifiées _par ces

_systèmes.

b.

_{L’origine quantique}

Le

_champ

_{électromagnétique}

_peut être

_décomposé

en

_modes,

_{correspondant}

à des ondes

planes progressives

caractérisées _par un vecteur d’onde

k,

et une

_polarisation

03B5.

Pour le

_champ

électromagnétique

libre,

ces modes évoluent comme des oscillateurs

_harmoniques

_{indépendants.}

En

_{mécanique quantique,}

on _peut associer à un mode des

_opérateurs

de création et d’annihilation

hermitiques conjugués

a+et a vérifiant la relation de commutation :

L’opérateur champ électrique s’exprime

alors comme une somme sur tous les modes d’une

combinaison des

_opérateurs

a et a+ associés à ces modes.

L’amplitude

du

champ

électrique

correspondant

à un mode donné _peut s’écrire :

avec

Le commutateur de

:E(t)

et de

E

+

(t)

vaut :

Le

_champ

_peut aussi se

_décomposer

sous la forme :

avec

Les

_{opérateurs E}

₁

_(t)

et

E

2

(t)

vérifient :

E

Puisque

les deux _composantes de

_quadrature

_E

₁

et

_E

₂

du

_champ

ne commutent _{pas, les}

dispersions

sur

E

1

et

_E

₂

_vérifient,

_pour tout état du _rayonnement, une

_inégalité

de

_{Heisenberg :}

où

L’incertitude sur la valeur des _composantes de

_quadrature

du

_champ

constitue le bruit

_quantique

de la

_lumière,

_qui

limite la

_précision

des mesures en

optique.

Si le

_{champ électromagnétique}

est dans l’état

vide,

la _{valeur moyenne} du

_champ

_électrique

est

nulle,

mais les variances

_{de E}

₁

_et

_E

_{2 ne} le sont _pas et vérifient :

Ces fluctuations sont

_appelées

fluctuations du vide.

Si le

_champ

est

_représenté

_par un état cohérent

_(c’est

à dire un état propre de

_{l’opérateur}

_a)

[Glauber

63],

les variances de

_E

₁

et

_E

₂

_vérifient

cette même relation.

c. Modèle de faisceau lumineux

L’état du

_champ

_{électromagnétique}

_peut être décrit _par un vecteur _{appartenant à}

_l’espace

vectoriel obtenu _par

_produit

tensoriel des _espaces vectoriels

_{correspondant}

à

_chaque

mode du

champ. Cependant,

en

_{optique quantique,}

on s’intéresse à des faisceaux

_lumineux,

le

_plus

souvent

issus de

lasers,

qu’on

peut décrire dans une

_{approximation}

_{quasi-monomode :}

on ne considère

qu’une

seule

_polarisation

et

_qu’une

seule direction de

_propagation

où les modes sont caractérisés

par leur seule

fréquence.

On note s la section du faisceau.

Sous ces

_hypothèses,

le

_{champ électrique}

_peut être

écrit,

comme les sommes de ses _composantes

de

_{fréquences positives}

et de

_{fréquences négatives (Appendice}

B

_équation

_{(I.84)) :}

avec

Le coefficient

_E

_03C9

_dépend

lentement de la

_fréquence

comme

03C9

1/2

et vaut :

Le

_champ

considéré étant

_{quasi-monomode}

de

_fréquence

03C9L, seul le mode de

_fréquence

_03C9L est

occupé,

les modes voisins étant dans l’état vide ou très peu

occupés.

La valeur moyenne du

champ

E est

_{monochromatique :}

En

_optique,

la

_fréquence

_03C9L est très élevée

_(~10

₁₅

Hz),

et on s’intéresse à des fluctuations

de

_fréquence

basse

_(~

10

9

Hz),

donc faisant intervenir des modes de

_fréquence

_proches

de 03C9L : on

par :

Les

_champs

_E(t)

et

E

+

(t)

s’écrivent

alors,

sous forme de transformées de Fourier :

E(03C9)

et

E

+

(03C9)

vérifient :

et les relations de commutation :

Notons _{que par suite} du _{passage dans} le référentiel tournant, les

fréquences

03C9 et 03C9’ dans les

équations

(I-15

à

18)

sont maintenant les écarts à la

_fréquence

_{moyenne 03C9}L, c’est à dire les

fréquences d’analyse qui

nous intéresserons _{pour les} fluctuations.

On a bien

_entendu,

si

|0>

_représente

le vide de _{rayonnement :}

La valeur moyenne du

champ

E est maintenant

_{indépendante}

du _temps. La normalisation introduite

par

l’équation

(I.14)

est choisie _{par commodité pour} ce

_chapitre.

Grâce à

_elle,

le module carré de la valeur moyenne du

_{champ représente}

le flux

_numérique

de

_photons

du faisceau lumineux décrit.

d. Détection des fluctuations de la lumière

La mesure des fluctuations de la lumière s’effectue à l’aide de

_{photodétecteurs (photodiodes}

ou

_{photomultiplicateurs), qui}

délivrent un

_signal

_I(t)

_{proportionnel}

à l’intensité lumineuse _reçue

[Cohen-Tannoudji

88,Complément

A-II].

Compte

tenu du très

_grand

flux de

_photons

dans un faisceau lumineux

intense,

ses fluctuations

sont

_toujours

faibles en valeur relative. On considerera donc que les fluctuations 03B4E du

_champ

E

sont

_petites

devant sa valeur moyenne, ce

_qui

_permettra d’utiliser des

_{approximations}

linéaires dans les calculs sur ces fluctuations. Les fluctuations de

E(t)

sont définies _{par :}

Dans

_{l’approximation}

_linéaire,

les fluctuations d’intensité sont _{données par :}

i. Bruit d’intensité

Il est

_{possible d’analyser expérimentalement}

les fluctuations de l’intensité à l’aide d’un

_analyseur

de _spectre. Ces fluctuations sont _{alors caractérisées par leur densité}

_spectrale

normalisée

_S

_I

_(03C9).

où

_03B4I(03C9)

est la transformée de Fourier de

03B4I(t).

Nous allons montrer _que

_{l’expression}

de

_S

_I

_(03C9)

fait

intervenir,

outre les valeurs _moyennes des

_champs,

_{quatre fonctions} de corrélation de 03B4E et

03B4E

+

.

Afin de

_simplifier

les

formules,

on introduit des notations

matricielles,

définies dans

_{l’appendice}

A de ce

chapitre.

On _peut alors

exprimer S

I

(03C9)

sous la

_{forme :}

où :

soit encore :

La matrice V est

_appelée

matrice des corrélations du

_{champ. Remarquons}

_que ces fonctions de corrélation ne sont définies ni dans l’ordre

_normal,

ni

_antinormal,

ni

_{antisymétrique}

_pour les

opérateurs

03B4E et

03B4E

+

.

_Compte

tenu des

_propriétés

des transformées de Fourier

_(appendice

A),

la

matrice V a la forme

_{générale :}

où

_{A, B, C}

et D sont _quatre fonctions réelles.

Il _{faut remarquer que}

_S

_I

_(03C9)

est invariant dans un

déphasage

du

_champ

donc par

_propagation,

alors

que ni la matrice V ni la valeur moyenne du

champ

ne le sont.

ii. Bruit sur une

_composante

de

_quadrature

_{quelconque :}

mesure

_hétérodyne

La méthode de détection

_précédente

ne _permet de mesurer _{que le} bruit d’intensité sur le faisceau

détecté. On ne _peut alors remonter

_qu’à

une combinaison

_{particulière}

des fonctions de corrélation

du

_champ.

Il est

_{cependant possible}

d’obtenir d’autres informations sur la matrice

_V

_M

des corrélations du

_champ

à mesurer, en s’aidant d’un faisceau

_plus

intense,

de même

_fréquence

_03C9L

que celle du faisceau à mesurer : un oscillateur local.

Pour

_cela,

on

_mélange

le faisceau à mesurer

_E

_M

à l’oscillateur local

_E

_L

sur une lame

séparatrice

50

%,

et on mesure le bruit sur la différence des intensités des faisceaux résultants

_E

₁

Figure

1.1

Les _composantes de

_{fréquence positive}

des

_champs

_E

₁

et

_E

₂

valent :

On en déduit aisément les intensités

_I

₁

et

_I

₂

des

_champs

_E

₁

et

E

2

Dans

_{l’approximation}

linéaire et en utilisant le fait _que l’oscillateur local est

_{beaucoup plus}

intense

que le faisceau à mesurer, les fluctuations de la différence des intensités

_I

₁

et

_I

₂

a _pour

expression :

Cette formule est très semblable à celle donnant les fluctuations d’intensité d’un faisceau lumineux

(I.22).

Dans ce

_premier

cas les fluctuations de l’intensité _peuvent être vues comme le

mélange

hétérodyne

du

_champ

_moyen et de ses fluctuations. Dans le cas

_présent,

le

_signal

de bruit

_(I.29)

correspond

au

_mélange

hétérodyne

du

_champ

_{moyen de} l’oscillateur local et des fluctuations du

champ

à mesurer. Il

_{dépend explicitement}

de la

_phase

relative de l’oscillateur local et du faisceau à

mesurer au niveau de la lame

_{séparatrice.}

La mesure de la densité

spectrale

de bruit de ce

_signal

donne accès au bruit sur la _composante de

_quadrature

03B8 noté

S

03B8

(03C9)

et _{défini par :}

où

La _composante de

_quadrature

03B8 est

_{l’opérateur}

iii. Le bruit

_quantique

standard ou shot noise

Le bruit

_quantique

standard ou shot noise est le bruit d’un faisceau lumineux monomode décrit par

un état cohérent :

_plus

_{précisément,}

l’état du

_champ

est un état cohérent dans le mode de

fréquence

03C9

L et dans l’état _{vide pour les} autres modes. En utilisant les relations de commutation

_(I.18),

on obtient pour un état

cohérent,

et donc aussi _pour l’état vide :

La matrice

V(03C9)

ne

_dépend

_{pas de la}

_{fréquence :}

le shot noise est un bruit blanc. Le bruit ne

dépend

pas non

_plus

de la _composante de

_quadrature

03B8.

Puisque

la densité

_spectrale

normalisée vaut

_1,

la

_puissance

de bruit du shot noise est

proportionnelle

à l’intensité du faisceau détecté

_(1.23).

iv.

_{Champ comprimé}

et bruit

_optimum

Un

_champ

est dit

_comprimé

ou

_"squeezé"

si une de ses _composantes de

quadrature

possède

des fluctuations dont une des _composantes de

fréquence

a un bruit inférieur au bruit

_quantique

standard,

c’est à dire s’il existe 03B8 et 03C9 tels _que

_(03C9)

_03B8

_S

< 1. Pour un état

comprimé,

on _peut

parler

du bruit

_{optimum S}

_opt

défini _{par :}

En utilisant la forme

_générale

de la matrice des corrélations

_(I.27),

on obtient :

Ce bruit minimum _peut être mesuré _{par la} détection

_hétérodyne

décrite

_plus

haut,

en faisant varier 03B8 _{donc la}

_phase

_{relative du}

_champ

_à mesurer et de l’oscillateur local.

2

Cadre

_théorique

Dans ce

_paragraphe,

on s’intéresse aux méthodes

_possibles

de calcul des

_propriétés

de bruit d’un faisceau lumineux. Dans la mesure où le faisceau lumineux issu d’un laser continu

correspond

le

_plus

souvent à un état

_proche

d’un état

cohérent,

on _peut se _{poser le}

problème

de la transformation d’un état cohérent en état

_comprimé.

Il est donc

_important

de savoir comment se transforment les fonctions de corrélation d’un

_champ

lors d’une interaction _pour savoir si cette interaction est

_susceptible

de

_comprimer

les fluctuations du

_champ.

a. Position du

_problème

Une fonction de corrélation telle _{que les composantes} de la matrice

_V

_03BB

_,

est une valeur

moyenne d’un

produit

d’opérateurs pris

à deux instants différents

_(ou

_pris

_{pour deux}

_fréquences)

qu’il

nous faudra calculer à

_partir

de

_{l’équation}

d’évolution à un _temps de la

_{mécanique quantique}

(l’équation

de

_{Schrödinger)}

et des "conditions initiales" sur les fonctions de

corrélation,

données

par les relations de commutation d’un

champ

libre

(I.18).

Par

ailleurs,

la

_plupart

des interactions

_qu’un

faisceau lumineux _peut subir ne sont _pas

aisément décrites _par un hamiltonien. Par

_exemple,

l’action d’une lame

_{partiellement}

absorbante n’est _pas hamiltonienne dans le sens où

_l’énergie

du faisceau transmis est inférieure à celle du faisceau incident. Les interactions résonnantes avec un milieu

atomique,

_gazeux ou solide font intervenir des variables

_dynamiques

autres _{que celles} du

_champ.

Ces variables sont

_susceptibles

très faibles. Il faut alors utiliser une cavité

_optique

contenant le milieu

actif,

afin de

_recycler

la

lumière et

_{d’augmenter}

les

_couplages

_par effet de surtension. On doit donc utiliser une

approche

permettant de calculer la modification des fonctions de corrélation d’un faisceau lumineux dans son interaction avec un

système complexe, composé

de

sous-systèmes plus

simples :

miroirs,

propagation,

milieux non linéaires...

b. Contrainte sur les commutateurs

La

_{mécanique quantique}

conduit à une

_{quantification}

du

_{champ électromagnétique}

où les relations de commutation du

_champ

libre sont données _{par les} formules

_(I.18).

Considérons un faisceau lumineux incident

_{(champ E}

in

)

sur un

système

S

quelconque

avec

lequel

il

_interagit

_pour se transformer en un faisceau

émergent (champ

E

out

).

(Figure

I.2)

Figure

12

Avant et

_après

_{l’interaction,}

la lumière se _propage librement : les deux

_champ

Ein et

E

out

sont

des

champs

libres. Ils vérifient donc nécessairement les mêmes relations de commutation : celles d’un

champ

libre.

Cette contrainte

_impose

donc une condition très forte sur les transformations d’un

champ

lors

d’une interaction : elles doivent

_préserver

les relations de commutation du

_champ

libre.

c. Une solution : théorie entrée-sortie et linéarisation

La méthode d’entrée-sortie consiste à

_décomposer

le

_{système complexe}

S avec

_lequel

le

champ

interagit

en

_{sous-systèmes}

_S

_j

_,

_{qui interagissent}

avec un ou

_{plusieurs champs.}

Elle repose sur les

_hypothèses

suivantes :

- Les fluctuations des

champs

intenses entrants ou sortants sont faibles devant leurs valeurs

moyennes. Cette

hypothèse justifiera

les linéarisations.

-

Chaque sous-système

du

_{système complexe}

_provoque une

petite

modification des fluctuations des

_{champs qui}

le traverse.

- La

dynamique

propre de

chaque sous-système,

ne

dépend

_pas des

caractéristiques

des fluctuations du

_champ

incident ou

_émergent

de ce

_{sous-système.}

Ces trois

_hypothèses

seront vérifiées dans les cas

_qui

seront traités dans les

_chapitres

II et III.

Cependant,

la troisième

_hypothèse

n’est _pas

_toujours

vérifiée : en

effet,

on _peut

imaginer

et réaliser

expérimentalement

des

cavités,

telles que la relaxation des atomes

_{(c’est-à-dire}

leur

_dynamique

propre)

soit contrôlée par la structure des modes de la cavité

_{[Houches 82],}

et _{par l’état du}

_champ

micro-onde dans la cavité

_[Courty

89 et

_89a].

On _peut

_cependant

étendre la théorie entrée-sortie

des fluctuations à ce cas

_{[Courty 90].}

Cette

_possibilité

est brièvement discutée à la fin du

_chapitre

III.

L’hypothèse d’indépendance

des

_{sous-systèmes}

_permet de considérer le ou les

_champs

sortants

d’un

_{sous-système}

comme des

_champs

_libres,

c’est-à-dire comme des

_champs

entrants _pour les

autres

_{sous-systèmes.}

Les

_hypothèses

de

_"petites

fluctuations" et de

_petites

modifications des fluctuations _permettent de

se limiter à une transformation linéaire des fluctuations par un

_{sous-système :}

si

[03B4E

(j)in

]

et

[03B4E

(j)out

]

sont

les

_champs

entrant sur le

_{sous-système}

_S

_j

_,

on écrira :

où

T

(j)

(03C9)

est une matrice

qui

décrit la modification des fluctuations _{par le}

sous-système j

et

F

(j)

(03C9)

les éventuelles fluctuations

_{qu’il ajoute.}

La transformation linéaire est écrite dans

_l’espace

de Fourier

(des

fréquences),

ce

_qui

_permet de

_prendre

en _compte les effets de retard. Une telle transformation de

_champs

entrant en

_champs

sortant doit bien sûr conserver les relations de commutation car les

_champs

E

(j)in

et

E

(j)out

sont libres. Cette transformation est

_appelée

transformation

_canonique

des

_champs.

La méthode d’entrée-sortie décrite _par des tranformations linéaires

_canoniques

conduit donc à un

système d’équations

linéaires dans le domaine des

_fréquences,

reliant les fluctuations du

champ

E

in

incident sur le

_système

S et celles du

_{champ émergent E}

out

à celles des différents

champs

entrant et sortant des

_{sous-systèmes}

_Sj,

E

(j)in

et

E

(j)out

.

Il suffit ensuite d’éliminer

algébriquement

les

_champs

intermédiaires

E

(j)

_pour obtenir une

expression

des fluctuations sortant du

_système

S en fonction des fluctuations entrantes et des fluctuations _{propres des}

_{sous-systèmes}

S

j

.

A ce

stade,

il ne faut pas oublier que nous ne sommes _{pas seulement intéressés par la} transformation des fluctuations du

_champ

incident,

mais aussi par la transformation de leurs fonctions de corrélation. Les fonctions de corrélation des

_champs

entrant sont des données du

problème.

La transformation donnée _{par la relation}

_(I.36)

ne _permettra de passer des fluctuations

aux corrélations de

E

(j)out

_{que si les fluctuations}

_ajoutées

F

(j)

sont

_{indépendantes}

des fluctuations de

E

(j)in

,

et _{que si les fonctions} de corrélation de

F

(j)

sont connues.

d.

_Exemples

Nous allons donner maintenant

_{explicitement}

les transformations

_{canoniques correspondant}

à

_quelques

interactions courantes _{telles que la}

_propagation

libre du

_faisceau,

ou l’action d’un miroir ou d’une lame

_{partiellement}

_{réfléchissante,}

_puis

nous résoudrons le

_{système d’équations}

obtenu dans le cas d’une cavité

_optique

contenant un milieu

_quelconque,

mais modélisable _par une

transformation

_canonique.

i.

_Propagation

libre

On considère ici la

_propagation

libre du faisceau lumineux sur une distance

l,

avec la célérité c. Le

Compte

tenu de la relation

(I.14)

définissant les

_champs

normalisés Ein et

_E

_out

_,

on déduit la transformation due à la

_propagation,

valable _{pour les}

_champs

_moyens comme _{pour les} fluctuations :

avec ~

=

03C9

L

l

/ c, où 03C9L est la

_fréquence

centrale du

_champ.

ii. Miroir ou lame

_{partiellement}

réfléchissante

Figure

I 3

Une lame est un

système

_comportant deux entrées et deux sorties

(les

deux faces de la

lame),

représenté

sur la

_figure

3 et _{modelisé par} un coefficient de transmission t et un coefficient de réflexion r

_supposés

réels _pour

_simplifier.

On note

_E

_A

et

_E

_B

les deux

_champs

entrants,

E

C

et

_E

_D

les deux

_champs

sortants. La transformation des

_champs

est donnée _{par :}

Le

_{signe -}

dans la deuxième

_équation

et la relation

+

r

2

t

2

= 1 assurent la conservation de

_l’énergie

transmise et réfléchie _par la lame. Les transformations

_canoniques

des fluctuations sont données

par :

Dans

_{l’hypothèse}

où le

_champ

E

A

a une valeur _moyenne non nulle et où le

_champ

E

B

est dans l’état

vide,

le

_premier

terme de ces

_équations

décrit la transformation des

fluctuations,

et le deuxième le

Il est élémentaire de vérifier _que les transformations de ces deux

_{premiers exemples}

conservent les

relations de

_commutation,

donc sont

_canoniques.

iii. Cas d’une cavité de

_grande

finesse

Figure

I 4 : Cavité _optique en anneau contenant un milieu non-linéaire

On _peut obtenir une forme très

générale

_{pour la} transformation des fluctuations _par une cavité

optique

en anneau de

_grande

finesse _ayant un ou

plusieurs

miroirs de

couplage

et contenant un

milieu non linéaire

_quelconque.

On va traiter le cas le

_{plus simple}

d’une cavité à un seul miroir de

couplage,

et d’un seul

_champ

incident. On note Ain le

_champ

entrant sur le

_système,

et

A

out

le

champ

sortant

_(figure

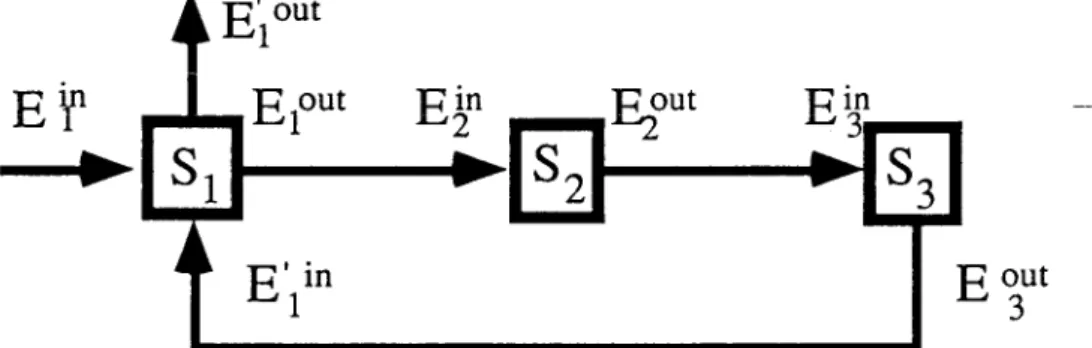
_(I-4)).

Cette cavité _peut être

_décomposée

en trois

sous-systèmes (figure

(I-5)) :

Figure

I 5 :

_{Décomposition}

de la cavité de la

_figure

14 en

_{sous-systèmes}

S

1

:

miroir de

_couplage,

caractérisé _{par les} coefficients de réflexion et de transmission r et t.

Ìl

_y a deux

_champs

entrants l’un venant de l’extérieur de la cavité

E

in

1

,

l’autre venant de

l’intérieur,

E

’in

1

,

et deux

_champs

sortants l’un réfléchi vers l’intérieur de la cavité

E

out

1

et l’autre transmis vers l’extérieur

_E

_’out

₁

_.

S

2

:

milieu non linéaire caractérisé _par une matrice

_T

₂

et un bruit

ajouté

F

2

.

Le

champ

entrant est noté

_E

_in

₂

_,

le

_champ

sortant

E

out

2

.

S

3

:

Propagation

du

_champ

dans la cavité de

_longueur

1. On note 03C4 =

l

_{/c , ~}

_{= 03C9L} 03C4. Le

champ

entrant est

E

in

3

,

le

_champ

sortant

E

out

3

.

La

_propagation

du

_champ

donne

_d’après

la formule

_(I.38):

Les

_champs

entrants et sortants sont reliés _{par :}

Il est

_possible

de résoudre ce

système d’équations

linéaires _pour obtenir :

Un des rôles du résonateur

_optique

est

_{d’augmenter}

les effets non linéaires _par effet de surtension

de la cavité. C’est

_pourquoi

on choisit une cavité de

_grande

finesse. Dans ces

_conditions,

on _peut

écrire :

On suppose ensuite _{que la}

_fréquence

du

_champ

est

_proche

d’une des

_fréquences

_{propres de la}

cavité

_03C9

_cav

_.

On définit l’écart

_~

₀

entre la

_fréquence

du laser et la résonance de la cavité en

posant :

On se restreint à des

_fréquences

03C9 telles _que 03C903C4 << 1. Tous les calculs ultérieurs seront faits à

l’ordre le

_plus

bas en _03C903C4,

_~

₀

et _03B3cav. On a alors :

et on obtient une relation _{entrée-sortie pour} les

_champs,

donnée _{par :}

On introduit alors une matrice de transfert

_{03BC(03C9), dépendant}

de la

_fréquence,

définie par :

et on en déduit les fluctuations des

_champs

sortants en fonction de celles des

_champs

entrants :

La méthode d’entrée-sortie linéarisée nous a

_permis

d’obtenir une relation linéaire donnant les

fluctuations du

_champ

sortant du

_système

en fonction des fluctuations du

_champ

entrant

_(qui

sont

connus

(dès

l’instant où on connaît les transformations

_canoniques

liées aux différents

sous-systèmes

du

_système

S).

La matrice de drift

_03BC(03C9)

décrit l’effet des éléments contenus dans la

cavité,

hormis l’interférence

entre les deux

_champs

entrant du miroir de

_couplage

_qui

donne le terme

_(-1)

de

_{l’équation}

(I.55),

car r ~ 1. La fonction

_03BC(03C9)

est donc la fonction de transfert des éléments de la cavité.

Le second terme de

_(I.55)

est un terme source de fluctuations

_{qui apparaissent explicitement}

comme les fluctuations émises _{par le}

_{sous-système}

_S

₂

et filtrées _{par la} fonction de transfert

_03BC(03C9)

de la cavité.

De la transformation des fluctuations

(I.55),

on obtient la transformation des fonctions de corrélation dont la définition est :

En utilisant

_{l’équation}

_(I.55)

et

_{l’indépendance}

des fluctuations _provenant du

_champ

entrant et du

sous-système S

2

,

la transformation des fonctions de corrélation

_prend

la forme très

_{générale :}

La matrice D dite de

diffusion,

contient l’ensemble des sources de bruit vues de l’intérieur de la

cavité : le bruit

_ajouté

_{par le}

_{sous-système S}

₂

_,

caractérisé _{par la} matrice _03C32

(03C9)

et le bruit entrant, caractérisé par

V

in

(03C9)

et filtré _{par la cavité.}

avec

03C3

2

(03C9)

est la matrice des fonctions de corrélation du bruit

_{ajouté F}

₂

_(03C9).

iv. Cavité de

_grande

finesse et état cohérent incident

L’expression

de

D(w)

se

simplifie beaucoup

dans le cas où le

_champ

entrant est un état cohérent. En

effet,

on _peut écrire :

En _reportant

_(I.54)

dans

_(I.58),

on obtient

_{l’expression}

de la matrice de diffusion :

L’expression

de D montre _{que la matrice} de diffusion ne

dépend

_{pas que du} bruit

ajouté

03C3

2

(03C9) :

un

_système

non linéaire non

_bruyant

_[Reynaud

_89],

_{[Fabre 89]}

donne une matrice de diffusion non nulle. La formule

(I.57)

montre _que la matrice D caractérise la

_capacité

du

_système

à modifier les fonctions de corrélation du

_champ

entrant.

leurs

fluctuations).

C’est le cas d’un

miroir,

ou de la

_propagation

dans le vide ou dans un milieu linéaire. La conservation de

_l’énergie

des

_{champs impose}

_{que la matrice}

_qui

définit cette

transformation linéaire est unitaire. Cette même matrice définit la transformation

_canonique

des

fluctuations.

Or,

une matrice unitaire _peut s’écrire

e

iH

où H est

_hermitienne,

soit 1 + iH si H est

une matrice de

petite

norme.

En

_remplaçant

_T

₂

_{par iH} dans

_(I.61),

on déduit

qu’un système

linéaire non

bruyant

ne _peut en aucun cas

_comprimer

les fluctuations d’un

_champ

décrit _par un état cohérent car dans ce cas on a

D(03C9)

= 0 _et donc

V

out

(03C9)

= Vin

(03C9).

e. Relation entre la

_compression

des fluctuations et la stabilité du

système

Dans le cas où le

_système

non linéaire utilisé _pour

comprimer

les fluctuations du

rayonnement

n’ajoute

pas de bruit propre, les

propriétés

de

compression

des fluctuations de

rayonnement sont étroitement correlées aux

_propriétés

de stabilité du

_système.

En

effet,

dans ce

cas, la relation entrée-sortie pour les fluctuations s’écrit :

La conservation des relations de commutation

_impose

_{alors que le} déterminant de la matrice

03BC(03C9)-1

soit

_égal

à 1. Cette matrice

_possède

donc deux valeurs _{propres de module}

_quelconque,

mais dont le

_produit

vaut 1. Un tel

_système

est

_susceptible

de

_comprimer

efficacement les

fluctuations d’une des _composantes de

_quadrature

du

_champ

si on l’utilise dans des conditions où une des valeurs _propres est

_petite

en module. Les fluctuations sur l’autre

quadrature

_propre seront

donc

_amplifiées.

La limite d’un

_{squeezing parfait}

sera obtenue _pour une

_divergence

des fluctuations

_conjuguées,

c’est à dire au seuil

d’apparition

d’une instabilité du

système.

f. Lien avec les autres méthodes de calcul

Le calcul des fluctuations

_quantiques

de la lumière sortant d’une cavité contenant un milieu non-linéaire _peut se faire de

_plusieurs

_façons.

Il existe à ce

_{jour plusieurs}

_types de méthode : celle

qui

vient d’être

_présentée,

une méthode dite

_{"semi-classique"}

et des méthodes dites

_{"quantiques".}

Les méthodes

_{"quantiques" s’appliquent}

aux non-linéarités

_{paramétriques,}

c’est à dire

qui

ne font intervenir _{que les}

_degrés

de liberté du

_champ,

et aux non-linéarités

résonantes,

faisant intervenir

d’autres variables

_dynamiques

comme _par

exemple

les

populations

et les cohérences d’une

transition

_atomique

_[Drummond

_{80] [Gardiner 83].}

Ces méthodes _partent de l’écriture d’un

hamiltonien effectif décrivant l’évolution du

_champ

dans la cavité non-linéaire : ce hamiltonien

prend

en _compte l’amortissement dû aux _pertes de la

cavité,

la non-linéarité et le

_couplage

avec le

champ

incident sur la cavité via le miroir d’entrée. De ce

hamiltonien,

on déduit

l’équation

d’évolution d’une fonction de distribution du

_champ

dans la cavité. Cette

_équation

est

Langevin

pour des variables

complexes stochastiques représentant

le

champ

intracavité. Il

_s’agit

d’une

_équation

d’évolution

_{généralement}

non-linéaire et contenant des "forces de

_Langevin",

c’est

à dire des termes sources de

bruit,

de valeur moyenne nulle. La forme de ces termes de bruit et leur

interprétation physique dépendent

de la

_{représentation}

_{choisie pour définir} la fonction de

distribution

_(ordre

_normal,

antinormal ou

_{symétrique). L’équation}

de

_Langevin

est linéarisée

autour d’une de ses solutions

stationnaires,

ce

_qui

_permet de déterminer l’évolution des fluctuations du

_champ

intra-cavité. Les trois calculs

_{correspondant}

aux trois ordres usuels conduisent aux mêmes résultats. Les calculs effectués avec la distribution de

Wigner

(ordre

symétrique)

conduisent à des

_équations

de

_Langevin

où les termes de bruit

_{s’interprètent}

aisément : dans le cas d’une interaction

_{paramétrique,}

la seule source de bruit est constituée _par les fluctuations

_quantiques

du

_champ

incident sur la cavité. On _peut montrer _{que la méthode}

"semi-classique"

est

_équivalente

à la méthode

_{quantique appliquée}

à la

_{représentation}

de

_Wigner

[Reynaud 89a].

La méthode

_{"semi-classique"}

ne

_{s’applique qu’aux}

non-linéarités

_{paramétriques,}

où seuls des

_degrés

de liberté du

_champ

interviennent. Elle _repose sur l’écriture des

_équations

d’évolution

classiques

du ou des

_champs

dans la cavité. Ces

_champs

évoluent sous l’action des éléments de la

cavité

_(pertes

sur les

miroirs,

_déphasage,

non-linéarité)

et des

_champs

incident sur la cavité

auquels

ils sont

_couplés

_{par les} miroirs. Ces

_champs

sources sont

_{représentés}

_{par des}

_{champs classiques}

fluctuants dont les fluctuations simulent les fluctuations

_quantiques

d’un état cohérent en

représentation

de

_{Wigner :}

les fonctions de corrélation des

_champs

sources sont

_égales

aux

fonctions de corrélation dans l’ordre

_symétrique

d’un

_{champ quantique}

dans un état cohérent.

L’équation

d’évolution

_classique

est ensuite linéarisée autour du

_point

de fonctionnement calculé par les

équations classiques

sans les termes sources

fluctuants,

_pour donner une

équation

d’évolution des fluctuations des

_champs

dans la cavité.

Une fois

_{l’équation}

d’évolution linéaire des _{fluctuations obtenue par} l’une ou l’autre de ces

méthodes,

on calcule à l’aide d’une transformée de Fourier les _composantes de

fréquence

des

fluctuations des

_champs

intra-cavité en fonction de celles des sources de bruit du

système.

Les fluctuations intra-cavité sont ensuite reliées aux fluctuations des

_champs

sortant de la cavité _par une

relation entrée sortie de la forme

_(1.42):

où 03B4E est le

_champ

_{intracavité,}

03B4Ain et

03B4A

out

les

_champs

incident et sortant.

On ne sait _{pas démontrer que les} différentes méthodes de calcul sont

_{équivalentes}

dans le cas

général.

On _peut

_cependant

retenir

_quelques

résultats :

La méthode

_{"semi-classique"}

est

_équivalente

à la méthode

_"quantique"

utilisant la

distribution de

_{Wigner lorsque}

le hamiltonien d’interaction est

_quadratique

en

_champ,

et

donc dans tous les cas où on linéarise les

_équations

d’évolution.

La méthode entrée-sortie _pour les

_opérateurs

de

_champ

_{donne les mêmes résultats que la} méthode

_{semi-classique}

_{pour les interactions}

_{paramétriques}

et, comme nous le verrons au

trois niveaux.

g.

Conclusion

Le formalisme entrée-sortie _pour les fluctuations

_quantiques

_permet donc de

_dégager

quelques

résultats

_généraux

très

_simples

sur les

_grandes

classes de

_{systèmes optiques}

_que l’on

peut faire

interagir

sur le

_champ

lumineux. Les fluctuations de

_champ

sortant d’un

_système

proviennent

de la transformation des fluctuations des

_champs

entrants, transformation

_qui

comporte éventuellement une

_compression,

et de fluctuations _propres,

_ajoutées

_{par le}

_système.

Ce formalisme sera utilisé dans les

_chapitres

suivants _{pour calculer le spectre} des fluctuations de la lumière sortant d’une

_cavité,

dans le cas où elle contient un milieu non linéaire

_{paramétrique (effet}

Kerr et oscillateur

_{paramétrique optique)}

au

chapitre

II,

et dans le cas où le milieu non-linéaire est