Publisher’s version / Version de l'éditeur:
Vous avez des questions? Nous pouvons vous aider. Pour communiquer directement avec un auteur, consultez la première page de la revue dans laquelle son article a été publié afin de trouver ses coordonnées. Si vous n’arrivez pas à les repérer, communiquez avec nous à PublicationsArchive-ArchivesPublications@nrc-cnrc.gc.ca.
Questions? Contact the NRC Publications Archive team at
PublicationsArchive-ArchivesPublications@nrc-cnrc.gc.ca. If you wish to email the authors directly, please see the first page of the publication for their contact information.
https://publications-cnrc.canada.ca/fra/droits
L’accès à ce site Web et l’utilisation de son contenu sont assujettis aux conditions présentées dans le site
LISEZ CES CONDITIONS ATTENTIVEMENT AVANT D’UTILISER CE SITE WEB.
Paper (National Research Council of Canada. Division of Building Research); no.
DBR-P-901, 1980
READ THESE TERMS AND CONDITIONS CAREFULLY BEFORE USING THIS WEBSITE. https://nrc-publications.canada.ca/eng/copyright
NRC Publications Archive Record / Notice des Archives des publications du CNRC : https://nrc-publications.canada.ca/eng/view/object/?id=34fead1f-2908-4133-b884-32784ef0826f https://publications-cnrc.canada.ca/fra/voir/objet/?id=34fead1f-2908-4133-b884-32784ef0826f
NRC Publications Archive
Archives des publications du CNRC
This publication could be one of several versions: author’s original, accepted manuscript or the publisher’s version. / La version de cette publication peut être l’une des suivantes : la version prépublication de l’auteur, la version acceptée du manuscrit ou la version de l’éditeur.
For the publisher’s version, please access the DOI link below./ Pour consulter la version de l’éditeur, utilisez le lien DOI ci-dessous.
https://doi.org/10.4224/40001694
Access and use of this website and the material on it are subject to the Terms and Conditions set forth at
The possibility of characterizing the severity of fires by a single
parameter
National Research Council of Canada Conseil national de recherches du Canada
THE POSSIBILITY OF CHAR
FIRES BY
A
SINGLE
PARAM
by T. Z. Harmathy
Reprinted from Five and Matevials Vol. 4, No. 2, June 1980 pp. 71-76
DBR Paper No. 901
Division of Building Research
Price $1 .OO
.ACTER
ETER
IZING THE SEVERITY OF
SOMMAIRE
Les canalisations sanitaires et de ventilation (DWV) en plastique ne seront pas des agents de propagation des flammes au travers d'un coupe-feu, mCme dans des conditions dkfavorables de diffkrence de pression, si des mkthodes de construction et des dispositifs d'arrCt appropriks sont utilists. Dans cet article l'auteur rapporte les rksultats d'un programme d'essai B
petite tchelle au cours duquel a ttt ktudit le passage de canalisations sanitaires et de ventilation en plastique dans des coupe-feu.
The Possibility of Characterizing the Severity of
Fires by a Single Parameter
T. Z. Harmathy
Division of Building Research, National Research Council of Canada, Ottawa, Canada KIA OR6
Because language conveys the idea of fire severity by a single expression, it has always seemed desirable to h d a
'1
single variable for its quantification. The earlier suggestion by the author that the total heat absorption per unitsurface area of the compartment boundaries during the period of full fire development, to be referred to as overall heat load, be used as a measure of destructive potential of fires, has been critically examined. It has been found that for many reinforced and prestressed concrete building elements, the overall heat load is indeed an approximate descriptor of the severity of compartment fires, irrespective of their temperature histories.
INTRODUCTION
The term 'fire severity' has different connotations for different researchers. Some look upon fire severity as characterizing the fire itself, others as characterizing the destructive potential of the fire with respect to the confining boundaries. The interpretation of fire severity in strict scientific terms comes naturally from an analysis of the heat balance for post-flashover compartment fires. If opportunely conducted, the analysis will yield a number of descriptors which are capable of fully characterizing the fire process, including the nature of the fire itself and the destructive potential of the fire with respect to the compartment boundaries. The author found that there are three such descriptors and recommended that they be referred to as fire severity parameters.1-3
T h e three fire severity parameters are as fol1ows:t
I . Overall penetration flux, g, i.e. heat flux penetrating
the compartment boundaries. averaged over all boundary urfaces, and temporally over the period of full dev
3
lopment.2. Duration of fully developed fire, T .
3. Average temperature of compartment gases,
Tg
(average 'fire temperature'), averaged over the compartment volume and temporally over the period of full development.A closer examination will reveal that of the three parameters two, either Tg and T or g and T , are sufficient
for unequivocally characterizing the fire process. If
Tg
and T are selected, the characterization is done fromthe point of view of the fire itself, whereas if
g
and Tare chosen, the effect of the fire on the compartment boundaries, in other words its destructive potential, is emphasized. Since this paper is concerned primarily with design for fire safety, the selection of
g
and T seemshere to be more appropriate.
Characterizing the fire by two parameters instead
I
t All symbols are listed at the end of paper.
0 Heyden & Son Ltd, 1980
of a set of process variables is already a significant step toward clarity and conciseness. Yet, since language conveys the idea of fire severity by a simple expression, it has always seemed desirable to have a single variable for its numerical representation. It has been thought3 that perhaps
g
and T could be permanently combined and used as a product,47,
as 'the' measure of fire severity. This product can be recognized as quantifying the total heat absorption per unit surface area of the com- partment boundaries during the period of full fire development. It will be referred to as 'overall heat load' on the compartment.SOME BASIC CONSIDERATIONS
Earlier studiesl-3 have indicated that, in the case of cellulosic fire load, the duration of fully developed fire, T , is independent of the nature of the compartment
lining materials, whereas the other two parameters,
g
andTg,
depend on it through the overall thermal inertia of the lining, dkpc. If, as usual, the various boundary surfaces of the compartment are lined with different materials, the overall thermal inertia of the compartment lining can be expressed as the weighted average of the thermal inertia for the individual boundaries :where
and the subscript i (= 1, 2, 3,
. .
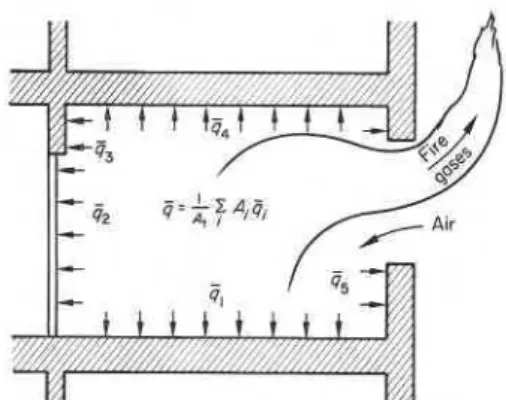
. ) refers to the various lining materials as well as the surfaces formed by them. Furthermore, as Fig. 1 shows, the overall penetration heat flux, 4, is the weighted average of the heat fluxes, qi, penetrating the individual boundaries:After multiplying Eqn (I) by
g / d k p c
and deductingCCC-0308-0501/80/00044071 $03.00
FIRE AND MATERIALS. VOL. 4. NO. 2.1980 71
T. Z. HARMATHY
Figure 1. Illustration of the overall penetration heat flux, (I, and
the component penetration heat fluxes, (It.
the equation so obtained from Eqn (3), a homogeneous linear equation results, the trivial solution of which is?
Clearly, the overall penetration heat flux, g, and the individual penetration heat fluxes, qi ( g ~ , 92, g3,
. . .
),are temporal averages taken over the period of full fire development. The instantaneous values of these variables, q and qi (ql,q2,q3,
. . .
), are subject to moderate variations.Although it is the overall penetration heat flux, g, which is obtained from the heat balance analysis, the individual penetration heat fluxes, qi, are of direct interest in the assessment of the performance of the various boundaries of the compartment. Of special interest are the products q i ~ (q17, 427, g37,
. . .
) which represent the total heat absorptions per unit surface area by the individual boundaries; they will be referred to as 'individual heat loads'.It follows from Eqn (3) that
reached as a result of fire exposure by some crucial load-bearing component (reinforcing bar, prestressing wire) as a measure of destructive potential. Thus, the answer to the first question is yes.
The answer to the second question is more involved, and therefore it will be developed in several steps. In the first phase of investigations, q and the qi's will be regarded as constant quantities, equal to
g
and qi, respectively, even though they are known to be subject to variations during the course of a fully developed fire. The tenability of this practice will be scrutinized later.To simplify the problem, only slab-like constructions will be examined. Knowing that, except for very thin slabs and unusually long fire exposures, conditions on the unexposed side of the slab have no noticeable effect on its temperature history (and, in turn, on the temperature history of an embedded steel component), the slab will further be idealized as a semi-infinite solid.
The formulation of the problem is this. A semi- infinite solid (i.e. a compartment boundary), originally (at t =0) at a uniform temperature (taken as zero), is penetrated at its surface (at x=O) by a constant heat flux,
g
(the subscripts i are omitted for convenience at this stage), for a period O< t < T. At t = T the heat penetration ceases and the solid becomes subject to Newtonian cooling to its surroundings (whose tem- perature is constant and taken as zero), a process characterized by a constant heat transfer coefficient, h. For convenience, all thermal properties, k, p, c and K ,are regarded for the time being as constant. The following equations apply:
1
47=-
z
Ai(gi7)At i ( 5 ) -hT+k-=O a T x=O, t > ~
ax
In words: the overall heat load is the weighted average
of the individual heat loads. T=O x>O, t=O
The solution for that particular case when h=O has MAXIMUM RISE OF TEMPERATURE been given by Carslaw and Jaeger.4 The temperature of the crucial component located at a distance x = a With interest focused on the destructive potential
of fires, an investigation into the possibility of using the product g~ as 'the' parameter of fire severity will consist of finding answers to the questions: Can the destructive potential of fires be quantified by a single variable? Then, if the answer is yes: Is there a unique relation between that single variable and the overall heat load ?
To answer these questions, a specific but very impor- tant group of building elements, namely reinforced and prestressed concrete constructions, will first be examined in detail. Since the structural performance of reinforcing and prestressing steels is a function of temperature and deteriorates at higher temperatures, it seems justifiable to regard the maximum temperature
7 Computer studies of heat transfer in fire test furnaces have
indicated that conditions characterized by the trivial solution are usually closely approximated after a transitional period.
below the surface of the solid (host material for the steel) is described by the following equation:
k~ = 2
(5)
112 (ier fc 1(xt)
112After differentiating with respect to t , and making dT/dt equal to zero, an expression5 is obtained for the time, trn ( > T), at which the temperature of the crucial component reaches its maximum, Trn:
THE POSSIBILITY OF CHARACTERIZING THE SEVERITY OF FIRES BY A SINGLE PARAMETER
On multiplication of both sides by ~ / t m this equation becomes
/ T I 2
Equation (12) represents a unique relation between tm/r and K7/a2 which can be written in the following general form
:t
By replacing T and t in Eqn (10) with Tm and tm, respectively, then substituting for ~t,/a2 its expression by Eqn ( l l ) , and finally taking account of Eqn (13), it can be proved that the maximum temperature reached by the crucial component is determined by two dimen- sionless products :
After multiplying the first with the square of the second, and inverting the product so obtained, Eqn (14) can further be brought into the following form:
If h#O, an additional variable enters the problem and, according to the
II
theorem, another dimensionless product, comprising h, is needed to complete Eqns (13) and (15). This additional product may be defined in several different ways. From the point of view of the subject discussed here, its most convenient form is h(r/kpc)l/2. Thus, the complete forms of Eqns (15) and (13) area
pca Tm (16)
When applying Eqn (16) (or Eqn (17)) to the individual boundaries of a fire compartment, mathematical rigor requires that subscript i be added to all symbols which represent quantities that may be different for the various boundaries. Thus, after some rearrangement, Eqn (16) becomes
This equation, after substituting for qi from Eqn (4), assumes the form
t
The dimensionless products that appear on the right-handside of Eqns (13) and (15) are both equivalent to the Fourier
number, K T / U ~ . They appear in these equations in somewhat
modified forms which were found to offer some convenience in the graphical presentation of the respective relations. The dimen- sionless presentation of the maximum temperature in Eqns (15) and (16) by the product cj~/pcaTm, rather than by its reciprocal which would seem more logical, has also been decided on, on the ground of ease in graphical presentation.
Equation (19) shows that for a given compartment (as characterized by a set of material properties) the maximum temperature attained by any crucial steel component embedded in any boundary is proportional to the overall heat load, q ~ . Unfortunately, (G)m also depends separately on the fire duration T which, in
addition to being part of the product 47, has additional roles to play by being part of the groups
and h1/(~/kspi~i)1/2. Whether or not these roles are significant will be decided after finding the explicit form of Eqn (16).
Naturally, Eqn (19) is valid only if ai > 0. If the crucial component of a compartment boundary is directly exposed to the fire, as in the case of unprotected steel constructions, (tm/7)6= 1, and (Ti)m will depend on qi~1/2 rather than
q i ~
(see Ref. 4). Consequently, for unprotected steel constructions, the heat load has no special significance in the assessment of the destructive potential of fire.Thanks to the convertibility between the individual and overall penetration heat fluxes,
qi
and4
(see Eqn (4)), and between the individual and overall heat loads, &T and47
(see Eqn (5)), it seems justified and convenient to dispense with the use of the subscript i in further discussions and in the figures.The relations expressed by Eqns (16) and (17) are presented graphically in Figs. 2 and 3. For h ( ~ / k p c ) ~ / ~ > 0, the curves were developed from numerical heat flow studies. It is noteworthy that for the range 0.8 < a / ~ l / ~ r l f ~
< 1.2 the value of the product qrlpcaTm is very nearly constant, about 2.3. This means that the maximum temperature reached by the crucial component is practically independent of such important variables as the thermal conductivity of the material in which the component is embedded, or the heat transfer coeffi- cient which characterizes the rate of cooling of the construction following fire exposure. The following approximate equation applies :
0
h
I 2 3d
4 50/kk2 ,'h
Figure 2. Dimensionless presentation of the maximum tem-
peratures attained by a crucial component embedded in a semi-infinite solid.
T. Z. HARMATHY
heat flux on the nature of the relation between T, and g ~ . In two of these studies the penetration heat flux was assumed to increase, in another two to decrease linearly over the period O< t < T, in such a way as to yield the same average values, as illustrated (cases A and C) in the insets in Fig. 4. Case B depicts the classical case discussed earlier, namely that for which q = const =
g.
From the point of view of non-constancy of q, cases A and C can be regarded as representing extreme conditions. In each group of two, one study was performed with a value h ( ~ / k p c ) l / ~ = 0.1, and another with h ( ~ / k p c ) l / ~ = 5 . These values can also be looked upon to represent rather extreme conditions to be met in practice.The results of the studies, together with two others borrowed from the earlier series (related to case B), are plotted in Fig. 4. The hatched areas can be regarded as representing the bands of possible error due to the
0 5 10 15 20 25 non-constancy of q. Clearly, the error is not expected
a 2 / x r to be more than
+
10% irrespective of the patternFigure 3. Dimensionless presentation of the times at which of the temporal variation of the penetration heat flux
maximum temperatures are attained by a crucial component Or, what means the same thing, the history of
embedded in a semi-infinite solid. the fire temperature. The error is considerably less in
the range 0.8 < u / K ~ / ~ T ~ / ~ < 1.2 which is of primary
Assuming a typical fire exposure of, say, 30 min duration practical interest.
(i.e. T - 1800 s), the ranges of values of a to which The effect of non-Newtonian cooling (by radiation
Eqn (20) is applicable are as follows: and convection) was studied in three series of calcula- tions. They involved three slabs (with imaginary crucial for (dry) weight 'OnCrete 0.025<a<0.039
component) made from (dry) normal weight concrete, for (dry) lightweight concrete 0.017 < a < 0.025 m (dry) lightweight concrete, and insulating fire brick. These distances can be recognized as typical of the (The last-mentioned is often employed as lining in location of the steel reinforcing bars or prestressing fire test furnaces.) The most important information strands in reinforced or prestressed concrete construe- used in the studies is summarized in Table 1. The values tions. That the fire duration appears in Eqn (20) only for g are typical of the average penetration heat fluxes in the product g~ substantiates that, for the type of occurring in a standard fire test of I h duration. The construction considered, the individual heat loads results of the calculations are plotted in Fig. 5 against and (by virtue of Eqn (5)) the overall heat load are the background of Curves representing Newtonian indeed suitable and sufficient for quantifying (by means cooling.
of the maximum temperatures) the destructive potential Also plotted in Fig. 5 are the results of two further of fire. An inspection of Fig. 2 will reveal, furthermore, series of calculations performed on normal weight and that even if the condition O . ~ < U / K ~ ~ ~ T ~ / ~ < 1.2 is not
strictly fulfilled, the role that the fire duration T may 8
play in the quantification by its presence in the groups
a / ~ l l z r l l z and h / ( ~ / k p c ) ~ / ~ is of secondary importance 7 in relation to its role as part of the product g ~ .
CONSIDERATION OF REAL-WORLD CONDITIONS
5
The real-world conditions may differ mainly in three k 8 ways from those discussed in the previous section: $. 4 -
1-
1. The penetration heat fluxes are never constant; q is 3 subject to moderate variation.
2. Following exposure to fire, the cooling of the
compartment boundary (or test specimen in 2 standard fire tests) is not Newtonian (i.e. h # const) ;
it takes place by a combined radiation-convection I
mechanism.
3. The presence of moisture may render the assumption
-
Case A Case B Case c
-
-
('3"
,--,
6 - k g G-
5 -<
P
-
.?z
-
-
0.1-
- l ~ r ~ , ~ I , ,of constancy of the thermal properties of the o 1 2 3 4 5
material hosting the crucial component untenable. O/K 2'' $2
Figure 4. The influence of the non-constancy of the penetration
Four studies were performed throw heat flux on the maximum temperature attained by a crucial
light on the effect of variability of the penetration component embedded in a semi-infinite solid.
74 FIRE AND MATERIALS. VOL. 4. NO. 2. 1980
0
Heyden & Son Ltd, 1980THE POSSIBILITY O F CHARACTERIZING T H E SEVERITY O F FIRES B Y A SINGLE PARAMETER Table 1. Information used in calculations related to the maximum rise of temperature in the interior of three slabs
k P C K V'kTc q
Slab material (W m - l K - I ) (kg (J k g - l K-l) (mz s-l) ( J m-z s-lI2 K-l) (W m-2)
Dry normal weight concrete 1.68 2200 1300 5 . 8 7 4 ~ 1 0 - ~ 21 92 28 890
Dry lightweight concrete 0.46 1450 1300 2 . 4 4 0 ~ 991 12 270
Insulating fire brick 0.25 722 1000 3 . 4 6 3 ~ 425 5 600
Duration of fire exposure: ~ = 3 6 0 0 s; cooling (following exposure) by radiation and natural convection.
lightweight concrete slabs (with imaginary crucial component) containing a normal amount of moisture (6% by volume). The effect of moisture on the thermal conductivity of concrete was taken into account in a way recommended by Cammerer,G and its effect on the specific heat in a way described by the a ~ t h o r . ~ The information in Table 1 was used, except that the penetration heat flux was increased by 6.2% in the case of the normal weight concrete slab and by 11.0% in the case of the lightweight concrete slab. Earlier studies had indicated that such increases were to be expected under realistic fire exposure conditions in the presence of moisture.
A comparison of Figs. 4 and 5 with Fig. 2 reveals that in the range of practical significance, namely in 0 . 8 < a / ~ l / ~ r l / 2 < 1.2, Eqn (20) remains valid under any practical condition, provided that the material in which the crucial component is embedded does not hold significant amounts of moisture. To make it applicable to moist concrete, the constant in it should be reduced, as Fig. 5 suggests, by 10-15%. (If applied to moist concretes,
g,
p and c in Eqn (20) so modified are to be selected as values pertaining to oven-dry conditions.)Equation (20) provides support for the claim that for the type of construction examined there is a 'reason- ably' unique relation between the heat load and Tm;
- Normal weight concrete
--- Lightwe~ghl concrete
.., Insulating f ~ r e brick
in other words, between the heat load and the destructive potential of fire.
GENERALIZATION
The preceding discussions were related to a type of construction characterized by crucial components of low heat capacity embedded in a massive protection. Under these conditions a substantial simplification was possible in the mathematical formulation of the heat flow problem. The question that arises now is this: Do the conclusions remain valid even if the said conditions are not fulfilled?
Because of the large variety of conditions that one can think of, most of which cannot be handled by simple mathematical analyses, it is difficult to give at this time an unqualified affirmative answer. There is some evidence, however, that the practice of using the overall heat load as a measure of destructive potential may have a wider applicability. Some time ago Law899 developed for massive steel columns with light insulation an empirical formula which presented the minimum fire resistance requirement (to counteract the destructive potential of fire) as directly proportional to the fire load and inversely proportional to the square root of the area of ventilation opening. Figure 3d in Ref. 3 shows that, for cellulosic fire load, the dependence of the heat load,
97,
on the fire load and the ventilation parameter (which, in turn, is proportional to the ventila- tion opening) indeed roughly reflects Law's finding. Law's work can therefore be regarded as implicit support for extending the validity of earlier conclusions.Because a number of incidental factors may influence the fire process, the nature of fire is rarely predictable with an accuracy better than 30%. The convenience offered by characterizing the destructive potential of fire by a single parameter, namely by the overall heat load, instead of a series of process variables, is probably worth losing some more of the accuracy.
CONCLUSION
Support has been provided for the earlier suggestion that the overall heat load on the compartment,
g ~ ,
be treated as a single descriptor of the destructive potential of fires.Figure 5. The influence of the non-constancy of the heat
transfer coefficient and the presence of moisture on the maximum Acknowledgements
temoerature attained bv a crucial comoonent embedded in This paper is a contribution from the Division o f Building Research. normal weight concrete,'lightweight concr'ete, and insulating fire ~ a t i o n a l Research Council o f Canada, and is published with the
brick. approval o f the Director of the Division.
T. Z. HARMATHY NOMENCLATURE Note: Without subscript i, symbols c, h, k, q,
q,
K and pare used either in a general sense, or represent overall values valid for the entire compartment. With a sub- script i, they represent values pertaining to an individual compartment boundary. a A C
f
h i ierfc k 4B
distance of the crucial component from the surface of the host material (m)
surface area (m2) specific heat (J kg-1 K-1) function
heat transfer coefficient (W m-2 K-1) = 1 , 2 , 3 , .
. .
integral error function
thermal conductivity (W m-1 K-1)
time-dependent penetration heat flux (W m-2) temporal average penetration heat flux for the period of full fire development (W m-2)
t time (s)
T temperature above its level at t = 0 (K)
spatial and temporal average temperature for the period of full fire development above the temperature level at t = 0 (K)
x distance from surface (m)
K thermal diffusivity (m2 s-l)
p density (kg m-3)
T duration of fully developed fire (s) Subscripts
g of compartment gases
i of or for the ith compartment boundary m maximum; pertaining to maximum temperature t total for the compartment
REFERENCES
1. T. Z. Harrnathy, in Design of Buildings for Fire Safety, ed. STP 464. American Society for Testing and Materials by E. E. Smith and T. Z. Harmathy, p. 198. ASTM STP 685. Philadelphia (1 969).
American Society for Testing and Materials, Philadelphia 8. M. Law, A relationship between fire grading and building
(1 979). design and contents. Fire Research Note No. 877. Joint Fire
2. T. 2. Harmathy, Fire Technol. 8, 196, 326 (1 972). Research Organization, London (1 971 ).
3. T. Z. Harrnathy, Fire Mater. 3, 49 (1979). 9. M. Law, in Prediction of Fire Resistance, p. 16. Symposium 4. H. S. Carslaw and J. C. Jaeger, Conduction of Heat in No. 5. Joint Fire Research OrganizationIHer Majesty's
Solids, 2nd Edn, p. 75. Oxford University Press, London Stationery Office, London (1973). 11 959).
5. T. Z. ~armathy, J. Appl. Phys. 35, 11 90 (1 964). Received 13 August 1979 6. J. S. Carnrnerer, Warme- Kaltetechn. 41, 126 (1 939).
7. T. Z. Harmathy, in Fire Test Performance, p. 209. ASTM 0 Heyden & Son Ltd, 1980
This publication is being distributed by the Division of Building Research of the National Research Council of Canada. It should not be reproduced in whole or in part without permission of the original publisher. The Division would be glad to be of assistance in obtaining such permission.
Publications of the Division may be obtained by mailing the appropriate remittance (a Bank, Express, or Post OGce Money Order, or a cheque, made payable to the Receiver General of Canada, credit NRC) to the National Research Council of Canada, Ottawa KIA 0R6. Stamps are not acceptable. A list of all publications of the Division is available and may be obtained from the Publications Section, Division of Building Research, National Research Council of Canada, Ottawa KIA 0R6.