Identification des coefficients aérodynamiques du Dirigeable AS500 du LAAS

Identification des coefficients aérodynamiques

du Dirigeable AS500 du LAAS

N° de Commande du LAAS : L 42960

SOMMAIRE

I) Généralités sur la modélisation des efforts aérodynamiques 1

II) L'enveloppe du Dirigeable 5

II-1) Efforts sur l'enveloppe du dirigeable 8

II-1-1) Effort normal : origine, modélisation et comparaison expérimentale 9

II-1-1-1) Effort normal : confirmation numérique du terme linéaire 15 II-1-1-2) Effort normal : confirmation numérique du terme non linéaire 20

II-1-2) Effort latéral : origine, modélisation et comparaison expérimentale 22 II-1-3) Effort tangentiel : origine, modélisation et comparaison expérimentale 22

II-2) Moment de tangage et de lacet sur l'enveloppe du dirigeable 27

II-2-1) Moment de tangage : origine, modélisation et comparaison expérimentale 28

II-2-1-1) Moment de tangage : confirmation numérique du terme linéaire 31 II-2-1-2) Moment de tangage : confirmation numérique du terme non linéaire 33

II-2-2) Moment de lacet sur l'enveloppe du dirigeable 34

III) Dirigeable complet 35

III-1) Efforts stationnaires sur le dirigeable complet en configuration lisse (gouvernes

non braquées) 35

III-1-1) Effort normal et latéral 35

III-1-2) Effort tangentiel 40

III-1-3) Moment de tangage et de lacet 43

III-1-4) Moment de roulis 48

III-2) Influence du braquage symétrique des gouvernes 48

III-2-1) Effort normal 48

III-2-2) Effort latéral 50

III-2-3) Effort tangentiel 51

III-2-4) Moment de tangage 58

III-2-5) Moment de lacet 60

III-2-6) Moment de roulis 60

III-3-1) Coefficient d'effort normal en braquage dissymétrique 62

III-3-2) Coefficient d'effort latéral en braquage dissymétrique 62

III-3-3) Coefficient d'effort tangentiel en braquage dissymétrique 63

III-3-4) Coefficient d'effort tangentiel en braquage dissymétrique 64

III-3-5) Coefficient d'effort tangentiel en braquage dissymétrique 64

III-3-6) Coefficient d'effort tangentiel en braquage dissymétrique 64

III-4) Efforts instationnaires 66

III-4-1) Méthode de Kirchoff : 67 III-4-2) Méthode de Bryson: 70

III-4-3) Comparaison des deux modélisations 75 III-4-4) Méthode de calculs des coefficients 81 III-4-4-1) Résultats concernant les quantités mij 82 III-4-4-2) Applications : Calcul des coefficients b11, c11, d11 86

III-4-4-3) Applications : Calcul des coefficients b22, c22, d22 86

III-4-4-4) Applications : Calcul des coefficients b12, c12, d12 87

III-4-4-5) Applications : Calcul des coefficients b13, c13, d13 87

III-4-4-6) Applications : Calcul des coefficients b23, c23, d23 87

III-4-4-7 ) Applications : Calcul des coefficients b33, c33, d33 87

III-4-4-8 ) Calcul des coefficients mi j, x mi j, x 2 m_{i j} 87

III-4-5) Comparaison résultats expérimentaux et méthode de Bryson 89

IV) Synthèse 92

V) Conclusions 104 Références bibliographiques 106

Annexe 1 : Données géométriques 108

1

Modélisation aérodynamique du Dirigeable AS500

La 1ère

partie de ce document est rédigée de façon didactique, de façon à ce que les lecteurs non familiarisés au monde de l'aérodynamique puissent comprendre les phénomènes qui apparaissent, leur complexité et percevoir le sens des modélisations adoptées.

On notera en effet que les essais en soufflerie, malgré leur qualité, ont également beaucoup de défauts : obligation de mettre la maquette sur des mâts, qui perturbent fatalement l'écoulement, sensibilité des balances quand les efforts sont de l'ordre du gramme force, mais surtout taille de la maquette, fatalement réduite, qui entraîne le non respect d'un paramètre important qui est le nombre de Reynolds dont la définition est donnée plus loin.

Il est alors extrêmement important de montrer que les calculs, associés à des modélisations, permettent de retrouver les valeurs expérimentales. Les mêmes calculs et les mêmes modèles sont ensuite utilisés pour déduire les résultats à l'échelle 1.

Tous les résultats en soufflerie sont des résultats stationnaires représentant simplement le dirigeable en phase de translation permanente.

Il est ainsi d'autant plus important de démontrer que calculs et modèles sont capables de restituer ce cas simple, de façon à donner une crédibilité à ces calculs et modèles qui traitent ensuite des cas complexes abordant à la fois les rotations, et les phases instationnaires. Ce dernier aspect est particulièrement important pour les "aéronefs allégés" comme il le sera vu par la suite.

La 2ème

partie est plus synthétique donnant l'ensemble de la modélisation avec les coefficients numériques attendus.

Une 3ème

partie regroupe des annexes diverses.

I) Généralités sur la modélisation des efforts aérodynamiques :

De façon très générale, les efforts aérodynamiques pour un obstacle quelconque,

• dont les longueurs caractéristiques selon les trois axes sont notées L (longueur dans le sens de l'écoulement), 2b (envergure) et e (épaisseur),

• se déplaçant à la vitesse aérodynamique V r _a

( )

t = V_a ( cos! cos", sin", sin! cos" ) , avec une vitesse de rotation ! tr

( )

de composantes

₍

p, q, r

₎

,

• au sein d'un fluide ayant pour propriétés physiques, à l'infini, une viscosité µ!, une

masse volumique !!, une célérité du son a!, un coefficient de conduction !c", et des

chaleurs spécifiques Cp et Cv,

• en présence d'une accélération de la pesanteur g, responsable d'un gradient statique de pression

vont être fonction de l'ensemble de ces paramètres et de leurs dérivées temporelles éventuelles, d'où : r F = r f L, 2b, e, V_a, V•a, !, ! • , ", "•, p, q, r, p•, q•, r•, a_#, $_#, µ_#,%c#, Cp, Cv, g & ' ( ) En fait, l'analyse dimensionnelle montre que les efforts rendus sans dimension, ne sont fonction que des paramètres sans dimension du problème.

Ainsi :

• au lieu de Va et a! , il intervient le nombre de Mach de l'objet M! = Va a!

• la viscosité intervient dans le nombre de Reynolds Re_L = !" Va L µ"

• les échelles de longueurs interviennent, entre autres, par leurs rapports respectifs, soit ! = 2b

L (allongement) et e = e

L (épaisseur relative),

• le coefficient de conduction apparaît dans le nombre de Prandtl Pr = µ! Cp "c!

, • les chaleurs spécifiques par leur rapport ! = Cp

Cv

,

• l'accélération de la pesanteur par le nombre de Reech-Froude1

Fr = Va g L

• l'accélération V•a intervient sous la forme de V • a = L V • a Va 2

• les composantes du vecteur rotation p, q et r et les dérivées angulaires !•, "• donnent, sous forme adimensionnelle x = L x

Va

, où x représente une quelconque des quantités précédentes.

• enfin, les accélérations angulaires p•, q•, r• ont pour forme adimensionnée y = L

2 _y

V_a2 où y est une quelconque des accélérations angulaires. Il vient alors : r F 1 2!"SrefVa 2 = r F M_", Re_L, Pr, #, Fr, $, e , %, &, V • a, % • , & • , p , q , r , p • , q •, r • ' ( ) * + ,

De façon analogue, le moment par rapport à un point O, va s'écrire :

1 _{Dans la littérature, le nombre de Reech-Froude est parfois Fr =} Va 2 g L

3 r M O 1 2!"LrefSrefVa 2 = r M M_", Re_L, Pr, #, Fr, $, e , %, &, V • a, % • , & • , p , q , r , p • , q •, r • ' ( ) * + ,

Dans ces relations, Sref et Lref sont respectivement une surface et une longueur de référence,

faisant fatalement intervenir les échelles L, 2b et e de l'objet.

Dans la liste des paramètres sans dimension ci-dessus, un choix a été effectué parmi plusieurs possibilités. En effet, les produits de paramètre sans dimension étant également sans dimension, un couple de paramètre

(

a , b

)

peut être remplacé, par exemple, par

(

a , a b

)

. En supposant que la liste des paramètres ait été exhaustive, le rôle de l'aérodynamicien est de déterminer les fonctions F r et M r ci-dessus.

Un tel travail est en général impossible. Toutefois, dans le cadre de l'utilisation "dirigeable" des simplifications importantes peuvent être envisagées.

• le Mach est très faible, de sorte que la masse volumique !! = ! du fluide reste

constante.

• la viscosité du fluide, très généralement fonction de la température ne subit, à faible Mach, que fort peu de modification et peut être considérée comme constante.

Des deux simplifications précédentes, il résulte un découplage entre la résolution du problème dynamique ( recherche de p et V ) et du problème thermique. Corrélativement, le nombre de r Prandtl qui n'apparaît dans le problème dynamique qu'en présence d'un couplage entre les deux problèmes n'intervient plus, de même que le rapport " des chaleurs spécifiques qui n'a d'importance que dans les problèmes compressibles.

Par ailleurs, il est possible de découpler les effets de la pesanteur qui interviennent par le nombre de Froude et les effets dynamiques. En effet, l'action de la pesanteur se retrouve sur le gradient statique de pression auquel s'ajoute les variations de pression dues au mouvement du fluide. En ce qui concerne le gradient statique de pression, il est responsable de la poussée d'Archimède, ou de son moment par rapport à un point. Cet effort et ce moment sont bien connus, respectivement égaux à P r archi = - ! Vol

r

g et M r O archi = - ! Vol OC "

r

g où C est le centre de carène défini par Vol OC = OM

D

!!!

d" .

En ôtant ces efforts pour ne conserver que la partie dynamique, on a :

r F dyn. 1 2!"SrefVa 2 = r F Re_L, #, e , $, %, V • a, $ • , % • , p , q , r , p • , q •, r • & ' ( ) * + (1) Et : r M O dyn. 1 2!"LrefSrefVa 2 = r M Re_L, #, e , $, %, V • a, $ • , % • , p , q , r , p • , q •, r • & ' ( ) * + (2)

Bien entendu, d'autres échelles de longueur auraient pu apparaître par exemple relatives aux empennages , à leur position par rapport à l'origine du repère ou celles caractéristiques de la case à équipement sous le dirigeable, mais ceci apparaîtra naturellement lors de la modélisation.

Il est ici plus important de souligner la dépendance vis-à-vis : • du nombre de Reynolds ReL

• des incidence et dérapage ! et " • et des quantités réduites V

• a, ! • , " • , p , q , r , p • , q • et r •

En ce qui concerne les paramètres !, e

(

)

ils sont ici égaux au rapport diamètre sur longueurs de l'objet. D'après les mesures effectuées sur l'AS 500, on a L = 7,80 m et D = 1,90 m (diamètre au maître - couple), soit :

! = e = D

L = 0,2436

Malgré les simplifications effectuées, les expressions (1) et (2) restent encore inaccessibles à la modélisation analytique. Par ailleurs, les codes de calcul complets type Navier - Stokes, déjà incapables de prédire avec précision les résultats stationnaires, sont a fortiori inopérants pour obtenir les efforts ici envisagés dans leur plus grande généralité.

Deux niveaux de simplification peuvent être alors envisagés :

A) on note que la viscosité de l'air, qui intervient dans le nombre de Reynolds est donnée par la formule de Sutherland :

µ = µ0 T T₀ 1 + S T₀ 1 + S T

avec, pour l'air S = 110.4°K et µ₀ = 1.711 10-5 kg.m-1.s-1 pour T0 = 273°K

La longueur L = 7.80 m étant choisie comme longueur de référence, le nombre de Reynolds, dans des conditions normales de température et de pression ( soit T! = 288,15°K ;

p! = 101325 N/m 2_{, d'où #} != 1.225 kg/m 3 _{et µ} ! = 1.785 10 -5 kg.m-1.s-1 est, à la vitesse maximale envisagée, soit V_a = V_max = 50 km/h = 13.89 m/s :

ReL =

!" Va L µ"

5 Même pour le dixième de la vitesse maximale, soit pour V_a = 5 km/h = 1.39 m/s , qui est la vitesse d'un homme au pas, le nombre de Reynolds reste élevé, ici Re_L ! 7.43 105.

Il est alors possible, dans un 1er

temps de supposer le nombre de Reynolds infini, ce qui constitue l'hypothèse "fluide parfait". La prise en compte d'une viscosité non infiniment faible est effectuée dans un 2ème

temps, à l'aide de l'approche "couche limite" 2

rendue possible par les valeurs élevées du nombre de Reynolds.

B) Une autre possibilité de simplification, consiste à considérer comme séparés les éléments constitutifs du dirigeable : on peut ainsi considérer d'une part l'enveloppe du dirigeable, corps de révolution, les ailettes stabilisatrices, de type faible allongement, et la case à équipement. Les phénomènes d'interaction peuvent ensuite être introduits pour améliorer le modèle.

II) L'enveloppe du dirigeable :

Par "enveloppe du dirigeable", on entend la carène nue après avoir ôté à la fois les ailettes arrière et la case à équipement. Il s'agit d'une certaine façon d'un corps pur, possédant une symétrie de révolution.

Cet obstacle a priori très simple est choisi pour montrer l'enchaînement des éléments théoriques qui permettent de comprendre la réalisation expérimentale.

L'ensemble des efforts et moments agissant sur un corps quelconque, en mouvement instationnaire de translation - rotation ont été déterminés, en fluide parfait, par Kirchoff, résultats en particulier rappelés dans la [ref.1], en supposant qu'aucune surface de glissement ne s'échappe de l'obstacle.

Ces efforts sont connus dès l'instant où est connue une matrice 6 x 6 , symétrique, comportant donc, dans un cas très général, 21 termes a_{i j} a priori distincts. Les obstacles présentant fréquemment des plans de symétrie, cette matrice peut notablement se simplifier : c'est notamment le cas pour un corps de révolution.

Pour un obstacle indéformable, en atmosphère illimitée, ces termes sont des constantes ne dépendant que de la géométrie de l'obstacle. On démontre en particulier que les éléments diagonaux de la matrice sont tous positifs.

• Pour i et j variant de 1 à 3, ces coefficients sont homogènes à une masse, et sont tous proportionnels à la masse correspondant à la poussée d'Archimède notée Ma avec

M_a = ! Vol . Pour les éléments de cette sous - matrice, il peut être défini une forme sans dimension, soit kij =

aij Ma

.

• Pour i et j variant de 4 à 6, ces coefficients sont homogènes à une inertie.

2 _{La taille caractéristiques des effets visqueux, ramenée à la longueur de l'obstacle décroît, en laminaire, comme}

1/ Re. En turbulent, le comportement est en 1/ Re1/ 6: à Reynolds infini, l'épaisseur de la zone visqueuse est donc nulle.

• Enfin, pour i variant de 1 à 3, et j variant de 4 à 6, ces coefficients sont homogènes à une masse multipliée par une longueur.

La littérature portant sur ce domaine parle de "masses ajoutées" en limitant donc le phénomène à la seule sous - matrice 3 x 3 des a_{i j} pour i et j variant de 1 à 3. De façon plus générale, nous parlerons de la matrice des coefficients de fluide ajouté. Cette terminologie provient du fait que, lors de mouvements instationnaires, impliquant donc des accélérations, le déplacement du fluide ambiant se traduit par des efforts sur l'obstacle dont une partie est directement proportionnelle aux accélérations.

Si un objet de masse M subit, dans la direction x, une accélération du1

dt , le fluide, opposant son inertie à cette mise en mouvement, créera une force instationnaire - a₁₁ du1

dt . L'équation de la mécanique selon cette direction prendra alors la forme :

M du1

dt = - a11 du₁

dt + ... où l'on rappelle que les akk sont positifs. Tout se passe comme si, selon la direction x, le corps avait en présence du fluide une masse M + a11. Il en serait de même selon les directions y ou z, la masse de l'obstacle en présence

du fluide, mise en évidence par les accélérations devenant respectivement M + a22 ou M +

a33. Comme les masses ajoutées sont proportionnelles à la masse de la poussée d'Archimède,

on est ainsi conduit à comparer les masses M et kjj Ma pour j = 1 à 3, où les kjj seront

appelés "coefficients de masses ajoutées", formes sans dimension des masses ajoutées. Dans le cas d'un plus lourd que l'air, M et Ma sont deux paramètres totalement

indépendants, et l'on a M >>> Ma de sorte que ces termes instationnaires sont classiquement

négligés. Par contre, pour un engin en sustentation Archimédienne (dirigeable, montgolfière, sous-marin, bateaux), soit M ! M_a, les masses ajoutées ne sont plus du tout négligeables, car, selon les directions , les kjj peuvent être très proches de l'unité. Pour le Hindenburg,

dont l'allongement était ! = D

L " 0.168, la valeur théorique de k22 = k33 est de l'ordre de 0.98 : pour les accélérations transversales, ce dirigeable de 130 tonnes se comportait donc comme un corps de masse 257.4 tonnes ! Même selon la direction longitudinale, pour laquelle le coefficient a11 est le plus petit, celui-ci représente toutefois une augmentation d'un

peu moins de 5% de la masse du dirigeable, soit plus précisément 5.9 tonnes de masse ajoutée pour ce dirigeable.

En ce qui concerne les aspects "rotation", le phénomène de "fluide ajouté" se retrouve en termes d'inertie ajoutée sur les coefficients ajk lorsque les indices varient de 4 à 6.

Les éléments théoriques ci-après permettent de mieux comprendre comment les efforts sont obtenus à partir des coefficients de fluide ajouté. Il faut noter également que si ces coefficients apparaissent sur les termes instationnaires, ils seront retrouvés également sur des termes purement stationnaires !

7 Si, dans une application très générale, on considère un obstacle en translation - rotation V r _G

( )

t , ! tr

( )

_{au sein d'un fluide animé d'une vitesse constante} V r _!, les efforts sont identiques à ceux agissant sur l'obstacle animé d'une translation - rotation V r _a = V r _G - V r _{! ,} ! tr

( )

baignant dans un fluide au repos. En notant u

(

₁, u₂, u₃

)

_{les composantes de la vitesse aérodynamique} V r _a exprimées dans le repère relatif attaché à l'obstacle et u

(

₄, u₅, u₆

)

_{celles du vecteur} ! tr

( )

dans ce même repère, alors, dans le cadre "fluide parfait incompressible", on montre que l'écoulement est irrotationnel et que le potentiel des vitesses est une combinaison linéaire de potentiel élémentaire ne dépendant que de la géométrie, donc des coordonnées x, y, z du repère relatif, combinaison linéaire dont les coefficients sont les uk(t).

L'énergie cinétique T du fluide mis en mouvement par le déplacement V r _{a ,} ! tr

( )

est alors une forme quadratique des composantes uk(t) dont les coefficients sont précisément les

coefficients de fluide ajouté, soit :

2 T = a_{i j} u_i u_j j=1 j =6

!

i =1 i= 6

!

(3)

La quantité de mouvement du fluide ainsi que son moment cinétique par rapport à un point G ont alors pour composantes, dans le repère relatif :

r p !T !u1 , !T !u2 , !T !u3 " # $ % & ' et r H _G !T !u4 , !T !u5 , !T !u6 " # $ % & ' où !T !u_k = i=1ai k ui i =6

"

(4)

Les variations par rapport au temps de cette quantité de mouvement ou ce moment cinétique sont liées aux efforts exercés par l'obstacle sur le fluide. Réciproquement, les efforts exercés par le fluide sur l'obstacle directement opposés au précédent, sont finalement obtenus par :

r F = - dp r dt ! " # $ a = - d r p dt ! " # $ r - % &r p r (5) et r M G = - dH r _G dt ! " # $ % & a - V r _a'r p = - d r H G dt ! " # $ % & r - ( 'r H r G - r V _a'r p (6)

Malgré leur apparente généralité, ces expressions ne constituent malheureusement pas le modèle le plus complet. Il suffit, pour s'en rendre compte de choisir quelques cas particuliers. En effet, en se limitant à une translation pure ( ! "r 0 ) permanente ( r duk

dt ! 0 ), il vient, pour les forces :

F = r 0 r

ce qui constitue le paradoxe de d'Alembert ( pas de traînée) généralisé ( pas de portance non plus). Ce résultat est insuffisant car, même si la portance des corps de révolution est largement plus faible que les ailes, elle n'en existe pas moins. Par ailleurs, l'existence d'une force de traînée est tout à fait évidente, ce que ne prédit visiblement pas cette théorie. Il faut

toutefois remarquer que ce résultat est cohérent avec le cadre dans lequel il a été établi : la théorie de Kirchoff se place dans le cadre fluide parfait (les efforts de frottement sont donc omis ainsi plus généralement que tous les efforts liés à la viscosité du fluide) et pour des obstacles non portants. La suite montrera les mécanismes qui finissent par créer de la portance sur la carène nue.

Pour les moments par rapport à G, en se limitant à un corps de révolution (a22 = a33, a12 = a23

= a31 = 0) et toujours dans le cadre de la translation pure permanente, il vient :

r

M G = 0, a

[

(

33 - a11

)

u1 u3, a

(

11 - a22

)

u2 u1

]

Soit avec : u1 = Va cos! cos" u2 = Va sin" u3 = Va sin! cos"

r M G = 1 2!Va 2 Vol Sref Lref 0, k

(

33 - k11

)

cos 2

" sin 2#

(

)

, k

(

11 - k22

)

sin 2"

( )

cos#

[

]

et en introduisant les coefficients sans dimension de moment de roulis Cl_G, de moment de tangage Cm_G et de moment de lacet Cn_G :

Cl_G = 0 CmG = Vol Sref Lref k

(

33 - k11

)

cos 2 ! sin 2"

(

)

(7) et CnG= Vol

S_ref L_ref k

(

11 - k22

)

sin 2!

( )

cos" (8)

Ces résultats, là aussi cohérents avec le cadre dans lequel ils ont été établis, et même s'ils permettent de comprendre l'instabilité des carènes3

sont sans nul doute également insuffisants puisque résultant d'une distribution de pression qui a conduit à un effort nul.

II-1) Efforts sur l'enveloppe du dirigeable :

Traditionnellement, deux termes de portance apparaissent lors des essais expérimentaux : a) une portance aux faibles incidences dépendant "linéairement" de l'incidence, b) le terme précédent est rapidement dominé par une portance, non linéaire, dite

portance tourbillonnaire.

Curieusement, c'est une méthode fluide parfait approchée, dite théorie des corps élancés4

dont les principes sont rappelés [Ref. 0], qui donne une évaluation du terme a) pour un corps tronqué à l'arrière, présentant de ce fait une section dite de culot Sq. Cette méthode,

qui fait partie des méthodes linéarisées, conduit aux coefficients aérodynamiques suivants (les

3 _{On note en effet que a}

22 = a33 > a11 et l'on trouve

!Cm !" > 0 et

!Cn

!" < 0 : compte tenu des conventions de signes sur les incidences et dérapages, ces deux moments correspondent à des instabilités.

4 _{Cette théorie est développée pour les objets dont les dimensions longitudinales sont beaucoup plus grandes} que les dimensions transversales, ce qui est ici le cas puisque l = D/L = e/L = 0.2436 <<< 1.

9 lignes trigonométriques n'ont pas été linéarisées pour plus de généralité), exprimés dans le repère lié à l'obstacle de révolution :

• coefficient d'effort tangentiel CT = CpA - Cpq - sin 2

! - sin2"

(

)

Sq

Sref

(9)

où Cp_A est un coefficient de pression moyen d'avant-corps, tandis que Cp_q est le coefficient moyen de pression qui s'applique au culot.

• coefficient d'effort normal CN = sin 2!

(

)

cos 2

" Sq Sref

(10) • coefficient d'effort latéral CL = cos! sin 2"

( )

Sq Sref

(11)

• coefficient de moment de tangage par rapport à un point A sur l'axe de révolution :

CmA = - sin 2!

(

)

cos 2

"

[

Sq

(

L - xA

)

- Vol

]

S_ref L_ref (12)

• coefficient de moment de lacet par rapport à un point G sur l'axe de révolution :

CnA = cos! sin 2"

( )

Sq

(

L - xA

)

- Vol

[

]

Sref Lref

(13)

- Pour un corps sans culot, soit Sq = 0, on retrouve sur ces formules la nullité des forces,

tandis qu'inversement la présence d'un culot donne des efforts proportionnels à la section de culot.

- Pour les moments, on note que la théorie des corps élancés traduit le comportement asymptotique quand l'allongement ! = DMC

L tend vers zéro. Dans ce cas, on montre, à partir des résultats fluide parfait exacts, que le coefficient a11 tend vers zéro, tandis que a22

égal à a33 pour un corps de révolution tend vers Ma = ! Vol, soit également k11 -> 0 et k22

= k33 -> 1.

Pour Sq = 0, les formules (12) et (13) sont bien cohérentes avec le comportement

asymptotiques des résultats exacts (7) et (8) .

Inversement, les formules (7) et (8), en présence d'un culot, traduisent une diminution systématique des valeurs absolues des moments, lorsque le point A est situé en amont de l'arrière de l'obstacle, ce qui est fatalement le cas du centre de gravité. Ainsi la présence du culot réduit l'instabilité de carène. L'explication physique de ce phénomène est traitée dans le paragraphe suivant simultanément avec le mécanisme d'apparition de l'effort normal.

II-1-1) Effort normal : origine, modélisation et

comparaison expérimentale :

L'apparition de l'effort normal provient de l'analyse suivante où l'on a seulement représenté une mise en incidence pure ( " = 0) :

Fig. 1 : Distribution théorique des efforts locaux en incidence

Le schéma précédent représente les efforts locaux à l'issue d'une intégration des pressions sur une couronne. On note que les efforts locaux sont positifs lorsque la section de l'obstacle est croissante et inversement.

Si l'intégration par rapport à la variable x est effectuée du nez à l'arrière, on trouve effectivement que les efforts positifs compensent les négatifs, d'où le résultat théorique énoncé F = r 0 , et le moment déstabilisant, qui est un couple pur. r

Si, par la pensée, on coupait l'arrière de l'obstacle à une abscisse xq, en gardant les deux

parties en présence, l'écoulement serait inchangé, et il apparaîtrait sur la face avant un effort normal proportionnel à la section Sq = S(x=xq) et sur la partie arrière un effort opposé.

Si dans un 2ème

temps, on ôte la partie arrière, l'obstacle est alors tronqué, présentant un culot de section Sq. L'écoulement n'apparaît pas singulièrement modifié car, incapable de

contourner les arêtes vives du culot, l'écoulement décolle, créant une pseudo - géométrie, distincte du corps initial, mais cette modification est insignifiante quand le corps est élancé, soit ! <<1 : corrélativement il apparaît maintenant sur l'obstacle à culot un effort normal :

Fig. 2 : Efforts locaux en présence d'un culot

Dans la zone décollée, les vitesses sont faibles, de sorte que la pression s'appuyant sur le culot est très voisine d'une constante, d'où le coefficient de pression moyen Cp_q qui intervient en particulier sur l'effort longitudinal.

x = x1 Va ! x = x₁ V!_a F ! zone décollée

11 On note également, à partir de ce schéma, que la disparition des efforts vers le bas de la partie arrière, diminue le moment cabreur qui traduisait l'instabilité de carène. Selon le culot, et la position du centre de gravité, l'objet par rapport à ce point peut être stable, ou encore instable. Or, dans le cas d'un l'obstacle n'ayant pas de culot, apparaît également, en raison de la viscosité du fluide, un décollement. Dès lors la section à laquelle a lieu le décollement joue le rôle d'une section de culot fictive, à la différence près qu'elle est inconnue, tant que les calculs de la zone visqueuse n'ont pas été effectués. Cette zone visqueuse, de taille caractéristique très faible aux grands nombres de Reynolds , est appelée "couche limite".

Ainsi, sur un corps sans culot, mais en fluide réel, il va également exister un terme d'effort normal, de la forme : CN = Sq Sref sin 2!

(

)

cos2" (14) où le coefficient !CN !" # $ % & " ='= 0 = CN"00 = 2 S_q

S_ref est soit à mesurer expérimentalement, soit à calculer en fonction de la géométrie de l'objet.

De même, pour le coefficient d'effort latéral, il vient un terme équivalent :

CL = Sq Sref

cos! sin 2"

( )

(15)

La théorie des corps élancés donnant les idées de base de traitement de ces obstacles, il existe ensuite une extension de cette théorie capable de prendre en compte le terme b) dit non linéaire, ou de portance tourbillonnaire.

En effet, cette théorie revient à calculer des écoulements transverses, ce qui, dans le cas d'un corps de révolution, est équivalent au calcul de l'écoulement autour d'un cylindre élémentaire de diamètre D(x) = 2 R(x), de longueur dx, attaqué par la composante transversale de V!.

Fig.3 : Coupe dans un plan x = cte

En plus de l'effort élémentaire fluide parfait, responsable du terme linéaire, déjà pris en compte, on considère que ce cylindre élémentaire possède une traînée dF , qui, en projection r sur les axes x2 et x3, fournit un terme d'effort normal et d'effort latéral.

Cet effort élémentaire de traînée est porté par le vecteur unitaire

r

t = -sin! cos" r

k - sin" r j sin2_{! cos}2_{" + sin}2_"

soit : d r F = 1 2! Va sin 2 " cos2# + sin2#

(

)

2 D(x) dx

(

)

Cx Re

(

_D

)

r t

où ReD est le nombre de Reynolds calculé à l'aide du diamètre local D(x) et la vitesse

transverse Va sin 2

! cos2" + sin2", soit :

Re_D = !Va sin 2 " cos2# + sin2# D x

( )

µ = ReL sin 2 " cos2# + sin2# D x

( )

où D x

( )

= D x

( )

L et ReL = ! Va L µ

La fonction Cx(ReD) est la courbe standard de coefficient de traînée d'un cylindre

bidimensionnel en fonction du Reynolds, obtenu en incompressible, telle qu'on peut la trouver, par exemple, dans la [Ref.2].

Partant de la constatation que le cylindre n'est pas 2D, soit à cause des évolutions R(x) soit parce que le corps n'est pas infini, des auteurs pondèrent le résultat précédent d'une fonction !(x) plus ou moins sophistiquée (elle peut notamment dépendre d'un Reynolds longitudinal

Rex =

!Vacos" cos# x

µ = ReL cos" cos# x où x =

x L), conduisant à : d r F = 1 2! Va 2

sin

(

2" cos2# + sin2#

)

D(x) Cx Re

(

_D

)

$ x

( )

r t dx y = x₂ z = x₃ dF -V_a sin! -V a s in " cos ! #

13 D'autres auteurs, au contraire, simplifient cette approche, en considérant que, intégrée de 0 à L, les fonctions de x vont donner un coefficient moyen de traînée Cx (la dépendance vis-à-vis de ! et " intervenant dans ReD est ainsi laissée de côté), conduisant au coefficient

d'effort non linéaire :

r F = 1

2! Va

2

sin

(

2" cos2# + sin2#

)

Cx S_lat r t

où Sm est la surface latérale de l'obstacle, soit Sm = D(x) dx 0

L

!

Soit en projection et en utilisant les coefficients d'effort normal (selon l'axe x3 = z) noté CN

et d'effort latéral (selon l'axe x2 = y) noté CL, avec :

F_x3 = - 1 2! Va 2 S_ref CN et F_x2 = - 1 2! Va 2 S_ref CL :

CN = sin2! cos2" + sin2" sin! cos" Cx Slat

Sref

(16)

et

CL = sin2_{! cos}2_{" + sin}2_{" sin" Cx} Slat

Sref

(17)

On note ainsi, qu'à partir de théories établies en fluide parfait, avec quelques extensions prenant en compte les effets de la viscosité, on arrive à modéliser le coefficient d'effort normal qui, en rassemblant (15) et (16) prend la forme :

CN = Sq Sref

sin 2!

(

)

cos2" + sin2! cos2" + sin2" sin! cos" Cx Slat Sref

(18)

En particulier, à dérapage nul, cette expression se simplifie en :

CN = Sq Sref

sin 2!

(

)

+ sin! sin! Cx Slat Sref

(19)

On trouve ce type de résultat sous la forme ₁ FN 2!V"

2 _{A sin}2

#

= a₀ cotg #

( )

+ C _D, donc à dérapage nul, tracé en fonction de cotg(!) (la modélisation devrait ainsi donner des droites) dans la [Ref.3] où l'auteur a choisi A , qui correspond à notre Sm , comme surface de

référence. Avec ce choix de surface de référence, le coefficient a0 de l'auteur s'identifie à 2 Sq

Slat.

tandis que le coefficient moyen de traînée (drag) C _D coïncide avec notre Cx.

Plusieurs dirigeables sont représentés, certains avec des contours circulaires, d'autres polygonaux, à des Reynolds ReL variant entre 18-13 10

6

et 0.38 106

, et des rapports diamètre sur longueurs variant entre 0.211 (S.S..Z) et 0.099 (R.29).

Les résultats expérimentaux confirment la forme générale du coefficient d'effort normal, avec des valeurs de a0 qui semblent très proches pour tous ces dirigeables. L'exploitation des

différentes courbes de cette référence, montre toutefois des valeurs numériques de a0 avec

des écarts sensibles (cf. Tableau 1 p.15).

Par contre, l'extrapolation pour cotg(!) = 0 donne des valeurs C D qui sont visiblement très

fortement variables. Évidemment, cette grandeur caractéristique de l'écoulement transversal, est très sensible à la forme de la section ( polygonale ou circulaire), au nombre de Reynolds transversal, et à l'allongement qui interviendrait sur la fonction de pondération "(x).

Les premiers essais sur la carène nue, tirés de la [réf.4] ont permis de déterminer les paramètres Sq

Sref

et Cx Slat Sref

sur la maquette à l'échelle 1/20ème

de l'AS 500, à partir d'un lissage de la courbe expérimentale par une technique de moindre carré :

Fig. 4 : Résultat expérimental et lissage par moindre carré- Expérience [Ref. 4]

Dans cette représentation, la surface de référence choisie est la surface frontale, ou surface du maître - couple SMC. Il vient alors :

C_N = 0.21059757 sin 2!

( )

+ 2.25999747 sin! sin!

Bien entendu la précision de ce résultat issu de la minimisation des écarts entre les points expérimentaux et les valeurs données par la fonction théorique CN(!) est illusoire, compte tenu des imperfections expérimentales, et le résultat précédent sera simplement écrit :

C_N = 0.21 sin 2!

( )

+ 2.26 sin! sin! (20)

Coefficient d'effort normal en fonction de sin(2!)

-0,2 -0,1 0 0,1 0,2 0,3 0,4 0,5 0,6 -0,4 -0,2 0 0,2 0,4 0,6 sin(2!) CN Expé Moindre carré

15 Une remarque peut être effectuée sur la répétabilité des mesures. La maquette, depuis les essais de la [Ref. 4] a été démontée, puis remontée pour la nouvelle série d' essais. À la date de ce rapport, seuls les fichiers de mesure de la [Ref.5] sont disponibles, avec en particulier un essai carène nue.

Fig. 5: Résultat expérimental de la 2ème

campagne d'essai- Comparaison avec le lissage Du résultat de la 1ère _{campagne d'essai - (20)}

Si une autre surface de référence avait été choisie, par exemple le volume à la puissance 2/3, il aurait fallu écrire :

F_x3 = - 1 2! Va 2 S_MC CN = - 1 2! Va 2 Vol2/3 CN' soit CN' = SMC Vol2/3 CN (21)

Les données géométriques du dirigeable telles qu'elles ont été approchées (cf. annexe Données Géométriques AS 500) fournissent :

S_MC

Vol2/3 ! 0.457 et le résultat expérimental (20) prendrait la forme, avec le volume à la puissance 2/3 comme surface de référence :

C_N' = 0.0962 sin 2!

(

)

+ 1.0323 sin! sin! (22)

Bien entendu, quel que soit le choix de la surface de référence, les efforts doivent être identiques.

Enfin, si la surface latérale Slat avait été choisie comme référence, on aurait un nouveau

coefficient d'effort normal CN", tel que :

C

N

en fonction de sin(2 !) - Carène nue

-0,2 -0,1 0 0,1 0,2 0,3 0,4 0,5 0,6 -0,4 0,1 0,6 sin(2 !) CN Expérience lissage M.C. Mazeran

CN" = SMC Slat CN ₍₂₃₎ Soit avec SMC Slat. ! 0.237111:

C_N" = 0.049793 sin 2!

( )

+ 0.535872 sin! sin! ou également pour ! positif :

CN"

sin2! = 0.099587 cotg! + 0.535872 (24)

En comparant avec les données extrapolées des courbes de la [Ref.3 - Fig IX.23] : Dirigeables " Reynolds CD moy a0 Section

Parseval 0,176 380000 1,129730 0,043784 Circulaire S.S 0,192 730000 0,627027 0,059459 Circulaire S.S.Z 0,211 730000 0,545946 0,072216 Circulaire R101 0,17 1140000 0,455135 0,059892 Circulaire AM 3(a) 0,182 1060000 0,455135 0,059892 Circulaire Akron 0,169 13 à 18 10^6 0,567568 0,074595 Circulaire R.32 0,106 1180000 0,437838 0,058703 polygonal R.33 0,123 1350000 0,335135 0,042162 polygonal AM 3(a) 0,182 1060000 0,654054 0,067676 polygonal AS 500 soufflerie 0,244 642000 0,535872 0,099587 circulaire Tableau. 1 : Comparaison des données de la [Ref.3] et de l'AS 500 en soufflerie

-> On constate que notre valeur du coefficient linéaire est beaucoup plus élevée que la majorité des dirigeables présentés. Toutefois, il faut nous comparer, d'abord avec d'autres carènes de dirigeable testées dans la même gamme de Reynolds, comme le S.S et le S.S.Z et ensuite avec le même ordre de grandeur pour l'allongement. Prenant précisément ces deux dirigeables, on constate bien que a0 croît en passant du S.S (" = 0.192) au S.S.Z (" =

0.211). Il est donc logique que notre carène, encore plus épaisse, présentant donc un décollement plus sévère ait une valeur de a0 la plus élevée.

-> Notre coefficient du terme non linéaire, soit C D est par contre tout à fait comparable aux valeurs de la [Ref.3]. Seuls le Parseval (Reynolds très faible) et le R.33 (section polygonale) s'écartent notablement des autres dirigeables. Effectuant la moyenne des

C D privée des deux dirigeables mentionnés, on trouve une valeur moyenne de C D ! 0.5347, à comparer avec notre valeur de 0.5359…

En conclusion, on peut dire que nos valeurs expérimentales restent cohérentes avec la [Ref.3]. Sur la base de la modélisation de notre carène donnée par (20) et en rappelant que

u₁ = V_a cos! cos" u₂ = V_a sin! u₃ = V_a sin! cos" , on obtiendrait, à dérapage nul pour l'effort normal :

17 F_N = - 1

2 ! SMC 0.42 u

[

1 u3 + 2.26 u3 u3

]

À titre d'application numérique, pour une vitesse Va = 10 m/s , soit 36 km/h, une incidence

de 10°, et une masse volumique de l'air aux conditions standard ! = 1.225 kg/3

, le Dirigeable AS 500 soit SMC = 2.835 m

2

, carène nue, et en supposant que les valeurs de (20) sont identiques à l'échelle 1, subirait un effort normal de :

F_N = - 24.3 N

Sur cet ordre de grandeur, on comprend aisément pourquoi il est d'usage de parler de corps "non portants" pour une carène, eu égard à la petitesse des efforts.

II-1-1-1) Effort normal : Confirmation numérique du

terme linéaire

Le résultat (20) étant acquis, il importe de vérifier par calcul que la distribution de pression sur l'obstacle conduit bien à un décollement dont la position donne accès à la section de culot fictive Sq.

Le calcul de l'écoulement en fluide parfait sur la carène du Dirigeable AS 500 a été effectué par une classique méthode des singularités. Ce code de calcul donne les coefficients de fluide ajouté et la distribution de pression. Bien entendu, cette dernière, intégrée sur l'obstacle doit donner un effort nul.

Dans un 2ème

temps, sont effectués des calculs de couche limite utilisant explicitement la distribution de pression précédente comme condition à l'extérieur de la zone visqueuse. Compte tenu du fait que C_N!00 = "CN

"! # $ % & !=0 = 2 Sq

S_ref , seul est utile un calcul à incidence nulle.

Un 1er

calcul en transition naturelle5

a été effectué [resCLlaas2611] aux conditions expérimentales, soit :

Va = 24 m/s L = 0.39 m soit un Reynolds de 6.42 10

5._{. Le taux de turbulence de la}

soufflerie étant de " = 0.7% : le calcul montre que, dans ces conditions, il existe une transition laminaire - turbulent à l'abscisse réduite x _T = xT

L = 0.8169 suivie d'un décollement turbulent très proche, à l'abscisse réduite x _D = xD

L = 0.8407. Avec cette valeur, le rapport Sq

Sref

avec la surface frontale comme surface de référence, s'écrit

Sq Sref = ! R 2 (xq) ! RMC 2 = R q R MC " # $ % & ' 2

et prend la valeur 0.530 au lieu des 0.210 qui ont été trouvés

5 _{À l'origine de l'obstacle, la couche limite est laminaire. Des mécanismes d'instabilités apparaissent ensuite} tendant à faire apparaître un régime turbulent. Des critères établissent alors si ces seuils d'instabilité sont atteints ou non. Dans la négative, le régime reste laminaire, sinon le calcul est poursuivi en turbulent.

expérimentalement. L'écart est même plus important car de façon plus complète, la couche limite en s'épaississant tout le long de l'obstacle, crée un effet de déformation caractérisée par une épaisseur !1(x) appelée "épaisseur de déplacement". L'obstacle baignant dans le fluide

visqueux apparaît ainsi épaissi, et corrélativement, le rayon effectif de l'objet au niveau du décollement est Rq + !

[ ]

1 q. En prenant en compte cet épaississement, il vient

S_q S_ref ! " # $ % & mod

= 0.5672 .L'explication de cet écart important avec la valeur expérimentale, provient du fait que, aux Reynolds testés, les résultats sont très sensibles à la transition laminaire - turbulente de la couche limite.

D'autres calculs ont alors été effectués en changeant la vitesse : - à Va = 27 m/s [ rescllaas2612], soit un Reynolds de 7.23 10

5

, la transition se déplace un peu en direction du bord d'attaque, soit x T = 0.8151 et le décollement turbulent est à

x D = 0.8428, soit, compte tenu de l'épaisseur de déplacement

S_q S_ref ! " # $ % & mod. = 0.5588. - puis à Va = 30 m/s [resCLlaas], soit un Reynolds de 8.03 10

5

, la transition continue d'avancer, soit x T = 0.8126 mais cette avancée est maintenant suffisante pour que

l'écoulement turbulent puisse maintenant pleinement se développer conduisant à un décollement turbulent beaucoup plus aval, à x D = 0.9680, soit, toujours avec

l'épaississement Sq S_ref ! " # $ % & mod.

= 0.1587, valeur maintenant inférieure à la valeur mesurée ! On peut objecter que le calcul précédent n'a pas de sens car l'essai s'est bien déroulé à 24 m/s et non à 30, mais d'autres facteurs entrent en jeu dans le mécanisme de transition : par exemple un fil sur la paroi6

peut déclencher artificiellement cette transition ou également les mâts supports de la maquette peuvent l'avoir fait, créant un écoulement turbulent à leur aval. Or, numériquement, il est possible de simuler ce déclenchement…

Ici, les mâts sont à l'abscisse x = 0.14 m, auquel correspond une abscisse curviligne réduite de s _T = 0.4043. Si l'on suppose que le déclenchement a eu lieu exactement en ce point (resCLlaas7], le décollement se produit à x D = 0.9553, soit

S_q S_ref ! " # $ % & mod. = 0.21958 !

En fait la contamination par les mâts se produit dans leur sillage et la couche limite n'est certainement pas turbulente dès les mâts, mais sans doute plus à l'aval. Un autre calcul

[ resCLlaas8] a alors été effectué en déclenchant la transition un peu en aval des mâts, soit à une abscisse curviligne réduite de s T = 0.50 auquel correspond l'abscisse x = 0. 1774 m sur

la maquette. Le décollement se produit alors à x D = 0.9605, soit

S_q S_ref ! " # $ % & mod. = 0.1991 !

On voit ainsi que la valeur du coefficient en sin(2") de l'effort normal est très sensible à la position du point de transition. Il est en fait inutile de chercher a posteriori de façon précise la

6 _{Il s'agit d'une technique classique pour fixer un point de transition. Sur nos maquettes l'épaisseur du fil est de} l'ordre de 0.1 mm. D'autres techniques existent comme une bande de carborundum qui a l'avantage d'être un moyen moins brutal que le fil.

19 position de la transition pour retrouver exactement la valeur 0.210. Il faut remarquer en effet que dans les conditions de l'expérience, soit 24 m/s, l'effort correspondant à ce que nous avons appelé le terme linéaire de l'effort normal, soit C_N = 0.21 sin 2!

( )

donne, par exemple à 10°, seulement 0,1796 N, soit 18.31 grammes force !

D'autres calculs ont alors été effectués, cette fois-ci grandeur nature, soit L = 7.8 m, pour des vitesses allant de 5 km/h (1.39 m/s) jusqu'à 50 km/h ( 13,9 m/s). Le taux de turbulence de l'air calme est plus faible que celui de la soufflerie, soit ! = 0,05 %

Pour Va = 5 km/h, soit Re = 7.44 10 5

, il n'y pas de transition à cause de la diminution du taux extérieur de turbulence, et un décollement laminaire apparaît à x D = 0.8328 et

S_q S_ref ! " # $ % & mod. = 0.5871 ! À Va = 10 km/h, soit Re = 1,49 10 6

, il y une transition naturelle x T = 0.8323 mais le

décollement turbulent suit immédiatement à x D = 0.8387 et

S_q S_ref ! " # $ % & mod. = 0.5608.

Pour les vitesses 20, 30, 40 et 50 km/h, une transition apparaît systématiquement, qui remonte progressivement vers le nez, et le régime turbulent a pleinement le temps de s'établir, avec un recul du décollement. Le rapport Sq

S_ref ! " # $ % & mod.

prend respectivement les valeurs suivantes : 0.1156, 0.1131, 0.1064 et 0.1129.

Ceci étant, on a observé que le dirigeable, même gonflé, comporte beaucoup de plis le long des coutures : il en résulte que vraisemblablement, ces irrégularités vont provoquer un déclenchement de la couche limite. La position de celui-ci est bien sûr mal connue, mais des calculs la supposant très près du nez, soit en abscisse curviligne réduite s T = 0.1, donnent

les résultats suivants :

Va en km/h 5 10 20 30 40 50

[Sq/Sref]mod. 0,2354 0,1996 0,1903 0,1833 0,1743 0,1713

Pour la plus basse vitesse, le nombre de Reynolds entre la soufflerie et l'échelle 1 sont comparables et l'on retrouve l'ordre de grandeur du résultat soufflerie, l'écart avec la valeur retenue 0.21 venant de la différence sur la position du point de transition.

Ensuite, on observe une décroissance du coefficient liée à l'augmentation du nombre de Reynolds, avec ici la transition fixée, d'où un recul du décollement.

Si une modélisation de cet effet Reynolds sur le décollement était souhaitée, se traduisant par une évolution du rapport Sq

S_ref ! " # $ % & mod.

, on pourrait par exemple utiliser la relation :

S_q S_ref ! " # $ % & mod. = 0,03428 + 1, 91427 Re1/6

Qui donne des résultats très proches des valeurs calculées.

II-1-1-2) Effort normal : Confirmation numérique du

terme non linéaire

On a vu que ce terme était lié à ce qui est nommé la "portance tourbillonnaire".

En effet, à une incidence suffisamment élevée, une coupe par un plan x = cte montre le champ des vitesses suivant :

Fig. 5 : Allure qualitative de l'écoulement transversal

C'est exactement ce type d'écoulement qui est retrouvé à l'arrière d'un cylindre circulaire infini, avec deux structures tourbillonnaires contrarotatives côté extrados de l'obstacle, ce qui explique la modélisation adoptée en ajoutant un terme de traînée.

Ceci étant, en bidimensionnel, le point de décollement est intimement lié, là encore, à la nature laminaire ou turbulente de l'écoulement, directement liée à la fois au Reynolds longitudinal et transversal.

Ainsi, si le Reynolds transversal est compris entre 104

et 2 105

, environ, le coefficient de traînée d'un cylindre de longueur L, est constant et égal à 1.2 en prenant la surface de référence 2 R L. Si notre carène, du nez à l'arrière, avait donc cette valeur constante du Cx, on obtiendrait "rigoureusement" un coefficient d'effort normal résultant de ces traînées élémentaires en : CN tourb. = sin 2 ! Cx Slat Sref = 1.2 sin2! Slat Sref soit CN tourb. = 5.06 sin 2 !

avec la surface du maître - couple comme surface de référence : les données géométriques de l'AS 500 fournissent effectivement Slat. = 11.9576 m

3

, soit Slat Sref

= 4.2174. On note que la valeur expérimentale obtenue 2.26 sin2

! est beaucoup plus faible pour deux raisons :

y = x₂

z = x₃ point de décollement

21 - d'une part le fait que l'obstacle est évolutif en x et non un cylindre 2D: c'est la fonction !(x) dont il a été déjà fait mention qui peut prendre en compte cet aspect. Pour illustrer de façon caricaturale ceci, si l'on appliquait à une sphère notre formule, on obtiendrait, puisque Slat = SMC = Sref, un coefficient de traînée de 1.2 alors que, dans cette

gamme de Reynolds, il n'est que de l'ordre de 0.45 [Ref. 2 p. 295]. Également, toujours d'après la [Ref. 2], on note qu'un cylindre non plus 2D, soit un rapport L/D infini, mais avec L/D = 5, soit " = 0.2, et dans la gamme de Reynolds entre 104

et 2 105

, voit son coefficient de traînée passer de 1.2 à un peu moins de 0.8 ce qui illustre également l'effet tridimensionnel.

- d'autre part, on a vu sur les calculs de l'écoulement longitudinal, que des transitions naturelles apparaissaient, ou étaient déclenchées vraisemblablement par les mâts, dans la situation "soufflerie", alors qu'à l'échelle 1, nous avons fait référence aux plis de l'enveloppe comme cause suffisante de déclenchement de la transition. Dans ces conditions, sur un cylindre 2D, l'écoulement transversal est également turbulent, et corrélativement, on assiste à un recul des décollements associé à une diminution du coefficient de traînée. La chute est très spectaculaire puisque, en 2D, on passe d'un coefficient de traînée de 1.2 à 0.3 à un Reynolds de 5 105

puis le coefficient de traînée recroît quand le Reynolds est supérieur à cette valeur. On peut mentionner également que la mise en incidence amplifie les phénomènes de transition par aggravation des gradients de pression positifs. Dès lors, si la transition apparaît à incidence nulle, elle existe a fortiori en incidence.

On peut alors pratiquement affirmer qu'un majorant de notre effort normal d'origine tourbillonnaire est la valeur 5.06 sin2! obtenue à partir de Cxcyl. = 1.2 et !(x) = 1 alors

qu'un minorant, obtenue avec Cxcyl. = 0.3 donne le quart, soit 1.265 sin 2

!.

Notre valeur expérimentale de 2.26 sin2! est donc parfaitement crédible comme le soulignait le paragraphe précédent [cf. Tableau 1], en ramenant ce terme à la surface latérale de façon à le comparer avec les résultats de la [Ref.3]. En termes de coefficient de traînée, la valeur obtenue, compte tenu de la valeur Slat

Sref

= 4.2174, est Cx = 0.5359 correspondant aux régimes de décollement avec écoulement turbulent.

Sur la configuration à l'échelle 1, ce coefficient ne va que peu évoluer et nous supposerons effectivement qu'il reste constant.

En généralisant au cas présentant un dérapage, le coefficient d'effort normal, avec la surface du maître - couple comme surface de référence, est de la forme :

• Dans la configuration soufflerie ( Re = 6.42 105

, transition au voisinage des mâts):

CN = 0.21 sin 2!

(

)

cos 2

" + 2.26 sin2! cos2" + sin2" sin! cos" • Dans la configuration échelle 1 ( Re variable, transition près du nez) :

C_N = 0.03428 + 1.91427 Re1/6 ! " # $ sin 2%

(

)

cos 2

II-1-2) Effort latéral : origine, modélisation et

comparaison expérimentale :

Ce paragraphe bénéficie de l'expérience du paragraphe précédent. On a vu en effet comment naissait l'effort normal, et l'origine de l'effort latéral, qui n'existe qu'en présence d'un dérapage et tout à fait analogue, résultant de l'addition d'un terme linéaire, et d'un terme non linéaire, soit :

CL = cos! sin 2"

( )

Sq

Sref

+ sin2! cos2" + sin2" sin" Cx Slat Sref

(26)

• Soit, dans la configuration soufflerie :

CL = 0.21 cos! sin 2"

( )

Sq

Sref

+ 2.26 sin2! cos2" + sin2" sin"

• Et dans la configuration échelle 1 : C_L = 0.03428 + 1.91427

Re1/6 !

"

#

$ cos% sin 2&

( )

+ 2.26 sin

2

% cos2& + sin2& sin& (27)

II-1-3) Effort tangentiel : origine, modélisation et

comparaison expérimentale :

On a vu que la théorie de Kirchoff donnait un effort global nul, donc un effort tangentiel également nul, puis, que la théorie des corps élancés fournissait un terme (9) de la forme :

CT = CpA - Cpq - sin 2

! - sin2"

(

)

Sq

Sref

Dans cette écriture, sont clairement pris en compte, soit un culot réel, soit un culot fictif, les deux situations conduisant au-delà d'une certaine abscisse à un coefficient de pression moyen constant Cp_q dans la zone décollée.

Malheureusement, cette expression :

- obtenue d'une part en fluide parfait, ne prévoit pas la prise en compte du frottement, présent même à ! et " nuls et qui se superpose aux termes de pression,

- limitée d'autre part aux petites perturbations, soit incidence et dérapage faibles, est incapable de prédire la disparition de ce terme pour ! ou " égaux à 90°.

Il faut remonter un peu au sein des éléments théoriques fluide parfait pour trouver une expression un peu plus générale, dont (9) est la forme simplifiée pour ! et " faibles, de la forme :

23 C_T = C_{T 0} cos2! cos2" + CT90 ( 1 - cos

2

! cos2") qui se réduit à dérapage nul à :

C_T = C_{T 0} cos2! + C_T90 sin2!

Bien entendu, dans le cadre "fluide parfait ", les deux coefficients CT0 et CT90 sont nuls,

mais cette relation incite plus généralement à chercher le coefficient d'effort tangentiel, sous la forme :

C_T = C_{T 0}

( )

! cos2! + CT90

( )

! sin 2

! dont seule la forme C_T = C_{T 0}

( )

! cos2! est conservée.

Aux petites incidences et compte tenu de la parité de ce coefficient quand on change ! en son opposé, on a : CT 0

( )

! " CT 0

( )

0 + #CT0 #!2 $ % & '

( )

0 ! 2 + ...

Le terme C_{T 0}

( )

0 contient deux contributions physiques distinctes, un terme de pression lié au décollement et le terme de frottement. Ce terme sera confronté entre expérience et calcul un peu plus loin.

En ce qui concerne la dépendance non linéaire en !, on trouve dans la littérature que, théoriquement pour un corps élancé, le rapport CT 0

( )

! - CT0

( )

0

CN " - !

2 quand ! tend vers zéro, ce qui signifie que l'effort aérodynamique uniquement dû à l'incidence est bissecteur de l'angle formé par l'axe de révolution et la direction V r _a. Les résultats expérimentaux sont loin de montrer un tel comportement, mais il faut mettre en avant que fait que le coefficient d'effort tangentiel est un coefficient très délicat à mesurer : expérimentalement, la balance donne accès aux coefficients de traînée Cx et de portance Cz, les coefficients d'effort tangentiel CT et normal CN étant ensuite déduits par les relations trigonométriques :

CT = cos! Cx - sin! Cz CN = sin! Cx + cos! Cz

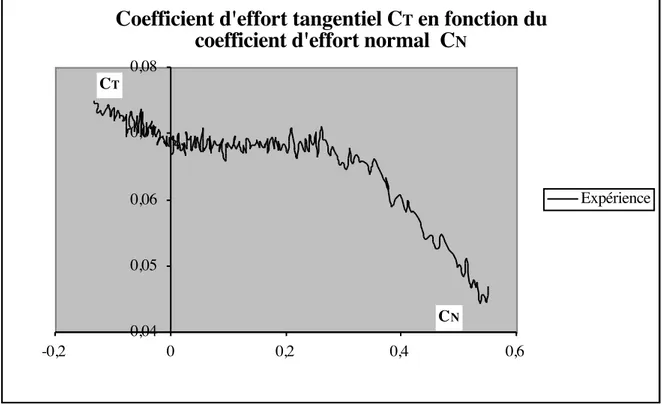
Dans le cas de la carène nue, le CT apparaît comme la différence de deux termes du même ordre de grandeur ce qui explique ses fluctuations importantes: le schéma ci-après [Fig.6] donne le tracé de ce coefficient, où l'on note que la parité vis-à-vis de l'incidence n'est pas retrouvée.

Gardant dans l'esprit le rôle censé être joué à la fois par le rapport CT

cos2! et par le produit CN !

2 , nous avons tracé [Fig.7] les résultats expérimentaux du CT sous la forme CT

( )

! cos2! " CT

( )

0 = F CN tg( ! 2) # $ % & .

Fig. 6 : Évolution du CT en fonction du CN carène nue

Fig. 7

La courbe ci-dessus, après détermination de la valeur CT(0) expérimentale, montre une légère dépendance vis-à-vis du paramètre CN tg(!

2) . Compte tenu de ce résultat, le coefficient d'effort tangentiel est finalement représenté par :

Coefficient d'effort tangentiel C

T

en fonction du

coefficient d'effort normal C

N

0,04 0,05 0,06 0,07 0,08 -0,2 0 0,2 0,4 0,6 CN CT Expérience

Courbe Y = C

T

/cos(!)^2 - C

T

(0) = F [ C

N

tg(!/2) ]

-0,10 -0,08 -0,06 -0,04 -0,02 0,00 0,02 0,04 0,06 0,08 0,10 -0,02 0,00 0,02 0,04 0,06 0,08 0,10 0,12 0,14 CN tg( !/2) Y Expérience

25 CT = 0.07178 - 0.0862 CN tg(! 2) " # $ % cos 2 !

On note la valeur CT( )0 = CT₀( )0 = 0.07178 qui correspond à l'effort tangentiel, ou au coefficient de traînée, à incidence nulle, et la suite de ce paragraphe montre la cohérence de ce résultat avec des calculs portant à la fois sur la détermination de la contribution en pression et en frottement

Les calculs par une méthode des singularités donnent la distribution théorique des coefficients de pression sur la carène nue, à incidence et dérapage nue :

Fig. 8

La solution analytique qui existe pour l'ellipsoïde a été superposée à la courbe obtenue pour l'AS 500. On note que la modélisation de la géométrie sous forme de trois tronçons est révélée par le calcul aérodynamique, car, malgré le raccord continu et à tangente continue des trois parties, il y a discontinuité des dérivées secondes, ce qui ne passe pas inaperçu, "aérodynamiquement" parlant… Ceci étant, on note qu'au-delà de 70% les distributions de pression sont suffisamment proches pour être confondues.

La prise en compte d'un décollement, au-delà d'une abscisse xq revient alors, dans

l'hypothèse de corps élancés, à prendre ce résultat de calcul valable de 0 à xq, puis de

supposer que dans la zone décollée, le niveau de Cp au point de décollement, Cpq, est

maintenu de xq à L.

Soit pour la contribution de la pression :

C_{T 0}

[

]

p = 2! Cp(x) R R' dx S_ref + 0 xq

"

2! Cpq R R' dx S_ref xq L

"

Distribution de coefficient de pression sur l'AS 500 à incidence et dérapage nuls -0,3 -0,1 0,1 0,3 0,5 0,7 0,9 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 x Calcul Ellipsoïde

D'où, puisque Cp(x) R R' dx S_ref = 0

0 L

!

et que Cpq est pris constant :

CT 0

[

]

p = - 2! Cp(x) R R' dx Sref - xq L

"

Cpq Sq Sref

Plutôt que d'intégrer numériquement le 1er

terme, nous avons utilisé la coïncidence des Cp(x) avec l'ellipsoïde sur la partie arrière, soit :

CT 0

[

]

p = - 2! Cpell.(x) R R' dx Sref - xq L

"

Cpq Sq Sref

Le résultat est alors analytique moyennant quelques calculs d'intégrales, soit :

C_{T 0}

[

]

p = 4 x q (1- x q) 1 - Cpq - 1 + k₁₁

(

)

2 1 - !2 " # $ % & ' + 1 + k₁₁

(

)

2 !2 1 - !2

(

)

2 Log 1- 4 x _q (1 - x _q) 1 - !2

(

)

!2 " # $ % & ' Compte tenu des calculs de couche limite évoqués pour les efforts normaux, pour chaque cas retenus, on accède à la fois à la position du point de décollement x _q et au niveau de Cpq

correspondant. La relation ci-dessus donne ensuite le coefficient

[

CT 0

]

p

À ce coefficient, il faut ajouter la contribution du frottement : la démarche retenue afin de donner une modélisation de ce terme, consiste à utiliser les résultats de plaque plane appliqués à notre surface mouillée.

En présence d'une couche limite mixte, laminaire turbulent ce coefficient prend la forme :

C_{T 0}

[

]

f = 1.328 Re_L x T 0.6 + ReL 0.4 59.281884 1 - x

(

T

)

! " # $ % & 5 6 _Sw S_ref

où Sw est la surface mouillée de l'obstacle, et x _T l'abscisse réduite de transition. Les données géométriques de l'AS 500 donne un rapport Sw

Sref

= 13.601. D'où le tableau suivant :

Coefficient d'effort tangentiel à ! = " = 0 : Calculs conditions Soufflerie

24 m/s TD mâts 24 m/s TD aval mâts dû à la pression 0,0453 0,0405 dû au frottement 0,0534 0,0493 CT0(0) 0,0987 0,0898

On rappelle que, sur la base du coefficient d'effort normal, les résultats expérimentaux se situent entre les deux cas ci-dessus.

27 On note ainsi que les calculs, dans la situation soufflerie, donnent un CT à incidence nulle compris entre 0.0987 et 0.0898 alors que les résultats expérimentaux ont fourni une valeur de l'ordre de 0.07178 : on retrouve là encore la difficulté intrinsèque pour l'aérodynamicien à déterminer de façon précise un coefficient de traînée, ici quantité extrêmement faible alors même que le choix de la surface frontale comme surface de référence amplifie cette valeur… En termes de force, le coefficient 0.07178, dans les conditions d'essai, correspond à une force de 0.18 N, soit environ 18 gramme force !

Les calculs équivalents, mais en conditions réelles, conduisent à : Coefficient d'effort tangentiel à ! = " = 0 : Calculs échelle 1

5 Km/h 10 Km/h 20 Km/h 30 Km/h 40 Km/h 50 Km/h dû à la pression 0,0458 0,0330 0,0349 0,0343 0,0301 0,0306 dû au frottement 0,0626 0,0552 0,0488 0,0454 0,0432 0,0416 CT0 0,10837 0,08816 0,08370 0,07973 0,07333 0,07211

On note donc un effet du nombre de Reynolds qui induit une diminution du coefficient CT0

lorsque la vitesse croît. De même que pour le coefficient d'effort normal, cette évolution peut être modélisée par une expression du type :

CT₀ = - 0,0054 + 1,0829 Re1/6

La modélisation du CT a été effectuée en l'absence de dérapage. Il convient alors de remarquer que, pour la carène nue, corps de révolution, la notion séparée de dérapage et d'incidence est purement arbitraire. Dans un référentiel qui contient à la fois l'axe de révolution et le vecteur vitesse V r _a, l'objet est seulement à l'incidence !a reliée à l'incidence a

et au dérapage b par :

cos!a = cos! cos" sin!a = 1 - cos

2

! cos2"

La modélisation du coefficient CT, sur la carène nue, en présence d'une incidence et d'un dérapage et à l'échelle 1 pourrait ainsi être, incidence et dérapage étant censés varier au pire de 0 à 90° : CT = -0,0054 + 1,0829 Re1/6 - 0.0862 CN 1 - cos! cos" 1 + cos! cos" # $ % & ' ( cos 2 ! cos2"

où le coefficient d'effort normal CN est donné par (25). On note qu'en l'absence de données supplémentaires le coefficient -0.0862 obtenu expérimentalement, est supposé gardé cette valeur aux Reynolds plus élevés.