Paramétrisation et classification de signaux en contrôle non destructif. Application à la reconnaissance des défauts de rails par courants de Foucault

HAL Id: tel-00006600

https://tel.archives-ouvertes.fr/tel-00006600

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

non destructif. Application à la reconnaissance des

défauts de rails par courants de Foucault

Latifa Oukhellou

To cite this version:

Latifa Oukhellou. Paramétrisation et classification de signaux en contrôle non destructif. Application à la reconnaissance des défauts de rails par courants de Foucault. Traitement du signal et de l’image [eess.SP]. Université Paris Sud - Paris XI, 1997. Français. �tel-00006600�

UNIVERSITÉ DE PARIS-SUD

Centre d'Orsay

THESE

présentée par

Latifa OUKHELLOU

pour obtenir le grade de Docteur en Sciences

de l'Université Paris XI Orsay

TITRE :

Paramétrisation et Classification de Signaux

en Contrôle Non Destructif. Application à la

Reconnaissance des Défauts

de Rails par Courants de Foucault

Soutenue le 4 juillet 1997 devant la commission d'examen :

MM P. AKNIN Examinateur G. DELAUNAY Rapporteur J. DEPREZ Examinateur G. DREYFUS Rapporteur B. DUBUISSON Président J.P. PERRIN Invité D. PLACKO Examinateur

Le travail de recherche que décrit ce mémoire de thèse a été mené au Laboratoire des Technologies Nouvelles (LTN) de l'INRETS. Je tiens à témoigner ici toute ma gratitude envers son Directeur, Monsieur Pascal, Directeur de Recherche à l'INRETS, pour m'avoir accueillie au sein de son Laboratoire et soutenue durant ces années de recherche.

Monsieur Aknin, Chargé de Recherche à l'INRETS, a dirigé mes travaux. Je tiens à le remercier pour son encadrement dynamique, son aide précieuse et son soutien permanent tout au long de ces années. Ses multiples compétences et sa rigueur ont beaucoup contribué à l'aboutissement de cette recherche. Qu'il trouve ici l'expression de toute ma reconnaissance. Je remercie vivement Monsieur Placko, Professeur à l'ENS-Cachan, pour ses conseils et ses suggestions, en particulier ceux liés aux aspects "contrôle non destructif".

J'adresse mes plus vifs remerciements à Monsieur Dubuisson, Professeur à l'Université de Technologie de Compiègne, d'avoir bien voulu participer à ce jury, ceci en dépit de ses multiples activités.

Je remercie vivement Monsieur Delaunay, Professeur à l'Université de Reims, pour l'intérêt qu'il a porté à mes travaux de recherche et pour avoir accepté de les évaluer.

Je tiens à remercier Monsieur Dreyfus, Professeur à l'Ecole Supérieure de Physique et de Chimie Industrielles de la ville de Paris, pour l'honneur qu'il me fait d'examiner ce travail en qualité de rapporteur. Ses avis et ses remarques constructives m'ont été précieux.

J'adresse également mes remerciements à Monsieur Deprez, Professeur à L'université d'Orsay (Paris XI), pour sa participation au jury.

Pour avoir accepté de participer à ce jury et pour avoir suivi cette recherche, j'exprime toute ma reconnaissance à Monsieur Perrin, Conseiller Scientifique à la RATP. Je remercie également Messieurs Plagne et Bleno du service Logistique de la RATP, pour avoir initié ce projet de recherche et pour leur collaboration durant ces années.

Enfin je remercie Angèle Darly et Pierre-Emmanuel Barjonet pour leur relecture du manuscrit et plus généralement l'ensemble du personnel du LTN pour avoir participé, directement ou indirectement, à l'élaboration de ce travail.

Résumés

Notations

Sigles utilisés

I . Introduction générale

II . Capteur à courants de Foucault pour la détection de défauts de rails

II.2 Différentes technologies pour le contrôle des rails. ... 6

II.3 Contexte ferroviaire II.3.1 Cahier des charges ... 8

II.3.2 définition de la cible ... 11

II.3.3 Cibles étalons ... 12

II.4 Généralités sur les capteurs inductifs II.4.1 Principe des capteurs inductifs ... 13

II.4.2 Plan d’impédance normalisée ... 15

II.4.3 Contrôle multifréquence et par Courants de Foucault pulsés ... 18

II.4.4 Différentes géométries de sondes CF ... 19

II.5 Prototype modulaire II.5.1 Géométrie d’un capteur élémentaire ... 21

II.5.2 Blindage passif ... 23

II.5.3 Simulations numériques par éléments finis ... 24

II.5.4 Réalisation et test de 3 capteurs modulaires ... 27

II.6 Multicapteur II.6.1 Mesures simples et différentielles ... 29

II.6.2 Blindage actif ... 33

II.6.3 Dimensionnement axial du dispositif ... 37

II.6.4 Conception du multicapteur ... 41

II.6.5 Choix des fréquences d’alimentation ... 45

II.7 Electronique associée II.7.1 Banc de mesure en laboratoire à détection synchrone ... 51

II.7.2 Chaîne de mesure pour les essais sur site ... 52

II.8 Essais sur site II.8.1 Description du site ... 54

II.8.3 Pré-filtrage et Trigger ... 57

II.8.4 Classe de défauts ... 58

II.8.5 Constitution de la base de données ... 62

II.9 Conclusion ... 63

III . Paramétrisation des signaux

III.2 Approches heuristiques III.2.1 Paramètres spatio-temporels et fréquentiels ... 67

III.2.2 Paramètres géométriques dans le plan de Lissajous ... 68

III.2.3 Transformation non linéaire dans le plan de Lissajous : angle local 69 III.2.4 Inconvénients des approches heuristiques ... 70

III.3 Modélisation Autorégressive III.3.1 Présentation ... 70

III.3.2 Mise en oeuvre de la modélisation AR ... 72

III.3.3 Choix de l’ordre ... 74

III.3.4 Intérêt pour la segmentation ... 76

III.3.5 Sensibilité du modèle AR aux invariants du problème ... 77

III.4 Descripteurs de Fourier III.4.1 Présentation ... 79

III.4.2 Coefficients de Granlund ... 81

III.4.3 Descripteurs de Fourier Modifiés (DFM) ... 83

III.4.4 Mise en oeuvre ... 84

III.5 Conclusion ... 85

IV . Sélection de paramètres

IV.2 Analyse en Composantes Principales (ACP) IV.2.1 Présentation ... 89

IV.2.2 Interprétation des résultats de l'ACP ... 91

IV.3 Classement par le critère de Fisher IV.3.1 Formalisme ... 96

IV.3.2 Définition du critère de Fisher ... 97

IV.3.3 Exemple de mise en oeuvre sur la base de défauts ... 98

IV.4 Classement des paramètres par des méthodes séquentielles "constructive" et "destructive" (SFS & SBS) IV.4.1 Principe des algorithmes d'ordonnancement ... 100

IV.4.2 Choix du critère de classement ... 102

IV.4.3 Exemple de mise en oeuvre sur la base de défauts ... 103

IV.5.3 Interprétation géométrique ... 110

IV.5.4 Exemple de mise en oeuvre sur la base de défauts ... 111

IV.6 Critères d’arrêt IV.6.1 Critères d'arrêt "classiques" ... 112

IV.6.2 Critère d'arrêt avec adjonction d'un paramètre aléatoire ... 114

IV.7 Conclusion ... 115

V . Classification Neuronale Supervisée

V.2 Panorama des méthodes de classification supervisée V.2.1 Règle de décision bayésienne ... 121

V.2.2 Conséquences pour les méthodes de classification ... 122

V.3 Influence des dimensions de la base d’apprentissage ... 124

V.4 Evaluation des performances des classifieurs ... 126

V.5 Classification par neurone élémentaire V.5.1 Formalisme ... 127

V.5.2 Séparation linéaire entre classes ... 129

V.5.3 Règles d’apprentissage ... 132

V.5.4 Mise en oeuvre ... 137

V.6 Architecture générale du classifieur à K classes V.6.1 Approche globale : Perceptron MultiCouche (MLP) ... 139

V.6.2 Approche par partition : sous-classifieurs élémentaires ... 144

V.6.3 Classifieurs élémentaires 1 parmi K ... 144

V.6.4 Classifieurs élémentaires 2 à 2 ... 147

V.7 Classifieur par neurones à Fonctions Radiales de Base (RBF) V.7.1 Formalisme ... 151

V.7.2 Apprentissage des réseaux RBF ... 154

V.7.3 Choix du nombre et du positionnement des noyaux ... 155

V.7.4 Choix de la métrique et de la largeur des noyaux ... 158

V.7.5 Architectures du classifieur ... 161

V.7.6 Résultats ... 164

V.8 Conclusion ... 165

VI . Conclusion générale

...

Annexe A :

Annexe D :

Annexe E :

Annexe F :

sous-problèmes à 2 classes. ... 187

Abstract : The work presented in this report deals with a device for the rail head defect detection and recognition. In the first section, a non contact eddy current inspection system dedicated to rail head non destructive testing in the exploitation situation is presented. The main conception options (differential measurement, bi-frequency, shielding...) are described and validated by in-situ experimental tests. A list of defect classes has been established and a representative data base has been also constituted to elaborate the processing system.

The first part of the defect recognition process concerns the representation mode of sensor output signals. The main properties required for the parametrization are a great descriptive potential as well as a strong insensitivity to problem invariants (as play-back operation, scale factor, lift-off). An original parametrization procedure referred to as "Modified Fourier Descriptors" has been elaboreted and compared to parametrization of an autoregressive type. A parameter selection must then be carried out in order to maintain only the parameters relevant to class separability. For the parameter classification, the orthogonalization method and the sequential backward and forward procedures are compared. In order to select a subset of parameters, many stop criterions are also presented. The application of those methods to our data base is illustrated.

The last section of this report is devoted to a supervised neuronal classification by means of multilayer perceptron and radial basis function. For these two types of networks, both global and partitioned approachs are exposed. In the first case, the muliclass problem is solved simultaneously while in the partial case, the problem of classification is subdivised into sub-problems. The classification performance are given for the two approaches and it will be shown that the partitionning results are better and bear more relevance to our application in correspondance with a small learning dataset size.

Key-words : Eddy Current Sensor, Non Destructive Control, Parametrization, Parameter Selection, Classification, Neural Networks.

à la Reconnaissance des Défauts de Rails par Courants de Foucault.

Résumé : Le travail présenté dans ce mémoire traite d'un dispositif embarqué de détection et de reconnaissance des défauts de rail débouchants. Une structure multicapteur à courants de Foucault permettant le contrôle non destructif de l'intégrité des rails en voie, sans contact et avec des conditions d'exploitation commerciale est détaillée dans le premier chapitre. Les principales options de conception (mesures différentielles, bi-fréquences, blindages...) y sont décrites, et validées a posteriori par des essais sur site dans des conditions de mesure réelles. Une liste des classes de défauts détectables par le capteur a été établie (fissures, écaillages...) ainsi qu'une base de données représentative du site pour la mise au point des traitements haut-niveau.

La première phase des traitements concerne le mode de représentation des signaux complexes issus du capteur. Cette paramétrisation doit posséder un fort potentiel descriptif tout en restant insensible à certaines opérations sur les signaux définies comme des invariants du problème (retournement, homothéties, lift-off). Une procédure originale de paramétrisation des signatures dénommée "Descripteurs de Fourier Modifiés", a été mise au point et comparée à des paramétrisations de type autorégressive.

Sur l'ensemble des paramètres d'une signature, une sélection doit ensuite être effectuée en termes de pertinence à la discrimination entre classes. Une méthode d'ordonnancement par orthogonalisation et des méthodes séquentielles constructive et destructive pour le classement des paramètres sont comparées. Différents critères d'arrêt permettent de choisir le nombre réduit de paramètres retenus; des résultats de mise en oeuvre sur la base de données de ces différentes méthodes sont présentés.

Le dernier chapitre de ce mémoire traite de la classification neuronale supervisée à l'aide de réseaux de type perceptron multicouche ou de réseaux à fonctions radiales de base. Pour ces deux types de réseaux, des approches globales de classification (discrimination des K classes simultanément) et des approches par partition (problème de classification initial décomposé en sous-problèmes de classification) sont exposées. Des performances de classification sont données pour les deux approches et nous montrons la supériorité de l'approche par partition dans notre application en relation avec la faible dimension de la base de données.

Mots clés : Capteur à courants de Foucault, Contrôle Non Destructif, Paramétrisation, Sélection de paramètres, Classification, Réseaux de Neurones.

Chapitre II

x, y, z : repère de mesure

h : distance capteur/cible

Dt : décalage transversal du capteur par rapport à l'axe x

Lf : largeur de fissure

m : perméabilité magnétique

s : conductivité électrique

f, w : fréquence et pulsation d'excitation

d : épaisseur de peau

iexc : courant d'alimentation du capteur en notation complexe

V : tension de mesure aux bornes d'un bobinage en notation complexe

DS0° : partie active de la tension V

DS90° : partie réactive de la tension V

Z : impédance complexe d'un bobinage

R : composante résistive de l'impédance d'un bobinage

X : composante inductive de l'impédance d'un bobinage

Z0 : impédance à vide (sans cible)

Zn : impédance normalisée

k : coefficient de couplage bobinage/cible

2a : largeur inter-plots

L : espacement entre capteurs élémentaires

Vdiff : tension de mesure différentielle entre deux capteurs élémentaires

V2diff : tension de mesure double-différentielle entre trois capteurs élémentaires

Chapitre III

DSi : partie du signal de mesure en phase avec le courant d'alimentation

DSv : partie du signal de mesure en quadrature avec le courant d'alimentation

s : abscisse curviligne

q : angle local dans le plan de Lissajous

s(n) : signal de mesure du capteur à l'instant tn

p : ordre du modèle AR

a : vecteur de paramètres AR dim : p x 1

ˆ

s : prédiction de la valeur de s

fk : coefficients de Fourier du signal de mesure complexe

gm k : Descripteurs de Granlund

dk : Descripteurs de Fourier Modifiés

Chapitre IV

d : dimension de l'espace de représentation (avant sélection)

N : nombre d'observations de la base de données

B : matrice d'observation pour une base complète dim : N x d

Xi : vecteur paramètre dim : N x 1

Yi : vecteur d'observation dim : d x 1

m : centre de gravité de la matrice d'observation dim : 1 x d

m_i, si : centre de gravité et écart-type de Xi

V_B : matrice de variance-covariance associée à B dim : d x d

li, ui : ième valeur propre de la matrice VB et vecteur propre associé

dr : dimension de l'espace de représentation réduit (après sélection)

U : matrice des dr premiers vecteurs propres de VB dim : d x dr

C : matrice d'observation après projection par l'ACP dim : N x dr

C_i : ième _{composante principale dim : N x 1}

VC : matrice de variance-covariance associée à C dim : drx dr

I : pourcentage d'inertie totale après projection

Wi : ième classe

K : nombre total de classes

N_Wi : nombre d'observations dans la ième _classe

Ns : nombre d'observations de la base de données extraite

X : sous-matrice d'observation dim : Nsx d

mX : centre de gravité de la sous-matrice d'observation dim : 1 x d

VX : matrice de variance-covariance associée à X dim : d x d

VWk _{: matrice de variance-covariance propre à la classe W}

k dim : d x d

mWk _{: centre de gravité de la classe W}

k dim : 1 x d

Vi n : matrice de variance-covariance intraclasse dim : d x d

J : critère de classement des paramètres

P : vecteur modèle de régression linéaire dim : Ns x 1

y : sortie du modèle de régression linéaire dim : Nsx 1

e : erreur résiduelle du modèle de régression linéaire dim : Nsx 1

H : sous-matrice d'observation après orthogonalisation dim : Ns x d

hi : ième vecteur colonne de H dim : Nsx 1

ai k : projection sur l'axe hi du vecteur Xk

Q : vecteur modèle de régression linéaire après orthogonalisation dim : Ns x

1

qi : projection de la sortie y sur l'axe hi

r : seuil d'arrêt de la méthode de sélection de paramètres par orthogonalisation

Chapitre V

Y : vecteur d'observation dim : drx 1

Prob(Wi Y ) : probabilité a posteriori d'appartenance à la classe Wi sachant Y

p( Y Wi) : densité de probabilité conditionnelle de Y sachant que la classe Wi est vraie

Prob(Wi) : probabilité a priori de la classe Wi

d(Y) : fonction discriminante

w : vecteur poids dim : drx 1

F : fonction d'activation

S_S : potentiel du neurone

S : vecteur sorties du neurone dim : N x 1

T : vecteur sorties souhaitées dim : N x 1

m : taux d'apprentissage

—_w J : gradient de la fonction coût

F : fonction radiale de base

ci : ième noyau ou centre

Nc : nombre de noyaux

A : matrice de normalisation pour le calcul des distances

CND : Contrôle Non Destructif

JE : Joint Eclissé

JIC : Joint Isolé Collé

JS : Joint Soudé

JA : Joint éclissé Avant coeur d'aiguille

E : Ecaillage

DFM : Descripteurs de Fourier Modifiés

ACP : Analyse en Composantes Principales

AFD : Analyse Factorielle Discriminante

SFS : Sélection séquentielle constructive (Sequential Forward Selection)

SBS : Sélection séquentielle destructive (Sequential Backward Selection)

OFR : Moindres carrés orthogonaux (Orthogonal Forward Regression)

MLP : Perceptron Multicouche (Multi-Layer Perceptron)

Chapitre I : Introduction générale

L'accroissement de la vitesse des trains, de la densité du trafic, des charges par essieux et de la puissance des engins moteur ont pour conséquence d'exercer sur les voies ferroviaires des sollicitations toujours plus grandes qui peuvent, à la longue, mettre en cause l'intégrité des rails. Jusqu'à présent, le contrôle non destructif des rails tel que les exploitants ferroviaires le pratiquent s'effectue hors exploitation commerciale à l'aide de voitures spéciales d'inspection. A l'aide de capteurs généralement à ultrasons, ils sont capables de détecter des amorces de fissures mais au prix d'une inspection avec contact.

Concernant les défauts importants comme les fissures complètes, des systèmes à poste fixe dénommés "circuits de voies" dont la fonction principale est de détecter la présence d'un véhicule sur un tronçon donné, renseignent également sur l'existence de tels défauts. Enfin le conducteur, grâce à son expertise, est à même de soupçonner l'existence de fissures transverses complètes qui entraînent le clignotement des feux et de forts délaminages du sommet du rail, qui altèrent la qualité du roulement.

La nécessité de développer un dispositif de contrôle de rail sans contact et en exploitation commerciale s'inscrit dans une perspective d'automatisation de la conduite des trains sur roulement fer. Dans ce cadre en effet, les circuits de voie n'existent plus, le conducteur n'est plus présent, mais, bien sûr, la sécurité du trafic doit être maintenue.

L'étude présentée dans ce mémoire décrit un dispositif embarqué de détection et de reconnaissance des défauts de rail. La spécificité de l'étude tant en ce qui concerne les conditions de mesure (vitesse d'auscultation et positionnement du capteur) que la particularité de l'environnement ferroviaire, ont porté notre choix vers une technologie courants de Foucault dont les propriétés de robustesse et de simplicité de mise en oeuvre ne sont plus à démontrer. Les capteurs disponibles sur le marché ne peuvent cependant pas répondre directement au cahier des charges. Une solution originale de capteur a donc été développée. Le chapitre II de ce mémoire fournit une description détaillée des principales options de réalisation, lesquelles ont été validées a posteriori par des essais sur site avec des conditions de mesure réelles. Des essais sur site d'une version prototype ont permis de révéler des aptitudes supplémentaires du dispositif qui concernent la détection de défauts de moindre importance et ont ouvert sur de

nouvelles perspectives d'utilisation du capteur en maintenance prédictive des rails. Une liste des différentes classes de défauts détectables a été établie, et la suite de ce mémoire porte sur l'élaboration d'une procédure de reconnaissance des défauts. Le dimensionnement du défaut au sens du contrôle non destructif n'est pas traité, seule son appartenance à une classe donnée est abordée.

Avec à notre disposition les signaux bruts issus du capteur, on peut décomposer l'ensemble de la procédure de reconnaissance comme indiqué sur la figure I-1.

Paramétrisation des signaux Sélection de paramètres Classe Signaux bruts numérisés dim≈100 dim≈1000 dim≈10 Classification

Figure I-1 : Synoptique de la procédure de reconnaissance des défauts

La somme d'informations issues du capteur est très grande. Cela autorise à penser que le dipositif offre une grande richesse descriptive des défauts mais conduit en contrepartie à "noyer" l'information utile. Il est donc nécessaire de diminuer la taille de l'espace de représentation des défauts par des phases successives de paramétrisation puis de sélection qui tenteront de diminuer d'un facteur 100 environ la dimension initiale.

La première phase des traitements concerne le choix du mode de représentation des signaux. Le choix de l'espace de représentation mérite une attention particulière car il conditionne toute la méthodologie mise en oeuvre ensuite dans la classification (complexité, performances du classifieur,....). Le chapitre III de ce mémoire traite de ce problème.

Contrairement à la méthodologie de modélisation telle qu'on l'effectue habituellement en "Traitement du Signal", la paramétrisation en vue d'une classification est menée de telle sorte qu'elle posséde au final un fort potentiel de discrimination des classes. Son insensibilité à certaines opérations sur les signaux définies comme des invariants du problème est également primordiale. Nous proposons dans le chapitre III une méthode originale de paramétrisation par Descripteurs de Fourier Modifiés (DFM). Une comparaison de ce nouveau mode de représentation avec la modélisation AutoRégressive (AR), plus largement répandue, sera également présentée.

Une diminution supplémentaire de la dimension de l'espace de représentation est obtenue ensuite à l'issue d'une sélection de paramètres. Ce point est traité dans le chapitre IV. Des

méthodes séquentielles constructive et destructive ainsi qu'une approche s'inspirant des travaux effectués pour la sélection de régresseurs dans un modèle linéaire sont proposées. Toutes ces méthodes fournissent un classement des paramètres par ordre de pertinence, relativement à un problème de classification donné. Pour ce qui concerne le nombre proprement dit de paramètres, divers critères existant dans la littérature sont examinés et des résultats de mise en oeuvre sur une base de données sont présentés. Enfin, une méthode originale avec adjonction d'un paramètre aléatoire est abordée avec l'avantage de mieux s'adapter aux cas où le nombre d'observations de la base de données n'est pas très supérieur à la dimension de l'espace de représentation.

Le chapitre V de ce mémoire est consacré à la partie classification. Ne disposant d'aucune hypothèse a priori sur les probabilités d'appartenance aux classes, nous avons écarté les classifieurs bayésiens et avons concentré notre étude sur des classifieurs neuronaux supervisés. Deux types de réseaux ont été étudiés : les réseaux de type perceptron multicouche (MLP) et les réseaux à fonctions radiales de base (RBF). Pour ces deux types de réseaux, à l'approche globale d'un apprentissage type "boite noire" sur l'ensemble des problèmes de classification, on a préféré une approche par partition qui définit des sous-problèmes de classification élémentaires dont les complexités sont de fait moindres. Pour les réseaux classiques MLP, cette simplification conduira même à définir des sous-classifieurs sans couche cachée, réalisant chacun des hyperplans séparateurs linéaires entre classes. Les règles de décision d'appartenance aux classes de défauts à partir des sorties des sous-classifieurs seront également détaillées. Pour ce qui concerne les réseaux RBF, nous nous sommes particulièrement intéressés à l'apprentissage de ces réseaux et nous proposons une transposition d'une méthode de sélection de paramètres à un problème de sélection de noyaux des réseaux. Les performances obtenues pour chaque classifieur seront présentées et comparées.

La succession des chapitres s'établit comme suit :

Chapitre II : Capteur à Courants de Foucault pour la détection de défauts de rails

Chapitre III : Paramétrisation des signaux

Chapitre IV : Sélection de Paramètres

Chapitre II : Capteur à Courants de Foucault pour la

Détection de Défauts de Rail.

II.1 Introduction

Le système dont nous exposons la structure dans ce chapitre est un dispositif de contrôle non destructif (CND) de l'intégrité des rails en voie, sans contact et avec des conditions d'exploitation commerciale. Ces conditions de mesure, en plus du contexte ferroviaire relativement hostile (perturbations électromagnétiques, température de mesure, milieu "pollué") nous ont amené à opter pour la technologie "courants de Foucault" dont les qualités de robustesse et de simplicité d'utilisation sont bien connues [ASH-87] [CAS-85].

A partir de cibles étalons représentatives des défauts à détecter, nous avons mené la conception en laboratoire d'un capteur qui répond au mieux au cahier des charges, auquel les capteurs disponibles sur le marché ne répondent pas directement. Cette phase de conception a été effectuée conjointement à l'aide de simulations numériques par éléments finis et avec des mesures en laboratoire sur une version prototype modulaire. Nous nous sommes particulièrement attachés à reproduire des conditions de mesure en laboratoire les plus proches de celles du terrain et à tenir compte de l'influence des différents paramètres de cible dont les plus importants sont le positionnement du capteur et le décalage transversal. L'étude des principales options de réalisation du multicapteur (alimentation, blindage, fréquence(s) d'excitation, paramètres géométriques) est détaillée dans la première partie de ce chapitre. Une description de l'électronique associée et de quelques prétraitements élémentaires est également donnée.

La dernière partie de ce chapitre est consacrée aux essais sur site menés avec ce multicapteur et la chaîne de mesure qui lui est associée. Il s'agit d'essais embarqués sur un véhicule du type de ceux utilisés en exploitation commerciale dans le métro parisien. Dans ce paragraphe seront traités plus particulièrement les points induits par des conditions de mesure réelles, comme les problèmes de position relative capteur/cible ou l'influence de la vitesse d'avancement. Nous définirons également les différentes classes de défauts détectables par le capteur et la base de données qui servira pour les traitements ultérieurs.

II.2 Différentes technologies pour le contrôle des rails

Dans ce paragraphe, seront présentées rapidement les diverses techniques mises en oeuvre pour le contrôle de rails en précisant pour chaque type de contrôle, ses caractères propres, ses possibilités et ses limitations.

• L'examen visuel

Chronologiquement le plus ancien. Cette procédure techniquement très simple fait toutefois appel à une véritable expertise et à un sens aigu de l'observation des agents qui l'effectuent. • Le ressuage

Cette technique, également très ancienne, consiste à pulvériser un liquide pénétrant à la surface préalablement nettoyée de la pièce à contrôler, et à appliquer ensuite un révélateur sur la surface, afin de visualiser toutes les discontinuités. De par son principe, cette technique ne permet de détecter que des défauts en surface et ne fournit pas leur degré de gravité. Elle reste, néanmoins utile lorsque le contrôle non destructif par courants de Foucault ou par magnétoscopie ne peut être utilisé. C'est le cas pour des pièces non conductrices de courant électrique ou non magnétiques.

• Magnétoscopie

Le principe de cette méthode repose sur le fait que dans une pièce aimantée, toute anomalie de structure provoque une distorsion des lignes d'induction. Si le défaut est situé au voisinage de la surface, la perturbation engendrée peut être décelée à l'aide de fines particules magnétiques qui s'accumulent à l'aplomb du défaut. Cette méthode à champ magnétique continu ne s'applique qu'à des matériaux ferromagnétiques. Elle est d'autant plus efficace que leur perméabilité relative est élevée. L'interprétation des résultats reste toutefois visuelle.

• Ultrasons

Dans un rail sans défaut, pouvant être assimilé à un milieu homogène, les ondes ultrasonores se propagent à une vitesse constante dépendant du milieu, mais se réfléchissent sur toutes discontinuités rencontrées. Par analyse des échos reçus (temps de parcours aller et retour de l'onde), l'anomalie est localisée dans l'espace. Dans la pratique, l'onde ultrasonore est émise par un élément piézo-électrique, sous forme d'impulsions de quelques micro-secondes. Lorsqu'elle est réfléchie par une surface de séparation, cette onde est détectée par l'élément piézo-électrique qui agit alors comme récepteur, et transforme la vibration ultrasonore reçue en

tension électrique.

Pour pouvoir identifier différents défauts de rails, plusieurs sondes sont utilisées avec des orientations adaptées aux directions des anomalies recherchées (cf. figure II-1) et dans une gamme de fréquence allant de 1 à 10 MHz [MAT-84] :

- un sondage vertical pour les fissures horizontales

- un sondage oblique pour les fissures transversales du champignon

palpeur oblique palpeur

vertical

Figure II-1 : Contrôle par ultrasons

L'ensemble peut être suspendu sous un véhicule de contrôle spécifique ou équiper plus simplement une "cane" manuelle. Dans tous les cas, ce type de contrôle nécessite un couplage acoustique entre la sonde et la pièce du fait que les ondes ultrasonores se propagent mal dans l'air. Ce couplage est assuré par un film liquide entre le rail et le palpeur (généralement de l'eau). Un guidage précis du palpeur est également nécessaire afin que la propagation des ondes soit assurée dans l'axe du rail. A noter que cette technique de contrôle ne peut être utilisée qu'à des vitesses d'auscultation relativement faibles et que le "sabot" de contrôle doit être escamoté au passage des appareils de voie [DUV-84]. Son implantation sur des véhicules en exploitation commerciale n'est donc pas envisageable.

• Capteurs inductifs

Le contrôle non destructif par capteurs inductifs est un procédé relativement répandu dans l'industrie ferroviaire [MON-84] [AST-93] [DOG-91]. C'est par l'intermédiaire d'un champ magnétique alternatif que s'établit l'interaction entre le dispositif de mesure et la cible. Puisque tous les milieux transmettent les ondes électromagnétiques, la mesure peut s'effectuer sans contact. Toutefois, une distance faible est recommandée du fait de la décroissance rapide des champs électromagnétiques dans l'air et afin de focaliser au maximum le champ produit vers la

zone utile. Le traitement des signaux issus de ces capteurs est fonction de l'application envisagée; il peut s'avérer très simple ou très complexe selon les performances attendues et le nombre de paramètres du défaut à identifier [STR-94].

L’auscultation des rails utilisant cette technique est possible aussi bien durant la phase de fabrication qu’une fois posés en voie. En sortie de laminoir, les contrôles concernent soit la mesure des variations de la hauteur du rail soit la détection de défauts de type fissure en surface ou en sub-surface, le choix de la fréquence d'émission conditionnant la profondeur de pénétration du champ dans le rail. Pour les contrôles en voie, les sondes inductives sont souvent associées à des sondes à ultrasons; de cette manière elles sont rendues solidaires du sabot de contrôle afin d'assurer une hauteur de mesure constante ou minimiser l'effet de la dynamique du véhicule sur la mesure [AKN-92]. Les sondes utilisées sont des sondes d'usage général et leurs formes ne sont pas étudiées spécifiquement pour le CND des rails. De fait, cette technique de CND est moins utilisée que la technique ultrasons qui, lorsqu'on s'autorise une mesure par contact, est plus riche d'informations. L’exploitation des signaux de mesure s’effectue par simple seuillage sur les amplitudes mises en jeu. L’interprétation des résultats est généralement relativement sommaire. Une fois qu’une alerte est fournie par le système, elle est validée ou annulée par un examen visuel de la zone suspecte.

II.3 Contexte ferroviaire

Sur le réseau RATP, la détection en voie des deux types d'anomalies est assurée en grande partie par le conducteur. Le bruit de roulement jugé anormal dans le cas d'arrachement de champignon de rail et le clignotement des circuits de voie lorsqu'il s'agit de rail cassé sont les deux moyens de détection utilisés par le conducteur jusqu'à présent. Dans la perspective d'une conduite automatique intégrale et des évolutions futures des systèmes de signalisation, d'autres dispositifs de détection doivent être développés.

Le CND des rails envisagé dans notre étude répond à cet impératif. Il doit s'effectuer sans contact, sur véhicule en exploitation commerciale et pour des vitesses d'auscultation pouvant atteindre 100 km/h. Dans un contexte industriel ferroviaire relativement hostile, certaines conditions de mesure sont inhabituelles pour le CND par courants de Foucault. Il s’agit notamment de la distance de mesure, qui doit être de 20 à 30 mm.

la rupture franche d'une file de rail (spécialement dans les zones de soudure). Le taux d'occurrence de ce type de défaut est d'environ 8 par an et par ligne sur un réseau ancien de métro type RATP. Moins fréquemment, il peut apparaître un autre type de défaut consistant en un arrachement d'une partie du champignon (la partie supérieure du rail). Ce second défaut résulte d'une fatigue de contact qui initie des fissures en surface ou sub-surface du champignon et dont l'évolution ne conduit pas à une rupture franche du rail mais à un arrachement, le plus souvent partiel, du champignon [ALI-86]. Selon que le tracé est en alignement ou en courbe, la dénomination anglo-saxonne de l'arrachement partiel est respectivement "schelling" ou "head-checking". Ce type d'arrachement de matière possède des caractéristiques géométriques très diverses. Il peut concerner l'ensemble du champignon (délaminage complet) ou se latéraliser (écaillage généralement sur la joue active regardant l'intérieur de la voie). Sa longueur est très variable, pouvant aller de 1 à 2 cm jusqu'à des valeurs de 50 cm !

Le système développé doit détecter les deux défauts type : - fissure complète ou partielle du champignon. - arrachement du champignon du rail.

Ces défauts sont dans un plan grossièrement perpendiculaire à la direction d'avancement. Le gabarit de mesure autorisé étant uniquement sur le dessus du rail (emplacement d'une roue), seules les fissures du champignon sont détectables.

Contrairement aux applications traditionnelles en CND [CEC-93] [AUL-84], le dimensionnement des défauts n'est pas demandé.

L'utilisation du capteur dans un environnement ferroviaire très perturbant induit également certaines contraintes de conception que l'on peut classer en différentes catégories :

• Contraintes thermiques et mécaniques

La température de fonctionnement peut varier dans une gamme allant de - 20°C à 60°C, avec présence éventuelle d'eau, de givre ou de neige sur le capteur et sur le rail. Le capteur sera fixé sur un châssis de bogie, lequel subit des accélérations pouvant atteindre 10g. De plus, il peut venir percuter des morceaux de ballast soulevés par le passage du véhicule.

• Contraintes de positionnement liées à la dynamique ferroviaire

relativement au rail (dynamique transversale des suspensions, usure des boudins de roues, surécartement des voies dans les courbes), et d'autre part des variations de hauteur de ±5mm (dynamique verticale des suspensions primaires). Par ailleurs, le châssis de bogie possède trois degrés de liberté en rotation autour des axes x, y et z.

• Contraintes géométriques

Pour ne risquer aucun choc destructeur, le capteur doit pouvoir se placer dans l'ombre de la roue, et afin de limiter les déformations de la patte de fixation, il doit être de faible poids. La largeur maximale autorisée est de 120 mm. Il n'y a pas de contrainte particulière sur la longueur du capteur (selon x) sinon que le dispositif doit pouvoir s'inscrire entre les deux essieux d'un même bogie dans un emplacement d'environ 1m. De plus, l'apparition de pièces métalliques telles que contre rail ou pointe d'aiguillage doivent perturber le moins possible la mesure des défauts du rail principal. La figure II-2 présente l'unité sensible en position de mesure et indique le choix des axes.

120 mm max y z Dt = + 30mm h =20 + 5mm Capteur 150-200 mm x z

Figure II-2 : Capteur en position de mesure

• Contraintes liées à l'environnement électrique de l a cible

Le capteur ne doit pas être sensible à la présence de forts courants hachés de traction (500 A) ni aux signaux 50 Hz de Contrôle-Commande circulant dans les rails. Il existe également sur les réseaux de métros modernes des signaux de pilotage automatique de la vitesse (tapis PA entre les rails) qui génèrent des champs électromagnétiques alternatifs de fréquences comprises entre 1 et 2 kHz.

En résumé, le capteur doit respecter les critères suivants :

- immunité aux variations de température et aux perturbations électromagnétiques externes. - bonne tenue mécanique vis à vis des contraintes mécaniques et thermiques.

- insensibilité de la mesure aux déplacements relatifs rail/capteur liés à la dynamique du châssis de bogie.

- optimisation du rapport portée/encombrement et du poids.

Afin de respecter ces critères, le développement d'un capteur spécifique a été mené et sa description est abordée en détail au paragraphe II.5.

III.3.2 Définition de la cible

La cible à contrôler est un rail (type U50) dont le gabarit théorique est présenté figure II-3. Son champignon a une largeur de 65 mm.

Champignon Table de roulement Joue Patin Ame 65 mm 140 mm 49 mm Portée d’éclissage 153 mm

Figure II-3 : Nomenclature et côtes principales du rail U50

Ces rails sont toujours réalisés par laminage d'acier au carbone avec deux nuances possibles [ALI-88] : une à 0,5% de carbone dite "ordinaire" (nuance 700) et une à 0,7% dite "dure" (nuance 900). Seules les pièces d'aiguillage sont moulées dans de l'acier amagnétique au manganèse.

Pour les coupons de rail en nuance "dure", la conductivité électrique est voisine de

σ= 4 106 Sm−1 et la perméabilité relative pour les champs faibles (100 A/m) a été estimée à

µr=25 environ. Cette valeur de perméabilité peut être sujette à variations à cause

principalement de deux facteurs :

- au cours du refroidissement lent des rails à la sortie du laminoir, il s'opère une décarburation totale du matériau en surface (absence de carbone dans une épaisseur de 100 à 200 µm). Les perméabilités du matériau en surface et en profondeur sont donc différentes (plus grande en surface). Cette épaisseur varie évidemment avec l'état d'usure du profil.

- à proximité des soudures de rails, il existe des trempes et des recuits partiels et les propriétés

magnétiques s'en trouvent changées (µr augmente avec le recuit et diminue avec la trempe).

II.3.3 Cibles étalons

Afin de disposer de défauts étalons pour l'optimisation du capteur, il a été nécessaire d’usiner, sur deux coupons de rail, les deux défauts majeurs (cf. figure II-4).

50 mm 10 mm

Cible 1 Cible 2

L_f

Figure II-4 : Cibles étalons

La cible étalon 1 représente une rupture de rail; la largeur de la fissure Lf est réglable à l’aide

d’une cale calibrée. La seconde cible étalon représente un arrachement partiel de la table de roulement de 10 mm de profondeur sur 50 mm de long, conformément au cahier des charges. Rappelons que sur site, les longueurs de ce second défaut sont variables et qu’il s’agit là, simplement d’une taille moyenne de défaut servant aux essais en laboratoire.

II.4 Spécificités de la technologie "capteur inductif"

Un capteur inductif est en principe constitué d'un circuit magnétique ouvert de grande perméabilité, sur lequel est bobiné un ou plusieurs enroulements parcourus par un courant alternatif. L'approche d'une cible conductrice et/ou magnétique dans l'entrefer du circuit modifie la répartition des lignes de champ et se traduit par une variation de réluctance et l'apparition de pertes électromagnétiques dues à la pénétration du champ à l'intérieur de la cible.

Remarque : Certains capteurs très simples ne possèdent qu'un bobinage et le trajet des lignes de champ a lieu alors intégralement dans l'air.

L’effet résultant de l’approche d’une cible peut être mis en évidence, puis analysé en mesurant l’impédance du bobinage d’excitation : l’enroulement primaire assure dans ce cas la double fonction d’alimentation et de mesure. On peut choisir de munir le circuit magnétique d’un second enroulement qui servira uniquement pour la mesure : on parle alors de mesure par trans-impédance ou de capteur à fonctions séparées. La réponse fournie par un tel capteur est, sur le principe, identique à celle d’un capteur à simple enroulement, avec en plus la possibilité d’optimiser de façon distincte l’inducteur et la bobine réceptrice (disposition, nombre de spires etc.).

Lorsque la cible est purement conductrice, le champ incident induit des courants surfaciques dénommés courants de Foucault, qui à leur tour génèrent un champ magnétique réfléchi, s'opposant au champ excitateur (loi de Lenz). On parle dans ce cas de "Capteurs à courants de Foucault" ou "CCF" (cf. figure II-5).

L'amortissement des courants de Foucault dans le matériau, dans le cas simple d’une onde plane harmonique d’incidence nulle, décroît exponentiellement en fonction de la profondeur du matériau en regard. On définit l'épaisseur de peau par :

δ = 1 / (π f µ σ )

avec f la fréquence d’excitation, µ la perméabilité magnétique et σ la conductivité électrique de la cible. Dans le cas général, cette formule n’est pas rigoureuse mais elle renseigne néanmoins assez précisément sur la profondeur au delà de laquelle les courants induits sont trop faibles pour être influants.

modification des lignes de champ, qui se trouvent attirées par le matériau en regard. Le dispositif fonctionne alors en "Capteur Magnétique" ou "CM" (cf. figures II-6).

CCF iexc Cible conductrice bobinage d'excitation ~

Figure II-5 : Capteur à courants de Foucault

Cible conductrice CM Cible magnétique bobinage d'excitation ~ iexc

Figure II-6 : Capteur magnétique

Cependant, dans le cas général plus complexe à étudier, où la cible présente à la fois de bonnes propriétés conductrices et magnétiques, seule la gamme de fréquence de l'alimentation du capteur distingue les deux technologies CCF et CM. A fréquence élevée, le champ développé ne pénètre quasiment pas dans la cible. Le dispositif fonctionne en CCF. Par

contre, lorsque la fréquence du champ d'excitation est faible (voire continue lorsque l'on utilise des aimants permanents) le capteur fonctionne en CM. Pour des fréquences d'excitation intermédiaires et à certaines distances de mesure, les deux phénomènes d'attraction et de répulsion du champ s’équilibrent et le dispositif peut être qualifié à la fois de capteur à courants de Foucault et de capteur magnétique. Les valeurs de ces fréquences intermédiaires dépendent de caractéristiques du matériau; on travaille en général assez peu à ces fréquences intermédiaires de manière à affirmer suffisamment le caractère CCF ou CM du capteur.

La topologie des lignes de champ et la répartition des courants de Foucault dépendent tout d'abord des paramètres de structure tels que la fréquence d’excitation, la géométrie du capteur et la position relative capteur/cible. Elles dépendent ensuite de la géométrie de la cible et de ses propriétés électriques et magnétiques. La présence de défaut dans la cible induit une variation d’un ou de plusieurs de ces paramètres qu’il est possible de mettre en évidence en mesurant l’impédance du bobinage d’excitation ou d’une bobine réceptrice.

Bien que la frontière entre ces deux technologies soit floue, le parti pris CCF ou CM dépend essentiellement, des propriétés électriques et/ou magnétiques de la cible, de la nature et de la géométrie des défauts à déceler et enfin de l'environnement d'utilisation du capteur.

En ce qui nous concerne, ce choix a été essentiellement déterminé par l'environnement de mesure. Un fonctionnement à champ continu (cas extrême des CM) a été évité car toutes pièces métalliques situées à proximité du capteur risquent alors de s'y coller. Et d’autre part, si le capteur fonctionne à faible fréquence, l'environnement électromagnétique ne serait pas favorable (fréquence de hachage des courants de traction, tapis piloté automatique). Ces remarques nous ont conduit à privilégier un fonctionnement en CCF. On notera au passage que la profondeur de pénétration qui limite le champ d'action du capteur par courants de Foucault aux défauts surfaciques n'est pas ici un problème puisque les deux défauts à détecter sont débouchants.

II.4.2 Plan d’impédance normalisée

Nous nous plaçons dans ce paragraphe dans le cas d'un capteur à double-fonction. L’interaction capteur/cible s’étudie en examinant l’impédance complexe du capteur. Pour un

bobinage de N spires parcouru par un courant alternatif sinusoïdal iexc, cette impédance est

définie par :

Z = V iexc

où V et iexc sont les vecteurs complexes de Fresnel associés à la tension et au courant

d'excitation. La grandeur V est mesurée à l'aide d'un voltmètre vectoriel et se décompose en

une partie active et réactive, en quadrature et en phase avec iexc :

V = DS0° + j DS90°

Sachant que la tension V et le courant iexc s’expriment en fonction de la réluctance complexe

du circuit magnétique R et du flux magnétique enlacé par la bobine Φ à l'aide des relations :

Niexc = R .Φ et V = j N ω Φ

où ω est la pulsation du courant d'alimentation. L’impédance Z s'écrit donc :

Z = j

ω N2

R = R + j X

Un capteur inductif est donc caractérisé par deux grandeurs : la composante résistive R qui englobe les pertes par courants de Foucault dues à la pénétration du champ dans la cible et les pertes internes du bobinage d’excitation, et le terme inductif X qui représente la réactance du bobinage d’excitation, liée à la topologie des lignes de champ magnétique émises par le capteur.

Pour ne conserver dans l'expression de l'impédance que les variations dues à la présence de la cible, on introduit traditionnellement la notion d'impédance normalisée [HAG-82]. Cette

impédance normalisée Zn se déduit de Z à l’aide de l’expression :

Z_n = Rn + j Xn =

Z − R0 X₀

où Z0 = R₀ + j X₀ est l'impédance à vide du capteur (impédance sans cible).

En procédant à cette normalisation, la mesure devient indépendante des caractéristiques propres de la bobine excitatrice (nombre de spires, pertes à vide) et de la croissance de la réactance en fonction de la fréquence. Elle dépend uniquement des paramètres de structure que sont la fréquence d’excitation f et la géométrie du capteur, et des paramètres de la cible à savoir sa géométrie, sa conductivité électrique σ, sa perméabilité magnétique µ et la distance

capteur/cible (lift-off). L’étude des variations de Zn s’effectue dans le plan d’impédance

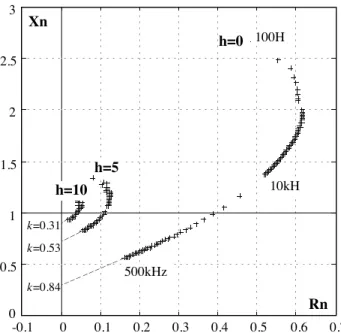
Pour un capteur donné, toutes variations de l’un de ces paramètres induit un déplacement du

point représentatif de Zn dans le plan d’impédance normalisée. La figure II-7 illustre l'allure

des trajectoires que décrit le point d’impédance du capteur pour des variations de conductivité électrique, de perméabilité magnétique ou de distance de mesure [ASN-86].

La prédétermination de ces trajectoires pour une cible quelconque est un problème relativement complexe qui nécessite une modélisation complète du dispositif. Les modélisations internes complètes sont rares car très complexes [MON-87] [PAL-80]. Seuls les cas de géométries de cible et de capteur simples peuvent être abordés. Des modélisations externes sont plus courantes [AKN-89]. Un modèle externe de type transformateur [DUF-93] a par exemple

permis d'identifier, à partir des deux mesures (Rn, Xn), la conductivité locale de la cible et la

distance séparant le capteur de la cible.

Xn 1 0 f h h variable σ, µ : constantes Rn Xn 1 f µ µ variable σ, h : constantes 0 Rn 1-k2 Xn 1 0 f.σ σ variable µ, h : constantes Rn 1-k2

Figure II-7 : Influence de µ, σ ou h sur le diagramme d’impédance normalisée

La présence de défauts ou d’inhomogénéités de la cible induit une modification de l’un ou de plusieurs des trois paramètres influants (σ, µ, h), qui se traduit dans le plan d’impédance

complexe (Rn, Xn), par un déplacement du point représentatif du capteur. Selon le type de

défaut considéré, les directions de ces déplacements sont celles correspondant aux variations locales de σ, µ ou h, ou bien une combinaison des trois directions, s’il s’agit d’une variation simultanée des trois propriétés.

Du fait de la décroissance rapide du champ électromagnétique, la notion de couplage capteur/cible est extrêmement importante dans le CND par courants de Foucault. Elle permet

d'évaluer la "partie" des ondes électromagnétiques atteignant la cible dont dépendra directement l'excursion des signaux de détection. Le plan d'impédance normalisée permet de caractériser le coefficient de couplage k entre le capteur et la cible. On montre en particulier

qu'à fréquence infinie, le point limite a pour coordonnées (0, 1-k2_{) [DUF-93].}

II.4.3 Contrôle multi-fréquences et par courants de Foucault pulsés

• Contrôle multi-fréquences

Le contrôle par courants de Foucault multi-fréquences est très utilisé pour l'inversion des données fournies par le capteur en vue de déterminer des paramètres du matériau en regard [ASN-86] [LE-95] [SAB-84]. Selon les applications considérées, ces paramètres peuvent être de différentes natures :

- distance capteur / cible (h).

- conductivité électrique de la cible (σ). - perméabilité magnétique de la cible (µ). - défauts dans le matériau.

- épaisseur du matériau à contrôler,...

Dans un problème d'inversion où il s'agit d'identifier n paramètres de la cible, il est nécessaire de disposer d'au moins n informations du capteur. Dans la majorité des cas, cette condition nécessaire n'est pas suffisante car d'une part, elle ne tient pas compte des dépendances qu'il peut y avoir entre les différentes mesures et d'autre part, des paramètres additionnels (à ceux recherchés) peuvent influencer la mesure. Ces deux remarques montrent clairement que le nombre d'informations disponibles ainsi que le degré d'indépendance entre celles ci influencent fortement le résultat de l'inversion.

Partant du principe que le comportement du capteur varie en fonction de la fréquence d'excitation, en particulier, selon que l'on se situe en basse, moyenne ou haute fréquence, les paramètres influants de la cible ne sont pas les mêmes (cf. figure II-7). La méthode multi-fréquences consiste à choisir judicieusement les multi-fréquences d'excitation du capteur de manière à recueillir des informations riches et complémentaires sur le matériau à contrôler. L'idéal serait que chaque paramètre ait une influence sur le signal de mesure à une fréquence et une seule. Ceci est évidemment difficile voire impossible à réaliser en pratique. Quant au nombre de fréquences d'alimentation nécessaire, il est étroitement lié aux nombres de paramètres à identifier et à la complexité du dispositif complet que l'on s'autorise.

Dans un problème de contrôle où il s’agit de discriminer plusieurs paramètres, une alternative à l'alimentation sinusoïdale multi-fréquences, consiste à émettre un champ magnétique large bande en excitant le capteur avec un signal impulsionnel ou quasi-impulsionnel. Ce mode de fonctionnement est communément appelé contrôle par courants de Foucault pulsés. Les premières applications de ce type de contrôle ont porté essentiellement sur l’évaluation d’épaisseurs de matériaux. De récents travaux dans ce domaine ont par ailleurs démontré l’intérêt du mode impulsionnel par rapport au mode sinusoïdal pour la détection de défauts profonds [LIB-71] [BOU-95].

La forme des signaux d’alimentation peut être rectangulaire, triangulaire ou semi-sinusoïdale, cette dernière étant la plus utilisée en raison de sa simplicité de mise en oeuvre. Dans ce type de contrôle, c'est l'évolution temporelle des signaux qui est utilisée.

Sur le principe, une telle méthode est plus riche en informations qu’un contrôle par courants de Foucault sinusoïdal mono ou multi-fréquences. Cependant, la quantité d’informations fournie dans la pratique dépend fortement du traitement des signaux bruts. Ceci justifie le nombre encore faible de développements que cette méthode a eu dans le domaine du contrôle non destructif.

La mise en oeuvre pratique de cette technique dans un contexte industriel est délicate. Le champ magnétique émis étant large bande, il risque de s’y superposer d’autres champs électromagnétiques externes perturbant ainsi la mesure de défauts de rail. Ce qui n’est pas le cas lorsque les formes d’ondes sont sinusoïdales et où le choix des fréquences d’excitation s’effectue "en évitant" les fréquences déjà présentes dans l'environnement électromagnétique.

II.4.4 Différentes géométries de sondes CF • Sondes élémentaires

La distribution du champ magnétique émis par le capteur, et par conséquent des courants de Foucault induits dans la cible à contrôler, dépend en premier lieu de la géométrie de la sonde utilisée.

Il existe plusieurs configurations possibles pour la disposition du bobinage d’excitation relativement à la cible; chacune est dédiée au contrôle de cibles de forme donnée. Sans dresser un panorama exhaustif de toutes les différentes méthodes d’auscultation, nous allons en citer trois principales (cf. figure II-8) :

- les bobines encerclantes : utilisées pour contrôler par l’extérieur des objets de faible section. - les bobines simples ou plates utilisées pour l’inspection des objets par leur surface [BIT-90].

bobine simple bobine plate

sonde interne sonde encerclante

Figure II-8 : Classification des sondes selon la méthode d'auscultation

Sur la figure II-8, les sondes ne comportent qu'un simple bobinage. Les champs qu'elles émettent s'épanouissent largement. Afin de limiter les zones d'interaction de la bobine, on couple généralement celle-ci avec un circuit magnétique de grande perméabilité. Celui-ci peut être réalisé en tôle feuilletée à basse fréquence ou en ferrite pour les fréquences plus élevées. Son rôle est de canaliser les lignes de champ magnétique vers la ou les zones de l'espace où l'on placera la cible à inspecter. La géométrie du circuit varie selon les applications et la figure II-9 en donne quatre exemples.

sonde en U

sonde en H

sonde en pot

sonde en E

On constate que dans le cas d’un capteur en "U", la direction des lignes du champ est principalement celle reliant les deux pôles alors que la structure en "pot" ne privilégie aucune direction particulière des lignes du champ. Les structures en forme de "E" ou "H" sont plus complexes mais elles offrent la possibilité de réaliser des mesures par différence ce qui diminue fortement la sensibilité du capteur aux différentes dérives. Le choix d’une structure plutôt qu’une autre est étroitement lié à la cible à inspecter et aux types de défauts qu'elle contient.

• Capteur multiple

Dans plusieurs applications, la constitution d'un multicapteur est nécessaire pour répondre à certains impératifs :

- pour les problèmes de CND d'une pièce selon un ou deux axes, la procédure d'inspection effectuée à l'aide d'un capteur unique peut s'avérer trop longue et nécessite l'association en ligne de plusieurs capteurs élémentaires. En multiplexant les informations issues de chacun d'eux, il est possible d'accéder plus rapidement aux propriétés de la cible. Sur ce principe, des multicapteurs permettant la restitution du profil de la cible en utilisant l’information sur les distances séparant chaque capteur élémentaire du profil ont été développés [AKN-89] [FEN-94].

- le deuxième type de problème pour lequel un multicapteur peut apporter une réponse est la détection de défauts de géométrie particulière. L'association en ligne de plusieurs capteurs judicieusement espacés en fonction de la taille des défauts à détecter permet de recueillir des signaux suffisamment riches en information.

II.5 Prototype modulaire

II.5.1 Géométrie d’un capteur élémentaire

La sensibilité de détection d’un défaut dans un matériau dépend de sa position (en surface ou en profondeur), de sa forme et de son orientation : la détection sera d’autant meilleure que le défaut est orienté perpendiculairement aux lignes de courants induits. En ce qui nous concerne, nous avons utilisé avec profit l'information suivante : les deux défauts-type à détecter sont dans un plan quasi perpendiculaire à la direction d'avancement du véhicule étant donné que les efforts principaux au contact roue/rail sont généralement développés parallèlement à l'axe du rail.

Il est donc préférable que le champ magnétique généré soit principalement parallèle aux anomalies, de telle sorte que les courants de Foucault créés soient perpendiculaires à la direction des défauts de type fissure complète; on obtient ainsi une perturbation maximale des courants induits, et par conséquent une variation maximale de l'impédance du capteur. Cette remarque nous a conduit à utiliser un capteur en "U". Par opposition aux structures à symétrie de révolution (généralement en "pot") qui ne privilégient aucune direction, cette géométrie particulière conditionne les lignes de champ comme la figure II-10 en donne l'allure.

x y z iexc 2a V = DS0° + j DS90° Φ courants induits défaut

Figure II-10 : Géométrie du capteur

Pour illustrer l'influence de l'angle entre la direction principale du champ magnétique et l'axe des défauts, nous présentons figure II-11, la variation de réluctance du capteur en U lorsque celui-ci se déplace selon x au dessus d'une fissure de 1 mm de large et pour 10 valeurs de cet angle comprises entre 0° et 90°.

Variation de réluctance y θ x ... x +100mm -100mm θ =90° ₈ 7 6 5 4 3 2 1 0 x 0

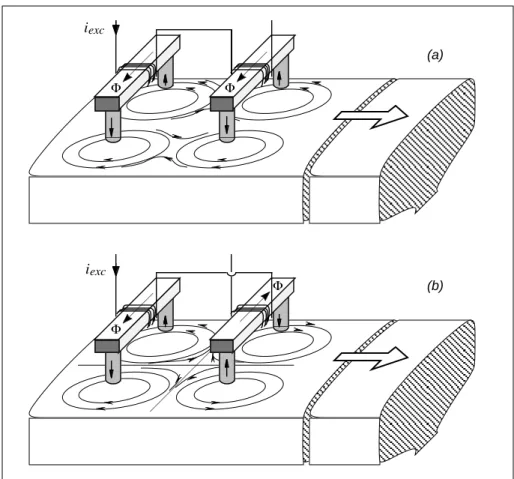
Au fur et à mesure que l'angle θ diminue, les perturbations des courants induits sous chaque plot ne s'effectuent plus simultanément. Au niveau du signal détecté, cela se traduit par l'apparition de deux lobes séparés d'amplitude réduite. Ces mesures nous confortent dans notre choix de placer le capteur en U perpendiculairement au rail de telle manière que la perturbation des courants de Foucault induits soit maximale.

II.5.2 Blindage passif

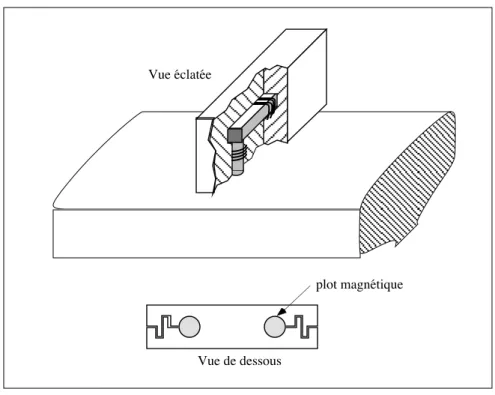
En disposant autour du circuit magnétique et des bobines un matériau conducteur qui ne laisse affleurer que les deux plots du capteur en U, on canalise le champ magnétique dont la progression dans le blindage est limitée à l'épaisseur de peau (très faible car le matériau est choisi très bon conducteur tel que le dural AU2GN). Le flux utile sortant par les plots du U est par conséquent augmenté et la sensibilité du capteur améliorée. La figure II-12 donne l'allure du capteur et son blindage réalisé en deux parties. On notera sur la vue de dessous la présence de saignées dans le blindage. Il convient en effet de ne pas enlacer les branches du circuit magnétique en U avec un blindage qui autoriserait la mise en court-circuit des courants induits en son sein. Le flux magnétique serait alors nécessairement nul dans le circuit magnétique. Dans ce but, des saignées de faible largeur sont réalisées par électroérosion. La forme en chicane de ces saignées minimise le flux de fuite (cf. figure II-12).

plot magnétique

Vue de dessous Vue éclatée

Disposer un blindage autour du capteur permet en résumé :

- de canaliser le flux magnétique sous la sonde afin d'augmenter la sensibilité. - de limiter l'influence des perturbations électromagnétiques externes.

- de donner à l'ensemble une rigidité mécanique.

Ce type de blindage sera qualifié de blindage passif (ou blindage par courants de Foucault [DUF-95]) par opposition au blindage actif que l'on abordera au paragraphe II.6.2.

II.5.3 Simulations numériques par éléments finis

Une fois choisie la structure en U pour le circuit magnétique, la largeur inter-plots 2a constitue avec la fréquence d’excitation les principaux paramètres de structure à optimiser lors de la conception d’un capteur élémentaire. Au vu du cahier des charges, les contraintes les plus pénalisantes à prendre en compte sont liées au positionnement du capteur. La distance de mesure imposée étant relativement élevée (20 ou 30mm), la valeur choisie de 2a doit assurer le meilleur couplage capteur/cible tout en minimisant l’influence de la dynamique transversale (± 30mm) et verticale (± 5mm) transmise par le châssis de bogie sur la détection des défauts de rail.

La modélisation par éléments finis constitue une approche intéressante des problèmes d’optimisation de structures de capteurs. Elle permet, en un temps relativement court, d’évaluer les performances de plusieurs structures sans avoir à les réaliser physiquement ou en développer des modèles analytiques, qui dans la majorité des cas s'avèrent complexes à mettre en oeuvre. Les outils de simulation existants sont nombreux à pouvoir traiter des problèmes bidimensionnels.

La nature foncièrement 3D de notre application justifierait l'emploi d'un outil de simulations tridimensionnel. Ces logiciels complexes et peu nombreux nécessitent un environnement informatique beaucoup plus lourd et leurs temps de calcul sont très importants. Pour notre étude, nous avons plutôt choisi de simplifier notre problème et d'utiliser le code 2D Maxwell de Ansoft Corporation [ANS-94]. Les simulations nous permettront d'estimer le couplage capteur/cible dans le plan (y, z) pour différentes largeurs inter-plots mais elles seront incapables de modéliser la réponse du capteur à un défaut situé sur la troisième dimension. Cette étape préliminaire de simulations doit nous fournir une description qualitative de l’évolution du coefficient de couplage capteur/cible (k) en fonction de la largeur inter-plots (2a). On peut noter que seules des tendances peuvent être déduites de ces simulations, étant

donné que la résolution d’un problème tridimensionnel à l’aide d’un logiciel de calcul 2D ne peut être qu'approchée.

Pour mener à bien ces simulations, il convient de procéder à :

1- la création, sous forme de dessin, de la structure géométrique du modèle.

2- l'affectation des propriétés électriques et magnétiques des matériaux constituants chaque élément.

3- la définition des conditions aux limites du problème et la configuration des sources de courants présentes dans la structure.

4- le réglage des paramètres de simulation tels que le pourcentage d’affinement du maillage par itération, l’erreur résiduelle souhaitée, le nombre d’itération maximal. Des calculs supplémentaires de certains paramètres tels que le flux à travers une section, la matrice d'impédance entre deux conducteurs peuvent être effectués.

5- l'analyse des résultats.

La structure géométrique que nous avons simulée est présentée figure II-13.

blindage 1 bob2 bob1 Rail Dt blindage 2 h 2a U ferrite

On distingue deux blindages (supposés infiniment longs dans la direction x non modélisée), le circuit magnétique en U, deux conducteurs et une section du rail de largeur 65mm. L'annexe A donne les caractéristiques complètes de la simulation sous l'environnement Maxwell.

Pour estimer le couplage capteur/cible, il convient de simuler le capteur seul. Cette simulation préalable fournit l'impédance à vide du capteur qui ensuite permettra d'estimer l'impédance normalisée (cf. § II.4.2). Pour calculer le coefficient de couplage, nous avons choisi de placer le système sur sa caractéristique d'impédance normalisée à la fréquence f = ∞; l'épaisseur de peau tendant alors vers zéro, l'impédance est uniquement réactive (le flux purement en phase avec le courant d'excitation) et la caractéristique du capteur coupe l'axe vertical du plan

d'impédance à l'ordonnée 1-k2_{. Pour la simulation, on se place fictivement en ce point de}

fonctionnement en réglant simplement σ = ∞ pour le rail.

L’allure des lignes de champ lorsque le rail est placé à 20mm du capteur est illustrée sur la figure II-14.