Constraining Effective Field Theories with Machine Learning
Texte intégral
Figure
Documents relatifs
The proposed plug-in enables to visually define and execute processes in terms of UML activity diagrams to reverse engineer or comprehend existing traditional
The objectives of this workshop are to carry out a situation assessment of computerization of health statistical information systems in the countries of the Eastern
Papers from the four main tracks at CICM 2014 (Calcule- mus, Digital Mathematical Libraries, Mathematical Knowledge Management, and Systems & Projects) will be published in
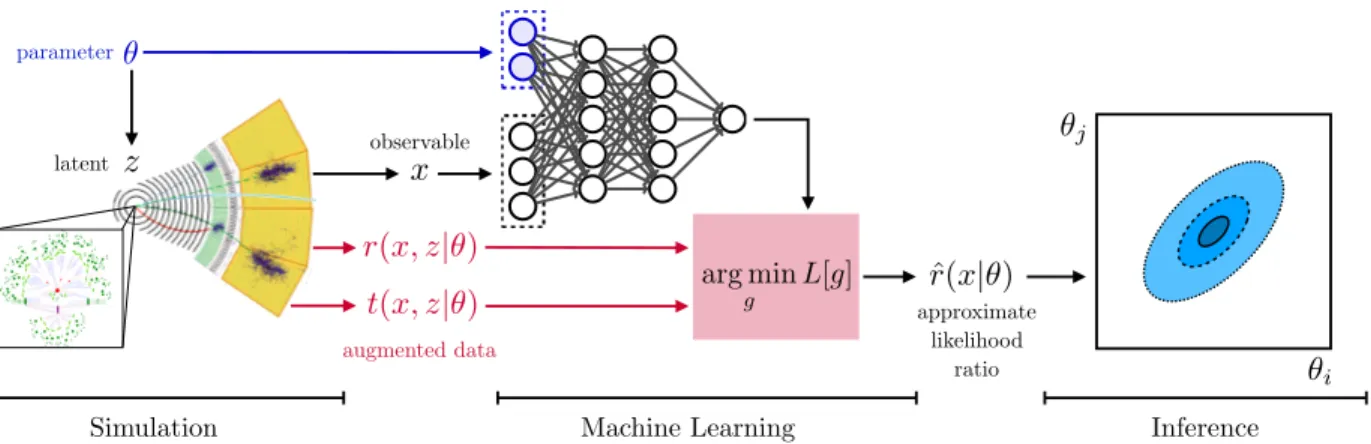
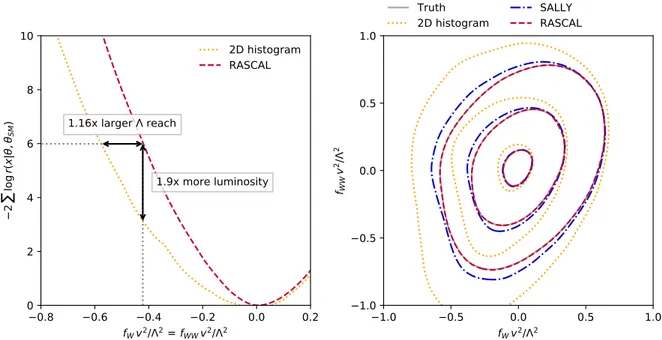
The idea behind maximum likelihood estimation is to choose the most probable parameter θ ∈ Θ for the observed data.. Hence, the high level idea of maximum likelihood estimation will
Joint Proceedings of Modellierung 2020 Short, Workshop and Tools & Demo Papers CEUR-WS.org Proceedings, Volume 2542 1.. Preface of the Joint Proceedings of Modellierung 2020
Zhu, A Uniformization Theorem Of Complete Noncompact K¨ ahler Surfaces With Positive Bisectional Curvature, J.. Zhu, On complete noncompact K¨ ahler manifolds with positive
(a) The average RASE as a function of bandwidth for the three estimation methods; (b) The scatter plot for the RASE of the local quasi- likelihood estimator with the imputed
30th March: Dr Robert Wilson (Mathematics and Statistics, University of Strathclyde) 25th May: Raphael Ximenes (Department of Mathematics & Statistics, University of