ARTheque - STEF - ENS Cachan | Bulletin de l'Association Amicale des Anciens Élèves de l'École Normale Supérieure de l'Enseignement Technique n° 115

Questions

d'aujouiti'hui

Les fascicules de cette série sont consacrés à un ou

plusieurs problèmes du monde d'aujourd'hui. Point

par point, chacune de leurs dimensions est abordée

à travers un texte, une illustration ou des statistiques,

éclairés, contredits ou approfondis par d'autres

textes ou d'autres documents.

Chaque fascicule constitue :

— pour les élèves ou les étudiants, un guide ou un

ouvrage de référence, maniable, adapté aussi bien

au travail en équipe qu'au travail individuel ;

— pour les professeurs, un outil qu'ils peuvent

mettre en œuvre selon le niveau et les intérêts des

groupes, sans être enfermés dans un schéma pré­

établi ou dans une progression impérative, et sans

être contraints à la lourde tâche de rechercher et de

reproduire des documents complémentaires.

Vient de paraître:

Vivre l'économ ie

Le q u o t i d i e n . S t r a t é g i e s é c o n o m i q u e s . P r o b l è m e s e t p e r s p e c ­

tiv e s.

p a r J . B o d in e t Y. P e l a n n e

168 p a g e s , 6 2 F

Egalement disponible, des mêmes auteurs :

L'univers des signes

S i g n e s e t s ig n ific a tio n s . L 'i n f o r m a t i o n . L 'art.

176 p a g e s , 40 F

Prix au 1.4.76

MASSON

120, Bd Saint-Germain 75280 Paris cedex 06

m

BULLfTin de

L’IISSOCiilTIOn m n i c f l u

des

f l i l c i f n s

f U V f S

ECOLE

NORMALE

SUPERIEURE

NSEÎGNEMEN

ECHNÎQUE

N° 115 - 1er trimestre 1976 Abonnement (un a n ) SO F Le num éro ... 15 F 61, avenue du Présldent-W llaon

---Une nouveauté dans la

Bibliothèque Professionnelle

chez DUNOD

LA CONSTRUCTION

DE BÂTIMENT

par Gérard BAUD

2 5 6 p a g e s , f o r ma t 21 x 29,7, r e l i é .

45 F

C e lu i q u e l'o n n o m m e a u j o u r ­

d 'h u i

“ Le c o n s t r u c t e u r d e

B â t i m e n t ” d o i t a v o ir a c q u i s

u n e s o l i d e f o r m a t i o n t e c h n o ­

lo g i q u e p o u r ê t r e à m ê m e

d ' a s s i m i l e r le s t e c h n i q u e s d i­

v e r s e s qu'il lui f a u t m a î t r i s e r

a u j o u r d 'h u i .

A v e c c e d o c u m e n t , le t e c h n i ­

c i e n , c o m m e le c o m p a g n o n

qualifié, d i s p o s e r a d 'u n o u ­

v r a g e c o m p l e t , clair, r i c h e ­

m e n t d o c u m e n t é e t a c t u a l i s é

s u r le g r o s œ u v r e . L e s j e u n e s

e n c o u r s d e f o r m a t i o n t r o u v e ­

r o n t d a n s c e m a n u e l un outil

d e tra v a il i n d i s p e n s a b l e .

dunod

37, rue Boulard

75680 PARIS CEDEX 14

nwonnetieetb^on^

nathan

technique

ELECIRICITC

collection JEAN N IA R D

électronique |

1è r e F 2 F3 Jear) N IA R D • Édition rouge ... 25,5 5 N O W E A i n C ^ Livre de l’élève (nouvelle é d itio n ) ... en préf>aration T e r m . F 1 Jean N IA R D

• Livre de l'élèv e... 2 2 ,9 5 T e r m . F 2 Jean N IA R D , R o b e rt M E R A T, , Yves R E N O U X

• É dition v erte ... 2 9 ,4 0 N O W E A V T E .^ Livre d e l'élève (nouvelle é d itio n ) en p ré p a ra tio n T e r m . F 3 Jean N IA R D , R o b e rt M E R A T

• Livre d e l'élève ... 2 8 ,1 0

mesures électriques

1ère F 2 F3 Jean N IA R D , Yves R E N O U X e t Jean-Claude Q U IZ Y

• Livre de l'élève ... 30 ,6 5

mesures électroniques

T erm . F2 Jean N IA R D e t Yves R E N O U X

• Livre d e l'élève ... 2 5 ,5 5

machines électriques

T erm . F I F3 Jean N IA R D

• Livre d e l'élève, éd itio n bleue ... 3 0 ,6 5 T erm . F 2 • Livre d e l'élève, éditio n noire ... 2 0 ,4 0

____________________ NOVVEAIFTES_____________________

T erm . F3 • Livre de l'élève en p ré p a ra tio n

T erm . F I , 2 , 4 • Livre de l'élève ... en p ré p a ra tion

cours d'électricité

L O I S G É N É R A L E S C O U R A N T C O N T I N U • É dition b leu e ... • Édition jau n e ... L O I S G É N É R A L E S C O U R A N T A L T E R N A T I F • Édition b leu e ... • Édition jau n e ... 39 ,0 0 3 1 ,9 5 3 2 ,3 5 19 ,1 0 D e m a n d e z le c a t a l o g u e n<> 6 3 N A T H A N T E C H N I Q U E à :

FERNAND NATHAN

9. rue Méchain 7 5 6 8 0 PARIS CEDEX 14 Salie d 'exposition : 18 rue M onsieur-le^rince 7 5 0 0 6 PARIS

publié so u s la direction de

G eorges Goudet

TRAITE

D'ELECTRICITE

en 3 tomes :

I. Phénomènes électriques et magnétiques indépen­

dants du temps, par G. Goudet.

380 p., 263 fig., 1 2 tab l.,6 2 F .

II. Phénomènes électriques et magnétiques dépen­

dants du temps, par G. Goudet, R. Bonnefille et

A. Maréchal.

372 p., 228 fig., 3 tabl., 66 F.

III. L’électricité et la matière par F. Bertein, J. Chanu,

M. Chemla, G. Fournet et D. Quemada.

372

p.,

188 fig., 7 tabl., 68 F.

Prix au 1.4.1976

Pour toute documentation sur le Nom et adresse TRAITÉ D ’ÉLECTRICITÉ publié _____________ sous la direction de G. Goudet Spécialité ___ adressez-vous à votre libraire ou

retournez ce bon aux E ditions M asson, 120 bd Saint-G erm ain,

G R A P H O P L E X

n o u v e a u t é

s t y l o à e n c r e d e c h i n e S T 2

r é g u l a t e u r S T 2

s é c u r i t é

+

r é s e r v o i r é c l i p t i q u e

S T 2

r e m p l i s s a g e

r a t i o n n e l

p r o p r e t é

+

g a i n

d e

t e m p s

SPÉCIAL ; ÉCOLE DESSIN - BUREAU ÉTUDES

S T 2 est r i n s t r u m e n t de t r a ç a g e à e n cr e

de c hi ne le plus p e r f e c t i o n n é du

m o m e n t

PHYSIQUE ELECTRICITE

collection NIARD

COLLEGES D'ENSEIGNEMENT TECHNIQUE

--- COURS

D'ÉLECTRICITÉ---L O IS G É N É R A D'ÉLECTRICITÉ---L E S C O U R A N T C O N T IN U

B.E.P.

• Le volum e (édition jaune) ... 3 5 ,5 0 L O IS G É N É R A L E S C O U R A N T A L T E R N A T I F • Le volum e (édition jaune) ... 2 1 ,2 0 É L E C T R O N IQ U E

• Le volum e (édition rouge) ... 2 8 ,4 0

LYCÉES TECHNIQUES

---

ÉLECTRONIQUE---Jean NIARD

“

jre p 2 - F3

• Le volum e (édition rouge) ... 2 8 ,4 0 • Le volum e (édition bleue) ... 3 9 ,9 0

Terminale F I

• Livre de l'élève ... 2 5 ,5 0 Jean NIARD, R obert M ERAT, Yves RENOUX

Terminale F2

• Le volum e (édition bleue) ... 4 8 ,8 5 Jean NIARD, R obert MERAT

Terminale F3

• Livre de l'élève ... 3 1 ,2 0 Jean NIARD, Yves RENOUX, Jean-Claude Q U I2Y

M E S U R E S É L E C T R IQ U E S

jre p 2 - F3

• Livre de l'élève ... 3 4 ,0 0 Jean NIARD, Yves RENOUX

M E S U R E S É L E C T R O N IQ U E S

Terminale F2

• Livre de l'élève ... 2 8 ,3 5 Jean NIARD

M A C H IN E S É L E C T R IQ U E S

Terminale F I - F3

• Livre de l'élève (édition b le u e ) ... 3 4 ,1 0

Terminale F2

• Livre de rélève (édition ja u n e )... 2 2 ,6 5

^^Term inale F3

• Livre de l'élève

sous presse

Terminale F I

• Livre de rélève

sous presse

F 2 - F 4

--- COURS

D'ÉLECTRICITÉ---Jean NIARD

F, H

L O IS G É N É R A L E S C O U R A N T C O N T IN U

• Le volum e (édition bleue) ... 4 3 ,3 0 • Le volum e (édition jaune) ... 3 5 ,5 0

FI , F2, F3, F5

L O IS G É N É R A L E S C O U R A N T A L T E R N A T I F

Terminales F I ,

• Le volum e (édition bleue) ... 3 5 ,9 0

F4, F5

_______________ 0 Le volum e (édition jaune) ... 2 1 ,2 0

|^ ^ 2 1 C3 Π!!Π[

C o rre s p o n d a n c e : 9, r u e M éch ain - 7 5 6 8 0 P aris C ed ex 14 S alle d 'E x p o s I tio n : 1 8 , ru e M o n sieu r-le-P rin ce • 7 5 0 0 6 Paris

SOMMAIRE

• U n ac c e sso ire logique ...

7

• U tilis a tio n d e m a tr ic e s r e c t a n t u l a i r e s

d a n s q u e l q u e s p r o b l è m e s de p h y s i q u e ...

14

• T r i b u n e libre

Les f a u x r a t t r a p a g e s o u la

m a lig n ité d e l 'i m p ô t

...

3 6

• Le vin e t l ' e a u ...

4 3

• B ib lio g ra p h ie

... 4 6

• Vie fa m ilia le

...

5 8

• O ffre s d ' e m p l o i s ...

5 9

•

6

e t 7 ju in , C a c h a n , c o n g r è s 1 9 7 6

6 0

• La vie d e n o s ré g io n s

... 61

• C o m i t é d u 19 o c t o b r e 1 9 7 5

6 3

• C o m i t é d u 2 9 fé v rie r 1 9 7 6 ...

6 4

• T r é s o r e r i e

...

6 7

• M o ts c ro isé s

...

7 3

Pour répondre aux nouveaux programmes

d'Électrotechnique et de servo-mécanismes :

Groupe de Regulation do uiiesso a Tiiiirisiors

avec moteur C/C à entrefer plan et rotor discoïdai

i

Pour les

besoins

de TEnsei-

gnement

Technique,

la CEM

a étudié

à partir de

constituants

industriels,

un Groupe

de régulation

de vitesse

à thyristors.

CONSTITUTION :

— 1 banc supportant : 2 moteurs courant continu à ro tor discoïdai A X E M — 500 W - 3000 tr/m n avec tachym étrie AXEM - (6 V par lOOOtr/mn) accouplés par manchon débrayable.

— 1 variateu r de vitesse à thyristors unidirectionnel à pont m ixte avec synop­ tique reprenant le schéma de principe de la régulation et perm ettant l'étude des signaux caractéristiques à partir de points tests.

La régulation peut se faire : par génératrice tachym étrique ou par compensation de la chute interne RI.

A lim entation : 220 V monophasé 50 Hz. Tension de sortie : 0 /1 70 v continue. Courant de sortie : 6 ampères continu.

— 1 self de lissage du courant d 'in d u it (20 mH - 6 ampères).

CE G R O U PE PER M ET :

— Les essais habituels des moteurs C /C conventionnels.

— Les essais propres aux caractéristiques du moteur AXEM (faible inertie - nom­ bre élevé de lames au collecteur - absence de fer au rotor) - Exemple : simulation de cycles de commande numérique.

— L'étude des circuits composant un variateur à thyristors.

C e t e n s e ig n e m e n t e st e x tra it d u c a ta lo g u e « Matériel Èlectrotecnlque pour l'enseignement » é d ité p a r la G E M .

S'adresser aux Agences régionales CEM ou écrire sous référence VEC 606 à :

C O U R C E L L O R

SE R V IC E 2, RUE CüRNO NSKY

UN ACCESSOIRE LOGIQUE

Quel autom obiliste q u itta n t sa voiture pour la jo u rn ée n ’a jam ais

oublié ses veilleuses restées allumées après un tunnel ou une nappe

de brouillard ?

Mon but ici n ’est pas de philosopher sur la faiblesse hum aine,

mais de proposer un petit accessoire susceptible de rappeler sa

négligence au conducteur distrait.

UN TEM O IN SONORE

Le m oteur de ce tém oin de veilleuses est un circuit intégré m onté

en oscillateur et d éb itan t sur un petit haut-parleur.

Le circuit intégré est le TAA

611 de la S.G.S. ATES, prévu

com m e am plificateur, que l’on fait osciller en couplant l’entrée à la

sortie par un condensateur de

4,7 nF. Le circuit travaillant à

saturation on le charge par un haut-parleur d ’im pédance relative­

m ent élevée

(20 à 30 ohms) pour lim iter l ’échauffem ent.

On pourra m odifier la fréquence du son émis en faisant varier la

valeur du condensateur C entre 4,7 juF et 25

juF-Ainsi réalisé le tém oin fonctionne en 6 V ou

12 V sans m odifica­

tion, avec une consom m ation négligeable d ’électricité.

LA COMM ANDE LOGIQUE

Le m ontage n ’étan t étudié que pour des véhicules conçus avec

le pôle négatif à la masse, j ’utilise pour le calcul les conventions de

l’algèbre de Boole en appelant niveau

0 la masse et niveau 1 le

potentiel + 6 V o u +

1 2 V selon le cas.

Soit A le fil d ’alim entation des veilleuses ou des lanternes arrières,

et a son niveau électrique, la variable booléenne a a la valeur 1

quand les veilleuses sont allumées et 0 quand elles sont éteintes.

Q uand les veilleuses sont éteintes le reto u r vers la masse se fait

éventuellem ent à travers les lampes elles-mêmes.

n i v e a u 1 n i v e a u 0 i n t e r r u p t e u r c o m m o d 0 n i v e a u a v e i l l e u s e ;

De même B éta n t le fil d ’alim entation de la bobine (contact

m oteur) et h son niveau électrique, la variable booléenne h a la

valeur 1 quand le contact est mis, et 0 contact coupé ; un reto u r

éventuel à la masse se faisant par les instrum ents de bord.

n i v e a u 1 c o n t a c t n i v e a u 0

o-1

n i v e a u b i n s t r u m e n t s ....

Pour com m ander le tém oin envisagé nous disposons donc de

quatre inform ations booléennes :

a

b

1

0

veilleuses allumées

contact m oteur

positif perm anent

masse

Trois principes de com m ande apparaissent alors, par ordre

d ’in térêt, utilisant une, deux, ou trois variables booléennes.

PREMIER MONTAGE

La solution triviale est de m onter le tém oin sonore en parallèle

sur les veilleuses.

a

v e 111 e u s e s t é m o i n

0 ^ 0 s o n o r e

r - O ---• t = a

Deux états sont alors possibles :

a t

0 0 les veilleuses so n t éteintes, le tém oin est éteint

1 1 les veilleuses sont allumées, le tém oin fonctionne

C ette solution simple n ’aura certainem ent pas l’agrém ent du

conducteur am ené à supporter longtem ps un tém oin sonore gênant.

SECOND MONTAGE

Une solution plus agréable est de ne faire fonctionner le tém oin

que lorsque le co n tact m oteur est coupé :

Pour réaliser cette option, il suffit d ’effectuer le reto u r à la masse

à travers les instrum ents de bord, une diode placée dans le circuit

bloquant la possibilité : “ contact ET non veilleuses” .

c o n t a c t

t é m o i n s o n o re

Q uatre états sont possibles :

a b t

0 0 0 veilleuses éteintes, co n tact coupé : tém oin éteint

0 1 0 veilleuses éteintes, co n tact mis : tém oin étein t

1 0 1 veilleuses allumées, co n tact coupé : tém oin fonctionne

1 1 0 veilleuses allumées, co n tact mis : tém oin étein t

Ce m ontage pratique ne perm et cependant pas de laisser in ten ­

tionnellem ent les veilleuses allumées en stationnem ent.

TRO ISIEM E MONTAGE

Pour perm ettre à l’utilisateur de rallum er ses veilleuses au sta tio n ­

nem ent il suffit que le tém oin ne se déclenche que si, les veilleuses

é ta n t allumées, il coupe le contact.

Pour réaliser cette condition j ’utiliserai une variable booléenne

tem porisée : la charge d ’un condensateur Ct de

0,47

mF-c o n t a mF-c t nI V e a u b

n i v e a u 0

X

n i v e a u c

La variable c n ’est pas indépendante de

la variable b : quand h

est au niveau 1, c est aussi au niveau 1, on d it que “b e n tra în e c ” .

Mais la variable c reste au niveau

1 quand on ram ène b à l ’état 0 .

Les six cas possibles sont alors :

a b c

0 0 0 m oteur arrêté et veilleuses éteintes

0 0 1 on vient d’arrêter le m oteur, veilleuses éteintes

0 1 1 m oteur en ro u te, veilleuses éteintes

1 0 1 on vient d ’arrêter le m oteur, veilleuses allum ées

1 1 1 m oteur en ro u te, veilleuses allumées

Seul l’avant dernier cas nous intéresse : t = a ■

b ■

c .

La tension c com m ande la gâchette d ’un th yristor Th qui devient

conducteur seulem ent quand les trois conditions sont réalisées :

Anode à un p o ten tiel positif

G âchette à un p o ten tiel positif

C athode au potentiel zéro

et reste co nducteur quand le courant de gâchette est supprim é.

V e 111 e u s e _ o -c o n t a -c t o ---b

-w-Tti c o m m a n d e l o g I qu e t é m o i n s o n o r e

Les six états possibles sont alors :

a b c

0 0 0 le tém oin n ’est soumis à aucune tension

0 0 1 le condensateur se décharge sans effet

0 1 1 son anode au potentiel 0 , Th est bloqué

1 0 0 sa gâchette au potentiel 0, Th reste bloqué

1 0 1 le thyristor Th conduit, le tém oin fonctionne

1 1 1 le tém oin n ’est soumis à aucune tension

Le seul cas où le tém oin fonctionne est l’avant dernier :

les veilleuses sont allumées et on arrête le m oteur.

Si le conducteur désire laisser ses veilleuses allum ées pour un

stationnem ent, il lui suffit d ’arrêter le m oteur, puis, le contact

é ta n t coupé, de rallum er les veilleuses.

R E A LISA TIO N PRATIQUE

Le m ontage peut être fait sur une plaquette de cablage imprimé

de

60 X 77,5 mm, d o n t voici le dessin côté cuivre et côté com po­

sants. On fera a tte n tio n à ne pas oublier le po n t “ strap ” .

ma s s e

LISTE DES COMPOSANTS

circuit intégré TAA

611 B ou équivalent

th yristor 1 am père, 100 volts

diodes silicium 1 am père, 100 volts

condensateur

220 juF, 63 volts

condensateur

100

63 volts

condensateur de

4,7 mF à 25 ixF, 63 volts (voir texte)

condensateur

0,47 mF métallisé

condensateur 0,1 juF

condensateur

4,7 nF

condensateur

1,8 nF céram ique

condensateur

100 pF céram ique

résistance

160 ohm s, 1/2 w att

résistance

24 000 ohm s, 1/2 w att

haut-parleur

7 cm, 20 à 30 ohms

Le boîtier au choix de l’utilisateur vous perm ettra de placer ce

petit accessoire, sous le capot ou derrière le tableau de bord, près de

la b o îte à fusibles de façon à le brancher facilem ent sur le fil des

veilleuses et sur le fil du contact m oteur.

utilisation de

MATRICES RECTANGULAIRES

dans quelques problèmes de physique

L’utilisation de m éthodes m atricielles est devenue banale ces

dernières années pour la résolution de tous problèm es faisant in ter­

venir des systèm es linéaires, su rto u t grâce au développem ent du

calcul par ordinateur. Les m atrices qui interviennent dans ces

problèm es (à part les m atrices lignes et colonnes), dans la très

grande m ajorité des cas sont carrées et l’usage de m atrices rectangu­

laires est à peu près ignoré. Il existe cependant des situations où la

m anipulation de telles m atrices est indiquée.

Les matrices carrées ont été utilisées intensivem ent d ’abord par

des m écaniciens étudiant les vibrations de structures aéro n autiqués*.

Ce sont encore des m écaniciens qui récem m ent ont in tro d u it la

no tion de m atrice de transfert (ou de transférance) rectangulaire^’^.

I - RAPPEL DE QUELQUES ELEMENTS DE LA TH E O R IE

DES QUADRIPOLES

Un quadripole est une “ b o îte noire’’ à quatre bornes qui assure

le transfert d ’une énergie, q u elqu’en soit la form e, sous la seule

restriction que les équations qui régissent le systèm e soient linéaires

(fig.

1). La co nstitution interne de la b o îte noire im porte peu. Un

tel systèm e s’appelle encore un transducteur. Les grandeurs interve­

n ant à l ’entrée et à la sortie peuvent être le plus couram m ent des

l e

6e

Es

Fig. 1 — Q uadripole électrique.

tensions et des courants électriques, des forces et des vitesses m éca­

niques, des longueurs et des angles optiques, des débits et des

pressions acoustiques, etc..."*.

Considérons l’exem ple classique du quadripole électrique. On

appelle Eg, E , la d.d.p. et le courant d ’entrée et

et E la d.d.p. et

le courant de sortie. On sait que les équations du quadripole s’écri­

vent, sous la form e m atricielle :

ou

Eg

A B

Es

E

C D

E

= [T]

La m atrice T qui perm et de passer des grandeurs d ’entrée aux

grandeurs de sortie s’appelle m atrice de transfert dans la plupart

des ouvrages français. Il y a six manières de grouper deux à deux les

bornes d ’entree et de sortie : on définit donc six m atrices exprim ant

des relations linéaires entre Eg, E et Eg, E- La plus im p o rtan te est

la m atrice de transfert T. Q uand celle-ci est régulière, on désigne

son inverse T'* sous le nom de m atrice caractéristique ou encore de

transfert arrière ou rétrograde. T est alors la m atrice de transfert

avant ou directe selon la term inologie des ouvrages anglo-saxons.

Une autre m atrice im portante est la m atrice im pédance définie par

2 i i

Z2 I

' 2 2

ou

= [Z]

h

Is

Q uand Z est régulière, son inverse est la m atrice adm ittance. Dans

la suite, nous n ’utiliserons que les m atrices de transfert et la m atrice

im pédance.

Il existe des relations entre les élém ents de ces différentes

m atrices. Le lecteur les trouvera dans les ouvrages de calcul

matriciel^

.

Dans le cas général, les grandeurs d ’entrée et de sortie sont des

quantités complexes. Les m atrices précédentes définissent donc une

application de

dans

. Les quantités apparaissant dans les

m atrices colonnes peuvent être considérées com m e les com posantes

d ’un vecteur que nous appellerons vecteur d ’état.

A ppliquons les notions précédentes à quelques exem ples simples

et classiques.

Exem ple

1 :

Soit le systèm e m écanique constitué par deux masses m j et m2

couplées par des ressorts de raideurs fei et ^2 et se déplaçant sans

fro ttem en t. Sur les masses on applique respectivem ent les forces

f i e ' “ ' et F2

,1 C J t

où Fi et F2 sont des constantes et on étudie les

vibrations sinusoïdales du systèm e (fig. 2).

/

h

>

i i e '

R i

Fig.

2 — Système m écanique à deux degrés de liberté.

Pour la résolution de cet exercice, nous utiliserons les équations

de L a g r a n g e ^ Désignons par Xj et X2 les déplacem ents des

masses m j et m2, par XiCt X2 les vitesses. L’énergie cinétique est

L’énergie potentielle est

k i x ] + - | ^2 (^2 - X i Ÿ

.

A partir du Lagrangien L — T — U, on déduit les équations de

Lagrange :

d

dt

d

df

(s)

3L

9x i

= m i ' x i + k i X i — fej (x2 —X i ) = F i e ' ^ ^ (1)

T - 1 : ^ 1 = " Î 2 ^ 2 + ^ 2 ( ^ 2 - ^ i) = - F 2 '“ ' O X j

En régime sinusoïdal de pulsation OJ : x = X e“*’

x = — OJ^x.

Les équations précédentes deviennent

{- m i

+ kl + fej ) -^1 ~ ^2 ^ 2 = -f^i

- ^2-^1 + (— m2

+ k2) X2 = p2 ,

ou, sous form e m atricielle,

Fx

- myCjJ^ + ky -1-^2

- ^2

F2

- ^ 2

— m2

-1- ^2

X2

(

2

)

Nous obtenons ainsi les solutions en régime perm anent. La

m atrice ci-dessus s’appelle m atrice d ’élasticité. La form e de ces

solutions ne perm et pas facilem ent des généralisations.

On sait que to u t systèm e vibratoire régi par des équations diffé­

rentielles linéaires à coefficients constants possède un analogue

électrique. Nous ne nous étendrons pas sur ce sujet qui à lui seul

nécessiterait de longs développem ents et ne citerons que l’analogie

force-tension ou analogie série. Ainsi, au systèm e m écanique am orti

à un degré de liberté de la figure

3 com prenant une masse m suspen­

due à un ressort de raideur k avec une constante d ’am ortissem ent

fluide c, régi par l’équation différentielle

correspond, dans l’analogie force-tension, le circuit électrique régi

par l’équation

Lq + R q + i =

.

/ U / / / / J

LU C

u

-nsam

L---/ywv—

R

Fig.

3 — Analogie force-tension.

A une masse correspond une self (m ^ L), à une raideur l’inverse

d ’une capacité (fe -»•

1/C), à un am ortissem ent fluide une résistance

[C ^ R), à une force une tension [ F V ) et à une abscisse une

charge électrique (x -> q).

Dans le cas de réseaux électriques, en régime perm anent où les

charges ne s’accum ulent pas, la n o tion même de charge est sans

intérêt. Les seules grandeurs que l’on recherche sont les tensions et

les courants. Pour conserver l’analogie entre systèm es m écaniques et

systèm es électriques, il est nécessaire, dans les équations des mouve­

m ents, de faire intervenir, non les déplacem ents, mais les vitesses

qui sont les analogues des courants.

Dans l’exem ple

1, les équations aux vitesses s’o btiennent par

intégration des équations de Lagrange (

1), en rem arquant que pour

des grandeurs sinusoïdales x = icox :

d x

J dx

J

F (t) d t

ou

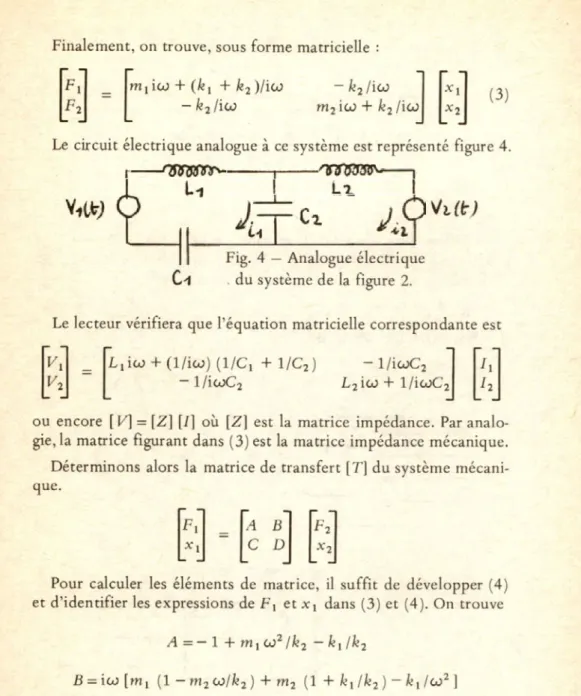
F in a le m e n t, on tro u v e, sous fo rm e m atricielle :

F i

F2

m iico + (fei + fei )/it^

- k 2 /icü

m2i(j0 + k2/'\u)

Xi

X2

(3)

Le circuit électrique analogue à ce systèm e est représenté figure

4 .

L x

I

^ i ( t )

Fig.

4 — Analogue électrique

du systèm e de la figure 2.

Le lecteur vérifiera que l’équation m atricielle correspondante est

I

L ,ico + (

1/ico) (1/C i + I/C2)

- l/icoC j

- l/icoC2

L2ico + l/icoC2

ou encore [ V] = [Z] [/] où [Z] est la m atrice im pédance. Par analo­

gie, la m atrice figurant dans (3) est la m atrice im pédance m écanique.

D éterm inons alors la m atrice de tran sfert [T] du systèm e m écani­

que.

F i

A B

C D

F

2

X2

Pour calculer les élém ents de m atrice, il suffit de développer (4 )

et d ’identifier les expressions de F j et Xj dans (3 ) et (4 ). On trouve

A = — 1 +

jk2 — kl Ik2

B =

[mi

(1 — m2 tj/fe2 ) + W2 {1 + kl Ik2) — kl

]

C = — ico/feo

D = 1 — m2

Ik^

N otons que si la m atrice [Z] est sym étrique, la m atrice [T] ne

l’est pas. Par analogie, on o b tie n t im m édiatem ent les élém ents de la

m atrice im pédance électrique.

Cas de plusieurs q u ad rip o les en c h a în e (fig. 5).

C n j

Fig.

5.

C T î l

La m atrice de transfert de l’ensemble est [T] = [Tj ] ■

[T2 ] • [T3 ] ,

produit des matrices de transfert de chaque quadripole, d ’où l’in té ­

rêt fondam ental de la n o tion de m atrice de transfert.

- N O T IO N DE M ULTIPOLE

C ’est une “ b o îte noire” possédant p entrées et n sorties (fig. 6).

0----—0

Fig. 6 — M ultipôle.

Fig.

7.

"%7—

17— '

^

e '

C

1

1 •

yâ

Dans la théorie des réseaux électriques^, on ne considère généra­

lem ent que des

2N pôles (ou 2N + 1 pôles s’il y a une borne

cofnm une aux entrées et aux sorties). Donc on prend 2N — p = n .

En m écanique, cette restriction ne s’im pose pas et il peut se

présen-ter des structures telles que celles de la figure 7 qui est une grille

com posée de barres m étalliques identiques et do n t on peut se

proposer d ’étudier les petits m ouvem ents. Cet exem ple est très

com pliqué, mais il m ontre com m ent, intuitivem ent, s’im pose la

n o tion de m atrice de transfert.

Au point A s’exercent des forces

, des couples

qui produi­

sent un déplacem ent

résultant de translations

et de ro tatio n s

• Il en est de même au point B. On peut, comm e déjà indiqué

plus haut, ranger les quantités F

a

--Q

a

et F

b

—O

b

dans des colonnes

appelées vecteur d ’é ta t ou état, et si le systèm e est régi par des

équations linéaires, on aura encore

F

a

F

b

C

a

= [T]

C

b Xa Xb

A

B

ou

[2 ]

p représente le vecteur des forces généralisées (forces et couples) et

d celui des déplacem ents généralisés correspondants (translations et

rotations) ; [T] est la m atrice de transfert.

Sur la figure

7, les points A et B jo u e n t les mêmes rôles géomé­

trique et m écanique. La m atrice [T] est donc carrée. Il n ’en est plus

de même pour les points C et D. Il y a moins de forces qui sollicitent

C que D et la situation est celle d ’un m ultipôle avec p entrées et n

sorties. Le vecteur d ’é ta t à l’entrée aura p com posantes et n à la

sortie. La m atrice qui perm ettra de passer de l ’entrée à la sortie sera

rectangualire avec p lignes et n colonnes. Si o;i...a!p désignent les

com posantes du vecteur d ’éta t à l’entrée et )

3i

celles du vecteur

d ’é ta t à la sortie, on a :

«1

a , 1 .

■ « in

“ 2

«2 1 •

«P

« p i • • «pn

( p x i ;

(p X n)

(n X

1 )

(5)

S i p > n, la m atrice a plus de lignes que de colonnes, nous l’appel­

lerons m atrice haute. S ip < n , elle a plus de colonnes que de lignes,

nous l’appellerons m atrice large. Dans l ’exem ple de la figure

7, il est

in tu itif que, connaissant l’é ta t en D, on peut déterm iner l ’éta t en C,

mais qu’il est impossible de rem onter de C en D si l’on ne co n n aît

que les états avals sans autre inform ation sur les états am onts. Pour

passer de C en D, on dispose de p équations linéaires à n inconnues.

Si le systèm e est bien conditionné, seulem ent p — n de ces équations

sont linéairem ent indépendantes. Par contre, pour passer de C en

D,

on ne dispose que de n équations linéaires pour déterm iner p

in c o n n u e s; il m anque précisém ent p —n équations. Le systèm e

m atriciel (

5) est donc essentiellem ent irréversible.

Ill - FO R M A TIO N DES MATRICES DE TRAN SFERT

RECTANGULAIRES.

Nous allons exposer m aintenant un procédé p erm ettan t de passer

de la m atrice im pédance carrée à la m atrice de transfert rectangu­

laire. Raisonnons sur un systèm e m écanique com m e celui de la

figure

7. Au point d ’indice i — 1, le vecteur des forces généralisées

est F,-. 1, celui des vitesses généralisées f,-. i , chacun ayant p com po­

santes. Au point d ’indice i, le vecteur des forces est F,-, celui des

vitesses v,- avec n com posantes [n < p ) . L’équation m atricielle

d ’im pédance faisant correspondre les F aux v s’écrit de la manière

la plus générale :

nn

n 1~ "

np

(6)

p n

p p

La m atrice carrée est d ’ordre n + p . En vertu du théorèm e de

réciprocité de Maxwell**®, [F ] = [R ]^ où [R]^ est la m atrice

* Pour des systèm es excités sinusoîdalem ent en régime perm anent, la force produit la même réponse sur la coordonnée que la force

Qs = Qr

p ro d u it sur la coordonnée q^.

transposée de [R]**. [Q] et [R] sont des m atrices sym étriques. Les

m atrices [Q] et [S] sont carrées, l’une d ’ordre n, l’autre d ’ordre p.

La sous-m atrice [R] est rectangulaire à p lignes et n colonnes. En

dévelopant (6), on a :

-F ,- = Q

Vi -f-

Vi

(n-1)

(n-n) (n-1)

{n-p) (p-1)

(7)

F,-. I = R

Vi + S

_{1 (}

₈

₎

(p-1)

(p-n) (n-1)

( p . p ) ( p . l )

Les indices sous les lettres rappellent la règle de m ultiplication

des m atrices rectangulaires : dans un pro d u it de deux m atrices

rectangulaires, le nom bre de lignes de la prem ière m atrice est égal au

nom bre de colonnes de la seconde.

Faisons intervenir m aintenant la m atrice de transfert. Ce ne

pourra être qu’une m atrice de transfert arrière ou caractéristique

qui perm ettra de déterm iner les com posantes du vecteur d ’é ta t en i

connaissant celles en / — 1.

n

n

En développant.

p . l ^ R/x

l r

fF ,.n

l ' ü

F,- = U ,F m +

U^Vi.i

Vi = U 3F i.i + U^Vi.i

P

P

(9 )

(

1 0

)

(

1 1

)

** Chez certains auteurs, on trouve [^ '] = “ [ R ] F Le signe de [R j^ p r o v ie n t de certai- nés conventions sur les signes des forces et des déplacem ents, à l’une des ex trém ités du systèm e. La même difficulté se présente pour les signes de et dans la théorie des quadripoles {voir référence 6). Selon le cas, on rencontre donc des m atrices sym étriques ou antisym étriques. Dans les réseaux électriques, on rencontre le plus souvent des m atrices sym étriques. Dans un systèm e m écanique, si l’on veut conserver la sym étrie de la m atrice im pédance, il faut ad o p ter le signe pour les forces généralisées supposées appliquées à la sortie.

Le

problèm e consiste à obtenir

Ui , U-^, U^, U4 connaissant Q,

R, S.

Il suffit pour cela d ’isoler

v,- dans l’équation (8) et de le

rep o rter dans l’équation (7). Dans le cas de matrices carrées, on

m ultiplierait à gauche par R ' * . Ici R est rectangulaire.

Pour

continuer la résolution, il faut donc définir l’inverse d ’une m atrice

rectangulaire. Nous définissons l’inverse à gauche d ’une m atrice R à

p lignes et n colonnes par :

R-® = ( R ^

R)-*

R ^

(12)

{n-p)

{n-p) [p-n]

[n-p]

On vérifie que R"*^R = ( R^R)' * ( R ^ R ) = / où / est la m atrice

unité d ’ordre n. Pour que cette définition soit valable, il faut que R

soit

de rang n***. L’inverse à gauche n ’existe que si u < p . On

définirait de même l’inverse à droite par R"^, R"^ - R ^ (R R ^ ) ‘*.

Celui-ci n ’existe que si n ^ p et si le rang de R est p. Si n = p , on

retrouve R"^ - R ' ^ = R

"1

En m ultipliant à gauche les deux m em bres de l’équation (8) par

R ' ^ , il vient :

R-<^ Fi-1 =Vi + R - ^

5vm

Vi = R- ^ Fi - i - R - ^ S v i . i

(13)

En rep o rtan t dans (7),

- F i = Q R -c Fi. 1 - Q R -«

5 v,-_ 1 -P R ^ v,-. 1 = Q R ' ^ Fi. , +

+ { R ^ - Q R - ^ S ) V i . i

(14)

Les équations (

13) et (14) peuvent se com biner en une seule

équation m atricielle

n

n

H ] ^ r - Q R - ^

- R ^ + Q R - ^ S ]

[ f m ] P

. . . .

D ’où,

Ui = - Q

R- ^

U2 ^ - R ' ^ +

Q

R- ^

S

in-p) , [n-n) {n-p)

(^’P) (^ ’P)

{n-n) {n-p) (p-p)

t/3 = R- ^

D4 = - R - ^

S

(16)

(n-p)

{n-p)

{n-p)

{n-p) {p-p)

La m atrice obtenue est une m atrice à

2n lignes et 2p colonnes

(n < p ) . Elle contient moins de renseignem ents que la m atrice

im pédance. Elle correspond à un systèm e linéaire de

2n équations

indépendantes alors q u ’au départ nous avions n + p équations

linéairem ent indépendantes. Il m anque donc p — n équations pour

revenir au point de départ.

Si l’on veut la m atrice de transfert avant, on écrira de la même

façon :

P

P

n

17)

n

^

'

et, dans le cas seulem ent où

n > p ,

on trouve, à partir des sous-

m atrices Q, R et S de la m atrice im pédance, les relations

| / i = - S ( P ^ ) - ^

V2 = R - S {R' ^) - ^Q

V 2 = - { R ' ^ ) - ‘^ V ^ = - {r T ) -d q ( 1 8 )

La n o tatio n ( R ^ ) ' ^ désigne l’inverse à droite de la m atrice trans­

posée de R.

Dans le cas n > p , nous obtenons encore une m atrice large à 2p

lignes et 2n colonnes. Si nous voulions revenir à la m atrice im pé­

dance (ou adm ittance), il nous m anquerait n —p équations.

I V - APPLICATIONS

A ppliquons ce qui précède à un réseau électrique et à un systèm e

mécanique.

A)

Considérons le réseau passif suivant à

8

mailles. Les tensions

d ’entrée sont F j-.-F g . On se propose de calculer les courants de

mailles /i.- ./g d ’où l ’on pourra déduire les tensions de sortie existant

entre les points

Les valeurs des résistances sont indiquées

sur la figure

8

.

^ V w

-vw

0

T Q

O

^

1 2 . i / | I j i /

3 T

Fig.

8

— Réseau électrique.

Fig. 9 — G raphe du réseau.

Le nom bre de mailles indépendantes est

8

, ce que l’on peut véri­

fier facilem ent en cherchant le graphe du réseau (fig. 9). En effet, il

y a 7 nœ uds, 14 branches et le nom bre m de mailles indépendantes

(ou degré de liberté du systèm e) est donné par la form ule :

où b est le nom bre de branches et n celui des nœuds* ^ . Pour établir

la m atrice im pédance Z du réseau, nous utiliserons la m éthode de

Kron* * désorm ais classique.

Nous choisissons un sens positif arbitraire pour les tensions et les

courants. Z se présente sous la form e :

[Z]

_

("R 11

. . .

R 1s i

I^R g 1 • • • R g s j

Les vecteurs d ’éta t sont ici les vecteurs tension [e] et intensité [/]

et l ’on a : [e] = [Z] [/]. Rrr est la résistance totale de la maille n°

r . Rrs est la résistance com m une aux mailles r et s . Le signe de Rrs

est positif si les courants Ir et

4

traversent cette résistance com m une

dans le même sens, sinon il faut le prendre négatif, ce qui est le cas

dans cet exem ple. Dans le cas d ’élém ents passifs, la m atrice Z est

sym étrique et Rrs = R$r • S’il n ’y a rien de com m un entre les

mailles r et s, Rrs = 0 . On fait ensuite la som m e des tensions dans

chaque maille en co m p tan t les tensions positivem ent si le sens du

courant est en accord avec le sens de cette tension et négativem ent

dans le cas contraire. S’il n ’y a pas de tension dans une maille, on

m arque zéro. L’inspection de la figure

8

fournit aisém ent les

élém ents de [ Z ] .

[ Z ] = R

1 0 0 0 0 0 0 0 0 1 0 0 0 - 1 0 0 0 0 1 0 0 0 - 1 0 0 0 0 1 0 0 0 - 1 0 0 0 0 1 0 0 0 0 - 1 0 0 0

5

- 1 0 0 0 - 1 0 0 - 1

5

- 1 0 0 0 - 1 0 0 - 1

5

(19)

Le vecteur des tensions est :

Le vecteur des courants est :

e =

Vl - V2

h

V

2

- V

3

h

V3-V^

_h

V^-Vs

h

Vs- Ve

m =

h

0

_h

0

0

Pour calculer les intensités en fonction des tensions, il faut

inverser la m atrice im pédance :

m = [Z]-‘ [ e ] .

E tan t donné l’allure de la m atrice Z, la m éthode la plus simple et

la plus rapide consiste à l’inverser par le procédé de la partition* ^ .

On décom pose la m atrice [Z] d ’ordre n en 4 sous-matrices. Soit Y

son inverse (m atrice adm ittance). On peut ainsi écrire Y sous form e

partitionnée :

,4i

A

2

_P

B,

B

2

[Z] =

[Y] =

A

3

A

4

_9.

B

3

B

4

avec p + q = n. Ici p = 5, n = 3.

De l’identité Y Z = / , on tire

B

3

A

2

+ B

4

A

4

= /

d ’où

De ZY = / , on déduit

d ’où

B3A

1 +

B^A

3 — 0

B 3 = — B ^ A j A

I

=:: — B/xF

B

4

(^4

- F / I

2

) = /

A

1

B

2

+ A 2 B h = 0

A i B i A A 2 B3 — I

82 = - A Ÿ A 2 B ^ = - E B ^

B i = A Ÿ - E B 4

Le calcul de Y com porte donc

8

étapes :

Inversion de A i

Produit

E = A ' i A

2

Produit

F = A ^ A Ÿ

Produit et soustraction G —A ^ — F A

2

Inversion de G :

—G'^

Produit

B

2

= ~ B h F

Produit

B

2

= — FB^

Produit et soustraction

—A Ÿ ~ F B j

L ’inversion de la m atrice A i est im m édiate puisqu’elle est diago­

nale. On trouve F = A

2

, F = A ^ et

1

)

2

)

3)

4)

5)

6

)

7)

8

)

G =

4

-

1 0

-

1

4

- 1

G

- 1

4

Pour inverser G on peut encore appliquer la m éthode précédente

utiliser celle des cofacteurs. Le calcul n ’est pas très long et l ’on

ou

trouve

15

4

1

G-‘

= ^ 4

= (1/56)

4

16

4

1

4

15

Les phases

6

, 7 et

8

s’ex écutent alors im m édiatem ent et, finale­

m ent on trouve

h

^ 2

^3

U

1

h

56R

h

7?

7g

D ’où :

56

G

G

G

0

71

4

1 0

4

72

4

0 1

4

71

G

G

G

G

G 15

4

1

G

4

16

4

G

1

4

15

0

0

0 15

0

0

36

0

0 15

0

0

h

- V

1

- V

2

R

0

4

0

1

4 16

4

1

4 15

0

4

4 16

1

4

0

1

4

15

Vi - V

2

V

2

- V

2

v ^ - v ^

V

4

- V S

Vs - V e

G

G

G

(

2 0

)

h =

71 [ V

2

- V ^ ) + A { V ^ - V ^ ) + { V ^ - V , )

56R

etc...

Supposons m aintenant que nous considérions non seulem ent les

tensions d’entrée

mais encore les c o u ra n ts /i

/g com m e des données (ce que l’on peut réaliser physiquem ent en

insérant dans les mailles des générateurs de courants convenables) et

que nous voulions seulem ent calculer les courants /g , I

t

, Ig, réalisant

ainsi un cas semblable à celui de la figure 7. On écrira alors une

m atrice de transfert arrière analogue à (15) sous la form e :

= [T]

K l - K j 1^2 - f ^ 3 V

3

- V

4

V ^ - V s V s - 6

II

h

I

3

u

T est une m atrice rectangulaire à

6

lignes et 10 colonnes. L’appli­

cation des form ules (16) au systèm e (19) récrit sous la form e

n = 3

p = 5

- P i

Q

G

5 -

1

G G

1

G

0

G

_l

₆

G

-

1

5 -

1

G

G -

1

G G

I?

_ _ 0

_ _

_

0

_

-

1

_5

_0 0

^

_G_ -

1 0

_J

_l

_.

Kl -

V2

G

G

G

1

G

G

G G

h

=

R

V 2 - V 3

-

1

G

G G

1

G

G G

h

K3-K4

G -

1

G G

G

1

G G

_I

₃

Ka-Ks

G

G -

1

G

G

G

1

G

U

Vs - Vs

G

G

G G

G

G

G

1

h

(2 1)

O n tro u v e ici

R

-G =

R ^

,

Ui —- Q R ^

,

U

2

=

R ^

_{( Q -}

_{f ) .}

0

0

5 - 1

0

_»1

0 - 4

R

R

0

0

0

0

- 1

5 - 1

_{0 | 0}

R -

4

R

R

0

_0_

0 _

0 -

_ 1 _ _

_{_5 _0 i}

0 _ _

_0

_

_ R _

_o

l 6

0

0

0

o | 0

1

0

0

0

R

1

h

0

0 -

1

0

0

0

1

0

0

R

1

^8

0

0

0 - 1

ol 0

0

0

1

0

R

1 F i - K 2 K j - F

3

F

3

- F

4

F

4

- F s

II

h

h

U

h

(2 2)

En développant (22) on trouve a in si/g = —

y

2

- y

3

R

+ I-i

etc...

On vérifiera q u ’en rem plaçant I

2

par sa valeur trouvée par le sys­

tèm e (

2 0

), on o b tie n t bien la même valeur de

que celle que

fournit (

2 0

) ;

Si on développe le systèm e (22), on s’aperçoit que les quantités

1 ^ 1

“

1

^

2

) b's ~ 1^6)

et /s n ’interviennent pas à cause de

4

colonnes de zéros de la m atrice de transfert rectangulaire. On m et

ainsi en évidence le caractère irréversible de cette m atrice. En

p artant de trois tensions (ici nulles) et de trois intensités, on ne peut

déterm iner que trois tensions et trois intensités. En d ’autres term es,

en p artant des mailles

6

, 7 et

8

, on rebâtira les mailles 2, 3 e t 4 mais

non les mailles

1

et

2

.

B)

E x e m p l e m é c a n iq u e .

Considérons le systèm e représenté sur la figure 10. Il s’agit d ’une

barre rigide de masse m, de m om ent d ’inertie J, mise en m ouvem ent

à l’aide de systèm es élastiques am ortis schém atisés par des ressorts

de raideur k et une constante d ’am ortissem ent C. La barre est

m obile dans son plan au to u r du centre de gravité G {AG = GB = h).

A l’entrée agissent les forces F j , F

2

, F

3

, les vitesses sont y ,, v^, Vj

une force unique - F appliquée au centre de gravité et un couple de

ro ta tio n de m om ent M. La vitesse de translation est v et la vitesse

angulaire

le déplacem ent x. Le vecteur d ’éta t à l’entrée a donc

trois com posantes [p = 3) et à la sortie deux com posantes {n — 2).

La m atrice im pédance s’o b tien t à partir des équations de

Lagrange.

c

Fig. 10.

Si T est l’énergie cinétique, U l’énergie potentielle, R l’énergie de

fro ttem en t, les équations s’écrivent :

i ( | I ) + P

+ | # = Q,

d f 0(j,- o q i o q i

où qi sont les coordonnées généralisées, q,- les vitesses généralisées et

Qj les forces extérieures. Ici :

T = i m x ^ + i 7 $ ^

2

2

U —

[ X i

~

X 2 ) ^

+ ^ k

[ X 2

~

X —

+ i f e ( X 3 —X +

Ù<L)2

D ’où les équations du m ouvem ent :

— F = m x + 3 cv + 3 k x — cvi — CV

2

~ cvj — fexj — fexj ~ k x j

— M = /

+ 2h^c<F — hcv

2

+ hcv^ + 2 h } k ^ — h k x

2

+ hk x ^

F j = k (xi — x) + c (Vi — v)

F

2

— k {x

2

— X — h ^ ) + c (vj ~ v ~ h ^ )

F

3

= fe (X

3

— X + ù<ï>) + c (V

3

— V + h'F).

Si l’on veut exprim er les forces uniquem ent en fonction des

vitesses, en régime sinusoïdal, on écrit :

X q = r - ^ (l^ = - 1 ) , iCq = iCOVq

ICU

De plus, pour sim plifier l’écriture, on pose m = m ic o , / =

_ 7 i c o

c = c + -— •

ICO

Il vient alors le systèm e m atriciel :

Q

- F

m + 3c

0

- M

_ _ 0

____

2

PF(J_ +

Fx

—

—~c

0

F

2

—F

~ Pic

Fz

— F

Pic

— c

c

0 0

F

0

0

R

S

L’application des form ules (16) donne

•

“ “

— C V

— Pic

è

f i

0

l

>2

F

1^3

2

3

1 / ( 3 F 2 ) 0 0 i / ( 2 ù ^ c ^ ; R - ^ = ( R ^ R ) - ^ R ^ =

1 /(3 F )

0

- 1 /( 3 F )

l / ( 2 ù c )

- 1 / ( 3 F )

l / ( 2 / i c )

u , =

1

+ m/ { 3 c )

0

1 + m l { 3 c )

h [ J / c + 1 ) 1 + m l { 3 T )

- h { J l c + 1)

=

m/ 3

—m /3

—m /3

0

- J h

J h

t / , =

[

- i / ( 3 c ;

0

- l / ( 3 c )

- 1 / ( 3 F )

- l l { 2 h c )

\ l [ 2 h c )

\

[

1/3

0

1/3

1/3

l i [ 2h)

- l / (

2

/j)

D ’où :

- F - M l + m _ 1 + JZL

3c

3c

0

3c

0

h { i + L )

3c

- 1 2hc 1 + iîL I — m

3 ^ I

3

- ù ( l + 1 ) I 0

______ Ç-J_____

Z i

I

1

3c

I

3

1 2hc

0

3

- h j

1

3

J_

2

ù

— m 3 F i F î hJ _F3 1 3 Vl V

2

V

3

2h

Si l’on développe cette équation m atricielle, on s’aperçoit que

- F et V s’exprim ent uniquem ent en fonction de Fi + F

2

F F

3

et

de

+ i

»2

+ U

3

, — M e t

en fonction de F

2

— F

3

et V

2

■ On

ne peut pas rebâtir le systèm e à partir des données de sortie car il

m anque les grandeurs F j et Vj .

CONCLUSION

C ette étude a permis de m ettre en évidence quelques aspects

encore peu connus du calcul m atriciel. Les m odes de raisonnem ent

qui o nt été exposés s’appliquent à tous les problèm es linéaires où le

nom bre d’inconnues à calculer est inférieur au nom bre de param è­

tres figurant dans les données.

BIBLIOGRAPHIE

1 R.A. FR A ZER , W J. DUNCAN and A.R. CO LLA R — E lem entary

matrices. University Press. 1960.

2 S. RUBIN — Transactions o f the A SM E . Février 1964. 3 E. PESTEL - Int. J. Mech. Sci. 5, 1963, 419.

4 B.U.P. - n° 444, 445, 446, 1959.

5 A. ANGOT — C om plém ents de m athém atiques. E ditions de la Revue d ’Op tique.

6 M. DENIS-PAPIN et A. KAUFM ANN — Cours de calcul matriciel

appliqué. Albin Michel.

7 R. G A BILLA RD — Vibrations e t p h én o m è n es de propagation. D unod. 8 M. SOUTIF — Vibrations, propagation, d iffusion. D unod.

9 R. BOITE et J. NEIRYNCK — A nalyse des circuits linéaires. G ord o n et Beach. 1971.

10 C.K. W A N G —M atrix m eth o d s o f structural analysis. S cranton, Pa. In tern atio n al T extbook.

11 G. KRON — Tensor analysis o f netw orks. N ex-Y ork, 1939.

12 J. WHITE and S. TA UB ER — S ystem s analysis. Saunders C om pany. 1969. 13 E. DURAND — Solutions num ériques des équations algébriques. Masson

et Cie.

TRIBUNE LIBRE

LES FAUX RATTRAPAGES

ou la malignité de l’impôt

A la dem ande de no tre cam arade G ayrard, agrégé de physique, nous publions l’article suivant qui a paru égalem ent dans le Bulletin de la Société des Agrégés. Nous lui laissons l’entière responsabilité de ses affirm ations.

Chaque année, à pareille époque, on fait des bilans : bilans de Noël pour les Enfants, bilans de fin d ’année pour les Sociétés, bilans négatifs des p o rte ­ feuilles après les Fêtes, bUans du m êm e genre mais dits d’augm entation des F o n ctionnaires par le M inistre des Finances...

C’est de ce dernier bilan que je voudrais parler.

On va nous annoncer to u t d ’ab o rd que la hausse officielle du co û t de la vie au cours de 74 aura ete de 12, de 14 ou de 19 % ... on ne saurait deviner le chiffre ta n t il est ordinairem ent loin des réalités q uotidiennes (surtout p our une famille) et des sauts d ’hum eur du prix du b ee f steack. Mais peu im porte d’ailleurs tel o u tel chiffre pour m on propos, car c’est sur une procédure générale, et non poin t sur son aspect particulier 73 ou 74 que je voudrais attirer l’atten tio n .

Ainsi donc nous pouvons nous aussi, choisir un ta u x arbitraire (...) pour servir de base à n o tre d ém onstration. Prenons par exem ple 18 % “ d ’augm enta­ tion reco n n u e” au cours de l’année, et adm ettons-la, un in stan t réelle.

S upposons m aintenant, dans une a ttitu d e euphorique, que les F o n ctio n ­ naires, et n o ta m m e n t les Agrégés qui en so n t to u t de m êm e une catégorie d o n t u n Concours sérieux atteste des m érites, voient leurs ém olum ents augm entés de 20 % en valeur num érique, au cours de la même période... enfin supposons toujours, puisque j ’écris ces lignes quelques heures avant la Nuit de Noël...

Eh bien, on ne m anquerait pas de dire que nous avons non seulem ent rattra p é, mais dépassé l’augm entation du c o û t de la vie ; et de 2 % écrirait- on ; com m e si les pourcentages s’ad d itio n n aien t aussi aisém ent. Ainsi il ap p a­ ra îtra it au Public, et beaucoup d ’en tre nous s’y laisseraient prendre sur le m om ent (q u itte à déchanter ensuite) que n o tre niveau de vie se serait am élioré.