THESE de DOCTORAT de l’UNIVERSITE de POITIERS
Ecole Doctorale "Ingénierie Chimique Biologique et Géologique" Secteur de Recherche : "Terres Solides et Enveloppe Superficielle"
présentée par
Anne KACZMARYK
pour l’obtention du Grade de DOCTEUR DE L’UNIVERSITE DE POITIERS
APPROCHES MULTI-CONTINUUM DE LA DUALITE
HOMOGENEISATION - INVERSION DES PROPRIETES
HYDRODYNAMIQUES EN MILIEU POREUX FRACTURE
Directeur de Thèse : Frederick DELAY
Soutenue le 6 novembre 2008 devant la Commission d’Examen :
MM. Michel BUES Professeur, ENS Géologie, Nancy, Rapporteur
Anis YOUNES Chargé de Recherche CNRS, IMFS Strasbourg, Rapporteur Jean-François THOVERT Directeur de Recherche CNRS, ENSMA Poitiers, Examinateur Olivier BOUR Professeur, Géosciences Rennes, Examinateur
Charles DANQUIGNY Maître de Conférences, Université d’Avignon, Examinateur Alain MEUNIER Professeur, Université de Poitiers, Examinateur
SOMMAIRE
INTRODUCTION 7
CHAPITRE I : INTERPRETATION DE TESTS D’INTERFERENCE EN MILIEU
POREUX FRACTURE PAR APPROCHES DOUBLE MILIEU 11
I.1. PRINCIPE ET ÉQUATIONS DU MODÈLE DOUBLE MILIEU 15
I.1.1. Double milieu homogène 17
I.1.2. Double milieu fractal 18
I.2. PROCÉDURE D’INVERSION 19
I.3. PRINCIPE DU CALCUL DES SENSIBILITÉS ANALYTIQUES 22
I.3.1. Sensibilités analytiques du double milieu homogène 22
I.3.2. Sensibilités analytiques du double milieu fractal 24
I.4. MÉTHODE DE CONDITIONNEMENT DE LA MATRICE JACOBIENNE 27
I.5. MODIFICATION DU MODÈLE DOUBLE MILIEU 30
I.5.1. Principe et équations 30
I.5.2. Procédure d’inversion 33
I.6. RÉSULTATS ET INTERPRÉTATIONS 34
I.6.1. Simple milieu fractal 34
I.6.2. Double milieu homogène 36
I.6.3. Double milieu fractal 38
I.6.4. Double milieu modifié 42
I.7. DISCUSSION ET ANALYSE CRITIQUE DES MÉTHODES PROPOSÉES 46
CHAPITRE II : INVERSION D’UNE METHODE LAGRANGIENNE DANS LE DOMAINE DES TEMPS (TIME DOMAIN RANDOM WALK – TDRW) POUR LA
RÉSOLUTION DU TRANSPORT 49
II.1. FONDEMENTS THÉORIQUES DE LA MÉTHODE TDRW 51
II.1.1. Equation de Fokker Planck Kolmogorov (FPKE) 52
II.1.2. Equivalence entre ADE et FPKE 57
II.2. LA MÉTHODE TDRW 59
II.3. AJOUT DE PROCESSUS DE RÉTENTION 61
II.3.1. Diffusion matricielle 61
II.3.2. Sorption avec cinétique de premier ordre 64
II.4. PROCÉDURE D’INVERSION DE LA MÉTHODE TDRW 71
II.4.1. Sensibilités analytiques pour un problème advectif-dispersif 73 II.4.2. Sensibilités analytiques pour un problème advectif-dispersif + diffusion matricielle 73 II.4.3. Sensibilités analytiques pour un problème advectif-dispersif + cinétique de sorption 74
II.5. RÉSULTATS ET INTERPRÉTATIONS 76
CHAPITRE III : ETUDE PROSPECTIVE DE L’UTILISATION DES EQUATIONS DE LANGEVIN POUR L’HOMOGENEISATION DU TRANSPORT EN MILIEU
FRACTURÉ 79
III.1. ECRITURE ET RÉSOLUTION DES ÉQUATIONS DE LANGEVIN 82
III.1.1. Résolution du système complet 84
III.1.2. Résolution du système simplifié 85
III.1.3. Comparaison des équations simplifiées et complètes 86
III.2. CALCUL DE LA DISPERSION LIÉE AUX DIFFÉRENTS TERMES DES ÉQUATIONS DE LANGEVIN 89
III.2.1. Dispersion pour un champ de forces homogène 89
III.2.2. Dispersion engendrée par un champ de forces hétérogène et corrélé 91
III.3. CONCLUSION ET PERSPECTIVES 96
CONCLUSION GENERALE 99
ANNEXES 101
REFERENCES BIBLIOGRAPHIQUES 139
PUBLICATIONS :
ADVANCES IN WATER RESOURCES : Inversion of interference hydraulic pumping tests in both homogeneous and fractal dual media. F. Delay, A. Kaczmaryk, P. Ackerer, 2007.
JOURNAL OF HYDROLOGY : Interference pumping tests in a fractured limestone (Poitiers-France) : Inversion of data by means of dual-medium approaches. A. Kaczmaryk, F. Delay, 2007. JOURNAL OF HYDRAULIC RESEARCH Special issue IAHR-GW 2006 : Interpretation of interference pumping tests in a fractured limestone (Poitiers-France) using fractal and dual-media approaches : Homogenization scale of hydraulic parameters. A. Kaczmaryk, F. Delay, 2007.
JOURNAL OF HYDROLOGY : Improving dual-porosity-medium approaches to account for karstic flow in a fractured limestone : Application to the automatic inversion of hydraulic interference tests (Hydrogeological Experimental Site, HES-Poitiers-France). A. Kaczmaryk, F. Delay, 2007.
ADVANCES IN WATER RESOURCES : Inversion of a Lagrangian time domain random walk (TDRW) approach to one-dimensional transport by derivation of the analytical sensitivities to parameters. F. Delay, A. Kaczmaryk, P. Ackerer, 2008.
LISTE DES FIGURES
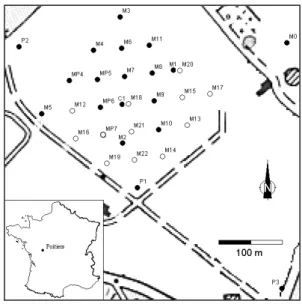
Figure 1 : Localisation des forages du Site Expérimental Hydrogéologique. En noir : puits testés
en 2004, en blanc : puits testés en 2005. 11
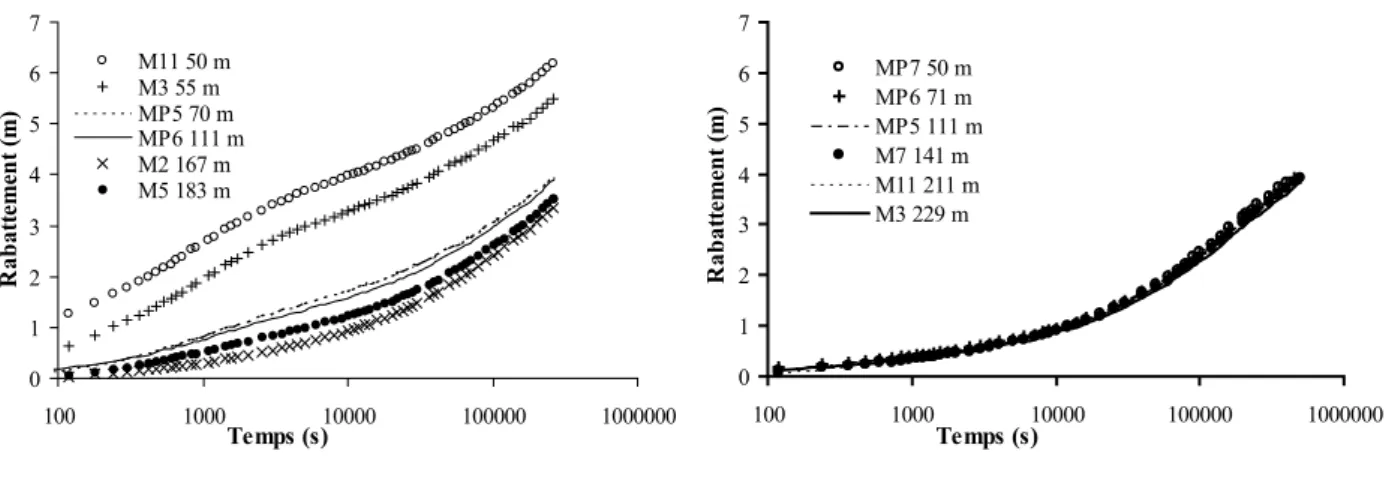
Figure 2 : Exemples de courbes de rabattement obtenues lors des tests de 2004 (à gauche,
pompage en M6) et de 2005 (à droite, pompage en M16). 12
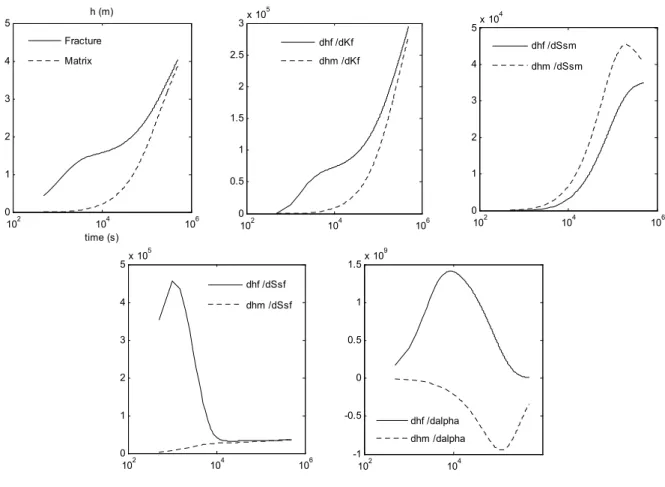
Figure 3 : Exemples de courbes de rabattement et de l’évolution des sensibilités du double milieu homogène aux paramètres en fonction du temps à 100 m du puits pompé. 23 Figure 4 : Exemples de courbes de rabattement et de l’évolution des sensibilités du double milieu
fractal aux paramètres en fonction du temps à 100 m du puits pompé. 24
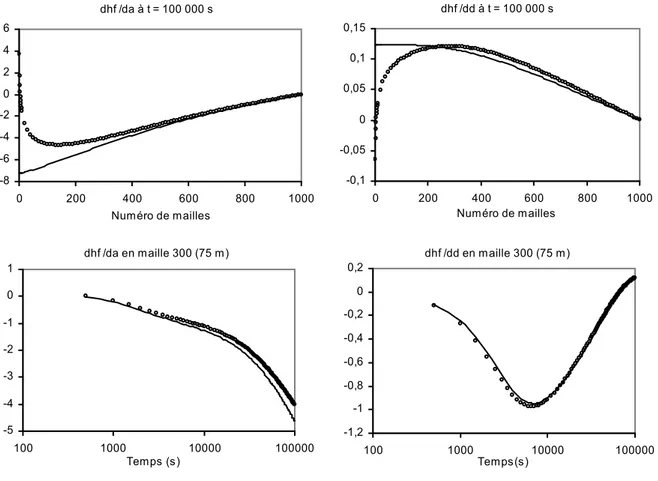
Figure 5 : Comparaison entre sensibilités exactes (traits pleins) et approchées (cercles) aux exposants de puissance du double milieu fractal (a = paramètre de la conductivité hydraulique et d = paramètre du coefficient d’échange). En haut : sensibilités pour un temps donné en fonction de la distance au puits pompé ; en bas : sensibilités à une distance donnée
en fonction du temps. 27
Figure 6 : Evolution de la conductivité hydraulique et de l’emmagasinement spécifique avec la distance puits pompé - puits observé pour t = 48 heures. Données de la campagne 2004 interprétées par l’approche simple milieu fractal (échelle log pour Ss t ).f
( )
35 Figure 7 : Evolution de la conductivité hydraulique de fracture, des emmagasinements spécifiquesde fracture et de matrice et du coefficient d’échange avec la distance puits pompé – puits observé. Données de la campagne 2004 interprétées avec l’approche double milieu homogène (échelle log pour Ssm, Ssf et α). Cercles, cercles pleins, triangles et carrés correspondent aux réponses des puits observés pour les puits pompés MP4, M7, M11 et M6
respectivement. 36
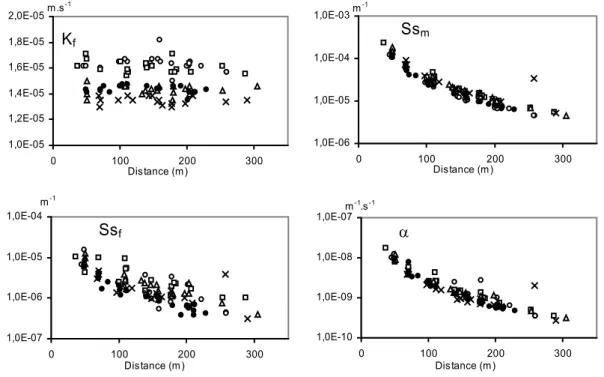
Figure 8 : Evolution de la conductivité hydraulique de fracture, des emmagasinements spécifiques de fracture et de matrice et du coefficient d’échange avec la distance puits pompé – puits observé. Données de la campagne 2005 interprétées avec l’approche double milieu homogène (échelle log pour Ssm, Ssf et α). Cercles, cercles pleins, triangles, carrés et croix correspondent aux réponses des puits observés pour les puits pompés M19, M16, M15, M22
et M20 respectivement. 37
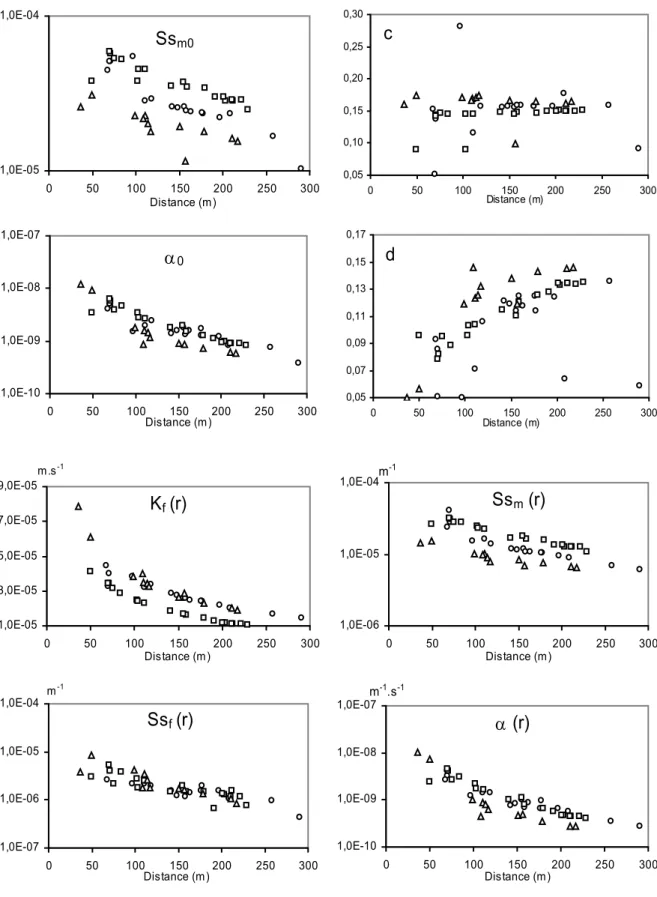
Figure 9 : Evolution de la conductivité hydraulique de fracture, des emmagasinements spécifiques de fracture et de matrice et du coefficient d’échange avec la distance puits pompé – puits observé. Données de la campagne 2005 interprétées avec l’approche double milieu fractal (échelle log pour Ssm0, Ssf0, α0, Ssm(r), Ssf(r) et α(r)). Cercles, triangles et carrés correspondent aux réponses des puits observés pour les puits pompés M20, MP7 et M16
respectivement. 40
Figure 10 : Evolution de la conductivité hydraulique de fracture, des emmagasinements spécifiques de fracture et de matrice et du coefficient d’échange avec la distance puits pompé – puits observé. Données de la campagne 2005 interprétées avec l’approche double milieu modifié homogène (échelle log pour Ssm et Ssf). Cercles et cercles pleins correspondent aux réponses des puits observés pour les puits pompés M16 et M20
Figure 11 : Evolution de la conductivité hydraulique de fracture, des emmagasinements spécifiques de fracture et de matrice et du coefficient d’échange avec la distance puits pompé – puits observé. Données de la campagne 2005 interprétées avec l’approche double milieu modifié fractal (échelle log pour α0, Ssm(r) et Ssf(r)). Cercles et cercles pleins correspondent aux réponses des puits observés pour les puits pompés M16 et M20
respectivement. 44
Figure 12 : Exemples de courbes de restitution obtenues par tests de traçage (données issues de traçages sur le SEH, résultats non publiés, Marion Chatelier, 2008). 50
Figure 13 : Représentation d’un réseau de liens avec une approche DFN. 50
Figure 14 : Exemples de courbes de restitution pour un problème advectif-dispersif + diffusion matricielle en réponse à une injection instantanée. A gauche : problème dominé par la diffusion (a = 5 x 10-3 [T-0.5] pour Pe = 5 et 500) ; à droite : mécanismes advectif-dispersif
prédominants (a = 5 x 10-5 [T-0.5] pour Pe = 5 et 500). 64
Figure 15 : Exemples de courbes de restitution en réponse à une injection instantanée pour un transport advectif-dispersif (Pe = 500) + cinétique de sorption. Trois couples de valeurs des
paramètres cinétiques sont testés. 69
Figure 16 : Courbe de restitution, concentrations cumulées et sensibilités analytiques du modèle aux paramètres u et D pour un problème advectif-dispersif (Pe = 500). 73 Figure 17 : Sensibilités analytiques du modèle aux paramètres u, D et a pour un problème
advectif-dispersif + diffusion matricielle. Le problème est dominé par le phénomène de
diffusion (Pe = 500, a = 5 x 10-3[T-0.5]). 74
Figure 18 : Sensibilités analytiques du modèle aux paramètres D, λ et μ pour un problème advectif-dispersif + cinétique de sorption avec Pe = 500 et (Daλ, Daμ) = (1, 0.5). 75 Figure 19 : Sensibilités analytiques du modèle aux paramètres D, λ et μ pour un problème
advectif-dispersif + cinétique de sorption avec Pe = 500 et (Daλ, Daμ) = (100, 50). 75 Figure 20 : Arbre binaire pour le test des capacités d’inversion du transport sur réseau de liens du
modèle TDRW. 79
Figure 21 : Courbes de restitution à la distance L (Tab. 9) pour différentes valeurs de β. A gauche : cas peu diffusif ; à droite : cas diffusif. Les pointillés et traits pleins correspondent aux résultats respectifs de la version simplifiée et complète des équations de Langevin (5000
particules déplacées). 87
Figure 22 : Evolution des vitesses moyennes en fonction du temps pour une résolution complète
des équations de Langevin et différentes valeurs de β. 88
Figure 23 : Comparaison des solutions analytiques (traits pleins) et numériques (figurés) pour le calcul de la dispersion Dx générée par les équations de Langevin avec un champ de forces
homogène et différentes valeurs de β. 90
Figure 24 : Evolution en fonction du temps de la solution analytique à la dispersion DF engendrée pour un champ de forces hétérogène corrélé. Différentes valeurs de longueur de corrélation
(∝ paramètre a) sont testées. 93
Figure 25 : Evolution en fonction du temps de la dispersion calculée par résolution numérique des équations de Langevin 1D avec un champ de forces homogène et hétérogène. 95
LISTE DES TABLEAUX
Tableau 1 : Gammes de variation de la conductivité hydraulique et de l’emmagasinement spécifique calculées pour t = 48 heures avec l’approche simple milieu fractal sur les données
de 2004. 35
Tableau 2 : Gammes de variation et moyennes de la conductivité hydraulique de fracture, des emmagasinements spécifiques de fracture et de matrice et du coefficient d’échange identifiés
par l’approche double milieu homogène sur les données de 2004. 36
Tableau 3 : Gammes de variation de la conductivité hydraulique de fracture, des emmagasinements spécifiques de fracture et de matrice et du coefficient d’échange identifiés
par l’approche double milieu homogène sur les données de 2005. 38
Tableau 4 : Gammes de variation et moyennes des paramètres de dimensionnement s0, des exposants de puissance λ et des paramètres effectifs s(r) identifiés par l’approche double
milieu fractal sur les données de 2004. 39
Tableau 5 : Gammes de variation des paramètres de dimensionnement s0, des exposants de puissance λ et des paramètres effectifs s(r) identifiés par l’approche double milieu fractal sur
les données de 2005. 41
Tableau 6 : Gammes de variation et moyennes de la conductivité hydraulique de fracture, des emmagasinements spécifiques de fracture et de matrice et du coefficient d’échange identifiés par l’approche double milieu modifié homogène sur les données de 2005. 42 Tableau 7 : Gammes de variation et moyennes des paramètres de dimensionnement s0, des
exposants de puissance λ et des paramètres effectifs s(r) identifiés par l’approche double
milieu modifié fractal sur les données de 2005. 45
Tableau 8 : Valeurs des paramètres des problèmes de référence et des paramètres identifiés
(signalés par *) pour les différents cas tests (L = 50 [L]). 76
Tableau 9 : Paramètres choisis pour les tests de validité des versions complète et simplifiée des
INTRODUCTION
L’étude d’un système passe par l’acquisition d’informations et de mesures de propriétés directes ou induites par l’objet concerné. Ces données résultent le plus souvent de tout un ensemble de phénomènes physiques inhérents aux mécanismes se développant dans le milieu mais aussi aux méthodes de mesure elles-mêmes. En général, le système reste mal investi tant à l’échelle macroscopique car les données n’échantillonnent pas la totalité du milieu, qu’à l’échelle locale ou l’échelle des hétérogénéités car les mesures sont souvent intégratrices de mécanismes sur un support mal cerné. Pour savoir quelles informations sur le fonctionnement du système on peut attendre des mesures, il est fréquent de devoir développer un modèle théorique d’interprétation. La première question à se poser est alors de savoir si l’interprétation n’est pas biaisée par le modèle défini pour une certaine physique alors que le milieu obéirait à une autre. La seconde question est de déterminer à quelle physique les mesures donnent accès et quelle panoplie de modèles sont-elles capables d’alimenter. Cela conduit finalement à : 1- des allers-retours entre physique expérimentale (ce qu’on mesure et comment) et physique théorique (comment on l’interprète) ; 2- l’utilisation de modèles d’interprétation avec toute la difficulté qu’on connaît à "essayer de mettre en boîte" les milieux naturels.
Les milieux souterrains, même dans le cas de sites expérimentaux dédiés (par exemple, le Site Expérimental Hydrogéologique SEH de l’Université de Poitiers), sont systématiquement sous échantillonnés par rapport à leur complexité. Le fait est que des mesures locales peuvent rester non pertinentes à l’échelle macroscopique malgré un échantillonnage important simplement parce que la physique change entre les échelles. Dans le cas des milieux souterrains, il est fréquent d’être astreint à un a priori sur la structure et/ou la dynamique du milieu pour pouvoir analyser les données disponibles dans leur ensemble. Très souvent, donner du sens à des données locales mais néanmoins intégratrices c’est avant tout avoir une vue simplifiée du milieu via un modèle conceptuel passant par une homogénéisation. Cette homogénéisation peut être qualifiée de "statique" si elle s’évertue à moyenner des grandeurs caractéristiques du milieu. Elle peut devenir "dynamique" si elle simplifie, voire remplace, la complexité d’une physique de processus et mécanismes locaux par une physique du "comportement moyen". In fine, on pourrait dire que construire un modèle c’est écrire par commodité le fonctionnement d’un système dont on ne connaît pas bien la physique en inventant en partie des mécanismes et processus pour mimer les données accessibles in situ. Prenons l’exemple de la modélisation de la dynamique sédimentaire. Les modèles de sédimentation utilisent souvent un régime de diffusion des particules pour représenter, à l’échelle des bassins, les observations faites sur le terrain. Or, on sait pertinemment que la physique du dépôt de sédiments est basée sur la mécanique du point, la dynamique des fluides et la chute des corps et non sur des équations de diffusion. Pour autant, les données sont correctement interprétées. Cela dit, si on est capable, via un outil d’interprétation, de donner du sens à la mesure, il ne faut pas perdre de vue que ce peut être au prix d’un modèle dont la physique est vraisemblablement fausse. Il est donc illusoire de vouloir utiliser les informations issues de l’interprétation de données dans un cadre très différent voire incompatible avec celui ayant conduit à ces informations.
Né en 2002 sur le domaine universitaire du Deffend dans le cadre du XIIième Contrat de Plan Etat-Région, le Site Expérimental Hydrogéologique (SEH) de Poitiers compte à ce jour plus d’une trentaine de forages et d’ouvrages verticaux. Les enjeux scientifiques ayant motivé sa création sont le suivi et la
modélisation du transfert et de la réactivité des eaux d’aquifères carbonatés hétérogènes, dans un souci de gestion et de protection de la ressource. Le SEH a fait l’objet de plusieurs campagnes d’expérimentations recueillant de nombreuses données géologiques, météorologiques, hydrauliques et chimiques. Parmi les tests hydrauliques menés jusqu’à présent, on retiendra deux campagnes (2003-2004 et 2005) de tests d’interférence et une série de chocs hydrauliques sur chaque puits avec parfois la mesure de charge en déporté (puits voisins). L’objectif des travaux présentés dans ce manuscrit est double. Dans un premier temps, il est question de développer des modèles d’interprétation des données de rabattement hydraulique acquises par tests d’interférence sur le site. Dans un second temps, une prospection est engagée sur la réalisation d’outils d’interprétation de données (non encore acquises sur le SEH) pour la compréhension du transport de soluté dans les réservoirs poreux fracturés. Deux étapes majeures sont indispensables dans cette confrontation modèle/données : 1- la conceptualisation et la paramétrisation du modèle pour un problème donné (écoulement ou transport de soluté) en fonction du type de données disponibles. Cette étape nécessite l’homogénéisation des propriétés macroscopiques du milieu et/ou l’intégration de mécanismes physiques réels ou fictifs pour mimer les observations ; 2- l’élaboration d’une procédure d’inversion des données (expérimentales voire synthétiques) passant notamment par la définition de la fonction objectif, le préconditionnement du problème inverse, l’écriture algorithmique et algébrique d’une procédure d’optimisation adaptée à l’outil d’interprétation.
Pourquoi avoir choisi d’entreprendre l’étude de l’écoulement et du transport de soluté dans les réservoirs poreux fracturés en appuyant la réflexion sur une approche "physique" ? C’est une question légitime quand on sait que la compréhension des systèmes souterrains est généralement vue d’abord selon une approche "naturaliste", les acteurs s’intéressant souvent aux modèles juste par le biais de leur utilisation. Même si l’objectif premier reste l’interprétation de données, il ne peut être ignoré que sans un minimum de compréhension du fonctionnement du milieu et sans un minimum de formalisme, il est possible d’inventer "tout et n’importe quoi" pour mimer des données. Utiliser intelligemment les mesures acquises et donner du sens aux paramètres d’un modèle suppose de nombreuses interrogations sur la physique et la dynamique des systèmes, ce d’autant plus qu’ils sont naturels. Les modèles ne remplaceront jamais les expérimentations in situ pour la compréhension du fonctionnement d’un milieu mais gardent néanmoins un intérêt certain s’il s’agit d’exploiter des données. Bien évidemment, on fera toujours de la physique "sale" en milieux naturels car ils sont beaucoup trop complexes pour être pleinement contraints. Cependant, il paraît plus rigoureux de s’appuyer sur des bases physiques pour modéliser un site, en extraire des paramètres et leur justification a posteriori. L’avantage indéniable de cette stratégie est de savoir ce qu’il y a derrière les interprétations. De plus, on peut espérer transposer, sinon le modèle, du moins la méthode à d’autres contextes.
Plusieurs modèles d’interprétation des mesures de rabattement hydraulique obtenues lors des deux campagnes de tests d’interférence sur le SEH ont été développés et font l’objet du premier chapitre du manuscrit. Basés sur une approche continue double milieu, ils distinguent les effets conducteurs du réseau de fractures, des propriétés capacitives de la matrice rocheuse. En termes d’interprétation, il est fait l’effort de donner du sens aux paramètres en fonction de la base physique des types d’homogénéisation utilisés et des observations faites in situ. A ce propos, les données montreront que la séparation en deux continuums imbriqués où l’écoulement est régi par des équations de diffusion et une cinétique de premier ordre peut s’avérer insuffisante pour la reproduction des effets macroscopiques visibles sur le site. Il faut alors ajouter une équation d’onde pour obtenir un calage
correct. Cet ajout et les paramètres attenants sont discutés au regard de leur sens physique (et/ou algébrique) mais aussi des données factuelles disponibles sur la géométrie des écoulements. La procédure d’inversion attachée à chaque modèle calcule analytiquement les sensibilités aux paramètres et fait appel à quelques astuces techniques pour éviter le mauvais conditionnement du problème en raison de très forts contrastes entre les valeurs de ces sensibilités. Concernant la partie transport de ce travail, il faut reconnaître que la philosophie d’approche évoquée plus haut a dû évoluer au sens où aucune donnée expérimentale n’était disponible à l’initiation de l’étude. Les chapitres II et III sont, de fait, consacrés à la proposition d’outils d’interprétation pour des données non encore acquises. Le développement de ces modèles suppose également une simplification du milieu, une homogénéisation à l’échelle macroscopique et l’inversion des paramètres. Dans le chapitre II, le milieu est simplifié en remplaçant le réseau de fractures réelles par un réseau de liens monodimensionnels [Ubertosi, 2008] et le transport advectif-dispersif est simulé par une méthode Lagrangienne dans le domaine des temps [Bodin et al., 2003a; Delay and Bodin, 2001]. Des mécanismes simples de rétention des particules sont ajoutés pour mimer les aspects ségrégatifs parfois complexes rencontrés dans les réseaux de fractures. L’outil d’interprétation ainsi établi est inversé via une méthode utilisant le calcul analytique des sensibilités aux paramètres. Cette dérivation analytique est une première pour une approche Lagrangienne et autorise un inverse précis, ce qui n’était jusqu’à présent pas possible en raison de l’aléa des calculs Lagrangiens. Ensuite, le chapitre III, propose de substituer l’équation d’advection-dispersion et le réseau de liens par des équations continues (équations de Langevin) afin de s’affranchir d’une complexité notable de paramétrisation des réseaux. En remplaçant le réseau par un champ de forces hétérogène, on simplifie la paramétrisation tout en espérant maintenir les capacités à simuler la chenalisation des écoulements fréquemment rencontrée dans les milieux fracturés. Si cette phase de prospection substituant une physique par une autre s’avérait opérationnelle, il est évident que l’inversion du transport y gagnerait beaucoup. Cela dit, les pré et le post-conditionnements sur des données restent obscurs et supposent des investigations bien au-delà du niveau de réalisation de ce travail.
Les publications rédigées et parues en cours sont insérées à la suite du manuscrit. Quatre papiers concernent le développement d’outils d’interprétation des tests d’interférence et ses applications aux données acquises sur le Site Expérimental Hydrogéologique. Un papier détaille la méthode d’inversion du transport de soluté par approche Lagrangienne dans le domaine des temps. Les travaux prospectifs sur les équations de Langevin sont pour l’instant inédits. Dans tous les cas, ce travail a souvent demandé de nombreux développements algébriques, soit novateurs, soit peu documentés dans la littérature. Lorsque cela est jugé utile pour la compréhension, ces développements sont reportés en annexe.
CHAPITRE I : INTERPRETATION DE TESTS D’INTERFERENCE EN MILIEU
POREUX FRACTURE PAR APPROCHES DOUBLE MILIEU
Section d'équation 1
Le test d’interférence est un essai standard largement utilisé en ingénierie de réservoir lors de toute étude d’un aquifère afin d’obtenir des informations sur l’hydrodynamique du système. Il consiste à pomper dans un puits et observer les réponses, sous forme de variations de charge hydraulique, sur un ou plusieurs piézomètres distants du puits pompé. Le test d’interférence renseigne alors sur la dynamique des écoulements à une échelle bien supérieure à l’environnement immédiat du forage. Problème diffusif par définition, l’écoulement radial convergent du test est intégrateur au sens où il ne permet pas d’accéder à une description complète (locale) de l’hétérogénéité du milieu. Le support spatial d’intégration est de surcroît difficile à cerner sans ambiguïté. Cependant, dans les milieux complexes, les informations recueillies en termes de rabattement au cours du temps permettent assez souvent de distinguer les effets "temps courts" (par exemple, le drainage par les fractures, la vidange de systèmes karstiques,…), des effets "temps longs" (drainage diffusif de matrice, effets de conditions aux limites,…). De principe, l’inversion d’un essai d’interférence a toujours pour objectif d’identifier les capacités conductrices du milieu (conductivité hydraulique, transmissivité) et les capacités de stockage (emmagasinement spécifique).
Nous nous intéressons aux réservoirs poreux fracturés, milieux où l’identification des paramètres hydrodynamiques est rendue complexe par la présence d’hétérogénéités spatiales à toutes échelles et génératrices de propriétés dynamiques fortement contrastées. Les données servant de base à ce travail ont été acquises par tests d’interférence sur le Site Expérimental Hydrogéologique de Poitiers (SEH). L’aquifère captif investigué, de 100 mètres d’épaisseur moyenne, est constitué de roches carbonatées fracturées et karstifiées du Jurassique moyen. La campagne de forage des puits a commencé en 2002 et s’est terminée en 2005 avec plus d’une trentaine d’ouvrages verticaux disposés selon un dispositif "five spot" (quatre tailles de mailles de 70 à 210 mètres de côté, Figure 1) permettant d’étudier les effets d’échelle. La campagne 2004 de tests d’interférence rassemble des essais hydrauliques effectués en 2003 et 2004 sur la première série de forages. Les puits forés en 2005 ont été testés lors de la campagne 2005.
Figure 1 : Localisation des forages du Site Expérimental Hydrogéologique. En noir : puits testés en 2004, en blanc : puits testés en 2005.
Deux exemples de tests issus des campagnes 2004 et 2005 sont reportés en Figure 2. Les tests d’interférence fournissent des courbes de rabattement de différentes formes [Bernard, 2005]. Certaines sont convexes et montrent une augmentation du rabattement plus importante qu’une fonction linéaire du log du temps. Elles ont été interprétées comme caractéristiques d’ouvrages fortement productifs dont la connexion avec le milieu en général et le puits pompé en particulier est importante. D’autres (non représentées ici) présentent une augmentation brutale du rabattement en fonction du temps et caractérisent des puits faiblement producteurs. Enfin, de nombreuses courbes ont "localement" une forme en baïonnette avec la présence d’une inflexion aux temps intermédiaires puis une forme convexe aux temps longs.
Figure 2 : Exemples de courbes de rabattement obtenues lors des tests de 2004 (à gauche, pompage en M6) et de 2005 (à droite, pompage en M16).
Les données recueillies par tests d’interférence au cours de la campagne 2005 montrent une réponse de l’aquifère très différente de celle observée en 2004. Toujours de forme convexe, les courbes de rabattement ne sont cependant plus différenciables en fonction de la distance entre le puits de pompage et le puits d’observation. Que l’éloignement entre le pompage et le point de mesure soit grand ou petit, les rabattements suivent la même évolution en amplitude avec des différences de temps de l’ordre de 104 secondes (ce qui est faible comparé aux temps caractéristiques de pompage de l’ordre de 5x105 s). Par comparaison avec les données de 2004, les rabattements de 2005 sont plus faibles aux distances courtes. L’aquifère réagit comme si la dépression engendrée par le pompage se propageait rapidement et identiquement dans un large rayon autour du puits pompé. Cette observation traduit un changement du comportement hydrodynamique du site. Voyons quelle peut en être l’explication physique.
Selon [Bernard, 2005], cette modification de comportement pourrait provenir de la succession de pompages d’essai en 2004 qui aurait décolmaté les chenaux d’écoulement, augmentant ainsi la connectivité des puits. Les nombreux forages effectués en 2004 auraient également participé à la réouverture d’anciens drains karstiques observés par [Audouin et al., 2008] en imagerie optique dans les ouvrages. Le marteau fond de trou activé par injection d’air sous pression est la technique utilisée pour la réalisation de la plupart des puits. Les surpressions d’air, visibles sur le site et se manifestant par de fortes oscillations de la charge hydraulique, pourraient avoir provoqué un "stress" du milieu favorisant le décolmatage progressif des chenaux. La répartition non uniforme des arrivées d’eau dans les puits ainsi que les diagraphies optiques et soniques permettent de souligner la présence d’horizons karstifiés de faible épaisseur mais largement ouverts et conducteurs. La présence de karst a également
0 1 2 3 4 5 6 7 100 1000 10000 100000 1000000 Temps (s) R ab att em en t (m ) M11 50 m M3 55 m MP5 70 m MP6 111 m M2 167 m M5 183 m 0 1 2 3 4 5 6 7 100 1000 10000 100000 1000000 Temps (s) R ab atte me n t (m) MP7 50 m MP6 71 m MP5 111 m M7 141 m M11 211 m M3 229 m
été mise en évidence par [Audouin and Bodin, 2008] grâce à l’analyse déportée de réponses à des chocs hydrauliques. Généralement, les variations de niveaux piézométriques lors d’un choc hydraulique ne sont enregistrées que dans le puits testé. Or, contrairement à ce qui était admis [Guyonnet et al., 1993], le volume d’investigation d’un choc hydraulique en termes de propagation de l’onde de choc (et non de déplacement du volume d’eau) peut être suffisamment important pour que soient observées des variations de niveaux dans d’autres puits. Sur le SEH, les réponses déportées aux chocs hydrauliques montrent que certaines connexions sont très diffusives et permettent la propagation d’onde de perturbation sur de grandes distances (100 m comme ordre de grandeur). Notons que l’évolution du comportement hydrodynamique de l’aquifère est amorcée sur les dernières données acquises en 2004, avec certains rabattements qui sont confondus en temps et en amplitude quelle que soit la distance puits pompé – puits observé.
La grande majorité des courbes de rabattement étant convexes sur des temps de pompage longs, elles sont difficilement interprétables avec la méthode classique de [Cooper Jr. and Jacob, 1946]. En effet, la non-linéarité des rabattements en fonction du log du temps rend l’essai non interprétable dans le cadre d’une hypothèse de milieu homogène à propriétés uniformes. Plus exactement, une interprétation Cooper-Jacob donnera des paramètres conducteurs et capacitifs évoluant au cours du temps de pompage. Une approximation combinant la solution analytique de Cooper-Jacob et des lois d’échelle sur les paramètres conductivité hydraulique K et porosité φ (ou emmagasinement spécifique Ss) est proposée par [Delay et al., 2004] et [Bernard et al., 2006]. Cette méthode est issue de travaux sur la théorie de la percolation et les milieux fractals [O'Shaughnessy and Procaccia, 1985; Stauffer
and Aharony, 1994]. La loi d’échelle fractale a déjà été utilisée pour des approches simple continuum
du réservoir [Acuna and Yortsos, 1995; Chang and Yortsos, 1990; Le Borgne et al., 2004] et s’écrit
( )
0s r =s r−α, s r étant le paramètre effectif pour une distance r, s
( )
0 le paramètre de dimensionnement et α l’exposant de puissance de la loi fractale en espace. Spécifiquement, pour un milieu fractal simple de dimension D dans un espace Euclidien de dimension d, l’emmagasinement étant proportionnel à la fraction volumique (cette dernière est le ratio du volume fractal sur le volume total) est par conséquent proportionnel à r rD d =rD d− . Les milieux fractals sont aussi caractérisés par une dimension dite "du
marcheur aléatoire" stipulant que les paramètres effectifs du transport sont soumis à loi d’échelle. Pour un écoulement typiquement diffusif, la diffusion hydraulique s’écrit DH=K Ss r≡ −θ, θ étant la dimension du marcheur aléatoire (ou encore l’exposant spectral). De fait, la conductivité hydraulique évolue en K r≡ D d− −θ. Le travail proposé par [Delay et al., 2004] est une approximation logarithmique
des rabattements en un point en fonction du temps comparable à la solution de Cooper-Jacob. Elle repose en partie sur la transformation des lois d’échelle spatiales en lois temporelles pour les deux paramètres K et Ss. Si la diffusion hydraulique du milieu fractal est en r−θ [L-θ], elle reste cependant de dimension [L2T-1]. L’identification de cette dimension à la loi en [L-θ] suppose une proportionnalité en régime diffusif T∝L2+θ. Il est donc aisé de transformer les lois d’échelles spatiales pour obtenir in fine : K t
( )
≡t ,−μ μ =(
d D− + θ) (
2+ θ)
; Ss t( )
≡t ,−ω ω =(
d D−) (
2+ θ .)
Dans la théorie d’un milieu fractal, la forme en "baïonnette" de certaines courbes de rabattement relatives au SEH est expliquée par le passage d’écoulements tridimensionnels à des écoulements bidimensionnels et un changement de la dimension fractale vue pendant l’essai alors que le rayon investigué augmente. Chaque courbe de la campagne 2004 a été re-interprétée avec ce modèle fractal simple continuum par [Kaczmaryk and Delay, 2007b]. Les paramètres identifiés montrent des valeurs scalaires décroissantes avec la distance puits pompé – puits observé. S’il est question de conductivité hydraulique, cette décroissance est conforme avec celle attendue d’un milieu fractal. Par contre,
l’emmagasinement décroît beaucoup plus fortement, invalidant en partie l’hypothèse que l’approche simple milieu fractal puisse représenter correctement l’aquifère au droit du site.
La question se pose alors d’identifier un concept, un type de milieu, un modèle, pertinents pour l’interprétation des données du site sans contradiction avec les hypothèses qui sous-tendent la méthode utilisée. Parallèlement, on pourra aussi s’interroger sur les capacités de ladite méthode à intégrer correctement les modifications évidentes de comportement du site entre les deux campagnes de tests. La philosophie de ce travail est basée sur l’idée du développement d’outils simples d’interprétation de tests d’interférences. Sous le terme "outils simples", on entend des outils faiblement paramétrés, qui soient inversibles et qui permettent d’obtenir les caractéristiques macroscopiques de l’écoulement (conductivité hydraulique et emmagasinement spécifique). La philosophie du développement d’un outil simple, dont l’utilisation est quasiment aussi facile qu’une solution analytique (sauf qu’elle nécessite un code de calcul), va à l’encontre d’une représentation détaillée de l’hétérogénéité. Sauf à représenter les hétérogénéités sous la forme de continuums statistiques décrits simplement (par exemple, la covariance spatiale de la grandeur d’intérêt), la piste la plus simple reste le milieu homogène, éventuellement décliné sous diverses formes : fractal, double continuum,…
Les hétérogénéités macroscopiques de l’aquifère étant essentiellement le fait d’un réseau de fractures et de conduits karstiques envahissant une matrice calcaire poreuse, la première idée traversant l’esprit est une représentation double milieu du réservoir. Proposé pour la première fois par [Barenblatt et al., 1960] et largement utilisé depuis en ingénierie pétrolière [Auriault and Boutin, 1992; Landereau, 2000; Landereau et al., 2001; Quintard and Whitaker, 1996; Warren and Root, 1963], le modèle double milieu décrit l’aquifère poreux fracturé comme l’assemblage de deux continuums interactifs et imbriqués : 1- la matrice aux propriétés capacitives importantes ; 2- le milieu fractures fortement conducteur. Les transferts de fluide entre ces deux milieux aux propriétés contrastées sont gérés par un terme d’échange dont la forme et la paramétrisation revêtent une importance particulière. Les modèles de [Barenblatt et al., 1960] et de [Warren and Root, 1963] sont qualifiés de modèles à écoulement pseudo-permanent (ou stationnaires) car ils supposent un échange entre matrice et fractures qui ne dépend du temps que par le biais de pressions (ou de charges hydrauliques) moyennes dans la matrice et les fractures. Cette hypothèse est une approximation simplifiant la résolution mathématique mais ne correspondant pas pour autant à la réalité physique de l’écoulement. Des modèles à écoulement transitoire ont été proposés [Barker, 1988; Boulton and Streltsova, 1977; Kazemi et al., 1976] et regroupent toutes les approches basées sur une forme non stationnaire des échanges matrice -fractures. Cette forme correspond mieux à la réalité car l’échange devient un phénomène diffusif d’intensité variable au cours du temps (et non plus uniquement variable par le biais des pressions dans chaque milieu). Comme ce terme diffusif complique la mise en équation, on simplifie généralement son expression par la mise en place d’un "effet mémoire" pour l’échange entre la matrice et les fractures. Il s’agit d’une technique assez classique en physique. Si on relie phénoménologiquement un signal S t à une entrée
( )
E t via une relation "stationnaire"( )
S t( )
=E t( ) ( )
α t , une approche non stationnaire remplace la relation précédente par un produit de convolution S t( )
=∫
E( ) (
τ α − τ τt)
d . Pour un processus sans mémoire(
α =δ(t) (t))
, on retrouve la relation phénoménologique initiale. On peut également trouver d’autres formes du genre : S t( )
E( ) ( )
t dt ∂ τ
= α − τ τ
∂
∫
. C’est cette dernière quiest assez souvent citée pour le caractère non stationnaire des échanges matrice – fractures des modèles double continuum. Dans une optique de paramétrisation simple, ce travail a fait le choix d’une
approche stationnaire pour le terme d’échange. L’hétérogénéité du réservoir poreux fracturé est alors portée par un milieu matriciel à fort emmagasinement et à conductivité hydraulique négligeable échangeant sous l’effet de la différence de pression avec un milieu fractures à forte conductivité et à faible emmagasinement. Ce modèle purement diffusif + cinétique du premier ordre (pour l’échange) sera l’outil d’interprétation des données acquises en 2004 par tests d’interférence. Cette approche double milieu devra ensuite être modifiée pour tenir compte des observations faites sur les données de 2005, à savoir l’identité des rabattements quelle que soit la distance à laquelle ils ont été mesurés. On verra que l’idée de propager très rapidement et uniformément la déplétion engendrée par le puits pompé peut se ramener à l’ajout d’une partie hyperbolique dans les équations du double milieu. Afin de concevoir un outil d’interprétation des tests d’interférence qui soit simple et sur lequel on puisse greffer une procédure d’inversion identifiant automatiquement les paramètres hydrodynamiques, chaque modèle double milieu est construit selon un schéma d’écoulement radial convergent à symétrie cylindrique. Les modèles sont développés suivant deux approches : une approche avec des paramètres uniformes sur tout le domaine, et une approche fractale reprenant ainsi l’idée que les réseaux de fractures puissent obéir à une géométrie dont la dimension est inférieure à celle de l’espace Euclidien qui les contient. L’inversion des données est effectuée selon une méthode classique de minimisation des moindres carrés et on s’attachera à calculer les sensibilités analytiques du modèle aux différents paramètres, technique donnant rigueur et précision à la procédure de recherche des paramètres optimaux. Chaque courbe de rabattement correspondant à un couple puits pompé - puits observé est inversée individuellement. On obtient donc pour chaque couple un jeu de paramètres hydrodynamiques. L’étalement statistique des valeurs trouvées pour l’ensemble des couples de puits testés permet de statuer sur le caractère adapté ou non du modèle à représenter le milieu au droit du site. Par exemple, si le modèle fait l’hypothèse de paramètres uniformes et que les paramètres ajustés par inversion varient beaucoup en fonction de l’interdistance entre les puits ou de leur position relative dans l’espace, il est peu vraisemblable que l’hypothèse d’uniformité soit un bon modèle de représentation.
I.1. Principe et équations du modèle double milieu
En conditions de validité de la loi de Darcy, les équations décrivant l’écoulement dans un double milieu se notent généralement sous la forme :
(
)
(
)
f f f f m / f f m m m m m / f m h Ss . K . h q q t h Ss . K . h q q t ∂ = ∇ ∇ + + ∂ ∂ = ∇ ∇ − + ∂ (I.1)Les indices f et m font référence au continuum fracture et au continuum matrice. h [L] est la variable d’état et correspond à la charge hydraulique, Ss [L-1] est l’emmagasinement spécifique et K [LT-1] la conductivité hydraulique. Le terme d’échange entre la matrice et les fractures se note qm / f [T-1]. Le terme puits – source q [T-1] est défini positif pour des flux entrant dans le milieu considéré (f ou m) et négatif pour des flux sortant.
Avec à l’esprit le développement d’un modèle conceptuel simple homogénéisant les aquifères poreux fracturés tels que celui du Site Expérimental Hydrogéologique, l’outil d’interprétation d’essais
d’interférence est construit sur la base d’un écoulement 2D (homogénéisé sur la verticale) radial convergent. La symétrie cylindrique du problème est conservée sur l’ensemble du domaine autour du puits sans anisotropie (horizontale ou verticale), ni stratification horizontale. L’écoulement dans la matrice rocheuse est supposé négligeable, éliminant de fait le terme faisant intervenir la conductivité hydraulique de la matrice. Le terme "puits-source" de l’équation de matrice en (I.1) est également éliminé car on suppose que les puits de pompage drainent localement le système par le biais des fractures interceptées. Le terme "puits-source" des fractures est alors noté q 0, t (puits pompé enp
( )
r 0= ). L’échange de flux entre la matrice capacitive et les fractures conductrices est développé selon une formulation stationnaire et dépend d’un coefficient d’échange α [L-1T-1] et de la différence de pression (ou de charge hydraulique) entre les deux milieux. Au vu des hypothèses énoncées, les équations (I.1) deviennent :( )
( )
( )
( )
( )
(
( )
( )
)
( )
( )
( )
( ) ( )
(
( )
)
f f 1 f f m f p m 1 m f m h r, t 1 h r, t Ss r r K r r h r, t h r, t q 0, t T t r r r h r, t Ss r r h r, t h r, t T t − − ∂ = ∂ ⎛ ∂ ⎞+ α − + ⎡ ⎤ ⎜ ⎟ ⎣ ⎦ ∂ ∂ ⎝ ∂ ⎠ ∂ ⎡ ⎤ = α − ⎣ ⎦ ∂ (I.2)avec r et t utilisés comme références spatiales ( r 0= au puits pompé) et temporelles (t = 0 au démarrage de l’essai). La discrétisation de ces équations et les conditions limites sont détaillées en annexe A (équations (A.1) à (A.4)). On obtient un schéma volumes finis du type :
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
i i i i 1 2 i 1 i i 1 2 i i 1 i i i i i i i n 1 n f f 2 n 1 n 1 n 1 n 1 f f f f f f f p 1,i 2 n 1 n 1 i m f n 1 n m m 2 2 n 1 n 1 m i f m h h i 1 2 Ss r i K h h i 1 K h h t Q i 1 2 r h h 2 e h h i 1 2 Ss r i 1 2 r h h t + + − − + + + + + + + + + + − − Δ = − − − − Δ δ + − α Δ − + π − − Δ = − α Δ − Δ (I.3)avec i la référence au numéro de la maille de taille rΔ (i croissant en s’éloignant du puits pompé), n la référence au temps découpé à pas régulier tΔ . On retiendra ici les quelques éléments suivants et déterminants pour une bonne simulation (directe) de l’écoulement radial convergent. Qp [L3T-1] est le débit pompé dans le puits localisé dans la maille 1 (la fonction Kronecker δ vaut 1 en i = 1 et 01,i ailleurs).
i i f m i
Ss ,Ss ,α sont des valeurs moyennes sur la maille i. Les paramètres capacitifs Ssf et Ssm étant des fonctions linéaires de la porosité du milieu, ils peuvent être considérés comme des propriétés additives. La signification physique du coefficient d’échange α est discutée plus loin. Cependant, puisqu’il régule les flux d’eau entre la matrice (Ssm) et la fracture (Ssf), il peut également être vu comme une propriété additive. Ce sens physique est conforté par la forme des sensibilités du modèle double continuum au coefficient d’échange (voir partie I.3.1.) mais également par le fait, qu’en milieu fractal, l’exposant de puissance de la loi d’échelle du paramètre soit sensiblement le même que ceux des emmagasinements (voir partie I.1.2.). La valeur moyenne de ces trois paramètres sur une maille i est alors simplement calculée par une moyenne arithmétique (annexe A). Les conductivités intermailles
i 1 2 f
K ± sont également des valeurs moyennes. Il est démontré en annexe A (équations (A.5) à (A.12)) qu’en dépit d’un écoulement radial convergent ces conductivités intermailles se ramènent classiquement à une moyenne harmonique.
Ainsi construit, l’outil numérique permet de simuler l’écoulement dans un milieu dont on comprend que l’hétérogénéité est réduite "au mieux" à des valeurs constantes par mailles concentriques autour du puits pompé. Rappelons pour mémoire que dans un souci de simplification et de paramétrisation minimaliste, on "dégrade" l’outil numérique à un double milieu homogène (HDM – Homogeneous Dual Medium) et à un modèle double milieu fractal (FDM – Fractal Dual Medium).
I.1.1. Double milieu homogène
Le milieu homogène uniforme est la paramétrisation la plus simple que l’on puisse envisager pour les équations (I.3) alors contraintes par quatre paramètres constants : Kf, Ssf, Ssm, et α. Le système discrétisé est simplifié (annexe A) :
(
)
(
)
(
)
[ ]
(
)
(
)
(
)
(
)
(
)
(
)
(
)
i i 1 i 1 i i i i i 2 f 2 n 1 n 1 n 1 f f f f f f p 1,i 2 f n 2 n 1 f m 2 m 2 n 1 2 m n 2 n 1 m m f Ss i 1 2 r 2i 1 K i 1 2 r h i K h i 1 K h t Q Ss i 1 2 r h i 1 2 r h t 2 e Ss Ss i 1 2 r i 1 2 r h i 1 2 r h i 1 2 r h t t + − + + + + + + ⎡ − Δ + − + − Δ α⎤ − − ⎡ − ⎤ ⎣ ⎦ ⎢ Δ ⎥ ⎣ ⎦ δ ⎡ ⎤ ⎡ ⎤ =⎢ − Δ ⎥ +⎣ − Δ α⎦ + Δ π ⎣ ⎦ ⎡ − Δ + − Δ α⎤ =⎡ − Δ ⎤ ⎡+ − Δ α⎤ ⎢ Δ ⎥ ⎢ Δ ⎥ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ (I.4)Ce système peut s’écrire sous la forme matricielle suivante :
n 1 n n 1 f f f f m n 1 n n 1 m m m m f + + + + ⋅ = ⋅ + ⋅ + ⋅ = ⋅ + ⋅ A h D h C h B A h D h C h (I.5)
Af est une matrice tri-diagonale tandis que Am, Df, Dm et C sont des matrices diagonales. B est le vecteur correspondant aux conditions aux limites. En r = 0, on écrit une condition de symétrie permettant de respecter le caractère radial convergent du problème et le débit pompé par le puits s’ajoute à la maille #1. Supposant que le milieu est infini, il est décrit par un nombre de mailles Nm (Nm suffisamment grand pour ne pas influencer les distances intéressées par le calcul) et la maille Nm se voit imposer une charge hydraulique constante H0.
Les deux équations (I.5) sont couplées par la présence de hm dans l’équation de hf (et inversement). Une méthode de résolution consiste à itérer jusqu’à convergence de la solution. Une autre méthode plus élégante (quand elle n’engendre pas de systèmes linéaires mal conditionnés) substitue la charge dans la matrice de la première équation par son expression obtenue par la seconde.
n 1 1 n 1 n 1 m m m m m f 1 n 1 n 1 n f m f f f m m m + − − + − + − ⎡ ⎤ ⎡ ⎤ =⎣ ⋅ ⎦⋅ +⎣ ⋅ ⎦⋅ ⎡ − ⋅ ⋅ ⎤⋅ = ⋅ +⎡ ⋅ ⋅ ⎤⋅ + ⎣ ⎦ ⎣ ⎦ h A D h A C h A C A C h D h C A D h B (I.6)
On obtient alors une équation où le vecteur inconnu n 1 m+
h est éliminé. La matrice 1
f m−
⎡ − ⋅ ⋅ ⎤
⎣A C A C⎦ est tri-diagonale et l’équation peut être résolue directement en utilisant l’algorithme de Thomas (détaillé
en annexe B). La résolution de n 1 1 n 1 n 1
m+ =⎣⎡ −m ⋅ m⎦⎤⋅ m+⎣⎡ m− ⋅ ⎤⎦⋅ f+
h A D h A C h est alors immédiate car n 1
f+ h est connu. Cette méthode est simple et rapide en temps de calcul. L’algorithme de Thomas transformant le
système tri-diagonal initial en système triangulaire, limite les éventuelles singularités numériques dues à de forts contrastes des grandeurs scalaires dans la matrice initiale (contrastes liés ici pour l’essentiel à des différences entre la valeur du coefficient d’échange et les termes d’emmagasinement de matrice et de fractures.
I.1.2. Double milieu fractal
Le double milieu fractal intègre une hétérogénéité spatiale décrite par des lois d’échelle. Ce type de loi a déjà été utilisé par [Bernard et al., 2006] pour un modèle simple milieu. Les quatre paramètres hydrodynamiques des équations (I.2) suivent une loi de puissance en espace de type s r
( )
=s r0 −λ. s0 est le facteur de dimensionnement, λ l’exposant de puissance. L’approche FDM est alors conditionnée par huit paramètres :( )
a( )
b( )
c( )
df f 0 f f 0 m m0 0
K r =K r ; Ss r− =Ss r ; Ss− r =Ss r ;− α r = α r− (I.7)
Voyons tout d’abord quelles sont les valeurs potentielles des exposants de puissance. Si ces exposants sont laissés à la dérive (non contraints dans l’inversion), ils engendreront probablement une grande variabilité des paramètres effectifs s r . De fait, l’inversion risque de diverger et de surcroît, chercher
( )
des paramètres dont le sens physique est discutable. Dans un milieu fractal, la porosité φ [-] évolue selon une loi d’échelle de la forme : φ ∝rD d− avec d la dimension Euclidienne (ici d = 2) et D ladimension fractale. Pour des objets fractals synthétiques ou naturels, des valeurs de D variant entre 1.5 et 1.95 sont proposées dans la littérature [Bonnet et al., 2001; Stauffer and Aharony, 1994]. L’emmagasinement spécifique peut s’exprimer en première approximation sous la forme Ss∝ φ ρc g avec c [M-1LT2] la compressibilité du milieu, ρ [ML-3] la masse volumique du fluide contenu dans le milieu et g [LT-2] l’accélération gravitationnelle. De ces relations, on peut déduire que les exposants b et c pour Ss r et f
( )
Ssm( )
r vont varier dans la gamme [0.05 - 0.5]. La signification physique du coefficient d’échange est celle d’un coefficient de diffusion intégrant une conductivité hydraulique moyenne sur une surface d’échange entre matrice et fractures. Les flux d’eau entre les deux continuum s’expriment par prise de moyenne volumique sur V [L3] : 1V− K h d
Γ ∇ Γ
∫
, avec Γ [L2] la surface d’échange entre matrice et fractures, K h∇ les flux [LT-1] traversant cette surface. En supposant l’homogénéité du milieu et en utilisant un schéma en différences finies, cette expression peut se simplifier en K(
ΓΔh)
(
V LΔ . La comparaison par identification à la forme du terme d’échange en)
(I.2) donne à ce dernier l’expression: KΓ(
V LΔ . V et L)
Δ sont indépendants de la nature fractale du milieu et les paramètres K et Γ obéissent aux lois d’échelle : K r≡ D d− −θ;Γ ≡rD 1− . Le coefficient αsuit alors une loi en α ≡r2D d 1− − −θ. θ variant entre 0.3 et 0.8 en milieu fractal bi-dimensionnel,
l’exposant d de la loi d’échelle pour α varie entre [0-0.8]. Le coefficient d’échange a un rôle "tampon" entre le fluide contenu dans la matrice dépendant de Ssm
( )
r et le fluide de la fracture conditionné par Ss r . En fait, ce coefficient régule les échanges d’eau entre les deux milieux. Onf( )
peut donc supposer qu’il suit une loi d’échelle similaire à celle des emmagasinements spécifiques des deux continuums. L’exposant d devrait donc également varier sur [0.05 - 0.5]. Il reste à borner les valeurs de a pour la conductivité hydraulique de fracture. Dans un milieu fractal, la diffusion hydraulique évolue selon DH∝r−θ [Stauffer and Aharony, 1994]. Connaissant la relationH f
D =K Ss et D d
f
Dans le système d’équations discrétisées en (I.3), la conductivité hydraulique intermaille doit être remplacée par sa moyenne harmonique tandis que les paramètres capacitifs et d’échange sont évalués par leur moyenne arithmétique. Le développement de ces moyennes en contexte fractal est détaillé en annexe A (équations (A.14) à (A.19)). Si on se trouve assez loin du puits pompé (voir annexe A, r grand, indice de maille i élevé) ces moyennes, harmoniques ou arithmétiques, tendent vers les valeurs locales du paramètre. Ainsi, pour la moyenne harmonique de la conductivité hydraulique à l’interface entre la maille i et la maille i+1, on obtient :
a fi 1/ 2 f0
H
K K (i r)−
+ ≈ Δ (I.8)
Pour la moyenne arithmétique des paramètres s = Ssf, Ssm et α sur la maille i, on aura :
(
)
i A 0
s ≈s (i 1/ 2) r− Δ −λ (I.9)
Finalement, les équations discrètes du double milieu fractal s’écrivent :
(
)
f 0 1 b 2 b 1 a 1 a a 1 d 2 d n 1 1 a a n 1 f0 0 fi f0 fi 1 f 0 p 1,i 1 a a n 1 1 b 2 b n 1 d 2 d n 1 f0 fi 1 fi 0 mi Ss (i 1/ 2) r i (i 1) r K (i 1/ 2) r h i r K h t Ss Q (i 1) r K h (i 1/ 2) r h (i 1/ 2) r h t 2 e (i − − − − − − − + − − + + − − + − − − − + − ⎡ ⎤ ⎡ ⎤ − Δ + + − Δ + − Δ α − Δ ⎢ ⎥ ⎣ ⎦ Δ ⎢ ⎥ ⎣ ⎦ ⎡ ⎤ δ ⎡ ⎤ ⎡ ⎤ −⎣ − Δ ⎦ =⎢ − Δ ⎥ +⎣ − Δ α ⎦ + Δ π ⎢ ⎥ ⎣ ⎦ m0 m0 1 c 2 c 1 d 2 d n 1 1 c 2 c n 0 mi mi 1 d 2 d n 1 0 f i Ss Ss 1/ 2) r (i 1/ 2) r h (i 1/ 2) r h t t + (i 1/ 2) r h − − − − + − − − − + ⎡ ⎤ ⎡ ⎤ − Δ + − Δ α = − Δ ⎢ ⎥ ⎢ ⎥ Δ Δ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ ⎡ − Δ α ⎤ ⎣ ⎦ (I.10)Sous forme matricielle, le système linéaire obtenu est comparable à celui du HDM en (I.6) avec matrices et vecteurs
(
A A C D D Bf, m, , f, m,)
modifiés pour intégrer l’hétérogénéité fractale du milieu. La résolution numérique est similaire à celle décrite pour l’approche HDM.I.2. Procédure d’inversion
Le problème inverse a pour but d’optimiser un jeu de paramètres s qui, via le modèle, reproduise le plus fidèlement possible le comportement observé. Mathématiquement cela se traduit par la minimisation d’une fonction objectif intégrant la différence entre la variable d’état simulée et la variable d’état observée. En fonction du type de problème résolu, plusieurs formes de fonction objectif sont envisageables. La bonne définition de la fonction objectif est un des éléments clés du problème inverse car ladite fonction doit être adaptée aux données que l’on souhaite mimer avec le modèle. En l’occurrence la minimisation est modulable en pondérant certaines valeurs d’erreurs entre variable simulée et variable observée par rapport à d’autres. Dans le cas d’un double milieu, les développements de formes algébriques et les calculs de valeurs (voir partie I.3.) des sensibilités du modèle aux paramètres montrent que tous les temps comptent, ne justifiant pas l’utilisation de pondérateurs. On peut également contraindre l’optimiseur par l’ajout de contraintes sur les valeurs des
paramètres (par exemple autoriser l’exposant a de la loi fractale de la conductivité hydraulique à varier sur [0.4 - 1.3]). L’essentiel des puits observés et qui présentent des rabattements interprétables sont connectés au continuum fractures. Par équilibre local des charges hydrauliques au puits sur toute la colonne d’eau, on peut raisonnablement penser que les mesures des tests d’interférence intéressent une charge correspondant localement à celle du milieu fractures (mais aussi du milieu matrice en supposant l’équilibre hydrostatique au puits observé). La variable d’état est donc la charge hydraulique dans le milieu fracturé. La fonction objectif est de type moindres carrés entre charges calculées C
f h et charges observées O f h et s’écrit:
( )
(
fi( )
i)
( ) ( )
n 2 C O T f i 1 1 1 F s h h . 2 = 2 =∑
s − = ξ s ξ s (I.11)s est le vecteur des paramètres à identifier (de taille p = nombre de paramètres). Le vecteur erreur ξ
est noté
( )
{
(
( )
)
}
i i C O i hf h , i 1 nf = ξ = − = s sξ , n étant le nombre de points de calage choisis entre
courbes de rabattement simulées et observées. Dans le cas présent, puisqu’une seule courbe de rabattement est ajustée, la notion de point de mesure fait référence à des temps sur la courbe d’évolution du rabattement local observé. L’inversion fournit un jeu de paramètres par couple puits pompé – puits observé et on regarde ensuite si le comportement de l’ensemble des paramètres sur Nc couples est compatible avec l’hypothèse attenante au milieu testé : uniforme, ou évoluant avec la distance r selon une loi s r
( )
≡r−λ.Le vecteur s contenant peu de paramètres (4 pour le modèle homogène et 8 pour le fractal), l’inversion s’appuie sur une méthode d’optimisation itérative de Gauss-Newton, réputée efficace tant que le problème comporte moins d’une vingtaine de paramètres [Carrera and Neuman, 1986]. A l’instar de nombreuses méthodes d’optimisation non linéaire, la méthode de Gauss-Newton est basée sur le calcul de la direction de descente d des paramètres entre deux itérations de convergence (k et k+1) jusqu’à ce que la fonction objectif atteigne un minimum local. Une approximation au second ordre de la fonction objectif à l’itéré k+1 est obtenue par développement de Taylor :
( ) ( )
k 1 k kT( )
k 1 kT 2( )
k k F F . F . F . 2 + = + ∇ + ∇ s s d s d s d (I.12)( )
k F∇ s est le gradient de la fonction objectif (vecteur de taille p) :
( )
k{
}
jF F s , j 1...p
∇ s = ∂ ∂ = ,
( )
2F k
∇ s est la matrice Hessienne (de dimension pxp) : ∇2F
( ) {
sk = ∂2F s s ,i, j 1...p∂ ∂i i =}
. La dérivéede F
( )
sk 1+ par rapport à sk 1+ ou, ce qui est équivalent, à dk =sk 1+ −s s’écrit :k( )
k 1( )
k 2( )
k kF + F F .
∇ s = ∇ s + ∇ s d (I.13)
Lorsqu’on atteint l’optimum ∇F
( )
sk 1+ =0. Par conséquent, la direction de descente entre les itérationsk et k+1 a pour expression :
( )
(
)
-1( )
k = k 1+ − k = − ∇2F k . F∇ k
Cette forme est connue sous le nom de méthode de Newton. La méthode dérivée dite de Gauss-Newton repose sur le calcul exact du gradient et sur l’approximation du Hessien. On peut montrer par quelques manipulations algébriques que le gradient s’exprime en fonction de la matrice Jacobienne des erreurs et du vecteur erreur : k
k T k F ξ . ∇ = J ξ . La Jacobienne s’écrit : k
{
}
k i s ,i 1...n, j 1...pj ξ = ∂ξ ∂ = = J etstocke les sensibilités du modèle aux paramètres :
i C i sj hf sj ∂ξ ∂ = ∂ ∂ . Le Hessien se note :
(
)
k k k 2 kF T. T . k ξ ξ ξ∇ =J J + ∂J ∂s ξ . En supposant ξ petit près de l’optimum, l’expression du Hessien estk
simplifiée : k k
2 kF T. ξ ξ
∇ ≈ J J . L’identification de la direction de descente par la méthode de Gauss-Newton s’écrit alors :
(
k k) (
k)
-1 k T. . T. k ξ ξ ξ = − d J J J ξ (I.15)La difficulté de cette approche réside dans le calcul de la matrice Jacobienne et certains défauts de convergence du problème (I.15) peuvent être liés à la mauvaise approximation du Hessien. Il existe une méthode d’inversion, a priori plus accessible, basée sur une approximation linéaire au premier ordre de la fonction objectif : F
(
sk+ λdk) ( )
F sk + λ∇F( )
sk T⋅d . Supposons k λ > , pour que F0diminue en
(
sk + λd , il faut choisir k)
λ∇F( )
sk T⋅d grand en valeur absolue et de signe négatif. Laksolution pour obtenir la diminution la plus forte de F
(
sk+ λd est de prendre k)
dk = −∇F( )
s . Cettekméthode dite "Steepest-Descent" calcule la direction de descente directement à partir du gradient. Intéressante sur les premières itérations de convergence, le plus souvent cette approche n’est pas assez précise lorsque la solution s’approche de l’optimum. Afin d’accélérer l’identification des paramètres, on peut coupler les deux méthodes (algorithme de Levenberg-Marquardt) et passer de la méthode Steepest-Descent aux premières itérations de convergence à la méthode de Gauss-Newton quand la fonction objectif se rapproche du minimum. Cet algorithme s’écrit :
(
)
(
k k)
kk T. . k T. k
ξ ξ ξ
η +I J J d = −J ξ (I.16)
Dans cette équation, I est la matrice identité et η un scalaire qui pondère le passage d’une méthode à l’autre. Si la norme de η I est largement supérieure à celle de k
k k T. ξ ξ
J J , l’algorithme tend vers une
forme Steepest-Descent alors que si η est nul, il est de type Gauss-Newton.
L’équation (I.16) met en exergue le rôle fondamental, dans la recherche d’une solution inverse, de la matrice Jacobienne dont on rappellera qu’elle porte les sensibilités du modèle aux paramètres :
{
}
k k i s ,i 1...n, j 1...pj ξ = ∂ξ ∂ = = J , i C i sj hf sj∂ξ ∂ = ∂ ∂ . La convergence du problème inverse est directement liée à la bonne estimation de cette matrice, d’où l’intérêt des efforts consacrés au calcul des sensibilités. D’utilisation fréquente au vu de sa relative simplicité, l’approximation des sensibilités par perturbations est généralement peu efficace. Les dérivées correspondant aux sensibilités sont approchées par un schéma au premier ordre nécessitant le re-calcul complet de la réponse du modèle pour une perturbation sδ ajoutée aux paramètres. Concrètement, on obtient les sensibilités selon :
(
k) ( )
k k i j j i j i k j j s s s s s ξ + δ − ξ ∂ξ ≈ ∂ δ (I.17)La difficulté réside dans le choix de la taille de la perturbation δsj : si elle est trop grande, l’approximation en (I.17) sera mauvaise, si elle est trop petite des problèmes numériques (division par zéro, erreurs d’arrondis…) peuvent survenir. La méthode analytique choisie dans ce travail consiste à écrire explicitement l’équation de chacun des termes de la matrice Jacobienne. Mise en avant par [Mc
Laughlin and Townley, 1996], cette méthode s’utilise plus communément pour des modèles directs
simples car le principe est de dériver les équations du calcul direct par rapport à chaque paramètre.
I.3. Principe du calcul des sensibilités analytiques
Formellement, le système d’équations matricielles (I.5) peut se réécrire :
n 1 f f f n 1 m m m + + ⋅ = ⋅ = A h W A h W (I.18) f
W et W sont les vecteurs correspondant aux membres de droite des équations (I.5). En dérivant cesm
équations par rapport au paramètre sj, on obtient :
n 1 n 1 f f f f f j j j n 1 n 1 m m m m m j j j s s s s s s + + + + ∂ ∂ ∂ ⋅ = − ⋅ ∂ ∂ ∂ ∂ ∂ ∂ ⋅ = − ⋅ ∂ ∂ ∂ h W A A h h W A A h (I.19) Les sensibilités n 1 f sj +
∂h ∂ sont accessibles en résolvant le système (I.19) comparable à (I.18) aux membres de droite près. Fondamentalement, le calcul des sensibilités est similaire à celui du problème direct (même matrice de "raideur"), se réalise conjointement (même boucle d’itérations sur le temps) et utilise le même algorithme (substitution de la charge dans la matrice dans l’équation de la fracture comme décrit par l’équation (I.6) puis résolution du système par l’algorithme de Thomas détaillé en annexe B). Cette similitude est bénéfique en termes de temps de calcul et de programmation car ici l’algorithme de Thomas triangulant la matrice A est calculé une fois pour toutes. Par exemple pour p paramètres, on résoudra un calcul direct et p calculs de sensibilités de type A h W dans la même⋅ = boucle d’itérations sur le temps. Autre avantage indéniable, les sensibilités seront calculées avec la même précision intrinsèque que les variables d’état hf et hm. Le seul bémol est l’effort nécessaire afin d’accéder "analytiquement" aux dérivées des matrices et vecteurs du système linéaire à résoudre (second membre de (I.19)). Parfois c’est impossible, dans le cas de discrétisations complexes ou de paramétrisations emboîtées (s est le paramètre recherché alors que c’est z =f(s) qui agit sur la variable
d’état du calcul direct). Dans les approches double milieu, ces difficultés ne se posent pas et les systèmes permettant de calculer les sensibilités analytiques s’acquièrent via quelques développements algébriques.
I.3.1. Sensibilités analytiques du double milieu homogène
Les expressions analytiques des sensibilités du modèle double milieu homogène sont données en annexe B de l’article de [Delay et al., 2007]. La Figure 3 illustre l’évolution des sensibilités aux quatre paramètres