Localisation relative à six degrés de liberté basée sur les angles et sur le filtrage probabiliste

Localisation relative à six degrés de liberté

basée sur les angles et sur le filtrage

probabiliste

Résumé

Lorsque des robots travaillent en équipe, il est avantageux de permettre à ceux-ci de se localiser mutuellement pour faire, par exemple, de la navigation en formation. La résolution de la localisation relative est d’une importance particulière pour des équipes de robots aériens ou sous-marins lorsque ceux-ci opèrent dans des environnements dépourvus de points de repère. Ce problème se complexifie davantage lorsque le système de localisation permet seulement l’utilisation de caméras légères et bon marché. Cette étude présente une solution analytique au problème de localisation relative à six degrés de liberté basée sur des mesures d’angle. Cette solution est intégrée à des filtres probabilistes pour augmenter sa précision. En utilisant deux robots mutuellement observables possédant chacun deux marqueurs et une caméra colinéaires, nous pouvons retrouver les transformations qui expriment la pose du premier dans le référentiel du second. Notre technique se distingue du fait qu’elle nécessite uniquement la mesure de deux paires d’angles, au lieu d’un mélange de mesures d’angles et de distances. La précision des résultats est vérifiée par des simulations ainsi que par des expérimentations concrètes. Suite à des expérimentations à des distances variant entre 3.0 m et 15.0 m, nous montrons que la position relative est estimée avec moins de 0.5 % d’erreur et que l’erreur moyenne sur l’orientation relative est maintenue sous 2.2 deg. Une généralisation approximative est formulée et simulée pour le cas où la caméra de chaque robot n’est pas colinéaire avec les marqueurs de celui-ci. Au-delà de la précision des caméras, nous montrons qu’un filtre non parfumé de Kalman permet d’adoucir l’erreur sur les estimations de la position relative, et qu’un filtre étendu de Kalman basé sur les quaternions peut faire de même pour l’orientation relative. Cela rend notre solution particulièrement adaptée pour le déploiement de flottes de robots à six degrés de liberté comme des dirigeables.

Abstract

When a team of robots have to collaborate, it is useful to allow them to localize each other in order to maintain flight formations, for example. The solution of cooperative localization is of particular importance to teams of aerial or underwater robots operating in areas devoid of landmarks. The problem becomes harder if the localization system must be low-cost and lightweight enough that only consumer-grade cameras can be used. This paper presents an analytical solution to the six degrees of freedom cooperative localization problem using bearing only measurements. Probabilistic filters are integrated to this solution to increase it’s accuracy. Given two mutually observing robots, each one equipped with a camera and two markers, and given that they each take a picture at the same moment, we can recover the coordinate transformation that expresses the pose of one robot in the frame of reference of the other. The novelty of our approach is the use of two pairs of bearing measurements for the pose estimation instead of using both bearing and range measurements. The accuracy of the results is verified in extensive simulations and in experiments with real hardware. In experiments at distances between 3.0 m and 15.0 m, we show that the relative position is estimated with less than 0.5 % error and that the mean orientation error is kept below 2.2 deg. An approximate generalization is formulated and simulated for the case where each robot’s camera is not colinear with the same robot’s markers. Passed the precision limit of the cameras, we show that an unscented Kalman filter can soften the error on the relative position estimations, and that an quaternion-based extended Kalman filter can do the same to the error on the relative orientation estimations. This makes our solution particularly well suited for deployment on fleets of inexpensive robots moving in 6 DoF such as blimps.

Table des matières

Résumé iii

Abstract v

Table des matières vii

Liste des tableaux ix

Liste des figures xi

Remerciements xiii

1 Introduction et présentation du projet 1

1.1 Concepts fondamentaux . . . 2

1.2 Description des objectifs de la recherche . . . 25

2 Localisation relative à six degrés de liberté basée sur les angles 29 2.1 Solution analytique au problème . . . 30

2.2 Simulation. . . 41

2.3 Expérimentations . . . 49

2.4 Généralisation au problème non colinéaire . . . 64

2.5 Conclusion . . . 75

3 Filtrage des mesures pour améliorer la précision des estimations sur la position relative et sur l’orientation relative 79 3.1 Description du filtre de Kalman basé sur la transformation non parfumée. . 80

3.2 Description du filtre étendu de Kalman. . . 87

3.3 Conclusion . . . 99

4 Conclusion 103 4.1 Travaux futurs . . . 105

A Appendice A : Code de localisation relative à six degrés de liberté 109

B Appendice B : Erreur 2D des caméras Logitech C905 119

C Appendice C : Simulation de la localisation coopérative pour le cas des

D Appendice D : Simulation du filtrage UKF sur la position 125

E Appendice E : Simulation du filtrage EKF sur l’orientation 129

Liste des tableaux

2.1 Précision des caméras OptiTrack . . . 55

Liste des figures

1.1 Le modèle du sténopé . . . 3

1.2 Description du modèle du sténopé inverseur.. . . 3

1.3 Flou créé par l’augmentation de l’ouverture du sténopé. . . 5

1.4 Le principe de la caméra avec une lentille. . . 5

1.5 Effet causé par le Rolling Shutter, une gracieuseté de Point Grey [2013]. . . 6

1.6 Architecture Full-Frame d’une caméra CCD, une gracieuseté de Quantum Scien-tific Imaging [2013] . . . 7

1.7 Architecture à transfert interligne d’une caméra CCD, une gracieuseté de Quan-tum Scientific Imaging [2013] . . . 8

1.8 Changement de coordonnées par transformations appliquées au repère. . . 11

1.9 Image d’un tryphon . . . 26

2.1 Problème de la localisation relative en trois dimensions . . . 31

2.2 Points de vue des caméras ~CA et ~CB dans le problème de localisation relative en trois dimensions . . . 33

2.3 Les trois angles ϕ mesurés par une caméra . . . 33

2.4 Localisation coopérative en deux dimensions. . . 35

2.5 Définition de l’angle β . . . 36

2.6 Simulation pour valider l’erreur sur l’estimation de β . . . 46

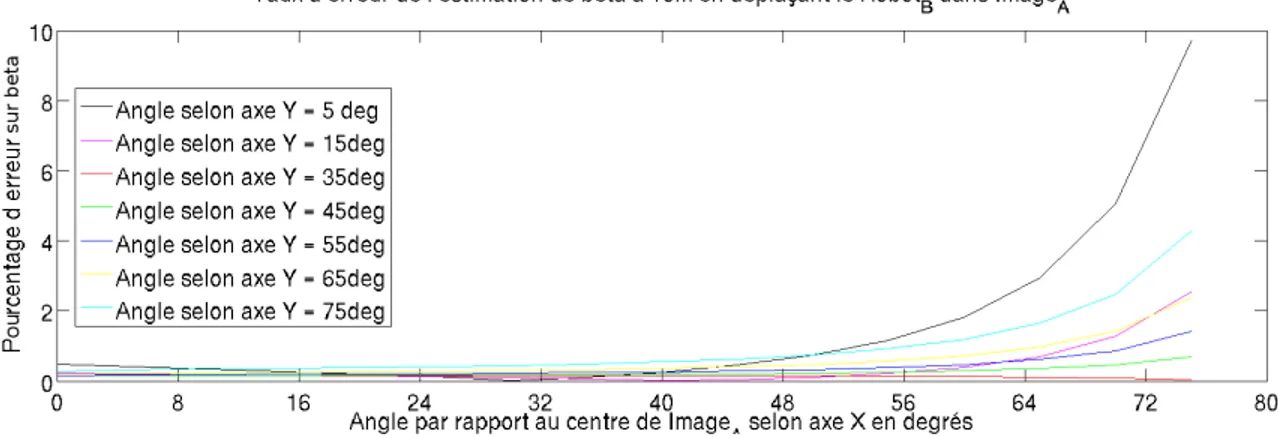
2.7 Erreur sur l’estimation de β . . . 46

2.8 Erreur sur l’estimation de la pose relative du RobotB à 10 m lorsque β est estimé 47 2.9 Simulation de l’erreur sur la pose relative entre les deux robots . . . 48

2.10 Logitech C905 [Logitech, 2013] . . . 50

2.11 Schéma électronique de l’assemblage des marqueurs lumineux . . . 50

2.12 Image du prototype RobotB . . . 51

2.13 Une des images ayant servi à calibrer une caméra. . . 51

2.14 Caméra V100 :R2 d’OptiTrack [NaturalPoint, 2013]. . . 52

2.15 L’OptiHub, servant à synchroniser les caméras d’OptiTrack et à gérer le flot de données. . . 53

2.16 Diagramme de branchement des OptiHubs . . . 54

2.17 L’OptiWand, la baguette de calibration d’OptiTrack. . . 55

2.18 Calibration des caméras V100 :R2 . . . 55

2.19 Équerre de calibration du système OptiTrack . . . 56

2.20 Évaluation de la précision des caméras C905 de Logitech . . . 57

2.21 Comparaison des positions réelles et estimées dans le plan X-Z avec calibration 60 2.22 Erreur sur l’estimation de la position du RobotB avec calibration . . . 60

2.24 Erreur sur l’estimation de la position du RobotB . . . 62

2.25 Erreur sur l’estimation de l’orientation du RobotB . . . 62

2.26 Comparaison des positions réelles et estimées dans le plan X-Z . . . 63

2.27 Comparaison des positions réelles et estimées dans le plan X-Z sur de longues distances . . . 64

2.28 Erreur sur l’estimation de la position du RobotB sur de longues distances . . . 65

2.29 Erreur sur l’estimation de l’orientation du RobotB sur de longues distances. . . 65

2.30 Visualisation de la non-colinéarité selon le plan Y − Z dans le cas de la caméra ~ CA . . . 66

2.31 Erreurs sur la localisation relative sans colinéarité pour la caméra ~CA. . . 71

2.32 Erreurs sur la localisation relative sans colinéarité pour la caméra ~CB . . . 72

2.33 Erreurs sur la localisation relative sans colinéarité. . . 73

2.34 Variation de l’erreur sur la position avec le déplacement dans l’image IA du RobotB . . . 74

2.35 Variation de l’erreur sur la position avec le déplacement dans l’image IA du RobotB et avec bruit . . . 74

3.1 Combinaison de filtres pour l’amélioration de l’estimation de la pose relative. . 80

3.2 Les points sigma du filtre UKF . . . 82

3.3 Simulation du positionnement avec le filtre UKF . . . 86

3.4 Linéarisation du filtre EKF . . . 90

3.5 Simulation de l’orientation avec le filtre EKF . . . 98

Remerciements

Je remercie Philippe Giguère pour son support et ses conseils. Je remercie David St-Onges pour son étroite collaboration. Je remercie également l’Université Laval pour nous avoir donné accès au matériel scientifique et aux laboratoires de recherche. Je remercie les techniciens du département de génie électrique et informatique, pour leurs nombreux services. Merci égale-ment à mes professeurs et mes chargés de cours, pour la passion qu’ils m’ont transmise. Merci à mes parents, pour leurs encouragements et leur soutien.

Enfin, je remercie Émilie Audet pour son amour et tout le support qu’elle m’a donné pendant mes études.

Chapitre 1

Introduction et présentation du projet

La robotique est la branche de la technologie qui est responsable de la conception, de la construction, de l’opération et de la mise en application de robots. Cela implique le dévelop-pement de systèmes informatiques pour assurer leur contrôle et l’analyse de l’information ob-tenue par leurs différents capteurs. De nos jours, la robotique est omniprésente dans notre vie. Nous utilisons maintenant des robots dans de nombreux domaines aussi variés que l’agricole, le domestique, l’industriel, le médical et le militaire. De plus, la récente visibilité de la robo-tique mobile, notamment par des compétitions comme le DARPA Robotics Challenge DARPA

[2013], a permis le développement rapide de cette technologie.

Plusieurs défis doivent être relevés afin de poursuivre l’essor de la robotique mobile. L’un d’entre eux est le problème de la localisation. Celui-ci est rencontré lorsqu’un robot doit se localiser dans son environnement en se servant de points de repère dans celui-ci et en utilisant ses multiples capteurs. Il est en effet impensable de concevoir un pilote automatique pour une voiture sans la capacité de se localiser dans une ville bondée, de se déplacer malgré les autres véhicules, ou encore d’apercevoir les piétons à temps pour ne pas les frapper lorsque ceux-ci traversent la chaussée.

L’utilisation du système de localisation mondial, ou Global Positioning System (GPS), a per-mis de nombreuses avancées pour la robotique mobile. Malheureusement, bien qu’utile pour une grande variété d’environnements et d’applications, ce système est inaccessible dans bien d’autres. Par exemple, le signal GPS ne peut pas être employé sous l’eau à des profondeurs appréciables. La même difficulté survient lorsqu’un robot tente d’utiliser ce système à l’inté-rieur d’un bâtiment, dans une caverne ou encore dans un tunnel. Aussi, puisque le système GPS implique des satellites en orbite autour de la Terre, celui-ci est inapplicable dans l’espace ou sur d’autres planètes.

Une alternative à l’utilisation du GPS est d’exploiter l’environnement lui-même. Les robots mobiles sont équipés de capteurs permettant d’observer des repères de leur environnement et de mesurer des angles et des distances par rapport à ceux-ci. En utilisant des points de repère

naturels d’un milieu, il est possible de déterminer la position des robots dans celui-ci. Cette solution s’avère efficace pour localiser des robots dans le cadre de nombreuses applications. Néanmoins, cette technique est complexe à utiliser dans des environnements qui ne possèdent pas ces repères naturels. C’est par exemple le cas pour les robots naviguant sous l’eau sans pouvoir observer le fond marin [Bahr et al.,2009].

Dans des environnements dépourvus de repères, il devient intéressant d’utiliser des équipes de robots mobiles afin de permettre une localisation relative de ceux-ci. Cette façon de procéder permet d’augmenter la précision des déplacements lorsqu’on la compare à celle du déplacement à l’aveugle d’un robot solitaire. Également, cette technique de localisation relative permet l’utilisation de flottes de drones, où il est nécessaire pour chaque robot de facilement repérer ses collaborateurs afin de naviguer en formation. Il devient aussi possible de faire collaborer des robots afin d’atteindre divers objectifs complexes.

La présente recherche porte sur le développement d’une nouvelle technique de localisation relative entre plusieurs robots dans un environnement sans repères. Cette étude s’intéresse particulièrement aux problèmes minimaux en vision numérique. Autrement dit, nous cherchons à utiliser le minimum d’information disponible afin de déterminer une équation analytique permettant de calculer la pose relative entre les entités observées. Nous souhaitons utiliser cette technique pour différentes applications, comme pour la collaboration de robots volants ou encore pour l’exploration de cavernes sous-marines.

1.1

Concepts fondamentaux

1.1.1 Terminologie liée à la vision numérique

Dans ce mémoire, nous utilisons des caméras comme capteurs de position relative. Ces caméras, de même que l’ensemble des caméras modernes, peuvent s’analyser à l’aide du modèle de caméra sténopé. Selon ce modèle, illustré à la figure1.1, un trou minuscule est percé sur l’une des faces d’une boîte afin d’y laisser entrer la lumière. Les rayons lumineux qui y pénètrent forment, au fond de la boîte, une image renversée de la réalité extérieure. Nous appelons donc ce modèle le sténopé inverseur.

La figure1.2affiche une description mathématique du sténopé inverseur et de différents termes associés. Cette description est tirée principalement deSonka et al.[1999], dont les travaux ont été traduits et synthétisés sous la forme de notes de cours par Laurendeau [2013]. Dans ce modèle, la longueur focale f est la distance entre le plan image de la caméra et le trou du sténopé. Le référentiel du modèle a pour origine O le centre de projection CP , qui correspond au trou du sténopé. Les axes x, y et z respectent la règle de la main droite de sorte que x et y soient parallèles au plan image et que z s’éloigne de ce plan. Toujours selon ce modèle, l’axe optique est l’axe parallèle à z et passe par le centre de projection de la caméra. Enfin, le point

Figure 1.1 – Le modèle du sténopé. L’image est gracieusement offerte par le professeur Laurendeau [2013].

principal d’une image représente le point où l’axe optique rencontre le plan image.

Figure 1.2 – Description du modèle du sténopé inverseur. L’image est gracieusement offerte par le professeur Laurendeau[2013].

Le modèle du sténopé implique que l’ouverture par laquelle passent les rayons lumineux est infiniment petite de sorte qu’un seul rayon atteigne chacun des points du plan image. En d’autres termes, dans la perspective de la caméra, un point à une distance inconnue a émis ou réfléchi un rayon lumineux en direction du centre de projection O. Pour exprimer cette réalité, les coordonnées homogènes sont employées. En coordonnées homogènes, les coordonnées du point [x, y, z]T _{s’expriment comme [hx, hy, hz, h]}T _{où h 6= 0. Afin de retrouver les coordonnées} réelles à partir de coordonnées homogènes, il suffit de diviser les premières coordonnées par h. L’approche des coordonnées homogènes est utile pour effectuer, par exemple, des opéra-tions de rotation ou de translation de points tridimensionnels [Laurendeau,2013]. Également,

cette technique est utilisée pour effectuer la projection de perspective, qui est l’opération ma-thématique permettant de calculer la formation des images sur le plan image à partir d’un environnement 3D. Tel que décrit parSonka et al. [1999], il existe différentes représentations matricielles pour faire des projections, comme les projections perspectives, orthographiques, sphériques et cylindriques. Cependant, nous n’utiliserons dans ce mémoire que la projection perspective, qui est exprimée par la matrice Tp suivante :

Tp =       1 0 0 0 0 1 0 0 0 0 1/f 0 0 0 0 1       . (1.1)

Nous notons ici que Tp est une version simplifiée de la véritable matrice de projection, car elle considère que les pixels dans l’image sont des carrés. La matrice de projection Tp est différente lorsque les axes de l’image ne sont pas perpendiculaires ou lorsque ces mêmes axes ne sont pas à la même échelle.

Une caméra physiquement construite selon le modèle sténopé possède d’importants incon-vénients. D’abord, il est impossible de faire physiquement un trou dans une boîte de taille infinitésimale. De plus, une petite ouverture implique que peu de lumière pénètre dans la caméra, ce qui rallonge la durée d’exposition nécessaire pour exciter suffisamment une sur-face photosensible. Également, selon le principe de la dualité onde-corpuscule en physique ondulatoire, un trou de très petite taille laissant entrer la lumière engendre un phénomène de diffraction qui provoque un effet de flou dans la formation de l’image sur le plan image. Inversement, une caméra construite selon le modèle sténopé avec un trou qui n’est pas infi-niment petit est également problématique. En effet, les objets photographiés qui émettent ou réfléchissent la lumière ne sont pas toujours à une distance infinie de la caméra. Ainsi, une ouverture trop grande fait en sorte que deux rayons lumineux provenant d’un même point dans l’environnement peuvent toucher le plan image à différentes positions. Ce phénomène, illustré à la figure1.3, résulte également en une image floue.

Afin de pallier ces difficultés, le trou de la caméra sténopé est remplacé par une lentille. Cette solution, illustrée à l’image1.4, permet aux caméras d’avoir une ouverture plus grande, tout en conservant un modèle mathématique similaire à celui du sténopé. En effet, la lentille redirige les rayons marginaux, qui sont les rayons ne passant pas par le centre de projection de la caméra, vers la position sur le plan image atteinte par le rayon principal émis par une position sur l’objet photographié. Cependant, un inconvénient est que seuls les points à une certaine distance entre ceux-ci et la caméra sont au focus, c.-à-d. lorsque le flou causé par la mauvaise concentration des rayons lumineux par la lentille est d’un diamètre inférieur à 1 pixel. Le modèle des caméras à lentilles possède cependant quelques différences par rapport au modèle des caméras sténopé. Il est notamment expliqué par Melles Griot[2013] que l’épaisseur et la

Figure 1.3 – Flou créé par l’augmentation de l’ouverture du sténopé. L’image est tirée des notes de cours gracieusements offertes par le professeurLaurendeau[2013].

Figure 1.4 – Le principe des caméras avec lentilles. Ce modèle de caméra respecte le modèle du sté-nopé inverseur. Cependant, la lentille est utilisée pour concentrer les rayons provenant d’un même point de l’objet afin d’augmenter l’intensité de la lumière qui éclaire le plan image. L’image est gracieusement offerte parMelles Griot[2013].

position de la lentille par rapport au plan image de la caméra ont une incidence sur la longueur focale de la caméra. Ainsi, il est important de calculer à nouveau la longueur focale de la caméra si l’un de ces éléments est modifié. Il y est également expliqué que la distorsion est une aberration particulière de la lentille qui fait en sorte que les objets sont projetés sur le plan image plus près ou plus loin de l’axe optique qu’ils ne l’auraient été sur une image parfaite. Ce problème est une propriété des lentilles et n’est pas causé par des erreurs de fabrication. Par conséquent, il est important de procéder à la calibration d’une caméra afin de calculer

la distorsion dans les images. Il est possible de déterminer la position parfaite d’un point en enlevant la distorsion dans l’image par un modèle approprié et une procédure de calibration des paramètres de ce modèle [voirBouguet, 2010] et ainsi obtenir une image utilisable par le modèle de caméra sténopé.

Il existe deux types de capteurs d’images dans les caméras modernes, soit les CMOS et les CCD. Comme l’a expliquéLitwiller [2001], l’application dans laquelle une caméra est utilisée a une grande importance dans le choix du type de capteur. Dans son article, Litwiller indique que les capteurs CMOS ont une plus grande rapidité de réponse, puisque la conversion de l’énergie photonique en voltage se fait individuellement sur chaque pixel. À l’opposé, cette conversion pour les capteurs CCD s’effectue en série pour tous les pixels en même temps. Pour ce qui est de la précision de l’image, les capteurs CCD sont plus efficaces que les CMOS parce que les circuits traitant l’image sont éloignés du capteur, ce qui réduit le bruit dans les pixels de l’image. En résumé, pour des applications nécessitant des caméras de petite taille, ayant une faible consommation électrique et où la qualité de l’image n’est pas requise, les capteurs CMOS sont idéaux. Inversement, les capteurs CCD doivent être utilisés là où la qualité de l’image et la flexibilité du capteur sont des éléments primordiaux d’une application.

Figure 1.5 – Effet causé par le Rolling Shutter, une gracieuseté dePoint Grey[2013].

Lors de la prise d’image, la plupart des caméras de type CMOS procèdent à un balayage progressif des pixels, technique mieux connue sous le nom de Rolling Shutter. Cette technologie permet de prendre des images très rapidement puisque certains pixels peuvent être excités par la lumière alors que d’autres sont figés afin de donner leur valeur de saturation actuelle. Cependant, cette technique a le désavantage de créer des images distordues lorsque les objets photographiés ou la caméra sont en mouvement. La figure 1.5 est un bon exemple de ce phénomène. À l’opposé de cette technique se trouve le balayage global, ou Global Shutter. Les caméras de type CCD et quelques rares caméras de type CMOS emploient ce type de balayage. Le résultat donne des images qui ne souffrent pas de distorsions pour des mouvements rapides.

Néanmoins, deux architectures sont disponibles pour les caméras CCD, soit celle à surface complète (Full-Frame) et celle à transfert interligne (Interline Transfert). La figure1.6montre l’architecture Full-Frame. Les caméras de cette architecture requièrent qu’à chaque image la valeur des pixels de chaque rangée soit transférée de rangée à rangée jusqu’à atteindre le registre de sortie. Cela force l’utilisation d’un obturateur mécanique afin de bloquer l’exposition de la surface photosensible. La figure 1.7 présente plutôt l’architecture à transfert interligne. Dans celle-ci, chaque colonne photosensible est associée à une colonne masquée. Lors de la prise d’une image, la valeur des pixels exposés est transférée dans la colonne masquée afin d’être enregistrée. Cela permet une plus grande vitesse de capture d’image, avec le désavantage d’une surface photosensible perméable. Au final, les caméras CCD à architecture Full-Frame rendront des images aux couleurs mieux définies, mais avec des effets de flou si un objet de la scène se déplace plus rapidement que la vitesse de l’obturateur mécanique. De leur côté, les caméras CCD à architecture Interline Transfer rendront des images parfaitement nettes, quoique plus sombres et aux couleurs moins bien définies.

Figure 1.6 – Architecture Full-Frame d’une caméra CCD, une gracieuseté de Quantum Scientific

Imaging[2013]

1.1.2 Problèmes minimaux et calculs de coordonnées

En vision numérique, les problèmes minimaux surviennent lorsqu’il faut résoudre des modèles géométriques à partir des données d’une ou de plusieurs images. Ces problèmes consistent à trouver, par exemple la pose d’une ou de plusieurs caméras, calibrées ou non, et ce avec le minimum d’information possible. Le site web du Center for Machine Perception [Pajdla et al.,

2011] offre un accès centralisé vers des articles résolvant différents problèmes minimaux. Nous présentons donc, ici, des problèmes se rapprochant du nôtre.

Un de ces problèmes minimaux est d’estimer la pose, soient la translation et l’orientation, d’une caméra calibrée à partir d’une image montrant trois points de référence dans l’espace dont les

Figure 1.7 – Architecture à transfert interligne d’une caméra CCD, une gracieuseté de Quantum

Scientific Imaging[2013]

positions sont connues.Fischler and Bolles [1981] s’attaquent à ce problème en commençant par introduire le paradigme du consensus d’échantillon aléatoire (Random Sample Consensus, ou RANSAC). Il s’agit d’une méthode itérative servant à estimer les paramètres d’un modèle mathématique reliant deux ensembles de données qui se ressemblent. L’hypothèse de base est que certains points d’un ensemble possèdent leur point correspondant dans l’ensemble de référence moyennant un certain niveau de bruit, alors que d’autres points sont des valeurs aberrantes.

De manière itérative, l’algorithme RANSAC sélectionne un sous-ensemble aléatoire de points de l’ensemble d’observations. Ces points sont hypothétiquement considérés comme des valeurs correctes alors que les autres points de l’ensemble sont initialement considérés comme aber-rants. Par la suite, l’algorithme tente d’ajuster les points sélectionnées à leurs correspondances dans l’ensemble de référence. Si suffisamment de points sont jumelés correctement, le modèle permettant d’aligner les deux ensembles est considéré comme correct et est conservé. Sinon, un nouveau sous-ensemble de points est pigé. Lorsque cette procédure est complétée, l’erreur du modèle est évaluée en analysant la distance qui sépare les points aberrants de leurs points correspondants dans l’ensemble de référence. Il est possible de répéter l’algorithme pour de nombreuses itérations afin d’améliorer les résultats de celui-ci. Pour ce faire, il suffit d’appliquer le modèle mathématique résultant de l’algorithme sur l’ensemble des données d’observation, puis de redémarrer la procédure jusqu’à une certaine condition de sortie, telle que l’atteinte d’un minimum d’erreur de correspondance. Ainsi, il est possible d’aligner des données qui, par exemple, ne sont pas dans le même référentiel de coordonnées.

Dans leur article,Fischler and Bolles[1981] utilisent le paradigme RANSAC pour résoudre le problème de la détermination de la pose d’une caméra non calibrée (dont la longueur focale

est inconnue) en présence de trois points visibles d’un tétraèdre. Leur solution suppose que les trois longueurs de la base du tétraèdre observée, Rab, Rbc et Rac, sont connues. De plus, elle suppose que l’angle des faces opposées θab, θbc et θac, de même que les trois segments restants du tétraèdre sont de longueurs a, b et c connues. Les auteurs présentent la solution analytique pour trouver les quatre solutions mathématiques possibles aux équations suivantes :

(Rab)2= a2+ b2− 2ab cos(θab); (1.2) (Rbc)2 = b2+ c2− 2bc cos(θbc); (1.3) (Rac)2= a2+ c2− 2ac cos(θac). (1.4) Ces quatre solutions possibles permettent de connaître les quatre poses possibles pour la caméra. Il suffit enfin d’utiliser une caméra calibrée (dont la longueur focale est connue) afin de déterminer la position réelle de la caméra en résolvant le problème des moindres carrés. Les auteurs démontrent ensuite qu’il est possible d’obtenir une solution unique dans le cas où une caméra non calibrée fait face à quatre points coplanaires. Lorsque le problème devient plus complexe et que la caméra observe quatre points ou plus qui ne sont pas coplanaires, l’algorithme RANSAC est utilisé. Celui-ci utilise de multiples sous-ensembles de trois points et tente de le faire correspondre au modèle du tétraèdre.

Un autre problème minimum en vision numérique est celui de trouver la pose relative de deux caméras calibrées à partir de cinq marqueurs visuels correspondants se retrouvant dans les images de chaque caméra en même temps. L’approche que présente Nistér [2004] permet de retrouver les transformations entre deux caméras observant une même scène en temps réel en utilisant la technique RANSAC pour augmenter la précision des résultats. Grâce à l’approche de l’auteur, il est également possible de calculer le déplacement d’une même caméra entre deux prises d’images en utilisant cinq marqueurs visuels immobiles. Une solution à ce problème minimum permet, entre autres, de reconstruire une virtualisation d’un objet réel.

Au lieu d’utiliser uniquement des points pour calculer la position d’une caméra, Ramalingam et al.montrent comment il est possible d’utiliser une combinaison de lignes et de points. Dans leur article, les auteurs expliquent qu’il existe quatre configurations minimales pour déterminer la pose d’une caméra calibrée dans un environnement contenant des marqueurs sous la forme de lignes et de points, soient trois points, deux points avec une ligne, un point avec deux lignes et trois lignes. Les auteurs établissent une technique générale permettant de déterminer la position d’une caméra en recherchant l’une de ces combinaisons de repères visuels dans une seule image. L’intérêt de leur approche est que celle-ci permet de déterminer la pose d’une caméra pour des combinaisons minimales de points et de lignes, ce qui n’avait pas encore été fait. Leur solution se base sur la colinéarité et sur la coplanarité liant les caméras et les marqueurs visuels entre eux. Pour le problème minimal requérant deux points et une ligne, les auteurs utilisent des contraintes d’orthogonalité impliquant les variables de rotation R11,

R21, R31, R22et R23 :

R2₁₁+ R2₂₁+ R2₃₁= 1; (1.5) R2₂₁+ R2₂₂+ R2₂₃= 1. (1.6) En résolvant ce système d’équations quadratiques, les auteurs obtiennent quatre solutions possibles pour l’estimation de la pose. Pour ce qui est du problème minimal avec deux lignes et un point, les contraintes d’orthogonalité et les variables de rotations sont plus nombreuses : R2₁₁+ R2₁₂+ R2₁₃= 1; (1.7) R2₂₁+ R2₂₂+ R2₂₃= 1; (1.8) R11R21+ R12R22+ R13R23= 0. (1.9) La résolution de ce système donne cette fois huit solutions possibles. Cependant les auteurs discutent peu de la technique utilisée dans cette situation pour déduire la solution réelle. Le problème minimum de la triangulation peut également être observé d’un point de vue différent, c.-à-d. lorsqu’il y a plusieurs caméras et un seul marqueur visuel.Hartley and Sturm

[1997] analysent ce problème lorsque deux caméras doivent positionner dans l’espace un même marqueur lumineux. Ils indiquent que pour des images montrant le marqueur visuel à des coordonnées souffrant d’un bruit gaussien, la triangulation est possible par la résolution d’un problème de moindres carrés. Les auteurs présentent enfin une solution non itérative qui permet de trianguler ce marqueur en retrouvant le minimum global. Afin d’accélérer le traitement et d’augmenter la précision de cette solution,Byröd et al.[2007] proposent une nouvelle approche utilisant trois caméras ou plus.

1.1.3 Changements de repères

Il est ici nécessaire d’expliquer comment il est possible d’exprimer un repère dans un autre en trois dimensions. Les matrices de rotation et celles de translation sont deux transformations de coordonnées permettant de déplacer des points ou des vecteurs dans un référentiel donné. Ces transformations s’expriment habituellement en coordonnées homogènes. En trois dimensions, une rotation R de θ autour des axes des x, y et z respectivement s’exprime par

Rx=       1 0 0 0 0 cos(θ) − sin(θ) 0 0 sin(θ) cos(θ) 0 0 0 0 1       (1.10) Ry=       cos(θ) 0 sin(θ) 0 0 1 0 0 − sin(θ) 0 cos(θ) 0 0 0 0 1       (1.11)

Rz=       cos(θ) − sin(θ) 0 0 sin(θ) cos(θ) 0 0 0 0 1 0 0 0 0 1       (1.12)

et une translation T de Tx, Ty, Tz autour de ces mêmes axes respectifs s’écrit comme suit.

T =       1 0 0 Tx 0 1 0 Ty 0 0 1 Tz 0 0 0 1       (1.13)

Figure 1.8 – Changement de coordonnées par transformations appliquées au repère, pour un problème en deux dimensions. Le vecteur ~Va, en noir, subit une rotation pour l’amener dans le repère bleu, puis

une translation pour être exprimé par ~Vc dans le référentiel vert.

Il est possible de construire des transformations de coordonnées en post-multipliant les chan-gements de repère [Laurendeau, 2013]. Nous pouvons ainsi retrouver les coordonnées d’un vecteur par rapport à des repères ayant subi plusieurs transformations. Le produit de matrices n’étant pas commutatif, l’ordre dans lequel les transformations sont effectuées est important. La figure 1.8 présente un exemple en deux dimensions, pour une représentation visuelle plus simple à comprendre. Cependant, le lecteur peut noter que la même théorie s’applique éga-lement pour les cas tridimensionnels. Soit le vecteur ~Va, exprimé par ses coordonnées dans le référentiel noir a. Nous souhaitons exprimer ~Va dans le référentiel vert c, et ainsi obtenir le vecteur ~Vc. Pour ce faire, nous appliquons une rotation B_AR à ~Va pour obtenir le vecteur dans le référentiel bleu b. À ce stade, les axes du référentiel b sont orientés comme ceux du référentiel vert c. Il faut ensuite faire correspondre l’origine de b et de c. Nous multiplions donc le vecteur résultant par une matrice de translationC

BTafin de trouver ~Vc. Nous obtenons ainsi l’équation 1.14:

~

Lorsque la performance d’une mesure de position ou d’orientation doit être évaluée, les cher-cheurs font régulièrement appel à la comparaison par rapport à des mesures réelles. Par exemple, si nous utilisons un système de localisation, nous avons intérêt à utiliser la posi-tion et l’orientaposi-tion réelle de l’objet mesuré, ou vérité terrain, comme critère de comparaison. Cette vérité terrain est obtenue par des appareils dont la précision est nettement supérieure aux appareils utilisés pour faire les expérimentations. Cependant, il arrive parfois que la vérité terrain ne soit pas dans le même référentiel que le système de localisation mis à l’épreuve. Dans une telle situation, nous utilisons l’algorithme Iterative Closest Point (ICP), la méthode actuellement dominante pour aligner des modèles tridimensionnels se basant sur la géomé-trie des ensembles de données. Cet algorithme, queRusinkiewicz and Levoy[2001] analysent rigoureusement, utilise deux ensembles de données en tentant par itérations de générer des transformations qui minimisent les différences entre les deux. Dans leur article, les auteurs dé-finissent les étapes logiques d’ICP et comparent les différentes variantes algorithmiques pour chacune de ces étapes par rapport à la précision et à la vitesse de convergence d’une variante servant d’étalon. L’analyse est conduite sur différents ensembles de données synthétiques et suite à cette analyse, Rusinkiewicz et Levoy optimisent ICP afin que celui-ci puisse s’exécuter en temps réel tout en préservant sa robustesse.

1.1.4 Localisation

Afin d’aider un robot à se localiser, celui-ci est muni de capteurs. En robotique, deux catégories de capteurs sont identifiées, soit les capteurs proprioceptifs et les capteurs extéroceptifs. Les capteurs proprioceptifs perçoivent les déplacements du robot d’un point de vue local à celui-ci et ne font pas usage de repères dans l’environnement, comme un accéléromètre, un gyroscope ou un odomètre. À l’inverse, les capteurs extéroceptifs renseignent sur le robot en fonction des données disponibles dans l’environnement, comme une caméra, un sonar, un télémètre laser ou un capteur de collision ou de proximité.

Le problème de la localisation est la capacité d’un système de déterminer la position et l’orien-tation de tous les agents présents dans le système en se basant sur les observations locales et relatives de chacun. En robotique, les agents de ces systèmes sont des robots possédant des capteurs et des effecteurs servant à se déplacer dans l’environnement. La localisation est un défi important en robotique collaborative, principalement lorsqu’une équipe de robots n’a pas accès à un système de positionnement global (GPS).

Comme cela est démontré par Dieudonné et al.[2010], lorsque chaque robot d’un groupe est en mesure d’observer la distance et la direction de tous les autres robots du même groupe, la pose relative de chacun peut facilement être établie. Cependant, dans tous les autres cas, et même en ajoutant à quelques robots la capacité de connaître ses coordonnées GPS, il y a un risque que l’information mesurée par les robots soit insuffisante. En effet, les auteurs ont montré que cette situation peut mener à des solutions multiples et que le problème de

déterminer la solution réelle de la localisation relative soit NP-difficile. Par conséquent, le problème de déterminer si suffisamment d’information est connue par l’ensemble des robots d’un groupe pour permettre la localisation relative du groupe est un problème NP-complet. Il importe donc de s’assurer, lors de la conception de robots collaborateurs, que les mesures relatives entre les robots sont suffisantes pour déterminer les poses relatives de chacun. Les robots utilisés pour effectuer différentes tâches en collaboration ne sont pas toujours ho-mogènes. En effet, les formes et les capteurs des robots peuvent être différents afin de pallier les limitations d’un problème. Par exemple, alors qu’un robot peut être doté d’une caméra et être de petite taille afin d’inspecter des endroits étroits, un second robot, plus gros, peut l’assister en lui procurant suffisamment de lumière pour que le premier puisse inspecter des en-droits sombres.Davison and Kita[2000] relèvent ce défi en simulant l’inspection d’une centrale nucléaire. La solution des auteurs permet au robot muni d’une caméra stéréo de se déplacer en se localisant relativement à des régions d’intérêt dans l’environnement. Le second robot, qui ne possède qu’une source lumineuse, se déplace en se fiant à son odométrie uniquement. Occasionnellement, le premier robot utilise sa caméra pour localiser le second afin de réduire l’incertitude dans les mouvements de ce dernier. Cette technique permet une collaboration efficace pour effectuer une tâche d’inspection.

Lorsqu’un capteur détecte un point de repère dans l’environnement, celui-ci peut être de na-ture anonyme, ce qui signifie qu’il ne possède pas de signana-ture permettant de se distinguer par rapport aux autres points de repère. Une telle signature correspond à de l’information addi-tionnelle davantage utile à l’identification qu’à la localisation, comme une couleur particulière du point dans une image. Dans le cas où le repère est un émetteur, par exemple, les messages que celui-ci envoie peuvent contenir un numéro d’identification. Par conséquent, les problèmes où les repères employés sont anonymes sont plus généraux et plus difficiles à résoudre que les problèmes avec des repères distinguables.

Un système peut être considéré comme observable lorsqu’il est possible, à partir de l’infor-mation disponible, d’estimer la pose de chaque agent d’un groupe et de chaque marqueur dans l’environnement avec une erreur qui est toujours bornée. La valeur de cette borne n’est pas essentielle à la définition d’observabilité, puisque celle-ci dépend fortement de la précision des capteurs utilisés par les agents du système. La question est donc de savoir à partir de quelle quantité d’information le système devient observable. Cristofaro and Martinelli [2011] font l’analyse de cette question pour permettre la localisation entre robots, mais aussi pour déterminer la cartographie de l’environnement étudié. Les auteurs démontrent que pour deux robots à six degrés de liberté munis de caméras, d’accéléromètres et de gyroscopes, il y a suffisamment d’information dans le système pour déterminer la pose relative des robots. Les auteurs constatent également que pour un grand groupe de robots ne s’observant pas tous mutuellement, il est parfois impossible d’estimer l’angle de lacet de quelques-uns des robots du groupe.

Lorsqu’il faut permettre à un seul robot de se localiser par rapport à son environnement, plusieurs solutions existent et celles-ci dépendent des capteurs possédés par le robot. Il est possible d’avoir un robot muni d’un grand nombre de caméras. Dans cette situation, Weber et al. [2012] développent une solution pour estimer la configuration de ce robot en temps réel. Pour ce faire, les auteurs produisent un algorithme en deux phases, soient une période d’estimation de la configuration des caméras entre elles et une phase de triangulation des points d’intérêts dans les images afin de déterminer les changements dans la configuration du robot. Bien que cette technique soit conçue principalement pour un robot avec de multiples articulations, les auteurs mentionnent que cette approche est potentiellement fonctionnelle pour tout système multi-caméras si celles-ci regardent dans des directions semblables et s’il est possible d’exprimer par certains paramètres l’homographie entre elles.

Les environnements sous-marins offrent de grands défis techniques pour la localisation de robots. En effet, en plus de ne pas avoir accès à un système de positionnement par GPS, les robots font face à de grandes difficultés de communication entre eux. Dans ces conditions,Bahr et al.[2009] décrivent un algorithme distribué basé sur l’acoustique pour permettre à des robots autonomes sous-marins de se localiser entre eux. Grâce à des émetteurs-récepteurs acoustiques, les robots peuvent estimer la distance les séparant les uns des autres afin de rectifier leur trajectoire lorsqu’ils naviguent à l’aveugle. L’algorithme, qui nécessite au moins trois robots, mais qui peut fonctionner avec un grand nombre de véhicules, utilise également les mesures et estimations précédentes pour augmenter la précision des nouvelles mesures.

L’identification des robots est un défi additionnel à relever lors de la collaboration d’au moins trois robots dans une même équipe. En effet, la localisation relative des robots ne peut se faire avant cette étape. Dans le cas où il n’y a pas de capteurs externes permettant de suivre les dé-placements des robots et ainsi mitiger ce problème, les robots doivent développer une technique collaborative permettant de se distinguer les uns des autres.Ishiguro et al. [1999] présentent une méthodologie fonctionnant grâce à une caméra omnidirectionnelle assemblée sur chaque robot. Ce type de caméra, qui permet en théorie de voir dans toutes les directions, consiste généralement en une caméra observant un miroir convexe de la forme d’une demi-sphère. La stratégie des auteurs est de mesurer, dans les images de chaque caméra, les angles entre les robots qui y sont perçus. L’algorithme bâtit des triangles en fonction des angles et élimine ensuite ceux-ci progressivement par propagation de contraintes. Leur solution peut fonctionner en temps réel pour des équipes allant jusqu’à sept robots. Pour de plus grandes équipes, la quantité exponentielle de triangles devient trop importante, mais les auteurs expliquent qu’il est possible de subdiviser les équipes en sous-groupes afin d’optimiser le traitement.

Pour deux robots s’observant mutuellement, il est possible de déterminer la pose relative de l’un d’eux par rapport à l’autre en se basant sur différentes stratégies. Par exemple, dans leur article, Trawny et al. [2010] introduisent une méthode algébrique permettant de calculer la translation et la rotation relatives entre deux robots en utilisant les déplacements connus de

chaque robot, ainsi que différentes combinaisons de mesures d’angle et de distances entre les robots. Pour ce faire, les auteurs utilisent plusieurs mesures dans le temps à des positions différentes afin de parvenir à estimer la pose relative entre les robots. Cet article leur permet également de présenter un estimateur non linéaire basé sur les moindres carrés servant à raffiner l’estimation des poses en présence de bruit dans les capteurs des robots.

Une variante de la stratégie qu’utiliseTrawny et al.[2010] est développée afin d’estimer la pose tridimensionnelle relative de deux robots. Lorsqu’un robot muni d’une caméra se déplace, il est possible d’évaluer le déplacement de la caméra en analysant l’égomotion. L’égomotion est définie par le mouvement d’une caméra dans l’espace 3D et se calcule en analysant le changement de position d’une scène rigide entre deux images subséquentes.Trawny et al.[2009] emploient cette technique jumelée à six mesures de distances entre deux robots aéroportés dans le but de localiser relativement ceux-ci. L’algorithme des auteurs est validé en simulation et démontre que la localisation peut se déterminer en temps réel.

Afin de déterminer la localisation relative entre deux robots, une technique répandue est de traduire la localisation en un problème de géométrie minimale, c.-à-d. en utilisant le plus petit nombre possible de mesures pour estimer les transformations géométriques pour passer du repère d’un robot à celui de l’autre. Zhou and Roumeliotis [2010] étudient ce problème en se basant sur différentes combinaisons de mesures entre deux robots à six degrés de liberté. Les mesures entre les robots que les auteurs analysent sont la distance séparant les robots et la direction d’un robot observé par rapport à l’axe optique de la caméra de l’autre robot. Les auteurs font également appel aux estimations de l’égomotion des caméras. Dans leur article, les chercheurs démontrent qu’il existe quatorze problèmes minimaux de base et que ceux-ci ont, en général, de multiples solutions dont la plupart sont complexes. Ils y développent aussi la solution algébrique pour trois de ces problèmes minimaux.

Zhou and Roumeliotis [2011] livrent une seconde partie à l’article mentionné ci-dessus [Zhou and Roumeliotis, 2010]. Les auteurs y présentent la solution algébrique des onze autres pro-blèmes minimaux de base. De tous ces propro-blèmes, cinq possèdent une solution réelle possible avec une forme analytique. D’autres utilisent diverses stratégies de calcul matriciel ou encore des algorithmes symboliques numériques afin d’éliminer des solutions impossibles. Certaines conservent plusieurs solutions réelles possibles qui doivent être éliminées par des techniques différentes qui ne sont pas explorées par les auteurs. De plus, puisque les problèmes mini-maux utilisent l’égomotion, le bruit dans les images fait croître rapidement l’erreur dans les estimations de pose relative.

Dans un article subséquent, Zhou and Roumeliotis [2013] réitèrent les résultats de leurs re-cherches précédentes (Zhou and Roumeliotis [2010] et Zhou and Roumeliotis [2011]). Ils uti-lisent les algorithmes permettant de résoudre les quatorze problèmes minimaux pour déve-lopper un programme qui évalue la performance de chacun par rapport à un algorithme de

référence pour obtenir la vérité terrain. Dans une expérience où des caméras sont distancées de moins de 60 cm et où des plaques de référence pour l’égomotion sont placées en arrière-plan de chaque caméra, les auteurs tentent de localiser relativement les caméras entres elles. Leur meilleur algorithme résulte en une erreur sur la position de 3.8 cm et en une erreur sur l’orientation de 0.0499 rad.

Lorsqu’un groupe de robots tente de se localiser, la capacité d’estimer les distances des ca-méras peut être défaillante ou imprécise. Puisque les caca-méras peuvent être utilisées comme d’excellents capteurs d’angles,Kennedy et al. [2012] tentent d’effectuer la localisation relative basée uniquement sur les angles. Les auteurs résolvent deux sous-cas de ce problème. D’abord, ils considèrent le cas tridimensionnel où chaque robot connaît un certain référentiel global dont l’origine est inconnue, mais dont l’orientation globale est connue. Par exemple, cette contrainte peut être respectée si chaque robot est équipé d’une boussole pointant le nord magnétique. Ainsi, lorsqu’un robot peut en observer un autre grâce à sa caméra, il est capable d’identifier le robot observé et d’estimer la direction vers celui-ci avec un angle en fonction du repère glo-bal. En combinant par triangulation tous les angles, les auteurs ont montré qu’il est possible de localiser tous les robots sauf dans les cas où la quantité d’information disponible rend le problème NP-difficile. Ensuite, les auteurs analysent le cas en deux dimensions où les angles de directions mesurés sont relatifs aux caméras des robots au lieu d’être globaux. L’algorithme de ces chercheurs permet de localiser les robots avec une grande précision si les mesures d’angle sont associées à une étiquette identifiant le robot observé et si la vision des robots n’est pas trop obstruée. Le cas tridimensionnel n’est pas résolu dans cet article.

L’identification d’un robot observé par une caméra lorsqu’une équipe de robot collabore pour se localiser n’est pas une tâche triviale. En fait, identifier un robot en particulier dans un groupe nécessite de l’étiquetage à vue et cela peut devenir un problème de taille en pratique. De plus, les auteursKennedy et al.[2012] ne définissent pas de solution tridimensionnelle basée uniquement sur les angles. Néanmoins, une solution est présentée par Cognetti et al. [2012]. Dans cet article, les chercheurs démontrent qu’il est possible d’utiliser les capteurs inertiels des robots conjointement à des mesures angulaires de direction des robots observées pour localiser ceux-ci. La technique utilisée est de calculer par triangulation toutes les combinaisons de poses possibles des robots et de leur donner un poids exprimant la probabilité de chaque triangulation. Les possibilités sont ensuite filtrées au fil des itérations dans le temps et la solution des auteurs permet de rapidement localiser les robots. Cependant, la solution requiert une puissance de calculs non négligeable, la communication entre les robots représente un goulet d’étranglement, le biais des capteurs inertiels n’est pas pris en compte et les mesures d’angle sont simulées par un système externe.

L’approche des auteurs de l’article mentionné ci-dessus [Cognetti et al.,2012] peut être com-parée à celle deSpletzer and Taylor[2003], publiée quelques années plus tôt. Dans l’article de ces derniers, la localisation est estimée et l’erreur de cette estimation est bornée en temps réel

pour une équipe de robots comportant autant de membres que désiré. La technique des auteurs se base sur les mesures angulaires de direction des robots observés par chaque membre. Celle-ci consiste en la construction d’un polytope convexe (un polyèdre de forme particulière) dont les sommets représentent l’ensemble de toutes les configurations possibles en fonction des mesures des capteurs des robots. Les chercheurs développent un algorithme distribué recherchant de manière itérative la localisation relative optimale selon les contraintes mesurées. En seule-ment quelques itérations, leur approche garantit une borne d’incertitude sur la localisation de chaque robot du groupe.

L’exploration d’un environnement inconnu par une équipe de robots implique de permettre une collaboration améliorant la précision des estimations faites par chaque membre du groupe. Cette précision est principalement déterminée par l’erreur sur les capteurs proprioceptifs lors des déplacements des robots. Il est donc nécessaire de développer une technique pour mini-miser cette dernière erreur. Kurazume et al. [1994] proposent une approche ne nécessitant pas de marqueurs dans l’environnement, comme c’est le cas généralement dans les territoires inaccessibles directement par l’homme, comme les milieux sous-marins, aériens et spatiaux. Les auteurs décrivent deux manières de procéder. La première requiert deux robots ou deux sous-groupes de robots capables de se localiser l’un l’autre. Alors qu’un groupe se déplace, le second reste immobile et agit comme un marqueur permettant de minimiser l’erreur sur le déplacement. La seconde stratégie implique trois robots dont la position est connue au départ. Alors qu’un robot se déplace, les deux autres restent immobiles et agissent comme des caméras stéréo, permettant ainsi de trianguler la position du robot qui a bougé. Bien que cette tech-nique soit théoriquement applicable en trois dimensions, elle est irréalisable pour les robots sous-marins ou aériens à six degrés de liberté parce qu’il est impossible pour eux de rester parfaitement immobile. De surcroît, la connaissance parfaite des positions initiales est souvent irréaliste, comme c’est le cas pour l’exploration extraterrestre.

Dans un article subséquent sur le même problème,Kurazume and Hirose[2000] implémentent leur stratégie d’exploration coopérative en effectuant des essais sur le terrain. De plus, les auteurs proposent une variante à leur méthode qui permet des déplacements plus rapides. Dans cette variante, un robot maître possède un système de localisation complet et deux robots esclaves possèdent des marqueurs facilitant la tâche du robot maître. Pour explorer, il y a alternance des déplacements entre le maître et les esclaves. Dans la première phase du mouvement, le robot maître reste immobile et mesure les déplacements des deux autres robots. Puis, seul le maître se déplace et utilise ses esclaves comme points de repère pour calculer ses propres déplacements. Bien que l’exploration soit ainsi plus rapide, car il y a plus d’un robot qui bouge à la fois, et malgré la grande précision de l’approche, cette nouvelle technique reste inapplicable pour des robots ne pouvant demeurer parfaitement immobiles.

Rekleitis et al. [1997] analysent également le problème de la minimisation de l’erreur sur l’odométrie pendant l’exploration d’un environnement avec une équipe de robot. Les auteurs

développent un algorithme d’exploration basé sur la triangulation qui implique que pour un groupe de robots, un seul d’entre eux doit rester immobile. Celui-ci agit ainsi comme repère pendant que les autres se déplacent dans l’environnement. Selon leur approche, l’environne-ment observé est découpé en triangles ou en losanges dont les sommets sont des zones où un robot doit se rendre à des fins d’exploration. Tour à tour, les robots vont à ces nouveaux points d’observation pendant qu’un des robots du groupe demeure immobile. Les auteurs effectuent une étude complète de la complexité analytique de leur algorithme d’exploration. Encore une fois, puisque les robots volants et les robots sous-marins à six degrés de liberté ne peuvent rester immobiles, cette stratégie ne peut s’appliquer au cas général des robots mobiles à six degrés de liberté, qui peuvent dériver suite aux vents ou aux courants marins.

Dans un second article, Rekleitis et al. [2003a] améliorent leur algorithme pour permettre l’exploration et la cartographie d’un environnement inconnu. En utilisant un sonar et un capteur laser, chaque robot longe les murs d’un environnement en préservant l’observabilité de l’autre. Les robots se déplacent à tour de rôle afin de permettre une localisation relative précise. Le sonar de chaque robot lui permet de suivre correctement les murs alors que le capteur laser permet d’estimer la position des autres agents. La méthode des auteurs permet une exploration optimale en précision des déplacements. Cependant, l’algorithme suppose que l’environnement est un polygone, ce qui rend l’approche inapplicable dans les environnements ouverts.

L’objectif derrière l’exploration d’un environnement inconnu avec une équipe de robots n’est pas toujours l’augmentation de la précision de celle-ci. En effet, il arrive parfois que l’objectif principal soit l’optimisation de la durée de cette exploration.Burgard et al.[2000] présentent dans un article une approche probabiliste permettant la coordination des robots pour accom-plir cette tâche. Pour effectuer cette technique, chaque robot doit bâtir un graphe de prochaines destinations en fonction de sa position actuelle. Afin de déterminer la meilleure d’entre elles, l’utilité de chaque destination possible est évaluée en fonction des déplacements estimés des autres robots de l’équipe, du coût de déplacement et de la visibilité espérée à destination. Les auteurs implémentent l’algorithme et effectuent des simulations dont les résultats démontrent qu’une exploration coordonnée est significativement plus rapide qu’une exploration indépen-dante de plusieurs robots dans un environnement.

Le présent mémoire propose une solution analytique à la localisation relative de deux caméras à six degrés de liberté basée sur des angles uniquement et sur une distance fixe séparant deux des marqueurs visuels.

Un article deDhiman et al.[2013] s’attaque à un problème similaire en suggérant une méthode différente de la nôtre. Les auteurs résolvent une minimisation des moindres carrés permettant de déterminer la pose relative de deux robots grâce à des marqueurs non colinéaires à la caméra de chaque robot. De plus, l’égomotion est employée au lieu de fixer à l’avance la distance entre

deux marqueurs. La stratégie des auteurs permet d’obtenir une précision d’environ 2 cm lorsque les robots sont distancés de 2 m. Enfin, leur approche ne permet pas d’obtenir une solution analytique au problème, ce qui empêche l’emploi de certaines méthodes de filtrage probabiliste comme le filtre étendu de Kalman. Aussi, l’absence de solutions analytiques ne permet pas d’obtenir de relations pour l’impact du bruit des mesures sur la pose estimée. 1.1.5 Filtrage probabiliste

Il est important de constater que les environnements dans lesquels les robots naviguent sont intrinsèquement imprévisibles. En effet, de nombreux facteurs rendent un environnement ro-botisé non déterministe. Les capteurs des robots peuvent être imprécis et retourner des valeurs qui diffèrent de la réalité ou des objets dynamiques peuvent provoquer des mesures différentes de celles attendues par les capteurs. Lorsqu’un robot se déplace sur le sol, ses roues peuvent être de diamètres légèrement différents dus à l’usure et peuvent aussi déraper, changeant ainsi la trajectoire de ses déplacements. Si un robot se déplace dans un fluide comme de l’air ou de l’eau, des courants imprévisibles peuvent le faire bouger celui-ci de manière aléatoire. Selon le livre Probabilistic Robotics [Thrun et al., 2006], tous les modèles internes du monde sont des approximations. Afin de tenir compte des aléas de l’environnement, des méthodes de calculs basés sur la théorie probabiliste sont développées. Ces méthodes probabilistes permettent de gérer les approximations plus efficacement. Ce faisant, ces méthodes surpassent les techniques déterministes dans de nombreuses applications du monde réel en manipulant des distributions de probabilités sur un ensemble d’information.

Dans le livre de Thrun et al. [2006], de nombreuses techniques de filtrage probabilistes sont présentées en détail. L’une des techniques principales est le filtre de Kalman. Ce filtre, dit gaussien, suppose un système linéaire gaussien, c.-à-d. que les mouvements du robot et les capteurs utilisés pour mesurer la pose de celui-ci sont basés sur des fonctions linéaires. Le filtre de Kalman est constitué de deux étapes principales. Dans la première, une estimation de l’état courant est effectuée selon la commande envoyée pour déplacer le robot, et les erreurs sur le déplacement sont intégrées aux estimations. À partir de cette estimation de l’état cou-rant, une estimation de la mesure actuelle la plus probable est calculée ainsi que l’incertitude sur cette prédiction. Dans la seconde, les observations de l’environnement sont utilisées pour corriger l’estimation de la pose actuelle du robot ainsi que l’incertitude sur cette estimation. De nombreuses variantes du filtre de Kalman ont été développées afin d’étendre son champs d’application.

Parmi ses améliorations les plus connues se trouve le filtre étendu de Kalman (Extended Kal-man Filter, ou EKF ). Ce filtre ne considère plus comme linéaires les transitions d’états ni les mesures puisque c’est rarement le cas en situation réelle. Le filtre EKF effectue la prédiction de l’état courant grâce à une fonction non linéaire et il utilise des jacobiennes pour calculer l’incertitude des estimations. La phase de mise à jour des estimations est également non

li-néaire pour représenter plus fidèlement les capteurs utilisés. Une autre variante importante du filtre de Kalman est le filtre de Kalman basé sur la transformation non parfumée (Unscented Kalman Filter, ou UKF ). Au lieu de n’utiliser que la pose du robot la plus probable comme seule mesure de départ, ce filtre effectue une linéarisation déterministe grâce à un processus de régression linéaire avec poids statistiques. En d’autres termes, le filtre utilise des points appelés points sigma à partir de la gaussienne représentant l’incertitude des estimations. Ces points sont utilisés lors des deux phases du filtre de Kalman afin de représenter statistiquement les variations dans l’incertitude sur la pose du robot à localiser. Le filtre UKF, de même que les filtres gaussiens basés sur une technique différente pour calculer des points sigma, est consi-déré comme supérieur à EKF parce qu’il permet d’estimer de manière plus fiable la variation de l’état et de la matrice de covariance représentant l’incertitude des observations. La bonne estimation de ces matrices de covariance est cruciale à l’obtention de bonnes performances des filtres de Kalman.

Cependant, les filtres de Kalman et les variantes introduites ci-dessus ne sont pas itératifs, c.-à-d. qu’ils n’itèrent pas sur l’entièreté des informations précédentes du système. Effectivement, au temps t, les filtres de Kalman non itératifs utilisent seulement l’information aux temps t et t − 1, au lieu d’utiliser la totalité des informations passées. Cela fait en sorte que leur étape de correction par les mesures ne permet pas l’atteinte de la solution optimale. En effet, nous devons poser l’hypothèse Markov, qui suppose que l’état précédent et les mesures courantes de celui-ci sont suffisants pour estimer correctement l’état présent d’un système. En d’autres termes, l’état du système est défini complètement lorsque l’état précédent et les mesures courantes sont connus, car celui-ci est indépendant de toute autre information passée (soit la notion de complete state). De plus, les filtres de Kalman non itératifs considèrent que toutes les erreurs sont exprimées par des fonctions gaussiennes. Ceci est faux en pratique, ce qui force les filtres gaussiens à surestimer l’erreur, les empêchant d’obtenir la solution optimale. En revanche,Dennis Jr and Schnabel [1996] montrent que les filtres probabilistes qui itèrent sur les mesures précédentes convergent vers la solution optimale et donc que ceux-ci sont idéaux pour les systèmes dont les erreurs sont fortement non gaussiennes. En se basant sur cette théorie,Sibley et al.[2006] décrivent une variation itérative des filtres de Kalman basés sur les points sigma. L’objectif des recherches des auteurs est d’améliorer la précision de l’estimation de distance avec les caméras stéréo, en ramenant la précision à l’ordre du subpixel. Dans cet article, les chercheurs montrent la dérivation mathématique menant au filtre de Kalman itératif à points sigmas (ISPKF ). Puis, ils démontrent mathématiquement que ce nouveau filtre ne sous-estime pas l’erreur des mesures et qu’il bénéficie des mêmes forces que le filtre UKF tout en étant itératif. En effectuant diverses expérimentations sur le terrain, les auteurs font la démonstration qu’ISPKF converge plus rapidement et obtient une plus grande précision que les autres filtres gaussiens utilisables en temps réel, tant ceux itératifs que ceux non itératifs. Une alternative populaire aux filtres gaussiens sont les filtres non paramétriques, dont l’un

d’eux est le filtre à particule. L’idée maîtresse derrière ce filtre est de représenter l’estimation de la pose d’un agent par des échantillons, appelés particules. Ces particules sont créées à partir de la position précédente estimée de l’agent et sont fonction de la distribution des différentes incertitudes de l’environnement. L’utilisation des particules permet de représenter des distributions multimodales, c’est à dire des distributions qui présentent plus d’une valeur maximale, mais également toutes les distributions non linéaires. En appliquant un poids à ces particules pour mesurer la probabilité de véracité de la particule, le filtre permet de converger vers une estimation de la pose réelle de l’agent dans l’environnement. Le filtre de Monte-Carlo est une variante du filtre à particule qui permet d’être robuste à la divergence des particules en générant continuellement de nouvelles particules aléatoirement dans l’environnement. Ainsi, ce filtre permet de trouver la position d’un robot dans un environnement sans connaître sa position initiale (soit le problème de localisation générale), et il permet également de retrouver un robot qui est perdu ou téléporté à un autre endroit sans que le filtre en soit informé (soit le problème du kidnapping).

Les méthodes probabilistes ont notamment été appliquées par Rekleitis et al.[2003b] au pro-blème d’exploration avec une paire de robots. Les auteurs proposent un algorithme de naviga-tion pour deux robots permettant de minimiser les erreurs d’odométrie. Selon leur approche, chaque robot possède un sonar pour longer les murs de l’environnement et un capteur laser pour estimer la distance le séparant du robot opposé. En utilisant un filtre à particules qui combine les données d’odométrie avec les mesures de distances des capteurs laser, les auteurs sont en mesure de modéliser la pose des robots et les incertitudes des estimations sur ces poses. Grâce à cette approche, les robots sont localisés en temps réel et peuvent explorer et cartographier l’environnement avec une grande précision.

Un problème avec le filtre de Monte-Carlo utilisé pour faire de la localisation de robots est que lorsque les capteurs sont précis, il peut arriver que ce filtre ne parvienne pas à converger vers la pose du robot. En effet, la première fois qu’un objet à traquer est observé, si aucune des particules échantillonnées n’est assez près de la position mesurée de l’objet, le filtre élimine toutes les particules susceptibles de définir celui-ci. Pour pallier à cette difficulté, Thrun et al.

[2001] suggèrent une amélioration significative au filtre de Monte-Carlo pour la localisation. L’idée des auteurs est de développer la forme duale du filtre de Monte-Carlo en inversant le processus de génération de particules et d’estimation du poids des particules créées : au lieu de générer les particules à partir de l’état précédent du système pour ensuite les évaluer en fonction des observations récentes, les particules sont générées d’après les observations et sont évaluées en fonction de l’état précédent du système. Bien que ce dual ne soit performant que lorsque les capteurs effectuant les mesures sont très précis, il est possible de créer un filtre combinant les approches du filtre de Monte-Carlo avec sa forme duale pour la génération des particules. Les auteurs montrent que ce filtre, le filtre de localisation par Monte-Carlo mixte (en anglais Mixture-MCL), produit des résultats supérieurs aux deux algorithmes l’ayant enfanté.

De plus, Mixture-MCL requiert une moins grande charge de traitement et est plus performant que ces prédécesseurs au problème du robot perdu ou téléporté. La principale difficulté avec l’implémentation de ce filtre est que pour certains capteurs, il peut être complexe de générer des particules selon la forme duale de Monte-Carlo, car la fonction de capteur peut être arbitrairement complexe à inverser.

Pour les équipes composées d’un grand nombre de membres, il n’est pas toujours possible de centraliser les calculs de la localisation relative. En effet, cette centralisation nécessite une com-munication entre tous les robots. De façon similaire, une majorité des algorithmes distribués de localisation font l’hypothèse que tout le réseau de membres est capable de communiquer parfaitement. Cependant, dans des environnements où la communication est limitée ou dif-ficile à établir, comme dans l’espace ou sur de longues distances, ces algorithmes s’avèrent inefficaces. Leung et al.[2010] décrivent un algorithme distribué qui individualise les calculs de localisation relative de tous les membres. La méthode des auteurs permet à chaque robot d’estimer la localisation des autres robots et, lorsque celui-ci en rencontre un autre et que la communication est établie, l’information est partagée afin d’améliorer les estimations. Cette technique n’oblige pas de connaître à l’avance le nombre total de robots dans l’équipe. De surcroît, l’utilisation de la mémoire sur chaque robot est limitée grâce à l’utilisation de points de contrôles basés sur l’assomption de Markov telle qu’expliquée notamment dans le livre deThrun et al.[2006].

Lorsque plusieurs robots doivent se localiser entre eux dans un environnement où la commu-nication est limitée, une stratégie collaborative peut être employée afin que deux robots qui parviennent à communiquer entre eux puissent partager leurs connaissances sur la position des autres.Prorok et al. [2012] considèrent ce problème lorsque les robots ont de la difficulté à communiquer et à se repérer dans l’environnement. Les auteurs supposent que les robots ne peuvent échanger d’information entre eux que lorsqu’ils sont mutuellement observables, et que la quantité d’information qui peut être communiquée est limitée. L’algorithme des auteurs emploie un filtre de Monte-Carlo pour chaque robot. L’évaluation des particules générées dans chaque filtre est basée sur l’observation des autres robots dans l’équipe. Lorsque deux robots peuvent communiquer, ceux-ci échangent des particules selon une technique de regroupement de particules de faible complexité. Bien que l’algorithme soit capable de fonctionner pour un grand nombre de robots, l’observation d’autres robots n’est pas anonyme et une source extérieure est utilisée afin de rendre globaux les angles d’observation.

La localisation d’un groupe d’agents implique souvent une forme de centralisation qui permet d’étiqueter physiquement ceux-ci afin de permettre à un seul agent de déterminer l’identité des agents observés. Ces systèmes souffrent d’une perte d’autonomie puisque les agents deviennent dépendants de cette centralisation afin de se localiser dans un environnement. Franchi et al.

[2010] présentent une solution probabiliste à ce problème. Dans leur article, les chercheurs expliquent le développement d’un filtre à particules pour estimer directement la fonction de