Impact de l'intervalle d'échantillonnage sur les tests d'efficience : application au marché français des actions

HAL Id: hal-01526523

https://hal.archives-ouvertes.fr/hal-01526523

Submitted on 23 May 2017

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Impact de l’intervalle d’échantillonnage sur les tests

d’efficience : application au marché français des actions

Hervé Alexandre, Kamil Cem Ertur

To cite this version:

Hervé Alexandre, Kamil Cem Ertur. Impact de l’intervalle d’échantillonnage sur les tests d’efficience : application au marché français des actions. [Rapport de recherche] Laboratoire d’analyse et de tech-niques économiques(LATEC). 1994, 25 p., tableaux, bibliographie. �hal-01526523�

LABORATOIRE D'ANALYSE

ET DE TECHNIQUES ÉCONOMIQUES

UMR 5601 CNRS

DOCUMENT DE TRAVAIL

�I

I

'1

Pôle d'Economie et de Gestion

UNIVERSITE

DE BOURGOGNE

2, boulevard Gabriel - 21000 DIJON - Tél. 03 80 3954 30 - Fax 03 80 39 54 43

n° 9316

IMPACT DE L'INTERVALLE D'ECHANTILLONNAGE SUR LES TESTS D'EFFICIENCE : APPLICATION

AU MARCHE FRANÇAIS DES ACTIONS

Hervé ALEXANDRE * - Kamil Cem ERTUR **

Janvier 1994

* LATEC, Université de Bourgogne

** LA TEC, Université de Bourgogne et Université de Neuchâtel

Une première version de cet article a été présentée au XXIXème colloque de VAssociation d'Econometrie Appliquée, les 14 et 15 octobre 1993 à Luxembourg.

Les auteurs remercient vivement M.C. Pichery, Professeur à l'Université de Bourgogne et M. Dubois, Professeur à l'Université de Neuchâtel, pour leurs nombreux commentaires. Les auteurs sont seuls responsables des insuffisances et erreurs qui pourraient subsister dans

I m p a c t de l'intervalle d'échantillonnage s u r les tests d'efficience : a p p l i c a t i o n a u m a r c h é f r a n ç a i s des a c t i o n s .

Hervé ALEXANDRE Latec, Université de Bourgogne

Kamil Cem ERTUR

Latec, Université de Bourgogne et Université de Neuchâtel

Janvier 1994

Résumé :

L'efficience des marchés financiers est un des thèmes les plus débattus de la recherche en finance. La formalisation de ce concept est réalisée à travers le modèle de la marche au hasard. De nombreux tests ont été développés pour valider l'hypothèse selon laquelle l'innovation est identiquement et indépendamment distribuée. Les résultats des travaux empiriques sont loin d'être unanimes ; l'acceptation de l'hypothèse de marche au hasard n'est pas systématique et dépend trop des caractéristiques de l'échantillon. Cette constatation nous conduit à étudier l'impact de l'intervalle d'échantillonnage sur les résultats en distinguant deux méthodologies distinctes de tests : les tests fondés sur la détection de la racine unitaire (DICKEY et FULLER 1979, 1981) et les tests fondés sur le ratio de variance (LO et MACKINLAY 1988). La question que nous nous posons est donc la suivante : le rejet ou l'acceptation de l'hypothèse nulle de marche au hasard est-il lié à l'intervalle d'échantillonnage et/ou à la méthodologie de test ?

Mots-clés

Efficience, tests de racine unitaire, tests de ratio de variance Abstract :

Efficiency of financial markets is one of the most studied subject in theoretical finance. Formalization of this idea is realised by the random walk model. Numerous tests have been developped to validate the hypothesis of identically and independantly distributed innovations. But the results of empirical works are not unanimous ; the acceptation of the random walk is not systematic and depend too much on sample features. This constatation leads us to study the impact of the sample frequency on empirical results by distinguishing two different methodologies of tests : the first one is based on unit root (DICKEY et FULLER 1979, 1981) and the other one on variance ratio (LO et MACKINLAY 1988). The question is the following : rejection or acceptation of the null hypothesis of random walk depend on the sample frequency and/or on the méthodologie of test ?

Keywords

Introduction

L'efficience des marchés financiers pose le problème de l'intégration de l'information dans les prix qui sont alors considérés comme des signaux non biaises reflétant cette information. FAMA (1970) définit un marché efficient comme un marché sur lequel les prix reflètent simultanément et complètement toute l'information disponible et pertinente : le meilleur prédicteur du cours de demain est le cours d'aujourd'hui. Cette définition suppose la nullité des coûts d'information et de transactions. Le processus spécifiant une hypothèse testable de cette version de l'efficience est la marche au hasard sur le logarithme des prix. Les taux de rentabilité sont alors identiquement et indépendamment distribués d'espérance mathématique nulle et de variance constante. Soit Pt le prix d'un actif financier au temps t et soit yt = \nPt> le processus

engendrant le log du prix s'écrit :

yt^P

~u.d

(o

,o£) (1)

JENSEN (1978) propose une autre définition de l'efficience : un marché est efficient si les prix reflètent toute l'information dont le coût d'acquisition est couvert par le bénéfice qu'un investisseur peut en retirer en l'intégrant dans sa stratégie. FAMA (1991) juge cette définition moins restrictive et économiquement plus vraisemblable que celle qu'il avait donné en 1970 car les coûts d'information et de transactions ne peuvent être considérés comme nuls. Les variations successives de prix peuvent alors être faiblement dépendantes et le processus de marche au hasard ne décrit plus les prix. Autrement dit, les hypothèses sur les erreurs ut peuvent être élargies sans

pour autant qu'on sorte du cadre de l'efficience.

De nombreux tests ont été développés pour valider l'hypothèse d'absence de corrélation des erreurs dans le modèle (1) en accord avec la définition restrictive de l'efficience (FAMA, 1970). Les résultats des travaux empiriques sont cependant loin d'être unanimes ; l'acceptation de l'hypothèse de marche au hasard n'est pas systématique et dépend des caractéristiques de l'échantillon. On est ainsi confronté à des conclusions divergentes en ce qui concerne l'efficience selon la taille de l'échantillon, l'intervalle d'échantillonnage et la provenance géographique ou temporelle des données. Pour tenter d'apporter une réponse à ce problème qui nuit à la généralité des conclusions, nous étudierons de manière empirique l'impact de l'intervalle d'échantillonnage sur les résultats des tests de marche au hasard fondés sur deux méthodologies distinctes : le test de la racine unitaire de DICKEY et FULLER (1979, 1981) et sa généralisation par PHILLIPS et

PERRON (1988) d'une part et d'autre part le test du ratio de variance de LO et MACKINLAY (1988) et sa généralisation par CHOW et DENNING (1993).

La méthodologie de DICKEY et FULLER (1979) repose sur le test de l'hypothèse nulle suivant laquelle le coefficient p dans le modèle (1) est égal à l'unité, en postulant que le terme

d'erreur

u

/./.d.(o

,o^)

de DICKEY et FULLER "augmenté" ou ADF (DICKEY et FULLER, 1981), ou encore de structure autorégressive moyenne mobile (SAID et DICKEY, 1984). Cette procédure nous permet de tester, outre la racine unitaire, l'hypothèse d'absence d'autocorrélation des résidus ; elle est donc plus appropriée que la procédure de test DF.

PHILLIPS (1987) ainsi que PHILLIPS et PERRON (1988) (PP) ont ensuite proposé une extension imposant des hypothèses très peu restrictives sur les erreurs. Elles peuvent être faiblement dépendantes temporellement et non identiquement distribuées. L'idée sous-jacente est l'indépendance asymptotique : des erreurs récentes peuvent être dépendantes, mais des erreurs très distantes l'une de l'autre dans le temps sont indépendantes. Soulignons le lien de cette procédure de test avec la définition moins restrictive de l'efficience de JENSEN (1978). Ce cadre d'analyse permet entre autres une modélisation ARCH des erreurs (ENGLE, 1982), et donc une représentation du processus selon le schéma de la Quasi Marche Aléatoire (ALEXANDRE, 1992), sous certaines conditions de régularités.

La méthodologie de LO et MACKINLAY (1988) repose quant à elle sur le fait que si une variable suit une marche au hasard, la variance des différences de cette variable doit être une fonction linéaire de la période retenue pour calculer ces différences, en d'autres termes, la variance d e c e s d i f f é r e n c e s T è m e doit être égale à 1 fois la variance des différences p r e m i è r e s (LOMAC1). Par exemple, la variance des taux de rentabilité mensuels (différences logarithmiques des cours corrigés des dividendes et des modifications de capital) doit être égale à quatre fois la variance des taux de rentabilité hebdomadaires. Ce test est ensuite étendu (LOMAC2) au cas où les erreurs sont hétéroscédastiques. CHOW et DENNING (1993) (CD1 et CD2) notent qu'il s'agit en fait d'un test joint, puisque cette propriété de la marche au hasard est vraie quel que soit T et proposent une modification de la procédure de test. Si l'on ne tient pas compte de la nature jointe du test de ratio de variance, on est conduit à rejeter trop souvent à tort l'hypothèse nulle de la marche au hasard ; la probabilité de rejeter l'hypothèse nulle est supérieure au seuil nominal de

test. L'existence de ce biais remet en cause certains résultats empiriques obtenus par LO et MACKINLAY.

Notre problématique est double :

- d'une part, nous allons comparer les résultats obtenus à partir des tests fondés sur les deux méthodologies décrites précédemment et étudier le comportement des tests dès lors que l'intervalle d'échantillonnage augmente. Autrement dit, le rejet ou l'acceptation de l'hypothèse nulle de marche au hasard est-il lié à la méthodologie de test et/ou à l'intervalle d'échantillonnage ?

- d'autre part, nous allons comparer les résultats des tests suivant la définition de l'efficience à laquelle ils font référence : définition restrictive de FAMA pour ADF et LOMAC1/CD1, ou définition moins restrictive de JENSEN pour PP et LOMAC2/CD2.

En théorie, le rejet de l'hypothèse d'efficience sur les données quotidiennes devrait conduire à un rejet global. En effet, si l'information n'est pas intégrée au bout d'une journée cela suffit à rejeter l'hypothèse d'efficience même si les tests l'accrédite à plus longue échéance. Simplement le délai d'ajustement du prix à l'information n'est pas nul et, s'il n'y paraît rien à l'échéance de cinq ou vingt séances, cela signifie que l'intégration totale de l'information se fait bien mais trop lentement pour que l'on puisse parler d'efficience du marché. Le cas inverse serait surprenant car on conçoit assez difficilement qu'un marché soit efficient quotidiennement et non efficient pour des intervalles d'échantillonnage plus importants. Le phénomène de "mean reversion" décrit par SUMMERS (1986) et FAMA et FRENCH (1988) n'est perceptible qu'à des horizons de quatre à cinq années. Il ne pourrait donc pas justifier un tel comportement des tests.

Nous présenterons les différents tests, avant de les appliquer à dix actions françaises du CAC 40. Les cours sont extraits de la banque de données AFFI-SBF. L'intérêt d'utiliser des données quotidiennes est de vérifier si les résultats issus d'études empiriques réalisées à partir de données mensuelles sur indices (FONTAINE, 1990a et 1990b) sont transposables. FONTAINE, en effet, applique chacune de ces méthodologies sur des indices boursiers internationaux et conclut à l'impossibilité de rejeter l'hypothèse nulle de marche au hasard. Nous concluerons ensuite sur l'effet de l'intervalle d'échantillonnage et l'influence de la méthodologie de test sur le résultat des tests de marche au hasard, suivant la définition de l'efficience adoptée.

1. Procédures de test de la racine unitaire1

1.1 Tests de DICKEY et FULLER (1979) (DF)

D é f i n i s s o n s l e s estimateurs des M C O et les statistiques t associées a u x c o e f f i c i e n t s estimés sous l e s hypothèses nulles correspondantes dans c h a c u n des modèles ( 1 ) , ( 2 ) et ( 3 ) lorsque

p < 1 p o u r u n é c h a n t i l l o n d e taille f i n i e T-I :

M o d è l e ( 1 )

y

+u

u

~U

.d.(o

,c%)

M o d è l e (2)

y

= c+py

_

u

t

M o d è l e (3) yt = c + bt + pyt^ + w, ( 4 )

S o u s l ' h y p o t h è s e n u l l e d e l a racine unitaire, les modèles ( 1 ) et ( 2 ) sont des processus d e m a r c h e a u h a s a r d sans d é r i v e , tandis que l e modèle ( 3 ) est u n processus d e m a r c h e a u hasard a v e c d é r i v e .

S o i e n t p * , p e t p l e s estimateurs des M C O d e p d a n s l e s m o d è l e s ( 1 ) , ( 2 ) et ( 3 ) r e s p e c t i v e m e n t . D I C K E Y et F U L L E R proposent des tests i n d i v i d u e l s fondés sur les estimateurs standardisés : r ( p * - l ) , T ( p - l ) et r ( p - l ) e t les statistiques / usuelles d u test d e l ' h y p o t h è s e n u l l e p = 1 : f . , et tp dans les régressions ( 1 ) , ( 2 ) et ( 3 ) respectivement. M a i s i l s proposent

é g a l e m e n t p o u r tester les hypothèses nulles jointes c = 0 et p = 1 dans l e m o d è l e ( 2 ) , c = b = 0 et p = 1 a i n s i q u e b = 0 e t p = 1 dans l e modèle ( 3 ) , d'utiliser les statistiques F u s u e l l e s , notées r e s p e c t i v e m e n t <ï>j, <J>2 et <ï>3.

S o u s l ' h y p o t h è s e n u l l e p = 1 , l'estimateur des M C O de p dans l e s m o d è l e s ( 1 ) , ( 2 ) et ( 3 ) est c o n v e r g e n t . I l c o n v e r g e m ê m e plus v i t e vers sa vraie v a l e u r lorsque p = 1 q u e lorsque p < 1 ( F U L L E R 1 9 7 6 , p . 3 6 9 ) , p a r c o n s é q u e n t l e facteur de standardisation r e q u i s p o u r obtenir l a distribution asymptotique d e c e t estimateur est alors T au l i e u d e T112. Toutefois les estimateurs des M C O d e p n e s u i v e n t p l u s asymptotiquement des lois N o r m a l e s et l e s statistiques t e t O n e s u i v e n t p l u s d e s l o i s d e S t u d e n t et d e Fisher-Snedecor. L e s procédures d ' i n f é r e n c e classiques n e permettent d o n c pas d e tester l'hypothèse nulle p = 1 .

C e p e n d a n t D I C K E Y et F U L L E R ont d é r i v é les v a l e u r s critiques d e c e s distributions asymptotiques n o n standard, m a i s aussi des distributions empiriques dans des échantillons d e taille f i n i e d e toutes c e s statistiques p a r des méthodes d e simulation ( F U L L E R , 1976 ; D I C K E Y et F U L L E R , 1981). C e s distributions dépendent d u modèle considéré, c'est-à-dire d e l a présence o u n o n d ' u n t e r m e constant et d ' u n e tendance linéaire déterministe.

1 Pour une présentation plus détaillée des ces procédures de test, le lecteur pourra se référer à ERTUR (1992a)

Nous pouvons également fonder le test DF sur l'estimation par les MCO des trois

modèles obtenus en soustrayant

Y

_

à chaque membre des modèles précédents : cette dernière

formulation a le mérite de faciliter la mise en œuvre de la procédure de test DF puisque les

statistiques

T

sont alors directement fournies par le programme des MCO.

1.2 TESTS DE DICKEY ET FULLER "AUGMENTÉS" (ADF) (1981)

Il est clair que la procédure de test DF n'est applicable que sous l'hypothèse suivant

laquelle les erreurs

U

sont i.i.d. Il va sans dire que cette hypothèse est trop restrictive et ad hoc ; il

faudrait la tester dans les travaux empiriques. Toutefois DICKEY et FULLER (1981) étendent

cette procédure de test à des séries chronologiques admettant une représentation purement

autorégressive d'ordre p, il s'agit alors des tests ADF ou tests de DICKEY et FULLER

"augmentés". Cette procédure de test est fondée sur l'estimation par les MCO, sous l'hypothèse

alternative, de trois modèles autorégressifs d'ordre p obtenus en soustrayant

Y

aux deux

membres des modèles (1), (2) et (3) et en ajoutant p-7 retards en différences premières :

P

Modèle (4)

AY

= JTY

_

+ ^FOT-J+I + U

U

~

/./.d.(0

,(7*)

(5)

J=2

P

Modèle (5)

AY

c

+

NY

_

+ £ <T>JAY

_

+ U

(6)

P

Modèle (6)

AY

c

BT

7TY

^

U

Le test de l'hypothèse nulle de la racine unitaire n'est autre que le test de significativité

du coefficient

N

que l'on effectue à l'aide des statistiques

T

usuelles

T^*, T^

et

T

dont les

distributions asymptotiques sont identiques, sous l'hypothèse nulle p = 7, à celles des statistiques

T +, TP

et

TP.

Les statistiques 0

<î>

^ 3

définies sur les modèles (5) et (6) suivent les mêmes

distributions asymptotiques que celles définies sur les modèles (2) et (3) et peuvent donc

également être utilisées pour tester les hypothèses nulles jointes correspondantes sous réserves de

quelques modifications mineures concernant les degrés de liberté (DICKEY et FULLER, 1981).

On peut noter par ailleurs que les coefficients estimés et^y des retards en différences

premières inclus dans les régressions suivent asymptotiquement une loi Normale sous les

hypothèses nulle et alternative et peuvent donc faire l'objet de tests standard de significativité

permettant d'évaluer l'ordre p du processus autorégressif. Un test de l'hypothèse nulle jointe

suivant laquelle les coefficients des retards en différences premières sont nulles est donc réalisable

par les procédures d'inférence traditionnelles (test F standard). Or le non rejet de cette hypothèse

nulle signifie que p = 0 dans (5), (6) ou (7) et par conséquent que les erreurs sont bien i.i.d. On retrouve alors les modèles DF avec, en plus, la possibilité de tester l'hypothèse sur les erreurs.

1.3 Tests de PHILLIPS (1987) et PHILLIPS et PERRON (1988) (PP)

PHILLIPS (1987) et PHILLIPS et PERRON (1988) adoptent une méthodologie radicalement différente. Leur approche est fondée sur une correction non paramétrique pour tenir compte de la structure d'autocorrélation et/ou d'hétéroscédasticité des résidus. Les hypothèses faites sur les erreurs ut dues à HERRNDORF (1984) sont ainsi beaucoup moins restrictives. Elles

peuvent être faiblement dépendantes temporellement et distribuées de manière hétérogène, c'est-à-dire non identiquement distribuées, mais asymptotiquement indépendantes. Leurs résultats asymptotiques sont fondées sur la théorie de la convergence faible fonctionnelle (BILLINGSLEY, 1968) et permettent de généraliser dans un cadre unifié les résultats antérieurs concernant la marche au hasard et des processus ARIMA plus généraux contenant une racine unitaire. Ce cadre d'analyse permet une modélisation ARCH ou GARCH des erreurs (ENGLE, 1982 ; BOLLERSLEV, 1986) tant que ces processus ne sont pas dégénérés ou quasi-intégrés2 (KIM et SCHMIDT, 1993 ; HECQ et URBAIN, 1993).

Lorsque les erreurs ne sont pas i.i.d., PHILLIPS et PERRON (1988) montrent que les distributions asymptotiques des statistiques de la procédure de test DF dépendent du rapport

T

<J2/crl où la variance des résidus est c\ = LimT^Y E[U}\ et la variance de long terme est

T a2 = l i m T- 1 YE ( S Î ) avec ST = Y u,.

Un estimateur convergent de a\ est simplement la variance estimée des résidus dans le modèle alternatif considéré ( o f ,<x„ oucr^). De nombreux estimateurs convergents de la variance de long terme sont envisageables, mais PHILLIPS et PERRON optent pour celui proposé par NEWEY et WEST (1987), défini de la manière suivante :

T i T

°TI

=

r

X " ,

+

K,-I

(8)

t=\ T=l f=T+l

où co(rj) = 1 - [ r / ( / +1)] et les ut sont les résidus du modèle alternatif estimé ( u*,ût ou iït). Les

pondérations affectées aux autocovariances estimées assurent que la variance estimée est

2 Dans l'équation de la variance conditionnelle ht - a0 + cc^^ + Pxht_x, cela implique a0 > 0 et <xx + p{ < 1 avec

positive. Gji a une interprétation naturelle pour ut stationnaires : il s'agit de 2Kfois l'estimateur de

la densité spectrale de o2 pour la fréquence zéro où on a utilisé une fenêtre spectrale triangulaire. Nous utiliserons une fenêtre de PARZEN dans notre étude empirique. PHILLIPS et PERRON suggèrent que le paramètre de troncature / soit une fonction croissante de la taille de l'échantillon [en fait / = o(Tlf4)] mais ne donnent aucune indication précise sur la valeur qu'il faut lui attribuer

en pratique. Une procédure fréquemment utilisée est alors de contrôler la sensibilité des résultats des tests lorsqu'on fait varier ce paramètre.

Les statistiques de PHILLIPS et PERRON, notées Z(...) (PERRON, 1988) sont des transformations des statistiques initiales de la procédure de test DF et nous permettent d'envisager des erreurs autocorrélées et distribuées de manière hétérogène. Les écarts types estimés o£, au, <ïu

intervenant dans les statistiques t sont maintenant remplacés par les écarts types estimés généralisés a^, a-n, c?n. Chaque statistique transformée contient, en outre, un terme de correction additif dont la taille dépend de la différence entre les variances estimées correspondantes

- o5*, OJI - crâ, ou Gj[ - Ou* Ces transformations sont conçues de manière à éliminer asymptotiquement les effets de l'autocorrélation et de la distribution hétérogène des erreurs.

Une caractéristique particulièrement intéressante des nouvelles statistiques de tests est que leur distribution asymptotique est identique à celles dérivées par DICKEY et FULLER sous l'hypothèse d'erreurs i.i.d.. Ceci implique que la procédure de test de PHILLIPS et PERRON peut être utilisée en se référant aux valeurs critiques asymptotiques tabulées par DICKEY et FULLER même si elle permet de spécifier de manière beaucoup plus générale les séries chronologiques étudiées.

L'avantage principal de l'approche de PHILLIPS et PERRON est que, même si on peut envisager une grande variété de modèles susceptibles d'engendrer les données, le calcul des statistiques transformées (PERRON, 1988, tableau 1, p.308-309) requiert seulement :

• l'estimation par les MCO d'un modèle autorégressif du premier ordre (correspondant à l'un des modèles de la procédure de test DF) et le calcul des statistiques DF associées.

• l'estimation d'un facteur de correction fondé sur la structure des résidus de cette régression.

Toutes ces procédures se heurtent cependant à une limitation importante : elles postulent que la composante déterministe de la série considérée suit une tendance linéaire. Or la mauvaise spécification, linéaire en l'occurrence, de la composante déterministe peut nous conduire à ne pas

rejeter l'hypothèse nulle de la racine unitaire et ceci à tort. Ces tests sont donc biaises en faveur de l'hypothèse nulle de la racine unitaire en cas de mauvaise spécification de la composante déterministe (ERTUR, 1992b).

1.4 STRATÉGIE DE TEST

Pour que toutes ces procédures de test soient réellement opérationnelles sur le plan empirique, il faut élaborer une stratégie de test indiquant le choix du modèle de régression et des statistiques appropriées, étant donné les règles de décision et leurs implications et la puissance des différents tests constituant ces procédures. Il est possible de distinguer trois approches dans la littérature sur les tests de la racine unitaire : celle de DICKEY, BELL et MILLER (1986), celle de PERRON (1988) et celle de HENIN et JOBERT (1990). Nous avons évalué leur limite et tenté de proposer une approche générale unifiée (ERTUR, 1992a, p. 159-173). Dans le cadre d'analyse dans lequel nous nous situons, la stratégie développée par PERRON (1988) nous paraît appropriée ; elle permet d'éviter des erreurs d'interprétation telles que celles faites par KLEIDON (1986, p.993). Nous présentons une version étendue de cette stratégie qui peut se décomposer en trois étapes.

Etape 1 : nous commençons la procédure de test DF en estimant le modèle (3) et effectuons les tests fondés sur les statistiques TP ou <D3.

• Si nous pouvons rejeter l'hypothèse nulle p = 1 ou l'hypothèse nulle jointe

(c, b, p) = (c, 0 , 1 ) dans le modèle (3), nous pouvons effectuer les tests de significativité

individuelle des paramètres p, c et b par les procédures d'inférence traditionnelles (loi de Student ou asymptotiquement loi Normale).

• Si l'hypothèse nulle p = 0 ne peut être rejetée et si b * 0 Vc, nous avons un modèle de tendance linéaire et bruit blanc centré ; si p = 0, c * 0 et b = 0, on revient au modèle (2) qui se réduit à un processus de bruit blanc non centré et si p = 0, c = 0 et b - 0, on revient au modèle (1) qui se réduit à un processus de bruit blanc centré.

• Si l'hypothèse nulle p = 0 est rejetée, i.e. si p est effectivement différent de zéro et si

b * 0 : la série yt suit un processus stationnaire en écarts à la tendance linéaire déterministe. Si

p * 0, b = 0 et c * 0 : la série yt suit un processus AR(1) avec constante asymptotiquement stationnaire. Si p * 0, b = 0 et c = 0 : la série yt suit un processus AR(1) sans constante

• Si nous ne pouvons pas rejeter l'hypothèse nulle : p = 1 et l'hypothèse nulle jointe : (c, 6, p) = (c, 0,1) dans le modèle (3), il nous faut tester si la dérive c est effectivement non nulle. Nous suggérons à ce propos d'utiliser la statistique $ 2

-• Si nous pouvons rejeter l'hypothèse nulle jointe (c, b, p) = ( 0 , 0 , 1 ) , la série yt suit un

processus de marche au hasard avec dérive, sinon, elle suit un processus de marche au hasard sans dérive.

Toutefois, si nous n'avons pas pu rejeter l'hypothèse nulle p = 1 et l'hypothèse nulle jointe (c, 6, p) = (c, 0,1) dans le modèle (3), ceci peut être dû à la faible puissance des tests fondés sur les statistiques du modèle (3) par rapport aux tests fondés sur les statistiques du modèle (2) lorsque la dérive est nulle. Par conséquent si nous, pouvons accepter l'hypothèse nulle jointe (c, b, p) = (0,0,1), nous suggérons de passer à l'étape 2 avant de conclure.

Etape 2 : nous estimons donc, dans une seconde étape, le modèle (2) et effectuons les tests fondés sur les statistiques tp et Oj.

• Si nous pouvons rejeter l'hypothèse nulle : p = 1 ou l'hypothèse nulle jointe : (c, p) = (0,1) dans le modèle (2), nous pouvons effectuer les tests de significativité individuelle des paramètres p et c par les procédures d'inférence traditionnelles (loi de Student ou asymptotiquement loi Normale).

• Si l'hypothèse nulle p = 0 ne peut être rejetée et si c * 0, le modèle (2) qui se réduit à un processus de bruit blanc non centré et si p = 0, c = 0, on se ramène au modèle (1) qui se réduit à un processus de bruit blanc centré.

• Si l'hypothèse nulle p = 0 est rejetée, Le. si p est effectivement différent de zéro et c * 0 : la série yt suit un processus AR(1) avec constante asymptotiquement stationnaire. Si p ^ 0 et

c = 0 : la série yt suit un processus AR(1) sans constante asymptotiquement stationnaire.

• Si nous ne pouvons pas rejeter l'hypothèse nulle p = 1 et l'hypothèse nulle jointe (c, p) = (0,1) dans le modèle (2) : la série chronologique yt suit un processus de marche au hasard

sans dérive caractérisé par une non stationnarité de nature purement stochastique.

Toutefois, si nous n'avons pas pu rejeter cette hypothèse nulle et l'hypothèse nulle jointe (c, p) = (0,1) dans le modèle (2), ceci peut être dû à la faible puissance des tests fondés sur les statistiques du modèle (2) par rapport aux tests fondés sur les statistiques du modèle (1) lorsque

c = 0. Nous pourrions alors envisager de tester l'hypothèse nulle c = 0 dans le modèle (2) et si

malheureusement l'estimateur de c n'est pas convergent sous l'hypothèse nulle de la racine unitaire. On ne peut passer à l'étape 3 que si on sait a priori que la moyenne de la variable considérée est nulle, par conséquent cette dernière étape est en quelque sorte "déconnectée" des deux étapes précédentes.

Etape 3 : dans le cas où on sait a priori que la moyenne de la variable considérée est nulle, nous estimons le modèle (1) et effectuons les tests fondés sur la statistique tp*.

• Si nous pouvons rejeter l'hypothèse nulle : p = 1 dans le modèle (1), nous pouvons effectuer le test de significativité de p par les procédures d'inférence traditionnelles. Si l'hypothèse nulle p = 0 est acceptée, le modèle (1) se réduit à un processus de bruit blanc centré. Sinon, la série yt suit un processus AR(1) sans constante asymptotiquement stationnaire.

• Si l'hypothèse nulle p = 1 ne peut être rejetée, la série yt suit un processus de marche au

hasard sans dérive.

La critique fondamentale que l'on peut adresser à la stratégie de PERRON (1988) est qu'elle n'est valide que sous le postulat suivant lequel la composante déterministe de la série étudiée admet une spécification linéaire. En effet, si le vrai processus engendrant les données est stationnaire en écarts à une tendance quadratique par exemple, les tests de type t fondés sur une régression n'incluant qu'une tendance linéaire [modèle (3)] seront biaises en faveur de l'hypothèse nulle de la racine unitaire. Le modèle (3) ne permettrait pas de discriminer un processus TS d'un processus DS parce que le régresseur yM contiendrait un terme de tendance inexpliqué t2 qui

dominerait la composante linéaire. La puissance asymptotique de la statistique tp pour tester l'hypothèse nulle p = 1 dans le modèle (3) sans t2 serait nulle (OULIARIS, PARK et PHILLIPS

1989, p. 10). Il se peut parfaitement que nous acceptions l'hypothèse nulle de la racine unitaire à tort dans le modèle (3) et que nous puissions la rejeter sous une spécification quadratique de la tendance en appliquant la procédure de test de OULIARIS, PARK et PHILLIPS. Le postulat de linéarité de la composante déterministe constitue donc une limitation importante de la stratégie de PERRON (ERTUR 1992b).

Il est clair que la stratégie présentée supra s'applique, sous réserve de quelques modifications mineures, à la procédure de test ADF ou à la procédure de test de PHILLIPS et PERRON. Dans le premier cas il suffit de remplacer les modèles (1), (2) et (3) par les modèles "augmentés" (4), (5) et (6); dans le second cas il suffit de fonder les tests sur les statistiques transformées Z(...).

2. TESTS DU RATIO DE VARIANCE

2.1 TESTS DE LO ET MACKINLAY (1988,1989) (LOMAC)

Ce test est fondé sur la propriété suivant laquelle la variance des variations d'une variable suivant une marche au hasard est une fonction linéaire de l'intervalle retenu pour calculer ces variations3.

Soit le processus de marche au hasard avec dérive:

YT = V + YT_X + UT UT~ I.I.D. N(0,AL) (9)

V(ÀTYT)=TV{AYT) (10)

L'hypothèse nulle testée porte sur la distribution des erreurs. C'est l'hypothèse d'une "marche au hasard homoscédastique", notée Hx, dans la terminologie de LO et MACKINLAY.

La statistique du test s'écrit (LOMAC 1) :

(H) Mr(r) =

4

| - 1

&L est l'estimateur centré de la variance des différences premières de ytet (r) est l'estimateur

centré de la variance des différences Tème de YT divisé par r, tandis que JL est l'estimateur de la

moyenne des différences premières.

Notons que Afr(r) est asymptotiquement équivalent à la somme pondérée des r - 1 premiers coefficients d'autocorrélation estimés des différences premières de YT dont les

pondérations décroissent arithmétiquement :

Mr( r ) = | X( T - l ) ^

/=1

(13) Tester l'hypothèse nulle revient en effet à tester la nullité de Mr(r). La distribution asymptotique de Mr(x) sous l'hypothèse nulle est la suivante :

•ZSÎ\ ₍₁₄₎

Le lecteur pourra se référer à LO et MACKINLAY (1998a,1988b) pour une présentation complète de ces tests. 11

ou encore en standardisant :

Z, ( t ) S 71 / 2Mr( T) ( 2( 2 T- l) ( T- l) / 3 T ) "1 / 2 ~N(0,1) (15)

L'hypothèse nulle est rejetée si zj^est supérieur à la valeur tabulée de la loi Normale pour un seuil fixé. Le test est effectué pour différentes valeurs de t ne devant pas excéder T/2 où T est la taille de l'échantillon (LO et MACKINLAY, 1989, p.225).

LO et MACKINLAY (1988) ont ensuite généralisé ce test pour intégrer une éventuelle hétéroscédasticité des erreurs. Les hypothèses sur les erreurs sont donc élargies suivant l'approche de WHITE (1980) et WHITE et DOMOWITZ (1984) mais sont cependant plus restrictives que celles adoptées par PHILLIPS et PERRON (1988) et maintiennent l'absence d'autocorrélation. L'hypothèse nulle est alors l'absence d'autocorrélation, la variance pouvant varier dans le temps. C'est l'hypothèse d'une "marche au hasard hétéroscédastique", notée H2, dans la terminologie de LO et MACKINLAY.

En tenant compte de la correction apportée par FONTAINE (1990a) la statistique utilisée s'écrit (LOMAC2) :

Z

( t )

S

M

{riy{T))~

~ N(0,1) (16)

(2(T-j)* SU) ( 1 7 )

où V ( t ) = £

et 8(j) est l'estimateur de la variance du coefficient d'autocorrélation d'ordre j :

S (;) = * z Z ± L _ ( 1 8 )

X ( ( ^ - A )

)

k=\

La statistique Z2( t) suit asymptotiquement une loi Normale centrée réduite. Le test

s'effectue de la même manière que précédemment. Les simulations en échantillons de taille finie effectuées par LO et MACKINLAY (1989) montrent que ces tests sont aussi puissants que les tests de DICKEY et FULLER contre l'alternative AR(1) stationnaire, mais plus puissants que ces derniers contre les alternatives ARI(1,1) et ARIMA(1,1,1)4.

4 L'alternative A R ( 1 ) stationnaire s'est révélée empiriquement intéressante dans SHILLER (1981) et PERRON et

SHILLER (1985), tandis que l'alternative ARI(1,1) est sugérée par les résultats empiriques de LO et MACKINLAY (1988a). L'alternative ARIMA(1,1,1) est une représentation du modèle de SUMMERS (1986) et FAMA et FRENCH (1988) qui supposent que le log du prix suit un processus qui s'écrit comme la somme d'un AR(1) stationnaire et d'une marche au hasard.

2.2 Tests de CHOW et DENNING (1993) (CD)

CHOW et DENNIG (1993, p.389) notent que l'approche de LO et MACKINLAY est appropriée pour tester un ratio de variance pour une valeur donnée de T, en comparant simplement

la statistique zx(r) et/ou Z2(T) à la valeur critique de la loi normale centrée réduite pour un seuil

fixé. Toutefois, sous l'hypothèse de marche au hasard, les ratios de variance doivent être égaux à l'unité quelque soit la valeur de T. Par conséquent il faut examiner les statistiques zx(r) et/ou

Z2(T) pour plusieurs valeurs de T et ne pas rejeter l'hypothèse nulle si seulement elle n'est pas

rejetée pour toutes les valeurs de T sélectionnées. Nous sommes donc confrontés au problème

statistique de comparaison multiple. Cela nécessite le contrôle du seuil du test, en effet utiliser une valeur critique au seuil nominal de 100<x% pour chaque valeur de % n'est pas approprié, il faut utiliser un seuil global de 100oc%. Ne pas contrôler le seuil du test conduit à rejeter beaucoup trop souvent l'hypothèse nulle alors qu'elle est vraie, le risque de première espèce est supérieure au seuil nominal du test. CHOW et DENNING propose alors la modification suivante des tests de LO et MACKINLAY.

Considérons un ensemble de ratios de variance estimés | Mr( r/) / / = l,2,...,m|

correspondant à un ensemble de valeurs {r,- / / = 1,2,...,m} choisies a priori. Soit T; un entier

naturel supérieur à un et différent de tj pour / * j . Sous l'hypothèse nulle de marche au hasard, on teste un ensemble de sous-hypothèses Hoi :Mr(r/) = 0 pour / = 1,2,...,m., le rejet de toute

hypothèse H0i entraîne le rejet de l'hypothèse nulle de marche au hasard. Notons la valeur absolue maximale des statistiques ^(r,-) et Z2(T,) :

Z*(T) = max IZ ^ TJ Z2(T) = max Iz^T;)! (19)

\<i<m1 1 \<i<m1 1

CHOW et DENNIG (1993, p.390) montrent qm :

Soit

Z

LO et MACKINLAY correspondant à \m ensemble prédéfini de m valeurs

{T,- / i = 1,2,.. .,m}telles que Tx(= 2) < r2 < • • • < rm < T12, où T est la taille de l'échantillon. Les

distributions des vecteurs Zx et Z 2 convergent asymptotiquement vers une distribution Normale

multivariée d'espérance mathématique nulle et de matrice de variance/covariance £lx et Q2

respectivement. L'intervalle de confiance d'au moins 100(l-oc)% pour la statistique maximale z*(r) ou Z2(T) peut être défini de la manière suivante :

Sous Hx : z*x{T)±SMM(a\m\oo) (20)

Sous H2 : z2(r)±5MM(a;m;oo) (21)

où SMM(a\m\<x>) est la valeur critique asymptotique au seuil de a% de la distribution de la valeur absolue maximale de m variables de Student pour <*> degrés de liberté (Studentized Maximum Modulus). L'intervalle de confiance joint d'au moins 100(l-a)% pour un ensemble d'estimations de ratios de variance est (respectivement CD1 et CD2) :

Sous Hx : r ^ M^ T^ l^ T , ^ (22)

Sous H2 : Mr(T¡)±[v(Ti)] SMM(a;m;oo) pour / = 1,2 m (23)

Le seuil d'un test multiple de ratio de variance peut ainsi être contrôlé en comparant simplement les statistiques de LO et MACKINLAY aux valeurs critiques de la distribution SMM. Pour 4 ratios de variance, la valeur critique asymptotique de cette distribution5 au seuil de 5% est de 2,491. CHOW et DENNIG montrent par simulations que la probabilité de rejeter l'hypothèse nulle à tort est supérieure à 6, 3 et 2 fois le seuil nominal pour les tests à 1, 5 et 10% respectivement si on ne suit pas la procédure qu'ils préconisent. Ils soulignent ainsi le biais qui peut résulter dans les travaux empiriques si l'on ne tient pas compte de la nature jointe des tests de ratio de variance. Il semble de plus que ce biais croît avec la taille de l'échantillon (1993, p. 394-396). Compte tenu de la modification qu'ils suggèrent, CHOW et DENNIG montrent aussi par simulation que ces tests sont d'une puissance comparable globalement à celle des tests de DICKEY et FULLER et PHILLIPS et PERRON contre l'alternative AR(1) stationnaire, alors qu'ils sont plus puissants contre les alternatives ARI(1,1) et ARIMA(1,1,1).

3. Résultats empiriques

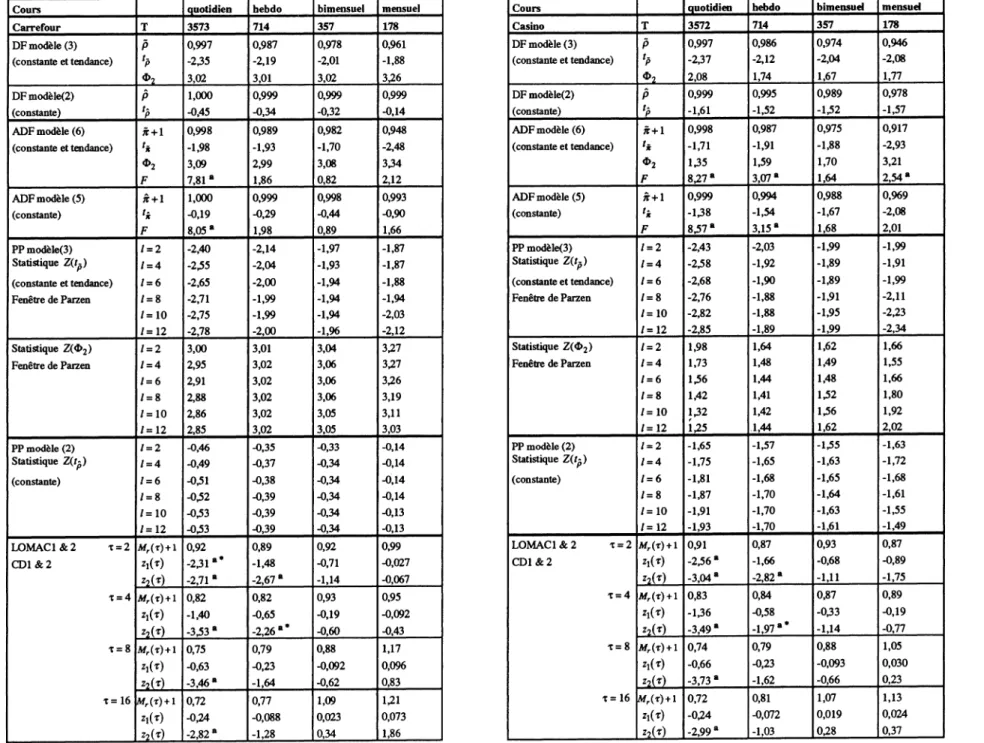
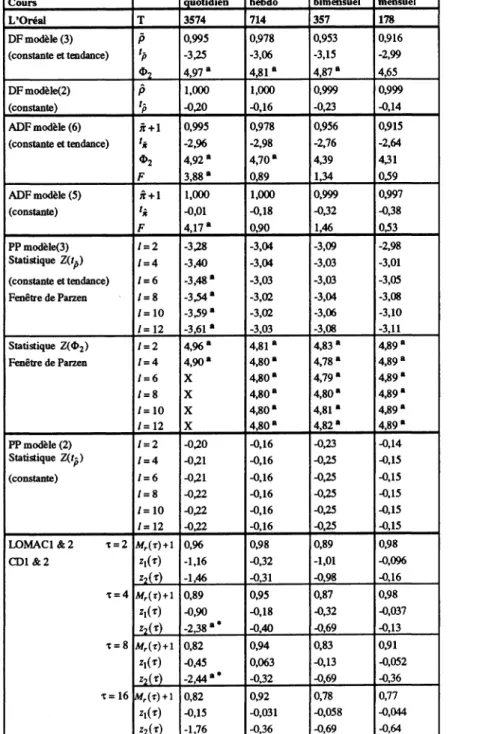
Nous avons analysé les cours et taux de rentabilité nominaux de 10 actions cotées sur le Règlement Mensuel à la Bourse de Paris et présentes dans le CAC40 : Carrefour, Casino, Club Méditerranée, Essilor, Legrand, Lyonnaise des Eaux, L'Oréal, Source Perrier, Peugeot SA, Valéo. Nous avons extrait ces séries de la banque de données AFH-SBF. La période d'étude s'étend du 4 janvier 1977 au 30 juin 1991, soit une taille d'échantillon supérieure à 3500 observations quotidiennes permettant d'exploiter pleinement les propriétés de convergence asymptotique des tests.

Nous avons adopté la stratégie décrite supra pour effectuer les procédures de tests DF, ADF et PP. Pour les tests ADF, nous avons fixé arbitrairement le nombre de retards en différences

5 Les tables des valeurs critiques de la distribution SMM se trouvent dans HAHN et HENDRICKSON (1971) et

supplémentaires inclus dans les régressions "augmentées" à 6 et nous avons effectué un test de l'hypothèse nulle jointe suivant laquelle tous les coefficients associés à ces retards sont nuls en utilisant la statistique F appropriée. Pour les tests PP, nous avons utilisé la fenêtre de Parzen pour l'estimation de la variance de "long terme". Le choix de la fenêtre de retard ne semble pas avoir de conséquence importante sur les résultats des tests (ERTUR 1992a, KDvI et SCHMIDT 1990) et nous avons contrôlé la sensibilité des résultats à la variation du paramètre / avec lmax= 12. Il

s'avère que les résultats sont généralement robustes à toute variation de ce paramètre. Nous avons utilisé la statistique Z2(T) de LO et MACKINLAY pour r = 2,4,8 et 16. Les résultats complets sont présentés dans l'Annexe. Nous présentons une synthèse de ces résultats dans le tableau A.

Nous allons classer les tests sur la base des hypothèses faites sur les erreurs : les tests DF, ADF, LOMAC1 et CD1 supposent l'homoscédasticité, les tests LOMAC2 et CD2 supposent l'hétéroscédasticité, tandis que les tests PP permettent de tenir compte à la fois d'une faible dépendance temporelle et de l'hétéroscédasticité.

La première constatation concernant l'impact de l'intervalle d'échantillonnage sur les résultats des tests est la suivante : il s'avère que les tests DF sont très peu sensibles à cet intervalle et conduisent généralement, au seuil de 5%, à la conclusion suivant laquelle les cours suivent un processus de marche au hasard qu'on considère les séries quotidiennes, hebdomadaires, bimensuelles ou mensuelles. Lyonnaise des Eaux, en données quotidiennes, est l'exception à cette règle. En outre la procédure de test DF n'est pas appropriée car elle postule que les erreurs sont i.i.d., mais ne permet pas de tester cette hypothèse.

Cependant lorsqu'on soumet l'hypothèse d'erreur i.i.d. au test par l'intermédiaire du test joint sur la nullité des coefficients des retards en différences premières dans la procédure ADF, les résultats sont loin d'être aussi unanimes. En effet, l'hypothèse nulle de la racine unitaire ne peut jamais être rejetée, mais les erreurs sont corrélées en données quotidiennes et parfois hebdomadaires comme l'indique la statistique F. Par conséquent l'hypothèse de marche au hasard est rejetée pour les séries quotidiennes dans la totalité des cas et parfois elle est également rejetée pour les séries hebdomadaires (Casino, Peugeot SA), alors qu'elle n'est pas rejetée pour les séries bimensuelles et mensuelles. La statistique O2 indique parfois la présence d'une dérive significativement non nulle (par exemple, l'Oréal pour tout intervalle d'échantillonnage, au seuil de 5%).

DF ADF homoscédasticité LOMAC1 / CD1 homoscédasticité LOMAC2/CD2 hétéroscédasticité PP faible dépendance et hétéroscédasticité Carrefour non rejet V intervalle rejet en quotidien non rejet V intervalle * rejet en quotidien et

hebdo

non rejet V intervalle

Casino non rejet V intervalle rejet en quotidien et hebdo

rejet en quotidien rejet en quotidien et hebdo

non rejet V intervalle

Club Méditerranée non rejet V intervalle rejet en quotidien non rejet V intervalle non rejet V intervalle * non rejet V intervalle Essilor non rejet V intervalle rejet en quotidien non rejet V intervalle non rejet V intervalle * non rejet V intervalle Legrand non rejet V intervalle rejet en quotidien non rejet V intervalle rejet en quotidien rejet en quotidien Lyonnaise des Eaux rejet en quotidien rejet en quotidien et

bimensuel

non rejet V intervalle * rejet en quotidien rejet en quotidien

L'Oréal non rejet V intervalle rejet en quotidien non rejet V intervalle non rejet V intervalle * rejet en quotidien Source Perrier non rejet V intervalle rejet en quotidien non rejet V intervalle rejet en quotidien non rejet V intervalle Peugeot SA non rejet V intervalle rejet en quotidien et

hebdo

non rejet V intervalle rejet en bimensuel et mensuel

non rejet V intervalle

Valéo non rejet V intervalle rejet en quotidien, bimensuel et mensuel

non rejet V intervalle non rejet V intervalle * non rejet V intervalle

T a b l e a u a : Synthèse des résultats

notes : tous les tests sont effectués au seuil de 5%. Intervalle signifie intervalle d'échantillonnage : quotidien, hebdomadaire, bimensuel et mensuel. * indique la détection d'au moins une erreur d'inférence lorsqu'on utilise la valeur critique issue de la Loi Normale (LOMAC1 &2) au lieu de la valeur issue de la distribution SMM (CD1 & 2) et donc le rejet à tort de l'hypothèse nulle au seuil de 5%. Le résultat indiqué est bien sûr celui corrigé des erreurs d'inférence.

Ces résultats sont cohérents avec la plupart des études empiriques utilisant des indices boursiers rencontrées dans la littérature et prouvent l'impact de l'intervalle d'échantillonnage sur les résultats des tests.

L'effet de l'intervalle d'échantillonnage sur le test LOMAC1 est inexistant. Ce test ne permet pas de rejeter l'hypothèse de marche au hasard. On ne constate pas de comportement systématique de la statistique utilisée en fonction du décalage temporel retenu. Mais il se pose un problème pour Casino, Carrefour et Lyonnaise des Eaux pour lesquels on rejette cette hypothèse en données quotidiennes lorsqu'on utilise la valeur critique issue de la Loi Normale. Toutefois si on tient compte de la nature jointe du test comme le préconisent CHOW et DENNING, l'hypothèse nulle n'est rejetée que pour Casino envdonnées quotidiennes en utilisant la valeur

critique issue de la Loi SMM. On détecte donc deux erreurs d'inférence.

Pour ce qui est du test LOMAC2, on constate qu'on ne peut pas rejeter l'hypothèse nulle de la marche au hasard en données hebdomadaires, bimensuelles et mensuelles (excepté Peugeot SA). Par contre en données quotidiennes, l'hypothèse nulle est rejetée dans la majorité des cas sauf pour Valéo et Peugeot SA. La procédure de CHOW et DENNING nous conduit à rejeter moins souvent l'hypothèse nulle en données quotidiennes : on ne la rejette plus pour Club Méditerranée, Essilor et L'Oréal. Là aussi des erreurs d'inférence sont donc mises à jour par cette procédure.

Dans le cas des tests PP, l'hypothèse nulle n'est généralement pas rejetée, les exceptions, au seuil de 5%, sont au nombre de trois : L'Oréal, Legrand et Lyonnaise des Eaux, pour lesquels on rejette l'hypothèse de la racine unitaire en données quotidiennes.

Par ailleurs, on constate sur les tableaux de résultats détaillés présentés dans l'Annexe que si l'on n'applique pas la stratégie de test suggérée supra, on s'expose à de sérieuses erreurs d'interprétation. Prenons l'exemple de Lyonnaise des Eaux, si l'on avait effectué le test sur le modèle (2) de DICKEY et FULLER (le modèle sans tendance), l'hypothèse nulle de la racine unitaire serait acceptée. Mais ce résultat est en fait dû au biais en faveur de l'hypothèse nulle lié à la mauvaise spécification de la composante déterministe. Lorsqu'on utilise le modèle ( 3 ) (le modèle avec constante et tendance) comme nous l'avons préconisé dans la stratégie, l'hypothèse nulle de la racine unitaire est rejetée au seuil de 5% en données quotidiennes.

Conclusion

D'un point de vue général, l'hypothèse nulle de marche au hasard ne peut pas être rejetée en données hebdomadaires, bimensuelles et mensuelles quelle que soit la série étudiée et le test effectué. Cette homogénéité est fortement remise en cause lorsqu'on s'intéresse aux données quotidiennes. L'impact de l'intervalle d'échantillonnage apparaît donc clairement lorsqu'on passe des données quotidiennes à des données de fréquence moins élevée pour les tests ADF, LOMAC2 et CD2.

Pour les données quotidiennes, des hypothèses restrictives sur les erreurs (non autocorrélation et homoscédasticité) conduisent à des conclusions opposées selon l'utilisation d'un test basé sur la racine unitaire (ADF) ou d'un test fondé sur le ratio de variance (LOMAC1 et CD1). Cette opposition est également présente lorsque les hypothèses sont relâchées. Mais dans ce cas les tests LOMAC2 et CD2 rejettent l'hypothèse nulle là où LOMAC1 et CD1 l'acceptent, et le test PP accepte l'hypothèse nulle là où le test ADF la rejette.

Chaque méthodologie, pour un même ensemble d'hypothèses, aboutit à des résultats opposés. Il semble donc que le choix de la méthodologie de test utilisée influence beaucoup le résultat. Les tests aux hypothèses moins rigides (LOMAC2, CD2 et PP) permettent cependant une première analyse des résultats. La prise en compte de l'hétéroscédasticité (LOMAC2 et CD2) ne suffit pas pour accepter l'hypothèse nulle. Il est nécessaire de relâcher encore les hypothèses en supposant de plus la faible dépendance temporelle (test PP). L'efficience selon JENSEN est alors pleinement vérifiée car l'hétéroscédasticité et la faible dépendance temporelle ne laisse pas la possibilité d'établir des prévisions engendrant un profit significatif.

Les tests réalisés ici portent uniquement sur les corrélations linéaires. Néanmoins les tests LOMAC2, CD2 et PP permettent d'envisager pour les erreurs des processus tels que ARCH et GARCH. Ces derniers introduisent des non linéarités empiriquement vérifiées de nombreuses fois et compatibles avec l'efficience des marchés.

Références bibliographiques.

Alexandre, H. (1992) "La Quasi Marche Aléatoire.", Finance, vol 13, n°2, p.5-21.

Billingsley, P. (1968) Convergence of Probability Measures. John Wiley, New-York, 253 p. Bollerslev, T. (1986) "Generalized Autoregressive Conditional Heteroscedasticity." Journal of

Econometrics, vol. 31, p.307-327.

Chow, K.V. et K.C. Denning (1993) "A Simple Multiple Variance Ratio Test" Journal of

Econometrics, vol. 58, p.385-401.

Dickey, D.A. et W.A Fuller (1979) "Distribution of the Estimators for Autoregressive Time Series

with a Unit Root" Journal of the American Statistical Association, vol. 74, p.427-431.

Dickey, D.A. et W.A Fuller (1981) "Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root." Econometrica, vol. 49, p. 1057-1072.

Dickey, D.A., W.R. Bell et R.B. Miller (1986) "Unit Roots in Time Series Models : Tests and

Implications." The American Statistician, vol. 40, p. 12-26.

Engle, R.F. (1982) "Autoregressive Conditional Heteroscedasticity with Estmates of the Variance of U.K. Inflation." Econometrica, vol. 50, p.987-1008.

Ertur, K.C. (1992a) Tests de Non Stationnante : Application aux PIB réel. Thèse de Doctorat,

Université de Bourgogne.

Ertur, K.C. (1992b) Tests de non stationnante et tendances non linéaires, Document de travail

IME n°9206, Université de Bourgogne.

Fama, E.F. (1970) "Efficient Capital Markets : a Review of Theory and Empirical Work." Journal

of Finance, vol. 25, p.383-417.

Fama, E.F. (1991) "Efficient Capital Markets : H" Journal of Finance, vol. 46, p.1575-1617. Fama, E.F. et K.R. French (1988) "Permanent and Temporary Components of Stock Prices."

Journal of Political Economy, vol. 92, p.246-273.

Fontaine, P. (1990a) "Les cours des marchés d'actions suivent-ils une marche au hasard?" Finance, vol. 11, p. 107-121.

Fontaine, P. (1990b) "Peut-on prédire l'évolution des marché d'actions à partir des cours et dividendes passés ? (Tests de marche au hasard et de co-intégration)." Journal de la

Société de Statistique de Paris, tome 131, n°l, p. 16-36.

Fuller, W.A. (1976) Introduction to Statistical Time Series, John Wiley, New-York, 470 p.

Hecq, A. et J.-P. Urbain (1993) Impact d'erreurs IGARCH sur les tests de racine unité. Communication au XXXIXème Colloque de l'Association d'Economie Appliquée :

Henin, P.Y. et T. Jobert (1990) "Persistance du chômage et hystérèse : une étude comparative." in

Association d'Econometrie Appliquée : Modélisation du marché du travail. Actes du Colloque I, Strasbourg : 5,6 et 7 décembre 1990, p.235-250.

Hernndorf, N. (1984) "A Functional Central Limit Theorem for Weakly Dependant sequences of Random Variables." Annals of Probability, vol. 12, p.141-153.

Jensen, M.C. (1978) "Some Anomalous Evidence regarding Market Efficiency." Jour anal of

Financial Economics, vol. 6, p.95-101.

Kim, K. et P. Schmidt (1990) "Some Evidence on the Accuracy of PHILLIPS-PERRON Tests Using Alternative Estimates of Nuisance Parameters." Economics Letters, vol. 34, p 345-350.

Kim, K. et P. Schmidt (1993) "Unit Root Tests with Conditional Heteroscedasticity." Journal of

Econometrics, vol. 59, p.287-300.

Kleidon, A.W. (1986) "Variance Bounds Tests and the Stock Price Valuation Models." Journal of

Political Economy, vol. 94, p.953-1001.

Lo, A et C. MacKinlay (1988) "Stock Market Prices Do Not Follow Random Walks : Evidence from a Simple Specification Test." The Review of Financial Studies, vol. 1, p.41-66. Lo, A et C. MacKinlay (1989) "The Size and Power of the Variance Ratio Test in Finite Samples :

A Monte Carlo Investigation." Journal of Econometrics, vol. 40, p.203-238

Newey, N.K. et K.D. West (1987) "A Simple Positive Definite Heteroskedasticity and Autocorrelation Consistent Covariance Matrix." Econometrica, vol. 55, p.703-708. Ouliaris, S., J.Y. Park, et P.C.B. Phillips (1989) "Testing for a Unit Root in the Presence of a

Maintained Trend." in Advances in Econometrics and Modeling, B. Raj eds., Kluwer Academic Publishers, Needham MA.

Perron, P. (1988) "Trends and Random Walk in Macroeconomic Time Series : Further Evidence from a New Approach." Journal of Economic Dynamics and Control, vol. 12, p.297-332. Phillips, P.C.B (1987) "Time Series Regression with a Unit Root." Econometrica, vol. 55,

p.277-301.

Phillips, P.C.B et P. Perron (1988) "Testing for a Unit Root in Time Series Regression."

Biometrika, vol. 75, p.347-353.

Said, S.E. et D.A. Dickey (1984) "Testing for Unit Roots in Autoregressive Moving Average Models of Unknown Order." Biometrika, vol. 71, p.599-607.

Summers, L.H. (1986) "Does the Stock Market Rationaly Reflect Fundamental Values ?" Journal

of Finance, vol. 41, p.591-602.

White, H. (1980) "A Heteroscedasticity-Consistent Covariance Matrix Estimator and a Direct Test for Heteroscedasticity." Econometrica, vol. 48, p.817-838.

White, H. et I. Domowitz (1984) "Nonlinear Regression with Dependant Observations."

Cours quotidien hebdo bimensuel mensuel Cours quotidien hebdo bimensuel mensuel

Carrefour T 3573 714 357 178 Casino T 3572 714 357 178

D F modèle (3) P 0,997 0,987 0,978 0,961 D F modèle (3) P 0,997 0,986 0,974 0,946

(constante et tendance) %P -235 -2,19 -2,01 -1,88 (constante et tendance) UP -2,37 -2,12 -2,04 -2,08

*2 3,02 3,01 3,02 3,26 *2 2,08 1,74 1,67 1,77

DFmodèle(2) P 1,000 0,999 0,999 0,999 DFmodèle(2) P 0,999 0,995 0,989 0,978

(constante) _'p -0,45 -0,34 -0,32 -0,14 (constante) lP -1,61 -1,52 -132 -1,57

A D F modèle (6) 7C + 1 0,998 0,989 0,982 0,948 A D F modèle (6) jt+l 0,998 0,987 0,975 0,917

(constante et tendance) '* -1,98 -1,93 -1,70 -2,48 (constante et tendance) -1,71 -1,91 -1,88 -2,93

02 3,09 2,99 3,08 334 1,35 1,59 1,70 3,21 F 7,81 a 1,86 0,82 2,12 F 8,27 a 3,07 a 1,64 2,54 a A D F modèle (5) jt + l 1,000 0,999 0,998 0,993 A D F modèle (5) 7t+l 0,999 0,994 0,988 0,969 (constante) -0,19 -0,29 -0,44 -0,90 (constante)

_'*

(constante et tendance) 1 = 6 -2,65 -2,00 -1,94 -1,88 (constante et tendance) 1 = 6 -2,68 -1,90 -1,89 -1,99

Fenêtre de Parzen / = 8 -2,71 -1,99 -1,94 -1,94 Fenêtre de Parzen / = 8 -2,76 -1,88 -1,91 -2,11

/=10 -2,75 -1,99 -1,94 -2,03 /=10 -2,82 -1,88 -1,95 -2,23

/=12 -2,78 -2,00 -1,% -2,12 /=12 -2,85 -1,89 -1,99 -2,34

Statistique Z(<D2) 1 = 2 3,00 3,01 3,04 3,27 Statistique Z(4>2) 1 = 2 1,98 1,64 1,62 1,66

Fenêtre de Parzen / = 4 2,95 3,02 3,06 3,27 Fenêtre de Parzen 1 = 4 1,73 1,48 1,49 1,55

1 = 6 2,91 3,02 3,06 3,26 1 = 6 136 1,44 1,48 1,66 / = 8 2,88 3,02 3,06 3,19 / = 8 1,42 1,41 132 1,80 /=10 2,86 3,02 3,05 3,11 /=10 132 1,42 136 1,92 /=12 2,85 3,02 3,05 3,03 /=12 1,25 1,44 1,62 2,02 PP modèle (2) 1 = 2 -0,46 -0,35 -0,33 -0,14 PP modèle (2) / = 2 -1,65 -1,57 -135 -1,63 Statistique Z(tß) _{/ = 4 -0,49} -0,37 -0,34 -0,14 Statistique Z(f-) 1 = 4 -1,75 -1,65 -1,63 -1,72 (constante) 1 = 6 -0,51 -0,38 -0,34 -0,14 (constante) 1 = 6 -1,81 -1,68 -1,65 -1,68 / = 8 -0,52 -0,39 -0,34 -0,14 / = 8 -1,87 -1,70 -1,64 -1,61 /=10 -0,53 -0,39 -0,34 -0,13 /=10 -1,91 -1,70 -1,63 -1,55 /=12 -0,53 -0,39 -0,34 -0,13 /=12 -1,93 -1,70 -1,61 -1,49 L O M A C 1 & 2 T = 2 Afr(r)-H 0,92 0,89 0,92 0,99 L O M A C 1 & 2 T = 2 Afr(r) + 1 0,91 0,87 0,93 0,87 C D 1 & 2 -2,31 a* -1,48 -0,71 -0,027 C D 1 & 2 -2,56 a -1,66 -0,68 -0,89 z2(t) -2,71 a -2,67 a -1,14 -0,067 Z2(T) -3,04 a -2,82 a -1,11 -1,75 x = 4 Afr(r) + 1 0,82 0,82 0,93 0,95 t = 4 A/r(r) + l 0,83 0,84 0,87 0,89 -1,40 -0,65 -0,19 -0,092 *iW -1,36 -0,58 -033 -0,19 z2(r) -3,53 a -2,26 a* -0,60 -0,43 z2(t) -3,49 a -1,97 a' -1,14 -0,77 t = 8 Mr(r) + 1 0,75 0,79 0,88 1,17 t = 8 Mr(r) + 1 0,74 0,79 0,88 1,05 -0,63 -0,23 -0,092 0,096 -0,66 -0,23 -0,093 0,030 z2(r) -3,46 a -1,64 -0,62 0,83 -3,73 a -1,62 -0,66 0,23 x= 16 Mr(T) + l 0,72 0,77 1,09 U l T= 16 A/r(r) + l 0,72 0,81 1,07 1,13 -0,24 -0,088 0,023 0,073 -0,24 -0,072 0,019 0,024 z2(r) -2,82 a -1,28 0,34 1,86 *2<T) -2,99 a -1,03 0,28 0,37

TABLEAU 1 : a : on rejette l'hypothèse nulle correspondante au seuil de 5%. Les valeurs critiques pour les tests DF, A D F et PP se trouvent dans FULLER (1976) et DICKEY et FULLER (1981). La valeur critique pour les tests de L O et M A C K I N L A Y est 1,96 au seuil de 5% . La statistique F suit une loi de Fisher-Snedecor à (6, T-k) degrés de liberté. Pour les tests de C H O W et DENNING la valeur critique de la distribution SMM(0,05 ; 4 ; ~) est 2,491 au seuil de 5%. * indique les erreurs d'inférence