Active network management for electrical distribution systems: problem formulation and benchmark

(1)

Active network management for

electrical distribution systems: problem

formulation and benchmark

Brussels, Belgium

1 Q. Gemine, D. Ernst, B. Cornélusse

Department of Electrical Engineering and Computer Science University of Liège

(2)

GREDOR - Gestion des Réseaux Electriques de Distribution Ouverts aux Renouvelables

Motivations

2

Installation of

wind and solar power generation resources

at the

distribution level

Environmental concerns are driving the

growth of

renewable electricity generation

Current

fit-and-forget

doctrine for planning and operating

of distribution network comes at

continuously increasing

(3)

Active Network Management

3

Curtail

the

production

of generators.

ANM strategies rely on

short-term policies

that

control the power injected by generators and/or taken

off by loads so as

to

avoid congestions or voltage

problems

.

Simple strategy:

Move

the

consumption of loads

to

relevant time periods.

More advanced strategy:

Such advanced strategies imply solving

large-scale optimal sequential decision-making

(4)

Observations

4

Several researchers tackled this

operational planning problem.

They rely on

different formulations of the

problem

, making it harder for one

researcher to build on top of another

one’s work.

We are looking to

provide

a

generic formulation

of the

problem and a

testbed

in order to promote the

(5)

Problem description

5

We consider the problem faced by a

DSO

willing to

plan the operation of its network over time

, while

ensuring that operational constraints of its

infrastructure are not violated.

This amounts to determine over

time the

optimal operation of a

set of electrical devices

.

We describe the evolution of the system

by a

discrete-time process

having a

time

horizon T

(fast dynamics is neglected).

12 6 9 3 8 7 5 4 2 1011 1

D

(6)

GREDOR - Gestion des Réseaux Electriques de Distribution Ouverts aux Renouvelables 6

Control Actions

Control actions are aimed to directly impact the

power levels of the devices .

0 1 2 3 4 5 6 7 8 Time P( M W ) Potential prod. Modulated prod.

Figure 3: Curtailment of a distributed generator.

We also consider that the DSO can modify the consumption of the flexible loads. These loads constitute a subset _{F out of the whole set of the loads C ⇢ D of the network. An activation fee} is associated to this control mean and flexible loads can be notified of activation up to the time immediately preceding the start of the service. Once the activation is performed at time t0, the

consumption of the flexible load d is modified by a certain value during Td periods. For each of

these modulation periods t _{2 [[t}0 + 1; t0 + Td]], this value is defined by the modulation function

Pd(t t0). An example of modulation function and its influence over the consumption curve

is presented in Figure 4. 1 2 3 4 5 6 7 8 9 1 0.5 0 0.5 1 t − t0(time) ∆ Pd (kW ) ∆E− ∆E+

(a) Modulation signal of the consumption (Td = 9).

0 1 2 3 4 5 6 7 8 9 T ime P (kW ) Standard cons. Modulated cons. t0+ Tf t0

(b) Impact of the modulation signal over the con-sumption.

Figure 4

Loads cannot be modulated in an arbitrary way. They are indeed constraints to be imposed on the modulation signal. Those are inherited from the flexibility source of the loads, such as an inner storage capacity (e.g. electric heater, refrigerator, water pump) or a process that can be scheduled with some flexibility (e.g., industrial production line, dishwasher, washing machine). In any case, we will always consider that the modulation signal Pd has to respect the following

conditions:

• A downward modulation is followed by an increase of the consumption, and conversely. It models the rebound e↵ect.

6 0 1 2 3 4 5 6 7 8 Time P( M W ) Potential prod. Modulated prod.

We also consider that the DSO can modify the consumption of the flexible loads. These loads constitute a subset _{F out of the whole set of the loads C ⇢ D of the network. An activation fee} is associated to this control mean and flexible loads can be notified of activation up to the time immediately preceding the start of the service. Once the activation is performed at time t₀, the consumption of the flexible load d is modified by a certain value during T_d periods. For each of these modulation periods t _{2 [[t}₀ + 1; t₀ + T_d]], this value is defined by the modulation function P_d(t t0). An example of modulation function and its influence over the consumption curve

is presented in Figure 4. 1 2 3 4 5 6 7 8 9 1 0.5 0 0.5 1 t − t0 (time) ∆ Pd (kW ) ∆E− ∆E+

Figure 4

Loads cannot be modulated in an arbitrary way. They are indeed constraints to be imposed on the modulation signal. Those are inherited from the flexibility source of the loads, such as an inner storage capacity (e.g. electric heater, refrigerator, water pump) or a process that can be scheduled with some flexibility (e.g., industrial production line, dishwasher, washing machine). In any case, we will always consider that the modulation signal P_d has to respect the following conditions:

6

Curtailment

instructions can

be imposed to

generators

.

0 1 2 3 4 5 6 7 8 Time P( M W ) Potential prod. Modulated prod.

We also consider that the DSO can modify the consumption of the flexible loads. These loads constitute a subset _{F out of the whole set of the loads C ⇢ D of the network. An activation fee} is associated to this control mean and flexible loads can be notified of activation up to the time immediately preceding the start of the service. Once the activation is performed at time t0, the

consumption of the flexible load d is modified by a certain value during T_d periods. For each of these modulation periods t _{2 [[t}0 + 1; t0 + Td]], this value is defined by the modulation function

Pd(t t0). An example of modulation function and its influence over the consumption curve

is presented in Figure 4. 1 2 3 4 5 6 7 8 9 1 0.5 0 0.5 1 t − t0(time) ∆ Pd (kW ) ∆E− ∆E+

Figure 4

Loads cannot be modulated in an arbitrary way. They are indeed constraints to be imposed on the modulation signal. Those are inherited from the flexibility source of the loads, such as an inner storage capacity (e.g. electric heater, refrigerator, water pump) or a process that can be scheduled with some flexibility (e.g., industrial production line, dishwasher, washing machine). In any case, we will always consider that the modulation signal Pd has to respect the following

conditions:

6

Cost:

_En

_curt

_[MWh]

_{⇥ Price}



e

MWh

Flexibility

service of

loads

can

be activated.

Cost: activation fee

Time-coupling effect.

(7)

Problem Formulation

The problem of computing the right control actions is

formalized as an

optimal sequential decision-making

problem

.

We model this problem as a

first-order Markov

decision process

with mixed integer and continuous

sets of states and actions.

s

_t

, s

_t+1

_{2 S}

s

_t+1

= f (s

_t

, a

_t

, w

_t+1

)

w

_t+1

_{⇠ p(·|s}

_t

)

(8)

System state s

t

The

electrical quantities

can be

deduced from the

power injections

of the devices.

Active power injections of loads

and

power level of

the primary energy sources of DG

(i.e. wind and

sun).

The

control instructions

of the DSO

that

affect the

current period and/or future periods

are also stored in

the state vector.

Upper limits on production levels and the number

of active periods left for flexibility services

in s

t

in s

t

(9)

Transition Function

3.3 Transition function

The system evolution from a state s

_t

to a state s

_t+1

is described by the transition function f .

The new state s

_t+1

depends, in addition to the preceding state, of the control actions a

_t

of the

DSO and of the realization of the stochastic processes, modeled as Markov processes. More

specifically, we have

f :

_{S ⇥ A}

_s

_{⇥ W 7! S ,}

where

_{W is the set of possible realizations of a random process. The general evolution of the}

system is thus governed by relation

s

_t+1

= f (s

_t

, a

_t

, w

_t

) ,

(12)

where w

_t

_{2 W and such that it follows a conditional probability law p}

_W

(

_·|s

_t

). In order to define

this function in more detail, we now describe the various processes that constitute it.

3.3.1 Load consumption

The uncertainty about the behavior of consumers inevitably leads to uncertainty about the

power level they withdraw from the network. However, over a one day horizon, some trends can

be observed. Consumption peaks arise for example in the early morning and in the evening for

residential consumers but at levels that fluctuate from one day to another and among consumers.

Finally, we model the evolution of the consumption of each load d

_{2 C by}

P

_d,t+1

= f

_d

(P

_d,t

, q

_t

, w

_d,t

) ,

(13)

where w

_d,t

is a component of w

_t

_{⇠ p}

_W

(

_·|s

_t

). The dependency of functions f

_d

to the quarter

of hour in the day q

_t

allows capturing the daily trends of the process. Given the hypothesis of

constant power factor for the devices, the reactive power consumption can directly be deduced

from P

_d,t+1

:

Q

_q,t+1

= tan

_d

_{· P}

_d,t+1

.

In Section 5, we describe a possible procedure to model the evolution of the consumption of

an aggregated set of residential consumers using relation (13).

3.3.2 Wind speed and power level of wind generators

The uncertainty about the production level of wind turbines is inherited from the uncertainty

about the wind speed. The Markov process that we consider governs the wind speed, which

is assumed to be uniform over the network. The production level of the wind generators is

then obtained by using a deterministic function that depends of the wind speed realization, this

function if the power curve of the considered generator. We can formalize this phenomenon as:

v

_t+1

= f

_v

(v

_t

, q

_t

, w

_t(v)

) ,

(14)

P

_g,t+1

= ⌘

_g

(v

_t+1

),

_{8g 2 wind generators ⇢ G ,}

(15)

such that w

_t(v)

is a component of w

_t

_{⇠ p}

_W

(

_·|s

_t

) and where ⌘

_g

is the power curve of generator

g. A typical example of power curve ⌘

_g

(v) is illustrated in Figure 5. Like loads, the production

of reactive power is obtained using:

Q

_g,t+1

= tan

_g

_{· P}

_g,t+1

.

A possible approach to determine f

_v

from a set of measurements is described in Section 5.

9 Curtailment instructions

for

next period and

activation

of flexible loads

.

Set of possible realizations of

a

random process

, with w

t

∈

W

that follows a

conditional

probability law

3.3 Transition function

The system evolution from a state s

_t

to a state s

_t+1

is described by the transition function f .

The new state s

_t+1

depends, in addition to the preceding state, of the control actions a

_t

of the

DSO and of the realization of the stochastic processes, modeled as Markov processes. More

specifically, we have

f :

_{S ⇥ A}

_s

_{⇥ W 7! S ,}

where

_{W is the set of possible realizations of a random process. The general evolution of the}

system is thus governed by relation

s

_t+1

= f (s

_t

, a

_t

, w

_t

) ,

(12)

where w

_t

_{2 W and such that it follows a conditional probability law p}

_W

(

_·|s

_t

). In order to define

this function in more detail, we now describe the various processes that constitute it.

3.3.1 Load consumption

The uncertainty about the behavior of consumers inevitably leads to uncertainty about the

power level they withdraw from the network. However, over a one day horizon, some trends can

be observed. Consumption peaks arise for example in the early morning and in the evening for

residential consumers but at levels that fluctuate from one day to another and among consumers.

Finally, we model the evolution of the consumption of each load d

_{2 C by}

P

_d,t+1

= f

_d

(P

_d,t

, q

_t

, w

_d,t

) ,

(13)

where w

_d,t

is a component of w

_t

_{⇠ p}

_W

(

_·|s

_t

). The dependency of functions f

_d

to the quarter

of hour in the day q

_t

allows capturing the daily trends of the process. Given the hypothesis of

constant power factor for the devices, the reactive power consumption can directly be deduced

from P

_d,t+1

:

Q

_q,t+1

= tan

_d

_{· P}

_d,t+1

.

In Section 5, we describe a possible procedure to model the evolution of the consumption of

an aggregated set of residential consumers using relation (13).

3.3.2 Wind speed and power level of wind generators

The uncertainty about the production level of wind turbines is inherited from the uncertainty

about the wind speed. The Markov process that we consider governs the wind speed, which

is assumed to be uniform over the network. The production level of the wind generators is

then obtained by using a deterministic function that depends of the wind speed realization, this

function if the power curve of the considered generator. We can formalize this phenomenon as:

v

_t+1

= f

_v

(v

_t

, q

_t

, w

_t

(v)

) ,

(14)

P

_g,t+1

= ⌘

_g

(v

_t+1

),

_{8g 2 wind generators ⇢ G ,}

(15)

such that w

_t

(v)

is a component of w

_t

_{⇠ p}

_W

(

_·|s

_t

) and where ⌘

_g

is the power curve of generator

g. A typical example of power curve ⌘

_g

(v) is illustrated in Figure 5. Like loads, the production

of reactive power is obtained using:

Q

_g,t+1

= tan

_g

_{· P}

_g,t+1

.

A possible approach to determine f

_v

from a set of measurements is described in Section 5.

9

3.3 Transition function

The system evolution from a state s_t to a state s_t+1 is described by the transition function f . The new state s_t+1 depends, in addition to the preceding state, of the control actions a_t of the DSO and of the realization of the stochastic processes, modeled as Markov processes. More specifically, we have

f : _{S ⇥ A}_s _{⇥ W 7! S ,}

where _{W is the set of possible realizations of a random process. The general evolution of the} system is thus governed by relation

s_t+1 = f (s_t, a_t, w_t) , (12) where w_t _{2 W and such that it follows a conditional probability law p}_W(_·|s_t). In order to define this function in more detail, we now describe the various processes that constitute it.

3.3.1 Load consumption

The uncertainty about the behavior of consumers inevitably leads to uncertainty about the power level they withdraw from the network. However, over a one day horizon, some trends can be observed. Consumption peaks arise for example in the early morning and in the evening for residential consumers but at levels that fluctuate from one day to another and among consumers. Finally, we model the evolution of the consumption of each load d _{2 C by}

P_d,t+1 = f_d(P_d,t, q_t, w_d,t) , (13) where w_d,t is a component of w_t _{⇠ p}_W(_·|s_t). The dependency of functions f_d to the quarter of hour in the day q_t allows capturing the daily trends of the process. Given the hypothesis of constant power factor for the devices, the reactive power consumption can directly be deduced from P_d,t+1:

Q_q,t+1 = tan _d _{· P}_d,t+1 .

In Section 5, we describe a possible procedure to model the evolution of the consumption of an aggregated set of residential consumers using relation (13).

3.3.2 Wind speed and power level of wind generators

The uncertainty about the production level of wind turbines is inherited from the uncertainty about the wind speed. The Markov process that we consider governs the wind speed, which is assumed to be uniform over the network. The production level of the wind generators is then obtained by using a deterministic function that depends of the wind speed realization, this function if the power curve of the considered generator. We can formalize this phenomenon as: v_t+1 = f_v(v_t, q_t, w_t(v)) , (14) P_g,t+1 = ⌘_g(v_t+1), _{8g 2 wind generators ⇢ G ,} (15) such that w_t(v) is a component of w_t _{⇠ p}_W(_·|s_t) and where ⌘_g is the power curve of generator g. A typical example of power curve ⌘_g(v) is illustrated in Figure 5. Like loads, the production of reactive power is obtained using:

Q_g,t+1 = tan _g _{· P}_g,t+1 .

A possible approach to determine f_v from a set of measurements is described in Section 5.

9

3.3 Transition function

The system evolution from a state s_t to a state s_t+1 is described by the transition function f . The new state s_t+1 depends, in addition to the preceding state, of the control actions a_t of the DSO and of the realization of the stochastic processes, modeled as Markov processes. More specifically, we have

f : _{S ⇥ A}_s _{⇥ W 7! S ,}

where _{W is the set of possible realizations of a random process. The general evolution of the} system is thus governed by relation

s_t+1 = f (s_t, a_t, w_t) , (12) where w_t _{2 W and such that it follows a conditional probability law p}_W(_·|s_t). In order to define this function in more detail, we now describe the various processes that constitute it.

3.3.1 Load consumption

The uncertainty about the behavior of consumers inevitably leads to uncertainty about the power level they withdraw from the network. However, over a one day horizon, some trends can be observed. Consumption peaks arise for example in the early morning and in the evening for residential consumers but at levels that fluctuate from one day to another and among consumers. Finally, we model the evolution of the consumption of each load d _{2 C by}

P_d,t+1 = f_d(P_d,t, q_t, w_d,t) , (13) where w_d,t is a component of w_t _{⇠ p}_W(_·|s_t). The dependency of functions f_d to the quarter of hour in the day qt allows capturing the daily trends of the process. Given the hypothesis of constant power factor for the devices, the reactive power consumption can directly be deduced from P_d,t+1:

Q_q,t+1 = tan _d _{· P}_d,t+1 .

In Section 5, we describe a possible procedure to model the evolution of the consumption of an aggregated set of residential consumers using relation (13).

3.3.2 Wind speed and power level of wind generators

The uncertainty about the production level of wind turbines is inherited from the uncertainty about the wind speed. The Markov process that we consider governs the wind speed, which is assumed to be uniform over the network. The production level of the wind generators is then obtained by using a deterministic function that depends of the wind speed realization, this function if the power curve of the considered generator. We can formalize this phenomenon as: v_t+1 = f_v(v_t, q_t, w_t(v)) , (14) P_g,t+1 = ⌘_g(v_t+1), _{8g 2 wind generators ⇢ G ,} (15)

such that w_t(v) is a component of w_t _{⇠ p}_W(_·|s_t) and where ⌘_g is the power curve of generator g. A typical example of power curve ⌘_g(v) is illustrated in Figure 5. Like loads, the production of reactive power is obtained using:

Q_g,t+1 = tan _g _{· P}_g,t+1 .

A possible approach to determine f_v from a set of measurements is described in Section 5.

9 0 5 10 15 20 25 30 0 v (m/s) P (MW ) Pn om in a l

Figure 5: Power curve of a wind generator.

3.3.3 Solar irradiance and photovoltaic production

Like wind generators, the photovoltaic generators inherit their uncertainty in production level from the uncertainty associated to their energy source. This source is represented by the level of

solar irradiance, which is the power level of the incident solar energy per m2. The irradiance level

is the stochastic process that we model while the production level is obtained by a deterministic function of the irradiance and of the surface of photovoltaic panels. This function is simpler that the power curve of wind generators and is defined as

P_g,t = ⌘_g _{· surf}_g _{· ir}_t ,

where ⌘_g is the efficiency factor of the panels, assumed constant and equal to 15%, while surf_g

is the surface of the panels in m2 and is specific to each photovoltaic generator. The irradiance

level is denoted by ir_t and the whole phenomenon is modeled by the following Markov process:

ir_t+1 = f_ir(ir_t, q_t, w_t(ir)) , (16)

P_g,t+1 = ⌘_g _{· surf}_g _{· ir}_t+1, _{8g 2 solar generators ⇢ G ,} (17)

such that w_t(v) is a component of w_t _{⇠ p}_W(_·|s_t). The technique used in Section 5 to build f_ir

from a dataset is similar to the one of the wind speed case.

3.3.4 Impact of control actions

The stochastic processes that we described govern the evolution of the state s(1)_t _{2 S}(1) of the

consumption of loads (flexibility services excluded) and of the power level of energy sources of DG. The following transition laws define the evolution of the components of the state of

modulation instructions s(2)_t _{2 S}(2) by integrating the control actions of the DSO:

8g 2 G : P _g,t+1 = p_g,t , (18) 8d 2 F : s(f )_d,t+1 = max(s(f )_d,t 1 ; 0) + a(f )_d,t T_d , (19) 8d 2 F : P_d,t+1 = ( P_d(T_d s(f )_d,t+1 + 1) si s(f )_d,t+1 > 0 0 si s(f )_d,t+1 = 0 . (20) 10

{

(10)

Reward Function

r :

_{S ⇥ A}

_s

_{⇥ S 7! R}

The reward function

associates an

instantaneous rewards for each transition

of the

system from a period t to a period t+1:

From vectors s(1)_t and s(2)_t , we can determine, for each node n _{2 N , the active and reactive}

power injections and thus obtain the value of the electrical quantities of the network: P P n,t = X g_2G(n) min(P_g,t; P_g,t) + X d_2C(n)\F(n) P_d,t +X d_2F(n) (P_d,t + P_d,t) , (21) Q P n,t = X g_2G(n) min(tan _gP_g,t; Q_g,t) + X d_2C(n)\F(n) Q_d,t +X d_2F(n) (Q_d,t + tan _d P_d,t) , (22) 0 = g_n(e, f , P P n,t, Q P n,t) , (23) 0 = h_n(e, f , P P n,t, Q P n,t) , (24)

and, in each link l _{2 L, we have:}

i_l(e, f ) = 0 . (25)

3.4 Reward function and goal

In order to evaluate the performance of a policy, we first specify the reward function r : _{S ⇥}

As ⇥ S 7! R that associates an instantaneous rewards for each transition of the system from a

period t to a period t + 1: r(s_t, a_t, s_t+1) = X g_2G max_{0, Pg,t+1 Pg,t+1 4 }C curt g (qt+1) | {z } curtailment cost of DG X d_2F a(f )_d,t C_df lex | {z } activation cost of flexible loads (s_t+1) | {z } barrier function , (26) where C_gcurt(q_t+1) is the day-ahead market price pour the quarter of hour q_t+1 in the day and

C_df lex is the activation cost of flexible loads, specific to each of them. The function is a

barrier function that allows to penalize a policy leading the system in a state that violates the operational limits. It is defined as

(s_t+1) = X n_2N [ (e2_n,t+1 + f_n,t+12 V 2_n) + (V 2_n e2_n,t+1 f_n,t+12 )] + X l_2L (_|I_l,t+1_| I_l) , (27)

where e_n,t+1, f_n,t+1 (n _{2 N ) and I}_l,t+1 (l _{2 L) are determined from s}_t+1 using equations (21)-(25) and

(x) = (

105 si x > 0

0 sinon . (28)

The higher are the operational costs and the larger is the number of violated operational limits, the more negative is the reward function.

We can now defined the return over T periods, denoted R_T, as the weighted sum of the

rewards that are observed over a system trajectory of T periods

R_T = T 1_X t=0 t_r(s t, at, st+1) , (29) 11

Because the operation of a DN must be always be

ensured, we consider the

return R

over an

infinite

trajectory

of the system:

where

_{2]0; 1[ is the discount factor. Given that}

t

< 1 for t > 0, the further in time is the

transition from period t = 0, the less importance is given to the associated reward. Because

the operation of a DN must be always be ensured, it does not seem relevant to consider returns

over a finite number of periods and we introduce the return R as

R = R

₁

= lim

T_!1 T 1

_X

t=0 t

_r(s

t

, a

t

, s

t+1

) ,

(30)

that corresponds to the weighted sum of the rewards observed over an infinite trajectory of the

system. Given that the costs and penalties have finite values and that the reward function r

is the sum of an infinite number of these costs and penalties, it exists a constant C such that,

8(s

t

, a

t

, s

t+1

)

2 S ⇥ A

s

⇥ S, we have |r(s

t

, a

t

, s

t+1

)

| < C and thus

|R| < lim

T_!1

C

T 1

_X

t=0 t

₌

C

1 .

(31)

It means that even if the return R is defined as an infinite sum, it converges in a finite value.

One can also observe that, because s

_t+1

= f (s

_t

, a

_t

, w

_t

), it exists a function ⇢ :

_{S ⇥ A ⇥ W 7! R}

that aggregates functions f and r and such that

r(s

_t

, a

_t

, s

_t+1

) = ⇢(s

_t

, a

_t

, w

_t

) ,

(32)

with w

_t

_{⇠ p}

_W

(

_·|s

_t

). Let ⇡ :

_{S 7! A}

_s

be a policy that associate a control action to each state of

the system. We can define, starting from an initial state s

₀

= s, the expected return R of the

policy ⇡ by

J

⇡

(s) = lim

T_!1 _{wt⇠pW (·|st)}

E

{

T 1

_X

t=0 t

_⇢(s

t

, ⇡(s

t

), w

t

)

|s

0

= s

} .

(33)

We denote by ⇧ the space of all the policies ⇡. For a DSO, addressing the operational planning

problem described in Section 2 is equivalent to determine an optimal policy ⇡

⇤

among all the

elements of ⇧, i.e. a policy that satisfies the following condition

J

⇡⇤

(s)

J

⇡

(s),

_{8s 2 S, 8⇡ 2 ⇧ .}

(34)

It is well know that such a policy satisfies the Bellman equation [9], which can be written

J

⇡⇤

(s) = max

a_2As w⇠pW (·|s)

E

⇢(s, a, w) + J

⇡⇤

(f (s, a, w))

,

_{8s 2 S .}

(35)

If we only take into account the space of stationary policies (i.e. that select an action

indepen-dently of time t), it is without loss of generality comparing to the space of policies ⇧

0

:

_{S⇥T 7! A}

because the return to be maximized corresponds to an infinite trajectory of the system [10].

4 Solution techniques

We identify in this section three classes of solution techniques that could be applied to the

op-erational planning problem. The first one is mathematical optimization, a technique for which

we also provide a review of the literature concerning research about solving multi-period OPF.

The second approach that we consider is constituted by techniques relying on the dynamic

pro-gramming framework, such as approximate dynamic propro-gramming and reinforcement learning.

Finally, simulation-based optimization techniques are discussed.

(11)

Optimal Policy

⇢(s_t, a_t, w_t) = r(s_t, a_t, f (s_t, a_t, w_t))

where

_{2]0; 1[ is the discount factor. Given that}

t

< 1 for t > 0, the further in time is the

transition from period t = 0, the less importance is given to the associated reward. Because

the operation of a DN must be always be ensured, it does not seem relevant to consider returns

over a finite number of periods and we introduce the return R as

R = R

₁

= lim

T_!1 T 1

_X

t=0 t

_r(s

t

, a

t

, s

t+1

) ,

(30)

that corresponds to the weighted sum of the rewards observed over an infinite trajectory of the

system. Given that the costs and penalties have finite values and that the reward function r

is the sum of an infinite number of these costs and penalties, it exists a constant C such that,

8(s

t

, a

t

, s

t+1

)

2 S ⇥ A

s

⇥ S, we have |r(s

t

, a

t

, s

t+1

)

| < C and thus

|R| < lim

T_!1

C

T 1

_X

t=0 t

₌

C

1 .

(31)

It means that even if the return R is defined as an infinite sum, it converges in a finite value.

One can also observe that, because s

_t+1

= f (s

_t

, a

_t

, w

_t

), it exists a function ⇢ :

_{S ⇥ A ⇥ W 7! R}

that aggregates functions f and r and such that

r(s

_t

, a

_t

, s

_t+1

) = ⇢(s

_t

, a

_t

, w

_t

) ,

(32)

with w

_t

_{⇠ p}

_W

(

_·|s

_t

). Let ⇡ :

_{S 7! A}

_s

be a policy that associates a control action to each state

of the system. We can define, starting from an initial state s

₀

= s, the expected return R of

the policy ⇡ by

J

⇡

(s) = lim

T _!1 _{wt⇠pW (·|st)}

E

{

T 1

_X

t=0 t

_⇢(s

t

, ⇡(s

t

), w

t

)

|s

0

= s

} .

(33)

We denote by ⇧ the space of all the policies ⇡. For a DSO, addressing the operational planning

problem described in Section 2 is equivalent to determine an optimal policy ⇡

⇤

among all the

elements of ⇧, i.e. a policy that satisfies the following condition

J

⇡⇤

(s)

J

⇡

(s),

_{8s 2 S, 8⇡ 2 ⇧ .}

(34)

It is well know that such a policy satisfies the Bellman equation [9], which can be written

J

⇡⇤

(s) = max

a_2A_s w_{⇠pW (·|s)}

E

⇢(s, a, w) + J

⇡⇤

_{(f (s, a, w))}

_,

8s 2 S .

(35)

If we only take into account the space of stationary policies (i.e. that select an action

indepen-dently of time t), it is without loss of generality comparing to the space of policies ⇧

0

:

_{S⇥T 7! A}

because the return to be maximized corresponds to an infinite trajectory of the system [10].

4 Solution techniques

We identify in this section three classes of solution techniques that could be applied to the

op-erational planning problem. The first one is mathematical optimization, a technique for which

we also provide a review of the literature concerning research about solving multi-period OPF.

The second approach that we consider is constituted by techniques relying on the dynamic

pro-gramming framework, such as approximate dynamic propro-gramming and reinforcement learning.

Finally, simulation-based optimization techniques are discussed.

12 Let be a

policy

that associates a control

action to each state of the system, the

expected return

of this policy can be written as:

⇡ :

_{S 7! A}

_s

Let be the

space of all stationary policies

. Addressing

the operational planning problem of a DSO consists in

finding an optimal policy

:

⇧

⇡

⇤

_{2 ⇧}

where

_{2]0; 1[ is the discount factor. Given that}

t

< 1 for t > 0, the further in time is the

transition from period t = 0, the less importance is given to the associated reward. Because

the operation of a DN must be always be ensured, it does not seem relevant to consider returns

over a finite number of periods and we introduce the return R as

R = R

₁

= lim

T _!1 T 1

_X

t=0 t

_r(s

t

, a

t

, s

t+1

) ,

(30)

that corresponds to the weighted sum of the rewards observed over an infinite trajectory of the

system. Given that the costs and penalties have finite values and that the reward function r

is the sum of an infinite number of these costs and penalties, it exists a constant C such that,

8(s

t

, a

t

, s

t+1

)

2 S ⇥ A

s

⇥ S, we have |r(s

t

, a

t

, s

t+1

)

| < C and thus

|R| < lim

T_!1

C

T 1

_X

t=0 t

₌

C

1 .

(31)

It means that even if the return R is defined as an infinite sum, it converges in a finite value.

One can also observe that, because s

_t+1

= f (s

_t

, a

_t

, w

_t

), it exists a function ⇢ :

_{S ⇥ A ⇥ W 7! R}

that aggregates functions f and r and such that

r(s

_t

, a

_t

, s

_t+1

) = ⇢(s

_t

, a

_t

, w

_t

) ,

(32)

with w

_t

_{⇠ p}

_W

(

_·|s

_t

). Let ⇡ :

_{S 7! A}

_s

be a policy that associates a control action to each state

of the system. We can define, starting from an initial state s

₀

= s, the expected return R of

the policy ⇡ by

J

⇡

(s) = lim

T _!1 _{wt⇠pW (·|st)}

E

{

T 1

_X

t=0 t

_⇢(s

t

, ⇡(s

t

), w

t

)

|s

0

= s

} .

(33)

We denote by ⇧ the space of all the policies ⇡. For a DSO, addressing the operational planning

problem described in Section 2 is equivalent to determine an optimal policy ⇡

⇤

among all the

elements of ⇧, i.e. a policy that satisfies the following condition

J

⇡⇤

(s)

J

⇡

(s),

_{8s 2 S, 8⇡ 2 ⇧ .}

(34)

It is well know that such a policy satisfies the Bellman equation [9], which can be written

J

⇡⇤

(s) = max

a_2As w⇠pW (·|s)

E

⇢(s, a, w) + J

⇡⇤

(f (s, a, w))

,

_{8s 2 S .}

(35)

If we only take into account the space of stationary policies (i.e. that select an action

indepen-dently of time t), it is without loss of generality comparing to the space of policies ⇧

0

:

_{S⇥T 7! A}

because the return to be maximized corresponds to an infinite trajectory of the system [10].

4 Solution techniques

We identify in this section three classes of solution techniques that could be applied to the

op-erational planning problem. The first one is mathematical optimization, a technique for which

we also provide a review of the literature concerning research about solving multi-period OPF.

The second approach that we consider is constituted by techniques relying on the dynamic

pro-gramming framework, such as approximate dynamic propro-gramming and reinforcement learning.

Finally, simulation-based optimization techniques are discussed.

(12)

Solution Techniques

We identified

three classes of solution techniques

that

could be applied to the operational planning problem:

• mathematical programming

and, in particular,

multistage stochastic programming;

• approximate dynamic programming

;

• simulation-based methods

, such as direct policy

(13)

Test Instance

Figure 6: Test network.

iteration k, parameter values ✓i(i2 I(k)) are evaluated by simulating trajectories of the system

which are associated to the policies ⇡✓i. The result of these simulation allows the selection of new parameter values ✓i (i2 I(k+1)) for the next iteration. The goal of such an algorithm is

to converge as fast as possible towards a parameter value ˆ✓⇤ that defines a good approximate optimal policy ⇡ˆ_✓⇤.

Another subset of simulation-based methods is the Monte-Carlo tree search technique [26, 27]. A each time-step, this class of algorithms usually rely on the simulation of system trajec-tories to build, incrementally, a scenario tree that does not have a uniform depth. These are the previous simulations that are exploited to select the nodes of the scenario tree that have to be developed. When the construction of the tree is done, the action that is deemed optimal for the root node of the tree is applied to the system.

5 Test instance

In this section, we describe a test instance of the considered problem. The set of models and parameters that are specific to this instance as well as documentation for their usage are accessible at http://www.montefiore.ulg.ac.be/~anm/ as a Matlabr class. It has been developed to provided a black-box-type simulator which is quick to set up. The DN on which this instance is based is a generic DN of 75 buses [28] that has a radial topology, it is presented in Figure 6. We bound various electrical devices to the network in such a way that it is possible to gather the nodes of this network into four distinct categories:

• each residential node is the connection point of a load that represents a set of residential 15

We designed a

benchmark

of the ANM

problem with the goal of

promoting

computational research

in this complex

field.

The set of models and parameters that

are specific to this instance as well as

documentation for their usage are

accessible as a Matlab class

at

www.montefiore.ulg.ac.be/~anm/ .

10 20 30 40 50 60 70 80 90 −30 −25 −20 −15 −10 −5 0 5 10 15 20 T e m p s ! d ∈ D Pd ( t)( MW ) T ime X d D Pd,t (MW )

Figure 8: Power withdrawal scenarios of the devices. Negative values indicate that DG inject more power than what is consumed by loads.

10 20 30 40 50 60 70 80 90 30 35 40 45 50 55 60 65 T emps /M W h € T ime

Figure 9: Market price of electricity per MWh over the day.

activation costs are proportional to the magnitude of the modulation signals (C_df lex _{/ P}_dnom). The approach used to build the transition functions of the stochastic quantities (i.e. the consumption of loads, the wind speed and the level of solar irradiance) is to learn from a dataset functions µi(si,t, qt) and _i2(qt), which predict the mean and the variance, respectively, for period

t + 1 of each of these quantities i. The input values used for this purpose are the realization si,t

of the quantity i at period t and the quarter of hour in the day qt to which it corresponds. The

following procedure has been used to build the approximate functions ˆµi and ˆ_i2:

1. formatting of the dataset into K tuples (s(k)_i,t , q_t(k), s(k)_i,t+1);

2. let ˆµ✓ be a neural network and ✓ its learning parameters, ˆµi is determined by solving

✓⇤_i = arg min ✓ K X k=1 [s(k)_i,t+1 µˆ✓(s(k)_i,t , qt(k))]2 with ˆµi = ˆµ✓⇤_i; 17

(14)

Example of Policy

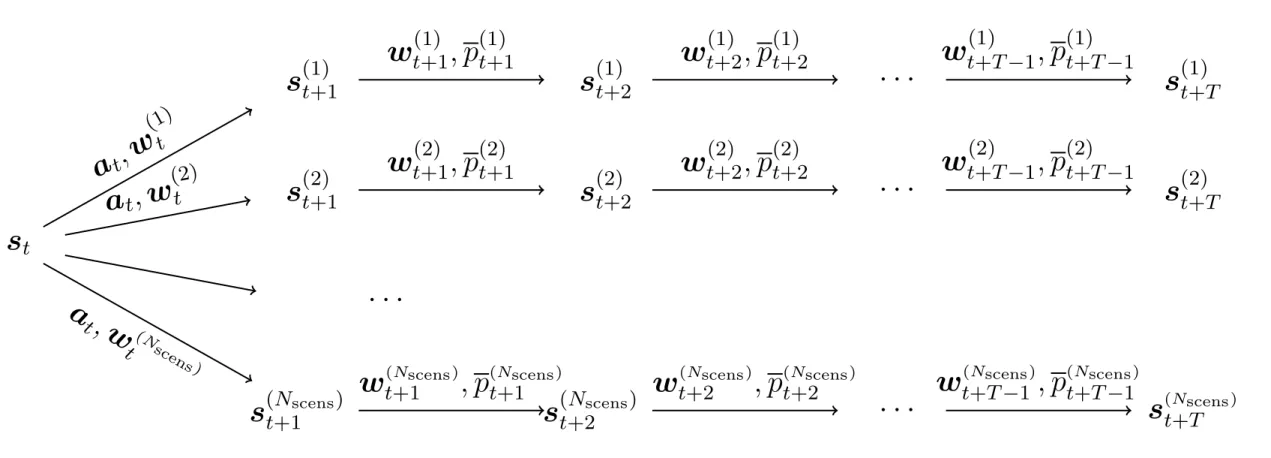
Figure 12: Scenario tree that is built at each time step.

presented solution technique can be written as

3 :

ˆ

⇡

⇤

(s) = arg min

a

_2A

_s

(s)

_8k2K

min

t

: s

k

,

8k2K

t

\{0}: a

Ak

X

k

_2K

t

\{0}

h

P

k

D

k

X

g

_2G

P

_g,k

4 C

curt

g

(q

k

) + ✏

2 P

g,k

2 ✏

₁

M

_g,k

+ ✏

₂

M

_g,k

2 i

+

X

d

_2F

h

C

_d

f lex

a

(f )

_d,0

i

(54)

s.t.

s

₀

= s

(55)

a

₀

= a

(56)

s

_k

= f (s

_A

_k

, a

_A

_k

, w

_A

_k

) ,

_{8k 2 K}

_t

_\{0}

(57)

a

_A

_k

_{2 A}

_s

_Ak

,

_{8k 2 K}

_t

_\{0}

(58)

a

(f )

_A

k

= 0 ,

8k 2 {k 2 K

t

| D

k

> 1

}

(59)

s

_k

_{2 ˆ}

_S

(ok)

,

_{8k 2 K}

_t

_\{0}

(60)

P

_g,k

= max(0, P

_g,k

P

_g,k

),

_{8(g, k) 2 G ⇥ K}

_t

_{\{0} (61)}

M

_g,k

= max(0, P

_g,k

P

_g,k

),

_{8(g, k) 2 G ⇥ K}

_t

_{\{0} ,(62)}

where Equation (59) enforces that the activation of flexible loads is not accounted as a recourse

action. The set ˆ

_S

_k

(ok)

is an approximation of the set

_S

(ok)

of the system states that respect

operational limits. For the test instance presented in this paper, this set is defined using a linear

constraint over the upper limits of active production levels and over the active consumption of

loads:

ˆ

S

(ok)

⌘

n

s

_{2 S}

X

g

_2G

P

_g

+

X

d

_2C

P

_d

+

P

_d

< C

o

,

(63)

where C is a constant that can be estimated by trial and error and with

P

_d,k

defined as in

Equation (20). The physical motivation behind this constraint is that issues usually occur when

a high level of distributed production and a low consumption level take place simultaneously.

In order to get control actions that are somehow robust to the evolutions of the system that

would not be well accounted in the scenario tree, the objective function of Problem (54)-(62)

includes, for each node k but the root node, the following terms:

P

k

D

k

X

g

_2G

✏

₂

P

_g,k

2 ✏

₁

M

_g,k

+ ✏

₂

M

_g,k

2 ,

(64)

where ✏

₁

and ✏

₂

are small positive parameters. The goal of these terms is to drive the solution

towards curtailment instructions that are as equally shared as possible among generators and

towards margins between the production upper limits and the forecasted production levels

that are as large as possible while being also equally shared among generators. By doing so, the

3

_{This formulation is used for the sake of understanding. It di↵ers from the exact implementation but defines}

an equivalent mathematical program.

20 In order

to illustrate

the operational planning problem

and the test instance, let’s consider a simple solution

technique. It consists in a simplified version of a

(15)

Example of Policy

In order

to illustrate

the operational planning problem

and the test instance, let’s consider a simple solution

technique. It consists in a simplified version of a

multi-stage stochastic program

:

Figure 12: Scenario tree that is built at each time step.

presented solution technique can be written as3:

ˆ ⇡⇤(s) = arg min a2As(s) _8k2Kmin_{t: s} k, 8k2Kt\{0}: a_Ak X k2Kt\{0} h Pk Dk X g2G Pg,k 4 C curt g (qk) + ✏2 Pg,k2 ✏1 Mg,k + ✏2 M_g,k2 i + X d_2F h C_df lexa(f )_d,0i (54) s.t. s0 = s (55) a₀ = a (56) s_k = f (s_Ak, a_Ak, w_Ak) , _{8k 2 K}_t_\{0} (57) a_Ak _{2 A}s_Ak , 8k 2 Kt\{0} (58) a(f )_Ak = 0 , _{8k 2 {k 2 K}_t _{| D}_k > 1_} (59) sk 2 ˆS(ok) , 8k 2 Kt\{0} (60) P_g,k = max(0, P_g,k P_g,k),_{8(g, k) 2 G ⇥ K}_t_{\{0} (61)} M_g,k = max(0, P_g,k P_g,k),_{8(g, k) 2 G ⇥ K}_t_{\{0} ,(62)}

where Equation (59) enforces that the activation of flexible loads is not accounted as a recourse

action. The set ˆ_S_k(ok) is an approximation of the set _S(ok) of the system states that respect

operational limits. For the test instance presented in this paper, this set is defined using a linear constraint over the upper limits of active production levels and over the active consumption of loads: ˆ S(ok) ⌘ ns _{2 S} X g2G P_g +X d2C P_d + P_d < Co, (63)

where C is a constant that can be estimated by trial and error and with P_d,k defined as in

Equation (20). The physical motivation behind this constraint is that issues usually occur when a high level of distributed production and a low consumption level take place simultaneously.

In order to get control actions that are somehow robust to the evolutions of the system that would not be well accounted in the scenario tree, the objective function of Problem (54)-(62) includes, for each node k but the root node, the following terms:

Pk Dk

X

g2G

✏₂ P_g,k2 ✏₁ M_g,k + ✏₂ M_g,k2 , (64)

where ✏₁ and ✏₂ are small positive parameters. The goal of these terms is to drive the solution

towards curtailment instructions that are as equally shared as possible among generators and towards margins between the production upper limits and the forecasted production levels that are as large as possible while being also equally shared among generators. By doing so, the

3_{This formulation is used for the sake of understanding. It di↵ers from the exact implementation but defines}

an equivalent mathematical program.

20

Figure 12: Scenario tree that is built at each time step.

presented solution technique can be written as3:

ˆ ⇡⇤(s) = arg min a_2As(s) min 8k2Kt: sk, 8k2Kt\{0}: a_Ak X k_2Kt\{0} h Pk Dk X g_2G Pg,k 4 C curt g (qk) + ✏2 Pg,k2 ✏1 Mg,k + ✏2 M_g,k2 i + X d_2F h C_df lexa(f )_d,0i (54) s.t. s0 = s (55) a0 = a (56) sk = f (sAk, aAk, wAk) , 8k 2 Kt\{0} (57) a_A_k _{2 A}s_Ak , 8k 2 Kt\{0} (58) a(f )_A k = 0 , 8k 2 {k 2 Kt | Dk > 1} (59) sk 2 ˆS(ok), 8k 2 Kt\{0} (60) Pg,k = max(0, Pg,k Pg,k),8(g, k) 2 G ⇥ Kt\{0} (61) Mg,k = max(0, Pg,k Pg,k),8(g, k) 2 G ⇥ Kt\{0} ,(62)

where Equation (59) enforces that the activation of flexible loads is not accounted as a recourse

action. The set ˆ_S_k(ok) is an approximation of the set _S(ok) of the system states that respect

operational limits. For the test instance presented in this paper, this set is defined using a linear constraint over the upper limits of active production levels and over the active consumption of loads: ˆ S(ok) ⌘ ns _{2 S} X g2G Pg + X d2C Pd + Pd < C o , (63)

where C is a constant that can be estimated by trial and error and with Pd,k defined as in

Equation (20). The physical motivation behind this constraint is that issues usually occur when a high level of distributed production and a low consumption level take place simultaneously.

In order to get control actions that are somehow robust to the evolutions of the system that would not be well accounted in the scenario tree, the objective function of Problem (54)-(62) includes, for each node k but the root node, the following terms:

Pk Dk

X

g_2G

✏2 Pg,k2 ✏1 Mg,k + ✏2 Mg,k2 , (64)

where ✏1 and ✏2 are small positive parameters. The goal of these terms is to drive the solution

towards curtailment instructions that are as equally shared as possible among generators and towards margins between the production upper limits and the forecasted production levels that are as large as possible while being also equally shared among generators. By doing so, the

3_{This formulation is used for the sake of understanding. It di↵ers from the exact implementation but defines}

an equivalent mathematical program.

20

Active network management for electrical distribution systems: problem formulation and

benchmark

Quentin Gemine, Damien Ernst, Bertrand Corn´elusse

Montefiore Institute, Department of Electrical Engineering and Computer Science University of Li`ege, 4000 Li`ege, Belgium

{qgemine,dernst,bertrand.cornelusse}@ulg.ac.be

Abstract

In order to operate an electrical distribution network in a secure and cost-efficient way, it is necessary, due to the rise of renewable energy-based distributed generation, to de-velop Active Network Management (ANM) strategies. These strategies rely on short-term policies that control the power injected by generators and/or taken o↵ by loads in order to avoid congestion or voltage problems. While simple ANM strategies would curtail the production of generators, more advanced ones would move the consumption of loads to rel-evant time periods to maximize the potential of renewable energy sources. However, such advanced strategies imply solving large-scale optimal sequential decision-making problems under uncertainty, something that is understandably complicated. In order to promote the development of computational techniques for active network management, we detail a generic procedure for formulating ANM decision problems as Markov decision processes. We also specify it to a 75-bus distribution network. The resulting test instance is available at http://www.montefiore.ulg.ac.be/~anm/. It can be used as a test bed for comparing existing computational techniques, as well as for developing new ones. A solution technique that consists in an approximate multistage program is also illustrated on the test instance.

Index terms— Active network management, electric distribution network, flexibility services, renewable energy, optimal sequential decision-making under uncertainty, large system

1 Introduction

In Europe, the 20/20/20 objectives of the European Commission and the consequent finan-cial incentives established by local governments are currently driving the growth of electricity generation from renewable energy sources [1]. A substantial part of the investments lies in the distribution networks (DNs) and consists of the installation of units that depend on wind or sun as a primary energy source. The significant increase of the number of these distributed genera-tors (DGs) undermines the fit and forget doctrine, which has dominated the planning and the operation of DNs up to this point. This doctrine was developed when DNs had the sole mission of delivering the energy coming from the transmission network (TN) to the consumers. With this approach, adequate investments in network components (i.e., lines, cables, transformers, etc.) must constantly be made to avoid congestion and voltage problems, without requiring con-tinuous monitoring and control of the power flows or voltages. To that end, network planning is done with respect to a set of critical scenarios consisting of production and demand levels, in

(16)

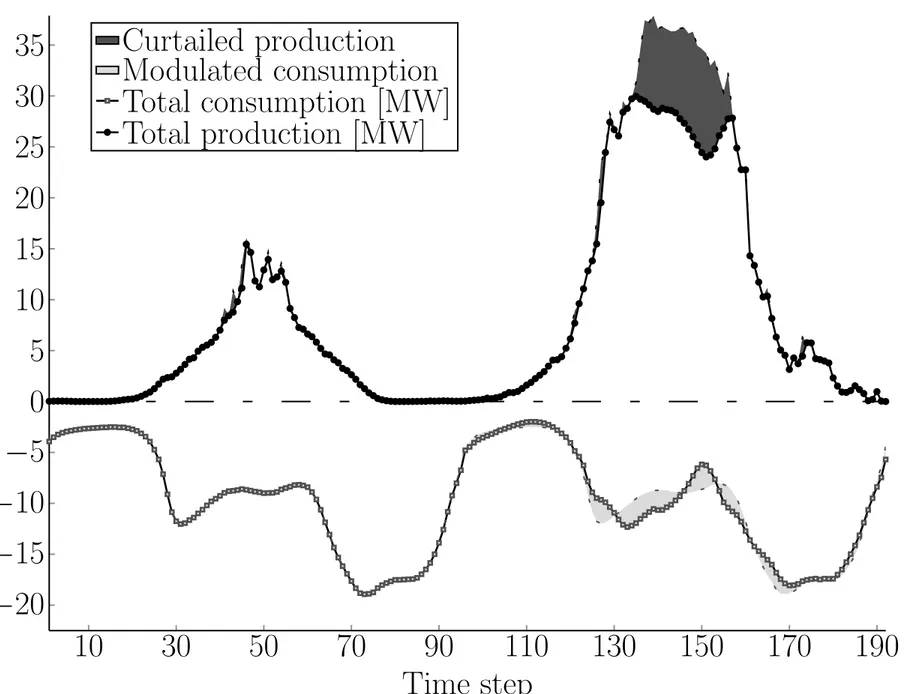
Example of Policy

Figure 14: Example of a simulation run of the system controlled by policy (54)-(62), over two

days.

which is supported by Matlab

r

code that implements a simulator of this test instance (cf.

http://www.montefiore.ulg.ac.be/~anm/). In addition, an example of solution technique

was presented and its performance was reported.

8 Acknowledgment

This research is supported by the public service of Wallonia - Department of Energy and

Sus-tainable Building within the framework of the GREDOR project. The authors give their thanks

for the financial support of the Belgian Network DYSCO, an Inter-university Attraction Poles

Program initiated by the Belgian State, Science Policy Office.

The authors would also like to thank Rapha¨el Fonteneau for his precious advices and

com-ments.

References

[1] D. Fouquet and T.B. Johansson. European renewable energy policy at crossroads – focus

on electricity support mechanisms. Energy Policy, 36(11):4079–4092, 2008.

[2] J.A.P. Lopes, N. Hatziargyriou, J. Mutale, P. Djapic, and N. Jenkins. Integrating

dis-tributed generation into electric power systems: A review of drivers, challenges and

oppor-tunities. Electric Power Systems Research, 77(9):1189–1203, 2007.

[3] S.N. Liew and G. Strbac. Maximising penetration of wind generation in existing distribution

networks. IET Generation Transmission and Distribution, 149(3):256–262, 2002.

[4] L.F. Ochoa, C.J. Dent, and G.P. Harrison. Distribution network capacity assessment:

Variable DG and active networks. IEEE Transactions on Power Systems, 25(1):87–95,

2010.

[5] M. J. Dolan, E. M. Davidson, I. Kockar, G. W. Ault, and S. D. J. McArthur.

Distri-bution power flow management utilizing an online optimal power flow technique. IEEE

Transactions on Power Systems, 27(2):790–799, 2012.

(17)

Thank you

www.montefiore.ulg.ac.be/~anm/

(18)

References

[1] Q. Gemine, E. Karangelos, D. Ernst, and B. Cornélusse. Active network management: planning under uncertainty for exploiting load modulation. In Proceedings of the 2013 IREP Symposium - Bulk Power System Dynamics and Control - IX, page 9, 2013.

[2] W.B. Powell. Clearing the jungle of stochastic optimization. Informs TutORials, 2014.

[3] B. Defourny, D. Ernst, and L. Wehenkel. Multistage stochastic programming: A scenario tree based approach to planning under uncertainty, chapter 6, page 51. Information Science Publishing, Hershey, PA, 2011.

[4] L. Busoniu, R. Babuska, B. De Schutter, and D. Ernst. Reinforcement Learning and Dynamic Programming Using Function Approximators. CRC Press, Boca Raton, FL, 2010.

[5] Q. Gemine, D. Ernst, and B. Cornélusse. Active network management for electrical distribution systems: problem formulation and benchmark. Preprint, arXiv Systems and Control, 2014.