Elasto-Dynamic Model of Robotic Milling Process Considering Interaction between Tool and Workpiece

HAL Id: hal-00667610

https://hal.archives-ouvertes.fr/hal-00667610

Submitted on 26 Jun 2019

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Elasto-Dynamic Model of Robotic Milling Process

Considering Interaction between Tool and Workpiece

Dmitry Bondarenko, Anatol Pashkevich, Sébastien Briot, Mathieu Ritou,

Benoît Furet

To cite this version:

Dmitry Bondarenko, Anatol Pashkevich, Sébastien Briot, Mathieu Ritou, Benoît Furet.

Elasto-Dynamic Model of Robotic Milling Process Considering Interaction between Tool and Workpiece.

ASME 2012 11th Biennial Conference on Engineering Systems Design and Analysis (ESDA 2012), Jul

2012, Nantes, France. pp.217-226, �10.1115/ESDA2012-82239�. �hal-00667610�

ELASTO-DYNAMIC MODEL OF ROBOTIC MILLING PROCESS CONSIDERING

INTERACTION BETWEEN TOOL AND WORKPIECE

D. Bondarenko(a,b) A. Pashkevich(a,b) S. Briot(a) M. Ritou(a,c) B. Furet(a,c)

(a)

Institut de Recherche en Communications et en Cybernétique de Nantes (IRCCyN), UMR CNRS 6497, 1 rue de la Noë, Nantes 44321, France

(b)

Ecole des Mines de Nantes, 4 rue Alfred-Kastler, Nantes 44307, France

(c)

University of Nantes, 1 quai de Tourville, 44035, Nantes, France

KEYWORDS

Robot elasto-dynamic model, cutting force model, vibratory analysis, milling.

ABSTRACT

In this paper, a reduced elasto-dynamic model of the robotic based milling process is presented. In contrast to previous works, it takes into account the interaction between the milling tool and the workpiece that depends on the end-effector position, process parameters and cutting conditions (spindle rotation, feed rate, geometry of the tool, etc.). To reduce the dimension of the problem, the robot dynamics is described as an equivalent mass-spring-damper system with six dimensions. This approach, based on the Rayleigh-Ritz approximation, aims at decreasing computational cost and at avoiding inaccuracy due to ill-conditioning in the full size model. To achieve a realistic modelling of the milling process, the machining efforts due to the interaction between robot, tool and working material are introduced into the robot model and calculated at each time instant. Using this global model that integrates the robot dynamics and the milling process particularities, it is possible to obtain the movement of the robot end-effector and corresponding quality of the final product (profile, macro and micro geometry, roughness, etc.). In addition, this model allows selecting the best process parameters and avoiding the vibratory behavior of this machining system which can dramatically affect the milling quality.

The developed model is applied to the behavior analysis of KUKA KR240 robot used for milling of an aluminum workpiece for automobile industry. This allows finding acceptable range for robot motion profile parameters.

1. INTRODUCTION

Parallel robots have increasingly been used in industry in the last few years, mainly for pick-and-place applications or high-speed machining [1], [2]. This interest is due to their main properties, i.e. their higher rigidity and dynamic capacities compared with their serial manipulator counterparts.

Having a good knowledge of the elasto-dynamic behavior of a manipulator plus its interactions is a crucial point. In this sense, accurate elasto-dynamic models are necessary at both the control stage [3]–[5] and design stage [6]–[8], in order to optimize the geometry, as well as the shape of the elements of the manipulator. This will lead to the creation of a mechanism in which vibrations will be minimized.

Several elasto-dynamic models have been proposed and used in the literature. Three main general methods can be distinguished:

 Finite element analysis (FEA); the FEA method is proved to be the most accurate and reliable, since the links/joints are modeled with its true dimension and shape [7], [9]–[12], but is highly time-consuming. This method is usually applied at the final design stage for the verification and component dimensioning.

 Matrix structural analysis (MSA) method is a common technique in mechanical engineering [13], [14]; it incorporates the main ideas of the FEA but operates with rather large flexible elements (beams, arcs, cables, etc.). This obviously yields reduction of the computational expense and, in some cases, allows analytical stiffness matrix to be obtained. However, this method can only be applied to links with simple shapes and requires improved skills in FEA.

 Virtual joint methods (VJM) [8], [15], which is also referred to as ‘‘lumped modeling”, is based on the expansion of the traditional rigid model by adding virtual joints (localized springs), which describe the elastic deformations of the manipulator components (links, joints and actuators).

Generally, lumped modeling is simpler to use than MSA and provides acceptable accuracy in reduced computational time. The main limitations of these models are:

 Because of the large number of elements they use, they are still highly time-consuming and can lead to few accurate results because of the problem dimension;

 They do not incorporate accurate modeling of the robot interactions, especially regarding the milling process.

The purpose of this paper is to propose a reduced elasto-dynamic modeling approach on parallel robots, based on VJM, combined with an accurate modeling of the milling process efforts. This approach is validated on a KUKA KR240 robot used for milling of an aluminum workpiece for automobile industry.

2. REDUCED ELASTO-DYNAMIC MODELING OF ROBOTS

2.1 Problem Statement

Let us consider a general robot made of n elements and m actuators. Considering that the robot is in an equilibrium position, its elastic potential energy is given by [9]

1 2 T

e tot

V  q K q, where Ktot is the global stiffness matrix of

size p×p, p being the number of elastic coordinates taken into account, and q the vector of elastic generalized coordinates. The robot kinetic energy is given by 1 2 T

tot

T  q M q, where

Mtot is the global mass matrix of size p×p. Starting from these

definitions, and considering that external forces F are applied, it can be demonstrated that the system is governed by the relation [9], [15]:

tot  tot 

M q K q F (1)

Solving this problem involves finding the p generalized of the problem and also inverting the p×p matrix Mtot, which is

highly time-consuming and can lead to few accurate results because of the problem dimension. In order to avoid such kind of drawbacks [16] has recently proposed a new procedure to compute the deformations of the robot when a force is applied at the end-effector. This procedure computes a stiffness (and also compliance) matrix Kr (and Sr, resp.) of dimension six that represents the behavior of the robot in terms of deformations. Moreover, during the procedure, only inversions of 6 dimensional matrices are involved, which considerably reduces computational time and avoids accuracy problems due to ill-conditioning of the large global stiffness matrix. Thus, the global p dimensional problem defined with respect to all variables q has been reduced to a 6 dimensional problem defined with respect to platform deflections t only. As a result,

the entire robot can locally be seen as a virtual spring of dimension six that deforms when applying a wrench on the end-effector.

Starting from these considerations, it would be interesting to reduce the dimension of the problem by expressing equation (1) as a function of the reduced stiffness matrix Kr, of the platform deflections t and, also, as a function of a reduced

mass matrix that will be denoted as Mr, which could represent the global behavior of the robot in terms of natural frequencies. The first section of the paper will be focused on this problem.

2.2 Computation of the Robot Natural Frequencies –

Rayleigh-Ritz Approximation

Considering the robot with free oscillations, equation (1) becomes M q K q_tot  _tot 0. A solution ql of this equation can

be found by solving the system:



2



l tot tot l



M K q 0, with



l2



fl (2) where ql represents the vectors of the shape of free vibrations of

the system for the l-th natural mode, fl and l are their

corresponding natural frequency and pulsation, respectively. If the matrix



_l2M_totK_tot is singular (which is always the case when l is one of the modal pulsation of the robot), ql

becomes non-null and is the eigenvector corresponding to the pulsation l. There is an infinity of vectors ql validating (2) (for

a given l), but all are proportional to the others. Vector ql is

not necessarily dependent of time, but almost represents the amplitude of the vibrations. Therefore, when only the l-th mode of the system is excited, the displacements of all springs may be written under the form:





*

sin l  l



lt



l

q q (3)

where l is a phase difference corresponding to the mode l.

When all modes are excited, the displacement q of all spring centers may be written in the form:





* 1 1 sin p p l l l l l l t     







 q q q (4)

The most common way to find the values of the pulsation

l is to solve the eigenvalue problem



2 1



det l tot tot 0



 

I M K (5)

where I is an identity matrix of dimension p.

Another way to find the natural pulsation l of the mode l

would be to know the exact amplitude l of the displacements ql for this mode. For the natural mode l, the potential and

kinetic energies of the system are given by:









* * 2 * * 2 2 1 2 1 2 sin 1 2 1 2 cos T T e l tot l l tot l l l T T l tot l l l tot l l l V t T t            q K q q K q q M q q M q (6)

From the principle of energy conservation, it follows that

 

 

max V_e max T 0, i.e. qlT





l2MtotKtot



ql0 (7) It is obvious that the exact knowledge of the amplitude ql

is an impossible task without a direct measure on the system of all the displacements of the robot nodes. However, this vector may be approximated by another denoted as qˆ_l that is close to the exact amplitude ql. Introducing this approximated vector qˆl

into (7) will allow us to find a corresponding value of



ˆ_l and, as a result, ˆf which is the approximated natural frequency of _l

the system. Such kind of elasto-dynamic problem resolution is called the Rayleigh-Ritz method [17].

The better the approximation, the more accurate the value of



ˆ_l. The designer’s skills in terms of understanding and analysis of robot physical behavior here are of the utmost importance. In this sense, let us recall that the first natural frequencies are associated with the highest level of energy due to vibrations, and represent the highest displacements of the structure.

Using the Rayleigh-Ritz approximation in order to compute the first natural frequencies, the stresses for which the maximal displacements appear have to be found. From our experience in elastic behavior of robots, it is assumed that a good approximation of these maximal displacements will be the deformation of the robot with a load applied at the end-effector, and it can be shown in the following that this hypothesis is valid. Using this assumption, the displacements ql of all springs

can be computed as a function of the end-effector displacements t, i.e. it is possible to define a matrix Jq such as:

l  p

q J δt (8)

As a result, introducing (8) into (7) will lead to



2



T T T

l tot tot



_{q p} _{q q} 

δt J M J J K J δt 0 (9)

where the matrices T tot q p J M J and T tot q q J K J are now of

dimension 6. It should be mentioned here that, in the case where an external load is applied at the end-effector only, the term T

tot

q q

J K J is equal to the reduced stiffness matrix Kr of the robot. Therefore, (9) can be rewritten as:



2



T l  _r _r  δt M K δt 0, with T tot  r q q M J M J (10)

In the following sections it is explained how to obtain expressions (8) and (10).

2.3 Reduction of the Link Mass Matrix

It is possible to decompose the previously cited task into two sub-problems. First, the displacements of a beam j can be expressed as a function of the displacement of its extremities. Then, one can express the beam extremity displacements as a function of the platform displacements t. Using this approach

will allow for a reduction in the size of the link mass matrices, and thus avoiding creating global mass matrices Mtot with very

large dimension.

Two main ways can be followed to reduce the size of the link mass matrices. The first one consists in discretizing the beam j into pj rigid links and springs and to express their

displacements as a function of the beam extremity displacements. However, such numerical method must be repeated for each link and, thus, increases the size of the algorithm and decreases its efficiency. As a result, it is preferred to use the following procedure which allows analytical expressions to be obtained for the reduced link mass matrices.

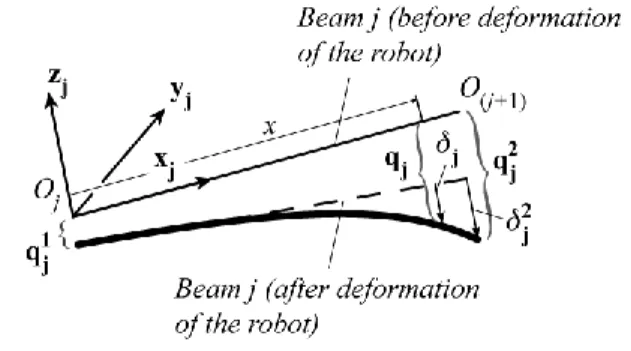
Figure 1: Displacements and elastic deformations of a beam.

Let us consider the link j, modeled as a beam (Figure 1). At this beam is attached a local frame represented by the vectors

xj, yj and zj. Before any deformation of the system, the beam j is linked (rigidly or by a passive joint) to beams (j–1) and (j+1) at points Oj and O(j+1), respectively (Figure 1). After deformation of the robot, the beam extremity located at Oj is

displaced from 1 1 1 1, 2, , 6 T j j j q q q      1 j

q and the one located at

O(j+1) is displaced from 2 21, 22, , 26 T j j j q q q      j

q , where the three

first components of each vector correspond to the translational displacements along local xj, yj and zj axes, respectively, and the three last components to the rotational displacements along the same axes. It should be mentioned that in the remainder of the paper, the left superscript “0” will stand for the coordinates expressed in the global frame. If no left superscript is mentioned, the vector is expressed in the local frame attached to the link j.

The general formula for the kinetic energy of an elastic Bernoulli beam is equal to [14]:





0 1 2 diag , , , , , j L T ij j p y z j j j j j j T dx A A A I I I   



j j j j q Q q Q (11)

In this expression, q_j represents the velocity of the beam cross-section located at position x from the local reference frame (Figure 1), Lj is the length of the beam j, j the mass

density at cross-section x, Aj its area,

p j

I its torsional constant and Iy_j, Iz_j , the quadratic momentums along yj and zj, respectively.

For the l-th natural mode, and from (4), the kinetic energy can be rewritten as:





2 2 0 1 2 cos j L T j l l l j T   t



 q Q q_{j j j}dx (12)

qj being the amplitude of the displacement of the beam cross-section located at position x from the local reference frame (Figure 1).

In the Rayleigh-Ritz approximation, considering that the deformations due to the natural vibrations are similar to those obtained when an external load is applied at the robot end-effector only, each link of the structure will deform due to the stresses transmitted through the robot joints at points Oj. As a

result, the deformations j of the beam cross-section (Figure 1) can be approximated by the deformations of a tip-loaded beam, given by [14]





diag f g g_j, _j, _j,f h h_j, _j, _j  2 j j δ δ (13) where 2





j x L   j j

δ δ represents the deformation of the beam at its tip and

 

 





 





2 3 2 , 0.5 3 , 0.5 j j j j j j j j f x x L g x x L x L h x x L x L      (14)

As a result, the global displacement qj of the beam cross-section at x can be expressed as a sum of two terms:

  3 3 3           1 j j j I D q q δ 0 I , with   0 0 0 0 0 0 0 D x x      _  _     (15)

In this sum, the left terms corresponds to the displacement of the undeformed beam due to the displacement of the node located at Oj.

Introducing (13) to (15) into (12) leads to the following equation:









2 2 0 0 0 0 0 1 2 cos red T j l l l j T   t _ 1 2_ _ 1 2_ j j j j q q M q q (16)

where the expressions of each components of matrix 0 red j

M are given in [18].

2.4 Reduction of the Robot Mass Matrix

Using the results of the previous section, the total kinetic energy of the system is given by:





2 1 2 cos T j l l l tot j T 



T   t q M q (17)

with Mtot diag



0M₁red,0M₂red, ,0Mredp



and

       

0 1 0 2 0 1 0 2

   

0 1 0 2 1 , 1 , 2 , 2 , , , T T T T T T T p p q   _  q q q q q q 

It is necessary to express the relationship linking all vectors

0 v j

q (v = 1, 2) to the end-effector displacements t. For a robot

composed of k legs and using the VJM [16], this displacement is equal to:

i i pi i



 

δt J θ J p (18)

where i represents the deformations of all virtual springs of the

leg i and pi the displacements of its passive joints, and Ji and Jpi are Jacobian matrices relying these displacements to the displacement t. These matrices can be obtained by the

differentiation of the global transformation matrix Ti of the chain i including rigid, passive and elastic coordinates [16].

After several mathematical derivations extracted from [16], the displacement pi of the passive joints of leg i can be expres-

Figure 2 : Architectural representation of a general parallel manipulator

sed as a function of t [18] and it can finally be shown that the

relation between q and t can be written as:

 _q

q J δt (19)

where the expression of Jq is detailed in [18]. Introducing this relation into (17) will lead to:





2 2

1 2 l cos l l T

T





t



δt M δtr (20)

where the expression of Mr is given at (10).

As a result, from (10), finding the robot natural frequencies relies on solving the 6 dimensional eigenvalues problem



2 1



6 det l 0   _{r r}  I M K (21)

2.5 Reduced Elasto-Dynamic Model

To conclude this section, it is necessary to mention that, from the previous obtained results, the robot free dynamic behavior can be modeled using the following expression:

 

r r

M δt K δt 0 (22)

As a result, if external milling forces F are applied on the tool, (22) becomes:

 

r r

M δt K δt F (23)

This expression will be used in the following sections in order to analyze the robot behavior during milling process. It should be mentioned that in order this model to be valid, the displacements of the robots should be sufficiently slow so that the vibratory phenomenon are mainly due to the milling process excitations. Let us now define the expressions for the computation of the milling forces.

3. CUTTING FORCE MODEL

In milling process, the cutting force F that appears in equation (23) is caused by the interaction between the tool and the workpiece. It is a contact force and it is distributed along the affected area of the tool cutting part [19]–[21]. In robotic machining, the tool is mounted on the robot end-effector. In that case, the cutting force serves as a source of an additional external loading for robot and influences its motion. To

evaluate this influence and to correctly analyze the robot behavior while machining, model of cutting force should be defined.

3.1 Basic Expressions

Most of existing works in the area of machining are based on Merchant’s model of cutting, where he assumed that the tool/workpiece contact force is distributed uniformly along the tool cutting edge [20]. Based on this hypothesis, a complex three-dimensional process of cutting can be analyzed referred to the one separated tool cross-section. In this cross-section the distributed cutting force can be presented as an equivalent point

force Fc applied to the cutting edge.

In general, the cutting force Fc has a nonlinear nature and

depends on many factors such as cutting conditions, properties of workpiece material and tool cutting part, etc. [22], [23]. But, for given tool/workpiece combination, the force Fc could be

approximated as a function of an uncut chip thickness h, which represents the desired thickness to cut.

The typical diagram Fc(h) is presented in Fig. 3 [24]. To

describe it analytically, different models (linear, exponential, fractional, etc.) can be found in literature. The linear model perfectly suits to conventional CNC based machining (especially with single-tip tools). Here, usually the high rate removal of working material produces large chip thickness and the relation Fc(h) could be correctly approximated with a linear

function [19], [24] (Fig. 3-a):

  



, 0

c T E

F h  k h k L h (24) where kT is the so called tool/workpiece cutting energy, kE is the

tool/workpiece edge force, L is the width of cut. The model parameters kT, kE are estimated experimentally for a given

combination of tool/working material.

However, in robotic based machining the robot compliance could be the source of considerable relative tool/workpiece displacement. Even, the loss of tool/workpiece contact can be observed. As a result of such behavior, the material removal rate and the corresponding cutting force depend on current position of the tool on its path. So, the linear model Fc(h)

cannot be applied correctly and some nonlinear approximations are required (exponential, fractional, etc.).

The exponential model [21] corresponding to Fig. 3-b is based on the equation

 

m , 0

c F

F h k h L h (25)

where kF is the so called specific cutting force and the power

m<1 depends on the properties of the workpiece and the tool

cutting part. The parameters kF, m are also estimated

experimentally for a given combination of tool/working material. This model is quite popular in industrial applications with machines CNC to analyze different machining operations with multi-edge tools [25]. But the exponential approximation does not fit well the physical phenomena of cutting process in case of small removal of material (i.e. for small h). The main reason for this is that the function (25) has infinite derivative when h tends to zero, which does not correspond to the reality.

In order to avoid this drawback, the fractional model [26] was proposed, that corresponds to Fig. 3-c and is based on the expression

 

0





2 , 0 1 s s c s h h r h h F h k L h h h     (26)

where rk k₀1 depends on the parameters k∞, k0 that

define the so called stiffness of the cutting process for large and small h respectively (see Fig. 3-c) and hs is a specific chip

thickness, which depends on the current state of the tool cutting edge. The parameters k0, hs, r are evaluated experimentally for a

given combination of tool/working material.

In this work, the cutting force will be computed using the fractional model (26). To take into account the latter phenomena, it is allowed for h to be either positive or negative, assuming that

 

0, if 0 c

F h  h (27)

For multi-edge tool the machining surface could be formed by means of several edges simultaneously. The number of working edges varies during machining and depends on the relative tool/workpiece position. Thus, the total force Fc of such

interaction is a superposition of forces Fc,i generated on each

tool edge i, which is currently in contact with the workpiece. Due to the presence of two different types of tool motion (spindle rotation, feed) the contact force Fc,i can be described

with its radial Fr,i and tangential Ft,i components. In accordance

with Merchant’s model [20], the t-component of cutting force

Ft,i can be computed with the equation (26). The r-component

Fr,i is related with Ft,i by following expression [27]

, ,

r i r t i

F k F (28)

where the ratio factor kr depends on the tool/workpiece

characteristics.

In robotic machining it is more suitable to operate with forces expressed in the robot tool frame {x,y,z}. Then, the corresponding components Fx, Fy of the machining force Fc are

expressed as follows , , 1 1 , , 1 1 cos sin sin cos z z z z n n x r i i t i i i i n n y r i i t i i i i F F F F F F             









(29)

where nz is the number of currently working cutting edges, φi is

the angular position of the i-th cutting edge (the cutting force in

z direction Fz is negligible here)

It should be stressed that the cutting force components Fr,i,

Ft,i mentioned in equation (29) are computed regarding the

corresponded chip thickness hi, which should be also evaluated.

Using mechanical approach of analysis of machining operation, the parameter hi is computed in general as the geometrical

distance between the position of the given tooth i and the current machining profile.

h Fc Usual range of h (a) Fc h (b) hs ~k∞ ~k0 Fc h (c)

Figure 3: Linear (a), exponential (b) and fractional (c) cutting force models Fc(h). hi vi ai i i i Fr,i Ft,i Fx Fy vf W TCP Workpiece Tool ai vi vf vWx vWy

Figure 4: The force interaction between the i-th tooth and workpiece and corresponding kinematics.

Let us present algorithms for the computation of hi during

process of robotic milling for three different types of tool fixation, assuming that machining is performed in aluminum workpiece with straight borders. The cutter of the external radius R=10mm with Nz=4 teeth distributed uniformly over the

tool is used. This tool/workpiece combination corresponds to the following cutting force model parameters k0=5 10 6N/m,

hs=1.8 105 

 m, r=0.1, kr=0.3. Let us suppose that the feed is

applied only in x direction (robot base frame). Below, the instant t=0 corresponds to the tool position when one of the teeth is in contact with the working material. Also, it will be supposed that the feed rate vf and the spindle rotational speed Ω

are constant during whole machining process.

3.2. Case A: Rigid Tool Fixation

The objective of this case study is to understand the mechanics of the tool/workpiece interaction, while any dynamic aspect related to the robot compliance is excluded from the analysis. In that case the applied feed rate and spindle rotational speed totally determine the position {xi, yi}, i1,Nz of all tool cutting edges referred to robotic base frame at each instant of machining t







cos , sin 2 1 , 1, i f i i i z i z x v R y R N i i N            W    (30)

The orientation αi of the i-th tooth velocity vi can be

defined by the feed rate vf and the spindle rotational speed Ω at

each instant as a_iatan2





v +v_{f Wx}



v_Wy



with

sin , cos

x i y i

vW  WR  vW  WR  . The angle αi provides

computing the chip thickness hi as the displacement of TCP

corresponding to the one tooth period 2



WN_z and referenced

(a) (b) (c)

Figure 5: Different phases of tool/workpiece interaction (case Nz=4) and corresponding machining forces; (a) – process of tool

engaging into the workpiece, only one tooth can be in contact with workpiece at the same time, (b) – process of tool engaging into the workpiece, several teeth could be in contact with workpiece at the same time, (c) – machining with fully engaged tool.

to the i-th tooth, when it is situated inside the working material. If the given tooth is located outside the working material, the corresponding chip thickness hi is equal to zero. The following

expressions allow evaluating hi for all possible positions of the

i-th tooth on its path while machining

0, sin , 2 , 1, 2 sin , 2 i z i i i i f z f z i i f z x R h x R x v N i N v N x v N a   a     _   W   _{W  W}  (31)

The advantage of the presented algorithm of computing the chip thickness is that different phases of tool/workpiece interaction illustrated in Fig. 5 can be identified.

It should be mentioned that the phase of tool approaching to the workpiece corresponding to the zero machining force is not considered here. For the remaining phases a detailed analysis is presented below:

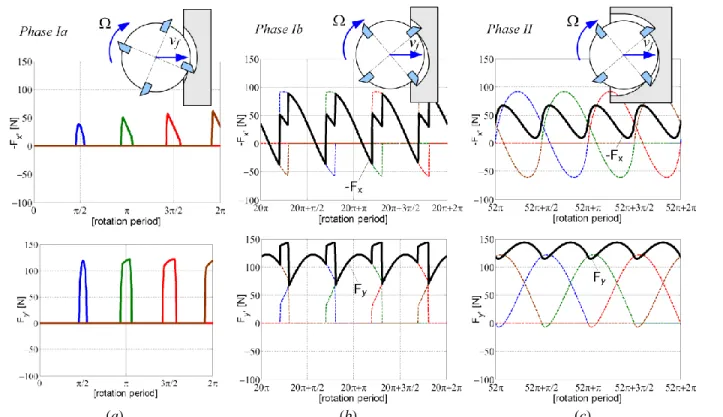
 The phase of tool engaging into the working material (phase I) corresponds to the variable contact area between the tool and the workpiece. The TCP during this phase is located always outside the workpiece. In fact, the phase I can be divided into two sub phases:

 Phase Ia: In the beginning of milling operation a small area of workpiece is affected by the machining process. This fact and presence of two types of motion (feed, spindle rotation) form the case, when only one tooth can participate in cutting at the same time (Fig. 5-a). Such behavior produces intermittent machining forces Fx and Fy with the frequency WNz 2



Hz. The sub phase 1 is very limited in time and its duration depends on the feed rate, the spindle rotational speed and the number of teeth Nz. For example, if

vf=4m/min, Ω=10

4

rpm, Nz=4 the duration of phase Ia

is only 0.04sec.

 Phase Ib: It corresponds to a case, when several teeth can participate in cutting at the same time, but the TCP does not reach the workpiece border (Fig. 5-b). As a result an oscillatory periodic behavior in machining forces Fx and Fy is observed. But, because of different

number of currently working teeth, the force patterns are not homogenous.

 The phase of machining with fully engaged tool (Phase II) starts when TCP reaches the workpiece border (Fig. 5-c). In that case always the same number of teeth (nc=2 for the tool

with Nz=4) is working at every instant of cutting process. It

produces harmonic periodic machining forces Fx and Fy

with the frequency WZ 2



Hz.

So, even with the analysis of tool motion during machining without any dynamic aspect, the oscillatory behavior of machining forces can be detected for whole process. The high frequency of such oscillation (for example, Ω=104

rpm, Nz=4

give frequency of 667Hz) does not affect the motion of robot but it can be crucial for robot control system and should be considered in design of robotic machining process.

0 2 4 6 8 x 10-3 -100 -50 0 50 0.09 0.092 0.094 0.096 0.098 -100 -50 0 50 0.2 0.202 0.204 0.206 -100 -50 0 50 0 0.05 0.1 0.15 0.2 0.25 -100 -50 0 50 Time, [sec] Fx (W o rkp ie ce ->T o o l), [ N ] Phase Ib Fxavg Phase II Phase Ia 0 2 4 6 8 x 10-3 0 20 40 60 80 100 120 140 0.092 0.094 0.096 0.098 0 50 100 150 0.202 0.204 0.206 0.208 0 50 100 150 0 0.05 0.1 0.15 0.2 0.25 0 50 100 150 Time, [sec] Fy (W o rkp ie ce ->T o o l), [ N ] Phase Ib Fyavg Phase II Phase Ia

Figure 6: Machining force patterns with average forces referenced to the frame {x,y}.

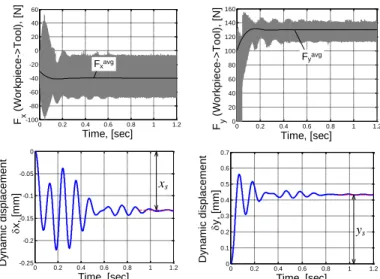
3.3 Case B: Tool Fixation with Compliance in x Direction

In contrast to Case A, the dynamic aspect of tool motion associated with the robot compliance is considered here. Thus, at each instant of machining, the position xTCP is defined as a

superposition of tool displacement xf due to feed and a dynamic

displacement δx due to compliance of the fixation: TCP f

x x x. The first component x_f v_f is known at each instant of process while the second one depends on the current position of the tool regarding to the machining profile. In this case, the dynamic displacement δx can be obtained by reducing the equation (23) to a one-dimensional problem and by introducing the damping related to the machining process and robot control algorithms

x x x

M x C







xK



xF (32) where M is the equivalent mass of the tool fixation, Kx and Cx

are its stiffness and damping respectively and Fx is the

machining force in x direction. The damping c_x 2



k m_x is related to the damping factor ζ, which can be estimated experimentally.

{xi,yi} τ TCP τ TCP τ-Dτ i τ-Dτ i τ Da R {xi,yi} τ-_Dτ W

A

i Workpiece area hi Dsx Dsy Nodes xf + x Dτ τ-Dτ

Figure 7: Evaluating the tool/workpiece intersection Ai and

computing the corresponding chip thickness hi.

0 0.2 0.4 0.6 0.8 1 1.2 -100 -80 -60 -40 -20 0 20 40 60 Time, [sec] Fx ( W o rkp iece -> T o o l) , [N ] Fxavg 0 0.2 0.4 0.6 0.8 1 1.2 0 20 40 60 80 100 120 140 160 Time, [sec] Fy ( W o rkp iece -> T o o l) , [N ] Fyavg 0 0.2 0.4 0.6 0.8 1 1.2 -0.2 -0.15 -0.1 -0.05 0 Time, [sec] D yn a m ic d is p lace m e n t  x, [m m ] τs xs 5%

Figure 8: Machining force patterns and TCP dynamic displacement in case of 1DOF model (M=100 kg, Kx=3 × 10 N/m, ζ=0.05, N5 z=4,

Ω=104

rpm, vf=4 m/min).

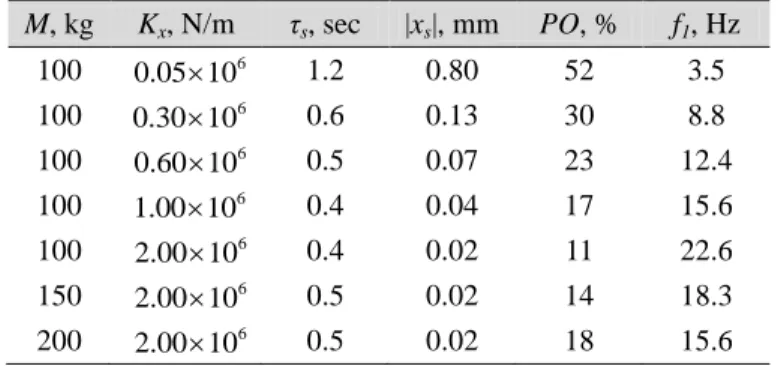
Table 1: Influence of tool fixation parameters on the tool motion; τs

is the settling time, PO is the overshoot, f1 is the first frequency of

the tool dynamic displacement in feed direction; ζ=0.05, Nz =4,

Ω=104 rpm, vf=4 m/min M, kg Kx, N/m τs, sec |xs|, mm PO, % f1, Hz 100 _{0.05 10} 6 _{1.2 0.80 52 3.5} 100 _{0.30 10} 6 _{0.6 0.13 30 8.8} 100 _{0.60 10} 6 _{0.5 0.07 23 12.4} 100 _{1.00 10} 6 _{0.4 0.04 17 15.6} 100 _{2.00 10} 6 _{0.4 0.02 11 22.6} 150 _{2.00 10} 6 _{0.5 0.02 14 18.3} 200 _{2.00 10} 6 _{0.5 0.02 18 15.6}

Next, the position of the i-th tooth in the robot base frame {x,y} can be easily determined:

sin , cos , 1, z

i TCP i i i

x x R



y R



i N .

Comparative analysis of this position with respect to the current machining profile defines the chip thickness hi

removing by i-th tooth. But, the main issue here is to define whether i-th tooth participates in cutting for given instant of process. For this reason, it is proposed to create a mesh on the

workpiece, where each node j ( j1,N_w, Nw is the number of

nodes) can be filled with “1” or “0”: “1” corresponds to nodes situated in the workpiece area with material, “0” corresponds to nodes situated in workpiece area that was cut away.

In order to define the number of currently cut nodes by the

i-th tooth, the previous instant of machining process should be

considered. Let us define Ai as an amount of working material

that is currently cut away by the i-th tooth. So, if node j filled with “1” is located inside the sector, it changes to “0” and Ai is

increasing by D Ds_x s_y (Δsx, Δsy are node steps in x and y

directions respectively). Analyzing all potential nodes and computing Ai, the chip thickness hi, removed at given instant of

process by the i-th tooth, can be estimated by hi A Ri D

a

i, 1, z

i N . The angle Δαi determines the current angular position

of the i-th tooth regarding to its position at the instant τ-Δτ (Δτ is the time step) and referred to the position of TCP at τ-Δτ.

Here, in contrast to the previous case, the dynamic aspect of the tool motion allows

 estimating of deviation in tool motion from the desired one because of the robot compliance in the feed direction. It should be mentioned that this deviation affects the Cartesian stiffness of robot but does not influence the machining profile quality. For example, following parameters M=100 kg, Kx=3 10 5 N/m, ζ=0.05, Nz=4, Ω=104 rpm, vf=4 m/min

provide deviation in the feed direction of 0.13mm (Fig. 8). But it is not essential for this application.

 detecting of vibratory behavior of tool motion while it is engaging into the workpiece. In some cases the low frequency of such motion can excite robot natural frequency, destabilize machining operation and even damage the tool or/and workpiece. For example, the milling process with following parameters M=100 kg, Kx=3 10 5

N/m, ζ=0.05, Nz =4, Ω=104 rpm, vf=4 m/min generates

vibration of f1=8.8Hz from the beginning of cutting process

in addition to the frequency 667Hz related to the spindle rotation.

More details on influence of the tool fixation parameters (M, Kx) on the dynamics of its motion during machining are

presented in Table 1, which covers the range of values for M, Kx

computed for different configurations of the robot KUKA KR 240 using equations presented in Section 2.

As it can be observed from the table, changing the fixation parameters (i.e. the robot configuration) influences low frequencies (about 10 – 20 Hz) of the tool motion.

0 0.2 0.4 0.6 0.8 1 1.2 -100 -80 -60 -40 -20 0 20 40 60 Time, [sec] Fx ( W o rkp iece -> T o o l) , [N ] Fxavg 0 0.2 0.4 0.6 0.8 1 1.2 0 20 40 60 80 100 120 140 160 Time, [sec] Fy ( W o rkp iece -> T o o l) , [N ] Fyavg 0 0.2 0.4 0.6 0.8 1 1.2 -0.25 -0.2 -0.15 -0.1 -0.05 0 Time, [sec] D yn a m ic d is p lace m e n t  x, [m m ] xs 0 0.2 0.4 0.6 0.8 1 1.2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 Time, [sec] D yn a m ic d is p lace m e n t  y, [m m ] ys

Figure 9: Machining force patterns and TCP dynamic displacements in case of 2DOF model (Mr,xx=Mr,yy=100 kg,

Kr,xx=Kr,yy=3 × 10 N/m, N5 z=4, Ω=10

4

rpm, vf=4 m/min).

Table 2: Influence of the tool fixation parameters on tool dynamic behavior; f1x, f1y are first frequencies of the tool dynamic

displacement in x and y directions respectively; Nz =4, Ω=104 rpm,

vf=4 m/min M r,xx=M r,yy, kg K r,xx=K r,yy, N/m |xs|, mm |ys|, mm f1x, Hz f1y, Hz 100 6 0.05 10 0.80 2.61 3.2 2.2 100 _{0.30 10} 6 _{0.13 0.43 8.2 7.3} 100 6 0.60 10 0.07 0.22 12.4 11.4 100 _{1.00 10} 6 _{0.04 0.13 15.6 14.6} 100 6 2.00 10 0.02 0.06 22.4 21.5 150 _{2.00 10} 6 _{0.02 0.06 18.3 17.4} 200 6 2.00 10 0.02 0.06 15.6 15.6 Suitable robot configurations to perform given machining operation could be defined. But, it should be mentioned that this one dimensional equivalent model presented here allows analysis of machining process dynamics in the feed direction only. In order to evaluate behavior of the tool motion more closely to the real machining operation, this model should be extended.

3.4 Case C: Tool Fixation with Compliance in x and y Directions

In this case, a dynamic aspect of tool motion in feed direction (x) and orthogonal to it (y) is considered. Then, similarly to the Case B, at each instant of machining process, the position of TCP is determined by

,

TCP f TCP f

x x x y y y, where x_f v_{f x,}, y_f v_{f y,}. The dynamic displacements δx, δy could be obtained from the equation (23) which, in this case, is reduced to

x y F x x x F y y y          _  _                    r r Μ C Κ (33)

where Mr (2×2) is the equivalent mass matrix of the tool fixation, the matrices Kr (2×2) and C (2×2), where

, 2 , , ,

i j 



i j i j i j

C K M characterize the fixation stiffness and damping respectively (which can be estimated experimentally),

Fx and Fy are the machining forces in x and y directions.

In contrast to the previous case, the position of the i-th tooth at each process instant t includes dynamic components in both directions: x_ix_TCPRsin



_i, y_iy_TCPRcos



_i,

1, z

i N . The algorithm of computing the chip thickness hi for

given position of tooth {xi, yi} is similar to Case B.

In order to illustrate the advantages of this two dimensional model and its ability to detect some phenomena (that are not visible in Cases A, B) the robotic milling process is simulated for KUKA KR 240 robot with the following parameters

5 5 100 0 3 10 0 550 0 , kg, , , , 0 100 0 3 10 0 550 sec N kg m        _{ } _{ } _{ }        r r M K C .

Here, the equivalent mass matrix Mr is computed in accordance with the method presented in the Section 2 of this paper. The stiffness Kr is the structural stiffness of the robot, referred to its end-effector. It should be noted that in practice the non diagonal elements in these matrices are non zero. But, with this simplified case it is possible to identify qualitatively the dynamic nature of the tool behavior in the direction (y) orthogonal to the feed. Simulation results corresponding to this case study are presented in Fig. 9.

It should be also stressed that the tool dynamic behavior in the feed direction (x) is similar to the results, which were obtained in the Case B. The displacement in y-direction has an essential dynamic component during the phase of tool engagement (Phase I) into the workpiece and becomes constant while machining with fully engaged tool. The corresponding frequency f1y=7.3Hz is comparable with the frequency

f1x=8.2Hz of the tool dynamic displacement in feed direction.

More details on the tool motion during milling process regarding to the parameters of the tool fixation are presented in Table 2 (it covers the range of values for Mr,xx, Mr,yy, Kr,xx, Kr,yy

computed for different configurations of the robot KUKA KR 240 using the methodology presented in Section 2)

It should be noted that changing the robot configuration affects the tool dynamics in y direction which is crucial regarding to the quality of the final product. Hence, considering the tool displacement orthogonal to the feed direction is essential and the Case C gives more realistic results comparing Cases A and B. As it is shown in Fig. 9, the deviation (0.31 – 0.56mm) in machining profile from the desired one has a vibratory behavior during the phase of tool engagement into the workpiece. Thus it cannot be suppressed by straightforward compensation methods and other compensation techniques should be proposed.

4. CONCLUSION

In this paper, a reduced elasto-dynamic model of the robotic based milling process has been presented. In contrast to previous works, it takes into account the interaction between the milling tool and the workpiece that depends on the end-effector position, process parameters and cutting conditions (spindle rotation, feed rate, geometry of the tool, etc.). To reduce the dimension of the problem, the robot dynamics have been described as an equivalent mass-spring-damper system with six dimensions. This approach aims at decreasing computational cost and at avoiding inaccuracy due to ill-conditioning in the full size model. To achieve a realistic modeling of the milling process, the machining efforts due to the interaction between robot tool and working material have been introduced into the robot model and calculated at each time instant. This model has allowed selecting the best process parameters and avoiding the vibratory behavior of this machining system which can dramatically affect the milling quality.

The developed model has been applied to the elasto-dynamic behavior analysis of KUKA KR240 robot used for milling of an aluminum workpiece for automobile industry. This allowed us estimating the deviation in motion of the robot end-effector during machining caused by the flexibilities in robot links and joints, which essentially influence the quality of the final product.

ACKNOWLEDGMENTS

The authors would like to acknowledge the financial support of the ANR, France (Project ANR-2010-SEGI-003-02-COROUSSO) and the Region “Pays de la Loire”, France.

REFERENCES

[1] Brogardh T. Present and future robot control development – an industrial perspective. Annual Reviews in Control, 31 (1):69–79, 2007.

[2] Chanal H., Duc E., Ray P. A study of the impact of machine tool structure on machining processes. Int. J. of Machine Tools and Manufacture, 46 (2):98–106, 2006.

[3] Singer N. Residual vibration reduction in computer controlled machines. PhD thesis, Department of Mechanical Engineering, MIT, Fall, 1988. [4] Singhose W., Singer N., Seering W. Comparison of command methods

for reducing residual vibrations. Proceedings of the 1995 European Control Conference, Rome, Italy 5-8 September, 1995.

[5] Pelaez G., Pelaez Gu., Perez J.M., Vizan A., Bautista E. Input shaping reference commands for trajectory following Cartesian machines. Control Engineering Practice, 13:941-958, 2005.

[6] Voglewede P.A., Ebert-Uphoff I. Overatching framework for measuring the closeness to singularities of parallel manipulators. IEEE Transactions on Robotics, 21(6):1037–1045, 2005.

[7] Bouzgarrou B.C., Fauroux J.C., Gogu G., Heerah Y. Rigidity analysis of T3R1 parallel robot uncoupled kinematics. Proceedings of the 35th International Symposium on Robotics, Paris, March, 2004.

[8] Briot S., Pashkevich A., Chablat D. On the optimal design of parallel robots taking into account their deformations and natural frequencies. ASME 2009 IDETC/CIE, San Diego, California, USA, August, 2009. [9] Shabana A.A. Dynamics of multibody systems. 3rd _{Ed. Cambridge}

University press.

[10] Cammarata A., Sinatra R. The elastodynamics of a 3-CRU spherical robot. Proc. of the 2nd _{Int. Workshop on Fund. Issues and Future Rob.} Res. Dir. for Parallel Mech. and Manip., Montpellier, France, September 21–22, 2008.

[11] Bettaieb F., Cosson P., Hascoët, J.-Y. Modeling of a high-speed machining center with a multibody approach: the dynamic modelling of flexible manipulators. Proceedings of the 6th International Conference on High Speed Machining, San Sebastian, Spain, March 21-22, 2007. [12] El-Khasawneh B.S., Ferreira P.M. Computation of stiffness and stiffness

bounds for parallel link manipulators. Int. J. of Machine Tools and Manufacture, 39(2):321-342, 1999.

[13] Deblaise D., Hernot X., Maurine P. Systematic analytical method for PKM stiffness matrix calculation. Proceedings of the IEEE ICRA, Orlando, Florida, May, pages 4213–4219, 2006.

[14] Imbert J.F. Analyse des structures par éléments finis. Cepadues ed.,1979. [15] Wittbrodt E., Adamiec-Wojcik I., Wojciech S. Dynamics of flexible

multibody systems. Springer-Verlag, 2006.

[16] Pashkevich A., Chablat D., Wenger P. Stiffness analysis of over constrained parallel manipulators. Mechanism and Machine Theory, 44(5):966–982, 2009.

[17] Birkhoff G., De Boor C., Swartz B., Wendroff B. Rayleigh-Ritz approximation by piecewise cubic polynomials. SIAM Journal on Numerical Analysis, 3(2):188-203, 1966.

[18] Briot S., Pashkevich A., Chablat D. Reduced elastodynamic modelling of parallel robots for the computation of their natural frequencies. 13th World Congress in Mechanism and Machine Science, 19 - 25 Juin, 2011, Guanajuato, Mexico.

[19] Altintas Y. Manufacturing automation, metal cutting mechanics, machine tool vibrations and CNC design. Cambridge University Press, New York, 2000.

[20] Merchant M.E. Mechanics of metal cutting process. I-Orthogonal cutting and type 2 chip. J. of Applied Physics, 16(5):267–275, 1945.

[21] Jayaram S., Kapoor S.G., Devor R.E. Estimation of the specific cutting pressures for mechanistic cutting force models. Int. J. of Machine, Tools and Manufacture, 41(2):pp.265-281, 2001.

[22] Merrit H.E. Theory of self-excited machine-tool chatter. Trans. ASME, J. of Engineering for Industry, 87(4):447-454, 1965.

[23] Tlusty J., Ismail F. Basic non-linearity in machining chatter. Annals of CIRP, 30(1):299-304, 1981.

[24] Armarego E.J.A., Brow E. The machining of metals. Prentice Hall Inc., Englewood Cliffs, NJ, 1969.

[25] Peigne G., Paris H., Brissaud D., Gouskov A. Impact of the cutting dynamics of small radial immersion milling operations on machined surface roughness. Int. J. of Machine, Tools and Manufacture, 44(11):1133-1142, 2004.

[26] Brissaud D., Gouskov A., Paris H., Tichkiewitch S. The Fractional Model for the Determination of the Cutting Forces. Asian Int. J. of Science and Technology – Production and Manufacturing, 1(1):17-25, 2008.

[27] Laporte S., K’nevez J.-Y., Cahuc O., Darnis P. Phenomenological model for drilling operation. Int. J. of Advanced Manufacturing Technology, 40:1-11, 2009.