Les Apports de l’Intelligence Artificielle aux Approches Probabilistes pour l’Optimisation de Portefeuille d’Actifs Financiers

(1)

UNIVERSITÉ MOHAMMED V – AGDAL

FACULTÉ DES SCIENCES

Rabat

N° d’ordre 2656

THÈSE DE DOCTORAT

Présentée par

EL HACHLOUFI Mostafa

Discipline : Mathématiques Appliquées

Spécialité : Mathématiques Financières et Statistiques

Les Apports de l’Intelligence Artificielle aux Approches

Probabilistes pour l’Optimisation de Portefeuille d’Actifs Financiers

Soutenue le 29/06/2013

Devant le jury :

Président :

SOUISSI Ali PES Université Mohammed V-Agdal, Faculté des Sciences – Rabat

Examinateurs :

GUENNOUN Zine El Abidine PES Université Mohammed V-Agdal, Faculté des Sciences – Rabat

BENBACHIR Saâd PES Université Mohammed V-Agdal, Faculté des Sciences Juridiques, Economiques et Sociales Agdal– Rabat HAMZA Faris PES Université Abdel Malek Essaâdi, Faculté

Polydisciplinaire de Tetouan

BENSOUDA Charaf PES Université Ibn Tofail, Faculté des Sciences – Kénitra BELMAHJOUB Faycal PH Université Ibn Tofail , Faculté des Sciences – Kénitra

(2)

Avant Propos

Les travaux présentés dans ce mémoire ont été effectués dans le laboratoire

Analyse, Algèbre et Aide à la Décision sous la direction de Monsieur Zine El Abidine Guennoun.

Je tiens tout d’abord à remercier mon directeur de thèse Monsieur Zine El Abidine Guennoun qui a su me communiquer toutes ces années son

enthousiasme et sa motivation. Ses commentaires et suggestions tout au long de ma thèse ont considérablement amélioré à la fois le contenu et la présentation de cette dernière. Je remercie également mon co-encadrant Monsieur Faris Hamza, Professeur d’enseignement supérieur à Université Abdel Malek Essaâdi, Faculté Polydisciplinaire de Tetouan, pour les conseils et les remarques qu’il m’a prodigués pendant cette période.

Je remercie également Monsieur Ali Souissi, Professeur d’enseignement supérieur à l’Université Mohamed V - Agdal, Faculté des Sciences de l’honneur qui’il m’a fait d’avoir accepté de présider mon jury de thèse.

Je remercie aussi Monsieur Saâd Benbachir Professeur d’enseignement supérieur à l’Université Mohamed V-Agdal, Faculté des Sciences Juridiques, Economiques et Sociales – Rabat pour l’intérêt qu’il a porté à mes travaux en acceptant la tâche fastidieuse de rapporteurs. Je remercie aussi Monsieur Charaf Bensouda et Monsieur Faycal Belmahjoub, Professeurs à l’Université Ibn Tofail, Faculté des Sciences –Kénitra d’avoir accepté d’être membres de jury.

Je tiens à remercier mes parents de leurs encouragements, ma femme pour son aide précieuse et ses conseils lors de la préparation de la soutenance et mes sœurs pour leur soutien.

(3)

Résumé

Dans ce travail, nous avons mis en œuvre de nouvelles approches basées sur les méthodes d’intelligence artificielle et statistiques pour l’optimisation d’un portefeuille d’actifs financiers. En effet, nous avons développé un algorithme appelé MinVaRMaxVaL basé sur les algorithmes génétiques permettant, pour une valeur de portefeuille fixée, de minimiser le risque mesuré par la valeur à risque (VaR), puis de maximiser la valeur de portefeuille, d’une manière dynamique, de telle sorte que le risque obtenu soit inférieur à celui obtenu précédemment et la valeur finale de portefeuille soit supérieure à celle fixée à l’avance. Cet algorithme est utilisé aussi pour optimiser un sous portefeuille d’actions. Ce dernier est obtenu par une méthode de classification K-Means et réalise le rendement espéré le plus élevé et la VaR moyenne la plus petite.

Un autre algorithme appelé MinMRSV est réalisé en se basant sur les algorithmes génétiques et les réseaux de neurones pour minimiser la mesure de risque semi-variance (MRSV) d’une manière dynamique en considérant que les proportions et les paramètres de cette mesure sont variables.

Nous avons aussi développé un algorithme qui permet de réduire la taille d’un portefeuille en extrayant de ce dernier un sous portefeuille afin de réaliser un surplus de gain financier en termes de réduction de coût et de performance au niveau de la réduction des charges de calcul. Ce résultat est obtenu par la sélection d’un nombre d’actions à partir de ce portefeuille qui a une contribution faible (respectivement élevée) sur le risque (respectivement la valeur) de portefeuille. Ce sous portefeuille subit une procédure d’optimisation. Le même objectif est atteint par un autre algorithme développé en se basant sur les algorithmes génétiques, les réseaux de neurones et la logique floue pour optimiser un portefeuille de meilleures actions sélectionnées, c'est-à-dire

(4)

celles ayant les rendements les plus élevés et les risques les plus petits en utilisant la prévision et la classification.

Egalement, nous avons réalisé une formule explicite pour estimer la CVaR d'un portefeuille d'actions investies dans un marché dont la distribution des rendements suit une loi log-normale.

Enfin, nous avons mis en œuvre une nouvelle approche permettant de choisir un portefeuille optimal de produits financiers Islamiques en utilisant des algorithmes génétiques de telle sorte que pour une valeur de portefeuille fixée, le risque de ce dernier est nul ou presque nul, vu que l'investissement dans le marché des produits financiers Islamiques est en pleine expansion.

Mots Clés :

Optimisation, Portefeuille, Actifs financiers, Risque, Algorithmes génétiques, Réseaux de neurones, Logique floue, VaR, CVaR, Produits financiers Islamiques.

(5)

Abstract

In this work, we have implemented new approaches based on artificial

intelligence and statistical methods to optimize the portfolio of financial assets we developed an algorithm called MinVaRMaxVaL based on genetic algorithms, for a fixed value of portfolio, we minimize the risk measured by the value at risk (VaR) and we maximize the value of the portfolio dynamically, such that the risk obtained is lower than who is obtained previously and the final

portfolio value is higher than that fixed in advance.

This algorithm is also used to optimize a sub portfolio. It is obtained by a method of K-Means classification and achieves the expected highest and the average VaR smallest.

Another algorithm called MinMRSV is made based on genetic algorithms and neural networks. This algorithm minimize the risk measure semi-variance (MSRV) dynamically, whereas the proportions and the parameters of this measurement are variable.

We have also developed an algorithm that reduces the portfolio size in order to make a portfolio in portfolio that achieve a surplus of financial gain in terms of cost reduction and performance at reduced loads.

This result is achieved by selecting a number of shares from the portfolio which has a low (respectively higher) contribution of the portfolio risk (respectively value). This sub portfolio undergoes an optimization procedure. The same result is achieved by another algorithm based on genetic algorithms, neural networks and fuzzy. This algorithm optimize a portfolio of the best stocks selected, i.e: the stocks whose have the highest returns and smaller risks using prediction and classification.

(6)

Also, we have made an explicit formula for estimating CVaR of a portfolio of stocks invested in a market whose return distribution follows a log-normal distribution.

Finally, we implemented a new approach to select an optimal portfolio of Islamic financial products using genetic algorithms such that for a fixed value of

portfolio risk, this risk is zero or almost zero. Because the investment in the market for Islamic financial products is in full expansion.

Keywords:

Optimization, portfolio, financial assets, Risk, Genetic Algorithms, Neural Networks, Fuzzy Logic, VaR, CVaR, Islamic financial products.

(7)

Tables des matières

INTRODUCTION GENERALE ... 1

CHAPITRE 1 : ETAT DE L’ART D’OPTIMISATION DE PORTEFEUILLE D’ACTIFS FINANCIERS ... 6

I. THEORIE ET CONCEPT DE RISQUE ... 7

1.DEFINITION ET CONCEPT DE RISQUE ... 7

2.COHERENCE DE MESURE DE RISQUE ... 9

II. APPROCHES D’OPTIMISATION DE PORTEFEUILLE D’ACTIFS FINANCIERS ... 11

1.APPROCHE DE MARKOWITZ (1952) ... 11

2.APPROCHE DE SHARPE (1963-1964) ... 18

2.1 Modèle à indice simple de Sharpe ... 18

2.2 Modèle de marché de Sharpe ... 19

2.3 Modèle d’équilibre des actifs financiers (MEDAF) ... 23

3.APPROCHE DE MARKOWITZ ET PEROLD (1981) ... 25

4.APPROCHE DE LAI (1991) ... 26

5.LE MODELE KONNO ET YAMAZAKI (1991) ... 28

6.LE MODELE DE SPERANZA (1993) ... 30

7.MODELE MOYENNE – SEMI-VARIANCES DE HAMZA &JANSSEN (1995)... 32

8.APPROCHE DE YOUNG (1998) ... 34

9.APPROCHE BASEE SUR LA VALEUR A RISQUE (2000) ... 36

CHAPITRE 2 : ESTIMATION DE LA CVAR DE PORTEFEUILLE D’ACTIONS INVESTIES DANS UN MARCHE LOG-NORMAL ... 38

I. ELEMENTS DE PROCESSUS STOCHASTIQUES APPLIQUES A LA FINANCE ... 38

1.LES PROCESSUS STOCHASTIQUES ... 38

2.PROCESSUS ET LEMME D'ITO ... 39

3.LE MODELE DE BLACK &SCHOLES ... 41

(8)

II. ESTIMATION DE LA CVAR DE PORTEFEUILLE D’ACTIONS

INVESTIES DANS UN MARCHE LOG-NORMAL ... 45

1.LA VALUE AT RISK (VAR) ET LA CVAR ... 46

2.LA VAR DE PORTEFEUILLE D’ACTIONS ... 49

3.LA CVAR DE PORTEFEUILLE D’ACTIONS ... 55

4.ESTIMATION DE LA CVAR DE PORTEFEUILLE D’ACTIONS INVETIES DANS UN MARCHE LOG-NORMAL ... 58

CHAPITRE 3 : OPTIMISATION DE PORTEFEUILLE D’ACTIONS A L’AIDE DES ALGORITHMES GENETIQUES ... 62

I. LES ALGORITHMES GENETIQUES (AG) ... 62

1.CODAGE DE DONNEES ET GENERATION DE LA POPULATION INITIALE... 63

2.EVALUATION DES INDIVIDUS ... 64

3.PRINCIPES DE SELECTION ... 64

4.OPERATEUR DE CROISEMENT ... 65

5.OPERATEUR DE MUTATION ... 65

II. OPTIMISATION DE PORTEFEUILLE D’ACTIONS INVESTIES DANS UN MARCHE LOG-NORMAL EN UTILISANT LA CVAR ET LES ALGORITHMES GENETIQUES ... 66

1.ALGORITHME D’OPTIMISATION... 67

2.PROCEDURE D’OPTIMISATION ... 67

III. OPTIMISATION DE PORTEFEUILLE D’ACTIONS A L’AIDE DES ALGORITHMES GENETIQUES ET LA VALEUR A RISQUE (VAR)... 69

1.ALGORITHME D’OPTIMISATION MINVARMAXVAL ... 70

3.APPLICATION NUMERIQUE ... 71

IV. OPTIMISATION DE PORTEFEUILLE D’ACTIONS EN UTILISANT LA CLASSIFICATION ET LES ALGORITHMES GENETIQUES ... 73

1.ALGORITHMES D’OPTIMISATION ... 73

CHAPITRE 4 : OPTIMISATION DE PORTEFEUILLE D’ACTIONS A L’AIDE DES ALGORITHMES GENETIQUES ET LES RESEAUX DE NEURONES ... 78

(9)

I. LES RESEAUX DE NEURONES ... 78

1.LE RESEAU DE NEURONES MULTICOUCHE ... 79

2.APPRENTISSAGE DES RESEAUX DE NEURONES ... 80

3.L’APPRENTISSAGE ET L’ALGORITHME DE RETROPROPAGATION ... 81

II. LE MODELE DE REGRESSION MULTIPLE ... 83

1.ESTIMATION DES PARAMETRES DU MODELE ... 84

2.ANALYSE DE VARIANCE ET LE COEFFICIENT DE DETERMINATION MULTIPLE ... 85

3.TEST D’HYPOTHESES... 86

II. MINIMISATION DE RISQUE SEMI-VARIANCE DE PORTEFEUILLE D’ACTIONS EN UTILISANT LES RESEAUX DE NEURONES ET LES ALGORITHMES GENETIQUES ... 88

1.ALGORITHME DE MINIMISATION DE MRSV ... 89

IV. OPTIMISATION DE PORTEFEUILLE D’ACTIONS EN UTILISANT LES ALGORITHMES GENETIQUES ET LES RESEAUX DE NEURONES... 95

1.REGRESSION PAR LES RESEAUX DE NEURONES ... 95

2.ALGORITHME DE SELECTION DE PORTEFEUILLE OPTIMAL D’ACTIONS ... 97

CHAPITRE 5 : OPTIMISATION DE PORTEFEUILLE D’ACTIONS A L’AIDE DES ALGORITHMES GENETIQUES,LES RESEAUX DE NEURONES ET LA LOGIQUE FLOUE ... 101

I.LA LOGIQUE FLOUE (LF) ... 101

1.OPERATIONS ET PROPRIETES DES ENSEMBLES FLOUS ...102

2.SYSTEME D’INFERENCE FLOUE...103

3.CONCEPTION DU CLASSIFICATEUR FLOU ...106

II. OPTIMISATION DE PORTEFEUILLE D’ACTIONS A L’AIDE LES RESEAUX DE NEURONES ET LA LOGIQUE FLOUE ET LES ALGORITHMES GENETIQUES ...107

1.PREDICTION DES RENDEMENTS ET DES RISQUES DES ACTIONS PAR LES RESEAUX DE NEURONES ...108

2.CONCEPTION DU CLASSIFICATEUR FLOU ...109

(10)

CHAPITRE 6: ALGORITHME D’OPTIMISATION DE PORTEFEUILLE DE

PRODUITS FINANCIERS ISLAMIQUE ... 113

1.NOTIONS DE BASE DE LA FINANCE ISLAMIQUE ... 113

2.LES PRODUITS FINANCIERS ISLAMIQUES ... 115

2.1 Mourabaha ... 115 2.2 Al Ijar ... 115 2.3 Salam ... 116 2.4 Istisna’a ... 117 2.5 Moudaraba ... 117 2.6 Moucharaka... 118

3.RISQUE DE PRODUITS ISLAMIQUES ... 118

3.1 Les risques de la Mourabaha : ... 118

3.2 Les risques de l’Istisnaa ... 119

3.3 Les risques de la Moudarabah ...120

3.4 Les risques de la Moucharaka ...120

4.ALGORITHME D’OPTIMISATION DE PORTEFEUILLE DE MODARABA ET MORABAHA ...122

CONCLUSION ...125

PUBLICATIONS...128

(11)

Liste de figures

FIGURE 1.1 : FRONTIERE EFFICIENTE DANS LE PLAN

ESPERANCE-VARIANCE ... 14

FIGURE 1.2 : RISQUE ET DIVERSIFICATION ... 23

FIGURE 3.1 : ALGORITHME GENETIQUE DE BASE... 63

FIGURE 3.2 : OPÉRATION DE CROISEMENT... 65

FIGURE 3.3: OPÉRATION DE CROISEMENT ... 66

FIGURE 3.4 :ALGORITHME MINVARMAXVAL ... 70

FIGURE 3.5 : REPRESENTATION GRAPHIQUE DE LA VALEUR DU PORTEFEUILLE EN UTILISANT L’ALGORITHME MINVARMAXVAL ET LES ALGORITHMES GENETIQUES. ... 72

FIGURE 3.6 : REPRESENTATION GRAPHIQUE DE LA VAR DU PORTEFEUILLE EN UTILISANT L’ALGORITHME MINVARMAXVAL ET LES ALGORITHMES GENETIQUES. ... 72

FIGURE 3.7 : CLASSES RETENUES PAR LA METHODE DE CLASSIFICATION ... 76

FIGURE 3.8: REPRESENTATION GRAPHIQUE DE LA VAR DE PORTEFEUILLE INITIAL (IP) ET SOUS PORTEFEUILLE (SP) POUR UN NOMBRE D’ACTIONS. ... 76

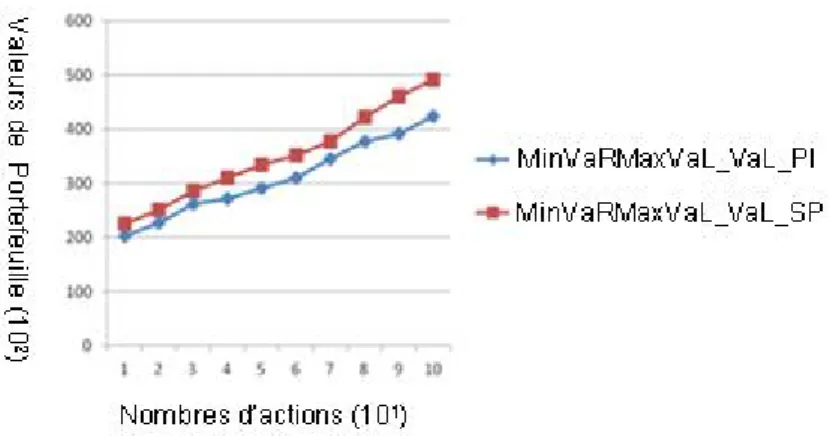
FIGURE 3.9: REPRESENTATION GRAPHIQUE DE LA VAL DE PORTEFEUILLE INITIAL (IP) ET SOUS PORTEFEUILLE (SP) POUR UN NOMBRE D’ACTIONS. ... 77

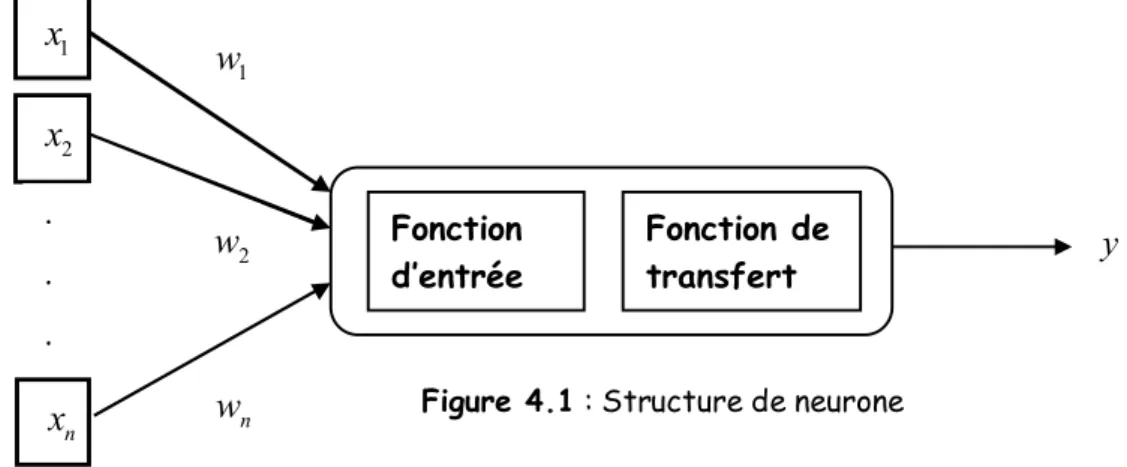
FIGURE 4.1 : STRUCTURE DE NEURONE... 78

FIGURE 4.2: BOITE NOIRE DE RESEAUX DE NEURONES ARTIFICIELS ... 79

FIGURE 4.3 : STRUCTURE DE RÉSEAUX MULTICOUCHE ... 80

FIGURE 4.4 : STRUCTURE DES AG UTILISEE DANS L’ALGORITHME MINMRSV ... 90

FIGURE 4.5 : STRUCTURE DES RN UTILISEE DANS L’ALGORITHME MINMRSV ... 92

(12)

FIGURE 4.6: ALGORITHME DE MINIMISATION DE MINMRSV ... 93

FIGURE 4.7: REPRESENTATION GRAPHIQUE DE RISQUE DE L’ALGORITHME MINMRSV ET DE L’ALGORITHME MRSV-HJ POUR UN CERTAIN NOMBRE DE RENDEMENTS INITIAUX ... 94

FIGURE 4.8: BACKWARD DE PROPAGATION DE CORRECTION D’ERREUR ... 96

FIGURE 4.9 : ALGORITHME DE SELECTION DE PORTEFEUILLE OPTIMAL . 98 FIGURE 4.10: LA VAR DE SOUS PORTEFEUILLE SP EN FONCTION DES NOMBRE DES ACTIONS ...100

FIGURE 4.11: LA VAL DE SOUS PORTEFEUILLE SP EN FONCTION DES NOMBRE DES ACTIONS ...100

FIGURE 4.12 : REPRESENTATION GRAPHIQUE DE RISQUE DE SOUS PORTEFEUILLE SP PAR L’ALGORITHME ASPO ET L’ALGORITHME BASE SUR L’AG POUR UN CERTAIN NOMBRE DE RENDEMENTS. ...100

FIGURE 5.1 : REPRESENTATION D’UN SOUS-ENSEMBLE FLOU ET PRINCIPALES CARACTERES...102

FIGURE 5.2 :STRUCTURE D’UN SYSTEME D’INFERENCE FLOUE ...104

FIGURE 5.3 : SCHEMA SYNOPTIQUE D’UN CLASSIFICATEUR FLOU ...106

FIGURE 5.4 : RESEAUX MULTICOUCHE ...109

FIGURE 5.5: REPRÉSENTATION DE LA FONCTION D'APPARTENANCE ...109

FIGURE 5.6 : BASE DE RÈGLES ... 110

FIGURE 5.7: REPRESENTATION GRAPHIQUE DE RISQUE DU PORTEFEUILLE INITIAL ET DE SOUS-PORTEFEUILLE DE L'ALGORITHME RMSV ET DE L'ALGORITHME HJSV POUR UN CERTAIN NOMBRE DE RENDEMENTS. ... 112

FIGURE 5.8: REPRESENTATION GRAPHIQUE DE RISQUE DU PORTEFEUILLE INITIAL ET DE SOUS-PORTEFEUILLE DE L'ALGORITHME MSRV_IP ET DE L'ALGORITHME MSRV_SP POUR UN CERTAIN NOMBRE DE RENDEMENTS. ... 112

FIGURE 6.1 : CONTRAT DE LA MOURABAHA ... 115

(13)

FIGURE 6.3 : CONTRAT DE SALAM ... 116 FIGURE 6.4: CONTRAT DE LA MOUDARABA ... 117 FIGURE 6.5 : CONTRAT DE LA MOUCHARAKA... 118

(14)

Introduction générale

Contexte du travail

L’optimisation de portefeuille ou le choix optimal de portefeuille d’actifs financiers est un sujet qui a occupé un intérêt particulier dans la recherche en mathématiques financières.

Dans ce cadre, Markowitz a été le premier à introduire un modèle appelé moyenne-variance en 1952 basé sur la variance des rendements de portefeuille observés autour de leur moyenne comme mesure de risque pour le choix optimal de ce dernier.

En effet, le modèle de Markowitz consiste à minimiser l’écart-type ou la variance pour un rendement donné ou de maximiser le rendement du portefeuille pour un risque donné.

Cependant, plusieurs critiques ont été adressées à ce modèle comme le choix de la variance en tant que mesure de risque, la charge de calcul et l’hypothèse sur le caractère quadratique de la fonction objectif, l’hypothèse sur la normalité des rendements des actifs financiers,…etc. Nous reviendrons plus en détails sur ces critiques dans le premier chapitre.

Ces critiques donnent lieu à plusieurs tentatives d’amélioration de ce modèle ou de développement de nouveaux modèles.

Dans ce cadre plusieurs modèles ont été proposés pour réduire la charge de calcul et linéariser le problème de choix optimal de portefeuille dont ceux de Sharpe et Stone sont les plus populaires.

D’autre part, plusieurs auteurs comme Konno, Konno et Yamazaki , Zenios et Pang

(15)

la forme linéaire au lieu de la forme quadratique pour développer des modèles de programmation linéaire afin de sélectionner un portefeuille optimal et inclure le critère de risque asymétrique pour faciliter l’optimisation.

D’autres auteurs comme Pedersen et Stchell ont généralisé une famille de fonctions de risques en introduisant une classe qui englobe la majorité des mesures de risque.

Egalement, Hamza et Janssen ont proposé une nouvelle mesure de risque sous la forme d’une combinaison convexe des semi-variances, et ce dans le but de généraliser les modèles standards de mesure de risque.

Dans le même sens, Homaifar, Grootveld et Huang ont développé des modèles de mesure de risque en se basant sur la minimisation de la semi-variance.

Quand à Chopra et Hlouskova, une variété de modèles a été réalisée en utilisant la variance comme mesure du risque dans diverses situations.

Tous les modèles précédemment soulignés ne permettent pas de calculer de manière explicite la perte que pourra subir un investisseur ou une institution financière (établissement de crédit , banque, compagnie d’assurance,…), d’où la naissance d’une nouvelle mesure de risque appelée value at risk (VaR) développée par la géante banque américaine J.P.Morgan en 1995.

Cette mesure permet de quantifier la perte maximale qui pourrait toucher un portefeuille pour une certaine probabilité sur une période donnée.

La VaR présente plusieurs avantages comme la facilité de comparaison et d'interprétation. Cependant, des études récentes, comme celle de Szergõ qui a montré que celle-ci souffre de plusieurs inconvénients, le plus marquant étant la non prise en compte du montant des pertes excédant la VaR et la sous-additivitée, ce qui signifie qu'avec cette mesure, toute diversification n'implique pas un risque réduit.

(16)

Pour surmonter les limites de la VaR, une nouvelle mesure de risque appelée VaR conditionnelle et notée CVaR définit comme étant la moyenne des VaR, de niveau supérieur à celui de la VaR, est adoptée à sa place.

Objectifs et contributions

Les différents modèles présentés précédemment agissent soit sur le rendement (en le maximisant pour un risque donné ) soit sur le risque (en le minimisant pour un rendement donné) afin d’optimiser un portefeuille d’actifs financiers, mais ils n’ agissent pas sur les deux en même temps d’une manière dynamique. En effet, cette dernière n’est que peu entamée dans la littérature. C’est ainsi que nous l’avons développée dans ce travail à travers un algorithme dynamique appelé MinVaRMaxVaL.

En outre, tous ces modèles s’appliquent sur le portefeuille afin de déterminer, à travers l’optimisation, les proportions du capital investies qui rendent optimal ce dernier (but recherché).

Cependant, ils ne s’appliquent pas sur une partie ou un ensemble d’actifs financiers de ce portefeuille pour atteindre le même but. Démarche qui est presque absente et aussi peu entamée dans la littérature, et que nous avons traité dans ce travail. Et ce, en faisant extraire à partir de ce portefeuille, appelé portefeuille initial, un ensemble d’actifs financiers, appelé sous portefeuille. Ce dernier est pertinent, c'est-à-dire donne lieu à un rendement plus élevé et un risque plus bas par rapport à celui du portefeuille initial, ce qui permet d’obtenir un sous portefeuille d'actifs financiers optimal d'une taille réduite par rapport au portefeuille initial. Cette démarche conduit à un surplus de gain financier en termes de coût et une performance à la réduction des charges de calcul.

(17)

Cette approche est développée en utilisant les algorithmes génétiques et la classification d’une part, les réseaux de neurones, la logique floue et les algorithmes génétiques d’autre part.

Dans un autre cadre, les modèles construits pour minimiser la mesure de risque semi-variance (MRSV), supposent que les paramètres de cette dernière sont constants et agissent seulement sur les proportions. Dans ce travail , nous avons considéré que les paramètres de risque mesuré par la combinaison convexe des deux semi-variances, ainsi que les proportions du portefeuille, sont variables et nous avons développé un algorithme dynamique appelé MinMRSV afin de déterminer en même temps d’une façon dynamique les proportions et les paramètres de risque (MRSV) conduisant au choix du portefeuille optimal. Egalement, nous avons réalisé des formules mathématiques explicites et une estimation de la CVaR pour les portefeuilles d'actifs financiers dans le cas où les rendements suivent la loi normale et la loi log-normale en utilisant le modèle de marché en temps continu développé par Merton.

Organisation du travail

Notre travail est organisé comme suit :

Dans le premier chapitre, nous avons traité la théorie et le concept de risque puis nous avons présenté les différentes approches d’optimisation de portefeuille d’actifs financiers existants dans la littérature, en expliquant les diverses critiques adressées à chacune de ces approches ainsi que quelques avantages et inconvénients de certaines d’entre elles.

Dans le deuxième chapitre, nous avons présenté des applications de méthodes statistiques pour l’estimation de la mesure de risque CVaR de portefeuille

(18)

d’actifs financiers investis dans un marché Log-Normal ainsi que la minimisation de risque de ce portefeuille mesuré parla CVaR.

Au niveau du troixème, du quatrième et du cinquième chapitre, un ensemble de procédures d’optimisation de portefeuille d’actions basées sur l’intelligence artificielle à savoir les algorithmes génétiques, les réseaux de neurones et la logique floue a été présentées.

Dans le dernier chapitre, nous avons défini un nouvel algorithme d’optimisation de portefeuille composé de deux produits financiers Islamiques à savoir : le produit Mourabaha et le produit Moudaraba afin d’encourager les investisseurs à s’orienter vers le marché de produits financiers Islamiques.

(19)

Chapitre 1 : Etat de l’art de l’optimisation de portefeuille

d’actifs financiers

L’optimisation de portefeuille d'actifs financiers est depuis longtemps un sujet d'intérêt majeur dans le domaine de la finance. Dans ce cadre les préoccupations majeures de l’investisseur se résument souvent à savoir si son portefeuille pourrait offrir un meilleur rendement sans que le risque auquel il est exposé ne s’en trouve accentué.

Markowitz fut le premier à introduire un modèle appelé moyenne-variance basé sur le risque dans l’optimisation de portefeuille en proposant la variance des rendements observés autour de leur moyenne, comme mesure de risque. Mais son modèle reste peu employé dans la pratique à cause des ressources importantes, le caractère quadratique de la fonction objectif et la charge de calcul de la matrice de variance-covariance.

Afin de simplifier les difficultés liées à la charge computationnelles du modèle de Markowitz, plusieurs modèles ont été proposés comme des modèles alternatifs à l’approche moyenne-variance. Certains auteurs ont tenté de linéariser le problème de choix de portefeuille comme Sharpe qui a proposé le modèle à indice, le modèle de marché et le modèle d’équilibre des actifs financiers (MEDAF).

D’autres ont développé plusieurs modèles de programmation linéaire pour la sélection de portefeuille optimal : Konno & Yamazaki et Speranza ont proposé de calculer le risque de portefeuille à l’aide de la forme linière au lieu de la forme quadratique Ils ont proposé un modèle basé sur le critère de risque asymétrique, ce qui permet d’éliminer les difficultés associées au modèle d’optimisation quadratique.

(20)

Hamza & Janssen ont généralisé les modèles standards en proposant une mesure de risque définie comme une combinaison convexe des deux semi-variances par la simplification du critère moyenne-écart absolu en utilisant la forme linèaire.

I. Théorie et concept de risque 1. Définition et concept de risque

La théorie du risque a été développée par Frank Knight qui s’est intéressé à démontrer qu’il existe deux types de risques. Le premier type de risque est probabiliste et il peut être assuré tandis que le deuxième type de risque est celui de risque d’entreprise qui est non assuré car lié à la politique de cette dernière et non pas aux aléas.

Le risque est un évènement préjudiciable et aléatoire qui ne répond à aucun facteur déterminé. Il correspond au hasard et non à l’incertitude.

Le risque est défini par l'imprécision au niveau de sa survenance, sa réalisation, la date de sa réalisation et son montant.

La mesure de risque se base sur l'analyse de la probabilité, de survenance d’un évènement et de son estimation.

La gestion des risques au sein des entreprises a suscité ces dernières années un intérêt croissant ce qui a conduit à des investissements importants pour le développement de systèmes efficaces et la mise en ouvre une série d’outils de gestion de risque.

La gestion des risques joue un rôle très important dans la stabilité financière des entreprises. En effet, plusieurs entreprises ont connu des pertes financières importantes, ou même des faillites à cause d’une mauvaise maîtrise des risques.

(21)

Généralement, il existe deux grands types de risques. Les risques non quantifiables, et les risques quantifiables.

Les risques non quantifiables sont des risques non mesurables et peuvent engendrer des pertes financières importantes. Le risque légal, le risque opérationnel, et le risque médiatique sont parmi les principaux risques appartenant à cette famille.

Le risque légal survient lorsqu’une entreprise effectue des transactions financières avec une autre non habilitée à effectuer une telle opération.

Le risque médiatique est dû à un événement qui entame la confiance ou nuit à l’image de l’entreprise.

Le risque opérationnel est le risque de pertes directes ou indirectes résultant d’une inadéquation ou d’une défaillance des systèmes internes, des personnes, ou provenant d’évènements extérieurs.

Concernant les risques quantifiables, nous citons le risque de crédit et le risque de marché.

Le risque de crédit (ou risque de défaut) survient lorsqu’une contrepartie ne peut ou ne veut remplir ses obligations contractuelles.

Le risque de marché qui résulte des variations d’un ou de plusieurs facteurs du marché. Les principaux risques de marché sont :

- Le risque de change :survient lorsque l’investisseur effectue des transactions dans une devise étrangère.

- Le risque de taux d’intérêt survient lorsque l’investisseur a des emprunteurs ou des prêteurs sur le marché. L’investisseur risque de voir des résultats défavorables grâce aux variations de taux d’intérêt.

(22)

- Le risque sur portefeuille d’actions dont l’évaluation du rendement dépend des fluctuations des actions dans le marché.

2. Cohérence de mesure de risque

Soit  l’ensemble des valeurs ou les rendements possibles d’un actif financier et une collection de sous ensemble de .

est un attribut de  si elle vérifie les conditions suivantes :    B B C  ₁ 1 ,..., _i i A A A =



Soient P:

[ ]

0,1 une mesure de probabilité et le couple

₍

,

₎

un espace mesurable.

On appelle une variable aléatoire sur

₍

,

₎

, toute fonction : Soit X  : une variable aléatoire, vérifiant donc:

]

(

)

1

, ,

X x x

Soit



, ,F P



l’espace de probabilité et V un ensemble non vide de variables

aléatoires -mesurable à valeurs réelle. On appelle une mesure de risque toute fonction :

:V

 

 

X X

Le risque auquel est soumis l’actif financier pour une période de temps est décrit par la variation de sa valeur ou son rendement dans cette période.

(23)

Dans ce cas, la mesure de risque est une fonction  faisant correspondre à un

risque X , un nombre positif noté 

 

X qui permet de quantifier le niveau de danger inhérent à ce risque.

Selon Artzner et Heath [Art 97], une mesure de risque est dite cohérente si elle vérifie les propriétés suivantes :

- Invariance par translation

Pout toute constante c et  X  on a :





Xc





 

X c



1.13



La propriété d’invariance par translation signifie que si on ajoute (ou soustrait) un montant initial c au portefeuille initial dans l’actif de référence, la mesure de risque  accroît (ou décroît) par c .

- Sous-additivité

Pour tous les risques X  et Y   on a :



X Y



 

X

 

Y

   



1.14



La sous-additivité traduit l’effet de diversification que signifie la réduction de risque et qui est mesuré par : _



X Y





 

X 

 

Y _0. Cela veut dire que si on a deux portefeuilles de risques séparés, le capital requis pour le portefeuille combiné est inférieur à la somme des capitaux requis pour chaque portefeuille.

Remarque :

Si 



X Y





 

X 

 

Y quelles que soient les risques X et Y , on dit qu’il y a

(24)

- Homogénéité

Pout toute constante c et  X  on a :





cX



c

 

X



1.15



La multiplication de chaque risque d’un portefeuille par un scalaire positif augmente la mesure de risque par le même scalaire.

L’homogénéité peut être vue comme un cas limite de la sous-additivité, lorsqu’il n’y a aucune diversification possible, c'est-à-dire :





XX ... X



c

 

X



1.16



- Monotonicité

Pour tous les risques X  et Y   on a :





X Y



 1 

 

X 

 

Y



1.17



Cette propriété exprime que si le risque d’un portefeuille est supérieur à celui d’un autre, le capital requis pour le premier portefeuille est supérieur à celui requis pour le deuxième.

II. Approches d’optimisation de portefeuille d’actifs financiers 1. Approche de Markowitz (1952)

Soit pt le prix d’une action a à la fin de la période t , la variation de prix



pt  pt1



désigne le gain, auquel s’ajoute éventuellement le revenu dt, appelé

dividende payé au cours de la période t .

Le rendement de cette action au cours de la période t est défini comme suit :



1



1 t t t t t p p d r p     



1.1



(25)

Soit P un portefeuille d’actions



A1,...,An



représenté par un vecteur



x xn



x  1,..., où xi désigne la proportion du capital C investie dans l’action ai

caractérisée par son rendement incertain ri



i1,...,n



.

Le rendement de ce portefeuille est défini comme suit :

 

1 n j j j R x r x  



_

1.2

_

La valeur et la variation de ce portefeuille sont définies respectivement comme suit : 1 n i i i VaL x p  

_



1.3



 

1 n i i i V x x p   

_





1.4



Harry Markowitz [Mar 52] a eu le premier, l'idée de mesurer la rentabilité d'un portefeuille par l'espérance de rendement et le risque par sa variance.

L’approche de Markowitz appelée aussi moyenne-variance consiste à minimiser le risque de ce portefeuille en fixant le rendement minimal  attendu par cet investisseur ou inversement, c'est-à-dire : Maximiser le rendement espéré en fixant le risque minimal souhaité par cet investisseur.

Le rendement du portefeuille est une variable aléatoire dont l’espérance sera donnée par :

 

1 1 n n j j j j j j E R x E r x x E r           _ _     







Donc E R x_

 

_ 1 n j j j x r  





1.5



(26)

La variance du rendement de portefeuille est donnée par :

 

2 2 2 1 1 n n i i i i i i R x E R x E R x E r x r x                       





Ce qui implique que :

2

 

R x  _ _ 1 1 n n i j ij i j x x   

_



1.6



L’algorithme d’optimisation de Markowitz qui en résulte s’écrit comme suit:

1 1 n n i j ij i j Min x x          



Sous les contraintes :

1 1 1 0 =1,..., n j j j n j j j x E r x x j n          



Il s’agit d’un problème de programmation quadratique qui engendre une combinaison moyenne-variance réalisable.

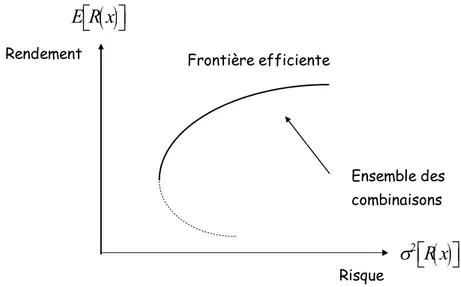
L’ensemble de combinaison possible des moyennes-variances de portefeuilles est dit efficace, si parmi tous les portefeuilles de même rendement espéré que lui, il n’existe aucun risque strictement inférieur. La frontière efficace est l’ensemble de portefeuilles efficaces (efficients).









2 2 2 1 1 1 1 1 1 cov , i j n n n n n n i i i i i i j ij i j i j i i i j i j E r r x x  x x x x r r           _  _    







 

(27)

Dans le cas où xj, =1,...,j n est quelconque, c'est-à-dire les ventes à découverte

sont autorisées et si la contrainte sur la rendement minimum attendu par l’investisseur est égal à  , on utilise la technique des multiplicateurs de Lagrange pour calculer la solution optimale. La fonction Lagrangienne utilisée est donnée par :





_                   

_

_

    1 , , ,..., 1 2 1 1 1 1 2 1 1 n j j n j j j n i n j ij j i n x x x R x x x L       Il s’ensuit que n i R x x L i n j ij j i ,..., 1 0 2 ₁ ₂ 1       



    0 1 1     



   n j j jR x L 0 1 1 2     



 n j j x L  Il en résulte que 1 . . C x K x C K    où

Figure 1.1 : Frontière efficiente dans le plan Espérance-Variance

Rendement

 

   Frontière efficiente Ensemble des combinaisons Risque

 

2 R x



_ _

 

E R x_ _

(28)

                 0 0 1 ... 1 0 0 ... 1 2 ... 2 ... 1 2 ... 2 1 1 1 1 11 n n nn n n R R R R C     avec :  xt 

_

x x₁, ₂,...,x_n, , ₁ ₂

_

 t 0, 0,..., 0, ,1 nfois K = ___

Supposons qu’on a un capital C0 qu’on désire répartir entre n actions (actifs risqués) et un actif sans risque caractérisé par un rendement fixe r0, une

variance nulle ( 2 0

1   n

 ) et une covariance nulle de son rendement avec les autres rendements des actifs risqués (_i_,_n_₁ 0 pour i1,...,n).

Soit xi la proportion du capital C investie dans l’actif i



i1,...,n



et par xn1 le pourcentage du capital investi dans l’actif sans risque. On a:

 

2 2 2 1 0 1 1 1 1 n n n n j j n j j i j ij j j i j R x σ R x x r σ R x x x  _                _ _ _ _   



 







Alors les contraintes sur le rendement espéré et le capital deviennent :

1 1 1 0 1 1   



    n j j n n j j j x r x R x 

La fonction Lagrangienne est donnée par :





_                    

_

_

       , , 1 , ,..., 1 1 2 0 1 1 1 1 1 2 1 1 1 n j j n n j j j n i n j ij j i n n x x x x R x r x x x L       Il s’ensuit que

(29)

n i R x x L i n j ij j i ,..., 1 0 2 ₁ ₂ 1       



    1 0 2 0 1        r x L n 0 0 1 1 1        



  x R x r L n n j j j 1 0 1 1 2     



  n j j x L  Il en résulte que: 1 . . C x K x C K    où :                      0 0 1 1 ... 1 0 0 1 0 0 0 1 0 2 ... 2 . . . .. ... 1 0 2 ... 2 0 1 0 1 1 1 11 r R R r R R C n n nn n n     avec : 

_

1, 2,..., , 1, ,1 2

_

t n n x  x x x x    t 0, 0,..., 0, 0, ,1 nfois K = _{}

(30)

L’approche moyenne-variance proposée par Markowitz reste peut employée dans la pratique à cause de plusieurs limites qui sont:

 La charge de calcul : le déroulement de l’optimisation nécessite le calcul de



1



2

n n 

covariances, alors il est clair qu’à l’époque, ce programme d’optimisation nécessitait des ressources importantes en terme matériel informatique.

 Le caractère non linèaire (quadratique ) de la mesure de risque utilisée par Markowitz est très sensible à la taille du programme d’optimisation utilisé pour la détermination de portefeuille optimal.

 La perception du risque par l’investisseur n’est pas symétrique par rapport à la moyenne, alors que la variance prend en compte de la même manière les variations au dessous et en dessus de la rentabilité espérée.

 La distribution de rendement : Markowitz suppose que le rendement des actifs suit la loi normale, cependant plusieurs études ont montré que ce résultat n’est pas toujours vérifié dans la réalité.

 Le coût de transaction : Les coûts de transaction ne sont pas pris en compte dans l’approche de Markowitz, alors ils sont incontrôlables dans la réalité.

 La mesure de risque introduite par Markowitz ne permet de mesurer de manière explicite la perte éventuelle que pourra subir l’investisseur. Il est intéressant de souligner que chacune de ces critiques adressées à cette approche a conduit à des tentatives de modifier de cette approche pour accommoder ces critiques émises sur un point ou un autre.

(31)

2. Approche de Sharpe (1963-1964)

2.1 Modèle à indice simple de Sharpe

Sharpe [Sha 63] a été le premier qui a tenté de simplifier le modèle de Markowitz en développant les modèles à indice qui se base sur la simplification de la matrice de variances-covariances afin de réduire la charge de calcul.

Sharpe a proposé une diagonalisation de cette matrice en se basant sur le modèle à un seul indice en supposant que les fluctuations des rendements des actions peuvent être exprimés à l’aide d’une régression simple.

Autrement dit,

ri aib Ri I i pour i1,...,n



1.7



où:

 R_I : est le rendement de l’indice I

 _i : est une variable aléatoire appelée bruit blanc qui vérifié les hypothèses suivant : o E

 

_i  0,et 2 _0 i   pour i1,...,n o



_i _j



i j j i, cov , 0,   _ _ ; o _, cov

_

, R

_

0, iI i I      pour i1,...,n

Le rendement de portefeuille devient :

 

n 1 i 1 1 1 n n n i i i i I i i i i i i i R x x r x a R x b x          _ _  



Soit

_

   n i i i n xb x 1 1 il en résulte :

 

_

      n i i i I n n i i ia x R x x x R 1 1 1 



1.8



Le rendement espéré est donné par :

(32)

 

 

n i 1 i 1 x _i _n _I E R x a x _E R       



,

La variance du rendement est :

2 2 2 2 2 1 1 i n P i n I i x _ x   _  

_





1.9



Donc on a besoin que de



n 1



termes à estimer au lieu de



1



2

n n 

variances et covariances pour l’approche de Markowitz.

Le concept de l’approche de Markowitz est basé sur la diversification qui permet de réduire davantage le risque du portefeuille. Malheureusement on ne peut réduire complètement le risque en augmentant indéfiniment la taille de portefeuille.

Sharpe a montré que le risque d’un portefeuille quelconque peut être décomposé en deux parties : le risque diversifiable ou risque non systématique et le risque non diversifiable ou risque de marché.

2.2 Modèle de marché de Sharpe

Sharpe [Sha 64] a remplacé l’indice I par l’ensemble du marché M dans le

modèle à indice simple. Dans ce cas, ce modèle porte le nom modèle de marché.

Le modèle de marché suppose une relation linéaire entre le rendement d’une action i et le rendement global du marché :

r_i _i _iR_M _i



1.10



où i est une variable aléatoire définie comme dans le modèle à indice simple.

Les paramètres i et i sont obtenus par la régression simple comme suit :









2 cov , var i M iM i M M r R R     



1.11



(33)

et

i E

 

RI iE



RM



RiRM



1.12



Selon les hypothèses précédentes, il en résulte:

 









2

i

var var var

i ri iRM i iRM i          _i2var





var

 

_i2 2 2 i M i M R _          où









2 cov , var i M iM i M M r R R     



1.13



 Le coefficient bêta i appelé le coefficient de risque systématique du

titre i permet de mesurer le pourcentage des fluctuations du rendement de ce titre .

 Le risque d’une action peut être décomposé en deux parties : o 2 2

iM

 : représente le risque systématique de l’action o 2

i



 : représente le risque non systématique .

Soit un portefeuille x



x1,...,xn



composé de n titres où xi représente la

proportion du capital investie dans iéme titre. Le rendement de chaque titre i

s’écrit comme suit :

riiiRM i pour i1,...,n.



1.14



Le rendement global de portefeuille est :

 

1 1 1 1 . n n n n i i i i M i i i i i i i i P M P R x x r x R x x R x                 



Le rendement du portefeuille est donné par :

(34)

où

_

  n i i i P x 1 

 est appelé le coefficient bêta du portefeuille. Le risque de portefeuille est :

 





 





2 2 P 1 Var P P M P M P n M P M i i i

Var R x Var R x Var R x

R Var x Var R Var x

            _ _ _   _ _  _     _ _  _ _ 



 Donc 2 2 2 2 2 1 . i n P P M i i x _       

_



1.16



Supposons que n x x x₁  ₂ ... _n  1. Alors :

_

   n i M P P _i n 1 2 2 2 2 2 1     



1.17



Posons 2 1 max i n i M _    , il en résulte que n M n nM n n i i   

_

 2 1 2 2 1 0 _ . Donc

_{ }

2 2 2 limn P  P M.

Comme dans le cas d’un seul titre, le risque de portefeuille peut être décomposé en deux parties :

 2 2 M P

 : le risque systématique de portefeuille 

_

 n i i i x 1 2 2 

 : le risque non systématique qui peut être éliminé en diversifiant le capital investi entre l’ensemble des actions.

Cette décomposition de risque est appelée l’effet de portefeuille ou l’effet de construction de portefeuille sur le risque, qui se décompose en deux éléments :

 L’effet Markowitz (ou effet des corrélations négatives)  L’effet de diversification (ou effet des non-corrélations).

(35)

Considérons un portefeuille contenant n titres à pondération égale :

n

x_i  1 pour tout i1,...,n.

Soit ij la corrélation entre les rendements ri et rj des deux titres i et j.

Si _ij  0  ,i j 1,...,n alors le risque de portefeuille sera :

Var R x



 



x n i ii i n i i n    



2



1 2 2 1 1  



1.18



Supposons que toutes les variances sont bornées, alors _i2  M pour tout

1,...,

i n. Il en résulte que Var R x



 



M

n

 . Donc lim_n_



Var R x



 



0 Il s’agit de l’effet des non-corrélations.

Par contre si ij  0 i j, 1,...,n



i  j



alors le risque de portefeuille devient:

Var R x

_

 

_

n i i n n ij j n i n i j      



1 1 2 2 1 2 1 1  



1.19



Pour n suffisamment grand, le risque de portefeuille devient

approximativement :



 



2 1 1 1 n n ij i j i j Var R x n     

_



1.20



Or ij  i j ,i j1,..., n



i j



, donc on aura ij   j n i n i j i j j n i n i j n M      







 1 1 1 1 2 2 . Posons j i n i n j ij moyenne n n Cov   



  1 1 ) 1 ( 1  _{. Il en résulte que}





2 2 1 M Cov n n n moyenne   ,

Alors lim_n_



Var R x



 



 où



moyenne



nCov

 lim

 .

(36)

 Le risque diversifiable : la partie de risque qui est dû à l’effet de diversification et que l’on peut éliminer en augmentant la taille de portefeuille.

 Le risque non-diversifiable (ou le risque de marché): la partie de risque que l’on ne peut éliminer.

Remarque :

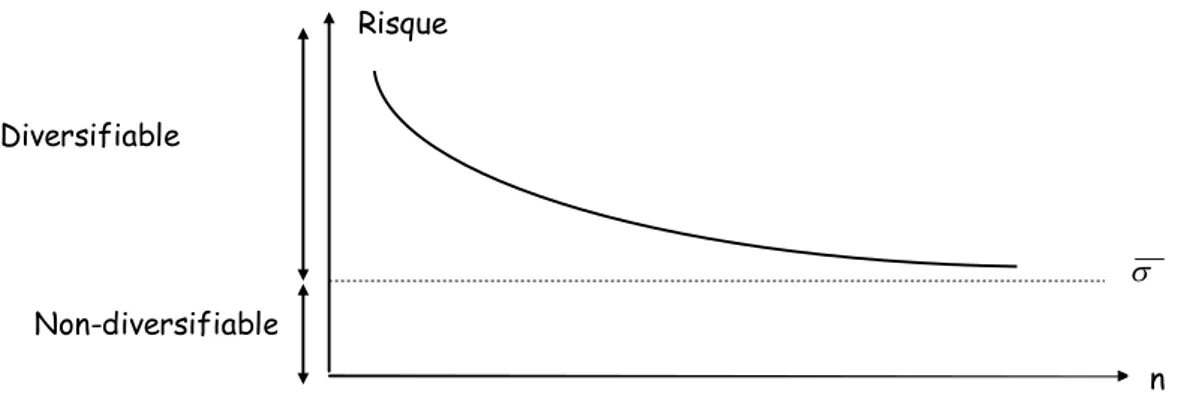
Il faut souligner que l’augmentation du nombre de titres au-delà d’un certain seuil ne permet pas de réduire le risque. La figure suivante montre bien cette situation:

2.3 Modèle d’équilibre des actifs financiers (MEDAF)

Suite à ses travaux concernant l’applicabilité de la matrice variances-covariances, Sharpe [Sha 71] a développé un nouveau modèle appelé le modèle d’équilibre des actifs financiers (MEDAF) qui consiste à mesurer le degré de sensibilité du rendement d’un actif par rapport à celui du marché.

Le modèle d’équilibre des actifs financiers se base sur plusieurs hypothèses :  Le marché est supposé parfait :

 Pas de coût de transaction.

 Les dividendes et les gains de capitaux ne sont pas taxés

n



Non-diversifiable Diversifiable

Figure 1.2 : Risque et Diversification

(37)

 Pas d’influence sur les prix par les acheteurs et les vendeurs qui interviennent sur le marché.

 L’emprunt et le prêt des investisseurs se fait avec un taux pur sans influence de son niveau et le taux d’emprunt est égal au taux de prêt.  Tous les investisseurs font le choix de portefeuille selon le critère de

moyenne-variance.

 Tous les investisseurs ont la même période de l’investissement.  Tous les investisseurs prennent leurs décisions en même temps.

 Tous les investisseurs détiennent leurs actifs pendant la même période.  Tous les investisseurs ont la même vision vis à vis les anticipations des

performances futures des actifs.

Etant donné un portefeuille constitué de n actions de rendements r r1, ,...2 et rn ;

et un actif sans risque de rendementr0.

Le rendement espéré de ce portefeuille est donné par :

1 n i i i r x r  

_

où xi représente la proportion investie dans l’action Ai pour i1,...,n.

La relation qui caractérise le modèle d’équilibre des actifs financiers MEDAF est donnée par :

ri r₀



RM r₀





1.21



où :

 r_i : le rendement espéré de l’action Ai

 RM : le rendement de portefeuille de marché

 2 M

(38)

 iM₂ M      1 n iM i ij i x    

_

3. Approche de Markowitz et Perold (1981)

Le modèle à indice simple de Sharp peut être généralisé à un modèle à plusieurs indices qui offre à l’investisseur la possibilité d’investir sur un marché international où figure plusieurs indices boursiers notamment le marché européen , marché américain ou le marché asiatique.

Dans ce cadre, Markowitz et Perold [Mark 81] ont développé un modèle multi-indiciels qui suppose qu’il y a une relation entre les titres sous la forme suivante :

Ri i i1 1F ... iKFK i , i1,...,n



1.22



où

 F_k représente le ème

k facteur aléatoire;  _i et i sont des constants

 _i est un bruit aléatoire de moyenne 0 et non corrélé avec F_k (pour tout 1,...,

k K) Si i E

 

i

2 2

 et _rs  cov



F F_r_, _s



alors on obtient la relation suivante :

_{ij i} _j     j n i n i i i n rs ir js i j s K r K j n i n x x x x x  



    











1 1 2 2 1 1 1 1 1



1.23



Le programme d’optimisation est :

2 2 1 1 1 n K K i i rs r s i r s Min  x  y y          



 

(39)

Sous les contraintes : 0 1 1 1 0 1,..., 1 0 =1,..., n j j j n jk j k j n j j j x E r x y k K x x j n               



4. Approche de Lai (1991)

Afin d’améliorer la qualité d’optimisation, Lai [Lai 91] a proposé la programmation multicritère pour l’optimisation de portefeuille en prenant en considération le Skewness.

Selon Lai, étant donné un portefeuille x 



x1,..., xn



où xi désigne la proportion

du capital C0 à investir par un investisseur dans les différents titres i i1,...,n. Le rendement et le rendement espéré de ce portefeuille sont donnés respectivement par :

 

1 n j j j R x r x  

_



1.24



et

 

1 1 n n j j j j j j R x E R x E r x r x    _ _

_



_



1.25



Les moments d’ordres deux et trois du portefeuille sont donnés respectivement par :

V R x



 



 E R x





 

r x

 



2





1.26



et

(40)

Lai a proposé l’espace variance- unité



x V R x/

_

 

_

 1



pour l’optimisation de

portefeuille. Selon cette hypothèse, l’algorithme d’optimisation multicritère à résoudre s’écrit comme suit:

 





Max R x ,

 





Max  _R x _{ ,} Sous les contraintes suivantes :

 





V R x x x j n j j n j    



1 1 0 1 1 = ,...,

Pour faire l’optimisation du portefeuille, Lai utilise les techniques de programmation polynomiale afin de résoudre le problème multicritère, et propose l’algorithme suivant :

 





1 2

p p

Min d  d

Sous les contraintes suivantes:

 

* 1 * 2 1 1 2 1 1 0 =1,..., , 0 n j j j R x d R x d V R x x x j n d d               



où:  *

r : est la valeur optimale de l’objective r x

 

dans l’algorithme uni-critère,

(41)

 *

 : est la valeur optimale de l’objective 



R x

 



dans l’algorithme uni-critère,

 d₁ : est la variable positive représente l’écart entre r x

 

et *

r

 d₂ : est la variable positive représente l’écart entre 



R x

 



et *



 p i i

_

1, 2

_

: paramètre subjectif positif qui mesure le degré de

préférence de l’investisseur entre les objectives.

5. Le Modèle Konno et Yamazaki (1991)

Konno et Yamazaki [Kon 91] ont définit une fonction de risque K x

 

appelé écart moyen absolu du rendement du portefeuille par rapport à sa moyenne en remplaçant la fonction quadratique de Markowitz par la fonction K afin de rendre l’algorithme d’optimisation linéaire pour l’optimisation de portefeuille. Ce modèle est exprimé comme suit:

 