Configuration optimale des aires de marché et coûts de transport

HAL Id: hal-01542071

https://hal.archives-ouvertes.fr/hal-01542071

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Configuration optimale des aires de marché et coûts de

transport

Agnès Basaille-Gahitte

To cite this version:

Agnès Basaille-Gahitte. Configuration optimale des aires de marché et coûts de transport. [Rapport de recherche] Institut de mathématiques économiques (IME). 1991, 19 p., ref. bib. : 6 ref. �hal-01542071�

INSTITUT DE MATHEMATIQUES ECONOMIQUES

LATEC C.N.R.S. URA 342

DOCUMENT de TRAVAIL

UNIVERSITE DE BOURGOGNE

FACULTE DE SCIENCE ECONOMIQUE ET DE GESTION

4, boulevard Gabriel -21000 DIJON - Tél. 80395430 -Fax 80395648

9101

CONFIGURATION OPTIMALE DES AIRES DE MARCHE ET COUTS DE TRANSPORT

Agnès BASAILLE - GAHITTE

Institut de Mathématiques Economiques Université de Bourgogne

CONFIGURA TION OPTIMALE DES AIRES DE

MARCHE ET COUTS DE TRANSPORT

GAHITTE Agnès

Institut de Mathématiques Economiques C.N.R.S et Université de Bourgogne 4, bd Gabriel - 21000 Dijon - France

Mots clés: Modèle de Places Centrales - Aires de marché Coûts de transport.

INTRODUCTION

La théorie des Places Centrales étudiée par LÖSCH (4) et CHRISTALLER (5) a pour objet l'examen et la construction d'un paysage hiérarchisé. Celui-ci est basé sur un système d'aires de marché qui possèdent des configurations précises (hexagonales et carrées principalement).

En fait raire de marché correspond à la zone d'influence d'un offreur. LÖSCH (4, p 130) a supposé que la libre entrée de firmes indépendantes localisées sur une plaine où sont situés des demandeurs équidistants entraine une transformation des aires circulaires en aires hexagonales et ainsi une maximisation du nombre de firmes par unité d'aire.

HARTWICK (2) examine analytiquement le théorème de LÖSCH concernant les aires de marché; il le traite comme un corollaire d'un théorème plus général (nous le résumerons dans une première partie). Or la démonstration qu'il nous propose contient quelques imprécisions et conduit à certaines erreurs développées et corrigées dans un second temps. HARTWICK (2) affirme que l'hexagone est une fonne optimale relativement au cercle, dans ce cadre d'analyse, et suppose (dans l'exemple chiffré qu'il traite) que les frais de transport sont unitaires. Nous tenterons dans une dernière partie d'élargir ce sujet en incluant des coûts de transport variables et constants ainsi qu'en envisageant des aires de marché triangulaires, pentagonales, circulaires, hexagonales et carrées.

L'auteur tient à remercier le Professeur Claude Ponsard pour ses commentaires, mais il reste seul responsable des erreurs qui pourraient encore s'y trouver. L'auteur tient également à remercier J.C Basaille (Centre de Calcul de l'Université de Bourgogne) pour les programmes et les tests qu'il a effectués.

Chapitre 1. UN MODELE SUR LES AIRES DE

MARCHE

/./

Exposé du modèle de HARTWICK

Nous reprendrons les mêmes notations que HARTWICK (2) pour, éviter toute ambiguité.

Les firmes possèdent des coûts de production décroissants :

C = A + kx

où C est le coût total, x la production, A e IRx f , k e IRX| . Les coûts de transport sont uniformes par unité de distance quelle que soit la direction, T = tu, où T est le coût de transport total supporté par le consommateur, et t est le coût par unité de distance par unité de produit et u est la distance.

Les consommateurs sont distribués uniformément sur une plaine ( D est la densité des consommateurs par mile élevé au carré).

Chaque consommateur a la même courbe de demande linéaire :

x r — a — b ( p + tu )

or, est la demande par consommateur, p est le prix FOB, a e [Rx+ b e 1RX+ . Les firmes peuvent se relocaliser à des coûts nuls et ne peuvent entrer dans un système d'entente intergroupes.

Pour un polygone régulier à s côtés, de cercle inscrit possédant un rayon uh, les ventes sont pour s = 6 (la configuration obtenue étant alors un hexagone) :

f —

x — 2 s D I I cos 0 a — b ( p + tu ) u dudd

•»o

d )

xh( p , u ) = 12 D u l{ ~ = - - - ~ T - 0,2027 b t uh )

uh est la distance de la firme au point le plus proche situé sur le périmètre de l'aire de marché. Il faut pour que la solution soit économiquement possible que les consommateurs reçoivent des quantités non négatives de biens c'est à dire que :

(1')

« -

bp

>

uh

ht ~ n

° 1 cos —

Pour un cercle de rayon uc on obtient :

(

2

)

~ „ i , a — bp b tu,.

xci P , u ) = 2nDuc (

--- --- -— )

La contrainte devient dans ce cas (

2

a — bp

---- ^

uc

Pour que cet équilibre soit lôschien les profits doivent être nuls et la pente de la courbe de recettes moyennes (A R ) doit égaler celle des coûts moyens (AC). Il vient donc :

(3) (4) et AR = p ( x , u ) dp | - 2 j 3 u est = ds '* ' 12h D u dP I 1 u est 2 ds c n h D u2 AC = —7-2— r + k (5) X( P , « )

(

)

C

X

Le revenu moyen Rh ou Rr et les profits Yh ou Yr sont donc :

(V)

2

n i

\

^

\'jLt)du \

(

8

)

(

)

On obtient pour l'hexagone et le cercle un équilibre lôschien quand un couple de solution ( p , u ) est obtenu respectivement pour les équations (7) , (9) et (8), (10). L'exemple donné par HARTWICK (2) montre que pour les mêmes coefficients, uh < uc , et

ph < p c, la densité de firmes par unité d'aire est supérieure dans le cas d'une aire hexagonale relativement à celle d'une aire circulaire.

1.2 Le théorème sur les aires de marché

I1ARTWICK (2) doit prouver que si l'équilibre lôschien existe alors uh < uc , sous les contraintes respectives ( 1 ) et (2'), avec ( p , u ) satisfaisant (7), (9) ou (8), (10).

Enoncé du théorème : s'il existe ( p , u ) h > 0 définissant xh > 0 et satisfaisant les

équations (7 ) e t (9 ) et s'il existe pour les m êm es param ètres dans les fonctions de demande et de coût un ( p , u )c > 0 définissant xc > 0 et satisfaisant les équations (8 ) et ( 10) alors

uh < uc.

Si on ne tient p a s com pte des contraintes ( 1’) et ( 2 ’), on peut affirmer que le théorèm e de L Ö SC H est un corollaire du théorème précédent; pour l'établir il suffit de les ajouter dans l'énoncé, respectivem ent après les équations ( 7), ( 9) ci ( 8), ( 10).

La preuve s'établit à partir du lemme suivant : Lemme :

S'il existe un ( p , u ) h > 0 déterm inant xh > 0 et satisfaisant (7 ) et (9 ) et s'il existe pour

les m êm es param ètres dans les fonctions de demande et de coût un ( p , u ) c > 0 déterm inant

xc > 0 et satisfaisant (8 ) et (10) alors : 1. pour p > 0, uc > uh dans (9) et (10) 2. pour p > 0, uc > uh dans (7) et (8) 3. ~~f~~ > 0 selon (7) et (8) duk 4. < 0 et —j - — < 0 selon (9) et (10). duh duc Preuve :

1. de (1) et (2) on peut dire que > 0 et < 0. De plus pour

( p , u ) > 0 , xh > xc . Ainsi pour p > 0 , pour que (9) et (10) soient vérifiées,

üh < üc , ( üh, et, tic sont considérées comme les valeurs solutions ).

p) Y F) Y ~ ~

2. - r — > 0et —z— < 0 dans ( 1 ) et (2). Pour u > 0 dans (7) et (8) alors ph > pr pour

ou dp

que (7) et (8) soient satisfaites .

dp

HARTW ICK ne prouve le résultat que pour l'hexagone et Rh. Démonstration : dRh = 2 f r 2 x h — 0,2021 b t u ( \ 2 D u2)

{ L--- 5--- J

2yf3

J

2^/3

* _ I ?

O p t dp

V

Les termes entre crochets sont respectivement positifs pour la première équation et négatifs pour la seconde équation. D ' où

dp

du

2 xh - 0,2027 h t u { 12 D u2) 12 D u2 b ( p — k )

2 j ï

(1 2 D u 2 b )

>

0

4. Yh et Yc ont des pentes négatives, < 0

Démonstration : 2 x h — 12 D u2 ( 0,2027 b t u) d Y k = du

+

12

Du2b

2 j ï

2 xh - 12 D u2 (0,2027 b t u ) 1 u I

< 0

Ék.

.

[

12

2V3-

J

/.J

Critique du modèle

N ous n'avons pas commenté en détail ce modèle, mais nous allons l'examiner dès à présent en profondeur.

Pour déterminer la pente de coût moyen d'une firme, ( les équations (5) et (6) ) il faut

d A C

calculer — — , or comme le coût moyen est :

dx AC = il vient x { p , u) + k d A C dx 2

On peut donc corriger les équations ci-dessus en :

(5 ')

est, p variable = — ——

pour l'hexagone et le cercle.

Ainsi les équations (7) et (8) sont justifiées car pour l'hexagone on égalise

d A C dp

c'est à dire

(5 ')

pour le cercle on obtient

(6') dx dx 2V3~ a 12 D b u x 2 1 A n D b u2 x 2 x 2 + A ( — n D h u2 ) = 0

L'exemple donné par H ARTW ICK (2) a été repris et les résultats diffèrent pour le couple solution dans les cas hexagonaux et carrés. On trouve dans le premier cas (2,710630;0,254561) au lieu de (2,752;0,254) et dans le second (2,718096;0,267275) au lieu de (2,745;0,267). Ces divergences peuvent s'expliquer par une prise en compte totale des chiffres après la virgule par le programme informatique.

Il convient maintenant d'examiner en détail l'équation suivante :

dRh = 2 xh On sait que 2 n / \ 2 , À f 12 6 D U \ /\ Rh( p , u ) = x + A { ---^ - j =--- ) = 0 donc 2 x k — 0,2027 b t u ( 12 D u2 ) — 12 D u 2b ( p - k ) 2 j ï du 12 D b u 2 2 j ï

dRh = 2xh dxh 2J2 dxh = b p — 0,2027 b tu

2

3

Ceci ne correspond pas à ce qui a été écrit par H ARTW ICK (2). On peut néanmoins supposer que c'est une erreur d'impression, l'accolade ayant été placée à un endroit inadéquat.

Ces erreurs ne sont malheureusement pas les seules. Dans l'expression

dP du [ 2 x h - 12 D u 2 (0,2027 b t u ) ] x — ( p — k )

12

2

Jf

J

H ARTW ICK (2) affirme que :

(a) xh - ( p - k ) 12 D b u > 0

Trouvons que cette inégalité n'est pas positive .

A

De (9) on peut tirer : xh = ---— avec p — k + 0 et de (8) on a : P ~ k

x = A \ \ 2 D b 2 j f

car xh est une demande positive. On peut donc écrire que :

Xh V 12 D b u

avec

Ainsi (a) s'écrit :

r 'Ï i — h ü — M D b u 2 _ / 12 D b u2

[a>

V 12

2J T

C'est à dire

12 D b u 2 1 1 2 D b u 2 _ Q

V 2

J

3

V 273

Le test de cette contrainte vérifie également le résultat précédent. Celui-ci a été effectué en "double précision" pour des valeurs de t telles que t varie par pallier de 0,05; de 0,05 à 6,42. 6,42 est le coût de transport qui ne respecte pas la contrainte (1).

La démonstration de H ARTW ICK (2) est donc inexacte et surtout incomplète car il n'essaie nullement de montrer que

x — ( p — k ) 12 D b u

2 j ï

est positif, il se contente de l'affirmer.

Bien entendu la démarche est correcte, mais nous n'allons pas tenter de redémontrer les affirmations de cet auteur ( ou de les infirmer ), nous nous contenterons de construire un modèle basé sur des coûts de transport dont une partie est constante et l'autre est va­ riable.

Chapitre 2. COUTS DE TRANSPORT ET AIRES

DE MARCHE

Dans sa théorie des régions LÖSCH (4) dispose les secteurs riches et pauvres on villes de façon à maximiser le nombre de centres de production et à optimiser le réseau de transport. Comme le plus grand nombre de centres coincident, le maximum d'achats peut être fait localement. D'un côté la distance qui sépare la résidence du consommateur du "centre commercial" est réduite, de l'autre la longueur des voies de communication est optimale et le coût de transport est minimisé.

En fait, la notion de coût de transport est très vaste et souvent utilisée en économie spa­ tiale. En général ce terme décrit le seul coût de transport d'un bien, ce qui est incomplet car il recouvre également d'autres éléments : ( HAGGETT, CI IORLEY (1) )

1. le coût de construction de l'infrastructure routière, ferroviaire... 2. le coût d'entretien des voies de communication

3f et le coût de flux ( coût de transport unitaire du bien ).

Dans le second chapitre, LÖSCH (4) traite exclusivement du troisième élément. Cette étude se propose d'intégrer le coût de construction et les conséquences de son in­ troduction sur l'optimalité des aires de marché hexagonales.

Trois approches sont possibles :

1. faire supporter les coûts de transport totaux par le consommateur 2. ou les faire supporter par l'entreprise

3. ou par le contribuable.

Nous nous contenterons ici de traiter et de développer la première approche ( la seconde

sera étudiée plus tard ). Un bref rappel du cadre d'analysç de la théorie régionale de

LÖSCH est nécessaire :

Les firmes peuvent entrer librement sur le marché; elles sont localisées sur une plaine homogène ainsi que les consommateurs qui sont équidistants les uns des autres.

Notre approche est analytique et déduite de l'analyse de CH AM BERLIN concer­ nant l'équilibre, analyse qui a motivé celle de LÖSCH. Dans une première section le modèle utilisé sera exposé et dans un second ternps l'esquisse de la démonstration du théorème sur les aires de marché sera donnée.

2.1 Le modèle

2.1.1 la fonction de coûts de production

La fonction de coûts, est de la forme :

C = A + k x

C est le coût total, A le coût fixe, k le coût de production unitaire ( k > 0 ) et x la quantité produite par la firme.

2.1.2 les coûts de transport

Ils ne sont pas uniformes en fonction de la distance quelle que soit la direction comme l'ont envisagé LÖSCH (4), HARTWICK (2), CAPOZZA ATTARAN (3). Ils sont de la forme :

M f ) = « + b f où h (f) est le coût de transport total par unité de distance a le coût de construction par unité de distance ( coût fixe ) b le coût de flux par unité de flux pour une unité de distance

f est le volume de flux ( dans le calcul qui suit on le considère comme unitaire ). Si u est la distance, le coût de transport total peut être représenté par la relation :

T = u h ( / ) = ti ( a + bf) = ua + u b f

En fait dans les calculs on donne une valeur à a + b f qui est parfois supérieure à 1 ( du fait du coût fixe de construction ) mais le modèle n'en tient pas compte.

2.1.3 la demande

Les consommateurs potentiels sont dispersés (avec une densité uniforme par kilomètre ou "mile" ) sur une plaine de qualité uniforme. Chaque consommateur a la même courbe de demande, fonction du prix :

xr= a — (i(p 4- uhf) = a. — fi ( p T)

Donc '

xr — a — P(p + ua + u bf)

xr est la demande individuelle du consommateur, p est le prix FOB, a > 0 fi > 0. Les coûts de transport sont supportés par les consommateurs.

2.1.4 l'offre

L'entreprise peut se relocaliser à coûts nuls, et on suppose qu'elle ne s'engage pas dans un comportement d'entente. Les ventes totales d'une firme sont calculées comme suit (on envisage le ças d'aires de marché polygonales et circulaires) :

!. Cas d'un polygone régulier à s côtés

“A

x = 2 s D I f I 005 b u xr dudOf cos 0uxr<

Jo Jo

s est le nombre de côtés, u la distance, D la densité de consommateurs, et 6 çst tel que Q; =

-f-f —

x — 2 s D * I cos 0 ( a — p p — (i au — Pu bf) u •*0 *^0

• cas d'un hexagone régulier

dudQ

xh(P> u) = 12 Dui

“

IT T

P -

0,2026621

m

ou u esj; la distance séparant la firme du ppint le plus proçhe sitqé pur le périmètre de l'aire de piarchp. Or pour que lp modèle soit çprreçt éçonomiquement il est indispensable que les consommateurs reçoivent des quantités non négatives de biens, CAPOZZA et ATTARAN (3). C'est à dire que

&P . u

P(a + bf) cos JL

6

— est la distance maximale jusqu'au périmètre ( c'est er> fait le " rayon c ° s T

de l'aire de marçhé ). Cas d'un carré

xr = 12 D u2 “ Pp - 0,25.5065238 u p( a + bf ) 3

J.a contrainte économique est dans ce cas :

a - Pp

¡ t ( a + b f ) 2

tT

7Z Cas d'un pentagonç, s = 5, 6 =

-j-jçr = 12 Du2 [0,3027260533 (a - p p) -, 0,217269833 u P ( a + f» /)]

U

La contrainte a - fiP _> fi ( a + bf) cos -J-• Cas du triangle, s = 3, 0 = -y = 12 D u2 [ ~ j ~ (a - fip) - 0,398421626 m /? ( a + 6 / ) ] La contrainte devient « - fiP u 2. Cas du cercle fi(a + bf) co s 'f" * = 2 n D u i a... ~ fi f i a + bf)l

u est le rayon de Taire de marché ; si les consommateurs reçoivent des quantités po­ sitives du bien, alors

~ fiP

> U

fi (a + bf)

2.1.5 le revenu moyen

Il est noté A R = p ( x, u ); il dépend de la quantité et de Y importance de la de­ mande, ainsi que de la distance et du prix du bien.

1. Cas d'un hexagone à s côtés • L'hexagone, s = 6 a JC fi 12 D u p - 0,202662135 u P (a + bf ) dAR_{, , u est ,} d s 'h d x dp - 2 j ï u est = 0

h

12

pDu

Le triangle, s = 3 P = 4 jc P 12 D u p J Ï 0,2428996226 u 4 p ( a + bf ) dAR I , dp :— MCSÎ = 7 -ds ' dx ucst = _{\2p f) u V 3} • Le carré, s = 4 3x P 12 Dpu - «0,255065238 3 (a + bf) dAR ds ucst = dp dx u est — _\2pDu 2. Cas du cercle - 2 j * - 2 n D u 2 [ ^ - - P j ( a + bf ) ] } 2 n Dpu donc dAR I , dp I — :— u est = —r~ u est — ds 1 dx 1 - 1 P Du n

2.1.6 le coût moyen d'une entreprise

Il s'écrit AC = — ( , m) 4- Æ, et la pente de coût moyen est :

dAC I . . . yi ---I u est p variable --- --- —

jf 1. pour yn polygone à s côtés • l'hexagone AC = --- - 1 12 D u

« -

PP

On peut écrire deux fonctions indiquant la condition de tangence de LÖSCH entre le coût moyen et la recette moyenne pour une firme ayant différents types d'aires de marché.

1. pour un polygone à s côtés • l'hexagone - 2 j 3 a 12 D ß u x 2 Rh { p , u) = x 2 - A ( 12 D ß ] = 0 le pentagone 0,30272605533 D \ 2 ß u x 2 Rp ( P , u) = x 2 - A (12 D ß u 2 0,30272605533) = 0 • le carré - 3 A 12 D ß u 2 x 2 <=> le triangle Ra ( p , u) = x 2 - a [ \2 D ß - y - ) = 0 - 4 = _ J _ \ 2 D ß u 2 j 3 x 2 2. Le cercle Rt ( p , u) = x 2 - A ^ \ 2 D ß u ~ ~ ^ j = 0 - 1 A n D ß u2 x 2 Rc ( p , u) = x 2 — A (tc D ß u2 ) = 0

2.1.7 les profits d'une entreprise

Les profits sont nuls ( c'est une condition du modèle ) et ils peuvent s'exprimer comme suit :

Yj = p x l ~ kxf — A = 0 i s'applique à des polygones à s côtés et au cercle

1. pour des polygones à s côtés • l'hexagone, s = 6 Yh — p xh - k xh — A = 0 • le pentagone, s = 5 Yp — p xp — k x p — A — 0 • le carré, s = 4 Yq p Xq k xa A 0 • le triangle, s = 3 Yt = p x t — k x t — A = 0 2. Pour le cercle Yc = P x c ~ k x c ~ A = 0

2.2 Preuve de l'optimalité et un hexagone

La démonstration du lemme posé par HARTWICK (2) n'est pas possible car on

dp

obtient un établi à partir de Yh, Yc.... ayant un dénominateur n u l.

Pour prouver le théorème de LÖSCH ( c'est à dire pour montrer que l'on obtient “a < K dans le cas d'une comparaison d'une aire hexagonale relativement à une aire carrée ) il faut trouver une autre méthode.

Compte tenu des relations (7), (8), (9), (10) il vient :

A x = --p — k et

2

2

ainsi u = A (p - k ) j 2 j Ï D ( i A ~ P ~ * V 2j3 DP pour l'hexagone et comme on a p — k x2 = A n D P u2 pour le cercle; on peut donc écrire

u = u — — ( p - k ) J n D p A 1 p — k V n D P Or et = 0,537284965 0,564189583 posons il vient alors et conclusion : uh < uc car 2 > 0 z = 1 p - k V Dp uh = 0,537284965 z uc = 0,56418953 z

La preuve est donc faite. Si l'on veut comparer les autres aires de marché la même procédure peut être utilisée. On obtient alors :

X = ---p p - k Xp — A 12 Dp u 2 0,30272605533 donc u 1 p - k V 12 DP 0,30272605533

Pour le carré on a x] = A4 D ß u 2 donc d'où u = — A D ß ua = 0,5 z Le triangle fournit les valeurs suivantes :

A p — k A 3vT Dßu donc d'où u = 1 P - k yj i j ï Dß ut = 0,43891337 z On peut donc conclure que : u, < u„ < up < uh < uc

Si la valeur de uh ( par exemple ) est inférieure à celle de uc, alors la densité de firmes par unité d'aire est supérieure pour un hexagone comparé à un cercle. Les comparaisons entre les valeurs de u conduisent à affirmer que la densité de firme par unité d'aire est supérieure dans le cas du triangle relativement aux autres configurations étudiées.

2.3 Comparaison des résulats obtenus avec deux méthodes

différentes

HARTWICK (2) prend un exemple et suppose que a — 5 , / ? = 5 , a + b f = l , D = l , A = 5 , et k = 0,6 .

La comparaison entre les distances et les prix obtenus selon son modèle donne les résultats suivants :

Tableau 1 : Les configurations des aires de marché pour des coûts de transport unitaires.

Configuration _P u X Cercle 2,710909 0,267273 2,368648 Hexagone 2,710644 0,254560 2,368945 Pentagone 2,710863 0,248556 2,3687 Carré 2,709307 0,237045 2,370447 Triangle 2,704080 0,208496 2,376336

ut < ua < up < uh < uc

Comme ce sont les consommateurs qui supportent le coût de transport , si la firme vend à un prix inférieur et si la distance séparant le demandeur de l'offreur est minimale alors ses produits seront plus concurrentiels relativement à des firmes ayant des types d'aires de marché différents. Par exemple si l'on compare l'hexagone et le cercle il est normal que la demande x soit supérieure dans le premier cas ( selon les hypothèses précédentes ). Si à présent on compare le carré et l'hexagone ( dans le même cadre d'analyse ) la de­ mande qui s'adresse à une entreprise possédant une aire de marché carrée est plus im­ portante que celle qui s'adresse à une firme ayant un type d'aire de marché hexagonal. On pourrait de même choisir entre le pentagone et l'hexagone. En fait la demande est supérieure dans le premier cas. Mais le pentagone ne recouvre pas l'espace donc il ne peut être utilisé comme configuration d'aire de marché d'une entreprise dans le modèle de LÖSCH.

En ce qui concerne le triangle la distance est effectivement la plus faible mais le prix est très supérieur aux autres prix. En fait la demande des consommateurs s'adressant à une entreprise ayant une telle aire est inférieure à toutes les autres, on ne peut donc pas retenir ce type d'aire de vente.

Donc si l'on résume, l'aire optimale recouvrant le plan est le carré , ensuite on trouve l'hexagone et enfin le triangle ( pour les confugurations qui recouvrent totalement le plan ).

Dans l'étude qui précède nous n'avons pas tenu compte des coûts de transport variable et constants, car a + b f — 1.

Si on veut intégrer ces facteurs il suffit de faire varier a + b f entre 0,1 et la variable maximale qu'il peut atteindre en respectant les contraintes du type ( ! ') ou (2') et en per­ mettant aux équations du type ~ j ~ > » et Æ, > K = 0 de déterminer des

solutions positives pour p et u . ( voir le tableau 2).

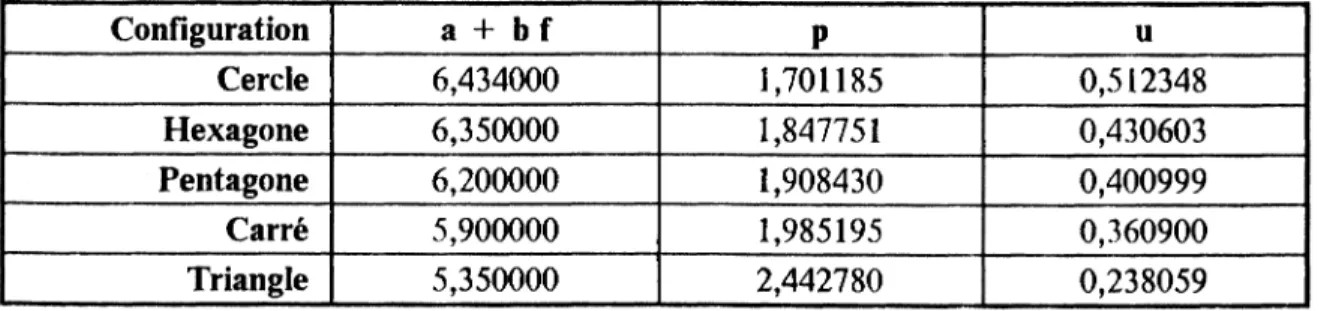
Tableau 2 : Coût de transport maximum pouvant être supporté par une configuration d'aire de marché donnée

Configuration a + b f _P u Cercle 6,434000 1,701185 0,512348 Hexagone 6,350000 1,847751 0,430603 Pentagone 6,200000 1,908430 0,400999 Carré 5,900000 1,985195 0,360900 Triangle 5,350000 2,442780 0,238059

Il est possible d'affirmer ( selon le tableau 2 ) que la configuration qui supporte les coûts de transport les plus élevés et les plus faibles est respectivement le cercle et le triangle.

Or comme nous avons prouvé que seuls le carré et l'hexagone conviennent, on peut dire que la zone d'influence carrée supportera des coûts de constructions plus élevés ( coûts de construction d'une "voie express" comparés à ceux d'une départementale par exemple ) si les coûts variables sont égaux ( et inversement ).

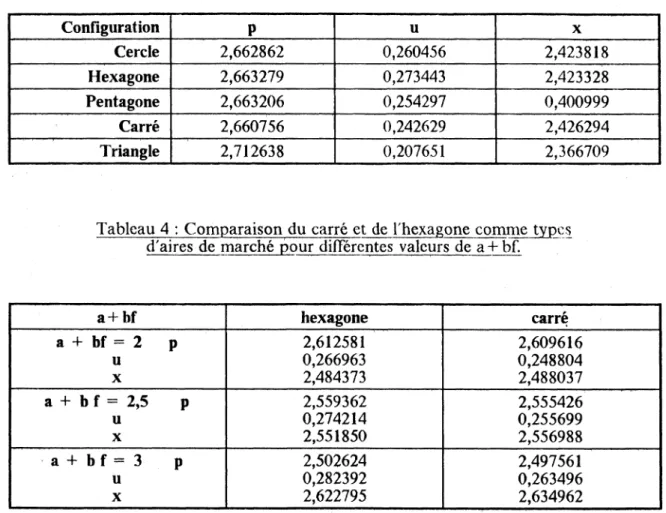
Tableau 3 : Aires de marché optimales avec des coûts de transport tels que : a + b f = 1,5 Configuration _P u X Cercle 2,662862 0,260456 2,423818 Hexagone 2,663279 0,273443 2,423328 Pentagone 2,663206 0,254297 0,400999 Carré 2,660756 0,242629 2,426294 Triangle 2,712638 0,207651 2,366709

Tableau 4 : Comparaison du carré et de l'hexagone comme types d'aires de marché pour différentes valeurs de a + bf.

a + b f hexagone carré a 4- bf = 2 p 2,612581 2,609616 u 0,266963 0,248804 X 2,484373 2,488037 a + b f = 2,5 p 2,559362 2,555426 u 0,274214 0,255699 X 2,551850 2,556988 a + b f = 3 p 2,502624 2,497561 u 0,282392 0,263496 X 2,622795 2,634962

Ces deux tableaux confirment les résultats précédents. Il est donc indispensable d'étudier le système de Places Centrales qui possède des aires de marché carrées. Ceci a été fait dans une précédente étude. Les principaux résultats de la comparaison hexagone-carré ainsi que les tests qui y sont liés ont été exposés ( GAHITTE (6) ).

Le théorème de LÖSCH établi par HARTWICK (2) est intéressant mais la démonstration fournie par son auteur est incomplète et incorrecte.

La preuve que nous avons donné est basée sur une méthode plus simple qui ne re­ met nullement en cause le résultat de ce théorème.

Le nombre de configurations possibles peut être important. HARTWICK (2) n'en a considéré que deux ( l'hexagone et le cercle ), le premier se déduisant du second par le jeu de la concurrence entre les firmes. Il ne faut pas oublier néanmoins que LÖSCH (4) a envisagé une troisième configuration, le carré, même s'il n'a pas développé son étude.

En géométrie trois polygones recouvrent parfaitement l'espace sans vide : l'hexagone régulier, le carré et le triangle équilatéral. Pour compléter ces trois configu­ rations nous avons ajouté dans notre étude le pentagone. Dans cette étude c'est la consommation qui supporte le coût de transport. L'hexagone est optimum relativement au cercle. Pour celui-ci en effet on obtient pour les mêmes coefficients uk < uc et

ph < pc. Ainsi la distance et le prix annoncés par une firme ayant une aire de marché hexagonale sont inférieurs à ceux annoncés par celle qui possède une aire de marché cir­ culaire.

On constate de la même manière qu'une comparaison aire de marché carré et aire de marché hexagonale donne le carré optimum car ua < tth et pa < ph.

BIBLIOGRAPHIE

(1) HAGGETT, CHORLEY : Network Analysis in Geography .Editor Edward Arnold, London, 1972.

(2) HARTWICK John M. : LÖSCH's Theorem on Hexagonal Market Areas, Journal o f Regional Science , vol. 13, n° 2, 1973.

(3) CAPOZZA Denis, ATTARAN Kazem : Pricing in urban areas under free entry, Journal o f Regional Science , vol. 16, n° 2, 1976.

(4) LÖSCH August : The Economics o f Location , translated by Woglom W I I and Stolper, New Haven, 1953.

(5) CHRISTALLER W. : Central Places in Southern Germany ( Die Zentralen Orte in Suddeuschland ) translated by W. Baskin, Prentice Hall, Englewood Cliffs.

(6) GAHITTE Agnès : Modèle löschien basé sur des aires de marché carrées, pa­ pier présenté devant le séminaire DELTA d'Ananlyse Economique Spatiale, Université Catholique de Louvain la Neuve, Mars 1987.