Threes problems on cycles in simple graphs

THREES PROBLEMS ON CYCLES IN SIMPLE GRAPHS

THESIS

PRESENTED

IN PARTIAL FULFILLMENT

OF THE MASTER' S DEGREE IN MATHEMATICS

BY

EBRAHIM ZARE

Avertissement

La diffusion de ce mémoire se fait dans le respect des droits de son auteur, qui a signé le formulaire Autorisation de reproduire et de diffuser un travail de recherche de cycles supérieurs (SDU-522 - Rév.1 0-2015). Cette autorisation stipule que «conformément

à

l'article 11 du Règlement no 8 des études de cycles supérieurs, [l'auteur] concède

à

l'Université du Québec

à

Montréal une licence non exclusive d'utilisation et de publication de la totalité ou d'une partie importante de [son] travail de recherche pour des fins pédagogiques et non commerciales. Plus précisément, [l'auteur] autorise l'Université du Québec à Montréal

à

reproduire, diffuser, prêter, distribuer ou vendre des copies de [son] travail de recherche

à

des fins non commerciales sur quelque support que ce soit, y compris l'Internet. Cette licence et cette autorisation n'entraînent pas une renonciation de [la] part [de l'auteur]

à

[ses] droits moraux ni

à

[ses] droits de propriété intellectuelle. Sauf entente contraire, [l'auteur] conserve la liberté de diffuser et de commercialiser ou non ce travail dont [il] possède un exemplaire.»

TROIS PROBLÈMES DE CYCLES DANS DES GRAPHES SIMPLES

MÉMOIRE

PRÉSENTÉ

COMME EXIGENCE PARTIELLE

DE LA MAÎTRISE EN MATHÉMATIQUES

PAR

EBRAHIM ZARE

Firstly, 1 would like to express my sincere gratitude to my supervisors, Prof. Gei'ia Hahn and Prof. Louise Laforest for the continuous support of my Master study and related research, for their patience, motivation, and immense knowledge. His guidance helped me in all the time of research and writing of this thesis. 1 could not have imagined having a better advisor and mentor for my Master study.

1 am also very grateful to my program's directors Dr. Olivier Collin and Dr. Steven Lu who helped me a lot through my study.

1 must acknowledge as well all the professors and friends at Department of mathematics who inspired and supported me and my efforts over these years. Particularly, 1 need to express my gratitude and deep appreciation to Jose Eduardo Blazek and Prof. Ben Seamone.

Last but not least, 1 would like to thank my parents who not only tolerated my absence, but also supported me while 1 was away from home, and my wife for supporting me and cheering me up and standing by me through the good times and bad.

LIST OF FIGURES RÉSUMÉ .. ABSTRACT INTRODUCTION CHAPTER I BASIC DEFINITIONS CHAPTER II

THE DECYCLING NUMBER OF GRAPHS

2.1 Decycling number of the Cartesian product of graphs 2.2 Decycling number of the strong product of graphs . . 2.3 Decycling number of the lexicographie product of graphs 2.4 Decycling number of the co-normal product of graphs CHAPTER III

THE BASIS NUMBER OF GRAPHS . . . . 3.1 Basis number of the join of two graphs . CHAPTER IV

THE MINIMUM CYCLE BASIS OF GRAPHS 4.1 Minimum cycle basis algorithms . . . . .

4.2 Minimum cycle basis of the Cartesian product of graphs 4.3 Minimum cycle basis of the jo in of two graphs . . . . 4.4 Minimum cycle basis of the direct product of graphs

4.5 Minimum cycle basis of the lexicographie product of graphs

lX Xl X111 1 3 15

20

24

27

30 33 37 41 41 45 49 50 50 4.6 A new minimum cycle basis of the lexicographie and co-normal products 54 CHAPTER V

Figure Page 1.1 A simple graph of 5 vertices and 6 edges. . . . . . . . . . . . . 4 1.2 An induced subgraph and a non-induced subgraph of the graph of

Fig-ure 1.1 . . . . . . . . . . . . . . . . 5

1.3 A graph with three connected components. 5

1.4 Various Products of P2 and P3 13

1.5 The join of P2 and P₃ .. 2.1 Petersen Graph. 2.2 Graph K20G

3.1 Edge Labelling of graphs 3.2 vVT. 0 • • • • • 4.1

4.2 P·uv

ab,w· · · · ·

4.3

P2

[

P3]

and P2 ~ P₃ where the edges belonging to P2 [

P3 ]

but not P2 I:8J P₃ are in red . . . .

4.4 Non-strong triangles in G[H]

4.5

C4 [

P3]

and C3 ~ P3 where the edges belonging to

C4

[

P

_3]

but not C

₃

I:8J P₃ 13 16 18 34 37 48 51 53 55 are in red. . . . . . . . . . . . . . . . . . . . . . . . 56

Le présent mémoire a pour sujet trois concepts différents concernant les cycles dans des graphes simples : indice de décyclage (la taille minimum d'un transversal de cycles), le nombre cyclomatique (la taille d'une base de l'espace des cycles) et la base mini-mum de l'espace des cycles. Ils ont tous de nombreuses applications en informatique ainsi que dans d'autres sciences appliquées. Nous nous intéressons à ce qui arrive à ces paramètres quand de nouveaux graphes sont construits comme produits divers à partir de graphes donnés. Nous survolons la littérature et nous présentons quelques nou-veaux résultats dans ces trois directions. Nous donnons également un contre-exemple à l'algorithme de Ka v eh et Mizrai pour trouver une base minimum de l'espace des cycles du produit lexicographique et nous en présentons une version correcte.

Mots-clés: Produits de graphes, jointure de graphes, indice de décyclage, nombre cy-clomatique, base minimum de cycles

ln the present thesis we study three different concepts concerning cycles of graphs: decycling number (feedback vertex number), basis number, and minimum cycle basis (MCB). They ail have many applications in computer science and other applied sci-ences. We are interested in what happens to these parameters when new graphs are constructed from given graphs by various product operations. We review old results and give sorne new results in these three directions. We also present a counterexample to Kaveh and Mirzaie's algorithm for minimum cycle basis of lexicographie product and present a correct way to construct a minimum cycle basis for this product.

Keywords: Graph products, join of graphs, decycling number, basis number, mini-mum cycle basis.

Cycles have an important role in graph theory and many applications in other sciences. In this thesis, we are concerned with three parameters connected to cycles in graphs (decycling number, basis number, and minimum cycle basis) and the way they can be obtained for the join of two graphs as weil as for various graph products. Our main aim is to find the decycling number, the basis number and the minimum cycle basis of lexicographie and co-normal products of graphs, painting out an error in [31] and giving a correct construction.

In the first chapter, we review basic concepts, definitions and results relevant to our research.

In the second chapter, we introduce the decycling number of a graph. After reviewing previous results on the decycling number of the Cartesian and strong products of two graphs, we give an upper bound for the lexicographie and co-normal products as weil as an exact formula wh en one factor of the product is a pa th, a cycle or a complete graph.

In the third chapter we study the basis number of graphs. We review the results on the basis number of the Cartesian, strong and lexicographie products and give a bound for the basis number of the join of two graphs.

the minimum cycle basis of the Cartesian, strong and lexicographie products of graphs and give new result on the minimum cycle basis of the join of two graphs. We also give sorne new results on the minimum cycle basis of the lexicographie and co-normal products of graphs obtained as extensions of the minimum cycle basis of the strong product of the components. In doing so, we point out a mistake in [31] and give a correct construction and a proof.

BASIC DEFINITIONS

A (finite simple) graph , G, is an ordered pair of sets (V, E) where V is a finite set of vertices and E is a subset of (~)

= { {

u, v} 1 u =1- v, u, v E V}. The elements of E are called edges. We write G

=

(V, E). When a graph is given only as G, we often write

V( G)

and

E( G)

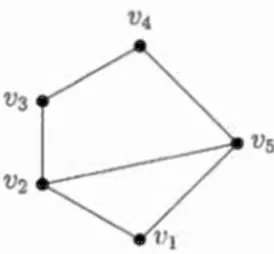
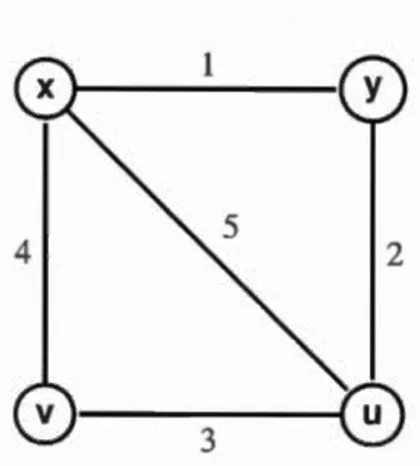
for its sets of vertices and edges, respective! y. The order of the graph Gis denoted by ICI and is the number of its vertices, IV(G)I. Often we denote IV(G)I and IE(G)I by p and q respectively. The edge e = {u,v} is usually denoted by uv; ·u is then said to be adjacent to v and vice versa. Also, u and v are said to be incident with e. For example, Figure 1.1 represents a graph with the set of vertices

V = {vi, v2, v3, v4, vs} and the set of edges E = {VI v2, v2v3, v3v4, V4Vs, vi Vs, v2vs}. A pa th of length n is an sequence of n+ 1 distinct vertices v₀ · · · vn such that vivi+I E E

for i

=

0, ... , n- 1. Allowing the first and last vertex to be identical we obtain a cycle. That is, a cycle of length n is a sequence of n distinct vertices v₀ · · · Vn-I such that vivi+I E E for i

=

0, ... , n - 1, addition modulo n. If vertices u and v are connected in G, the distance between u and v in G, denoted by dc(u, v), is the length of a shortest path between u and v in G; ifthere is no path connecting u and v we define dc(u, v) to be infinite. A chord in a cycle C is an edge of the graph G that is not part of the cycle but connects two vertices of the cycle. That is, a chard in a cycle VI ... Vn, n ~ 3, is an edge vivj E V such that 1

<

l

i

-

j

1

<

n - 1. The edge v2vs in the graph of Figure 1.1 is a chard of the cycle vi _v2v3v4vs.

Figure 1.1: A simple graph of 5 vertices and 6 edges.

A subgraph H of graph C, is a graph whose vertex set is a subset of the vertex set of G, and whose edges are a subset of the edge set of G (by the definition of a graph, only edges connecting vertices in V ( H) can appear in E( H) ). We write H Ç G

to show that His a subgraph of G. A subgraph H of G is induced (by the vertex set V(H)) if E(H) = (v~f)) nE(G). Forexample, Figure 1.2 shows an induced subgraph on vertices { v1, v2, v₅}, and a non induced subgraph on vertices { v₁, v₂, v_{3 , V}4, v_{5 }} the graph of Figure 1.1. The graph induced by the

setS

Ç

V(G)

is denoted by G(S) or

G

is

but when the graph

G

is clear from the context, we write sim ply (S). Sirnilarly, the subgraph induced by

G

\ S is denoted by

G

lv

-

s

or G(C- S), or, more simply, by G - S; it is the subgraph obtained from G by deleting the vertices in S together with the edges incident to them. If S = {v} we write G - v for G - {v}.

The degree of vertex u of a graph G is the number of edges which are incident with the vertex and is denoted by d( u). If a graph G has n vertices, the degree sequence of G is the non-increasing sequence of the degrees of its vertices d1, d2, · · · , dn with di

2:

di+l for i = 1, ... , n - 1.

The union of graphs G and H is a graph with vertex set V ( C) U V ( H) and edge set E( G) U E(H). If Gand H have no vertex in common, the union is disjoint and is often

denoted by G

+

H. Note that this allows for G

+

G where the vertex sets are made disjoint in sorne standard manner. The intersection G

n

H of G and H is a graph with vertex set

V(G)

n

V(H)

#

0

and edge set

V(G)

n

V(H).

Figure 1.2: An induced subgraph and a non-induced subgraph of the graph of Figure 1.1

A graph is connected, if there is a path between each pair of its vertices. Otherwise the graph is disconnected. A maximal (vertices) induced connected subgraph of a graph Gis called a connected component of

G.

The number of connected components of a graph

G

is denoted by

w(

G). For example, Figure 1.3 shows a graph with three con-nected components.

~4.

Figure 1.3: A graph with three connected components.

Two graphs G and H are isomorphic , written G ~ H, if there are bijections

r.p

:

V(G)

- t

V(H)

and 'ljJ :

E(G)

- t

E(H)

such that

e

=

ab

E

E(G)

if and only if

'1/J(e

)

=

r.p

(a)

r.p

(b);

such a pair (

r.p, '1/J)

of mappings is called an isomorphism between Gand H.

• A path graph, or simply a path , denoted by

P

n

, is a graph

isomorphic to the graph with vertex set

V(P

n

) =

{

v

a

,

..

.

,

Vn

-

d

and edge set

• A cycle graph, or a cycle, denoted by

Cn,

is a pa th with an extra edge { v₁,

Vn

}

between the first and last vertices. Thus a cycle of length n is a graph isomorphic to the graph

Cn

on the vertex set

{

v

a

,

.

..

,

Vn-

d

and edge set {

{

vi

,

Vi+

d

1 0

<

i

S

n - 1} with addition modulo n. Any such cycle is denoted by

Cn

• A tree is a connected graph with no cycles, that is, a connected acyclic graph, and is usually denoted by T. An acyclic graph is a forest; its connected components are trees.

• A complete graph is a graph with aU possible edges, i.e. E =

G)

.

If a complete graph has n vertices, it is denoted by Kn.

• A bipartite graph is one whose vertex set can be partitioned into two subsets

X

and Y, so th at each edge has one end in X and one end in Y; the partition (X, Y) is called a bipartition of the graph.

• A complete bipartite graph is a bipartite graph with bipartition (X

,

Y)

such that each vertex of X is adjacent to each vertex of Y; if

lXI

=

n and

IYI

=rn, such a graph is denoted by Kn,m·

• A planar Graph is one which can be drawn in the plane in such a way that the edges intersect only at their endpoints.

• A hypercube, denote by Qn, is the graph whose vertices are the ordered n-tuples of O's and 1 's, two vertices being joined if only if they differ in exact! y one coordinate.

For a given graph G

=

(V, E) we define two related graphs.

• A spanning tree, denoted by Tc, of connected graph G is a subgraph of G that is a tree and con tains all the vertices of G, i.e. V (Tc)

=

V (

G).

Cl earl y Tc is not unique unless G itself is a tree.

• A complement of a graph G, denoted by G, is a graph on the same vertex set as G such that two distinct vertices of G are adjacent if and only if they are not adjacent in G.

• A null graph is a graph with no edges. A null graph with n vertices is denoted by Kn.

One other concept will be needed. Given a simple graph G, a minimum distance tree rooted at vertex v is a spanning tree T of G, such that the path distance from root v to any other vertex u in

T

is the shortest path distance from v to u in G. Let

T

ê

be a minimum distance tree (breadth-first search tree) rooted at a vertex a. This induces a breadth-first search numbering of the vertices of G with a0

=

a, , a1, a2, · · · , aiV(C)I wi th the obvious property th at d( a0 , ai) :::; d ( a0, aj) if i :::; j and in particular d ( a0, ai) :::; d(a1, ai+I)

=

d(a1, ai)+ 1.

The removal of an edge from a tree results in a forest with two connected components. Thus each edge of a tree defines a partition of the vertex set. In a connected graph G with a spanning tree Tc we have the same phenomenon- the removal of an edge from

Tc defines a partition of the vertex set of G, each inducing a connected subgraph. The fondamental cutset in a connected graph G with respect to Tc and an edge e E E(Tc)

is defined as the set of edges that must be removed from G to obtain the same partition as that resulting from the removal of e from Tc. Thus, each spanning tree defines a set of V - 1 fundamental cutsets, one for each edge of the spanning tree.

An independent (vertex) set in graph C is a subset of V no two of whose vertices are adjacent in the graph C. The independence number of a graph C, denoted by

a(C),

is the maximum number of vertices in an independent set in

C.

A vertex cover of a graph C is a subset of V such that every edge of C is incident with a vertex in it. The covering number, noted by

(3

(

C) is the minimum number of vertices in a vertex cover. There is an elementary but useful connection between the independence and covering numbers of a graph. For graph theoretic terms not defined here see [ 6].

Theorem 1.1. [6] For a graph C,

a(C)

+

f3(C)

=IC

I.

Proof. SupposeS is an independent set in the graph

C.

By definition, there is no edge of C with endpoints in S, and so each edge has at !east one endpoint in V\ S, that is

V

\

S

is

a vertex cover of

C.

Now ifS is a maximum independent set of

C,

and

Ka

minimum covering of

C,

then

V\

K

is an independent set and V

\ S

is

a covering set of C. We have

ICI-

f3(C)

=IV\

KI

:::;

a(C) and

I

C

I

-

a(C)

=

IV

\

S

I

2:

f3(C) and hence

a(C)

+

f3(C)

=ICI.

D

Recall that the Cartesian product of two non-empty sets A and B is the set of ordered couples

A

x

B

=

{(a

,

b)

1

a E

A

,

bE B}.

We can now define the operations on graphs that interest us in this thesis. Suppose C and

H are two graphs with vertex

sets V(C) and

V(H), a

nd edge sets

E(C) and

E(

H

).

We define the following new graphs.

Join of two graphs: The jo in of two disjoint graphs C and H, written C V H, is the graph obtained from the disjoint union C

+

H by adding the edges {

{'U

,

v} 1 ·u E

V(G), v E

V(H)}.

It follows that G V

H

has IV(G)I

+

IV(H)I vertices and IE(G)I + IE(H)I

+ IV(G)IIV(H)

I edges.

In ali the following products of two graphs, the vertex set of the product graph is the set V(G) x V(H) Cartesian product of the two vertex sets) and so contains IV(G) x V(H)I = IV(G)I x IV(H)I vertices. The difference in the various graph products is in the definition of their edge sets. Since the vertices are couples

(a, u)

we denote the edges by

(a

,

u)(b,

v)

for readability. For more information on product graphs we refer to [22].

Cartesian product: The edge set of the Cartesian product GDH of Gand H is defined by

E(GDH)

=

{(

a

,

u)(b

,

v)

1

[a=

b

1\

'

uv

E E(H)] V

[

u

=v

1\

a

bE

E(G)]}. By definition, the Cartesian product GDH con tains IV ( G) 1 copies of the graph H and IV (

H)

1 copies of the graph

G

and so has IV ( G) IlE(

H)

1

+ IV (

H) IlE( G)

1 edges.

Direct product: The edge set of the direct product (also called categorical product)

G x H of G and H is defined by

E(G x

H)

={

(a

,

u)(b

,

v

)

1

ab

E

E(G) 1\

uv

E E(H)}.

Note that IE(G x H)l = 2IE(G)IIE(H)I.

Strong product: The edge set of the strong product G ~ H of G and H is defined by

lt is easy to see that fE(Gt8J H)f

=

fV(G)ffE(H)f + fV(H)ffE(G)f + 2fE(G)ffE(H)f.

Lexicographie product: The edge set of the lexicographie product G[H] of G and H is defined by

E(G[H])

=

{(a,u)(b,v) f abE E(G) V

[a= b

i\ uv E E(J-I)]}.

An easy way to visualise the lexicographie product of graphs G and H is as the graph obtained from graph G by replacing each vertex a by a (disjoint) copy Ha of H and adding ali edges between Ha and Hb when a and b are adjacent in G. (i.e Ha V Hb

replaces abE E(G)).

The edge set of the graph G[H] consists of fV(G)ffE(H)f edges for the copies of

H

and fV(H)i2fE(G)f edges thatjoin copies of H. Thus fE(G[H])f

=

fV(G)ffE(H)f

+

fV(H)i2fE(G)f.

Co-normal product The edge set of the co-normal product

G

•

H of

G

and

H

is defined by

E(G • H) ={(a, u)(b, v) f abE E(G) V uv E E(H)}.

There is fGf copies of graph H and [Hf copies of graph G in G • H such that any two copies of graph G are joined to each other if their corresponding vertices in H are adja-cent, as well as any two copies of graph H if their corresponding vertices in G are adja-cent, then there is

[V(

G)f2fE(H) 1

+

fV(H)i2fE( G)f edges, but there is 2[ E(G) IfE(

I-l)

1 common edges in this visualisation then G • H has [V( G) [2

[E(H) 1

+

1 V(H)f2IE( G)l-2fE(G)IIE(H)I edges.

By the definition it is clear that the Cartesian, direct, strong and co-normal products are commutative while the lexicographie product is not. Moreover GOH Ç G t8J fi Ç

G[H]

ç

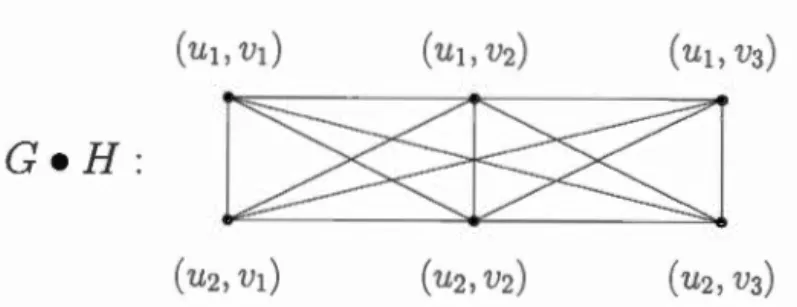
G• H

In Figure 1.4 there are the various products of graphs G = P2 and H = ?3 :

Vz

(u1,v1)

(u1

,

vz)

(u

1

,

v3)

G

DH

:

l l l

(uz

,

v

1)

( uz,

vz)

(uz

,

v3)

G

[5<J

H

•

e><c><J

G[H]:

G

•

H

:

Figure 1.4: Various Products of ?₂ and ?₃

G

V

H:

THE DECYCLING NUMBER OF GRAPHS

The first subject that we want to consider is the decycling number of a graph. Decycling of graphs has a variety of applications in applied sciences for example in the areas of combinational circuit design [28], deadlock prevention in computer systems [37] and other problems.

Suppose

G (V

,

E)

is a simple connected graph. If

S

Ç

V ( G)

and

G - S

is acy clic, we cali

Sa

decycling (vertex) set of

G;

it is also known as a feedback vertex set . Let us agree that to decycle a graph is to remove a set of vertices (and the edges incident to the vertices in the set) so that the remaining graph is acyclic. The smallest size of a decycling vertex set of G is the decycling number or feedback vertex number of G and is denoted by

cp

(G).

The problem of finding maximum arder of an induced forest is equivalent to this problem since the sum of these two parameters is the size of the vertex set. The analogous concept for edges is the cycle rank, the minimum number of edges whose deletion from a graph G leaves an acyclic graph. lt is known that the cycle rank of a graph

Gis

lEI- JVI

+

w(G),

see [46] for example.

Karp in [29] has shawn that the decision problem of finding if

cp

( G) ::; k

for an arbi-trary graph G and k a na tura! number is NP-complete but for sorne families of graphs (permutation graphs [35], interval and comparability graphs [36]) there are polynomial

-Vs

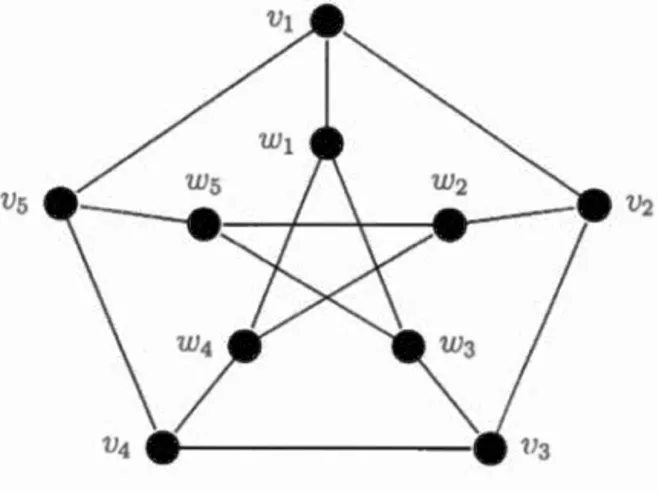
Figure 2.1: Petersen Graph.

time algorithms. Exact values of decycling numbers have been obtained for sorne fam-ilies of graphs such as grids and hypercubes [5, 42], generalized Petersen graphs [14].

One list of results on the feedback set problem and the decycling number can be found in the survey by Pesta et al. in [ 12].

It is easy to see that c/J( G) = 0 if only if G is an acyclic graph and c/J

(

G) = 1 if only if G has at least one cycle and there is sorne vertex that is on all the cycles. To remove ail cycles from a complete graph

K

n

,

we have to remove the vertices one by one to reach

K

3 and to decycle

K

3 it suffices to remove just one vertex. Thus

c!J

(K

n

)

=

n - 2. In

the case of a complete bipartite graph

K

n,m

with n

2

m, we need to remove all but one vertex in one of the sets of the bipartition. Thus

c!J

(

K

n,m)

=

min{n,m} - 1. For another example consider the Petersen graph P, Figure 2.1. To decycle P, we have to remove at least one vertex from external cycle and one vertex from internai cycle. Suppose vi is the vertex which is deleted from external cycle, if we remove one of the vertices wi, w2 or w3 , one cycle will be remain. Then by symmetry of Petersen graph

c/J

(

P

)

2

3. But vertex set {vi, v3 , w4} is a decycling set, so

c!J

(

P

)

=

3.

we review the problem of finding the decycling number of the Cartesian and strong products of graphs and, finally, we will study the decycling number of the lexicographie and co-normal products of graphs.

We begin with a trivial upper bound for an arbitrary graph.

Lemma 2.1.

[

5

] For

an

y

non null

g

raph

G

,

cp

(G)::;

f3

(G)-

1.

Proof. Suppose a graph G bas at !east one edge and consider the subgraph induced by a maximum independent setS of G and any vertex of

V(G) \S

.

Clearly this subgraph is acyclic and so

cp

(G

)

::;

I

C

I

- (

a

(G

) +

1)::;

f3

(G)-

1. 0

Lemma 2.2.

[

5

] If

n

e

ither

G

nor

JJ

is a

null

graph

,

then

cp

(G

V

H

)::;

min{IV

(G)

I

+

cp

(

H

)

,

IV

(

H

)

I

+

cp

(G)

}

.

Proof. In G V H we have two different kinds of cycles, those in G and in H, and the cycles which are produced by the edges between G and H. To deJete the latter kind of cycles, one can del ete ali vertices of one of G or H. This also triviall y de-stroys ali cycles in the graph removed. To destroy the cycles of other graph we need

cp

(

H

)

(or

cp

(

G)) vertices. Hence, and by the commutativity of the jo in

G

V

H,

we have

cp

(G

V

H

) ::;

min{

IV(G)

I

+

cp

(

H

)

,

IV(

H

)

I

+

cp

(G)}

. 0

Theorem 2.3.

[

5

]

For an

y

graph

G

,

2

cp

(G) ::;

cp

(

K

2

D

G) ::;

cp

(G)

+

(3

(G)

.

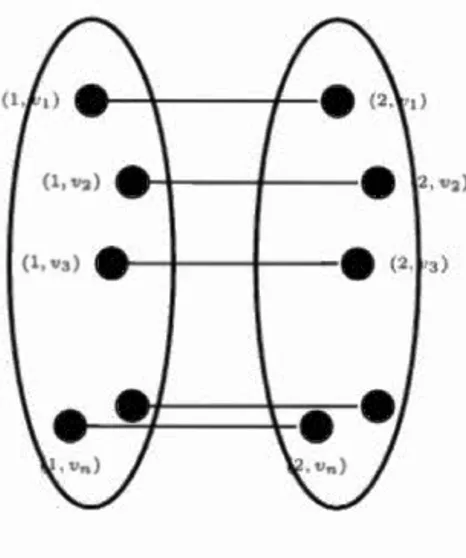
Proof. The graph K20G consists of two disjoint copies of G such that the corres pond-ing vertices are adjacent, see Figure 2.2. To decycle it, we have to remove ali cycles

(l,v3) -~1---~1----· (2, '3)

Figure 2.2: Graph K2DC

of each copy and the first inequality is obvious. Suppose A

= {

u₁, u₂, ···un} is a maxi-mum independent set ofvertices in one copy of Gand let B

= {

v1, v2, · · · , viV(G)I-a(G)} be a vertex set such that

G

l

8 is a maximum induced forest in the other. The subgraph

induced by AU Bis acyclic, so cj>(K₂DG) :::;

cj>(G)

+

IGI -a(G). D

For sorne special graphs, the bounds ofTheorem 2.3 is sharp. When G is the null graph

K

n then

cj>(K2DG) = 0 and bath bounds hold. For graph

G

=

K

n

the lower bound is

sharp because cj>(

K

2

D

K

n)

=

2

n

-

4

=

2

cj>(

K

n)

·

lt is shawn in the next section that ci>(

P2

DP

n)

=

l

~

J,

which equals the sum of ci>(

P

n)

and

f3

(Pn)

since

cj>

(

P

n)

=

0 and

(3

(

P

n)

=

l~J.

Lemma 2.4. [5] Suppose d1, d_{2 , · ·} · , dp is the degree sequence of a connected graph

G

with p vertices and q edges respective/y. If

cj>

( G)

=

s, then

s

2._)d

i

-

1

)

~ q- p

+

1.

Proof. Suppose

S

with ISI = s is a decycling set for

G

.

Then

G - S

is a for-est containing at most p - s - 1 edges. Since by removing s vertices of G at most

d1

+

d2

+

·

·

· +

ds

edges will be removed, we have that q -

:z=

:=l

(di)

:=::; p -

s

-

1 and so

:z=

:=l

(di) -

s

2:

q - p

+

1 and the result follows.D

An edge uv is subdivided if it is replaced by the pa th UWuv v with Wu v a new vertex. The graph G' = (V', E') obtained from the graph G = (V, E) by subdividing the edge uv is then defined by

V'= vu

{

Wuv}, Wuv tf.

v

andE'= { WuvU, WuvV}

u

(E \

{uv}). A subdivision of the graph

G

is any graph obtained from

G

by a sequence of subdivisions of edges.

Definition 2.5. Two graphs are said to be homeomorphic

if

each is a subdivision of the same graph.

Theorem 2.6. [5] Suppose Gand H are homeomorphic graphs, then cp(G)

=

cp(H).

Proof. Suppose that a graph K' is obtained by one subdivision from the graph K, that is, an edge ·uv is replaced by the path uwv, w a new vertex. The graph

K'

does not contains more cycles than K and so every decycling set of K is also a decycling set of K'. Thus cp(K') :=::; cp(K). Conversely, suppose S is a decycling set for K'. If w

tt

S, then

S

is a decycling set of

K

and if w E

S

then

S

-

{

w

}

U { u} is a decycling set for K. Thus cp(K) ::::; cp(K') .

Suppose N, N1, N2, · · · , Ni, Ni+l, · · · , Nn-l, Nn =Gand N, N{, N~, · · · , Nf, N{+₁, · · · , N:n = H are the two different edges subdividing sequences of the graph N to produce the

graphs H and G ( graph Ni+l is a obtained by one edge subdividing from the graph

cj;

(N:r,

=

H)

and the result follows. 0

The following usefullower bound for any connected graph Gis also given in [5].

Corollary 2.7. [5] IfG is a connected graph with maximum degree 6., then

Proof. Let d1, . . . , dp be the degree sequence of the gr a ph G and cjJ ( G) = s. We have ~;=l

(

d

i

-

1)

=

~;=l

(d

i

) -

s :=;; sb.- s. By Lemma 2.4, ~;=l

(d

i

-

1)

2:

q- p

+

1 and putting these together gives q - p + 1 ::;

s(

6. - 1), which leads to the result. 0

2.1

Decycling number of the Cartesian product of graphs

The grid graph, P

n

DP

m is one of the first graphs one studies when new parameters are

investigated for the Cartesian product. The decycling number is no exception. Still, we know of no exact formula for the decycling number of

Pn

D

P

m general! y. Sorne researchers focused on finding a tight bound for the decycling number of grids, while others looked for an exact formula for their subgraphs. In ali cases we assume that m, n

2:

2 in order to avoid trivialities. We choose a standard labelling for the vertices of

P

nDP

m

that corresponds to matrix notation, the ith vertex in the

jth

copy of P

n

is denoted Vij. We sometimes speak of the copies of

Pn

and

P

m

as the columns and rows, respectively, of

PnDPm

.

ln

PnDP

m,

each vertex of a decycling set can break at most 4 cycles of lengths 4, P₂DP₂. This allows Luccio in [38] to obtain an easy lower bound of (n-I)(;-l)+l for

find a decycling set of the size that agrees with the lower bound.

Theorem 2.8. [5] <P(P20Pm)

=

l

~

J.

Proof. In P2DPm there are

l

~

J

disjoint 4-cycles, so any decycling set must contain at least

l

~

J vertices

. Therefore, it sufficient to fi nd a decycling set with

l

~

J

ver-tices. Suppose that V(P2 )

=

{1,2}, V(Pm)

=

{1,2, ...

,

m

}

and k

=

l~J. Then {(1, 2), (1,4), · · · , (1, 2k)} is such a decycling set. Therefore <P_(P20Pm) =

l

~

J.

D

In [5] Beineke and Vandell presented the next lower bound. Proposition 2.9. [38] lfn, m ~ 3,

Observation 2.10. [47] IfG1 Ç G, G2 Ç Gand V(G1)

n

V(G2) =

0

then <P(G) ~ <P(Gl)

+

<jJ(G

2

)

.

Observation 2.11. [5] Let 1

<

r

<

m

.

Then

Furthermore, suppose

t

is the number of vertices of a decycling set of S in the rth column of PnD P m• then

Using these results, and applying sorne standard techniques, Beineke and Vandell in proved the following formulas.

Theorem 2.12. [5] For m ~ 4, we have

• c/J(P2 x

Pm)=

l~J;

• c/J(

P3

X

Pm)

=

l

3:

J

;

• cP ( P5 X

Pm)

=

l

3;

J

-

l

W

J

-

1;

•

c/J

(P6

x

Pm)

=

l

5

;'

J

;

Hartnell and Whitehead in [19] obtained sorne sharp bounds for the decycling number of the Cartesian product of two graphs when one of the factors is a complete graph.

They obtained a result analogous to Theorem 2.3 for any graph G with p vertices,

max{3c/J(G),p + c/J(G)}::; c/J(GDK3 )::; p + 2c/J(G),

So when G is a forest c/J( GDK3)

=

p

.

Also they proved when G is a bipartite graph of order p ~ 2 or when G is a graph of order p ~ 2 with ~(G)

=

3, then c/J(GDK_{3 )}

=

p+

c/J(

G)

.

Wh en one of the graphs is a complete gr a ph with order larger th an 4, [ 19] gives a lower bound.

Lemma 2.13. [ 191 Let G be a graph of arder p

2::

2. Then for r

2::

4,

ciJ(

GDKr)

2::

max{p(r-

2)

,

rc/J(G)}.

Proof. By the definition of Cartesian product of graphs, there are r copies of the graph

G and to remove the cycles we need

r

</J

(

G) vertices. Also there are p copies of the

graph

K

r

and

<P(Kr)

=

r

-

2,

soto decycle the graph

GDKr

we need at least

p(r-

2)

vertices. This gives the result. 0

Theorem 2.14. [ 191 Let G be a bipartite graph of arder p

2::

2. Thenfor r

2::

4,

c/J(

GDKr)

=

p(T-

2).

For the Cartesian product of two complete graphs, Hartnell and Whitehead have a

for-mula.

Proposition 2.15. [19

1

Suppose that n, T are integers with n

2::

r

2::

3.

Then

Decycling sets of the Cartesian product of two cycles were studied by Pike and Zou in

[ 42]. They started with the following Lower bound.

Proof. CmDCn is a 4-regular graph and so by Corollary 2.7 the result holds.D

The next result is proved in [ 42] by a series of lemmas:

Theorem 2.17. [42] Let m

2::

3

and n

2::

3

be integers. Then

r32nl

1 m=4

n=4

rmn+2l th ·

1- 3- o, ,erwv:;e

Decycling numbers of the Cartesian product of other classes of graphs are not known. In the next section we study the decycling number of the strong product of graphs.

2.2

Decycling number of the

strong

product of

graphs

ln the case of strong product, J. Xie in [47] obtained exact formulas. First we review sorne definitions, simple observations and Iemmas.

Suppose the vertex sets of Gand H are respective! y V( G) and V(H). There are 1 V( G) 1

copies of H and 1 V ( H) 1 copies of G in G [gj H. The induced subgraphs GY

=

(

G [gJ H )r{(x,y)lxEV(GJJ is a copy of G where y E V(H) and called a row of G [gJ H. Also x H = (G [gJ H)r{(x,yJiyEV(HJJ is a copy of J-1 where x E V(G), and called a column of G [gJ H. Aiso GY and x H are called the fibers of G [gJ H.

Observation 2.18. [47] For any graphs Gand J-1,

By the definition of the strong product of graphs there are JGJ copies of

H

and JHJ copies of Gin G C8l H. So <j;(G [8J H)

2:

JGJ.</J(H) and </;(G C8l H)

2:

JHJ.</J(G). Then

the following result follows.

Lemma 2.19. [47] For any graphs Gand J-1,

max{JGJ.</J(H), JHJ.</J(G)}

S

<P

(G

[8J H).

The following lemma is useful when one wants to calculate the decycling number of the strong product of graphs by induction.

Lemma 2.20. [47] Suppose that G

=

(V1, EI), H

=

(V₂, E_{2 ).} For each V{ Ç V₁ and

v;

ç

V2, we have

Lemma 2.21. [47] For graphs Gand H,

Proof. Suppose

A

= { u1, u2, · · · , Ua(G)} is a maximum inde pendent set in the graph

Gand B = {vi, v2 · · · , viHI-<I>(H)} is a vertex set such that Hia is a forest. let N =

GIA IZIH1a bethegraphwithvertexsetofV(JV) =

{(u

i,vj

)li

= 1,2,· ·· ,a(G);j =

1, 2, · · · , IHI -

cp

(H)}.

Since A is an independent set in

G,

for any

ui

,

Uj E

A

,

i =1=

j,

(ui,

uj)

tl.

E(G),

there is no edge whose two ends lie in different rows of

N

=

GIA IZl Hia· Hence

E(N)

=

{

((ui, Vs), (ui,

Vt))

l1

:::;;

i :::;; a(G),

(vs

,

Vt

)

E Hia}. Since

Hia is a forest and every row in GIA IZl Hia is a copy of Hia• N is a forest which has

a(G) copies of forest Hia· Then there is no cycle in N and INI = a(C).(IHI-

cp(

H)).

So

cp(G

~

!-!

):::;;

IGIIHI -INI. That is,

cp(G

IZIH):::;; IGIIHI- a(G).(IHI-

cp(

!-!

)).

By symmetry

cp(

G

IZl

H)

:::;;

IGIIHI- a(H).(ICI - cp(G)) and by Observation 2.10 the

Lemma holds. 0

By these two lemmas X. Chen and J. Xie proved the following formulas for the

de-cycling number of the strong product of graphs when one or both of the product factors

are complete, path or cycle graphs.

Theo rem 2.22. [ 48]

•

cp(Cm

IZl

Cn)

=min{

n.

l

~

J

+

1~1, m.l~J

+

f~l}, where m and n are even.

In the next two sections we investigate the decycling number of the lexicographie and co-normal products of graphs and give our new results.

The co-normal product is the less known of the two. It was introduced by Ore [41] in 1962, but only a few papers (for instance [9], [43]) have appeared about it since. The co-normal product is also known as the disjonctive product [ 43] and is clearly commutative [18] and [33].

2.3

Decycling number of the lexicographie product of graphs

In the case of lexicographie product we prove these results:

Theorem 2.23. For graphs Gand H,

IGi

rfJ

(H)

:S

r/J

(G[H])

~

j9

(G)IHI

+

a

(G)

cj;

(H)

Proof. The left inequality is clear because

G[H]

contains

IGI

disjoint copies of the graph H that we may index by the vertices of G: Hu is the copy of H induced by the vertex sets

{'U}

x

V(H).

Two copies

H

u and

ff

v

are joined to each other when 'uv

belongs to E ( G); "joined" means th at ali edges between the two copies are present. Therefore the re are four kinds of cycles in

G[

H], the cycles of copies of H, the trian-gles that appear in joins of copies of

H,

the cycles between two copies of

H

that are not triangles and the cycles induced by those in G. To find an acyclic subgraph of

G

[H],

we first del ete the

set

S

x

V (H

) of vertices

such that S

is

a vertex cover of G; there are ,B(G)IHI of them. In the remaining graph there are cycles only within copies of H of which there are IGI -

,B

(

G)

=

a(

G).

So cp(G[H]) ~ ,B(G)IHI

+

a(

G

)

cp

(

H

).

0

We computed the decycling number of the lexicographie product of various graphs

using a small programming written in Sagemath and we conjecture that equality holds

for ali graphs but we can only prove it when the first factor of the lexicographie product is a path, a cycle, a complete graph or a complete bipartite graph. First we present a

!emma that is useful in the sequel.

Lemma 2.24. Suppose that G

=

(V1, E1) and H

=

(V₂, E2 ), for each V{ Ç V1, we

have

Proof. For each

V{

Ç V1, G1 _V1

n

G1 1

= 0

.

Hence, by the definition of lexicographie

1 v1-v1

product Glv [H]

n

G1 ~[H]

=

0.

The result follows by Observation 2.10. 0

1 Vt- V₁

In particular when the graph G is a path

P

n

and 1

V{l

=

2 then

cp

(

P

n

[G])

~ cp(P2[G])

+

cp(Pn-2[G]).

This allows us to derive an exact expression for this case.

Theorem 2.25.

cp

(

P

n[G])

=

IGil~J

+

l~lcp(G).

Proof. We have

,B

(P

n

)

= l~J and

a(

P

n

)

= l~l By Theorem 2.23,

cp

(

P

n[G]) :'S

ICil~J

+

l~lcp(C). To prove

cp

(

P

n

[

C])

~ ICil~J

+

l~lcp(G) we use induction on n, the length of the pa th graph. For n = 2,

cp

(

P2 [ G]) =

cp

( G

V

G)

=

cp

( G)

+

1 Gl. Suppose for n

<

k the inequality holds. For n = k, by Lemrna 2.24, we have

cp

(P

n

[

G

])

~ cp(P2[G])

+

cp(Pn-2[G]) ~ IGI

+

cp

(G)

+

IGil n;2 J

+

rn;

2l cp(G) = IGI

+

cp

(G)

+

IGI(l~J -

1

)

+

(l~l

-

l).cp(G)

=

IGil~J

+

l~lcp(G), and the result

follows. 0

Since

cp

(P

m

)

=

0 we have the following. Corollary 2.26.

cp

( P

n

[

P

m

D

=

m

l

~

J.

When the first graph is a cycle we have the next result. Theorem 2.27.

cp

(

Cn

[

G

])

=

l~liGI

+

l~Jcj;(G).

Proof. For the graph Cn[G] we canuse the same argument as in Theorems 2.23 and 2.25,withthedifferencethat,B(Cn)

=

1~1 anda(Cn)

=

l~J. 0

Proposition 2.28.

cp

(

K

n

[G

])

::; (n-

l

)IG

I

+

cp

(G)

.

Proof. Kn[G] is a complete graph where vertices are copies of

G

,

which are joined to each other. By an argument similar to that in the computation of

cp

(

K

n

)

,

we have

cp

(

K

n

[

G

])

=

IGI(n-2)+

cp

(G

V

G)

=

IGI(n-2)+

1

GI+

4>

(G)

=

(n

- l)

IGI

+

4>

(G).

D

Proposition 2.29.

cp

(

K

n,m

[

G])::;

miGI

+

n

cp

(G)

where m

<

n

.

Proof. The Cartesian product Kn,m[G] looks like

K

n

,

m

with each of its vertices re -placed by a copy of

G

and two copies

G

u

and

G

v

of

G

replacing the vertices u and v, respectively are joined (ail vertices of

G

u

are adjacent to all vertices of

G

v

)

if

u

v

E

E(K

n

,

m)

.

lt follows from the structure of complete bipartite graphs that each copy of Gin one class of the bipartition of

K

n

,

m

joined to all vertices of the other class.

We need to remove

f3

(

K

n

,

m)

= m copies of

G

to delete all cycles that are produced by the joining of the copies. The remaining

n

disjoint copies of G need

n

ep

(

G) vertices to remove the cycles. 0

2.4

Decycling

number of the co-normal product of graphs

Lemma 2.30.

For

graphs

G

and H

,

max{IGI.c/J(H), IHI.c/J(G)} ::;

cp(

G •

H

).

Proof. By the definition of co-normal product of graphs, there are ICI copies of H and

lill

copies of G in

G

•11

.

So

cp

(G

•

H

)

2 IGI.c/J(H) and

cp

(C

•

H

)

2 IJJI.</J(G). 0

Lemma 2.31.

[

49

] For

an

y g

raphs

G

and

H

w

e

hav

e

a

(G

• H

)

=

a(G)a(

H

)

Proof. Suppose Sc and SH are the maximum independent sets in graphs G and H

respective! y. Clearly Sc x S H is an independent set in G • I-1. Therefore

a

(

G •

J-1

)

2

a

(G)a(

H

)

.

Suppose S is a maximum in dependent set in G • I-1, let Sc =

{

a

E V ( G) 1 :J'u E

V(

H

)

,

(a, u)

E S} and SH

=

{u

E V(H)I:Ja E V(G), (a,

u)

ES} be projections of S on V(G) and V(I-1) respectively. Clearly Sc and SH are independent set and ISI ::; ISciiSHI· On the other hand ISciiSHI ::;

a(G)a(

H

)

so

a(G

•

H

)

=

ISI::;

a(G)a(

H

)

and the result follows.

Lemma 2.32.

cp

(G

•

H

)::;

IGIIHI-

a

(G)a(

H

)

-

1.

Also we have the next result when the graph G is complete.

Corollary 2.33.

qy(

K

n

•

G)

=

(n-

1)IGI

+

qy(G).

Proof. By definition oflexicographic and co-normal product

Kn

•

G

~

Kn[G]

and the result follows from Theorem 2.28.

0

The bound in 2.32 is tight indeed, if both Gand H are complete, we have, by Corollary 2.33

qy(

K

n

•

Km)

=

(n - 1)1Kml

+

qy

(Km)

=

(n- 1)m

+

(m- 2)

=

nm- 2 while the

up-perboundinLemma 2.32is

IKniiKml-a(Kn)a(Km)-

1

= nm-1x1- 1 = nm-2.

Lemma 2.34.

Suppo

se

that

G

=

(Vi

,

E1 ),

H

=

(V2, E2 ).

For

eac

h

V{

c

V1

and

V~

ç

V2 ,

we

hav

e

0.

And it is obvious that G1 , •

H

Ç

G

•

H

and G1 , •

H

Ç

G

•

H.

By Obse

r-~ ~-~

vation 2.10 we have

qy(G

•

H)

2:

qy(GI , •

H)

+

qy(GI , •

H).

For each V~ Ç V2,

VI Vl- Vl

by symmetry of co-normal product,

c/J(

G

•

H)

2:

qy( G

•

H1,,)

+

qy( G

•

H1 , ) . This

v2 v2-v2

completes the proof the lemma.

0

Observation 2.35.

Ind

ee

d

G

•

P2 ~ GVG

so qy(G

•

P2 )

=

qy(GvG)

=

IGI

+c/Y(G)

and

then

qy(Pn

•

P2)

=

n.

So

qy(P3

•

P2)

=

qy(P3VP3)

=

3andqy(C3

•

P2)

=

qy(C3VC3)

=

4.

Lemma 2.36.

qy(

?3

•

Pn)

2:

2n - 2 -

l

n~3

J

Proof. By induction on n we prove

_qy(P3

•

Pn)

2:

2n - 2 -

l

n~3

J.

By Observation

length less than n

= k.

We will prove it is satisfied when n

= k +

1. By Lemma 2.34 we have

cp

(P

3

•

P

k+

l)

~

cp

(P3

•

P2)

+

cp(P3

•

H

-

1)

~ 3

+

2(k- 1) - 2-

l

k-~-3

J

~ 2k - 1 - l~J

+

1

=

2k- l~J ~ 2k-

l

k~2

J.

0

We conjecture that equality actually holds.

Conjecture 2.37.

cp

_(P3

•

P

n)

=

2n- 2- ln~3

J

Similarly, we have the following.

Lemma 2.38.

cp

(

C

3 •

Cn)

~ 2n

+

1

Proof. By induction on n we prove

cp(

C

3 •

C

n

)

~ 2n

+

1. Since C3 ~

K

3 by Corollary

2.33

cp(

C3 • C3) = 2 x 3

+

1 = 7 and the inequality holds. By Lemma 2.34 and Obser-vation 2.35 we have cp(C3 • Ck+1 ) ~ cp(C3 • P2 )

+

cp(C3 • Ck-1) ~ 4

+

2(k-1)

+

1 =

2k

+

3

=

2(k

+

1)

+

1 0

And we think this should be equality.

THE BASIS NUMBER OF GRAPHS

The set all of su bsets of the edge set E of the gr a ph G forms an

1

E

1-

dimensional vector space over

GF(2)

with vector addition

X+ Y

:=(X

U

Y)- (X

n

Y)

and scalar multiplication l.X = X O.X =

0

.

lt suffices to assign a fixed and arbitrary numbering { e1, ... , e₁e(G)I} of the edge set of the graph G and allocate a characteristic vector with

length of 1

E(

G)

1 to each subset of the edges. Assign 1 at the i-th coordinate of this vector if the edge ei is in the subset, otherwise put O.

A (generalized) cycle is a subgraph whose every vertex has even degree. lt is denoted by its edge set,

C.

The vertex set of a generalized cycle is denoted by

V (

C

).

An elementary cycle is a connected minimal (with respect to number of edges of the cycles) subgraph whose every vertex has degree two. The set C of all generalized cycles forms a linear subspace of

(P(E)

,

+,

.)

which is called the cycle space, C(G), of the graph G, where

P(E)

is the set of all subsets of

E(

G). So a set

B

= {

C1, C2, C_{3 ,} · · ·} is called a cycle basis of C ( G) if and only if every element of C ( G) can be written in a unique way as a fini te linear combination of cycles from the set B.

Theorem 3.1. [45] The dimension of the cycle space of the graph Gis the cyclomatic number (jirst Betti number)

v(

G)

=

dim(C)

=

1

E(

G) 1 -

IV(

G)

1

+

w(

G)

(where

w(

G)

is the number of connected components of G ).

Proof. It suffi ces to prove the claim for

w(

G)

=

1, when the graph is connected, because the cycle space of a graph is the direct sum of the cycle spaces of its connected

y

4 2

v

1----

3

---0

Figure 3.1: Edge Labelling of graphs

components.

Now suppose Tisa spanning tree of the graph G. For each edge e E E(G)- E(T), edge set TU { e} constructs a unique cycle. The set these cycles is independent because each one has an edge that is not in any other cycle. Si nee 1 E(T) 1

=

1 V (T) 1 - 1, there are IE(G)I - (IV(G)I - 1) such cycles. Therefore dim(C)

2:

IE(G)I - IV(G)I + 1.

On the other hand, suppose

S

and

S

are vertex sets of the two connected components formed by removing an edge e E E(T) from T. The set (S, S) is a fundamental eut set in G. For each eut set, we define the characteristic vector of a eut to be a vector in GF[2]1E(G)I that has 1's in components corresponding to the edges of Gin the eut and O's in the remaining components. There exist lVI - 1 such vectors each defined by an edge of

T.

Each cycle of

G

must intersect each eut set an even number of times, so the set of characteristic vectors of eut sets are orthogonal to the cycle space of G. In addition these characteristic vectors are linearly independent, because each eut is different in at least the tree edge defining the eut. Therefore the dimension of the orthogonal complement to the cycle space is at least IV (

G)

1 - 1. Therefore dim( C) :S 1 El - IV 1

+

1 and this completes the argument D

We associate vector [11 0 0 1] to the cycle C1

=

(x

,

y,

u

,

x),

vector [0 0 1 11] to the cycle

C2

=

(

x,

u

, v, x

)

and vector [1111 0] to the cycle

C3

=

(.r

,

y,

u

,

v

,

x).

We can write

c3

=

cl

+

c2

and consider {

cl

'

c2

} as a

cycle basis.

Given a basis

Bof

the cycle space

C

(G),

let

J(B)

=

max{

k :

:J

e

E

E(

G):JC

1, ... , Ci E

B}

such that e E

Ci

for i

=

{1, ... , k}. That is,

J(B)

is the maximum number of cy-cles of

B

containing any given edge. We call

f

(

B

)

the fold of

B.

A basis for C ( G) is called a k-fold basis if each edge of G occurs in at most k of the cycles in the basis, i.e.

J(B)

=k.

The basis number of

G,

denoted by

b(G)

is the smallest integer

k

such that

C

(G)

has a k-fold basis. For each edge

b

E

E(G),

J

8

(

e

)

is the number of cycles

in the basis B in which e occurs.

The basis number was introduced by Schmeichel [44] in 1981. He proved that for any integer

r

,

there is a graph with basis number greater than or equal to

r.

MacLane in 1937 [39] proved the following well-known result.

Theo rem 3.2. [ 39] Graph G is planar

if

and only if b( G) :::; 2.

Schmeichel [44] proved that

b(K

n

)

= 3 whenever

n

2

5 and

b

(

K

n

,

m) :::;

4 for each

n

and m. In 1982, Banks and Schmeichel [4] proved that

b(

Qn)

=

4 whenever n

2

7. Many papers appeared investigating the basis number of certain graphs, especially the graph products, see [2], [27], [1].

Ali and Marougi in [3] gave the following upper bound for the basis number of the Cartesian product of graphs.

max{b(G)

+

D..(TH ), b(H) + D..(Tc)}, where TH and Tc are spanning trees of H and G, respective/y, such that the maximum degrees D..(TH) and D..(Tc) are minimum with respect to ali spanning trees of H and G.

In [24] M.M. Jaradat proved sorne results for the basis number of the strong product.

Theorem 3.4. LetT1 andT2 be two trees. Then b(T

1

~T

2

) ::; max{ l36.(~I)+l

J

,

l

3(6.(;2)+l

J}

where 6.(~) is maximum degree ofvertices of~ for i = 1, 2.

Theorem3.5.!JG isabipartitegraphand Tf isanygraph, thenb(G~TJ)::; max{b(TJ)+

1

,

26.(H) +

b(G)

-

1

,

l

3(6.(;2)+1

j

,

b(G)

+2

}.

The basis number of the lexicographie product of graphs was studied by Jaradat and

Alzoubi in [26] who proved the following results.

Lemma 3.6. [26] Suppose Mis a null graph on vertex set { u₁, u₂, · · · ,

un

}

and P₂

=

ab is a path of order 2. Then

is a 4-fold basis ofC(P2[M])

Lemma 3.7. [26] LetT be a tree and P2 =uv be apath oforder 2. Then b(P2[T]) ::; 4. Moreover ifiV

(T)I

~ 14, then equality holds.

They used a special decomposition of a tree into an edge-disjoint union of subtrees to find a cycle basis for the lexicographie product of trees and then by computation fold

of the cycle basis, they fou nd a upper for b(T1 [T2]).