Translated Title:
Reprint Status:
Edition:
Author, Subsidiary:
Author Role:
Place of Publication:
Québec
Publisher Name:
INRS-Eau
Date of Publication:
1973
Original Publication Date:
Volume Identification:
Extent of Work:
42
Packaging Method:
pages, 4 annexes
Series Editor:
Series Editor Role:
Series Title:
INRS-Eau, Rapport de recherche
Series Volume ID: 22
Location/URL:
ISBN:
2-89146-015-4
Notes:
Rapport annuel 1973-1974
Abstract:
25.00$
Call Number:
R000022
INRS-Eau
Université du Québec
C.P. 7500, Sainte-Foy
Québec G1V 4C7
RAPPORT SCIENTIFIQUE No 22
1973
Rapport rédigé pour
INRS-Eau
par
B. Bobée
Etude de la loi log-Pearson type III
et ses applications.
L'emploi de plus en plus fréquent de la loi
10g~Pearson
type III pour
re-présenter des séries de données et plus particuliêrement des séries
de
données hydrologiques nécessite une connaissance plus approfondie
des
propriétés mathématiques et statistiques de cette loi que nous
considé-rons sous sa forme la plus générale. La partie mathématique de
l'étude
met en évidence la grande souplesse de cette loi et la grande variété des
formes de la fonction densité.
Dans l'étude statistique de la loi, on s'amène
â
considérer le
problème
de l'existence des moments et
â
calculer de maniêre systématique les
mo-ments importants et les divers coefficients caractéristiques en fonction
des paramêtres de la loi. Les résultats obtenus permettent en particulier
de tracer les courbes reliant les coefficients de variation et
d'asymé-trie, ce qui est d'un grand intérêt pratique pour l'ajustement de la loi
aux séries observées.
Mots clé: Distribution de la loi log-Pearson type III, formes de la
fonc-tion de densité, moments, coefficient de variafonc-tion,
coeffi-cient d'asymétrie.
Référence: Bobée, B.
(1973). Etude de la loi log-Pearson type III et
ses applications. INRS-Eau, rapport scientifigue no 22,42 p.,
4 annexes.
1.
Rappel des propriétés de la loi Pearson III
1.1
Forme générale de la loi
1.2
Fonction caractéristique de la loi
1.3
Détermination des cumulants et moments
2.
Etude mathématique de la loi log-Pearson III
2.1
2.2
2.3
2.4
2.5
3.
Etude
3.1
3.2
3.3
3.4
3.5
3.6
Fonction densité de la loi log-Pearson III
Mode de la distribution
Etude des points d'inflexion
Signe de g'. Valeurs aux limites de g et g'
Forme des distributions
statistique de la loi log-Pearson III
Calcul des moments
Relation entre
(1-1')
et les cumulants de Pearson III
r
L
Détermination des principaux coefficients de
log-:pearson III
Cas particulier de la loi log-Gamma
Calcul numérique des moments et coefficients de
log-Pearson III
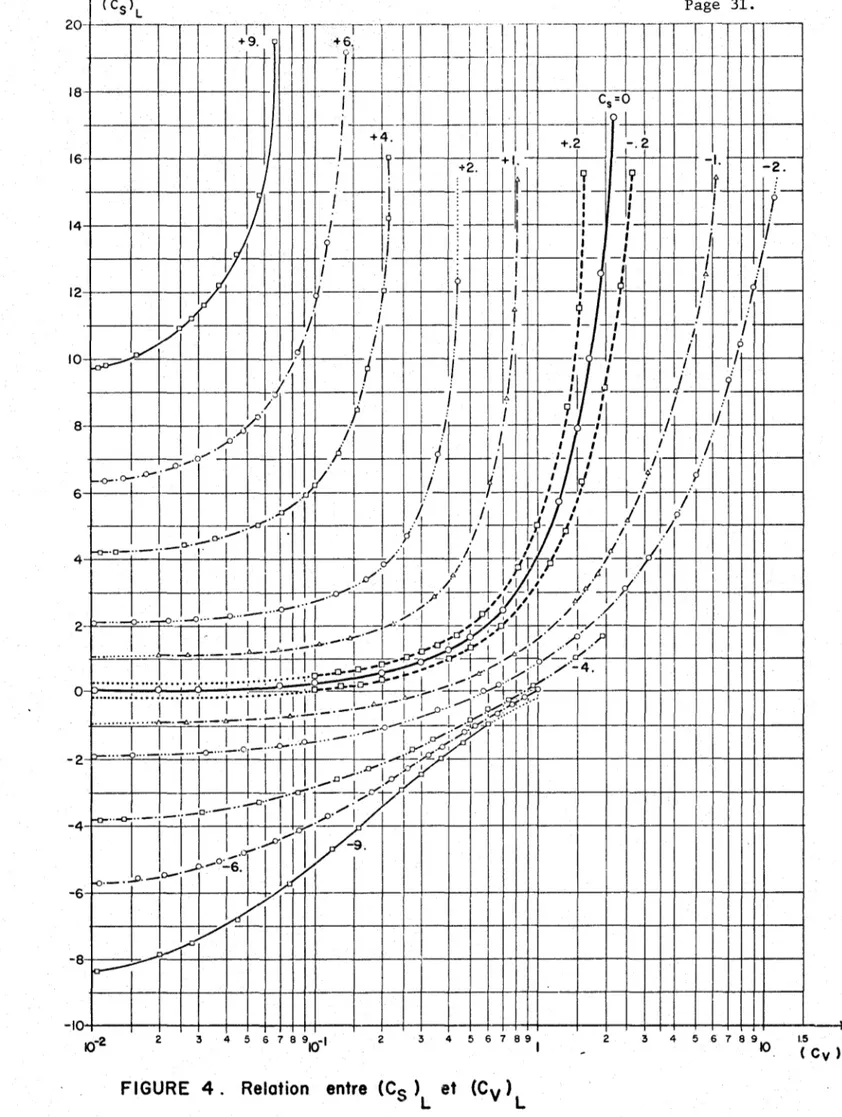
Etude de la relation entre (C )
4.2
Conclusion
Annexe A
Annexe
B
Annexe C
Annexe
D
.
CI.
>
CI.
>
CI.
<
CI.
<
0,
0,
0,
0,
Application en hydrologie
logarithme népérien
lagarithme décimal
logarithme népérien
logarithme décimal
hydrologiques concernant les crues (Water Resources Council 1967).
Cette loi semble par ailleurs adéquate pour représenter de
nombreu-ses séries de données.
Le but de cette étude est de déterminer les
principales caractéristiques mathématiques et statistiques de cette
loi et de la comparer
à
la loi Pearson III dont elle est déduite.
On considère la forme générale à trois paramètres et on examine
également l'influence de la base des logarithmes utilisée.
La densité de probabilité de la forme la plus générale de la loi
Pearson type III est
f(x)
=
W
{a
(x-m~
1..-1
e-
a
(x-m)
r(À)
1
avec:
À
>
0
et
_00<
m
<
+
00on peut considérer les 2 cas:
a)
a
>
0
l'intervalle de variation est m
~
x
<
+
00b)
a
<
0
l'intervalle de variation est -
00<
x~
m
La synthèse des 2 cas est donnée par
o
~ ~
(x-m)
<
+
00m est un paramètre d'origine;
lorsque m est nul, on est ramené au
cas particulier de la loi gamma.
(1)
Il existe d'autres formes de la loi Pearson
I I I
que l'on peut obtenir
par changement de variable
à
partir de
(1),
mais la forme la plus
souple pour représenter des séries de données est la forme
à
3
para-mètres.
La fonction caractéristique de la distribution existe toujours puisque
l'on a:
dx
'" J
1
e
itx
1
f(x)
dx '"
J
f(x) dx
=
1
6
6
1.3
~(t)
=
1
e
itx
rl~~ [~(x-m)}
;\-1
e-~(x-m)
dx
(2)
avec
(
m,co) si
(-co,m) si
0.<0
a
>
0
en effectuant le changement de variable v
=
(a -
it)
(x-m)
la
relation
(2)
devient:
donc:
l/J(t)
=
itm
e
-v
À-1
e
v
dv
Détermination des cumu1ants et des moments
Soit
K.
le cumulant d'ordre
j
de la distribution, on a
J
Ln
l/J(t)
=
L:
j
K.
J
Donc
K.
est
J
Ln
(l/J(t») ,
Pearson
I I I
le coefficient du terme
--.-,-
(it)j
du développement de
J,
On peut en déduire les cumu1ants de la distribution
en effet:
Ln
l/J(t)
=
itm -
À
Ln
(1 -
~t
1
=
itm
+
À
L:
(it
a
lj
1
'"'T'"j
J
Ln
l/J (t)
(3)
Donc le cumulant d'ordre
j
est
=
À
(j-l)
j
=
2,
3,
K.
...
J
a
j
(4)
=
À
KI
m
+ -
a
A
partir des cumulants, il est possible de déduire les expressions
des moments centrés par rapport
à
la moyenne et des moments non
centrés
(Kendall et Stuart
1969).
On a, en particulier:
moyenne
variance
~'
=
KI
=
m
+
À/a
l
~3
=
K3
=
n/a
3
2
2
114
=
K4 .. 3K2
=
L
4
(3
a
6
+ -
)
À
Il est également possible de déduire les principaux coefficients
caractéristiques de la distribution:
Donc:
coefficient de variation
C
v
C
v
C
v
=
-v;
1
=
1 al .
- À
=
=
Yî
+
-À+ma
Vî
- À+ma
m+
-a
si
si
1.
11
2
_
2
_
C
,
-v
111
a
>
0
a
<
0
(5)
2À
2
hlc
C
c
_
~
s.
3
À
"Vi:
a
Donc:
2
>
0
a
>
0
C
=
+ - -
s.
s
~
1-s
1
-
~I
--
2
a
-v:;:-C
S
-(6)
2
<
OJSi
a
<
0
-v:;
Le coefficient d'asymétrie est indépendant du paramètre d'origine
et montre que la loi relative
à
a
>
0 s'applique pour des données
à
asymétrie positive et la loi correspondant
à
a < 0 est
caractéri-sée par une asymétrie négative.
On peut vérifier que dans le cas de la loi gamma (m
=
0) on a
C
=
2 C
s
v
coefficient de finesse
(7)
Parfois on définit la finesse par C
k
=
C
k
- 3
Le coefficient C
k
est indépendant du signe de a.
Les propriétés d'invariance des cumulants permettent de déduire
les cumulants et les moments des formes simplifiées de la loi
Pearson III,
à
partir de ceux de la loi générale.
En effet, si nous considérons la variable y
=
lx
+
p
on a:
K
=
.t
r
K
r,y
r,x
r
=
2, 3, •.•
K
l,y
=
.t
K
l,x
+
P
K
et
K
sont respectivement les cumu1ants d'ordre r
des
r,y
r,x
variables y et x.
Dans le cas de la loi gannna
à
1 paramètre par exemple:
f (y)
=
1
1
00e-y
À-1
dy
r(À)
y
0
on a y
=
ax
- ma
donc
K
=
a
r
K
=
À (r-1)
r,y
r,x
À
À
K
=
a
K
-
m a
=
a(m ... - ) - m a
=
l,y
l,x
a
2.
ETUDE MATHEMATIQUE DE
LA
LOI LOG PEARSON III
Si
Y
=
log x suit une loi Pearson III, x suit une loi
log~
a
Pearson III, la function densité de y est d'après (1)
f(y)
=
lai
rc\)
e
-a(y-m) [ (
a
y-m
))À-1
y
y/k
Y
=
log x
=
k Ln x ... x
=
a
=
e
a
avec k
=
log e
a
=
1
Ln
a
k est
>
0
si a
>
1 (Ln est le logarithme népérien de base e)
on a:
g(x)
=
lai
T(À)
À-1
-a(log x-m) (
]
k
e
a
a(log
a
x-m)
x
avec 0 < À et
_00< m <
+
00L'intervalle de variation est D tel que
si
a
>
0
Si
a
<
0
m _ m/k
a - e
~x<+oo
O
" x " a
<
< m -
- e
m/k
La fonction g(x) peut encore s'écrire:
g(x)
=
lai
k
r(À)
am
e
1
l ..
ak
x
r,
)~
À-1
La
(k
Lux-m
'J
Le calcul des dérivées première et seconde de g(x) donne
g' (x)
=
1
a
1
ka
f(À)
e
am
2+ak
x
[a(k Lnx-m )] À-2
*
A
avec
A
=
(À-1)
k - (1 + ak) (k Ln x - m)
g"(x)
avec
=
lai
k
f(À)
am
e
3..-ak
x
r
~
À-3
l
a(k Ln
x - m)J
*
T
(8)
(9)
(10)
T
=
u
2
(l+ak) (2+ak) - U a k (À-1) (3+2ak) +a
2
k 2 (À_1) (À-2)
(11)
2.2
Mode de la distribution
Le mode de la distribution est obtenu lorsque
A
s'annule.
La valeur modale x
M
est telle que
(À.-l)k -
(1
+,
exk)
(k
Ln
~
-m)
=
0
puisque l'on a toujours quelque soit le signe de ex
ex
(k
Lnx-m)
?- 0,
le mode n'existe que si:
(:\-1)
ex
k
1
+
ex
k
>
0
En tenant compte du fait que
k et
À
sont positifs, la table
l
indique les cas où la distribution possède un extremum
1
1
ex
< 0
ex
>
0
ex
< -
- - <
k
k
0<
À
< 1
Pas de mode
Extremum
Pas de mode
À
>
1
Extremum
Pas de mode
Extremum
TABLE l
La valeur modale lorsqu'elle existe est atteinte pour
(À-l)
1 ...
ex k
(12)
e
m
k
e
1
À-l [
]
À-l
(À-l)
a
k
1
+
a. k
quand À=l l'extremum est atteint à une borne.
Cas particuliers
(13)
Si
ID
=
0, on est dans le cas de la loi Log-gamma, c'est-à-dire
que y
=
log x
suit une loi gamma.
a
Dans ce cas, le mode
~,o
et la fonction densité
g(~
,
0)
sont données par:
À-l
l-tak
~,O
=
e
(14)
[ r-
1
g
(~
,
0)
=
\ a \ • k
f(À)
1
À-l
(À-l)ak
l+ak
(15)
e
Quel que soit m on a
~
• g
(~)
=
~
,
0 g
(~
,
0)
=
constante.
Donc le point de coordonnées
[~, g(~~
se déplace sur une
hyperbole quand m varie pour À et a fixés.
Suivant la base
a
considérée dans y
=
log x, le paramètre k
a
prend différentes valeurs en particulier:
Si
y
=
Ln
x
(base e)
on a k
=
1
Si
y
=
10glO
x
(base 10) on a k
~
0.434
Dans tout ce qui suit, on ne considèrera que les valeurs k
>
0
(qui correspondent à a
>
1 ).
Les points d'inflexion sont obtenus lorsque
d'après l'expression
(10)
si
le trinome
T
g" s'annule donc
s'annule.
La
recher-che des points d'inflexion nous conduit
à
déterminer les racines
positives de
T
puisque l'on a toujours
U
=
a(k
Ln x - m)
>
O.
1
/