Hydraulique fluviale

(1)

de l'Ecole polytechnique fédérale de Lausanne

Volume 16

HYDRAULIQUE FLUVIALE

Ecoulement et phénomènes de transport

dans les canaux à géométrie simple

Walter H. Graf

Mustafa S. Altinakar

PROGRAMMES et ANIMATIONS

(2)

TABLE DES MATIERES

I . INTRODUCTION 6

I.1) GUIDE GÉNÉRAL 6

I.2) ANIMATIONS EN VIDÉO QUICKTIME 8

I I . CONTENU DU CD-ROM 1 0

III. EXPLIC 1 1

III.1) GÉNÉRALITÉS 11

III.2) GÉNÉRALISATION DE L'ÉQUATION DE CONTINUITÉ 11

III.3) EQUATION DYNAMIQUE ETSA DISCRÉTISATION 13

III.4) STABILITÉ DES SOLUTIONS NUMÉRIQUES ET

GÉNÉRALISATION DE LACONDITION DE STABILITÉ DE COURANT 14

III.5) EXEMPLE D'UTILISATION DU PROGRAMME EXPLIC 14

I V . MOCREG 2 0

IV.1) GÉNÉRALITÉS 20

IV.2) MÉTHODE DE CARACTÉRISTIQUES AU PAS DE TEMPS FIXE 22

IV.3) CONDITIONS AUX LIMITES 26

IV.3.1) Débit d'entrée est connu en amont (écoulement fluvial)

(voir Fig. IV.4a) 27

IV.3.2) Relation entre le débit et la vitesse est connue en aval

(écoulement fluvial) (voir Fig. IV.4b) 27

IV.4) LA MÉTHODE DE NEWTON-RAPHSON 28

IV.5) EXEMPLE D'UTILISATION DU PROGRAMME MOCREG 30

IV.5.1) Définiton du domaine de solution : 30 IV.5.2) Discrétisation des équations pour la méthode des

caractéristiques au pas de temps fixe 31

IV.5.2.1) Conditions initiales 31

IV.5.2.2) Stockage des informations dans le programme 31 IV.5.2.3) Discrétisation des équations 32 IV.5.2.4) Conditions de bord en amont 32 IV.5.2.5) Conditions de bord en aval 32

IV.5.3) Structure du programme MOCREG 33

IV.5.4) Solution de l'Ex.5.B en utilisant le programme MOCREG 35 IV.5.5) Analyse des résultats de calculs et commentaires 36

V . DELTA 5 1

V I . GRAVIT 5 4

VII. DIFFUSION PURE ET CONVECTION-DIFFUSION 5 6

VIII. DIFFTUR 6 0

VIII.1) GÉNÉRALITÉS 60

VIII.2) STRUCTURE ET FONCTIONNEMENT DU PROGRAMME DIFFTUR 64

VIII.3) EXEMPLE D'UTILISATION DU PROGRAMME DIFFTUR 67

I X . DIFDIS 7 8

IX.1) GÉNÉRALITÉS 78

IX.2) STRUCTURE ET FONCTIONNEMENT DU PROGRAMME DIFDIS 79

IX.3) EXEMPLE D'UTILISATION DU PROGRAMME DIFDIS 81

X . DISPTUR 8 5

X.1) GÉNÉRALITÉS 85

X.2) STRUCTURE ET FONCTIONNEMENT DU PROGRAMME DISPTUR 86

X.3) EXEMPLE D'UTILISATION DU PROGRAMME DISPTUR 89

X.4) REMARQUES 93

X I . REFERENCES 1 0 1

(3)

LISTE DE FIGURES

Fig. I.1 barre de commande du déroulement de l'animation (suivant le logiciel de vidéo et de sa version, l'apparence de la barre peut être plus ou moins différente).

9

Fig. 5.5 Maillage de différences finies autour du point P, projeté sur le plan, x - t.

12 Fig. Ex.5.B.2 Schéma numérique explicite et conditions limites aux extrémités

amont et aval du domaine de solution.

12

Fig. IV.1 Le maillage irrégulier formé par les lignes caractéristiques (écoulement fluvial).

21 Fig. IV.2 Comparaison entre la grille des caractéristiques et une grille

régulière.

23 Fig. IV.3 Méthode des caractéristiques (écoulement fluvial). 24 Fig. IV.4 Conditions aux limites pour écoulement fluvial. 27 Fig. IV.5 Représentation géométrique de la méthode de Newton-Raphson. 29 Fig. Ex.5.B.1 Le domaine de solution et sa discrétisation. 31

Fig. IV.6 Organigramme du programme MOCREG. 34

Fig. IV.7 Dialogue interactif avec MOCREG pour introduire les données du problème à partir du clavier.

37 Fig. IV.8 Dialogue interactif avec MOCREG pour introduire les données

du problème à partir d'un fichier de données.

39 Fig. IV.9 Fichier de données lu par le programme MOCREG. Les noms

des variables sont inclus pour faciliter la lecture par l'utilisateur. Ils sont ignorés par le programme MOCREG.

39

Fig. IV.10 Fichier de sortie du programme MOCREG. 40

Fig. IV.11 Comparaison des résultats obtenus avec les programmes MOCREG et EXPLIC: (a) débit d'écoulement ; (b) profondeur d'eau.

42 Fig. IV.11 Comparaison des résultats obtenus avec les programmes

MOCREG et EXPLIC: (c) vitesse d'écoulement ; (d) courbe de tarage.

43

Fig. VII.1 Systèmes de coordonnées. 57

Fig. VIII.1 Principe de fonctionnement de la méthode des sources imaginaires.

61 Fig. VIII.2 L'application de la méthode des sources imaginaires pour la

solution de la diffusion transversale dans un canal rectangulaire de largeur B.

62 Fig. VIII.3 Organigramme du programme DIFFTUR (suite à la page

suivante).

65 Fig. VIII.4 Explication du contenu du fichier d'entrée COUPEXY.DAT. 69 Fig. VIII.5 Dialogue interactif avec le programme DIFFTUR pour calculer

la répartition de la concentration des eaux usées à des stations L₁ = 0.5 [km] et L₂ = 20 [km]. Les points de calcul sont introduits à partir d'un fichier et les résultats sont imprimés sous forme adimensionnelle.

70

Fig. VIII.6 Dialogue interactif avec le programme DIFFTUR pour calculer la répartition de la concentration des eaux usées à des stations L₁ = 0.5 [km] et L₂ = 20 [km]. Les points de calculs sont introduits manuellement au clavier en donnant les limites du domaine de calcul et le nombre de points à considérer dans chaque direction. Les résultats sont imprimés sous forme dimensionnelle.

(4)

Fig. VIII.7 Résultats des calculs de la répartition de la concentration des eaux usées aux stations L₁ = 0.5 [km] et L₂ = 20 [km] avec le programme DIFFTUR: (a) Résultats adimensionnels obtenus avec le dialogue interactif à la Fig. VIII.5.

72

Fig. VIII.7 Résultats des calculs de la répartition de la concentration des eaux usées aux stations L₁ = 0.5 [km] et L₂ = 20 [km] avec le programme DIFFTUR: (b) Résultats avec dimensions, obtenus avec le dialogue interactif à la Fig. VIII.6.

72

Fig. VIII.8 Démonstration de la méthode des sources imaginaires en utilisant les données de l'Ex.8.C.

75 Fig. 8.9 Evolution de la répartition de la concentration, c*_(x*_,y*_{), pour}

une source positionnée au centre, y*_{= 0.5, et à la paroi latérale,}

y*_{= 0.0, d'un canal.}

76

Fig. IX.1 Organigramme du programme DIFDIS. 80

Fig. IX.2 Dialogue interactif avec le programme DIFDIS pour introduire les données.

82 Fig. IX.3 Contenu du fichier de résultat RESULT.DAT obtenu avec le

programme DIFDIS.

83 Fig. 8.7 Evolution de la concentration, C(x,t), pour une concentration,

Co, introduite de façon continue dans un écoulement à vitesse

moyenne, U.

83

Fig. X.1 Organigramme du programme DISPTUR 87

Fig. X.2 Dialogue interactif avec le programme DISPTUR pour le scénario A de l'Ex.8.E.

90 Fig. X.3 Dialogue interactif avec le programme DISPTUR pour le

scénario B de l'Ex.8.E.

91 Fig. X.4 Dialogue interactif avec le programme DISPTUR pour le

scénario C de l'Ex.8.E.

92 Fig. X.5 Dialogue interactif avec le programme DISPTUR pour calculer

l'évolution de la concentration aux stations L1∗ = 180 [km] et L2∗ = 310 [km] dans le cadre de l'Ex.8.F.

94

Fig. X.6 Dialogue interactif avec le programme DISPTUR pour calculer l'évolution de la concentration aux stations L1∗ = 180 [km] et L2∗ = 310 [km] dans le cadre de l'Ex.8.F.

95

Fig. 8.11 Evolution de la concentration, C(x,t), introduite uniformément sur toute la section : a) de façon instantanée, b) de façon à temps

fini et c) de façon permanente et constante.

(5)

LISTE D'ANIMATIONS

Animation III.1 (voir le fichier EXPLIC01.MOV ou EXPLIC01.AVI) 16 Animation III.2 (voir le fichier EXPLIC02.MOV ou EXPLIC02.AVI) 17 Animation III.3 (voir le fichier EXPLIC03.MOV ou EXPLIC03.AVI) 18 Animation III.4 (voir le fichier EXPLIC04.MOV ou EXPLIC04.AVI) 19

Animation IV.1 (voir le fichier MOCREG01F.MOV ou MOCREG01F.AVI) 46 Animation IV.2 (voir le fichier MOCREG02F.MOV ou MOCREG02F.AVI) 47 Animation IV.3 (voir le fichier MOCREG03F.MOV ou MOCREG03F.AVI) 48 Animation IV.4 (voir le fichier MOCREG04F.MOV ou MOCREG04F.AVI) 49 Animation IV.5 (voir le fichier MOCREG05F.MOV ou MOCREG05F.AVI) 50

Animation V.1 (voir le fichier DELTAMOVF.MOV ou DELTAMOVF.AVI) 53

Animation VII.1 (voir le fichier DIFFPUREF.MOV ou DIFFPUREF.AVI) 58 Animation VII.2 (voir le fichier DIFFCONVF.MOV ou DIFFCONVF.AVI) 59

Animation X.1 (voir le fichier EX8ESA01F.MOV ou EX8ESA01F.AVI) 98 Animation X.2 (voir le fichier EX8ESB01F.MOV ou EX8ESB01F.AVI) 99 Animation X.3 (voir le fichier EX8ESC01F.MOV ou EX8ESC01F.AVI) 100

(6)

I. INTRODUCTION

I.1) GUIDE GÉNÉRAL

La CD-ROM que vous tenez en main contient 7 programmes permettant de résoudre les exercices présentés dans le livre :

HYDRAULIQUE FLUVIALE

Ecoulement non permanent et phénomènes de transport

W.H. GRAF et M.S. ALTINAKAR Traité de Génie Civil

de l'Ecole polytechnique fédérale de Lausanne Volume 16

Presses polytechniques et universitaires romandes (mars 2000)

EXPLIC : Programme pour résoudre les problèmes d'écoulement non permanent dans les canaux à section trapézoïdale, rectangulaire ou triangulaire en utilisant un schéma explicite en différence finie.

Il a été utilisé dans le Chap. 5 pour résoudre le problème : - Ex. 5.B, pp. 300-321

MOCREG : Programme pour résoudre les problèmes d'écoulement non permanent dans les canaux à section trapézoïdale, rectangulaire ou triangulaire en utilisant la méthode de caractéristiques sur un maillage régulier (schéma explicite).

Il constitue une alternative à l'EXPLIC pour résoudre certains problèmes du Chapitre 5, par exemple :

- Ex. 5.B, pp. 300-321

DELTA : Programme pour le calcul unidimensionnel du transport de sédiments par charriage dans une rivière en tenant compte de la modification du profil du lit par les processus d'érosion et de déposition.

Il a été utilisé dans le Chap. 6 pour résoudre le problème : - Ex. 6.C, pp. 412-447

GRAVIT : Programme pour résoudre les équations d'écoulement non uniforme des courants de gravité (conservatifs ou non conservatifs) unidimensionnels et permanents, en régime torrentiel (Ri<1), avec la méthode de Runge-Kutta d'ordre 4.

Il a été utilisé dans le Chap. 7 pour résoudre le problème : - Ex. 7.A, pp. 491-515

DIFFTUR : Programme pour résoudre les problèmes de convection-diffusion en régime turbulent (dans le plan vertical ou horizontal) dans un milieu limité (par exemple dans un canal à section rectangulaire) en utilisant la méthode des sources imaginaires.

Il a été utilisé dans le Chap. 8 pour dessiner la Fig. 8.9 et pour résoudre les problèmes :

- Ex. 8.B, pp. 576-581, - Ex. 8.C, pp. 582-585.

DIFDIS : Programme pour résoudre les problèmes de convection-dispersion d'une source continue dans un écoulement turbulent.

Il a été utilisé dans le Chap. 8 pour dessiner la Fig. 8.7 et pour résoudre le problème :

(7)

DISPTUR : Programme pour résoudre les problèmes de convection-dispersion longitudinale (uni–dimensionnelle), avec ou sans réaction, dans un canal. Ce programme peut résoudre des problèmes avec injections multiples dans l'espace ou dans le temps.

Il a été utilisé dans le Chap. 8 pour dessiner la Fig. 8.11 et pour résoudre les problèmes :

- Ex. 8.E, pp. 590-597, - Ex. 8.F, pp. 598-603.

Les programmes sont écrits en FORTRAN 77 standard. Le style d'écriture est didactique et n'a pas la prétention d'être optimisé. Les programmes ont une structure modulaire. Dans la mesure du possible, le nom des variables est choisi de façon à rappeler la notation utilisée dans le texte. Une liste exhaustive de variables avec leur type, complétée d'explications, figure au début du programme principal et des sous-programmes. Les codes complets des programmes EXPLIC, DELTA et GRAVIT sont présentés dans le livre et les explications y sont données. Dans ce texte supplémentaire, on donne d'abord quelques informations supplémentaires sur EXPLIC et ensuite on présente la structure et l'utilisation des programmes MOCREG, DIFFTUR, DIFDIS et DISPTUR d'une manière détaillée.

Les programmes ont été vérifiés avec beaucoup de soin. Toutefois, c'est l'utilisateur qui est responsable de leur utilisation. Les auteurs et les Presses polytechniques et universitaires romandes (PPUR) ne donnent aucune garantie, directe ou suggérée, concernant le contenu de ce CD-ROM, les performances que vous pourrez obtenir en utilisant les programmes, la possibilité de commercialisation ou l'aptitude à un but quelconque. En aucun cas les auteurs et/ou PPUR ne peuvent être poursuivis pour les dommages directs ou indirects (spéciaux, accidentels) y compris toute perte de profits ou d'épargne, résultant de l'utilisation ou de l'impossibilité d'utilisation de ce CD-ROM. Les programmes NE SONT PAS PROTEGES. En achetant le livre, vous avez obtenu le droit de les utiliser. Vous pouvez les copier et/ou les modifier selon vos besoins personnels. Après modification, le fichier source doit être recompilé et passé par l'édition des liens pour obtenir un nouveau fichier exécutable.

Les fichiers exécutables des programmes sur la disquette ont été compilés de la manière suivante :

IBM-PC : Les fichiers exécutables (fichiers avec l'extension .EXE) des programmes ont été créés en compilant les fichiers sources (fichiers avec l'extension .FOR) à l'aide du compilateur "DIGITAL Visual Fortran" Version 5.0 (développé par Digital Equipment Corporation, Copyright(C) 1997), à partir de l'environnement "Microsoft(R) Developer Studio" (développé par Microsoft Corporation, (C)1991-1997).

Les fichiers .EXE sont des applications Win32 et ils nécessitent un ordinateur IBM-PC ou compatible équipé d'un processeur Pentium(R) (ou 100% équivalent) travaillant sous le système Microsoft(R) Windows NT(TM) Version 4 ou Microsoft Windows 95(R).

Si vous disposez d'un compilateur sur votre ordinateur, nous vous conseillons de recompiler les fichiers sources avec les options de compilation plus adaptées à votre machine. Cela permettra de raccourcir le temps de calcul des programmes.

(8)

MACINTOSH : Les fichiers exécutables (fichiers avec l'extension .A) des programmes ont été créés en compilant les fichiers sources (fichiers avec l'extension .F) à l'aide du compilateur "Absoft Pro Fortran -Fortran 77", développé par Absoft Corporation, Copyright(C) 1991-1999), 2781 Bond Street, Rochester Hills, Michigan, 48309, USA. Absoft Pro Fortran a été utilisé dans l'environnement MPW Shell (Macintosh Programmer's Workshop).

La compilation a été effectuée sur un Power Macintosh de type G3 travaillant sous Mac OS8. Pour tourner les fichiers exécutables, vous avez donc besoin d'un Power Macintosh(TM).

Si vous disposez d'un compilateur sur votre ordinateur, nous vous conseillons de recompiler les fichiers sources avec les options de compilation plus adaptées à votre machine. Cela permettra de raccourcir le temps de calcul des programmes.

Les codes sources peuvent être compilés sans trop de difficultés sur d'autres machines. Les programmes présentés sur cette disquette ont pu également être compilés et exécutés sur un ordinateur VAX de DEC sans aucune modification.

I.2) ANIMATIONS EN VIDÉO QUICKTIME

La CD-ROM contient plusieurs animations créées à l'aide de MATLAB®_{, un logiciel}

développé par MathWorks, Inc. Les fichiers d'animations ont une extension : - ".MOV" sur les ordinateurs Macintosh, et

- ".AVI" sur les ordinateurs IBM-PC et compatibles.

Pour visionner ces animations vous avez besoin d'un logiciel de vidéo, tel que : - Quicktime Player©

Ce logiciel est distribué par Apple Computer, Inc. Il peut être téléchargé à partir du site :

http://apple.com/quicktime/download/

pour les plates-formes Macintosh (Mac OS) et IBM-PC et compatibles (Windows 95/98/NT).

- Movie Player™.

Ce logiciel est distribué par Apple Computer, Inc. Il peut être téléchargé à partir du site :

http://apple.com/quicktime/download/ pour les plateformes Macintosh (Mac OS).

- Real Player™.

Ce logiciel est distribué par RealNetworks, Inc. basé à Seattle, EU. Il peut être téléchargé à partir du site :

http://www.real.com/player/

pour les plates-formes Macintosh (Mac OS) et IBM-PC et compatibles (Windows 95/98/NT).

- Windows Media Player™.

Ce logiciel est distribué par Microsoft Corp. Il peut être téléchargé à partir du site : http://www.microsoft.com/windows/mediaplayer/en/default.asp pour les plates-formes IBM-PC et compatibles (Windows 95/98/NT).

Pour visionner une animation, cliquer deux fois sur l'icône du fichier avec extension ".MOV" ou ".AVI". Si votre ordinateur est correctement configuré, le logiciel de vidéo démarre automatiquement. En général, la fenêtre de visionnement contient plusieurs boutons pour contrôler le déroulement de l'animation. Pour plus d'information, lisez le manuel du logiciel spécifique que vous avez sur votre ordinateur.

(9)

Les animations sont également insérées dans le fichier "PDF" (acronyme pour Portable Document Format) que vous êtes en train de lire à l'aide du logiciel Acrobat™ Reader. Vous pouvez donc les visualiser directement depuis l'Acrobat™ Reader. Quant on commence à utiliser Acrobat™ Reader, le pointeur de la souris a la forme d'une main. Quand le pointeur de la souris est placé quelques parts dans la fenêtre d'une animation (entourée d'une cadre bleue), il change de forme et il prend l'apparence d'un film de cinéma. Il suffit alors de cliquer quelque part dans cette fenêtre pour démarrer l'animation.

Fig. I.1 Barre de commande du déroulement de l'animation (suivant le logiciel de vidéo et de sa version, l'apparence de la barre peut être plus ou moins différente).

Une fenêtre flottante se détache de la cadre contenant l'animation et l'animation commence à dérouler dans cette nouvelle fenêtre. En bas de cette fenêtre, il y a une barre contenant les boutons de contrôle apparaît (voir Fig. I.1). Suivant le logiciel de vidéo et de sa version, l'apparence de la barre de commande peut être plus ou moins différente. En général, la barre de commande contient un bouton à gauche et deux boutons à droite. Il y a également un curseur qui glisse horizontalement de gauche à droite au fur et à mesure que le film déroule. Quand le visionnement de l'animation touche à sa fin, la barre de commande disparaît et la fenêtre reprend sa forme initiale.

Pour reprendre le contrôle du déroulement de l'animation en main, cliquer sur le bouton à gauche avec deux lignes verticale. L'animation s'arrête aussitôt mais la barre de commande reste visible.

- Le bouton à gauche montre maintenant une flèche vers la droite. En cliquant sur ce bouton l'animation recommence depuis le moment où elle a été arrêté.

- Les deux boutons à droite de la barre de commande permettent de faire avancer l'animation image par image vers l'avant ou vers l'arrière.

- Ramener le pointeur de la souris sur le curseur horizontal. Appuyer sur le bouton de la souris et le maintenir enfoncé. Vous pouvez maintenant glisser le curseur à gauche et à droite pour vous placez sur la séquence désirée.

Pour plus de détail concernant le visionnement des filmes vidéos à partir de l'Acrobat™ Reader, consulter le manuel de votre ordinateur, le manuel de l'Acrobat™ Reader ainsi que le manuel du logiciel de vidéo installé sur votre ordinateur.

La version la plus récente de l'Acrobat™ Reader peut être téléchargé à partir du site : http://www.adobe.com/products/acrobat/readstep.html

(10)

(11)

III. EXPLIC

III.1) GÉNÉRALITÉS

Le programme EXPLIC a été écrit pour résoudre les problèmes d'écoulements non permanents dans les canaux à section trapézoïdale, rectangulaire ou triangulaire en utilisant un schéma explicite en différence finie. Le programme a été utilisé pour résoudre l'Ex.5.B, p. 300 à 321.

Dans le livre, les explications sont données sur la base de la discrétisation des éqs. 5.23 et 5.25 et ne sont valable que pour des canaux à section rectangulaire. Le programme EXPLIC a été écrit d'une manière plus générale. Pour démontrer le principe de fonctionnement de l'EXPLIC, il est nécessaire de reprendre les équations de base et de les développer d'une manière plus générale que celle suivie dans le livre.

III.2) GÉNÉRALISATION DE L'ÉQUATION DE CONTINUITÉ

L'équation de continuité est donnée par :

∂

∂ + ∂∂ =

Q S

t

x 0 (2.1)

où Q est le débit, S la surface mouillée. Etant donnée que Q = US and dS = Bdh, on peut écrire : ∂ ∂ + ∂∂ = ∂∂ + ∂∂ + ∂∂ = (US) B h t S U U S B h t x x x 0 (2.3 et 5.1)

Les éléments géométriques pour un canal trapézoïdal sont présentés dans le Tableau 1.1 : Surface mouillée : S=(b+mh h) =bh+mh2

Largeur à la surface : B= +b 2mh

Considérons maintenant la dérivée de la surface mouillée, S, par rapport à la distance, x :

∂ ∂ = ∂∂ + ∂ ∂ = ∂∂ + S b h mh h h b mh x x 2 x x( 2 ) (III.1)

En introduisant cette relation dans éq. 5.1, on obtient : b mh h+

(

)

∂_∂U x + U b

(

+2mh

)

∂ ∂ h x + (b+2mh) ∂ ∂ h t = 0 (III.2)

Eq. III.2 peut être simplifiée en divisant tous les termes par la largeur à la surface libre, c.-à-d. par B = (b+2mh) : b mh b mh h + +     2 ∂ ∂ U x + U ∂ ∂ h x + ∂ ∂ h t = 0 (III.3)

Le multiplicateur du terme d'accélération, ∂U/∂x , n'est rien d'autre que la profondeur

hydraulique pour un canal trapézoïdale (voir éq. III.2 et Tableau 1.1) :

D S B b mh b mh h h = = + +   2  (III.4)

(12)

Il convient de noter que pour un canal rectangulaire, c.-à-d. quand m = 0 et b > 0, le rayon hydraulique est égal à la profondeur d'écoulement, Dh = h , et l'éq. III.3 se réduit à l'éq. 5.2 présenté dans le livre.

h ∂ ∂ U x + U ∂ ∂ h x + ∂ ∂ h t = 0 (5.2)

Il est également intéressant de relever que pour un canal à section triangulaire, m > 0 et b = 0, la profondeur hydraulique est égale à la moitié de la profondeur d'écoulement, Dh = h/2 . t t = t + ∆t t = t t = t - ∆t ∆x ∆x ∆t ∆t L M P R x

Fig. 5.5 Maillage de différences finies autour du point P, projeté sur le plan, x - t.

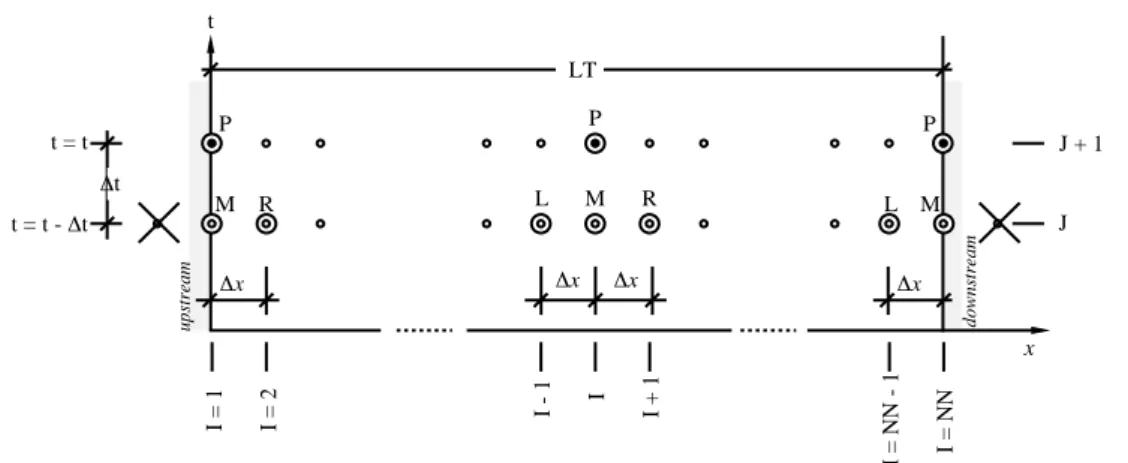
∆x ∆x M P R t ∆x L P M ∆x t = t t = t - ∆t J + 1 J M P R L x I = 2 I = 1 I = NN - 1 I - 1 I I + 1 I = NN LT upstream downstream ∆t

Fig. Ex.5.B.2 Schéma numérique explicite et conditions limites aux extrémités amont et aval du domaine de solution.

En se référant à la Fig. 5.5 et à la Fig. Ex.5.B.2, l'éq. III.3 peut être discrétisée en utilisant les quotients de différences finies suivants (voir éq. 5.22) :

∂ ∂ = − U U U M R L x 2∆x ou ∂ ∂ = − + − U U U i j i j i j x , x 1 1 2∆ (III.5a) ∂ ∂ = − h h h M R L x 2∆x ou ∂ ∂ = − + − h h h i j i j i j x _, x 1 1 2∆ (III.5b) ∂ ∂ = − U t U U t P P M ∆ ou ∂ ∂ = − + + U t U U t i j i j i j , 1 1 ∆ (III.5c)

(13)

∂ ∂ = − h t h h t P P M ∆ ou ∂ ∂ = − + + h t h h t i j i j i j , 1 1 ∆ (III.5d)

qui ont été obtenus en utilisant un schéma centré pour les dérivées spatiales, ∂/∂x , et un schéma progressif pour les dérivées temporelles, ∂/∂t . En introduisant ces relations dans l'éq. III.3, on obtient : b mh b mh h i j i j i j + +       2 U_ij₊₁−U_ij₋₁ 2∆x + Ui j hi h j i j +1− −1 2∆x + h h t i j i j +1₋ ∆ = 0 (III.6)

d'où on tire une équation pour la profondeur au prochaine pas de temps, j+1, en fonction des valeurs connues au pas de temps actuel, j.

h_ij+1 = h_ij + ∆ ∆ t 2 x U h h b mh b mh h U U i j i j i j i j i j i j i j i j − − + − +

(

)

+ + +      

(

−

)

      1 1 1 1 2 (III.7)

C'est l'éq. III.7 qui a été codée dans le programme EXPLIC dans le but de pouvoir l'utiliser pour résoudre des problèmes d'écoulement non permanent dans les canaux à section trapézoïdale, rectangulaire et triangulaire.

L'éq. III.7 est basée sur le schéma centré pour l'approximation des dérivées spatiales. Elle ne peut être utilisée que pour des noeuds d'intérieur, i = 2 à NN-1, où les noeuds en amont, i-1, et en aval, i+1, sont disponibles.

A l'extrémité amont du domaine de solution, i = 1, le noeud i-1 n'existe pas. Les dérivées spatiales dans l'éq. III.3 sont discrétisées en utilisant le schéma progressif qui ne contient que les noeuds, i and i+1 (voir Ex. 5.B, c.4) :

i j h +1 = i j h + ∆ ∆ t x U h h b mh b mh h U U i j i j i j i j i j i j i j i j −

(

)

+ + +      

(

−

+ + + + + + 1 1 1 1 2 2 1 (III.13)

III.4) STABILITÉ DES SOLUTIONS NUMÉRIQUES ET GÉNÉRALISATION DE LA

CONDITION DE STABILITÉ DE COURANT

Pour une solution numérique stable en utilisant le schéma explicite, il est toujours nécessaire, mais pas suffisant, de respecter la condition de stabilité de Courant partout dans le domaine de solution. Cette condition est exprimée par :

∆t ∆ U c ≤ + x (5.21) où c représente la célérité relative de l'onde par rapport à un observateur qui se déplace avec une vitesse égale à celle de l'écoulement, U. Dans le cas particulier d'un canal à section rectangulaire, cette célérité relative est donnée par :

c2 =gh donc c= ± gh (2.27)

Pour des canaux trapézoïdaux, il faut utiliser l'expression générale suivante :

c2 =gD_h donc c= ± gD_h (III.14)

qui est valable pour les canaux à section trapézoïdale. C'est cette relation qui a été codée dans le programme EXPLIC.

L'expérience montre que, le pas de temps, ∆t, pour obtenir une solution stable avec un schéma numérique explicite doit être plus petit que 20% de la valeur indiquée par la condition de stabilité de Courant. Le lecteur est encouragé à lancer le même problème avec différents pas de temps et d'espace afin de se faire une idée sur le problème de la stabilité.

III.5) EXEMPLE D'UTILISATION DU PROGRAMME EXPLIC

Le programme a été utilisé pour résoudre l'Ex.5.B, p. 300 à 321. Ex. 5.B

Dans un canal rectangulaire prismatique en béton rugueux ayant une largeur de B = 5 [m], l'écoulement est uniforme avec une profondeur d'eau de h_n = 1.20 [m]. Pendant le passage d'une crue, le débit augmente linéairement jusqu'à une valeur de Q = 50 [m3/s] dans un temps t' = 20 [min] et redescend linéairement au débit initial dans un temps t'' = 60 [min]. Le canal a une pente de fond de J_f = 0.001 et son coefficient de frottement est estimé à n = 0.020 [m-1/3s]. La longueur du canal étudié est de 3 [km]. En utilisant la méthode explicite, déterminer :

(15)

i) l'hydrogramme aux deux stations L₁ = 1.5 [km] et L₂ = 3 [km];

ii) quand se produit le débit maximum, Q_max , aux stations L₁ et L₂ respectivement;

iii) l'atténuation de la profondeur maximale d'eau aux stations L₁ et L₂ ;

iv) le temps nécessaire pour que la profondeur d'eau devienne enfin uniforme à la station L₂ .

Le code complet du programme ainsi que des explications détaillées se trouvent dans le livre. Le répertoire EXPLIC contient les fichiers suivants :

Pour la version IBM-PC ou compatibles :

EXPLIC.FOR : Fichier texte (ASCII) qui contient le programme source EXPLIC. EXPLIC.EXE : Fichier exécutable du programme EXPLIC. Cliquer deux fois sur

son icône EXPLIC pour démarrer le programme.

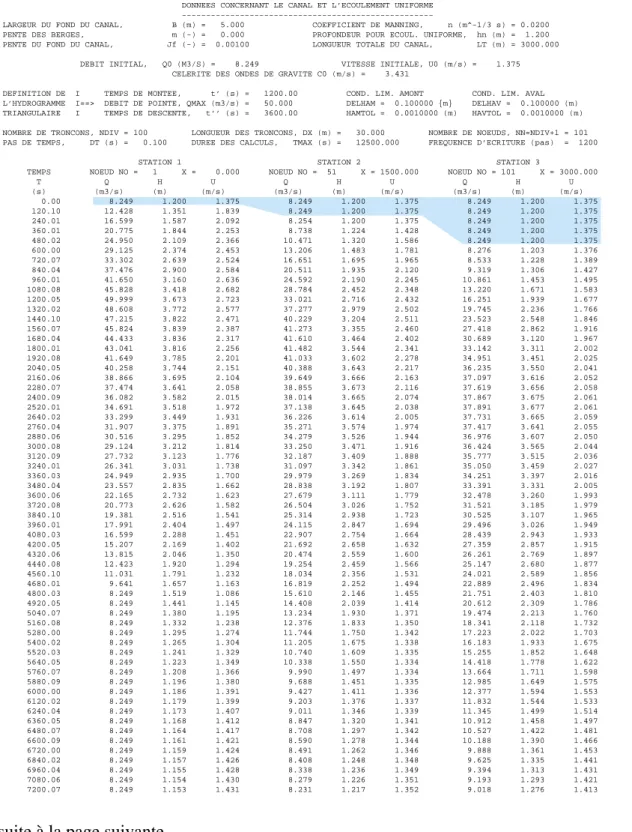
RESULT.DAT : Fichier de résultats pour la résolution du problème Ex. 5.B, pp. 300-321.

DIALOG.DAT : Fichier texte généré automatiquement par le programme EXPLIC. Il contient le dialogue interactif entre l'utilisateur et l'ordinateur pour la résolution du problème Ex. 5.B, pp. 320-321.

Pour la version Macintosh :

EXPLIC.F : Fichier texte (ASCII) qui contient le programme source EXPLIC. EXPLIC.A : Fichier exécutable du programme EXPLIC. C'est un fichier de

type application. Cliquer deux fois sur son icône pour démarrer le programme.

RESULT.DAT : Fichier de résultats pour la résolution du problème Ex. 5.B, pp. 300-321.

DIALOG.DAT : Fichier texte généré automatiquement par le programme EXPLIC. Il contient le dialogue interactif entre l'utilisateur et l'ordinateur pour la résolution du problème Ex. 5.B, pp. 300-321.

(16)

Animation III.1

(voir le fichier EXPLIC01.MOV ou EXPLIC01.AVI)

Cette animation montre l'évolution temporelle de la profondeur d'eau, du débit d'écoulement et de la vitesse d'écoulement le long du canal pour le problème résolu Ex. 5.B.

Les trois variables sont représentées sur des graphiques séparés. L'axe horizontal représente la distance, x , en mètres le long du canal. Le temps courant est affiché en bas, à droite de la fenêtre.

Au début, t = 0 [min] , l'écoulement est uniforme avec h_o = 1.2 [m], Q_o = 8.249 [m3_/s]

et U_o = 1.374 [m/s].

On peut faire les observations suivantes :

- A la station x = 3000 [m], l'effet de l'onde de crue ne se manifeste qu'à partir du temps t = 12 [min].

- Au temps t = 20 [min], le débit à la station x = 0.0 [m] atteint sa valeur maximale, Q = 50 [m3_{/s], ensuite il diminue. A ce moment là, la vitesse aussi atteint sa valeur}

maximale, U = 2.655 [m/s]. La profondeur d'eau, toutefois, continue à augmenter. - Au temps t = 26 [min], la profondeur d'eau à la station x = 0.0 [m] atteint sa valeur

(17)

Animation III.2

(voir le fichier EXPLIC02.MOV ou EXPLIC02.AVI)

Cette animation montre l'évolution du profil instantané de la surface libre le long du canal, pour le problème résolu Ex. 5.B, dans une représentation 3D de l'espace-temps, x-t. Le plan horizontal est formé par l'axe x (distance le long du canal) et l'axe t qui représente le temps. L'axe vertical représente la profondeur d'eau, h.

et U_o = 1.374 [m/s]. La ligne d'eau initiale (écoulement uniforme) est représentée par une ligne rouge. Une ligne verte est dessinée à la hauteur maximale, h = 3.904 [m], qui sera atteinte à la station x = 0.0 [m] au temps t = 26 [min].

Quand l'animation démarre une ligne bleu, correspondant au profil instantané de la surface libre le long du canal, se détache de la ligne rouge et évolue entre la ligne rouge et la ligne verte. Les trois lignes se déplacent le long de l'axe du temps. L'indicateur du temps en haut, à droite de la fenêtre affiche le temps courant, c.-à-d. la position des lignes le long de l'axe de t.

(18)

Animation III.3

(voir le fichier EXPLIC03.MOV ou EXPLIC03.AVI) Pour le problème résolu Ex. 5.B, cette animation montre :

• l'évolution du profil instantané de la surface libre le long du canal et • la variation du niveau dans le temps aux 5 stations

dans une représentation 3D de l'espace-temps, x-t.

Le plan horizontal est formé par l'axe x (distance le long du canal) et l'axe t qui représente le temps. L'axe vertical représente la profondeur d'eau, h.

Quand l'animation démarre, une ligne bleu épaisse, correspondant au profil instantané de la surface libre le long du canal, se détache de la ligne rouge et évolue entre la ligne rouge et la ligne verte. Les trois lignes se déplacent le long de l'axe du temps. L'indicateur du temps en haut, à droite de la fenêtre affiche le temps courant, c.-à-d. la position des lignes le long de l'axe de t.

Les limnimètres placés aux 5 stations x = 0.0, 750.0, 1500.0, 2250.0 et 3000.0 [m] enregistrent et dessinent la variation de la profondeur d'eau dans le temps.

(19)

Animation III.4

(voir le fichier EXPLIC04.MOV ou EXPLIC04.AVI) Pour le problème résolu Ex. 5.B, cette animation montre :

• l'évolution du profil instantané de la surface libre le long du canal et • la variation du niveau dans le temps aux 5 stations

dans une représentation 3D de temps, x-t. La ligne d'eau évoluant dans l'espace-temps dessine une surface (voir également Fig. Ex.5.B.7a). La surface est coloriée en fonction de la profondeur d'eau en allant du bleu (peu profond) vers le rouge foncé (profondeur maximale) en passant par les différentes teintes de vert, jaune et orange. Le plan horizontal est formé par l'axe x (distance le long du canal) et l'axe t qui représente le temps. L'axe vertical représente la profondeur d'eau, h.

Quand l'animation démarre, le profil instantané de la surface libre le long du canal se détache de la ligne rouge et évolue entre la ligne rouge et la ligne verte tout en laissant une surface enveloppe coloriée derrière elle (pour t ≤ temps courant). L'indicateur du temps en haut, à droite de la fenêtre affiche le temps courant, c.-à-d. la position des lignes le long de l'axe de t.

Les limnimètres placés aux 5 stations x = 0.0, 750.0, 1500.0, 2250.0 et 3000.0 [m] enregistrent et dessinent la variation de la profondeur d'eau dans le temps.

(20)

IV. MOCREG

IV.1) GÉNÉRALITÉS

Le programme MOCREG a été écrit pour résoudre les problèmes d'écoulements non permanents dans les canaux à section trapézoïdale, rectangulaire ou triangulaire en utilisant la méthode de caractéristiques avec un maillage régulier. Il constitue une alternative au programme EXPLIC pour résoudre l'Ex.5.B, p. 300 à 321.

Dans le livre, les quatre équations différentielles ordinaires résultant de la méthode des caractéristiques, éqs. 5.15, sont présentées sans donner les détails sur leur développement. Pour mieux comprendre le fonctionnement du programme MOCREG, il convient de reprendre les équations de base, c.-à-d. les équations de Saint-Venant (voir éq. III.3) : D U U h h t h ∂ ∂x + ∂∂x + ∂∂ =0 (IV.1) 1 g U t U g U h J_f J_e ∂ ∂ + ∂ ∂x + ∂∂x = − (IV.2)

Dh

Dt g Jf Je

+λ =

(

−

)

(IV.5)

en admettant que les relations suivantes sont valides :

U D d dt h +

(

λ

)

= x et U g d dt +   _λ = x (IV.6) On écrit alors : U+λDh = +U g λ (IV.7)

et on obtient une relation pour le coefficient λ :

λ2 = g = D gB S h ⇒ λ = ± g = ± D gB S h (IV.8)

(21)

La célérité relative pour des ondes de gravité a été définie comme :

c= ± gDh (IV.9)

En introduisant cette définition dans l'éq. IV.8, on obtient la relation suivante entre λ et c:

λ = ±g

c (IV.10)

En introduisant l'éq. IV.10 dans les éqs. IV.5 et IV.6 (une fois la valeur positive, une fois la valeur négative) on obtient un système de 4 équations différentielles ordinaires:

DU Dt g c Dh Dt g Jf Je + =

(

−

)

(IV.11) d dt U c x = + (IV.11a) DU Dt g c Dh Dt g Jf Je − =

(

−

)

(IV.12) d dt U c x = − (IV.12a)

Ces quatre équations sont les mêmes que les eqs. 5.15. Les équations sont groupées pour mettre l'accent sur le fait que les éqs IV.11 et IV.12 ne sont valables que le long des lignes qui vérifient respectivement les équations IV.11a (lignes C+_{) et IV.12a (lignes C}-_),

dans l'espace x-t (voir Fig. IV.1).

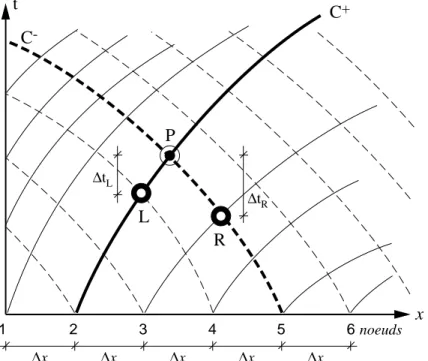
P L R C+ C -t x ∆x ∆x ∆x ∆x ∆x noeuds 1 2 3 4 5 6 ∆t_L ∆t_R

(22)

Dans le livre, les relations de différences finies sont directement introduites dans ces quatre relations. Ici, on va suivre un chemin légèrement différent pour mieux comprendre les simplifications introduites dans la procédure de calcul. En se référant à la Fig. IV.1, on multiplie les éqs. IV.11, IV.11a, IV.12 et IV.12a avec dt et on les intègre le long des lignes caractéristiques correspondantes (de L à P le long de C+_{et de R à P le long de C}–_);

=

∫

(

−

)

(IV.14a)

Pour évaluer ces intégrales, il faut connaître c et J_e le long des lignes C+_{et C}–_{. Or, c et J} e

dépendent de U et h, le long des lignes C+_{et C}–_{, que l'on cherche à calculer. Il est donc}

nécessaire de procéder à une simplification. La méthode la plus simple est d'admettre que c et J_e (donc U et h) sont constantes le long des lignes caractéristiques et leur valeur est égale à celles calculées aux points L (le long de C+_{) ou R (le long de C}–_{). Dans ce cas, on}

obtient : U U g c h h g J J t t P L L P L f _{e L} P L −

(

)

_{+ } _

(

−

)

=

(

−

)

(

)

_{− } _

(

−

)

=

(

−

)

Ces quatre équations sont identiques aux eqs. 5.16 dans le livre. Elles peuvent être considérées comme des approximations à différences finies des éqs. 5.15. Elles ont été obtenues en admettant que c et J_e (donc U et h) sont constantes le long des lignes caractéristiques. D'autres méthodes de simplification sont possibles. Le lecteur peut consulter Lai (1986) pour une information plus complète.

IV.2) MÉTHODE DE CARACTÉRISTIQUES AU PAS DE TEMPS FIXE

La Fig. IV.1 montre le réseau de caractéristiques pour l'écoulement fluvial, projeté sur le plan x-t. Les intersections des lignes caractéristiques constituent les noeuds. Le schéma numérique décrit dans la sect. 5.2.2 du livre permet de calculer la vitesse, U , et la profondeur d'écoulement, h , dans tous les noeuds du réseau en partant d'une condition initiale donnée (c.-à-d., une série de points où les valeurs de U et h sont connues).

(23)

Cette méthode a malheureusement un inconvénient majeur. Elle ne permet pas d'avoir un contrôle sur l'emplacement des noeuds où les résultats sont obtenus. A la Fig. IV.1, le réseau est constitué par des caractéristiques partant d'une série de points régulièrement espacés le long de l'axe x. Au fur et à mesure qu'on avance dans le temps, la répartition des noeuds devient plus ou moins irrégulière. Notez aussi que, le pas temps ∆t_L = t_P - t_L n'est pas forcément égal au pas de temps ∆t_R = t_P - t_R (voir Fig. IV.1).

P L R C+ C -t x ∆x ∆x ∆x ∆x ∆x ∆t ∆t ∆t ∆t ∆t ∆t noeuds 1 1 2 3 4 5 6 7 2 3 4 5 6

Fig. IV.2 Comparaison entre la grille des caractéristiques et une grille régulière. Il est souvent préférable de travailler avec un maillage régulier obtenu en discrétisant le domaine de solution avec un pas d'espace de ∆x (ou dx) et un pas de temps ∆t (ou dt) convenablement choisis. Le maillage régulier constitue un avantage non négligeable car il permet de suivre l'évolution temporelle d'une variable (vitesse, profondeur, débit, etc.) à une station donnée et/où à déterminer la répartition d'une variable le long du canal en un instant donné. Notre but est de développer un schéma numérique qui utilise la méthode de caractéristiques sur un maillage régulier.

La Fig. IV.2 montre un maillage régulier dans le plan x-t, obtenu en utilisant un pas d'espace de ∆x et un pas de temps ∆t constants. Les noeuds qui se trouvent à l'intersection des lignes verticales et horizontales sont répartis d'une manière uniforme dans tout l'espace. On admet que sur une ligne horizontale (c.-à-d. à un temps donné, t) les valeurs de U et h sont connues à tous les noeuds. Il s'agit de calculer les valeurs de U et h à tous les noeuds au prochain pas de temps, t+∆t.

La superposition du réseau de caractéristiques de la Fig. IV.1 sur le maillage régulier de la Fig. IV.2, révèle un problème. Les noeuds du maillage régulier ne se trouvent pas forcement sur l'intersection des caractéristiques. La méthode à intervalle de temps fixe présentée ci-dessous permet de contourner ce problème à l'aide des interpolations.

Considérons la grille représentée à la Fig. IV.3. Les valeurs de U et h sont connues aux points i-1, i et i+1 au temps t. Deux lignes caractéristiques, une C+_{et une C}–_{se croisent}

au point P. Les points L et R se trouvent à l'intersection des lignes C+_{et une C}–_{avec la}

ligne de temps t. Il s'agit de calculer U et h au point P, c.-à-d. au noeud i au temps t+∆t. On récrit les éqs. IV.15 et IV.16 sous la forme suivante :

(24)

P ∆x x x+∆x t t+∆t x-∆x ∆x ∆t i-1 L R C+ C -t x i+1 i

Fig. IV.3 Méthode des caractéristiques (écoulement fluvial)

U g c h K P L P pos +   = (IV.17) U g c h K P R P neg −   = (IV.18)

Les paramètres K_pos et K_neg regroupent tous les termes (U, h et J_e) connus aux points L et R respectivement : K U g c h g J J t pos L L L f _{e L} = _{+ } _ +

(

−

)

∆ (IV.19) K U g c h g J J t neg R R R f _{e R} = _{− } _ +

(

−

)

∆ (IV.20)

La vitesse U_P et la profondeur h_P peuvent être calculées en résolvant le système d'équations formé par les éqs. IV.17 et IV.18 :

U K K K c c c K K K c c P neg pos neg R L R neg pos neg R L = + − +     = + − +     1 1 1 (IV.21) h K K g c c P pos neg L R = − +     1 1 (IV.22)

On notera toutefois que, dans le cas le plus général, les points L et R ne coïncident pas forcement avec les noeuds i-1 et i+1 ou les valeurs de U et h sont connues. Pour pouvoir calculer K_pos et K_neg , il faut d'abord déterminer U et h aux points L et R en fonction des valeurs connues aux noeuds i-1, i et i+1.

(25)

Notons que le point L se trouve entre les noeuds i et i-1. En admettant que la vitesse varie linéairement entre les noeuds i et i-1, on peut écrire la relation d'interpolation suivante :

U U U U i L i i i L i i − − = − − −1 −1 x x x x (IV.23)

Les noeuds I et P étant sur la même ligne verticale, on peut remplacer xi par xP pour obtenir : U U U U i L i i i L i i P L i i − − = − − = − − −1 −1 −1 x x x x x x x x (IV.24)

Le dénominateur de la dernière fraction est, par définition, égal au pas d'espace, i.e. (x_i - x_i-1) = ∆x. Considérons maintenant le nominateur de la dernière fraction. Une

perturbation partant du point L voyage le long de la ligne de caractéristique C+_{avec une}

célérité de (U_L + c_L) et arrive au point P après un temps ∆t. La distance parcourue est exprimée par éq. IV.15a. En introduisant ces relations dans l'éq. IV.24, on obtient.

U U U U U c t i L i i i L i i P L i i L L − − = − − = − − = +

(

)

−1 −1 −1 x x x x x x x x x ∆ ∆ (IV.25)

De la même manière, on peut écrire les relations d'interpolation linéaire suivantes pour la célérité et la profondeur : c c c c U c t i L i i i L i i P L i i L L − − = − − = − − = +

(

)

−1 −1 −1 x x x x x x x x x ∆ ∆ (IV.26) h h h h U c t i L i i i L i i P L i i L L − − = − − = − − = +

(

)

−1 −1 −1 x x x x x x x x x ∆ ∆ (IV.27)

UR −cR

)

(

hi−hi+

)

∆ ∆x 1 (IV.36)

Les équations IV.21 et IV.22 ensemble avec les éqs. IV.28, IV.29, IV.30, IV.34, IV.35 et IV.36 permettent de calculer U et h au point P (i, t+∆t) en connaissant U et h aux points (i - 1, t), (i, t) et (i+1, t)

Notons que la méthode présentée ici est limitée aux écoulements fluviaux. Pour un écoulement torrentiel, le point R se trouve aussi entre les noeuds i et i-1 et les équations IV.34, IV.35 et IV.36 doivent être récrites en tenant compte de cette situation. Le programme MOCREG a été écrit avec les éqs. IV.34, IV.35 et IV.36 et il est uniquement valable pour des écoulements fluviaux.

Nous encourageons le lecteur à modifier le programme MOCREG de sorte qu'on puisse traiter également les problèmes d'écoulement torrentiel.

IV.3) CONDITIONS AUX LIMITES

Pour résoudre la vitesse et la profondeur à un point P donné, on a besoin de deux équations (voir éqs. IV.17 et IV.18), chacune valable le long d'une des deux caractéristiques qui se croisent au point P; l'une le long de C+_{en partant du point L et}

l'autre le long de C–_{en partant du point R.}

Les points aux extrémités amont et aval du domaine de calcul présentent une situation particulière et doivent être traités spécialement (voir Fig. IV.4).

(27)

P P t t+2∆t t+∆t L R C+ C -t x i-1 i i+1 i ∆x ∆x ∆x ∆x ∆t ∆t L R C+ C -1 2 3 NN-2 NN-1 NN (a) (b)

Fig. IV.4 Conditions aux limites pour écoulement fluvial.

IV.3.1) Débit d'entrée est connu en amont (écoulement fluvial) (voir Fig. IV.4a)

L'éq. IV.18 pour C-_{, qui va du point R au point P, est toujours valide:}

U g c h K P R P neg −   = (IV.37)

Le point L n'est pas dans le domaine de calcul. L'équation pour C+_{ne peut pas être}

utilisée. Toutefois, le débit au noeud 1 est donné en fonction du temps: Q(x = 0, t). La vitesse au noeud 1, c.-à-d. au point P, peut être exprimée par :

U Q t S Q t t h b m h P P P = = = = + +

(

)

(x 0, ) (x 0, ∆ ) (IV.38) ce qui donne un deuxième relation entre U_P et h_P . En éliminant U_P entre ces deux équations, on obtient une relation où la seule inconnue est la profondeur au point P :

Q t t h b m h g c h K P P R P neg (x= , + ) +

(

0 ∆

)

−   = (IV.39)

En simplifiant, on a un polynôme de troisième degré :

f(h ) m g (x , ) c h b g c m K h bK h Q t t P R P R neg P neg P =   3 + _  + _ 2 + − =0 +∆ =0 (IV.40)

La profondeur au point P, h_P , peut être résolue à l'aide d'une méthode numérique, par exemple, la méthode de Raphson (voir sect. d). La méthode de Newton-Raphson utilise également la dérivée l'éq. IV.40 par rapport à h_P , qui s'écrit comme suit :

f' (h ) df dh m g c h b g c m K h bK P R P R neg P neg = = _ _ +  _ _{ +}    + = 3 2 2 0 (IV.41)

IV.3.2) Relation entre le débit et la vitesse est connue en aval (écoulement fluvial) (voir Fig. IV.4b)

(28)

U g c h K P L P pos +   = (IV.42)

Le point R n'est pas dans le domaine de calcul. L'équation pour C-_{ne peut pas être}

utilisée. Toutefois, le débit au noeud NN, c.-à-d. au point P, peut être calculé à l'aide de l'équation de Manning-Strickler (voir éq. 3.16) :

)

          +

(

)

+ +         +   = 2 3 2 2 1 2 1 2 1 0 1 2 2 2 2 2 2 2 1 3 (IV.45)

IV.4) LA MÉTHODE DE NEWTON-RAPHSON

Il existe plusieurs méthodes itératives pour calculer numériquement les racines d'une équation donnée. La méthode de Newton-Raphson est probablement la méthode la plus populaire. Elle se distingue des autres méthodes par le fait qu'elle nécessite l'évaluation à la fois de la fonction et de sa dérivée.

Considérons l'expansion d'une fonction analytique, f(x) , en série de Taylor au voisinage du point x_o (ou centrée sur le point x_o) :

f x( ) f x( ) (x x ) f x( ) (x x ) f x ! ( ) ... ≅ o + − o ′ o + − ′′ + o o 2 2 (IV.46)

Si la fonction a une tendance consistante, on peut espérer avoir une bonne approximation en gardant uniquement les deux premiers termes de cette série :

f x( )≅ f x( o)+ −(x xo) f x′( o) (IV.47)

Si x est une solution de la fonction f(x), c.-à-d. si x est une racine de la fonction f(x), on a f(x) = 0. En introduisant cette condition dans l'éq. IV.47, on obtient une expression pour x : x x f x f x = − ′ o o o ( ) ( ) (IV.48)

(29)

qui peut être généralisée en une formule d'itération comme suit : x x f x f x n n n n +1 = − _′ ( ) ( ) (IV.49)

Dans cette équation, x_n est une estimation pour la racine de la fonction f(x) et x_n+1 est la nouvelle estimation.

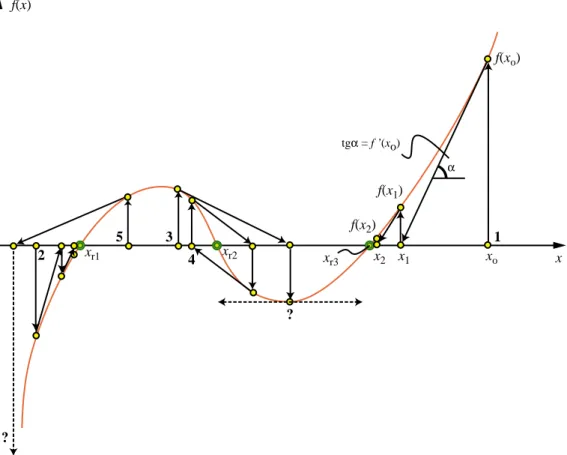
La Fig. IV.5 montre l'interprétation géométrique de la méthode de Newton-Raphson dans différents cas de figure. Considérons la fonction f(x) dessinée à la Fig. IV.5. Cette fonction a trois racines désignées par x_r1 , x_r2 , x_r3 . Considérons le point 1, c.-à-d. le point x_o , comme une estimation de départ pour une racine de la fonction f(x). En calculant f(x) et f'(x) et en utilisant l'éq. IV.49, on trouve une nouvelle estimation de la racine au point x₁ . En appliquant la procédure itérative plusieurs fois, on converge vers la racine x_r3 .

Le point de départ est bien entendu très important car il détermine la racine vers laquelle la solution converge. En partant du point 2, par exemple, la méthode fournit cette fois la racine x_r1 .

Notons que dans certain cas, la méthode de Newton-Raphson ne converge pas. Trois cas de figure où la méthode ne peut pas fournir une racine sont démontrés à la Fig. IV.5 : - En partant du point 3, on tombe sur un minima où la tangente est parallèle à l'axe x.

La formule de Newton-Raphson, éq. IV.49, produit une division par zéro et elle ne peut pas fournir une nouvelle estimation.

- En partant du point 4, l'itération aboutit dans une boucle qui se répète à l'infini. - En partant du point 5, on obtient une nouvelle estimation pour laquelle la fonction

n'est pas définie.

f(x) x_o x₁ x_r1 x_r2 _x r3 x2 f(x_o) f(x₁) tgα = f ’(xo) f(x₂) ? ? 1 3 5 4 2 α x

(30)

IV.5) EXEMPLE D'UTILISATION DU PROGRAMME MOCREG

Le programme a été utilisé pour résoudre l'Ex.5.B, p. 300 à 321. Ex. 5.B

Dans un canal rectangulaire prismatique en béton rugueux ayant une largeur de B = 5 [m], l'écoulement est uniforme avec une profondeur d'eau de h_n = 1.20 [m]. Pendant le passage d'une crue, le débit augmente linéairement jusqu'à une valeur de Q = 50 [m3/s] dans un temps t' = 20 [min] et redescend linéairement au débit initial dans un temps t'' = 60 [min]. Le canal a une pente de fond de J_f = 0.001 et son coefficient de frottement est estimé à n = 0.020 [m-1/3s]. La longueur du canal étudié est de 3 [km]. En utilisant la méthode des caractéristiques, déterminer :

i) l'hydrogramme aux deux stations L₁ = 1.5 [km] et L₂ = 3 [km];

ii) le moment où se produit le débit maximum, Q_max , aux stations L₁ et L₂ respectivement;

iii) l'atténuation de la profondeur maximale d'eau aux stations L₁ et L₂ ;

iv) le temps nécessaire pour que la profondeur d'eau devienne enfin uniforme à la station L₂ .

Le programme MOCREG est écrit en FORTRAN standard et peut être exécuté sur la plupart des micro-ordinateurs. La structure du programme est très similaire à celle du programme EXPLIC. Le programme est écrit de manière didactique et n'a pas la prétention d'être optimisé. Un grand nombre de commentaires insérés dans le code expliquent le déroulement du programme pas par pas. Dans la mesure du possible, le nom des variables est choisi de façon à rappeler la notation utilisée à la sect. 5.2 et dans les explications données ci-avant. Une liste complète des variables avec leur type, ainsi que des explications, figurent au début du programme.

S'il le souhaite, l'utilisateur peut introduire les données du problème de façon interactive (voir Fig. Ex.5.B.5), en répondant aux questions posées par le programme. De nombreux commentaires glissés dans le dialogue rappellent les sujets traités dans le livre et guident l'utilisateur dans ses choix. Le programme teste les erreurs éventuelles dans l'introduction des données. En cas d'erreur, la question est reposée jusqu'à ce que l'utilisateur réponde correctement. Les erreurs relatives à la stabilité de la solution (non-respect de la condition de stabilité de Courant) sont également détectées et signalées par un message d'erreur; ce dernier indique également la modification à apporter.

Le programme peut également lire les données du problème à partir d'un fichier de données, préparé à l'avance par l'utilisateur.

IV.5.1) Définition du domaine de solution

Comme c'est le cas dans le programme EXPLIC, l'espace-temps est visualisé comme un système de coordonnées cartésiennes, x-t, sur un plan horizontal (voir Fig. Ex.5.B.1 et Fig.5.4). L'axe du canal, d'une longueur de LT = 3 [km], coïncide avec l'axe x. Il est divisé en plusieurs tronçons de longueur ∆x (variable DX). Le nombre de noeuds ainsi

obtenu est de NN.

Perpendiculaire à l'axe de l'espace, x, l'axe de temps (variable T) commence au temps t = 0 à l'origine et va jusqu'à l'infini, par pas de temps ∆t (variable DT). Pour les besoins du problème, on admettra toutefois que la solution s'arrête au temps t = TMAX. La valeur de TMAX sera fournie par l'utilisateur comme donnée d'entrée.

On désire connaître les profondeurs, h(x,t) (variable H), et les vitesses, U(x,t) (variable U), à chaque point de cet espace-temps. De telles variables peuvent être représentées sous forme d'un troisième axe perpendiculaire au plan de l'espace-temps, x-t; ce qui donne un espace à trois dimensions.

(31)

t L M R x t = TMAX J J + 1 t = 0 x = 0 x x - ∆x x + ∆x x = LT I I - 1 I = 1 I = NN I + 1 ∆x ∆x t = t + ∆t t = t ∆t (DT) P (DX) (DX) h_n Q0 , U0 h(x,t) ou U(x,t)

Fig. Ex.5.B.1 Le domaine de solution et sa discrétisation.

IV.5.2) Discrétisation des équations pour la méthode des caractéristiques au pas de temps fixe

IV.5.2.1) Conditions initiales

On utilise les mêmes conditions initiales que celles utilisées dans l'Ex. 5.B : hn ( H0) = 1.20 [m] ; Uo (U0) = 1.374 [m/s] ; Qo (Q0) = 1.374 [m/s] Fro = Uo

√



gh_o = 1.374 √

(9.81) (1.2) = 0.40 [-] ⇒ l'écoulement est fluvial Pour les détails, voir les explications données dans l'Ex. 5.B.

IV.5.2.2) Stockage des informations dans le programme

Les variables représentant la profondeur d'eau, la vitesse d'écoulement, le débit d'écoulement, la célérité absolue et la pente de la ligne d'énergie aux noeuds du domaine de solution sont stockées dans des matrices à deux dimensions; respectivement H(J,I), U(J,I), Q(J,I), C(J,I) et JE(J,I). L'indice J (numéro de ligne) représente le temps, tandis que l'indice I (numéro de colonne) représente le numéro du noeud, c.-à-d. la position le long de l'axe x.

Afin de réserver la place nécessaire au stockage des matrices dans la mémoire de l'ordinateur, il y a lieu de fixer des limites quant au nombre maximum de lignes et de colonnes que l'on peut avoir. Le nombre de colonnes est dicté par le nombre maximum de divisions que l'on désire le long de l'axe x. Dans le programme, ce nombre a été fixé arbitrairement à MAXDIV = 100, ce qui permet d'écrire que le nombre maximum de noeuds sera de NNMAX = MAXDIV + 1 = 101. Pour augmenter le nombre autorisé de divisions, et par conséquent le nombre autorisé de noeuds, il suffit de changer la valeur du paramètre MAXDIV et de recompiler le programme.

Pour économiser de la place de stockage dans la mémoire, les matrices (H, U, Q, C et JE) sont déclarées avec seulement deux lignes (J = 1 et J = 2). Au début des calculs, les valeurs initiales de H, U, Q, C et JE sont stockées sur la ligne J = 1 en utilisant les conditions initiales. A chaque pas de temps, les calculs sont faits pour obtenir les valeurs sur la ligne J = 2 et les résultats sont immédiatement écrits sur un fichier. Ensuite, les valeurs de la ligne J = 1 sont remplacées par les valeurs de la ligne J = 2, et ainsi de suite.

(32)

IV.5.2.3) Discrétisation des équations

Les éqs. IV.21 et IV.22 sont récrites sous la forme suivante:

U K K K c c c K K K c c P neg pos neg R L R neg pos neg R L = + − +     = + − +     1 1 1 ; h K K g c c P pos neg L R = − +     1 1

Les variables K_pos et K_neg sont calculées directement à l'aide des éqs. IV.19 et IV.20.

La vitesse, la profondeur d'eau, la célérité absolue, et la pente de la ligne d'énergie au point L (U_L, h_L, C_L et JE_L) et au point R (U_R, h_R, C_R et JE_R) sont calculées respectivement à partir des équations IV.28, IV.29, IV.30, IV.34, IV.35 et IV.36, qui sont sous une forme utilisable directement. Ces équations peuvent être utilisées pour calculer la profondeur et la vitesse pour les noeuds de I = 2 à I = NN–1. Elles ne conviendront par contre pas pour les noeuds I = 1 et I = NN. Les calculs pour ces noeuds doivent utiliser les conditions de bord définies dans les données du problème.

IV.5.2.4) Conditions de bord en amont

En amont du canal, I = 1, on connaît l'hydrogramme de crue, c.-à-d. le débit en fonction du temps, comme le montre la Fig. Ex.5.B.3. Le débit au pas de temps J+1, Qj+1

i , est donné par la forme de l'hydrogramme imposé à l'entrée. Dans le

cas présent, l'hydrogramme est triangulaire (voir Fig. Ex.5.B.3). On le décrira par interpolation linéaire :

si T ≤ TP : Qj+1 i = Q0 + QMAX – Q0 TP T si TP < T ≤ TP+TPD : Qj+1 i = QMAX – QMAX – Q0 TPD [T – TP] si T > TP+TPD : Qj+1 i = Q0

En sachant le débit entrant au prochain pas temps Q(x = 0, t+∆t), la profondeur d'eau, hj+1

i , est calculée en résolvant la racine du polynomial cubique dans l'éq.

IV.40 à l'aide de la méthode numérique de Newton-Raphson. La vitesse, la profondeur d'eau, la célérité absolue, et la pente de la ligne d'énergie au point R (U_R, h_R, C_R et JE_R) sont calculées respectivement à partir des équations IV.34, IV.35 et IV.36, qui sont sous une forme utilisable directement.

Ensuite la vitesse d'écoulement est obtenue par la continuité : Uj+1 i = Qj+1 i Sj+1 i

où la surface mouillée, Sj+1

i , correspondant à la profondeur, h j+1

i , est calculée

selon la forme de la section du canal. IV.5.2.5) Conditions de bord en aval

A l'extrémité aval du canal, on admet que la courbe de tarage est définie par la relation de Manning Strickler (voir éq. 3.16). En utilisant cette condition la profondeur d'eau, hj+1

(33)

de la méthode numérique de Newton-Raphson. La vitesse, la profondeur d'eau, la célérité absolue, et la pente de la ligne d'énergie au point L (U_L, h_L, C_L et JE_L) sont calculées respectivement à partir des équations IV.28, IV.29 et IV.30, qui sont sous une forme utilisable directement.

Ensuite la vitesse d'écoulement est obtenue par la continuité : Uj+1 i = Qj+1 i Sj+1 i

où la surface mouillée, Sj+1

i , correspondant à la profondeur, h j+1

i , est calculée

selon la forme de la section du canal.

Voir les remarques dans le texte du programme EXPLIC dans le livre concernant les conséquences de l'admission de la validité de la courbe hauteur-débit correspondant à l'écoulement uniforme, Q =

f

(hn), au noeud NN.

IV.5.3) Structure du programme MOCREG

Le programme MOCREG a une structure modulaire. Il est composé d'un programme

principal et de plusieurs sous-programmes, chacun exécutant une tâche bien définie.

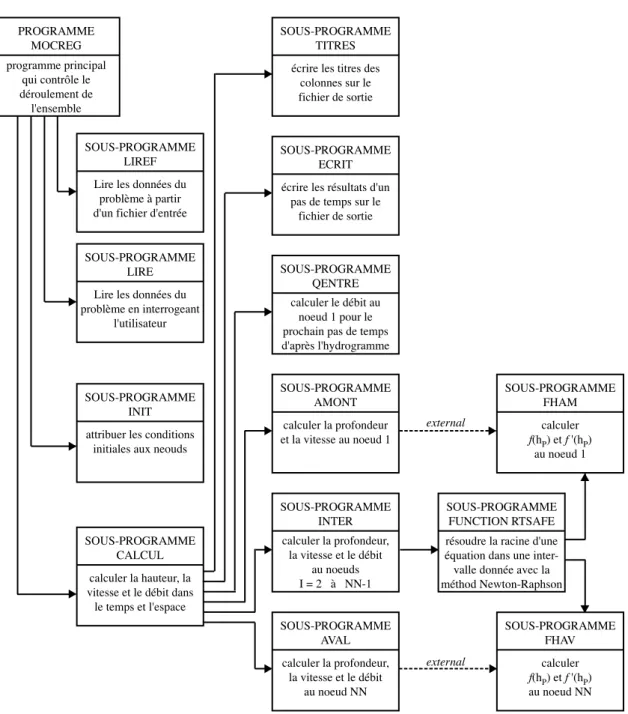
L'organigramme du programme présenté à la Fig. IV.6 montre les liaisons entre les différents modules. Pour une meilleure compréhension, on conseille au lecteur de prendre le temps de suivre la logique du programme directement à partir du code. Des commentaires sont abondamment utilisés pour en faciliter la lecture. Une description complète de toutes les variables se trouve au début du programme principal. Les tâches exécutées par les divers modules sont décrites ci-après (voir Fig. IV.6) :

- Le programme principal EXPLIC contrôle le déroulement de l'ensemble du programme en appelant quatre sous-programmes :

- Le sous-programme LIREF lit les données du problème à partir d'un fichier de données dont le nom est fourni par l'utilisateur en tapant au clavier. Il calcule également les différents paramètres utiles ainsi que les valeurs du débit, Q0, et de la vitesse, U0, au temps t = 0 selon la formule de Manning (éq. 3.16).

- Le sous-programme LIRE lit les données du problème en questionnant l'utilisateur. Il calcule également les différents paramètres utiles ainsi que les valeurs du débit, Q0, et de la vitesse, U0, au temps t = 0 selon la formule de Manning (éq. 3.16). - Le sous-programme INIT attribue les conditions initiales à tous les noeuds au temps

t = 0. Ce sous-programme reçoit la valeur de HN donnée par l'utilisateur et les valeurs de Q0 et U0 calculées par le sous-programme LIRE et les attribue à tous les noeuds en remplissant les premières lignes des trois matrices H, Q et U. Il calcule également la célérité absolue et la pente de la ligne d'énergie à tous les noeuds pour remplir les premières lignes des matrices C et JE.

- Le sous-programme CALCUL contrôle le déroulement de calculs d'écoulement non permanent selon le schéma explicite. Ce sous-programme avance le temps, T, par des incréments, DT, constants et arrête les calculs quand T = TMAX. Il appelle six autres sous-programmes pour exécuter les différentes tâches:

- Le sous-programme TITRES est appelé une seule fois tout au début pour écrire les titres et les données du problème sur le fichier de sortie.

- Le sous-programme ECRIT, comme son nom l'indique, écrit les résultats sur le fichier de sortie à la fin de chaque pas de calcul.

(34)

PROGRAMME MOCREG programme principal qui contrle le droulement de l'ensemble SOUS-PROGRAMME LIREF Lire les donnes du

problme partir d'un fichier d'entre

SOUS-PROGRAMME INIT attribuer les conditions

initiales aux neouds

SOUS-PROGRAMME CALCUL calculer la hauteur, la vitesse et le dbit dans

le temps et l'espace

SOUS-PROGRAMME TITRES crire les titres des

colonnes sur le fichier de sortie

SOUS-PROGRAMME ECRIT crire les rsultats d'un

pas de temps sur le fichier de sortie

SOUS-PROGRAMME QENTRE calculer le dbit au

noeud 1 pour le prochain pas de temps d'aprs l'hydrogramme SOUS-PROGRAMME AMONT calculer la profondeur et la vitesse au noeud 1 SOUS-PROGRAMME INTER calculer la profondeur, la vitesse et le dbit au noeuds I = 2 NN-1 SOUS-PROGRAMME FUNCTION RTSAFE rsoudre la racine d'une quation dans une inter-valle donne avec la mthod Newton-Raphson SOUS-PROGRAMME AVAL calculer la profondeur, la vitesse et le dbit au noeud NN SOUS-PROGRAMME FHAM calculer f(hP) et f '(hP) au noeud 1 SOUS-PROGRAMME FHAV calculer f(hP) et f '(hP) au noeud NN SOUS-PROGRAMME LIRE Lire les donnes du problme en interrogeant

l'utilisateur

external

Fig. IV.6 Organigramme du programme MOCREG.

- Le sous-programme QENTRE calcule le débit entrant dans le canal à l'extrémité amont selon l'hydrogramme triangulaire spécifié par l'utilisateur.

- Le programme AMONT reprend la valeur du débit calculée par le sous-programme QENTRE et calcule la profondeur et la vitesse pour le noeud I = 1. Il fait appel au sous-programme RTSAFE de type "FUNCTION" pour résoudre numériquement la racine d'un polynôme cubique codé dans le sous-programme, FHAM. Le nom FHAM est passé au RTSAFE dans la liste des arguments. A noter que, suivant les règles standard de Fortran, la variable FHAM est déclarée comme étant "EXTERNAL" .