Structures d'ondes forcées sur une sphère en rotation

..

STRUCTURES D'ONDES FORCEES SUR UNE SPHERE EN ROTATION

'de

René Laprise

r

Cette thèse est présentée à la Faculté de la recherche et des études graduées comme partie des exigences

requises pour le grade de Maître ès Sciences.

Département de météorologie Juin 1977. Université McGill

Montréal, Québec.

c'

t

1

1

l ' j ii RESUME

Le but della présente

..

~echerche bonsiste à étudier des structures d'ondes forcées dans l'atmosphère à l'aide de modèles numériques. 6n compare, sur un plan 'théorique, divers systèmes d'équations linéarisées, allant des équa-tions primitive~ jusqu'à la simplification la plus

pous-, ,

sée du géostrophisme. Puis on utilise un modèle numé-rique'des équations primitives linéarisées pour ~ênére~ , des ondes forcées par l'orographie. Des expér~ences de

"

sensibilité réyèlent que les structures des ondes forcées sont sensibles aux conditions particulières régnant dans les plus hauts niveaux de l'atmosphère.

Une ~rève étude des grandeurs d'échelle des équa-tions du mouvement montre que les ondes forcées da nom-bre d'onde zonal' l et 2 ont â'peu près le même degré de , , géostrophismei de plus, on trouve que la: c'omposante-u' du vent associée à la perturbation est plus géostrophi-que géostrophi-que la composante-v'.

".

•

,

, j

' "

1-The aim of this research is to study the

struc-,

tures of forced atmospheric planetary waves in hemis- , ~

pheric rnodels. The behaviour of various linearized models i5 compared from a theoritical point of view. Then a nurnerical model based on a linearized version

.

of the primitive equations ~s used to simulate pla~

netary waves due to orographie forcing. Sensitivity experiments reveal that forced waves are rather sen-sitive, even in their low'level

structu~e,

to parti-cula'r conditions in the upper atmosphere.

, A comparative study of waves with zonal wave-" numbers l"(and 2 reveals that

~both

wavês have about the same degree of geostrophy , with ,the ul-component

1

of the perturbation veloci~y being more geostrophic than the vl-component.

!

-"

(

.-'

1

\, {'

f'

'~

i

;t,~· j. " iv !ŒM1R~I EMEN'l'S , , .,

L'auteur veut remercier Dr J. Derome qui a supervisé

la présente rech~rche: son intêr~t pour le problême étudi~,

sa disponibi l i té de tous lés ins tants et son assis tance

\

dans l'orientation et l'exéc'ution· ~ette

----

étude ont été

grandement appréciés.

\

L'auteur veut aussi témoigner sa gr~ti tude à M1le

,

Nicole Nartel pour son soutien de tous les instants et pour son travail de dactylographie.

~

Je dois aussi remerçier le Service de l'environnement

atmàsphériqVe (Pê.ches et

envi~onnemen

t _Canada) pour l'aide

f1nanC1ere qU1 m a e e accor · . ... . , '" t'" dé\

f

d t . . . . ur:an mon seJour a . ...

l'Uniyersitê McGill. l \

--,

.

" '!

:i

4 •

/

v

, \

t

..

TABLE DES MATIERES

PAGE ... , RESUME ••.•••.••••

...

·

...

,

ii co "ABSTRACT" • . . . • • • . . . • • . . . •

·

... .

iii" ,

'7

\, , , llliMERCIEMENTS ••• , ••••••••••••••••••

· ... '1' ... .

iv

TABLE DES MA.TIERES . . . • • . . . .

·

... .

.

' v

TABLE DES FIGURES . . • • • . . • . . • • • • • . • • ix

'II- ,

LISTE DES SY.MBOLES . . • . . . • • • • • • . • • • • • . • • • • • • • • • • • • • • • 1 • • • xii ,

INTRODUCTION ••••••.•••••••••• 1 C • • • • 1 • • • • • • 1 . . . . l

'CHAPITRE I: LES 'EQUATIONS PRIMI'rIVES

A.

EQUATIONS DIFFERENT-IELLE DE ~

Î

B. ATMOSPHERE EN ROTATION SOLIDE

1. Fonctions de Hough ..••...• '. • . . . . . .

q

2. Fréquence équivalente ...•... ' . . •. .

11

3. Valeur propre . . . ~ . . . ; .... -; I • • • • • • ~ • • , . , 14-3.1 Ondes libres . . • . . . • . , . . . l~ 3.2 Ondes forcées... 11 4.1 Ondes de ROssby •••.••••..•..••.• ;-... 1~ 4.2 Ondes de grav~t€...

... ... ...•.. ...

20

''\, / _, "

/

/"

/

vi

,

"

_PAGE

CHA~ITRE II: _{LE MODELE NUMERIQ'UE}

\

'A.

GRI~LE

_{•••.••••••••••••••••••.•••}

\.~.

B .. CONDITIONS AUX FRONTIERES NORD ET S

23

1. Pôle . . . --.~ . . . . ---t! 2. Equateur . . . ~~ . . . . ---~, C. FORME MATRICIELLE 1. Equation générale... . . . 2'

2.1 Condition à la limite supérieure... ... ~q

, j

2.2fondition.à la limite inférieure . . . '"

31

\

l.

CHAPITRE III: _{LA VERIFICATION}

Dï

_{MODELE •••.••••••••••••••} CHAPIT.RE IV: STRUCTURES D'ONDES FORCEES

A. CONDITIONS GENERALES... . • •

.

4'3

'

B • EXPER~ENCES NUMERIQUES ••.•••••••••.•• '.' ••••••• \ ••

, \

1er g:çoupe dl expériences . . . ,' . . . ~

Expérience lA . . . -. . . " . . . " Expérien_~B •.•••...•...•. . .., .•... ---Expérience le ... ~ . . . . Expérience ID •••••••••••••••••.•••.•••••••• Expérience lE . . . • . . . 1 ~I ".;6i

2ième groupe d exper1enc~s • • . . .

.,r'

3ième groupe d' ~xpériences. ',r---' •••••• _. ';' ••••••.•

. 4ièrne groupe d' e~périences . . . .

Qil

,

41

47

47

51

.5'1-5q

6Q. 6~

7'-80

(

o

vii

PAGE

•

CHAPITRE V: GEOSTROPHIISME

A. INTRODUCTION...

_,

83

B. ETUDE DES GRANDEURS D'ECHELLE •••••••••.•••••• ' •• '" VS r ' ,,) ! CONCLUSION .•.•••••..••.•••.••••••••••••••••.••••••• ' . . .

9'

\ y APPENDICE 1: ATMOSPHERE ISOTHERME...

93

Cas 1: lJ2 positif . . . • . . . .

Il...

94

Cas 2:

-1

< lJ.2 <

O...

95

Cas 3: lJ 2 <

-1 ...

9 '

APPENDICE 2: RESONNANCE •..••••.•••....•.•.•••.•...•••.•.••

91

APPENDICE 3: MODELES APPROXIMES... 100

, . A. EQUATIONS QUASI-NON-DI~RGENTES

1. Equations générales •••••••.••••••.••••• ~ • • •• 100

2. Ondes 'libres . . . I l • • I l

lof

3. Ondes forcées... IOa

4. Parallèle ondes libres - - ondes forcées ••••• 103

ere ni

B. EQUATIONS QUASI-GEOSTROPHIQUES DE 1 .SORTE ••••• 106

,1

C. EQUATIONS QUASI-GEOSTROPHIQUESDE 2ieme SORTE ••••• 110

J

D. CONCLUSION ••••••••••••••••••••.••••••••••••••• - ••• III

a

, ,

viii

PAGE

1\PPENDICE 4: ME'rIlODE DE LINDZEN ET KUO EN ~EUX DIMENSIONS 114

APPENDICE 5: GENERATION D'UN MODE DE GRAVITE ••••••••••••• 117

REFEREN~S •••••••••••••••••••••••••••••••••••••••• " •••••• ',

l:l"

•

\, ,.. \ \

•

" _, ' /

J

"

i,

.----:.

\

~ " V

"

,

'. ix

TABLE DES FIGURES • 1

"

1. Courbe de À/m vs , -

Qin . . ' .. " ... ' ... '.' ...

~ ~

...

~.

2. Fréquence propres des mo~es pour m = 1 . . . .

31\. Champ des valeurs de ( t E)

-!

pour les modes de .R<?ssby

des équa tians primi ti ves, pour m L . • . . . •

3B. Champ des valeurs de (E:)-! pour les modeS' qe gravité

des équations primitives, pour m 1 . . . .

4. Grille ut'ilisée pour le calcul de <1>' •••• ' . . . .

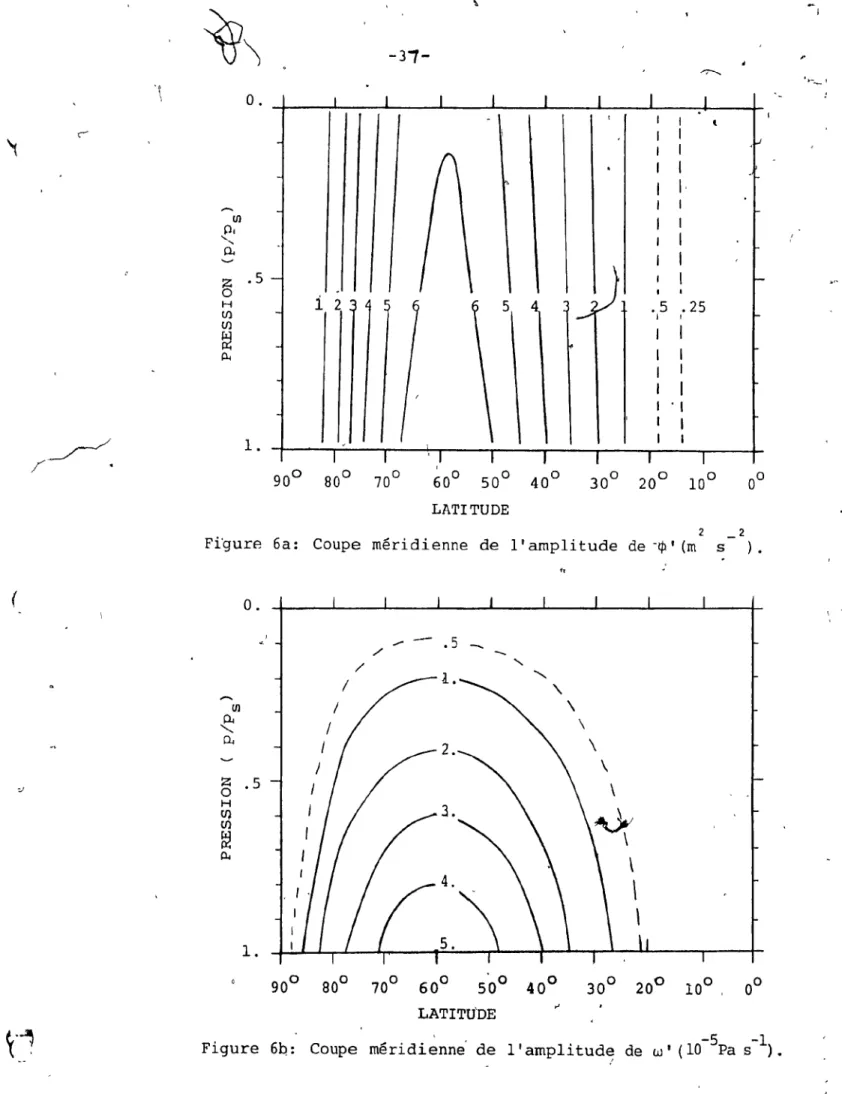
5. Coupe nord-sud de lJamplitud~ .de la contrainte w

s:

mode de Rossby (À

=

-O.li m = li n - m = 2) . . . ..

6. Coupe mér~dienne des • ampli tudes de ~' et w' •.•••••••••

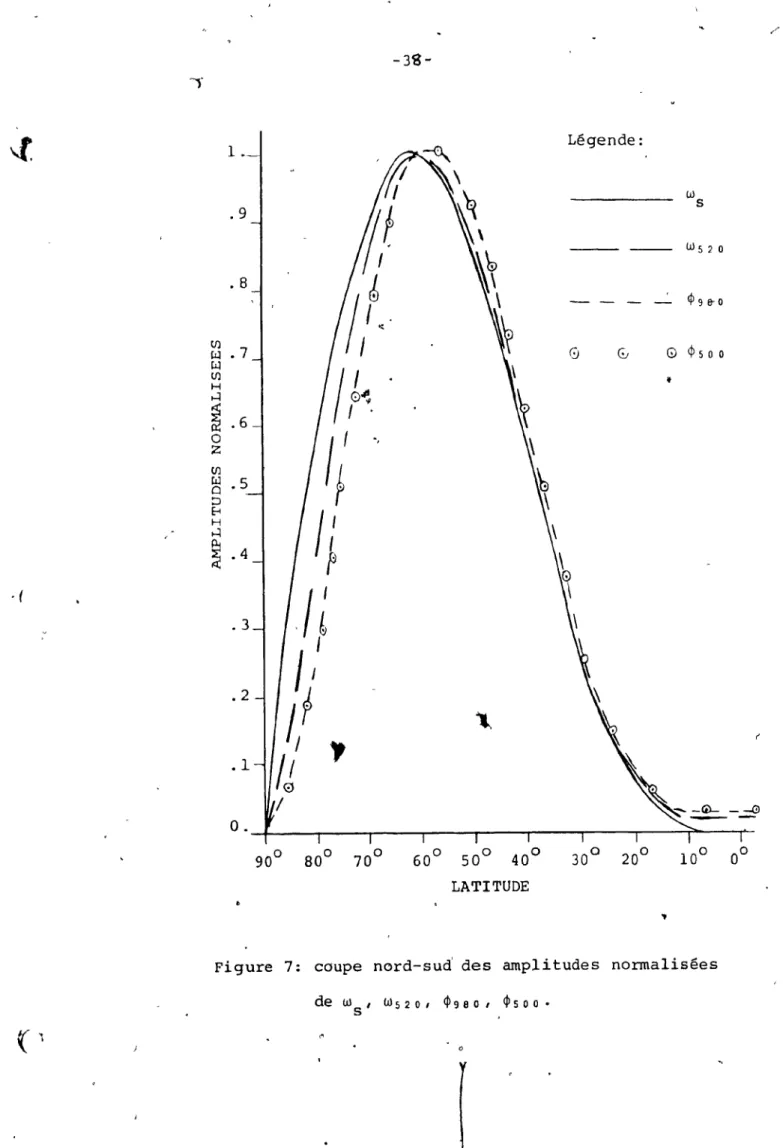
7. Coupe nord-sud des amplitudes normalisées de w , w ,

S 520

~9\80

et 4>500 . . . 1

• • • • • • • , • • • • •

8A. Coupe verticale de ~I à 60 N . . . • . . . , 0 .

,

8B. Coupe verticale de w'à 60 N . . . , .••... o ~ ....•..

...

, 9. Profil modifié de vents zonaux Ü caractéristiques des

conditions d'hiver . . . · . . . ~., . . . . 10. Coupe 'verticale du coefficient de refroidissement

linéaire Cl • • • • • • • • • • • • ~ • • • • • • • • • • • • • • • • • • • ~ • • • • • • • • • • •

11. Coupe méridienne de l'onde forcée de l'expérience lA ..

12. Coupe nord-sud ~e la valeur de a utilisée aux

expé-PAGE 21 24 3S'

3i1

3~ 40 4~

45

4~

50

riences

lB

et {

2B...

,

5

'3

13 •• Coupe méridienne de l'onde forcée de l' expérience

~lC.

• 5

é

l '

-

l ~ , ~

1

.+

,~:

,

. ,

.

le " "

1

x PAGE - 0 '

14. Coupe verticale à 60 N des ondes forcées du groupe

dl expériences 1 . . . - .--:-: .... .. f • • • • • lit • • • • • .. • • • • • • • • • • 57

, t \

15. Coupe vertiqale à 36. SON des ondes forcées "du groupe

d' expériences l~ . . . • . . .

1&. Profil de vents zonaux utilisés aux expériences ID et

2D:

TI

consta,nt au-dessus de 200 rob •.•••••.••••..••••.•

17. Coupe méridienne de l'onde forcée de 1.' expé:r:ience, 10 ..

18. Profil de vents tzonaux utilisés aux expériences lE et

sg

60

61

2E: U ~ntensi fié aU,dessus de 200 mb... .. .. . . ... . • .. .. 63

19. ~oupe méridienne de l'onde forcée de l' exp~rience lE..

6if

20. Coupe méridienne de l'onde forcée de l'e'Wérience 2A..

66

21. Coupe méridienne de l'onde forcée de l'expérience 2C.. 6'l

b ~

22. Coupe méridienne de l'onde forcée de l'\exp~érience 2D ••

. 23. Coupe méridienne de l'onde forcée de l'expérience - 2E ..

,

24. Coupe verticale à 600N des ondes fo~cées du groupe

d r expérience 2... 70l.

2S. Coupe verticale à 36. SON des ondes forcées du groupe

d'expériences 2 ... I l • • • • I l • • • • I l • • • • I l • • • • I l • • • • l ' '

73

26. Coupe méridienne de l' onde f~rcée de l'expérience 3A.. 75'

~7. Coupe méridienne de l'onde forcée de l'expérience 38.. 76

28. Coupe méridienne de l'onde forcée de l'expérience 3C.. 7T/

29. Coupe méridienne de l'onde forcée de l'expérience 3D..

79

30. Coupe n'ard-sud à 500 rnb des ondes forcé~s du groupe

d1expér~iences 3, ..•...•.•.. t • • • • • • • • • • • • , • • • • , . . . . • • • •

7tt

1

31. Coupe m~ridienne de l'onde forcéé de l'expérience 4... B

l

•

t

Xl

PAGE

32. Coupe nord-sud à 500 mb des termes de l'équation-u

pour m = 1 ....•...•...•. , ..•••.... •

t...

8b

33. Coupe nord-sud à 500 mb des termes de l'équation-v

pour m 'T"

1...

Bl

34. Coupe nord-flud à SOO mb des termes de l'équatlon-u

pour m =

2...

aB

3S. Coupe nQ,.rd-sud à 500 mb des termes de l'équatlon-v J

t

pour m = 2 ... " • . . . • • • . • • • • • . . • • • • . . . • • • . • • • • . . . • • . . ~q

tl

!

A~-l. Champ des valeurs de (:t E) des équatl0ns

quasl-non-divergentes . . .

10J.j-A3-2. Champ des valeurs de ( t É:)

-!

de~

équations

quasi-ère Q

géos trophique s de l

_,.

sorte. . . . . . . . . . . . . . . . . . . . . . 10 1

AH.

~~~:e

1

~O:d~~~~

:e

_l~; c:n~r:~) ~~:

..

~~~~. ~~

.

~~~~

...

AS-2. Coupe méridienne de l'amplitude de~' -Gt de w' . . . 120

AS-3. Coupe verticale à S5.90N de l'amplltude de w' ... 12r

AS-4. Coupe verticale à SS.90N de "l'amplitude de ~' . . . 12~

AS-5. Coupe nord-sud à 500 rob des champs de' -i~, -iu et v· 12'1'

A~6. Représentation schématique des champs du

gébpoten-tiel et du vent pour une onde de gravi té . . . ~.. 125

"

.

./

/

jiiiD •

t

1

1.

•

symboles (unités) a d e f 9 h i J k K l L x m ( m) ( m) (m) (m) xii

LISTE DES SYMBOLES

définition

rayon moyen de la terre dénvée totale

2. 718 ...

paramètre de Coriolis (= 2rlsin8) accélératl'on gravitationnelle épaisseur de l' 9tmosphère homogène

nombre entier ordonnant les nivèaux de latitude constante dans le modèle numé-rique: l!: J L JF

nombre d'onde zonal (= 2D/A ) x

nombre d'onde vertical en preSSlon

(~\ 2nps/Ap)

longltude (radians)

longueur d'échelle lohgltudinale de ~' longueur d'échelle latitudinale de ~' opérateur générateur des polynômes asso-ciés de Legendre

opérateur générateur des fonctions de Hough nombre d'onde zonal non-dimensionnel

(= ka cosS)

n N p Ps P r R 0 Of,

S

..

t u u'

TI

v v' v (Pa) (Pa) ( m) ( s) (m s-l1/ (m s -1) -1 (m s ) '/ xiiI

'degré du polynômè associé de Legendre qui admet la relation de valeur propre

L8P~ (8) = -n (n + 1)- P~ ,(8), .

. paramètre qUl ·ordonne. les fopctions de

Hough:

~()"

m, n)

l'

nombre entier ordonnant les niveaux de pression constante dans le modèle

numé-rique: l b. N {; NF

pression

pression à la

surf~ce

(posée égale à I05pa )

pression_non-dimensl0nnelle (= p/ps)

distance du centre de la terre nombre de Rossby 2 nn8 stabilité statique (=

:P-ap p p temps

composante longitudinille du vent 2

a)

composante longitudinale de la perturbation dans le vent

moyenne zonale de la composante longitu-dinale du vent

composante latitudinale du vent

rfcomposante latitudinale de la perturbation dans le vent

moyenne zonale de la composante latitudi-nale du vent

l "

...

\,

f

l

!Ix !I p 1\ '1. TI p cr CP'

x

...

'"

--~-~-) (m) (pa) (m) " (kg m-3 ) (m4s2kg-2) (m2 s-2) (m2s"72) (m2s-2 ) (m2 s-2) xiv

long~eur d'onde longitudinale

longueur d'onde verticale en coordonnée de pression

\ longueur d'onde verticale en coordonnée de hauteur

nombre d'onde vertical non-dimens~onnel en coordonnée de hauteur (= 2ITh/z)

-i"t fréquence d'une onde de la forme e

pi = 3.14159 . . . densité

-i

dln0 stabili té statique (= P '\. 3p 'géopotentiel (:: gz) (éq. 1.1, 1. 2 et 1. 3) • ampli tude de la perturbation du

géopoten-ikx

tiel (CP\,=cjJ(Y,p) e ) (ailleurs) perturbation dans le géopotentiel moyenne zonale du géopotentiel

transformation de variab.le (= <pe

-Zj2

fonction de Hough; mode propre de l'opé-rateur

L

6

fonction du potentiel divergent:

ryx =

V

vent irr'ationnel et

X

ry2X : divergence horizontale

:Çonction de cou'rant:

-

~

.

k x V~ = v~

:

vent non-d1vergent et

ry2~ = ç composante,verticale du

tour-billon

~.~a

______

~

_________ . _____________

~

__________________

--~---

-! i w _s

n·

n'

..

-1 (Pa s ) " -1 (Pù s ) (s -1) (s -1) xv

vi tesse verticale en coordonnée de pression

(= dp/dt)

contrainte dans la vitesse verticale _{à P}

s

,

taux de rotation de la terre

taux de rotation de l'atmosphère en

rota-tion solide (=

TI

)

a cosS

" ,<

"

...

-.---

...

_---

....

---.-~--- -~- -~ - ~,~--~

- ~ '1

-1-INTRODUCTION

Les ondes forcées 'dans l'atmosphère représentent un do~aine

de la météorologie dynamique qui ne fait l'objet d'études poussées que depuis un peu plus d'une décennie. Les études de

...

propagat~on verticale des ondes planéta~res forcées dans les

'.

-bas niveaux de l'atmosphère faites par Charney et Drazin (1961) 1

placent ces derniers au rang de pionni~rs.

Il s'est vite développé un intérêt accru pour l'étude de l'interaction des ondes forcées avec le cour~nt zonal lorsqu'on y a vu une explication possible du phénomène de réchauffement soudain associé au renversement de la circulation dans la stra-tosphèr'e (Dickinson, 1969 et 1970; Matsuno, 1971; ,Holton, 1976).

Des études conduites avec des modèles linéarisés et sta-tionnaires dans le temps ont permis de simul'er la réponse de l'atmosphère à diverses contraintes thermiques ou orographiques

(Derome et Wiin-Nielsen, 1971) et d~ mieux co~prendre la

, '

structure des ondes forcées et les transport~ thermiques ou d'énergie -associés avec celles-ci (Eliassen et Palm, 1961;

Matsuno, 1970). \

On a alors été amené à étud'er la condition appliquée à la limite supérieure de l'atmosphèr et les effets de la résolution verticale des modèles numerlques. A caus~ de la stratification, moyenne' de la stabilité statique de l'atmosphère, les ondes

forcées prése'ntent "des longueurs d

'o~de

verticàles à peu près uniformes en hauteur pour un COurant zonal Ü constant: ainsi le choix de niveaux linéairement espacés en hauteur (modèle-Z)'

.

~ devient judicieux pour l'étude des ondes forcées si on dé'sire une'

pu •

-~-Toutefois, dah~ les mod~l~s de prévision

d'ex-ploitation, on ne peut pas, ! ce moment-ci, dé,finir les' vents et les fonctions de dissipation à une altitude uffisante

à cause d'un manque d'observations synoptiques à ces

Il nous reste donc" à btiliser des profils évalués à par 'r de données climatologiques ou extrapolé~ d'une quelconque ma ière: cependant on a enco~e peu d'idée des répercutions possible des erreurs d'évaluation de ces profils sur les strUGtures d'o des

1 1 - -_

fo'rcées obtenues. Nous nous proposons içi d'étudier la sensi.,. bilité des strUctures d'ondes forcées aux conditions régnant dans la stratosphère.

\,

Notre étude se fait en utilisant une version li éarisée des équations primitives appliquée à l'étude des onde sta-\ tionnaire.s dans le temps sur une sphère en rotation. N

\

\ liserons un modèle-P avec w = 01 à P = 'Ü comme condition ra

,frontière SUPérie.urj afin de 'se rapprocher des

n\>dèle~

de \pré-visio'n _ opérationnel . Les"

~tructures

obtenues' ne seront

~~s

nécessairement cell s que l'atmosphère choisirait, ~ais cellés qu'on obtient avec fi modèle da résolution verticale donnée et

avec ses conditions aux limites imparfaites.

La contrainte à la base sera donnée en spécifiant la structure horizontale de w 0., A

l' S

notre ~onnai~sance, c'est~la

l ,

premièr.e lois qu'on utilise une telle c,ontrainte dans une étude

d'ondes forcéès Sur une sphère~ habitue1lement les chercheurs

utilis~nt.plutÔt une contrainte qui définit le géopotentiel à

,un certain niveau de référence.

.

.

Le syst.me~d'êquations ~st

qu'à l "obtenti6n d,tune équation géopotentiel de la perturbation férentierle est du 1er degré et

• 1

\

-~

"

sol uHo/né anal

~tique~en

t j

us-différe~ierle en te~es du ,

seulement. Cet~e équation

dif-du 2ième orâre en y ~t en P ,

t

t

, i

1

'1

~\ ~ .. --;-.'

\

\

\

' -3- ,

\

, \ "

avec un terme mixte

a

2

/ayap.

_{Pour les cas les plus'généraux}

de profils du vefit zonal et de dissipation, les dépendances' en y et en P ne sont pas séparables et cette équation doit être' résolue numériquement: on utilise ici une méthode de

, ' li

solution ~laborée par Lindzen et Kuo (1969).

On a préféré le système des équations primitives au système quasi-géostrophique à cause de sa généralité

èt

du fait que

l'équation di fférentielle à résoudre n'est' guère plus complexe ~ seul le terme mixte est ajouté; mais ceci ne crée pas de pro-blème de solution numérique à cause d~s conditions appliquées aux frontières qui sont ici<>,relati vernent simples ..

Le chapitre l et ~'appendice 3 font une étude comparative sur le' plan théorique -des structures des ondes forCées qu'bn

obtient analytiquement de quatre systèmes d'équations linéarisées déJà connus et on établit le parallèle entre ondes libres et ondes forcées: an chapitre 1, on applique les résultats de

Longuet-Higgins (1968) avec les équations primitives; à l'appen-dice 3A, on applique les résultats dè Moura (1976) avec les

équations quasi-non-divergentes et à l'appendice 3E et

3e;

on étudie les sysCèmes d'équations quasi-géostrophiques de l:re,

sorte et 2ième sorte, respeotivement.-

~

Les chapitres II et III" décrivent le modèle numérique avec ses conditions aux frontières etd1es tests de vérification.

Le chapitre IV

regroup~

les

e~périenc~s d~

sensibilité. \

Le chapitre

v~rmi~

par

u~e

qrêve

~tudè,des ~randeurs

dl échelle des termes des équations du mouvement afin d' éva'iuer

_.

_. le degré de gé~strophis~e des ondes planétaires forcées.

! -"'1

(

\

l LES EQUATIONS PRIMITIVES

A. EQUATION DIFFERENTIELLE DE ~ _r

.

-, "

Nous allons considérer les équations eulériennes du mou~ vément d'un fluide sur une sph~re en rotation constante. On apprpxime la' terre conune une sphê"re parfaite et on 'néglige

l'accéléra~ion cen~rifuge de l'atmosphère. 'On constate que

#l ,

l'épaisseur de l'atmosphère est petite comparée au rayon de la terre: ceci

s~gère

de poser r = a et

ir

=

~z

• De plus on modifie les équations par l'approxi~ation hydrostatique du fait que les mouvements verticaux sont généralement plus faibles que

~.

les horizontaux.

Phillips (1966) a montré que le principe de conservation d'énergie exige alors de n'égliger les

tE;rm~s

de 'courbure où la vitesse verticale intervient (vw et uw) et la force de Coriolis

, . a a ~

due à la composante horizontale du vecteur de'rotation de la terre (2~~cose};' cOJTU11e ce d~ernier terme est soustrait à .

2Dv sinS dans l'équation du mouvement selon x, et'que, ,à l'é-chelle qui nous intéres~e v » w, on peut conclure que le terme 2Dw coa9 ne peut devenir comparable à 2Dv sine que près de l'é-quateur où sine tend vers zéro.

On obtient alors un systême fermé de quatre équations!

"

.

avec les .~a-riables u, v, w et <t>. Les équations sont ici écri-tés sous forme de flux, avec la coordonnée

vert~ale

p:

!

1

1

1

..

_-~~~--- -(

'-"

)

..

-5-/ "

1.1 Equation du mouve t selon x :

~~

f

~(':') ,~iv

< ...

'OJ;

it~wJ-.(JlArM-n~f#.

0

1.2

1.3

,1. 4

Si on s€pare les variables en moyennes latitudinale~ (~) et en perturbations ( )', on obtient deux ensembles d'équations,

.

l'un régissant la moyenne zonale de la circulation, l'autre la perturbation. On linéarise ces équations en supposant que les perturbations sont beaucoup plus petites que les moyennes zona-

_.

les': on ~êglige alors les teqnes qui contiennent de.s produits de perturbations. Comme on s'intéresse ici à la structure sta-tionnaire des ondes forcées dans un courant zonal prédéfini, on annule les dérivées temporelles

(~t

= 0) .

"

. ,

On peut simplifier grandement les équations en supposant que la m9yenne zonale de la circulation est en balance géostro-,

phiqu~ (car alors

V

= 0

=

w)

et en supposant que la contribution

du tourbillon relatif au tourbillon total du syst~me est petite dans, cette balance (Ü.

~

-

~ ~~).

Nous' allons de plus négliger

•

. 't

, ,

-"

-b-l'advection verticale de la quant~té de mouvement par la

perturbation. On obtient alors le système d'équations suivant pour la structure des perturbations:

1.5

u

~',

-

f

1

~x.

~

Uk

,

1

f~1

]..6

*

-à

X-1.7

U

~~

-

+~'M

o )(,

_d1

" 1.8 ₊ où

et a.~' est une approximation newtonienne (linéaire) du

re-p

froidissement.

Ce systèrn~ d'équations est semblable à celui utilisé par

Holton (1976), sauf que le nôtre ne décrit que les perturbations stationnaires et la coordonnée verticale' est la pression.

Considérons une perturbation ayant une structure zonale

_..

sinusoïdale 1 A..JJ 1

m-U) Il •

<p'

•

r

» $ 4f;.I> ~ _{~ ,}

f

,-

,.

1 ~ (--~'

1

..J

...

-1-On peut alors obtenir des équations 1. 5 et 1. 6 les

expres-sions explicitas de u et v en termes de '~

\t2'

1.9 1.10 "Ir

-

[

F

G

tL-]

.~

0'1

i1 où D

-

j.

1 ,

(lfB)TT

.

_~,k( E (. +-

B

F

~

/-tE G

-(H-

B)

Liu

avec B

-

;.l

u

:t

A (

A

-

_.k

1

U+:lU~)

- J . ' Cl.. t-

U

'

t' C

-(i1un

J

- ..L-

fyr

ii

~

Il])

c..tJ<J!J

•

... M ~-- -.1" 1

.,.,

~ ! ',\

4

,'~ , 'f

---~--~ - - - ~

-

-'a-o

, De 'l' éQUaQde la thermodynamique (éq, L 7), on peut

obteni r une expression pour w

. 1.11

w

où v'est donné par l'équation l.10 et où

II

J

. ,

En substituant u, v et w dans l'équation' de corttinuité, on obtient une équation différentielle partielle pour ~

1.12 où

(,

f..-'F

T - ' -

J...[

q

~~G]

-

~

[#-]

cC<JB

dY

'Of

(J"

-~

--.

/

, '

\..1

-9-B. ATMOSPHERE EN ROTATION SOLIDE

1. Fonctions, de Hough

-L'équation différentielle partielle (éq. 1.12) est du

deuxi~me

ordre, en Y ,ct en p avec un terme mïxte

a a

~

•

{Dans

• , c y p

le cas le plus général, elle a des coefficients va~iables dans l'~space et n'est donc pas séparable. tependant'si on donne à _,

_.

_,

l'atmosph~re un taux' de rotation up~qrrne rotation solide --Ü (8,p) -

?i

a cos6 où

n

est.une

cort.·nt~,"

. .J..'éqUation peut deve-nir séparable .si la

stabiiit~t/ati~ue

cr (6 ',p) ,a une

struc~ure

simple. On commencera par considérer le cas particulier cr cons-tante et aucune dissipation: a(8,p) = O. (t~appendice 1 montre

l'effet d'employer une atmosphère isotherme on alors cr est

pro-portionnelle à IIp 2). L'équation di ffér~tielle (éq. 1.12) pe1ut alors se réécrite 1.13 D on et / avec

où m

k

t

cose est le nomtire d'onde zdnal non-dimenp~onnel. 1 / \

-:)

\(~ .. ft j,.'{i, ; h ~ \,'î 1 1 ;' ,i {

"

..

( • "

C',f

" '10

-J

e

est l'opérateur générateur des fonctions de Hough, tel que défini par Longuet-H1gg1ns (1968). Celles-cl sont donc les modes propres du système et admettent une relatIon de valeur propre

!.14

où ~(À,n,m) est un mode propre et (, la constante de séparation,

est la valeur propre correspondante. On obtIent l'équation de la structure vert1cale : . 1.15 > où On peut pour la définIt

+

1<~cp

-D

1re:

=

longu ur d'onde i·/\ c p la /...,

'1

TT a.,

J1 (

1

+

.l1...) .

E. -'11 . 0- 'I;!..

JL

,f

=

verticale lorsque ( > 0 Si ( < 0, on "pénétration " verticale de l'onde qui a alors une structur~ verticale exponentielle.

On notera gue les structures des modes ~ropres et leur va-leur propre E dépendent du nombre d'onde zonal (m), de l'inten-slté du courant zonal dans le paramêtre À et aussi~du paramètre' n qui ordonne les modes propres. Lorsqu~ € tend vers zéro, les

structures d~s modes/propres deviennent semblables A celles des harmoniq.ùes sphériqu,es

P~

(6) • eiml<ll et alors ,l'indice n' définit

\

-11-, m

le degré du polynôme associé de Legendre P (8) (Longuet-Higgins

n

1968); dans le cas plus général, le paramètre n deVlent un in-dlce plus abstrait et, pour un À et un m donné, la strùcture

nord-sud des modes correspondant à des valeurs petites du para-mètre n - m ~ 0 est assez grave et devient de plus en plus fine

lorsque n - r,l a ugmen te.

Dans les sections du chapitre l qui suivent, nous repre-nons l'analyse de Dlckinson ( 1968a) qui applique les résultats de Longuet-Higgins sur l'étude des ondes libres au·problème des ondes forcées dans une atmosphère en rotatlon sollde sur une sphère.

2. Fréquence équivalente

Historiquement, les fonctions de Hough sont nées du pro-blème des ondes libres appliquées aux marées sur une sphère en rotation: on s'intéresse alors à la vitesse angulaire (ou fré-quence) d'une onde llbre dans un fluide au repos par rapport à

la terre. Longuet-Higgins. (1968), que l' ôn abrévlera L. H., a

i (ml - vt)

étudlé une onde de la forme e , où 1 est la longitude, en Si lntéressant à la variation temporelle de celle-ci en l'

ab-sence de courant zonal.

En comparant

l'oPérateur~e

défini précédemment avec la définition donnée par L.H. pour le traitement des ondes libres, on constate que le paramètre À a une interprétation différente:

ondes libres

(atmosphère au repos)

( ,À

_Î

ondes forcées (courant zonal

TI)

/

•

-

-l~-Dans notre problème, on s'intéresse aux ondes forcées sta-tionnaires dans un courant ~onal ayant une vitesse angulaire

n.

Donc il s'établit un paralièle entre les deux problèmes: la fr6guenc~ de l'onde libre v de L.H. est remplacée par son mou-vement par rapport au courant zonal, luttant contre l'advection par ce dernler, pour rester stationnaire.

;

ondes libres ondes forcées

-v

+---~ mQ

Ainsi les ondes, dans une atmosphère en rotation solide

Q,

ne peuvent rester stationnaires par rapport à la terre gue si leur vitesse angulaire par rapport au fluide v/m est exactement l'opposé de celle du fluide (dqnc -n): ceci correspond à l'ef-fet Doppler.

Cependant la fréquence inertielle d'un fluide en rotation par rapport à la terre est modifiée par cette rotation, qui s'a-Joute algébriquement à celle de la terre. Ceci revient à dire que le tourbillon total (ou absolu) du système est donné par la somme des tourbillons planétaire 20 et relatif 2~.

La figure 1 montre la valeur du paramètre À/m en fonction de

Q/n

et nous permet de faire le parallèle entre le problème ~ des' ondes libres dans une atm~sphère au repos et celui des ondes forcées stationnaires dans une circulation zonale.

Pour une circulation zonale faible l~1 «

n,

À/m varie

\lin~airement

avec

n .

Cependant pour Jde'forts vents

~onaux,

le

tourbillon relatif devient important.

• $

--

_{l '} -13- Q

·

,..,

ln

·

·

..-f 0 1/ 0

~

-

-

...

_,

-,

₊

,<

~ • ~ 1

}tligure 1: Courbe d'e À/m' vs

A)/L,

1

,

Pour de forts vents d'ouest, l'onde doit se propager à

grande vitesse par 'rapport au fluide pour rester stationnaire ear rapport à la terre; cependant le r~pport de cette vi~esse angulaire à la fréquence inertielle ~u système reste fini et À/m tend vers une valeur limite. Pour établir le parallèle avec le problème des

on~s

libres, on doit

cons~d~~ue

ces ondes ont une fréquence finie -- même si mÔ tend vers l'infini.

J'

Un courant zonal d'est va diminuer le tourbillon absolu de l'atmosphère. Ainsi lorsque

n

s'approche de

-n,

la fréquenc~

tnertielle tend à devenir nulle; alors une onde se déplaçant à

une vitesse finie

(~~n)

pour rester stationnaire par rapport à

l,a terre' cor.respondra à une onde de très haute fréquence dans l~,

. ,

problème des ondes libres de L.H.

3. Valeur propre

c

Revenons à la valeur pfopr€, s qui est ,la constante de sépa-ration entre les équations des structures horizontale et verti-cale d~ l'onde, On note gue E est fonction du nombre d'onde'

zonal m, du paramètre horizontal n et aussi du paramètre non-dimensionnel À.

3.1 Ondes libres

( 'Dans le problème ,des ondes libres, le paramètre E est

obte-~u

en solutionnant

l~€quation

de la structure verticale:,

d~ns

, '>

le cas d'un fluide homogène, il est directement fonction ~é

l'é-, 4122 ₁

paisseur h du fluide. E = gh' Si on s'intéresse à une

certai-~ ne perturbation de nombre Q' ondEi zonal \ m, il existe une- var,iêté de modes discrets possibles correspondant à des paramètrès

hori-l '

..

, l (

V

--~-J 1

-15-zontaux n entiers (avec n - m ~ 0) qui définissent la structure nord-sud de ce mode qui a une fréquence propre À(E, m, n).

c'est l'approche qu'a utilisée L.H. en ~ariant l'épaisseur h du !luide homogène. Ses résultats sont présentés sous forme de 'figures qui montrent les lignes du lieu de n -6m -- dont les

valeurs sont discrètes' -- dans l'espace

J

vs

E-~{h),

pour dif-férentes valeurs de m. Les courbes correspondànt à m = 1 sont

reproduites à la figure 2~

La structure des équations primitives permet deux types d'o$des: d'dne part, les ondes de Rossby, aussi appelées ondes de classe 2 (L.H.), ondes, quasi-géostroph~ques ou ondes plané-taires; d'autre part, les ondes de gravit€, aussi appelées ondes de classe l (L.H.) qui incluent les ôndes équatoriales de

1

Kel vin .. Pour être rigoureux, les ondes de classe 2 ne sont géostrophiques que lorsque E + ±O; cependant, nous

appelle-rons ici "modes de Rossby'~ toute onde provenant de, lq.

continua-'"

.J

t

tion analytique des modes de Rossby, même lorsque ( + ±oo (ces

modes tendent alors à rester concentrés autour de l'équateur), De plus, l'es ondes se subdivisent en deux groupes selon qu'elles se déplacent vers l'ouest ou vers l~est.

Les figures 2A et 2B correspondent au cas E > '0, qui est une condit\ion nécessair~ pour les ondes libres. Les modes li-bres du type de' Rossby se déplacent tous vers l'ouest (À < 0: famille de courbes au bas de la figure 2A). Certainq modes li-bres du type de gravi té se déplacent vers ,1'ouest (k' < 0:

fa-mill,e de courbes au haut de la figure 2A), tandis que d'autres

se d~placent vers l'est (À > 0: figure 2B). Les

modes

corres-1

pondant à E < 0, qui sont nécessairement ,des mocl~s - forc'és, sont,

'\

tous du type de Rossby: les modes ~e déplaçant vers l'ouest

1

(À < 0) sont montrés à la 'figure 2C et ce~x qui se déplacent

vers l'est 0,

,>

0), à la figure, 20', "

-1.

,...---~

..

1,7"

.!

1 1 "

(

t

V

l,-l

,.

-.:-) \

-16-~ ~1

À

-1

10

).

1 3 1 ~--o.Ot

,'-

O.t ~.001.~~~~~~~~~~ __ ~~ 0.01 ~ ______ ~~ . . .-~ __ ~~~ 0.01 0.1 1 E·~I 10 . '0.01 0.1 1 ,.'11. 1

A:modes se

dépJaçant

-

~""'O

').

-.01

vers

11

ouest; B: modes se déplaçant

ve~s

l'est.

€,.

0 1 /'t-P1' 0

)

1-O~1 '3 .01 -.OO4-~~ __ ~ ____ ~~ __ ~~+ .oo~~~--~---~----~~~ 0.01 1 0.1 , (-.:)-Y110 0.01 0.1 ' 1 r-e)".1.10 C:

modes

se dé'plaçan~ ~

<

0'

vers ltouestiD:modes se déplaçant vers

l'est.

f. .( ,0

#

1

F~gùre

2:,

Fréque~ces

propres des modes pour m

/ "

=

1.

(D'après L.H.1968) :', ) :~ ,) ..~ 1 ( ):

•

-11"

Dans l'étude des dndes libres, les valeurs négatives ,de E:

arrivent un peu comme un artifice mathématique. L'appendice 2

montre que s,euls les modes 'de. structure verticale sinusoïdale

(E > 0) .peuvent être des "modes libres" du système Î et seulement

,

.

.

si -0 est choisi de sorte que leur structure~ verticale rencontre

les conditions aux frontières. Cependant, conurie 1e dit L.H.:

"Les modes correspondant à des valeurs négatives

de c sont nécessaires pour former un ensemble

complet de fonctions propres li~éairemen~

indé-pendantes à partir desquelles an peut former toute onde, quelle que soit sa structure."

Les modes correspondant'à E < 0 prouvent pleinement ~eur

utilité dans l'ét~de des ondes forcées (ws(e)

r

0) où elles

seules peuvent satisfaire les conditions aux fFontières. Il n'y

a pas de r~sonnance possible puisqu'il n'existe pas de tels

modes libres: il'n'y a que les modes forcés qui' ont E < ,0.

3.2 Ondes forcées

~

Pour le cas des ondes forcées dans un fluide en rot~ion

sol~de TI,' le problème ,est posé différemmen~ du cas ~es ondes

libres. Du fait que ra contrainte soit orographique, Jes ondes,

'pour rester stationnai:res par rapport à la te'rre, ~oivent 'se

-déplacer avec une vitesse de phase

_.

_.

-TI par rapport au fluide,

ce dernier ayant une fréquence inertielle 2 (n

+

TI) i donc À

.

est connu dès le début. De plus on détermine à priori n et m

.

,

en choisissant la structure. horizontale de la' contrainte. Alors

â partir des figures de L.H., 'qui reprêsentent la solution de

v • ,'\ \

l'équation de structure horizontale, bn peut qéterrniner la

• "

(

,-' -l~-)

,)

Comme notre pro~~ème est posê de façon diffêrente, on a cru bon. de reconstruire, à partir des 'rêsul tats de L.H., l~s fi9ures 3A et 3B qui présentent quelques isolignes du Ghamp des valeurs de (±E)-! dans le plan n - m vs

TI/n,

pour le

cas-particu~

lier m = 1. Les lignes sont tracêes continues même si, pour

,

être rigoureux, seules les valeurs entières de n - ID sont

possibles.

_..'

" , ~"-,

De l'êquation 1.15, on voit que (±E)-! est une mesure

nO~""di~ensionnelle de la longueur d'onde verticale (si E > 0,

solutidn sinusoïdale, iso1igne.s au

~rai

t contiJlu,) ou de "la pénê-tratiOn\{Si E <

Q,

solution verticale exponentielle, isolignes

en trai s pointillés) • •

li

p~r

une êpaisseur de l'atmosplière donnêe h, toutes les valeursJde E sont possibles pour les ondes forcées. Cependant certaines valeurs posi ti ves dei E - . - qui, à cause du choix par.,.

,

ticulier de 0, correspondent aussi à des modes libres du système - peuvent prés'enter une condition dE{ ~êsonnance (voir l'appen-dice 2).

4.1 Ondes de Rossby

La figure 3A nous montre, pour le cas m = 1, que, selon les valeurs des paramètres TI/n et n - m, é peut prendre des

valeurs positives ou négatives.

1 ,

Les valeurs positives de E s'obtiennent pour des valeurs

de

n/n

_{, ' ,} comprisent

da~s

l'intervalle [ O',

ni/m .

_crl tJ où

(O/O>crit

est

infini pour n - m - 0 et

diminue

au'

fur

et à

mesure que n - m au~mente.* Ainsi il exist~ une bande'permise

, *

valeurs obt~nues de la famille de courbes du bas dé la figure q

1

2A. _If

. . $Z

-L

-0.5

..

-1.0

-1.

"

~

\ L

! ,~

i

..J

-_ -

.1-/

~égende: 'I

t

~ 0 : - -

É

-~

---.:..'---.Ih.

é

l.. 0

l fE)

-r

N-M ~--- 0 _.~---~%~/---­ l '

Figure 3.-A: Champ des valeurs de (±

é

)-~

pour les' modes de ROBS

Èi

des équations primitives"

pour m

=

1. • ~i

•

L " _, ~

L

a • ! , (

--20 ..

'.

de vents d'ouest, celle-ci étant d'autant plus petite que le paramètre ~n - m est g~and, qui permet la propagatibn verticale ,des ondes forcées (On dit qutune onde forcée se propage si sa

structure vert1cale est sinuso1dale, do~c E > 0). On note que

E -

~

varie entre zéro (pour

TI/n

= 0) et l'infini "(pour

m/fl)

.

t) .

, crI

,

Les vents d '.ouest supérieurs à (njn) 't \ ne permettent pas

, crI

la propagation des ondes ,de Rossby~ les structures verticales de celles-ci sont alors exponentielles. * Les vents d'est empê-chent aussi la propagation des ondes de Rossby.** On remarquera qu'il y a une bande interdite pour les valeurs de

TI/n

comprises dans 11 intervalle [-2,

-2/3]

pour m = l, (ce qui correspond aux

valeurs de À en dehors de l'intervalle -1.( À < 1). pour laquelle

il ni existe pas de modes de Rossby. Ceci nous mène à penser que

s~ules les o~des de gravité forcées peuvent avoir, dans le

langage des ondes libres, des "fréquences" assez élevées pour pouvoir rester stationnaires pour ces valeurs de~

IT/n.

Les

ondes de Rossby forcées redeviennent possibles pour

TI/n

< -2

***

et représentent la continuation analytique des modes pour

TI

>

TI

crit à travers

TI/n

infini. 4. 2 ~

,

Ondes de gravi té

f

Sahs entrer dan~ les détails, notons que les ondes de gravité forcées ont des modes propres définis pour tout

TI;n

\

*

valeurs obtenues, de la famille de co'urbes de la figure 2e

avec -.5 < À < O.

**

valeurs obtenues de la famille de courbes de la figure 2D

1

***

valeurs obtenues de la famille de C'ourbes du haut 'de la ,figure \W avec -1 < À < -::,.5.

, ,

jiiiiP • 1

'-"

(' , (" ~

v--, ~

t

r

l JI j

-1 •

O.

o~

-O.

-1. += -21-.03

/

.0

z.

.01 • DOS' i l 0 13

'4

'S- N~M .01 .03 _ .10 _ .30 1.0 dJ 1.0

.3D

/

FJgure ' 3-B: Champ des'

valeurs

de

e":~

pour les'

'modes de eravité' des

équa~ioQs

primitives,

pour

m, ~

1.

\ r / , '\ " ~ 1

i

---~---

---jii'* _!' , , l • c,

(

\- 1..:-

-2~-et ont toutes des structures verticales sinusoidales lE > 0;

figure 3B*)'. On notera ,cependant que la valeur de

é-!,

'qui

est proportionnelle à la longueur d'onde verticale, reste petite

sauf lorsque

TI

s'approche de -Ili ce qui correspond à ~a bande

interdite des modes de Rossby. Kasahara (1976) trouve, dans

~-,

une analyse spectrale de la hauteur du niveau de pression de

500 rnb dans l'atmosphère en termes d 'une ~érie tronquée de

fonctions 'de Hough, que moins de 5% 'de l'énergie des ondes libres

eS,t placée dans les modes de gravi t~, ce qui est de l'ordre de

~

grandeur des erreurs d'observations.

L'appeI}dice 3 étudie la propagation des ondes forcées dans des modèles aux équations simplifiées.

\, \

*

La figure 2B contribue

.

~ous

/

donner les valeurs de €

-!

à

.1' intérieur .de

~'inter~e

-1 < Gill < 0 et la figure 2A

pour lés valeurs à l'extérieur de cet~V.lle,

\ \ - , , ~\

J

1

.~ 1

..

..

••

'~1

l

-23-II LE MODELE NUMERIQUE

_,

_r

A. GRILLE

Pour les cas plus gênêrau~ de profils de vents zonaux U , de

stabilitê statique

cr

et de structure' nord-sud de la contrainte

orographique' i~sée, l'équation différentielle de CP' (éq. 1.12)

ne peut se réso':l~re que pa..]:" de~ procédês numériques. Cbrnme 1 en

général, les" structures verticales et méridiennes ne sont pas

séparables, l'équation différentielle' est résol ue par ~l f"f,é

ren-ces /inies sur une grille à de-ux di~ensions. Afin de mieux

simuler les modèles opérationnels, on utllise unf! distributlon

linéaire en pression des niveaux dans la vertica,le. La grIlle

utilisêe es t'J1lontrêe à la fig1;l~ 4.

"'"

Le cal,cul de ~' s'effectue sur les points de grille définis

par l'intersection des lignes de niveau de pression (N vari~nt

~ ,

de l à NF) et des lignes de lqtitude constante (J variant de

l à JF). Le pôle est situé à J = l et l'équateur entre les

lignes de J L.; JF - 1 et J = JF. Le niveau de pression

N, = NF est situé à une hauteur Llp/2 au-dessus de la surface

du sol et le niveau de pressiOn N = 1 à une hauteur Llp/2 en

dessous du sommet de l'a trnosphère.

Par les équations diagnostiques 1.9, 1.10 et 1.11, on peut). ,

éval'uer les champs de u l

, VI et w' à partir du champ de ~'

obtenu. Les champs de u' et VI sont calculés surola même grille

LJ

que <p'; le champ de w' est calculé sur les mêmes lignes de

latitude constante, mais sur des" niveaux de pression

'intermé-o

diaires, de sorte que le premier niveau est à p ='0 et le

dernier

a

..

r, p = p . s 1 î \ / , 1

iD

.

>

J

ji ( '. , ,

,

.

l"

Ap

.1'_

1

.

.

-

,

-~ < ~ : , 1 1 j \

.

.

-2.lf-J-1 J J+1 --...,.. - . , . -

...

-.

.

~ . • j 1 -1 *AY~

- ' -

- ' -

-

-F'ir:urei: Grille utilisée :pour le c.a.lcul\de~'

..

" JF-2 JF'-1 JF

-..,...-..,....,....,.

1

,

1 1 1 ₂

..

1 e , 1 3 1 1 1 1 1 lu _-1 1 1 1 .. 1 1 ~T ₊₁ 1 1 , ₁ 1 1 00

_F-2

,

1 N

F-1

1 1 _{N F} _ _ 1_. 1 1 Equat3~ 9=0 ~

•

t

.J

s;s

-25-On a~optera la notation suivante pour décrire une variable

sur la grille JF X NF: ,

L'éyuatlon dlfférentlelle de~' (éq. 1.12) est résolue numérlquement sur la grl11e JF X NF par une méthode directe falsant intervemr l'lnver::;ion de matrices de coefficients. Cette méthode fut élaborée par Lindzen et Kuo (1969) en une dlmenSlon, malS a été reprl~e èn deux dimensions par plusieurs auteurs (volr Beaudoln, 1974; Holton, 1976; Matsuno, 1970).

B. CONDITIONS AUX FRONTIERES NORD ET SUD

1. Pôle

Comme on utilise une structure d'onde périodique le long d'un cercle de latitude et que la valeur de ~' doit rester unique en tout point, 11 est évident alors que ~n(l) doit être nul. CeCl est notre condition à la frontière du pôÎe.

2.1 iP (1)

n

o

2. Equateur

Il n'existe pas de condition naturelle à l'équateur

puisque l'atmosphère réelle est sphérique et non hémisphérique. Généralement les chercheurs en ondes forcées utilisent une

condition d'antisymétrie par rapport à l'équateur dans le champ ~' et posent ~' = 0 (Matsuno, 1970~ Holton, 1976; Beaudoi~,

eq

1974). On justlfie cette condition par le fait qu'il Y

/

l'

a peu dè contrainte orographique aux basses latitudes èt qu'on observe peu d'amplitude dans $' dans la haute atmosphère près de l'équateur.

Les mo~èles de prévision opérationnels utilisent plutôt

une condition de non-échange à travers 'l'équateur: par exemple

Sl Vi _.eq • 0 il n'y a pas de transfert de masse entre les deux _,

hémisphères. L'équation 1.10 nous montre que ceci correspond

a

une condi tlon de <symétrie par rapport à l'équateur dans le

champ ~' et ainsi:

a~'

1

-oy

éq - 0

Le choix entre antisymétrie et symétrie '~este cependant artificiel: la seconde alternative a été retenue ici. A cause de ce choix, il s'avère avantageux ùe placer l'équateur entre les n~ veaux J JF - l et JF, de sorte que la condltion à la frontlêre sud du mod~le s'écrit simplement:

C. FORME MATRICIELLE

1. Equation générale

En utilisant les différences finies centrées du deuxième 1

ordre en Y, l'équation 1.12 se réécrit:

2.3 a..,N

(:r).

cfN(.r-~

-t)N(J)·

q" .

.J:r)

4-

t(.r)

·-4N

(.Tn)

, '

- eN

(J).

ti

1

(.F-I)

t

c(

(r)

U

1

(s)

+

eN

(:r

).Qj

1.

(:rH)

dt

N

?'1

N

Of

N

~

j.,(J)

~,l

(J)

jN

(3)

~

, , àt·

J\J J •

. . p

t

.J

(2.3b)

~ Il _{• i} OÙ (tN(J) ::::

Q:e.I

_(:J)

bN

(.r)

,'y

~y~ _~

_6Y

1

_N

(J')

' :

~N (J'~,

+

6

N

r-.r)

!J

y

J. ::J.~y/

eN

(J)

::

ê

_{N (J)}

;;J.t::.Y

d

Al

(I)

:-

dN(J)

jN

(J')

' :

j

_N

(.1 ")

~N(,r)

::;

;tN(r) -

_;1

~tJ.{:r)

6Y~

jN

(:r)

':::

0

En utilisant les conditions aux frontières (éq.' 2.1 et 2.2),

l'équation 2. 3 peut être écrite sous forme matricielle:,

~

et

~

sopt'des vecteurs horizontaux de dimension JF - 2:

n n

2.5

» a

1

--~ ... JF - 2): 2.6

G' ::

_N

(0 )

, ,

, ':-- j

N

(.J

~

.

1 )' , \ .

X et Y sont des roatrices tridiagonales (JF! 2 X JF - 2)~

n n 2.7

X ::

_kI

(0 )

Y

N

dNh)

-t)3)

2.8

-

-eNh)

dt\)'{3)',

c'N (3), _,

.

, ,

lo )

,

, ...

_,

, ...

'

' , " " ,

"

, ". " 'a.,

(JF-))

" ""h:

(JF-J) +

1

N

(.rF-~:

SI

(0 )

"

~ "

" "

,

"

" . '-c.I\J{.:r,./)

\

\", "·JN{JFwl)

-f~tJ(.rF·D

..

(

-Si la dépendance verticale est exprimée sous forme de différen-ces finies c~nt~ées du deuxième ordre en p, l'équation peut s~

réécrire: 2.9 2.10 où

~

:2

At

1

J

-

6~

Cl

11.

-t

YN

~L:lt

2.1 Condition â la limite supérieu~e

Afin de se rapprocher autant que possible des modèles opérationnels, on utili$e la condition w(p = 0) = O.

Cepen-dant des études ont montré que poser une tell~ conditiori â

LI 1 imi te s\1p6rieurc peut entraîner des réflexions artificielles des ondes forcées (Kirkwood, 1976). On devra donc être prudent dans l'interprétation des résultats.

Afin d'obtenir une formulation en terme de différences finies centrées. du deuxiême ordre en p, on applique l'équation de èontinuité au niveau N = 1.

2.11

+

JI ____

-Cc()f)

• a

-,.

t ~. "

--pa

-30-" Ici w! =,0" et ,w

3/ 2 est tiré de, l'équation de thermodynamique (éq. 1.11) appliquée au niveau intermédiaire N = 3/2. Les variables u et v sont êvaluées par ~es équations 1.9 et 1.10.

• • t

En substituqnt ces valeurs dans l'équation 2.11, on obtient alors l'~quation: 2.12

'"

q,

où CLt =

bt:

_-=

Er -

_I

F,

+

...L-

L[4,

co<o&] -

J2-

(~)

Co<J

a

~y,

J6t

~

"1/j.. A Q ( ) Ct :;-

-.-1-

Cid

~t~t'

~

3/::>. \) 1

,1

₌

_.~

_{(11.) .}

_~ -L-

[ Ef)

'/1

"t,

;2hf

q

61

1 ' -;

1'17.

l,r

~

']),'0.-.1-

ii:[F.

<~IJ

-

L

(lL)

-t

_{J -}

(f~

,~~

d'l

bt"l.

0-'

-~/~ ~f

i

~.,

r~

-,

D·

, ,

•

_.

_.

"

~

j

" , ,1

-<l-i

" ,,' " 1 } t

f

,

J

l, . \

L~l

( ~ -~ \ V ' .... l~ -

31-En utilisant les conditjons données par les équations

2.1 et 2.2 au pôle et à l'équateur, et en expriMant 'la dépen-dance nord-sud de l'équation 2.12 sous

fi~ies

centrées du deuxième

ordr~

en

se réécrire sous forme matricielle:

2.13

y

_{t ,}

=

forme de différences <il ~ YI l'équat10n 2.12 peut

(J'

1 _ )

;2

sont de la forme donnée par l'équation

2.5

et ft est un vecteur horizontal de dimensi9n JF - 2~

es matrices X

t et Yt

\

s var:iables a

t , ,bt , 2.3B où les indices n

s~obtiennent des équations 2,7 et 2.8, QG Ct' dt et ht sont obtenues de la relation sont remplacés par t.

/

..

2.2 Condition à la limite inférieure

\

.

On veut forcer les ondes pa'r une contrainte orograph1quej on a chpi~i ici de spécifier la vitesse verticale w à la surf~ce~

La condi t~on à la limite i\nférieure s'obtient de faç,on semblable '5 ccllc'dft!sornrnet de l'atmosphère. On applique l'équation de

contin~ité au niveau NF. Çeci fait interve~ir w_NF

+!'

qu~ est ,

spécifié par\la contraintè, et w_NF

-!'

qui s'obtient de, l'appli-cation de l'équation de la thermodynamique au niveau NF-!.

Oh

obtient alors 'une équation semblable â l' êq~ation 2,.12:

-',

, ·t

ft ')~,

.'

l' r:~ \ ~ )~

\ ' \ .... 1 \ " \ , -, , \ , i l , 1

(

2.14 1 où ::. -3~- 1

Y:!..s-L:.t

(

En utilisant les ~onditions données par les équations 2.1 et 2.2 a ôle et à l'équateur, et en exprimant la dépendance nord-sud 2.14 sous forme de différences finies centrées

du deuxi~me dre en Y, on obtient la forme matricielle:

2.15

où

$N~

et

$NF-~

Sont de la forme donnée par

l'~quation

2.5 et

lb

est' alissi "un vecteur horizontal de dirnel)sion (JF ~ 2):

...

1 •

(

.

V

-33-2.16 ,

~ et Yb s'obtiennent des équations 2.7 et 2.8,Où les variables

~b' _{bb' cb ' db ,et hb sont obtenues de la relation 2.3B où les}

indices n sont remplacés par b.

L'appendice 4 explique la méthode de Lindzen et Kuo (1969) appliquée sur une grille à deux dimensions.

J

...,

1

> • ,

f'

\

1

"

=

III LA VERIFICATION DU MODELE

On a v~ au chapitre l que l'on peut définir des modes _,

\

propres pour le système d'équations primitives si l'atmosphère

U8t cn rotation solide, que la stabilité statique est constante

,

et qu'il ,n!y a pas de dissipation. Les dépendances verticale et horizontale de la perturbation deviennent alors séparables, et la structure verticale est connue de façon analytique si on définit les conditions aux frontières supérieure et inférieure .

.

,

Il est facile de montrer par l'équation 1.11 que $' et

w'

admettent alors les mêmes modes propres. Si on utilise une contrainte orographique ~ dont la structure nord-sud est celle

s

d'un mode propre du système, alors on peut résoudre le problème de façon analy'tique et se servir de cette solution pour vérifier le modèle numérique.

~

On choi~i t, pour ,une première expérienc'e 1 un courant zonal

TI

~/4 (donc À -0.1) et le mode propre de Rossby m = l et

n - m = 2. Sur l~ figure 3A , on constate que la vitesse du

~ .\ courant zonal choisi est supérieure â la vitesse critique de propagation pour cette perturb~tion; l'onde forcée aura alors une structure verticale exponentielle. A partir du tableau de valeurs calculées par L.H. qui a servi à tracer la figure 2C, on trouve

(~E)-!

= 0.523, donc E = 3.66. Pour cette expé-rience, on a posé

cr

= 5.83 lO-6m4s2kg-2 L'équation

1.~5

,nous donne K. = 0.398, donc la pénétration

verti-l 5

cale 'est de 15.8 .10 Pa. K. est la partie imaginaire de K. ₁

f

La structure nord-sud du mode propre antisymétrique choisi

,

(m = li n - rn = 2; À = -O. '1) a été obtenue graphiquement à

partir des résultats de L.H. 1 ~t est reproduite â la figure ~.

l '

"

5. 4. ~ 1 Ul lU

..

" p.. _3. III 1

.

0

-.-1 III 3 Cl) 'Cl r.1 _2.

l'

Cl ::J _{1 .}

(

, f-i H H p,

~

1.

o.

60° 50° 40° ,30° 200 Ibo ,0° LATITUDE (deg.)

Figure 5: Coup~ nord-sud de ~'amplitude

_..

de la contrai\nte w : rrode de Rossby

s ,

(À == -O.li m = 1; n-m = 2).