Conception des pseudo-articulations à col paraboique

Conception des pseudo-articulations à col

parabolique

J.F. DEBONGNIE

Université de Liège, A&M, Méthodes de Fabrication Chemin des Chevreuils 1, 4000 Liège, Belgique 1. Introduction

Le laboratoire de Méthodes de Fabrication de l’Université de Liège s’était déjà consacré dans le passé à l’étude de pseudo-articulations à col circulaire [3,4], dans le but de les utiliser dans certains micromécanismes médicaux dans lesquels il fallait éviter le frottement et les particules d’usure, au prix, naturellement, d’une amplitude de mouvement limitée. Ces travaux ont été étendus récemment par l’auteur au cas des cols elliptiques [1]. Nous présentons ici nos résultats dans le cas de cols paraboliques.

Notre démarche est la suivante :

- Tout d’abord, on calcule la solution exacte au sens de la Résistance des Matériaux – elle est souvent compliquée. - On dégage la forme asymptotique de cette solution pour de très faibles épaisseurs de col.

- La solution générale est alors présentée comme une correction de la solution asymptotique par un facteur dépendant de l’épaisseur relative.

- Par voie d’une analyse numérique, on dégage une expression simplifiée suffisamment précise du facteur correctif.

Cette démarche originale fournit des solutions très bien approchées et beaucoup plus simples que celles de la littérature [2,5,6], ce qui constitue un argument appréciable au niveau de la conception.

2. Géométrie

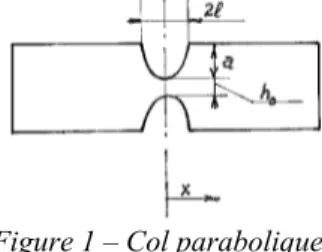
Nous nous proposons dans ce qui suit d’étudier le comportement élastique de cols paraboliques tels que celui de la figure 1.

Figure 1 – Col parabolique.

Le col a une épaisseur minimale h0. Pour le réaliser, on a découpé d’un bloc rectangulaire, symétriquement de chaque côté, des entaille paraboliques de profondeur a et de longueur 2_. Le rapport h /₀ a est supposé relativement petit et, en tout cas, inférieur à 0,5, ce qui suffit à tous les besoins pratiques. Nous utiliserons la coordonnée x prise suivant l’axe moyen de l’articulation, l’origine étant le point le plus étroit du col. L’épaisseur du col perpendiculairement au dessin est notée b. Comme le montre la figure 1, l’épaisseur du col dans le plan du dessin a la forme générale ) 1 ( 2 _{2 0} 2 2 0   h a x h h  (1) en faisant usage de la variable réduite

 x h a 0 2   (2) 3. Flexion pure dans le plan du dessin

Figure 2 – Flexion pure 3.1 – Forme générale

Sous l’effet d’un moment uniforme Mf , la rotation d’extrémité f () est donnée par

1 3 12 ) ( I Eb M h dx Eb Mf f f 



      _où



    3 1 12 h dx I

(3) Le calcul complet de cette intégrale, assez long, peut être consulté dans la référence [7]. Le résultat est

1 2 / 5 0 1 2 2 h I a a I   (4) avec





































a

h

a

h

a

h

a

h

h

a

2

1

2

1

4

1

1

2

1

2

12

2

arctg

9

0 0 0 0 0 1

I

(5) expression fort lourde et peu pratique.

3.2 – Valeur asymptotique

Pour les faibles valeurs du rapport h /0 a, on obtient à partir de (6) le résultat suivant :

2 9 , 1 1   I _as I ce qui donne Eb M h a a f as f _5/2 0 2 2 2 9 ) (     (6) 3.3 – Coefficient correcteur

Pour les valeurs usuelles de h /₀ a, c’est-à-dire allant jusqu’à 0,5, proposons-nous d’écrire la solution sous la forme ) / ( 1 . ) ( ) ( 0 1 h a K as f f      ₍₇₎

ce qui revient à dire

1 1 ₂ 9 I   K (8) Un ajustement numérique donne l’expression suivante de

1 K : 2 0 , 1 1 1 0,0264          a h K K _app (9)

1

avec une erreur inférieure à 0,018% pour h₀ /a0,5. Le calcul peut donc se faire simplement par la formule

app f f K Eb M h a a 5/2 _1, 0 1 . 2 2 2 9 ) (     (10)

On notera que le déplacement de flexion en x est donné par

 

_{  f(}) f v   ₍₁₁₎ 4. Raideur en torsion Figure 3 – Torsion

Pour un moment de torsion M appliqué à l’extrémité dut

col, la rotation de torsion ()se calcule par

1 3 ₄ 1 3 ) ( I Gb M dx Gbh Mt _ t 



    

où l’on retrouve la même intégrale qu’en flexion pure, ce qui permet d’écrire directement

1 2 / 5 0 1 . 2 2 8 9 ) ( K Gb M h a a t      (12)

avec le même K que ci-dessus. 1 5. Raideur en extension

Figure 4 – Extension 5.1 – Expression générale

Sous l’effet d’un effort normal d’extrémité N, le déplacement axial d’extrémité u()vaut



     ) 2 ( I Eb N h dx Eb N u (13)

On calcule sans grande difficulté [7] la valeur de I2 :

0 0

2 2_2a 2_ha arctg 2_ha

I   (14)

5.2 – Valeur asymptotique

Pour les très petites valeurs de h /₀ a, on déduit de (13) et (14) 0 2 2 ) ( h a a Eb N u  _as    (15) 5.3 – Coefficient correcteur Pour le cas général, on peut écrire

2 1 . ) ( ) ( K u u _{   as (16)} avec a h h a K 0 0 2 1 0,56 2 arctg 2     (17)

la valeur approchée étant exacte à 1,61% près pour 5 , 0 / 0 a h .

6. Raideur en flexion pure dans le plan transverse La rotation due à un moment uniforme M fT dans le plan perpendiculaire à celui du dessin est donnée par

2 3 3 12 12 ) ( I Eb M h dx Eb M fT fT



       (18)

Il s’agit de la même intégrale qu’en extension, ce qui nous permet d’écrire directement

2 as 0 3 1 . ) ( ) ( et 2 2 12 ) ( K h a a Eb M_fT as           (19) 7. Raideur en translation latérale pure dans le plan On peut obtenir la translation d’une extrémité sans rotation parasite en appliquant une charge latérale Q au droit du col, ce qui se réalise par l’artifice représenté en figure 5. Le moment de flexion a alors pour expression Mf Qx.

La déformée inclut un terme de flexion et un terme de cisaillement : vvf vc.

Figure 5 – Translation latérale pure 7.1 – Contribution de la flexion 7.1.1 – Expression exacte On a 3 f 12 dx d où ) ( Ebh Qx dx dx d x dx vf 



f 



f           

Tous calculs faits (voir [7]), cela donne

3 I Eb Q v_f  (20) avec

2









































_













_





























₂ 0 0 0 0 2 / 3 0 3 3

2

1

2

1

2

h

a

2

arctg

2

.

2

3

a

h

a

h

a

h

h

a

a

I



(21) 7.1.2 – Valeur asymptotique

Pour les très faibles valeurs de h /₀ a, on obtient

2 / 3 0 3 2 2 2 3 . ) ( _             h a a Eb Q vf  as   (22) 7.1.3 – Coefficient correcteur

Dans le cas général, nous écrirons encore

44 , 1 0 3 3 455 , 0 1 avec 1 . ) ( ) ( _         a h K K v v_{f  f  as} (23) l’expression approchée de K étant correcte à moins de3 0,25% pour h₀/a0,5.

7.2 – Contribution du cisaillement Elle s’évalue par





          2 5 6 5 6 6 5 ) ( I Gb Q h dx Gb Q dx Gbh Q v_c (24) On retrouve encore la même intégrale qu’en extension, ce qui permet d’écrire directement

2 0 1 2 5 6 ) ( K h a a Gb Q vc     (25)

Cette contribution est en général négligeable devant celle de flexion.

8. Raideur en translation latérale pure hors plan Il s’agit de la même sollicitation que ci-dessus, mais dans la direction transversale au plan du dessin. La charge appliquée sera ici notée R et le déplacement w se décomposera encore en un terme de flexion wf et un terme de cisaillement w . Les calculs se font comme ci-c

dessus. 8.1 – Contribution de la flexion 8.1.1 – Expression exacte Le calcul donne [7]





















0 0 3 3

₂

arctg

2

1

12

)

(

h

a

a

h

a

Eb

R

w

f





(26) 8.1.2 – Valeur asymptotique

Pour les très faibles valeurs de h /₀ a, on obtient

a Eb R w_{f  as}   3 2 12 ) (  (27) 8.1.3 – Coefficient correcteur

Dans le cas général on peut écrire 1 ) ( ) ( 4 K w w_{f   f  as} (28) avec 0 0 4 2 arctg 2 1 1 h a a h K   (29)

Ce coefficient peut être approché par l’expression suivante

a h a h K 0 0 4 470 , 0 111 , 1 1 1   

(30) à vrai dire pas tellement plus simple et conduisant à une erreur inférieure à 0,7% pour h0/a0,5.

8.2 – Contribution du cisaillement

Le déplacement dû à la déformation de cisaillement vaut



      2 5 6 5 6 ) ( I Gb R h dx Gb R w_{c (31)}

où l’on retrouve l’intégrale I que nous avons rencontrée2 en extension. On a donc immédiatement

2 0 1 2 2 5 6 ) ( K h a a Gb R w_c     (32) Il faut noter que cette contribution n’est en général pas négligeable devant celle de flexion.

9. Conclusions

Les résultats qui précèdent permettent de traiter toute sollicitation du col. Il faut en effet remarquer que tout champ de flexion peut être décomposé en une flexion simple (moment constant) et une translation pure (moment linéairement variable).

Notre approche fournit les solutions exactes, en général compliquées et les solutions asymptotiques, qui peuvent être considérées comme de premières approximations. L’idée de relier, comme nous l’avons fait, les solutions exactes aux solutions asymptotiques par un coefficient correcteur et de donner de ce dernier une approximation simple est la principale originalité de la présente communication. Cette approche permet d’obtenir une évaluation rapide des raideurs, ce qui est particulièrement commode au niveau de la conception où il faut nécessairement procéder par essais et corrections.

Références

[1] J.F. Debongnie – « Comportement des articulations flexibles à col elliptique » -VII èmes journées d’études techniques 2012, Marrakech, mai 2012.

http://hdl.handle.net/2268/121676

[2] N. Lebontiu – Compliant mechanisms – design of flexure hinges, CRC press, Boca raton Florida, 2002. [3] P. Merken – “La fonction guidage en micromécanique” - Thèse de D.E.A., Université de Liège, 2006.

http://hdl.handle.net/2268/33713

[4] P. Merken et J.F. Debongnie – « Le col circulaire comme articulation flexible » - 6ème _{congrès national de} mécanique théorique et appliquée, Gent, mai 2003.

http://hdl.handle.net/2268/16101

[5] J.M. Paros et L. Weisbord – « How to design flexure hinges » - Machine Design 25 (1965), p. 151-156.

[6] S. Henein – Conception des guidages flexibles – Presses polytechniques et universitaires romandes, collection META, Lausanne, 2001.

[7] J.F. Debongnie – « Pseudo-articulations à col parabolique » - Rapport LMF/D52, Université de Liège, 2012.

http://hdl.handle.net/2268/126088