LES INDICES BIOLOGIQUES EN HALIEUTIQUE

(1)

MODULE

TITRE

Préparés par :

D

r

_{. KHERRAZ ALI}

Année Universitaire 2016/2017 Laboratoire Réseau de Surveillance Environnementale

Université Des Sciences et de la Technologie d’Oran Mohamed Boudiaf Faculté des Sciences de la Nature et de la Vie

Département du Vivant et de l’Environnement

Travaux Dirigés

3

ème

_{année LICENCE}

PARCOURS : HALIEUTIQUE

HALIEUTIQUE II

(2)

Ce document porte sur « Les indices biologiques en halieutique ». Ce TD est destiné aux étudiants de 3ème_{année Licence «Halieutique » au niveau du Département des Sciences de la}

Mer et de l’Aquaculture à l’Université de Mostaganem.

Ces Travaux dirigés sont inspirés du programme proposé dans le canevas de la Licence Halieutique pour la matière Halieutique II.

(3)

LES PRINCIPAUX INDICES BIOLOGIQUES EN HALIEUTIQUE I. État des connaissances :

La croissance est définie comme une modification de biomasse (positive ou négative, exprimée en taille ou en masse) qu'il s'agisse d'un organisme dans son intégralité, de l'un de ses constituants ou encore de sa population (in WEATHERLEY et GILL, 1987).

La détermination du sexe et les changements des stades de maturité au cours d’une année est d’une très grande importance pour une connaissance précise de la biologie générale d’un stock exploité. Les résultats qui en résultent sont à l’origine de la détermination de l’âge et de la taille auxquels les poissons atteignent leur maturité sexuelle, la période et le lieu de ponte. Des indices de condition dérivent de l'analyse de la croissance relative, ou croissance allométrique, existant entre les différentes composantes d'un organisme, par exemple la taille corporelle ou masse d'un organe par rapport à la masse corporelle totale. Si l'on considère que la qualité de l'habitat est une fonction positive de la croissance et/ou de la condition, les performances de croissance d'une espèce dans son milieu, au regard de performances connues, témoignent donc de la qualité de l'habitat.

D'autre part, les multiples sources de variations de la croissance en font un indice potentiellement sensible, rendant compte des modifications à moyen terme de l'habitat.

Dans ces travaux dirigés on abordera les principaux paramètres essentiels à toute étude halieutique : reproduction, âge et croissance, afin de contribuer à l’amélioration et à l’évaluation d’une pêcherie.

II. Les indices biologiques

1. Les Indices de la reproduction

a. Le Rapport Gonado-Somatique (R.G.S)

BOUGIS (1952) a été le premier à avoir utilisé le rapport gonado-somatique. Il le définissait comme étant le rapport du poids de la gonade p sur celui du poids total de l’animal P exprimé en pourcentage.

p : Masse des gonades (g). P : Masse totale de l’animal (g).

L’évolution pondérale des gonades tout au long de l’année nous permet de cerner l’époque de R.G.S = (p/ P) *100

(4)

Les variations du (R.G.S) sont fonction de l’inactivité, de l’élaboration et de l’émission des produits sexuels. Elles permettent de mettre en évidence les phases de repos, de pré-maturation, de maturation et de ponte d’une espèce.

MOUHOUB (1986); HEMIDA et DJABALI (1987) proposent une relation dérivée de celle élaborée par BOUGIS (1952).

Ces premiers estiment que le (R.G.S) choisi est le paramètre caractérisant le mieux les poids de fortes maturations.

Il est calculé suivant l’expression:

Avec :

Wt : Poids total de l’animal(g). Wg : Poids des gonades (g).

C’est cette même relation qu’avait utilisé CHABANE en 1988, afin de déterminer la période de ponte de la bogue de la baie de Bou-Ismail.

En 1987, CHERABI ayant travaillé sur le pageot commun (Pagellus erythrinus) de la baie d’Alger trouve que la relation définissant le (R.G.S) comme étant égal à:

Avec

Wg : Masse des gonades (g). We: Masse éviscérée (g).

Est la mieux appropriée malgré certains inconvénients soulignés par KARTAS et QUIGNARD, (1984).

D’autres indices peuvent être également utilisés afin de caractériser les phases évolutives des glandes sexuelles, nous citerons:

L’Ovary index (Oi) ou l’indice ovarien utilisé par les anglo-saxons. Cet indice a la particularité d’utiliser la longueur (L) au lieu du poids (W). On définit (Oi) par la formule suivante:

W: Poids des gonades (g). L : Taille de l’espèce (cm).

Certains auteurs suggèrent également l’utilisation de la longueur en supposant la croissance R.G.S = (Wg / Wt – Wg) *100

R.G.S = (Wg/We) * 100

(5)

BOUCHEREAU (1981) définit l’indice gonado-somatique comme étant égal à 100 fois le poids des gonades sur le poids théorique de l’animal.

Les valeurs de l’I.G.S sont évaluées à partir de la relation: Wth=a*Lb

Wth: Poids théorique.

a et b : Constantes.

BARON (1983) utilise l’indice d’évolution gonadique (I.E.V) qui permet de supprimer une source d’erreurs en éliminant le poids des viscères. Il est donné par la formule suivante: Pe=α*Ltβ

Pe : Poids éviscéré. Lt : Longueur totale. α et β : Constantes.

L’utilisation du poids éviscéré permet de supprimer une source d’erreur en supprimant l’état de réplétion du tube digestif et de celle du poids des gonades (HEMIDA, 1987).

b. Le Rapport Hépato-Somatique

L’évolution du rapport hépato-somatique (R.H.S) renseigne sur l’éventuelle participation du foie dans la maturation des gonades.

Il se définit comme étant le rapport entre le poids du foie et celui du corps et s’écrit:

Wh: Poids du foie (g).

Wt: Poids total de l’animal (g).

Les variations du R.H.S permettent de décrire le cycle des réserves hépatiques, et de préciser l’apport du foie dans la maturation des produits génitaux.

c. L'indice de condition

C’est un indice biométrique couramment utilisé en multiculture pour rendre compte le degré de remplissage des coquilles des animaux.

Parmi les nombreuses formules proposées, nous avons choisi l’indice AFNOR. Exprimé par l’équation :

I.G.S= (Wg / Wth) * l00

I.E.V= Wg / Pe

R.H.S = (Wh/Wt) * 100

(6)

IG= (POIDS HUMIDE DE LA GONADE(g) / POIDS TOTAL(g)) * 100

IG= (POIDS HUMIDE DE LA GONADE(g) / DIAMETRE AU CUBE (cm³)) *100

IG= (POIDS SEC DE LA GONADE(g) / DIAMETRE AU CUBE (cm³))* 100

PTSEP = Poids des Tissus mous Sans l’Eau Palléale. d. Les indices physiologiques

Pour déterminer les périodes de reproduction et les divers étapes du cycle reproducteur de l'espèce, ainsi que la relation entre l'alimentation et le développement gonadique.

Deux indices physiologiques sont réalisés à savoir l'indice gonadique (IG) et l'indice de réplétion (IR).

 Indice Gonadique

L'indice gonadique (IG) est une relation entre un descripteur quantitatif de l'appareil reproducteur et un descripteur quantitatif des organes somatiques. Il a été utilisé pour la première fois par MOOKE, 1934 sur les Echinoides, c’est un rapport, généralement exprimé en pourcentage, entre le volume des gonades et le volume du test, tous deux exprimés en ml.

Ainsi, FENAUX ,1968 a utilisé l'indice calculé par la formule suivante:

REGIS, 1978 a utilisé pour sa part un autre indice qui est:

Les indices gonadiques proposés par SAN MARTIN, 1990: Le premier:

Le second est le:

Le troisième est :

IG= (VOLUME GONADE /VOLUME DU TEST) * 100

IG= (VOLUME GONADE /POIDS HUMIDE DE CORPS (mg)) * 100

(7)

 Indice de Réplétion

L'indice de réplétion représente l'intensité de collecte de la nourriture macroscopique (REGIS, 1978). Il est calculé par le rapport entre le poids sec du contenu digestif en mg et le cube du diamètre horizontal du test, en cm3_{qui est représenté par l'expression suivante:}

e. Facteur de Condition (F)

 Le facteur de condition (F) de Fulton (1911) est défini comme suit : F=W/L3

avec W le poids en gramme et L la longueur en cm ; cette relation implique que plus le poisson est gros plus il est dans de meilleures conditions environnementales. Les limites de la signification biologique de F ont été posées plus tard et LE CREN (1951) propose le calcul d’un facteur de condition relative.

 Le facteur de condition relative (Kn) de Le Cren (1951) a été utilisé par Swingle et Shell (1971) pour éditer des abaques de calculs des facteurs de conditions de quelques espèces de poissons d’eau douce. La formule de Kn proposée par Le Cren est la suivante : Kn =W/^W avec W= poids individuel du poisson et ^W le poids calculé à partir de la formule W=aLb_.

Pour vérifier le rôle éventuel des réserves musculaires dans la gamétogenèse, le coefficient de condition (FC) a été déterminé.

Avec :

LT = Longueur Totale du poisson en mm. Me = Masse du poisson éviscéré en grammes.

f. Taille de Première Maturation Sexuelle (PMS)

La taille à la première maturité sexuelle est définie de plusieurs manières, selon les auteurs. Dans le cadre de cette étude, elle sera la longueur à laquelle 50 % des individus sont matures. (BOUGIS, 1952).C’est-à-dire au stade III ou au-delà.

Une fonction logistique reliant les proportions des individus matures et la longueur totale du poisson (GHORBEL et al.2002) a été utilisée. Cette fonction permet en effet de suivre le degré de maturité sexuelle selon la taille et d’estimer avec précision les longueurs (L25), (L50) IR= [POIDS SEC DU CONTENU DIGESTIF (mg)) / (DIAMETRE HORIZONTAL DU TEST) ³ (cm) ³] *100

(8)

et (L75) souvent utilisées par la majorité des modèles d’évaluation des stocks. Cette fonction

de forme sigmoïde s’écrit :

Avec :

P : Pourcentage des individus mature. a et b constants.

LT: La longueur.

2. Les Indices de la Croissance a. Sex- ratio:

C’est un indice représentant l'abondance d'un sexe par rapport à l'autre dans une population d’une espèce donnée, il est l’un des paramètres qui contribuent au maintien dans une certaine limite, de la capacité reproductrice de l’espèce ; il s’exprime sous différentes formes :

 Pourcentage de femelle ou taux de féminité  Pourcentage de mâle ou taux de masculinité  Rapport du nombre de mâle au nombre de femelle.  Nombre de mâle pour 100 femelles

La valeur de la sex-ratio est donnée par l’expression :

Ou

L’intervalle de confiance au risque de 5% est calculé à partir de la formule suivante (SCHWARTZ, 1983).

P : Pourcentage des femelles dans la population étudiée q : Pourcentage des mâles

n : Nombre total des mâles et des femelles.

P=1/ (1+e

-(b+a*L T)

)

TAUX DE FEMINITE = EFFECTIF DES FEMELLES / (EFFECTIF DES FEMELLES +EFFECTIF DES MALES) * 100

TAUX DE MASCULINITES =EFFECTIF DES MALE/ (EFFECTIF DES FEMELLES +EFFECTIF DES MALES) * 100

(9)

 Sex-ratio en fonction de la taille

Cette étude nous permet d’étudier la distribution des sexes par rapport aux différentes classes de tailles.

 Sex-ratio en fonction des saisons (mois)

La détermination du Sex-ratio en fonction des saisons permet de voir la dynamique de la proportion des deux sexes durant les mois de prélèvements.

b. Relations biométriques

L’étude des relations allométriques se réfère aux relations entre variables aléatoires telles que le poids, la longueur, le diamètre ou la hauteur.

Les valeurs obtenues par lecture directe sur une balance ou avec un pied à coulisse ; elles sont par conséquent sujettes à erreur. Les deux variables sont aléatoires.

Dans ce cas, le modèle de régression qu’on doit utiliser est celui de l’axe principal réduit. Nous calculons cependant la droite de régression par la méthode qui est la plus fréquemment utilisée, celle des moindres carrés, ainsi nous pouvons comparer nos résultats avec ceux trouvés par d’autres auteurs.

Chez les poissons dont l’âge ne peut pas être lu on détermine à partir des ossements (écaille, otolithe, rayon osseux) et surtout dans le cas des espèces de poissons tropicaux dont la croissance est dite régulière durant toute l’année, l’analyse des fréquences des classes de longueurs permettent de déterminer l’âge des individus.

L’âge lu sur les fréquences modales des classes de longueurs est souvent adéquat pour les premières classes d’âges (1 à 4 ans) mais devient difficile à détecter et donc subjective pour les individus plus âgés. Les âges, après détection sur la distribution multimodale, permettent de construire la fonction VBF et faire des calculs d’autres paramètres de la dynamique des populations au même titre que dans la scalimétrie, otolithémétrie, etc.

L’étude de la croissance et de la mortalité peut aider le scientifique des pêches à prendre des décisions adéquates pour une production optimale soutenue qui permet de maintenir l’équilibre de la dynamique du stock de poissons de la pêcherie. Deux types de croissance préoccupent l’halieute:

(10)

1- La croissance pondérale ou corporelle (elle est liée à l’individu ou gain de poids individuel) qui relève du souci de récolter ou de capturer des poissons de taille pêchable ou marchande.

2- La croissance en nombre qui est un phénomène lié à l’augmentation de population ou du stock.

 La croissance corporelle

La relation poids-longueur

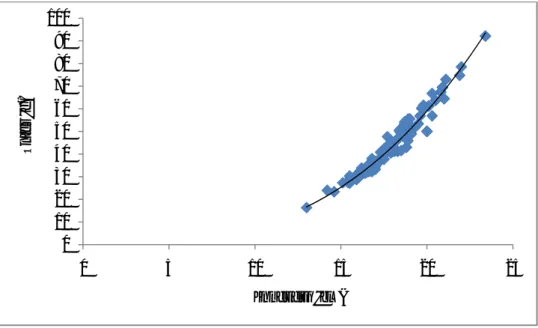
La croissance en longueur ou en poids d’un individu est évaluée entre deux périodes d’échantillonnage. Très souvent les biologistes établissent une relation entre le poids et la longueur corporelle. En effet il existe une corrélation linéaire entre le poids et la longueur comme l’indique la figure suivante :

Figure 1 : Relation taille-poids chez les Poissons.

La relation est une fonction de puissance : W=a *Lbavec W = le poids en g

L= Longueur en cm a et b sont des constantes.

Ln W = ln a + b ln L : Ceci est une équation de droite avec : 0 10 20 30 40 50 60 70 80 90 100 0 5 10 15 20 25 Po id s ( g) Longueur (cm)

(11)

b: la pente de la droite de régression ln a: la valeur de l’ordonné à l’origine.

Il existe une valeur de référence de b=3 qui indique que le poisson a une croissance isométrique ou symétrique ; c’est à dire que le corps du poisson est bien conformé, symétrique. Si b>3 ou b<3 on dit que la croissance est allométrique ou asymétrique ; le poisson est respectivement plus lourd ou moins lourd que sa taille. Lors des pontes par exemple les poissons ont un b>3. Autrement dit la valeur de b est affectée par la nourriture disponible, le stade de reproduction. Si des données poids-longueur existent ont tenté de comparer les individus de poissons; dans ce cas on calcul des facteurs de conditions qui décrivent l’état de santé ou de bien être des poissons. Le facteur de condition le plus utilisé est celui de Fulton (1911).

 Relation entre le diamètre (D) et la hauteur (H) du test

Afin de caractérisé d’un point de vue biométrique de la population des Oursins nous avons établi la relation allométriques entre le diamètre, hauteur du test (mm) et poids frais (g). Nous avons corrélé ces variables au moyen du modèle puissance :

D : Diamètre du test (mm). H : Hauteur du test (mm). a et b : Paramètres des équations.

 Relation entre le diamètre de test (mm) et le poids humide (PH)

L’équation qui lie le diamètre et la masse est : PH: Poids frais (g).

D: Diamètre (mm).

a et b : Paramètres de l’équation.

 Relation entre le poids humide et la hauteur

L’équation utilisée est : PH : Poids frais (g).

H= a Db

PH= aDb

(12)

H : Hauteur du test (mm). a et b : Paramètres des équations.

Pour chaque équation trouvée la valeur observée à la ponte est comparée à la valeur théorique qui est égale à 1 lorsqu’il s’agit d’une allométrie simple (variables de même dimensions tel que la hauteur, le diamètre), et elle est égale à 3 lorsqu’il s’agit d’une allométrie cubique, les variables sont de dimensions différentes poids frais, hauteur, etc.

Si la pente a ne diffère pas significativement de 1 ou 3, la croissance est isométrique, c'est-à-dire que les deux variables croissent proportionnellement au même rythme. Si la pente est significativement > 1 ou 3 la croissance est majorant c'est-à-dire que la proportion du corps considéré croît proportionnellement plus vite que la variable de référence.

Si elle est significativement < 1 ou 3 la croissance de la proportion du corps considéré est minorant c'est-à-dire qu’elle croît proportionnellement moins vite que celle de l’organe de référence.

Les allométries observées sont comparées entre elles, par le biais d’un test d’indépendance entre deux variables x et y, à partir d’un échantillon de n. Ce test est basé sur la valeur de la pente en coordonnées réduites :

Où mx et my désignent les moyennes observées des x et y.

Le risque α correspondant à r peut être obtenu, soit par la table de corrélation pour d.d.l = n-2, soit, lorsque celle-ci est insuffisante, en formant :

Et en cherchant le risque correspondant dans la table de t pour d.d.l = n-2.Si α>5%, la Liaison n, n’est pas significative (à 5 %). Si α ≤ 5%, la liaison est significative, est α mesure son degré de signification.

c. Croissance linéaire

L’étude de la croissance est une entreprise délicate en halieutique. Pour parvenir à ses fins, chaque biologiste des pêches essaye toujours de trouver la méthode qui s’adapte le mieux au

r = ∑ (x-mx) (y-ym) /√∑ (x-mx)2 _{∑ (y-ym)}2

∝=

(13)

données taille-âge, que pour le choix du modèle décrivant la relation entre ces deux variables. De plus, même avec l’aide des techniques les plus récentes, un facteur reste toujours difficile à appréhender, il s’agit du facteur temps, c’est à dire la détermination de l’âge exact des organismes qui est souvent peu sûre, assez approximative et même voire impossible dans certains cas.

d. Les données taille-âge

Trois approches sont généralement utilisées pour obtenir les données taille-âge :

Détermination directe de l’âge : Le principe général est la lecture des marques qui se

forment sur les structures dures (écailles, otolithes, épines et autres pièces squelettiques). Ces marques se répartissent en deux catégorie: celles à période longue, de l’ordre de plusieurs mois, de la saison ou de l’année, et celles à période courte, de l’ordre de la journée. Pour les invertébrés celles-ci ne peuvent être obtenu car il n’existe pas de structures dures.

Marquages : Ils peuvent donner de bons résultats lorsque l’espèce et son environnement s’y

prêtent. Toutefois, il existe toujours une incertitude qui subsiste sur la croissance et qui est liée à l’effet du stress provoqué par la pose de la marque.

Analyse des structures des tailles : Elle est toujours délicate, même avec l’aide des

techniques statistiques les plus élaborées, l’analyse visant à la séparation des différentes composantes d’une distribution de taille est souvent faite avec une interprétation plus ou moins subjective. Pour cette raison, l’emploi des méthodes d’analyse des tailles a été souvent discuté. Cependant, ces méthodes restent, malgré tout, les plus employées, d’une part parce qu’elles constituent souvent le seul recours, d’autre part parce qu’elles sont les plus faciles à mettre en œuvre.

Les études de croissance que nous présentons dans le cadre du présent travail utilisent uniquement comme matériel de base, des données de mesures de fréquences de taille.

e. Principe de base de l’équation de croissance de VON BERTALANFFY (1938) Il existe plusieurs modèles mathématiques pour exprimer la croissance. Une revue détaillée en a été faite par BEVERTON et HOLT (1957), URSIN (1967), RICKER (1980), GULLAND (1983), PAULY (1984), SPARRE et VENEMA (1996) et PAULY et MOREAU (1997). Le modèle le plus utilisé reste celui de VON BERTALANFFY (1938). Partant des observations physiologiques, VON BERTALANFFY (1951), dans PAULY et MOREAU (1997) montre que la croissance pondérale des poissons et des Crustacés est le résultat de deux processus

(14)

- l’anabolisme ou processus de synthèse, dont le taux, proportionnel aux surfaces absorbantes, tend à augmenter le poids.

- le catabolisme ou processus de dégradation, dont le taux, proportionnel au poids, tend à diminuer ce dernier. Ces deux processus interviennent continuellement et simultanément pendant toute l’existence de l’animal; la différence entre eux à un instant quelconque définit le taux de variation de poids par l’équation différentielle :

Où S = surface absorbante W = poids

dW = variation de poids pendant le temps dt H = coefficient d’anabolisme

D = coefficient de catabolisme.

La croissance étant supposée isométrique, S est proportionnel au carré de la longueur et W à son cube. Ainsi, de l’équation ci-dessus, on peut déduire le modèle décrivant la variation du taux instantané de croissance en longueur en fonction de la taille tel que :

L’intégration de cette équation différentielle conduit à la forme qu’on rencontre le plus couramment en halieutique.

Croissance linéaire :

Bien que VON BERTALANFFY ait justifié son modèle par des considérations métaboliques, il est préférable de le voir comme un modèle descriptif, et être prudent de ne pas attribuer trop de signification biologique aux paramètres L ∞, K et to qui ne font que résumer l’ensemble

des données disponibles. En voici les définitions actuelles:

L∞ =est la longueur asymptotique. Théoriquement, c’est la taille moyenne qu’atteindrait un

poisson qui pourrait vivre et grandir indéfiniment ;

K = est le coefficient de croissance (ou paramètre de courbure). Il caractérise la rapidité avec

laquelle le poisson croît vers la longueur asymptotique;

dW / dt = HS - DW

DI / dt = H - DI

(15)

to= est l’âge théorique pour lequel l’espèce a une longueur nulle. Il désigne le point de départ

de la courbe de croissance sur l’axe des temps si le Poisson avait grossi selon le modèle de croissance de VON BERTALANFFY (1938).

Ces paramètres sont donc des valeurs mathématiques et n’ont pas de significations biologiques précises dans le sens strict du terme. Les courbes de croissance ne sont valables en toute rigueur que dans l’intervalle d’âge ou de taille correspondant aux données observées.

f. Méthode d’ELEFFAN 1

 Les principes de fonctionnement d’ELEFAN1

On constitue d’abord une base de données, c’est –à-dire un ensemble de distributions de fréquences de tailles ; les dates de prélèvements étant également précisées. ELEFAN1 peut être mis en œuvre avec un seul mais aussi avec plusieurs échantillons séparés d’intervalles éventuellement irréguliers et répartis sur une année ou davantage.

Le premier travail d’ELEFAN1 est la préparation des échantillons pour l’analyse ultérieure, c’est-à-dire l’identification des maxima et des minima des distributions de fréquences. Cette opération est appelée dans la suite « restructuration des échantillons ».

Ces derniers sont tout simplement « filtrés ». En effet, chaque fréquence observée est comparée à la moyenne mobile centrée sur la classe de longueur considérée et calculée sur cinq classes de tailles. La différence est une nouvelle fréquence positive ou négative selon le cas. Les fréquences positives permettent de visualiser les maxima, sans hypothèse sur la normalité des distributions ainsi mises en évidence.

g. Expression de l’âge

Il existe trois façons d’exprimer l’âge considéré de manière individuelle, ou l’âge moyen d’une cohorte. Ce sont :

L’âge absolu : il est défini par rapport à la date exacte de naissance de l’espèce ou à la date

moyenne de naissance de la cohorte ;

L’âge relatif : il est fixé en référence à un événement remarquable dans la vie ou de la

cohorte. Le plus souvent on se réfère au recrutement, et l’âge est alors compté à partir de la date ou (la date moyenne) de recrutement, auquel est associée une taille (moyenne) de recrutement ;

(16)

conventionnel est alors égal au nombre de 1er janvier que l’espèce a connu dans sa vie. Quelle que soit l’expression de l’âge utilisé, l’équation du modèle de VON BERTALANFFY (1938) reste naturellement inchangée. En outre, la valeur des paramètres K et L∞, qui déterminent la vitesse de croissance et la taille asymptotique sont également indépendantes de la manière dont l’âge est compté. En revanche, le paramètre de to, qui fixe l’âge théorique de

longueur nulle diffère selon cette expression de l’âge. A ce propos, SPARRE (1987) conclut que "mathématiquement il n’y a aucune différence entre un modèle de croissance basé sur l’âge absolue et celui basé sur la taille associée à un âge conventionnel (ou arbitraire) d’une cohorte. Ces deux modèles ne diffèrent que dans l’interprétation du paramètre de condition initiale toet du concept d’âge.

Où : to= âge conventionnel théorique pour lequel l’espèce à une longueur nulle.

L(1) = taille moyenne du premier mode correspondant au premier groupe d'âge. K et L∞ = paramètres de croissance de l'équation de Von Bertalanffy (1938).

h. Méthode graphique de GULLAND et HOLT

La méthode graphique de GULLAND et HOLT (1959) a été introduite par l’équation qui s’écrit aussi :

Dans l’équation la longueur L(t) représente l’étendue des longueurs depuis L(t) à l’âge t jusqu’à L(t+_{t) à l’âge (t+}_{t). Il est alors naturel d’introduire dans l’équation la longueur}

moyenne

Lorsque t est petit, alors L(t) peut être une approximation raisonnable de la longueur moyenne. Cependant, il n’est pas nécessaire que ∆t soit une constante, ce qui représente un avantage important par rapport aux autres méthodes.

Si l’on retient L (t) comme variable indépendante et ∆L/∆t comme variable dépendante, l’équation devient une régression linéaire :

∆L/∆t= (K * L∞)- (K *L(t))

2 )

(

)

(

t

L

t

L









t0=1+ [ln (1-[L(1)/L∞])/K]

(17)

Les paramètres de croissance K et Lsont obtenus comme suit : K= -b et L= -a/b

i. Méthode graphique de FORD-WALFORD

La méthode introduite par FORD (1933) et WALFORD (1946) a été largement appliquée dans la mesure où le graphique permettait d’avoir une rapide estimation de L, sans calculs. De nos : jours, elle n’est plus très employé.

En partant de l’équation de croissance de VON BERTALANFFY, on déduit d’une série d’opérations algébriques que :

Où a = L*(1-b) et b = exp (-K*_t)

Étant donné que K et L, sont des constantes, a et b deviennent des constants si. t est une constante. Les paramètres de croissance K et L, sont déduits de :

K=-t 1 *Ln b et L= b a  1

j. Méthode graphique de VON BERTALANFFY

La première méthode permettant d’estimer les paramètres de croissance de VON BERTALANFFY a été suggérée par VON BERTALANFFY (1934). On peut l’utiliser pour estimer K et t0 à partir de données âge/longueur, étant entendu qu’il faut disposer d’une

estimation de L∞ comme donnée d’entrée.

On peut réécrire comme suit l’équation de croissance de VON BERTALANFFY

Avec l’âge, t, comme variable indépendante (x) et la partie gauche comme variable

dépendante (y), l’équation définit une régression linéaire où la pente b = K et l’ordonnée à l’origine a = -K*t0.

k. Méthode de BHATTACHARYA

On s présenté plusieurs modes de représentation graphique d’une distribution normale. L’un d’entre eux est la méthode de BHATTACHARYA (1967), qui a son utilité lorsqu’on veut scinder une distribution composite en distributions normales distinctes, c’est-à-dire lorsque le

L (t+_{t) = a + b*L (t)}

(18)

même échantillon Certifient plusieurs groupes d’âge (cohortes) de poissons. Cette méthode sera discutée en détail, l’ensemble des distributions normales qui composent l’échantillon global. Il est par conséquent possible de vérifier la validité du résultat de l’analyse.

 Base des procédures de calcul de la méthode de BHATTACHARYA

La méthode de BHATTACHARYA consiste à séparer des composantes normales, représentant chacune une cohorte de poissons, de la distribution globale, en partant du côté gauche de celle-ci. Une fois déterminée la première composante normale, celle-ci est retirée de la distribution totale et ainsi de suite tant qu’il est possible de séparer des composantes normales de la distribution totale. L’ensemble du processus peut être divisé en étapes successives :

Étape A : Déterminer une pente non perturbée (nette) d’une distribution normale à la partie

gauche de la distribution totale.

Étape B : Déterminer la distribution normale de la première cohorte par la transformation en

droite.

Étape C : Déterminer les effectifs des poissons par classe d longueur appartenant à cette

première cohorte, puis les soustraire de la distribution totale.

Étape D : Répéter le processus pour la distribution normale suivante à partir de la gauche,

jusqu’à ce qu’on ne trouve plus de distribution normale nette.

Étape E : Rapporter les longueurs moyennes des cohortes déterminées aux étapes A et D à la

différence d’âge entre les cohortes.

Comme on l’a déjà montré, une distribution normale est transformée en droite lorsque : 1) on remplace les nombres par leurs logarithmes

2) on calcule les différences entre les valeurs logarithmiques consécutives. Soit N le nombre, dans un échantillon de fréquence de longueur, revenant à la classe de longueur.

Où dL est la taille de l’intervalle, x est le centre de l’intervalle, x - dL/2 la limite inférieure et

x + dL/2 la limite supérieure de l’intervalle.

Si une certaine gamme de longueur de l’échantillon ne contient qu’une cohorte, cette partie de l’échantillon de fréquence devrait être conforme à une distribution normale. Dans ce cas, la relation linéaire :

[X- dL/2, x + dL/2]

(19)

Se trouverait comprise entre la différence du logarithme du nombre d’une certaine classe de longueur et le logarithme du nombre de la classe précédente, ou encore

Comme variable dépendante (y)

Et la limite supérieure de la classe de longueur la plus petite : Comme variable indépendant x.

Ne pas oublier que l’écart- type de la distribution normale et la moyenne s’obtiennent de la manière suivante :

s = dL/b et X = -a/b l. Méthode de PETERSEN (1891):

La méthode proposée par PETERSEN en 1891 consiste à suivre dans le temps les modes successifs observés dans les distributions des tailles avec les tailles moyennes des différents groupes d’âge de la population.

Grâce à cette technique, on assure que les valeurs modales successives d’une distribution de taille correspondent à différents groupes d’âge, déterminés à partir d’intervalle de temps égaux.

Cette méthode est généralement peu fiable et représente de nombreuses lacunes:

-Si les cohortes ne sont pas (ou peu) représentées, on peut les détecter car des jeunes classes d’âge peuvent être complètement oubliées car la taille des individus qui les composent est inférieur à la taille observée la plus petite d’où l’attribution d’un âge relatif (r, r +1, r+2,…) aux différentes cohortes mises en évidence.

Pour chaque distribution uni-modale. Caractérisée par son mode, on attribue une. Or. Les plus petits individus d’un âge r donné peuvent appartenir à la distribution Uni-modale précédente d’âge r-1, dont le mode peut être déplacé.

Cependant la méthode de PETERSEN rend encore de nombreux services notamment lorsque les marques naturelles sur les structures osseuses sont inexistantes ou difficile à interpréter. Elle permet aussi de distinguer, dans de nombreux cas, les différentes cohortes d’espèces de la zone intertropicale se reproduisant plusieurs fois par an.

m. Méthode de POWELL-WETHERALL :

Cette méthode connue sous l’appellation de "méthode POWELL-WETHERALL" est basée sur d’autres descripteurs statistiques que les modes. Elle est issue des travaux de POWELL

Ln N = ln N(x + dL/2,x + 3dL/2) - ln N(x - dL/2,x + dL/2)

(20)

(1979) et de WETHERALL (1986). Les démarches suivies par ces deux auteurs dans la construction de leur modèle sont décrites par PERODOU (1994). La méthode de POWELL (1979) repose sur la détermination de la moyenne et de la variance de la distribution. Celle de WETHERALL (1986) est plus exigeante, puisque doit être connue, à chaque classe de taille, la longueur moyenne des individus dont la taille est supérieure à la classe considérée.

Considérons une distribution de fréquence de longueur et supposons qu’à la longueur L100, qui

est la longueur de pleine sélectivité de l’engin de pêche, le recrutement ait déjà eu lieu. Supposons aussi que la courbe de croissance est définie par l’équation de VON BERTALANFFY(1938) avec K et L∞ comme paramètres de croissance. Alors fonction de distribution de fréquences en longueur s’écrit d’après WETHERALL(1986) :

Ce modèle suppose que la courbe de sélectivité est en lame de couteau, et qu’au-dessus de la longueur L100, le coefficient Z est constant. Partant de ces considérations, WETHERALL et

al. (1987) ont proposé une application de l’équation de BEVERTON et HOLT(1956)

permettant d’estimer L∞ et Z/K :

Où L : est la longueur moyenne des Poissons de longueur L’ et plus et L : étant la longueur à partir de laquelle tous les Poissons sont supposés pleinement exploités. Sous sa forme modifiée, l’équation de WETHERALL et al. (1987) est:

Les paramètres a et b sont estimés par régression linéaire. L∞ et K sont obtenus ainsi qu’il suit :

La variable K peut être estimée à partir de la relation empirique de PAULY et MUNRO (1984). Ces auteurs ont montré que pour les espèces dont la croissance suit l’équation de VON BERTALANFFY(1938), les paramètres de croissance L∞ et K sont liés par la relation :

L - L’= a+b*L’

L∞ = -a / b et Z / K = -(1+b) / b

Z=K*(L∞-L)/(L-L’)

L - L’= a+b*L’

L∞ = -a / b et Z / K = -(1+b) / b

Z=K*(L∞-L)/(L-L’)

L - L’= a+b*L’

L∞ = -a / b et Z / K = -(1+b) / b

(21)

Toujours, selon ces auteurs Ø’ est caractéristique de l’espèce et les valeurs de Ø’ d’une espèce donnée suivent une distribution normale, ce qui implique que leur moyenne permet d’estimer K. Par ailleurs, quelle que soit la méthode utilisée pour estimer L∞ et K, les valeurs de Ø’ d’une espèce donnée devraient être voisines. Pour l’espèce que nous avons étudiées, nous allons calculer Ø’ à travers la méthode de PAULY et MUNRO (1984).

Références bibliographiques:

BERTALANFFY, L. V., 1938. - A quantitative theory of organic growth (Inquiries on growth laws II). Hum. Biol. 10 : 181-213.

BEVERTON, R.J.H., et HOLT, S.J. 1956 - A review of methods for estimating mortality rates in exploited fish populations, with special reference to sources of bias in catch sampling. Rapp. P.-V. Réun. CIEM, 140 : 67-83.

BEVERTON, R.J.H., et HOLT, S. J. 1957 - On the dynamics of exploited fish populations. U.K. Min. Agric. Fish., Fish. Invest (Ser. 2) 19 : 1-533.

BEVERTON, R. J. H., et HOLT, S. J. 1959 - A review of the life spans and mortality rates of fish in nature, and their relation to growth and other physiological characteristics. In CIBA Foundation, colloquia on ageing. Vol. 5. The lifespan of animals, edited by G. E. W. Wolstenholme and M. O’Connor. London, Churchill, Vol. 5 : 142-80.

BHATTACHARYA, C.G. 1967 - A simple method of resolution of a distribution into Gaussian components. Biometrics, (23), 115-135.

BOUGIS, P., 1952. Recherches biométriques sur les rougets (Mullus barbatus ., Mullus surmuletus) Arch. Zool. Exp. gén., 89 (2) : 57-174.

BOUGIS, P., 1976. Océanographie biologique appliquée. Exploitation de la vie marine. Ed. Masson, Paris: 320p.

CHERABI, O. 1987- Contribution à l'étude de la biologie du pageot commun Pagellus erythrinus (Linné, 1758) et à l'écologie de la famille des Sparidés de la baie d'Alger. Université des Sciences et de la Technologie Houari Boumediene, Algérie, 203 p. Thèse de Magister.

GHORBEL, M., JARBAOUI, O. & BOUAN, A., 1997. - Evaluation du stock de pageot (Pagellus erythrinus,Sparidae) dans le Golfe de Gabès (Tunisie) par analyse de pseudo-cohorte. Cybium, 21 (1) : 55-65.

GULLAND, J.A., 1971- The fish resources of the ocean. Fishing News (Books) Ltd., London, 255 p. GULLAND, J.A., 1983 - Fish stock assessment. A manual of basic methods.Ed. John Wiley and Sons/FAO Series on Food and Agriculture, Vol.1.223 p.

HEMIDA, F., DJABALI, F., MOUHOUB, R., 1987- Résultats des travaux réalisés sur les stocks de sardines et d'anchois des côtes algéroises. FAO Fish. Rep., 395:112-120.

(22)

KARTAS F. & QUIGNARD J.P., 1984- La fécondité des Poissons Téléostéens. Masson Ed., Paris. 117 p.

KHERRAZ, A., MOUFFOK, S et BOUTIBA, Z., 2010. Paramètres d’approches de la croissance d’un Mullidés: le Rouget de roche Mullus surmuletus (Linné, 1758) exploitée au niveau de la façade maritime mostaganémoise. Acte de Workshop international « Bel 02 », 28,29 et 30 Nobvembre 2010, Oran.

KHERRAZ, A., KHERRAZ, A., BENGHALI, S. MOUFFOK, S et BOUTIBA, Z., 2014. Age and growth of Mullus surmuletus (L.) in Mostaganem coast, Northwest Algeria. Journal of Biodiversity and Environmental Sciences (JBES) ISSN: 2220-6663 (Print) 2222-3045 (Online) Vol. 5, No. 2, p. 37-43, 2014

KHERRAZ, A., KHERRAZ, A., BENGHALI, S., MOUFFOK, S et BOUTIBA, Z. 2014. Reproductive Biology and growth of red Mullet, Mullus surmuletus (Linné, 1758) in Western Algeria Coasts. Journal Academica Vol. 4(4), pp. 121-129, December 31 2014 - Environmental Science - ISSN 2161-3338 online edition www.journalacademica.org © 2014 Journal Academica Foundation

LE CREN, E. D., 1951. The length weight relationship and seasonal cycle In gonad weight and condition in the perch (Percafluviatilis).J.Anim.Ecol.20(2),201-219.

RICKER, W.E., 1975. Computation and interpretation of biological statistics of fish populations. Bulettin of the Fisheries Research Board of Canada.191:1-382.

MOUHOUB, R., 1986- Contribution à l’étude de la biologie et de la dynamique de la population exploité de la sardine sardina pilchardus (Welb, 1792) des côtes algéroises. Thèse de Magister, USTHB : 163p.

PAULY D., 1984 Length-converted catch curves. A powerfull tool for fisheries research in the tropics (Part 2).ICLARM, Fishbyte, 2 (1): 17-19 p.

PAULY, D et MUNRO, J.L. 1984 - Once more on the comparison of growth in fish and invertebrates. ICLARM Fishbyte, 2 (1): 21.

PAULY, D et MOREAU J., 1997 - Méthodes pour l'évaluation des ressources halieutiques. Collection POLYTECH de l'I.N.P. de Toulouse, Cépaduès-Editions, France. 288 p.

SCHWARTZ D., 1983- Méthodes statistiques à l’usage des médecins et des biologistes. Flammarion Ed., 3éme Ed., 7éme tirage : 318 p.

SPARRE, P., VENEMA, S.C., 1996 - Introduction à l'évaluation des stocks des poissons tropicaux. Première partie: Manuel. FAO Doc. Tech. sur les Pêches, 306(1), Rome. 401p.

URSIN, E., 1967- A mathematical model of some aspects of fish growth, respiration and mortality. J. Fish. Res. Can., 13: 2355-2454 p.

VON BERTALANFFY, L., 1938 - A quantitative theory of organic growth. Hum. Biol., 10, 181-213. WEATHERLEY A.H et GILL H.S., 1987. The Biology of Fish Growth . A cademic press: 433pp.

(23)

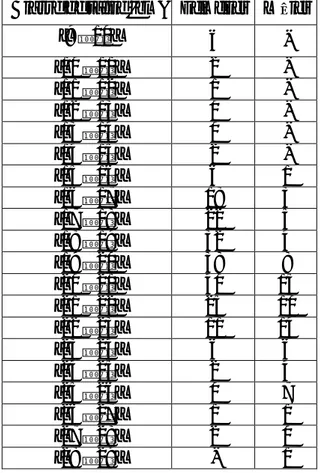
Tableau 1 : Variation du sex-ratio en fonction de la taille chez P. erythrinus Classe de taille (cm) Femelles Mâles

[9 – 10[ ₆ -[10 – 11[ 2 -[11 – 12[ 1 -[12 – 13[ 0 -[13 – 14[ 0 -[14 – 15[ 2 -[15 – 16[ 6 1 [16 – 17[ 18 3 [17 – 18[ 22 5 [18 – 19[ 32 4 [19 – 20[ 38 8 [20 – 21[ 40 15 [21 – 22[ 25 10 [22 – 23[ 11 14 [23 – 24[ 6 6 [24 – 25[ 2 4 [25 – 26[ 0 7 [26 – 27[ 1 1 [27 – 28[ 2 0 [28 – 29[ - 1

(24)

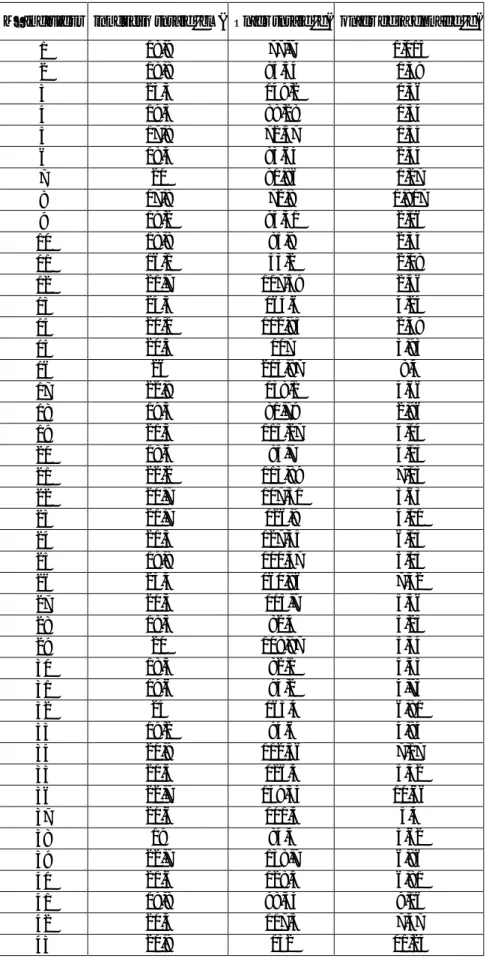
Tableau 2: Base de données pour l’étude des paramètres de la reproduction chez P. erythrinus.

N° individus longueur totale (cm) Poids totale (g) poids de la gonade (g)

1 18,9 77,7 1,015 2 18,8 85,54 1,49 3 23,3 149,2 1,56 4 19,3 88,28 1,34 5 17,8 72,37 1,34 6 18,4 83,64 2,54 7 20 91,86 1,27 8 17,8 72,8 1,817 9 19,2 85,31 2,06 10 18,8 83,9 2,34 11 16,1 53,2 2,08 12 21,7 117,39 2,46 13 24,5 164,6 4,24 14 20,1 102,95 2,49 15 20,5 117 3,93 16 26 215,87 8,4 17 22,9 138,1 4,66 18 19,5 81,79 2,96 19 21,5 115,27 4,04 20 18,6 85,7 4,03 21 22,2 113,89 7,13 22 20,7 107,31 3,63 23 21,7 126,9 4,01 24 21,5 127,45 6,13 25 19,8 100,37 5,03 26 23,4 160,86 7,32 27 20,3 105,7 5,36 28 18,3 82,4 5,23 29 20 108,97 5,34 30 18,5 82,1 4,33 31 19,6 94,2 4,73 32 24 165,4 6,81 33 19,2 94,6 4,84 34 20,9 112,56 7,17 35 21,5 126,4 5,42 36 22,7 139,34 10,66 37 20,6 101,5 5,4 38 19 84,4 5,62 39 22,7 138,7 6,86 40 21,6 128,4 6,81 41 19,8 98,33 9,16 42 20,4 117,3 7,47

(25)

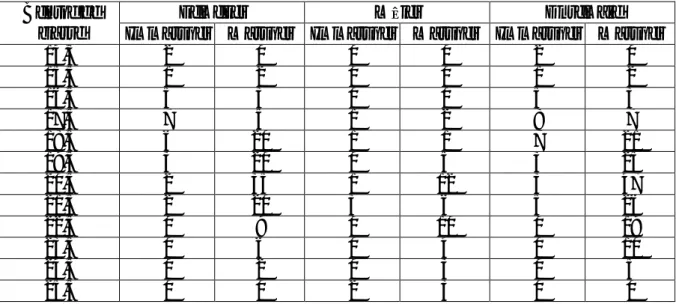
Tableau 3 : Distribution des individus mâtures en fonction de la taille chez P. erythrinus Centre de

classe Immatures Matures Immatures Matures Immatures MaturesFemelles Mâles Ensemble

14,5 2 0 0 0 2 0 15,5 1 2 0 0 1 2 16,5 5 3 0 0 5 3 17,5 7 5 1 2 8 7 18,5 6 20 1 1 7 21 19,5 3 20 0 5 3 25 20,5 2 35 1 12 3 47 21,5 2 20 3 6 5 26 22,5 0 9 0 10 0 19 23,5 0 6 0 4 0 10 24,5 0 2 0 3 0 5 25,5 0 0 2 3 0 0

(26)

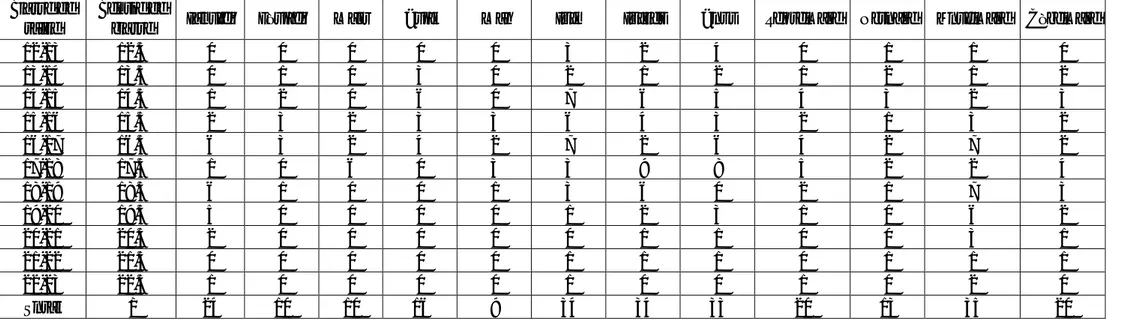
Tableau 4 : Base de données pour l’étude des paramètres de la Croissance (Échantillonnage de 2012 du Mullus surmuletus Femelles)

Classe de

taille Centre declasse Janvier Février Mars Avril Mai Juin Juillet Aout Septembre Octobre Novembre Décembre

12-13 12.5 0 0 0 0 0 3 2 4 0 1 1 0 13-14 13.5 0 1 0 3 0 2 1 2 1 2 1 2 14-15 14.5 1 2 0 6 0 7 6 5 4 3 2 3 15-16 15.5 2 3 2 3 3 6 4 3 2 1 3 2 16-17 16.5 6 3 2 4 2 7 2 6 4 2 7 2 17-18 17.5 1 0 6 0 3 3 9 8 5 2 2 4 18-19 18.5 6 1 0 0 1 3 6 0 2 1 7 3 19-20 19.5 5 0 0 0 0 1 2 3 1 0 6 2 20-21 20.5 2 0 0 0 0 0 1 1 0 0 3 1 21-22 21.5 0 0 0 0 0 1 1 1 0 1 1 1 22-23 22.5 1 0 0 0 0 1 0 0 1 0 2 0 Total / 24 10 10 16 9 34 34 33 20 13 35 20

(27)

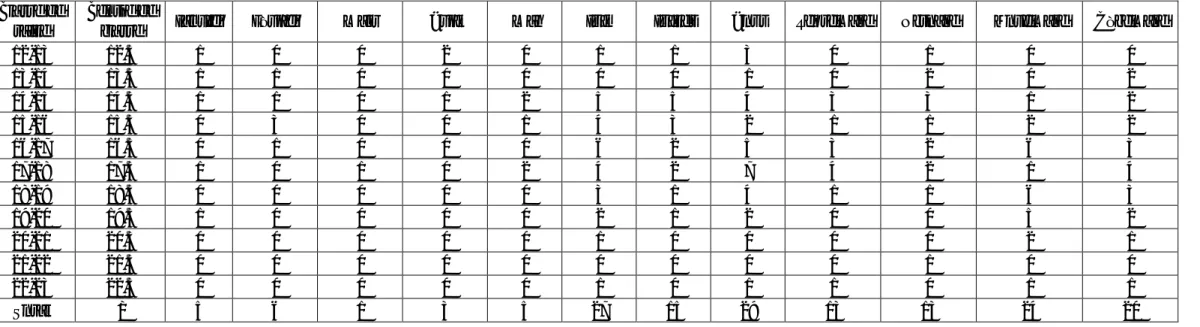
Tableau 5 : Base de données pour l’étude des paramètres de la Croissance (Échantillonnage de 2012 du Mullus surmuletus Mâles)

Classe de

taille Centre declasse Janvier Février Mars Avril Mai Juin Juillet Aout Septembre Octobre Novembre Décembre

12-13 12.5 1 0 0 2 0 1 1 3 0 1 0 0 13-14 13.5 1 1 0 0 0 0 0 1 0 2 0 2 14-15 14.5 1 1 0 1 2 5 5 4 3 3 1 2 15-16 15.5 0 3 0 0 1 4 3 2 1 1 2 2 16-17 16.5 0 1 0 0 0 6 2 5 3 2 6 3 17-18 17.5 1 0 1 0 2 4 2 7 4 2 1 4 18-19 18.5 0 0 0 0 0 3 1 4 1 1 6 3 19-20 19.5 1 0 0 0 0 2 1 2 0 0 5 2 20-21 20.5 0 0 0 0 0 1 0 0 0 0 2 1 21-22 21.5 0 0 0 0 0 0 0 0 0 1 0 0 22-23 22.5 0 0 0 0 0 1 0 1 1 0 1 1 Total / 5 6 1 3 5 27 15 29 13 13 24 20

(28)

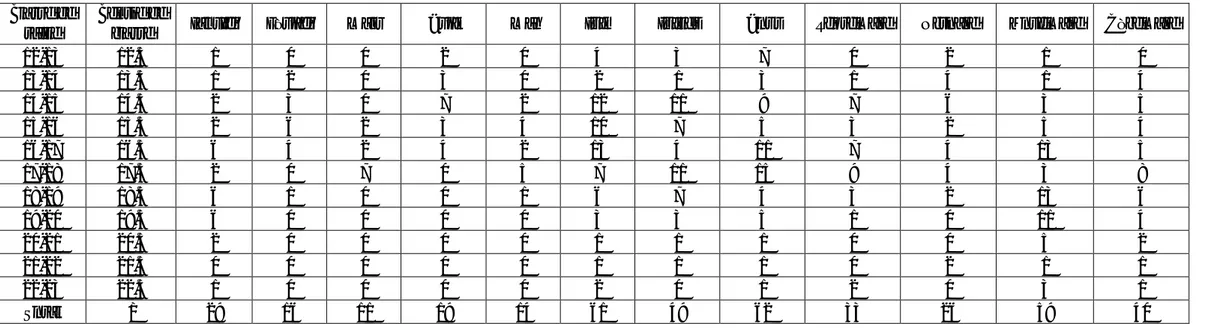
Tableau 6 : Base de données pour l’étude des paramètres de la Croissance (Échantillonnage de 2012 du Mullus surmuletus sexes confondus) Classe de

taille Centre declasse Janvier Février Mars Avril Mai Juin Juillet Aout Septembre Octobre Novembre Décembre

12-13 12.5 1 0 0 2 0 4 3 7 0 2 1 0 13-14 13.5 1 2 0 3 0 2 1 3 1 4 1 4 14-15 14.5 2 3 0 7 2 12 11 9 7 6 3 5 15-16 15.5 2 6 2 3 4 10 7 5 3 2 5 4 16-17 16.5 6 4 2 4 2 13 4 11 7 4 13 5 17-18 17.5 2 0 7 0 5 7 11 15 9 4 3 8 18-19 18.5 6 1 0 0 1 6 7 4 3 2 13 6 19-20 19.5 6 0 0 0 0 3 3 5 1 0 11 4 20-21 20.5 2 0 0 0 0 1 1 1 0 0 5 2 21-22 21.5 0 0 0 0 0 1 1 1 0 2 1 1 22-23 22.5 1 0 0 0 0 2 0 1 2 0 3 1 Total / 29 16 11 19 14 61 49 62 33 26 59 40