Ability of a Robot to Travel Through its Free Work Space in an Environment with Obstacles

Ability

of

a

Robot

to

Travel

_Through

ree Work

Space

in

an

Environment

with Obstacles

Philippe

Wenger

Patrick Chedmail

Laboratoire _{d’Automatique} de Nantes

Ecole Nationale _{Supérieure} de

_{Mécanique}

Nantes, France

Abstract

This article presents a new _geometric

_{analysis of the free}

work _space

_{of a}

robot among obstacles.

The free

work space

(FW)

is

_defined

as the set

_{of positions}

and orientations that

the robot’s end

_effector

can reach,

_according

to the _joint

limits and the various obstacles

_lying

in the environment.

The aim is to _give

global descriptions of the

robot’s

_ability

to

move in the

operational

space

(which

coincides with

Carte-sian _space when

only

position coordinates are

_specified).

The main contribution

_of

this work is the characterization

of the effects of obstacles

on the work space geometry, as well

as on its

_topology.

The

_{ability of a}

robot to

_{move freely}

in its

work space

(called

the

"moveability")

is

difficult

to describe and needs stringent

formalizations.

The concept

of

move-ability

is introduced

_through

various _properties and their

cor-responding

necessary and

sufficient

conditions. Using a

Con-structive Solid

_Geometry

_(CSG)

_{Computer-Aided}

_Design

(CAD) description of robots

and obstacles and an octree

model

of the

FW, these properties permit characterization

_of

selected

_moveability

areas in the FW, where,

for

instance,

any n _points can be linked

together

or where any continuous

trajectory can be achieved without

_{changing configuration.}

This new

_{global description}

is

_{of great}

_{interest for}

the user

_of

CAD _systems when

designing

robotic cells.

1.

Introduction

Automatic

_Design

or

Computer

Aided

_Design

of

ro-botic cells is

_actually

an

_{important challenge}

in

in-dustry

and involves several difficult

geometric

prob-lems :

. the choice of a

_robot;

the

difficulty

is to find the

morphology (type

and number of

_joints,

_length

of

links, ...)

that is best suited to the

_family

of tasks to be achieved.

. the

_geometric

_layout

of the

_cell;

one has to

posi-tion the

robot(s)

and the other components of the cell in such a _way that the robot is able to work

conveniently

in the environment

_{(accessibility}

of the

_specified

work areas, as well as

mobility

in

them,

should be

_ensured).

. _{Collision-free}

_{paths planning;}

the

_problem

is to

find a continuous

_path

_among obstacles between

one

_specified

location to another.

This third

_problem

has drawn the interest of many

authors,

and its theoretical solution is now well known

(Schwartz

and Sharir

1982; Brady

et al.

_{1982; Canny}

and Reif

_1987).

The

_techniques

are various: for

in-stance, the local

approaches

with

_potential

methods

(Khatib

1985;

Koditschek

₁₉₈₇₎

or the

_global

ones

based on the

configuration

space

analysis

and

using

cell

_{decomposition}

_(Faverjon

1984;

Brooks

_1983a,b;

Lozano-P6rez

₁₉₈₆₎

or retraction

techniques

such as

stratified sets

_{(Canny 1987)}

and Voronoi

_diagrams

(O’Dunlaing

et al.

_{1984; Canny}

and Donald

_1988).

These studies have

_already

_given

rise to

_operational

systems

(Lozano-P6rez

et al.

1987).

On the other

_hand,

the first two

_problems

have not

been so

_extensively

studied. Softwares of current

ro-botics

computer-aided design

(CAD)

systems

(such

as

ROBCAD from

_Teknomatix,

MACAUTO from

McDonnel-Douglas,

CATIA from Dassault

_System,

or

ROBOT PLUS from

Computervision)

all

_require

the

action of a human operator who selects the

_right

solu-tion,

validates the

_choices,

and modifies the

parame-ters if necessary

(Bernard 1984;

Dombre et al.

1986;

Deligneres

1987).

This article deals with these first two

problems.

For both of

_them,

characterization and

analysis

of the free work space are well-suited aids.

is the _space of

positions

and orientations of the end effector

_according

to the

_joint

limits and the various

obstacles.

_Concerning

the first

problem,

criteria such

as

volume, connectedness,

_compactness of the work

space, or

dexterity

in it are _very convenient for the

optimization

of the robot’s

_morphology,

as

_they

_give

a

good

evaluation of the

_geometric

_performances

of the

manipulator (Vijaykumar

et al.

_1986;

Lenarcic et al.

1988).

A

_possible

solution to the second

_problem

is the characterization of selected

_regions

of

&dquo;moveabil-ity&dquo;

in the work space. The aim is then to ensure the

feasibility

of tasks defined as areas to be

_freely

reached

(Deligneres

1987) and/or

to be &dquo;travelled

_{through&dquo;}

in

a certain sense

by

the robot

(e.g.,

areas of continuous

welding

or

painting).

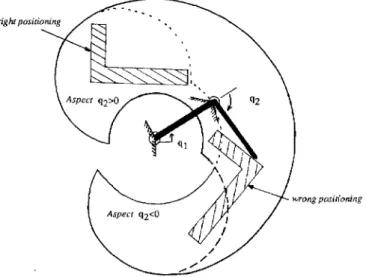
In

Figure

_1,

the

piece

cannot be

placed anywhere

in the free work space; it must be enclosed in a

_region

reachable from

_{configurations}

q2 > 0 or _{q2 <} 0

_separately.

The

_goal

of our

_study

is to

_give

a

_global

_description

of the obstacles in the

_operational

space

(space

of

posi-tions and orientations of the end

_effector;

this _space coincides with the Cartesian _space when

_{only position}

coordinates are

specified).

This is achieved

_through

geometric

and

_{topologic analysis}

of the FW. This new

description

is of _great interest for the

_designer

of

ro-botic cells.

A lot of work has

_already

dealt with work space

analysis. Typical geometric

characterizations of a work space are:

1. Its well-known

_projections

in the Cartesian space:

&dquo;reachable work

_space&dquo;

_(projection

of the whole

Fig. 1. The task to be achieved is continuous

_{welding of a}

piece. The piece must be

_{carefully placed}

in the work space to

avoid

_{configuration changing during}

the _operation. The end

effector

must remain in the same _aspect.

work

_space)

and &dquo;dextrous work

_space&dquo;

(projec-tion of the work _space part where every orienta-tion of the end effector is

_{possible) (Kumar}

and Waldron

_1981).

2. The

_analysis

of holes and voids in the work _space

(Gupta

and Roth

_1982).

3. The

_{approach angles}

and

_{lengths (Hansen}

et al.

1983).

4. Work area

_analysis

_(Yang

and Chiueh

1986).

5. Characterization of the so-called

_{&dquo;aspects&dquo; (set}

of

positions

and/or

orientations reachable under

given configurations)

(Borrel 1986).

6. &dquo;Well-connectedness&dquo;

(ability

to move between

any two

_points

in the work space without

chang-ing

configuration)

(Paden

and

_{Sastry 1988).}

However,

none of these take into account the effects

of obstacles. The

_proximity

of obstacles not

_only

modi-fies the

_shape

of the work space, but also reduces the

moveability

of the robot within

_it,

as has

already

been

shown in Chedmail and

_{Wenger (1987; 1988). Figure}

~A shows a _very

simple example

where the FW is

connected but does not allow the robot to travel

through

it. In

_Figure

2B,

the

_mobility

between _any

two

points

within the FW is

_ensured,

but not

necessar-ily

along

a

given

continuous

trajectory.

In this

article,

we _propose five

_stringent

character-izations of the

_moveability

in the FW for a robot

among obstacles. We attach five necessary and

suffi-cient conditions to these characterizations. These

con-ditions are tested

_using

a constructive solid _geometry

(CSG)

CAD

_technique

_(Martin

et al.

₁₉₈₅₎

and an

octree model of the FW.

_Finally,

an

algorithm

is

de-scribed to check the various

_properties,

and results are

presented.

2.

Definitions

We

_give

in this section some definitions before

pro-ceeding

further.

Let a robot - called

R OBO T(q) -be

defined

by

its ~t

_degrees

of freedom:

ROBOT(q),

enclosed in

_1~3,

is defined as a set of n

solids,

as in

_Wenger

₍₁₉₈₅₎

and Yu and Khalil

(1986).

Let an environment with obstacles be defined

by

Ob = _set of the

physical

obstacles of the

environment,

enclosed in R3

Let f:

f~8~ ~ _{Rm be the}

_geometric

_operator of the

robot

_(Khalil

and

KJeinfinger

1986),

where m is the number of

_operational

coordinates of the end effector

Fig. 2A, A two-DOF

_plannar

_linkage

with one circular obsta-cle and -120° ::::; _q, ::::; _{1200,- 1800 ::::; q2 ::::;} 1800.

_{The free}

work space is connected; however, the robot cannot travel

through

it but can

_only

move

_separately

within part 1 or _part

2B, A

_{two-DOF plannar}

_linkage

with one

_rectangular

obsta-cle and - 90° ~ q, - 90°,-100° - q2 -- 1200. The robot can

join any two _points in its

_free

_{work space} but not

along

any

trajectory

(the

given continuous _trajectory is

unfeasible;

point X, can be reached

_only

in aspect 1 because

_{of the}

_{joint limits,} and point

X2

can be reached

_only

in _aspect 2 because

of the

obstacle).

Let .9 =

_(q

E R&dquo;

_~/1,

_{CJl&dquo;~ ~}

_~’i ~

_~’imin)

_{be the}

con-figuration

space,

according

to the

_joint

limits. Let

_{Qf be}

the

_{configuration}

collision-free space of

ROBOT(q):

Let

_{Wf be}

the FW of

ROBOT(q).

It is the

_image

of

Qf under

the

_geometric

_operator:

The

_free

work space is the space of

positions

and ori-entations of the end effector

_according

to the

_joint

limits and the various obstacles in the environment. A

point

X in

_{Wf is}

a vector of m

_operational

coordinates.

We suppose that there are N connected _components

of

_Qf.

We shall denote them as:

The

_following

relations hold:

not connected. Then:

d i E I:

_{Wf = f(Qf )}

is the

_image

of

_Qfi

under the

geometric

operator.

The

_following

relation holds:

Define: The _aspects are defined as in Borrel

_(1986);

an _{aspect is} a

_subspace

A enclosed in

_{Qf such}

that: l. A is

connected,

2. V _{q E}

_A;

the determinant of any m X m matrix

extracted from the Jacobian matrix J is not

_equal

to zero, except if this minor is

equal

to zero

ev-erywhere

in 2. The components of J are:

where qj

is the

_jth

_component

_{of q,}

_{and x; is the}

ith

_operational

coordinate of X

_{= f (q)}

₍₁

_ i ~ m

and 1

_{; j =}

_n.).

The number _{of aspects is} finite.

_(14~),zj

is a

_partition

of 2.

3. Characterization of

the

Robot’s

Ability

to

Move

_Through

_Wf

We expose in this section the five characterizations of

the

_moveability

in the FW of a

_robot,

and their

corre-sponding

necessary and sufficient conditions.

3.1. First

Characterization

and

_{Corresponding}

Necessary

and

Sufficient

Condition

The FW can be travelled

through

_by

the robot in the sense of

_{P, if, by definition,}

_any two

_points

in

_{Wf can}

be

_joined

_by

the end effector. This means that for any

two

_points

in the

_FW,

a connected _component of the

configuration

collision-free _space exists such that its

image

under f contains

both of these

_points:

Note: This first property can be

_expressed

in a more

succinct _way:

Wf satisfies P,

if and

_only

if

_{Wf is}

_connected,

and there exists a

family (I, , 1~2,

... ,

Ip) _

(Iklk c

K)

of subsets of I such that:

(See

the demonstration in

_Appendix

_A.)

Example:

If

_{Qf is}

_composed

of three connected

components, the

_following

relations hold:

Assume:

and

Then

_{Wf satisfies}

_P,

_(Fig.

_3).

COROLLARY 1

_Wfp

c

_{Wf satisfies}

the

_generalized

property

P1 ( Wfp)

where:

if and

_only

if there exists a

_family

_{I~,

_12,

... ,

Ip~ _

(Iklk

E

_K)

of subsets of I such that:

which can be written in the

_following

more succinct

way:

Note: Because _any subset of set

_{satisfying P, { Wfp)}

also satisfies

_{P, (Wfp),}

such subsets are not

_necessarily

connected.

Fig. 3. A case where

_{the free}

work space can be traveled

through

in the sense

of P, .

Definition I

The maximal parts

Wfp

of

_{Wf satisfying Pi}

₍

_Wfp)

are

defined as follows:

There exists a

_{family ~I~, I2, . _ . ,}

_{Ip} _}

_(Iklk

E

_K)

of subsets of I such that:

Note 1:

_Any

_part

_satisfying

_PI(Wfp)

is enclosed in such

a maximal part. The converse

_being

_true, it is

interest-ing

to find the _{maximal parts}

_satisfying

_{P, (see}

_Fig.

4A;

in the case where

Card(I)

=

3,

there are four

max-imal _parts

_satisfying

_{P1 ( Wfp)).}

Note 2: The

_{properties P,}

and

_P1(Wfp)

do not take into account initial and final

_{configurations.}

More-over, every

trajectory

in the FW between

X1

and

X2

is

not

_necessarily

achievable. That is

_why

we will

com-plete

this definition in the

_following

_property;

_then,

in the next two

_properties,

we will

_successively

take into

account the

_{configuration}

at

_point

_{X, (or X2 )}

and then

at

_points

X

_{1 and X2 ; finally,}

we will _propose a

prop-erty of

mobility

along

any continuous

trajectory

through

the FW.

3.2. Second

_{Definition (Pz)}

and

_{Corresponding}

Necessary

and

_Su,fj~cient

Condition

The FW can be traveled

through by

the robot in the

sense

_{of P2}

_{if, by definition,}

_every discrete

_trajectory

_Td

in

_{Wf is}

_achievable,

which means:

Fig. 4. The

different

maximal parts

of the free

work space

satisfying

(A) P, (Wfp),

P2(Wfp)

(B),

P3(Wfp)

(C) and

P¢(Wfp)

(D) when the

_{configuration collision-free}

space has

three connected components.

Note: A discrete

_trajectory

is an

_arranged

_sequence of

points.

Wf satisfies

P2

if and

_only

if

(See

the demonstration in

_{Appendix B.)}

COROLLARY 2

_Wfp

c

_{Wf satisfies}

the

_generalized

property

P2( Wfp),

where:

(PZ( W.~P))

V Td discrete _trajectory in _Wfp, 3 i E I such that Td C W£ n _Wfp

if and

_only

if

Definition

2

The maximal _parts

_{Wfp satisfying P2(Wfp)}

are defined as follows:

(see Fig.

4B;

in the case where

_Card(I)

=

3,

there are

three maximal parts

satisfying

PZ(Wfp)).

3.3. Third

Characterization

and

_{Corresponding}

Necessary

and

_{Su~cient.Condition}

The FW can be traveled

_through

_by

the robot in the

sense of

_{P3 if,}

_{by definition,}

_any two

_points

in

_{Wf can}

be

_joined

_by

the end

_effector,

whatever the initial or

(exclusive or)

final

_{configuration:}

Note: This third

_property

can be

_expressed

in a more

succinct _way:

Wf satisfies P3

if and

_only

if:

(See

the demonstration in

_{Appendix C.)}

then

_Wfp

satisfies the

_generalized

_property

_P3(Wfp),

where:

if and

_only

if:

for some sets I’ of indices in I.

_(See

the demonstration

in

_{Appendix D.)}

Definition 3

The maximal _parts

_{Wfp satisfying}

_P~,(Wfp)

are defined as follows:

for _any subsets I’ of I such that

_Wfp

is

_nonempty.

_(See

Fig.

4C;

when

_Card(I)

=

3,

there are seven maximal

3.4. Fourth

_{Characterization}

and

Corresponding

Necessary

and

_Su~tcient

Condition

The FW can be traveled

_{through by}

the robot in the

sense of

_{P4 if, by definition,}

_any two

_points

in

_{Wf can}

be

_joined

_by

the end

_effector,

whatever the initial and

final

_{configurations:}

Wf satisfies P4

if and

_only

if

_{Qf is}

connected

_{(the proof}

is

_obvious).

COROLLARY 4 Let

_Qfp

be defined as in

_previous

corollary

3.

_Wfp

c

_{Wf satisfies}

the

_generalized

_property

P4( Wfp)

where:

if and

_only

if:

(See

the demonstration in

Appendix

E.)

Definition 4

The _{maximal parts}

_Wfp

_satisfying

_{P4 Wfp)}

are defined as follows:

(See Fig.

4D;

in the case where

Card(I)

=

3,

there _are

three maximal _parts

satisfying

P4(Wfp).)

Note:

_{Properties P4}

up to

_P,

characterize four

in-creasing

levels

_{describing point-to-point}

motions in the

FW of a robot:

3.5.

_Fifth

Characterization

and

_{Corresponding}

Necessary

and

_SuJ,~icient

Condition

This fifth _property will concern

_only

nonredundant

robots,

for which the

_geometric

_operator is

_bijective

on

the _aspects.

The FW can be traveled

_{through by}

a nonredundant

robot in the sense of

_Pg

if, by definition,

any two

points

in

_{Wf can}

be

_joined

with any continuous

trajec-tory

T~

without

_{changing configuration}

and

_regardless

of the initial or final

_{configuration.}

For

_{any j}

in J

(set

describing

the _aspects

_Aj),

define the

_single

_partition

_{(Aik )kElj}

of the _aspects

_{A j}

in

con-nected _components

_Ajk

as:

We _note,

_{for j}

E J and k E

_Ij:

is the

_{image under f of}

the _{connected component k of} the

_{aspect j}

in the

_operational

space.

Similarly,

we note,

for j

E J:

is the

_image

of the

_{aspect j}

in the

_operational

space.

According

to the results obtained

_by

Borrel

₍₁₉₈₆₎

and

_generalizing

them in the case of environments

with

_obstacles,

this fifth property can be

expressed

as:

Wf satisfies

property

Ps

if and

_only

if

The

_proof

is

_quite

_analogous

to that of theorem 3. COROLLARY 5 Let

_Qjp

be defined as in

_previous

corollary

3. Then

_Wfp

C

Wf satisfies

the property

Ps(Wfp),

where:

if and

_only

if:

where J’ is a set of indices in

_{J, and,}

for

_{any j}

in

_J’,

I’( j )

is a set of indices in

_I(j).

The

_proof

is

_{quite analogous}

to that of

_corollary

3.

Definition

5

The maximal parts

Wfp satisfying

PS ( Wfp)

are defined as the connected components of:

4.

_Algorithmic

_Analysis

of

the

Robot’s

Ability

to

Travel

_Through

_Wf

Let

_Wfp

be enclosed in

_(or

_equal

_to)

_Wf.

There exists

an

infinity

of parts

Wfp

that

verify

P, ( Wfp)

or

_{P2 ( Wfp)}

(any

subset of _any

_Wfi,

for

_instance).

The

_following

algorithm

tests the

_properties

_{P~ , P2 , P3 ,}

and

_P4

for

_Wf

and leads to all the maximal _parts

_{Wfp satisfying}

P, (Wfp) or P2(WfP).

The robot and its environment are modeled

using

a

CSG CAD

_technique.

It makes it

_possible

to

_perform

collision detection between the robot and its

1. Determination of

_I,

_{(<2/,),e~ {Wf,-}lEr, Wf, Qf: in}

the case where n - 3 and 7~ ~

_3,

we use an

oc-tree

(octal tree)

description

of these _spaces in a

similar way as in

_{Faverjon (1986). If r~ - 3,}

the

wrist may be modeled

by

a

_{circumscribing}

sphere.

The FW and the

_{configuration}

collision-free space are obtained

_{by sweeping}

the

configu-ration

_{space 2 according}

to the

joint

limits.

Col-lision detection is

_{performed using}

an efficient

algorithm

described in Yu

(1987).

Finally,

analy-sis of the connected components of

Qf,

as

de-scribed in Samet

(1979)

and Chedmail and

Wenger

( 1988)

leads to I and to the octree defini-tion of

_Qfi

and

_W¡;.

2. Verification of the _property

_{P4: If Card(I)}

=

_1,

then

_{Qf is}

_connected;

therefore

_{P, (and}

so

_{P1, P2 ,}

P3 )

is true for

_Wf;

end of the

_algorithm.

else

3. Verification of the _property

_{P3 : If d i E I, W£}

=

Wf,

then

_P3

is true for

_Wf;

end of the

_algorithm.

else

4. Verification of the property

P2

and determination

of the maximal

_{Wfp satisfying P2( Wfp):}

_{If ~ i E I,}

Wf

= Wf,

the

_PZ

is true for

_Wf;

the maximal

parts

satisfying

P2(Wfp)

are the

_{Wf ;}

end of the

algorithm.

else

5. Verification of the _property

_P,

and determination

of the maximal

_{Wfp satisfying}

_{only P,}

_{( Wfp):}

a. Enumerate all

possible

families of nonempty

subsets of I. For each such

_family,

_say

{Ik/kEK},

determine

Note: the deternnination of B is

performed

using

the octree model with _very

_simple

and fast boolean

_operations.

b. If B is nonempty, then it satisfies

_{P~ ( Wfp);}

go

to 5a.

End of the

algorithm.

We can make the

following

remarks

_concerning

the

part 5 of the

_algorithm:

Note 1: It is

_possible

to

_considerably

reduce the number of cases as a lot of them do not have to be

studied:

1.

_Card(Ik)

= _{1. Then} the _{element i of}

Ik

satisfies

Wf

=

Wfp,

already

seen

2. There

_{exists jo}

such that V k E

_{K, jo c Ik.}

Then

Wfp

C

_{W, f~}

and

_Wfp

is not maximal. In

particu-lar,

if Card(K)

= _{1: there exists i in I such that}

Wfp

C

_{Wf ,}

and

_Wfp

is not maximal.

3. A _great number of _sequences

_{Ik}kEK

do not have

to be tested as

they

_generate nonmaximal _parts.

For

instance,

in the case where N =

4,

the

se-quence

{( 1,

2),

(2, 3), (1, 3,

4)}

does not have to

be

_studied,

because the

_{subspace generated by}

it is enclosed in the maximal

_Wfp

_{generated by}

the

sequence

f ( 1, 2), (2, 3), ( 1,3)}.

Note 2: it is useless to

_study

the case

_where,

in a

sequence

{Ik~k~K,

there exists k and k’ such that

Ik C

Ik..

Indeed,

let

_{A k}

= B for

any k

E

_K;

then

and so

Wfp generated

by

is

_equal

to

_Wfp,

_{generated by}

and do not have to be tested. For

_example,

in the case

where N =

3,

it is useless to test the sequence:

Therefore we

verify

that for N =

2,

out of the cases

where

_{Wf = Wf,}

no subset of

_{Wf exists}

that satisfies

P, ( Wfp).

For N =

3,

then}{ = 127. Out of the _cases where

_Wf

_{= Wf,}

one

_single

set of subsets

_{of I may}

lead to _{parts of}

_{Wf that satisfy}

the condition

_PI(WfP):

{( l, 2), (1, 3), (2, 3))

where

_card(K)

= ₃

(see

Fig.

4A).

Similarly,

for N =

4,

then = _{32767. Out} of _the

cases where

_Wf

=

Wf,

_we

verify

that

_only

27 sets of

subsets

_{of I may}

lead to parts of

Wf that satisfy

the condition

_{P1 ( Wfp).}

5.

Results

We have

_developed

a

package

that enables us to

_study

any type of robot in _any

_{environment, by}

_only

deal-ing

with three-dimensional spaces. In this

section,

we _present some

_examples,

_using

_planar

robots for

graphic

convenience,

that illustrate the

_algorithmic

analysis

of the

_moveability

in the FW of a robot _among obstacles.

5.1.

_Example

1

The FW is not connected

_(Fig.

_5).

In this

_example,

the

algorithm

detects two connected _components in the Cartesian _space and concludes that the FW cannot be traveled

_through

in the sense of

_{PI (it}

cannot enter the

box).

Two maximal _parts

_Wf

and

_Wf2

are detected as

satisfying

P 1 ( Wfp)

and

_{P~ ( Wfp).}

5.2.

_Example

2

The FW is

_connected,

and the

_{configuration}

free space is not connected

_(Fig.

_6).

In this

_example,

the

algo-rithm detects two connected _components

_Qfi

and

_Qf2

in the

_{configuration}

_space. It verifies that FW cannot

be traveled

_through

in the sense

of PI

_(the

robot cannot

move

_completely

around the

_{spherical obstacle),}

but the

_algorithm

exhibits two _parts

_Wfi

and

_Wf2

as

satis-fying

PI(Wfp)

and

_{P2 ( WfP).}

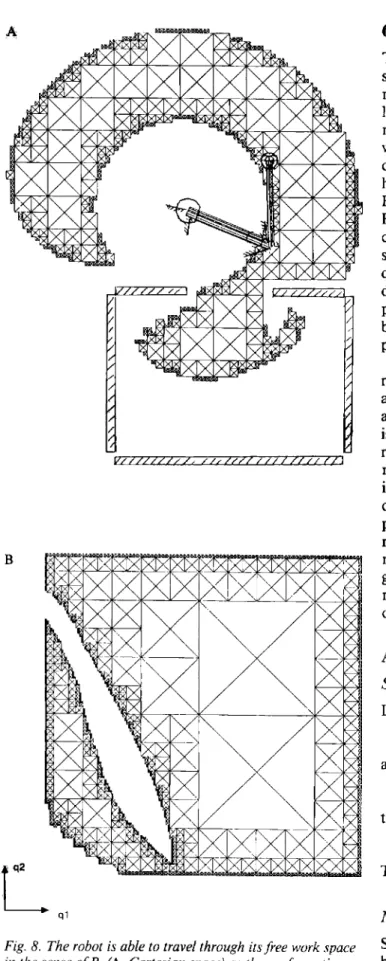
5.3.

_Example

3

The FW is

_connected,

and the

configuration

free space

is not connected

_(Fig.

_7).

In this case, the

algorithm

Fig. 5.

_{The free}

work space is not connected _(A, Cartesian

space);

the

configuration collision-free

space is

composed of

two connected components

Qh

and

_Qf2

_(B,

_{configuration}

detects two _{connected components}

_(2f,

and

_Qf2

in the

configuration

free space and exhibits two _parts

_Wf

and

_Wf2

such that

_Wf2

c

_{Wf and Wfi}

_{= Wf.}

So the

al-gorithm

concludes that the FW can be traveled

through

in the sense

of P2 ( Wfp)

(and

P, ( Wfp)).

We

_verify

that

_Wf2

can be traveled

through

in the sense

of P3( Wfp)

and the

subspace

Wf - Wf2

in .the sense of

_P4(

_Wfp).

5.4.

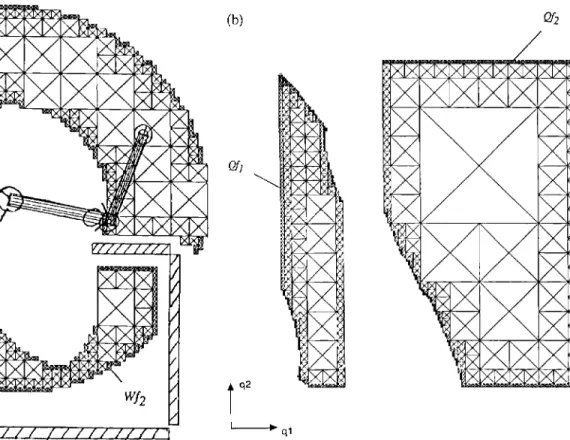
_{Example 4}

The FW and the

_{configuration}

collision-free space are

both connected

_(Fig.

_8).

In this

example,

the

algo-rithm finds

_only

one

_single

connected _component in

the sense of

_{P4 (not}

in the sense of

_P5,

as we could

verify

that the

_{configuration}

space is

composed

of two

aspects, whose

_images

in the

_operational

_space are

different).

5.6. Comments

As it has been shown in these

_{examples, a}

simple

con-nectivity

analysis o.f’the configuration collision-free

space is not

_sufficient

to characterize the

_geometric

space), and their image in the

_operational

space

(Wf

and

Fig. 7. The robot is able to travel

_{through its free}

work space in the sense

_{of P2}

_(A, Cartesian

_space)

and

through

the

sub-space

Wf2

in the sense

_{of Pj}

_(Wfp)

_(B). The

configuration

properties

of the free

work space. The

configuration

collision-free _{space may} be

_{nonconnected,}

whereas the FW can be traveled

_through

_(in

the sense of

_{P, ,}

_P2,

or

P3;

see

_{example 3).}

On the other

hand,

the

configura-tion collision-free space may be

_connected,

whereas

collision-free

space is

composed

of two

connected components

(C, configuration space).

the FW cannot be traveled

through (in

the sense of

_{P 5;}

see

example

4).

The

_analysis

of this

_paradox

and the

characteriza-tions of the

_moveability

of the robot in its FW are the

Fig. 8. The robot is able to travel

_through

_{its free}

work _space

in the sense

_{of P4}

_(A, Cartesian _space) as the

_{configuration}

free

space is connected (B,

configuration

space).

6. Conclusion

This article presents a

_{classification,}

in the

_operational

space, of

regions

where the robot is able to achieve motions

_according

to its

_joint

limits and the obstacles

lying

in the environment. Five characterizations of the

moveability

in the work space have been

explained,

as

well as the five

corresponding

_necessary and sufficient

conditions. Based on these

_conditions,

an

_algorithm

has been

developed

that tests whether

_{Wf satisfies}

_PI

or

P2

or

_P3

or

_P4

and finds all the _parts of

Wf satisfying

P, ( Wfp)

or

P2 Wfp).

_Any

robot in _any environment

can be

studied, provided

that the dimensions of the

spaces are not _greater than three

_(our

algorithm

is

quite

general

and could

_{theoretically}

deal with k-dimensional trees, with k >

_3,

but this would lead to

prohibitive computational

time;

when k %

_3,

the

num-ber of tests is reasonable and

_compatible

with the

ca-pacity

of current

_{minicomputers).}

This work is a new contribution to the

_design

of robotic cells. The

_geometric

_performances

of the robot among the various obstacles of the cell can be

evalu-ated

_through

the five characterizations of its FW. This

is an

interesting

aid for the

morphology

choice of a

robot. In

_addition,

the

_geometric

_layout

of the cell

may be realized

by

determining

the suitable

moveabil-ity

areas in the environment.

Independently,

we have

developed

a

_methodology

that

performs

the automatic

positioning

of a robot in its environment in order to

reach a

_given

area

(Chedmail

and

_Wenger

1989).

This

methodology

and the present

study

are

_currently

inte-grated

in a software

_package

that defines the

auto-matic

_positioning

of a robot _among the various

obstacles.

Appendix

A.

Demonstration of

Property

Pt

1

Sufficient

Condition

and so

therefore:

That is the _property

_Pi.

Necessary

Condition

Suppose

Wf is

not

_connected,

then no

_trajectory

exists between the different connected _{components of}

_it,

and

So we _suppose that

_{Wf is}

connected and satisfies the property

Pl:

Let Hence as

_PI

is satisfied. Therefore such that and Elsewhere

K is obtained

_by

_sweeping

the finite set of the _parts

of I,

the cardinal of which is finite:

_Card(K)

:s:; 2N - 1.

Finally

from

₍₁₎

and

_(3),

and

from

₍₂₎

and

_(3);

therefore i and ii are satisfied.

Appendix

B. Demonstration of

_Property

_P2

Sufficient

Condition

It is obvious.

Necessary

Condition

Suppose

that: V i E

I,

Wf

C

_{Wf (strictly).}

_Thus,

for any i in

I,

Df

= Wf -

WjE’is

nonempty.

Let Td = (Xl, X2,

... ,

Xp)

be a discrete

trajectory

in

_{Yljf, where p}

is the number of connected

compo-nents of the

_{configuration}

collision-free space: p =

Card(I).

This

_trajectory

is chosen such that for

_{any j %}

p,

_Xj

is in

_Dfj.

Thus there exists a discrete

_trajectory

in

WJ~such

that V i E

_I,

_Td

n

_{Df,. ~}

_0,

which means:

Appendix

C. Demonstration of

Property

P3

Sufficient

Condition

Similarly,

let

_X~

E

_Wh

then ‘d i E

_I,

_X~

E

_WJ;,

and so

P3

is satisfied.

Necessary

Condition

Suppose 3

i E I such that

_~

C

_{Wf (strictly);}

_{let qi} E

Qfi

and let

_X~

E

_{Wf -}

_{Wf ;}

then

_P3

is false.

Appendix

D.

Demonstration of

_Corollary

3

(Property

P3 ( Wfp))

Sufficient

Condition

Let

_Wfp

C

_(U~,.

_{Wf ) -}

_(Uk~l·

_Wfk)

for some I’ in I. Let qi in

_Qfp

and let

_X

_{I = f (q, ).}

As

_{X i £ Wfk}

for

_{any k}

not

_belonging

to

_I’,

there

exists

_io

in I’ such that _ql E

_Qfp

n

_QfiO.

Let

_X~

in

Wfp:

d i E

_I’,

_X~

E

_Wfp

n

_~

and thus

X2 E Wfp n WfiO.

Necessary

Condition

Let

_D(I’)

=

(niEI’

Wx) -

(Uk~l’

Wf~).

The sets

_D(I’)

make a

partition

of

Wh

when

considering

all

possible

subsets I’ in I.

Indeed,

they

are

_clearly

all

disjointed,

and moreover:

Now,

let

_Wfp

in

W£

and _{suppose V} I’ C

_I,

_{Wfp /}

D(I’).

Then,

there exists

1’,

and

_{1’Z in I}

such that

_Wfp

n

D(I’1) ~ ~

and

_Wfp

n

_{D(I’ 2) =1=}

ø.

_{If 1’1 ct}

_I’2,

then there exists _ql

_{in f-’(Wfp}

n

_D(I’,))

such that q,

be-longs

to

_(2fio

for

_io

in

_{I’, - 1’2.}

Let

_X2

in

_Wfp

n

_D(I’2);

then the

_property

_{P3( Wfp)}

is false.

_{Similarly, if I’, C}

I’~ ,

there exists q,

in f -’( Wfp

n

_{D(I’ 1 ))}

such that _ql

belongs

to

₆₄

_{for io}

in

_{1’2 -}

_{IZ .}

Let

_X2

in

_Wfp

n

D(I’2);

then the property

P3 ( Wfp)

is false.

Appendix

E. Demonstration

of

_Corollary

4

( Property

P4 ( WfP))

and

Necessary

Condition

Acknowledgment

This work has been

_partially

_{supported by}

the MRES

contract

_{MEC/ 10/ 10:}

&dquo;Choix d’architectures de robots&dquo;

_{(Robots morphology}

_choice).

References

Bernard, F. 1984. CATIA: du dessin au _volume, de la

cin&eacute;-matique

aux calculs

_{scientifiques,}

de la commande

nu-m&eacute;rique

&agrave; la _robotique, un outil _complet de C.F.A.O.

Proc. _{M.I.C.A.D., (2):1082-1097.}

Borrel, P. 1986. A

_study

of _multiple

_manipulator

inverse kinematic solutions with

_applications

to

_trajectory

plan-ning

and _workspaces determination. IEEE

_Conf

Robot. Automat., pp. 1181-1185.

Brady, M., Hollerbach, J. M., Johnson, T. L., et al. 1982. Robot Motion:

_Planning

and Control.

_Cambridge,

Mass.: MIT Press.

Brooks, R. A. 1983a.

_Planning

collision free motions for

pick-and-place operations.

Int. J. Robot. Res. 2(4):19-44. Brooks, R. A. 1983b.

_Solving

the

path-finding

problem

by

good

representation of free space. IEEE Trans.

Sys.

Man.

Cybernet.

SMC-13:190-197.

Canny,

J. F. 1987 _(Los

_Angeles).

A new

_algebraic

method

for robot motion

_planning

and real _geometry. Presented at

IEEE 28th

_symposium.

Canny, J. F., and _Reif, J. 1987

(Los

Angeles). New lower bound _techniques for robot motion

_planning

_problems. Presented at IEEE 28th

_symposium.

Canny,

J. _F., and _Donald, B. R. 1988.

_Simplified

Voronoi diagrams. Discrete _Computat. Geomet. _{3(3):219-236.}

Chedmail, P., and _Wenger, P. 1988 _{(Karlsruhe, F.R.G.).}

Ability

of a robot to move between two _points within car-tesian free _workspace with an encumbered environment. IFAC _Symposium on Robots Control, pp. 73.1-73.6.

Chedmail, P., and

_Wenger,

P. 1987 _(Nantes,

_France).

Do-maine

_atteignable

par un robot: G&eacute;n&eacute;ralisation de la

no-tion _d’aspects a un environnement avec obstacles.

Appli-cation aux robots articul&eacute;s

_plans.

Proc. AUM _Symposium

(2):312-313.

Chedmail, P., and _Wenger, P. 1989 _{(Scottsdale, Arizona,}

May

14-19).

Design

and

_positioning

of a robot in an environment with obstacles

_using

optimal research. IEEE

Conf

Robot. Automat. Vol. 2.

Deligneres,

S. 1987. Choix de

_morphologies

de robots. Ph.D. thesis, E.N.S.M., Nantes, France.

Dombre, E., Fournier, A.,

Quaro,

C., and _Borrel, P. 1986.

Trends in CAD/CAM systems for robotics. IEEE

_Conf

Robot. Automat., pp. (3):1913-1918.

Faverjon,

B. 1984

(Atlanta).

Obstacle avoidance

_using

an octree in the

_{configuration}

_space of a

_manipulator.

1st

IEEE

Conf.

Robot. Automat., pp. (1):504-512.

Faverjon, B. 1986.

_Object

level

_programming

of industrial

robots. IEEE Int.

_Conf

Robot. Automat. 3:1406-1412. Gupta, K. _C., and Roth, B. 1982.

_Design

considerations for

manipulators workspace. ASME J. Mechan. Des.

104:704-711.

Hansen, J. _{A., Gupta,} K. C. and _Kazerounian, S. M. K.

1983. Generation and evaluation of the _workspace of a

manipulator.

Int. J. Robot. Res. _2(3):22-31.

Khalil, W., and

_Kleinfinger,

J. F. 1986. A new

_geometric

notation for open and _closed-loop robots. IEEE Int.

_Conf.

Robot. Automat. 2:1174-1179.

Khatib, O. 1985 (St. Louis). A real time obstacle avoidance for

manipulator

and mobile robots. IEEE

_Conf.

Robot.

Automat. pp. 500-505.

Koditschek, D. 1987

_(Raleigh).

Exact robot

_{navigation by}

means of

_potential

functions: Some

topological

considera-tions. Proc. IEEE Int.

Conf.

Robot.

_(1):1-6.

Kumar, A., and Waldron, K. 1981. The _workspaces of

me-chanical

_{manipulators.}

ASME J. Mechan. Des.

103:665-672.

Lenarcic, J., Stanic, U., and Oblak, P. 1988

_(Ljubljana,

Yugoslavia).

Optimum

design

of robot mechanisms based on _{workspace analysis.} Proc. Adv. in Rob. Kin., (1):59-165. Lozano-P&eacute;rez, T. 1986

_{(Philadelphia).}

A

_simple

motion

planning algorithm

for _general robot _{manipulators.} Proc.

Fifth

Nat.

_{Conf. for the Am.}

Assoc.

_{of Art.}

Int., pp. 626-631.

Lozano-P&eacute;rez, T., et al. 1987.

Handley:

A _{robot system that}

recognises,

planes and

_manipulates.

Proc. IEEE Int.

Conf.

Robot. Automat.,

(2):843-849.

Martin, D., Martin, P., Plemenos, D. 1985. La mod&egrave;lisation des solides. Nantes, France, Universit&eacute; de Nantes, Institut de

_{math&eacute;matiques}

et

_{d’informatique.}

Res. rep.

IMI-INFO-R20.

O’Dunlaing, C., Sharir, M., and _Yap, C. 1984. Generalized Voronoi

_diagrams

for

_moving

a ladder. NYU-Courant Institute, Robotics Lab., Technical rep. no. 32-33.

Paden, B., and _Sastry, S. 1988. Optimal kinematics

_design

of 6R

_{manipulators.}

Int. J. Robot. Res. _7(2):43-61.

Samet, H. 1979. Connected component

labeling

using

quad-trees.

_College

_Park,

_Maryland,

_Computer

Science Depart-ment,

University

of _Maryland.

Schwartz, J., and _Sharir, M. 1982. On the _piano mover’s problem: General

_techniques

for

_{computing topological}

properties of real

_algebraic

manifolds. New _{York, N.Y.,}

Computer

Science Department, New York

_University,

Vijiaykumar,

R., Waldron, J., and _Tsai, M. J. 1986. Geo-metric _optimization of serial chain _manipulator structures

for

_working

volume and

_dexterity.

Int. J. Robot. Res.

5(2):91-103.

Wenger,

P. 1985. Mod&eacute;lisation du robot et de

l’environne-ment en vue de la d&eacute;tection de collision. _{Nantes, France,} D.E.A., Universit&eacute; de Nantes, E.N.S.M.

Yang, D. C. _H., and _Chiueh, T. S. 1986. _Workspace of

6-joints

robots with fixed hand orientation. Int. J. Robot.

Automat.

_1(1):23-32.

Yu, Z.

_Q.,

and _Khalil, W. 1986 _(Vienna, Dec. _3-5). Table look up for collision detection and safe operation of robots. IFAC

_Symposium

on

_{Theory of Robots,}

_pp.