Etude numérique du modèle de Boussinesq de la convection naturelle , laminaire et permanente, entre deux cylindres excentrés horizontaux

REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE MINISTERE DE L'ENSEIGNEMENT SUPERIEUR

ET DE LA RECHERCHE SCIENTIFIQUE UNIVERSITE MENTOURI CONSTANTINE

FACULTE DES SCIENCES EXACTES DEPARTEMENT DE PHYSIQUE N° de Série :………

N° d'ordre :……….

MEMOIRE

Présenté pour obtenir le diplôme de MAGISTER EN PHYSIQUE Spécialité: ENERGETIQUE Option : PHOTOTHERMIQUE Thème :

ETUDE NUMERIQUE DU MODELE DE BOUSSINESQ DE LA CONVECTION NATURELLE, LAMINAIRE ET PERMANENTE, ENTRE DEUX CYLINDRES

EXCENTRES HORIZONTAUX.

Par

GHERNOUG CHAHINEZ Soutenue le : /06/2008

Devant le jury :

Présidente : A.CHAKER Professeur Univ. Mentouri Cne Rapporteur : M. DJEZZAR M. de Conférence Univ. Mentouri Cne Examinateurs : N.ATTAF M. de Conférence Univ. Mentouri Cne

N.BELLEL M. de Conférence Univ. Mentouri Cne A.MOKHNACHE M. de Conférence Univ. Mentouri Cne

Je dédie ce mémoire à mes parents. A tous mes neveux et mes nièces.

A tous les membres de ma famille, grands et petits. A tous mes amis

REMERCIMENTS

Je tiens à exprimer toute ma gratitude à Monsieur Djezzar Mahfoud, Maître de conférence à l'Université Mentouri Constantine de m'avoir guidé tout le long de cette recherche, et de n'avoir jamais cessé de me prodiguer ses conseils et suggestions.

Je tiens à remercier sincèrement Madame Chaker Abla, Professeur à l'université Mentouri Constantine qui a bien voulu présider mon jury d’examen et ce malgré ces nombreuses occupations, qu’elle trouve ici l’expression de mes sincères remerciements.

Je tiens à remercier aussi de tout cœur, messieurs Attaf Nadir, Bellel Nadir et Mokhnache Ammar Maîtres de conférence à l'Université Mentouri Constantine, qui m'ont fait l'honneur d'examiner ce mémoire et de participer à mon jury d’examen.

Enfin, je tiens à remercier tous ceux qui ont contribué de prés où de loin à la réalisation de ce travail.

Nomenclature

Lettres latines

a constante définie dans le système de coordonnées bicylindriques. (m)

C1 rapport des rayons.

C2 excentricité de l'espace annulaire formé par les deux cylindres excentrés.

cp chaleur massique à pression constante. (j.kg-1.k-1) →

g accélération de la pesanteur. (m.s-2)

Gr nombre de Grashof défini par Gr g a₂ T

3

∆ υ β

= .

Grm nombre de Grashof modifié défini par q

a g Gr ₂ 4 m λυ β = .

h coefficient métrique dimensionnel défini dans la relation (2.15). (m) H coefficient métrique adimensionnel.

Kéq conductivité thermique équivalente locale.

éq

K conductivité thermique équivalente moyenne. Nu nombre de Nusselt local.

Nu nombre de Nusselt moyen. P pression au sein du fluide. (at) Pr nombre de Prandtl défini par

λ ρ ν = cp Pr .

q densité de flux de chaleur. (W.m-2)

r1, r2 rayons du cylindre intérieur et extérieur. (m)

SФ Terme de source figurant dans l'équation (3.3).

T température du fluide. (K)

T1 Température du cylindre intérieur. (K)

T2 Température du cylindre extérieur. (K)

Td écart de température Td=T-T2. (K)

→

V vecteur vitesse. (m.s-1)

x, y, z coordonnées cartésiennes. (m)

Lettres grecques

α angle d'inclinaison. (°)

β coefficient volumique d'expansion thermique du fluide. (K-1) ГФ coefficient de diffusion figurant dans l'équation 3.3.

λ conductivité thermique du fluide. (W. m-1. K-1) υ viscosité cinématique. (m2. s-1)

ρ masse volumique du fluide. (kg. m-3)

ij

τ

tenseur des contraintes visqueuses. η, θ, z coordonnées bicylindriques. ψ fonction de courant. (m2. s-1) ω vorticité. (s-1)

Ф fonction générale figurant dans l'équation 3.3.

Exposant + Paramètres adimensionnels. Indices i Intérieur. e Extérieur. η Suivant la coordonnée η. θ Suivant la coordonnée θ.

Sommaire

INTRODUCTION 1

CHAPITRE 1 – RECHERCHE BIBLIOGRAPHIQUE 3

CHAPITRE 2 – ANALYSE THEORIQUE 7

2.1 Description du problème 7

2.2 Hypothèses simplificatrices 7

2.3 Formulation vectorielle du problème 8

2.3.1 Formulation indicielle 9

2.4 Formulation des équations en coordonnées cartésiennes 9

2.5 Elimination du terme de pression de l'équation du mouvement 10

2.6 Introduction des coordonnées bicylindriques 10

2.7 Adimensionnalisation 12

2.8 Formulation des conditions aux limites adimensionnelles 14

2.9 Coefficients d’échange de la chaleur 14

2.9.1 Valeur locale du nombre de Nusselt 14

2.9.2 Nombre de Nusselt moyen 15

CHAPITRE 3 – FORMULATION NUMERIQUE 16

3.1 Introduction 16

3.2 Méthode de résolution numérique 16

3.2.1 Volume élémentaire d'intégration 17

3.2.2 Discrétisation de l'équation générale de transfert d'une variable Ф

dans le volume de contrôle 18

3.3 Discrétisation de l'équation de la chaleur 22

3.3.1 Discrétisation des conditions aux limites 25

3.4 Discrétisation de l'équation de quantité de mouvement 25

3.4.1 Discrétisation des conditions aux limites 27

3.5 Discrétisation de l'équation de la fonction de courant 28

3.5.1 Discrétisation des conditions aux limites 29

3.6 Discrétisation des composantes de la vitesse 29

CHAPITR 4 – RESULTATS NUMERIQUES 32

4.1 Introduction 32

4.2 Etude du maillage 32

4.3 Comparaison de résultats issus de ce code de calcul avec des résultats de la 33 littérature

4.4 Première condition pariétale thermique : Paroi interne isotherme 34

4.4.1 Influence du nombre de Grashof 34

4.4.1.1 Isotherme et ligne de courant 34

4.4.1.2 Nombre de Nusselt local 41

4.4.1.2.1 Variation du nombre de Nusselt local sur la paroi du cylindre intérieur et

extérieur 41

4.4.1.2.2 Variation du nombre de Nusselt local sur la paroi du cylindre extérieur 45 4.4.2 Effet de la variation de l'angle d'inclinaison α 47

4.4.2.1 Cas où l'angle d'inclinaison α est nul 47

4.4.2.2 Cas où l'angle d'inclinaison α=45° 47

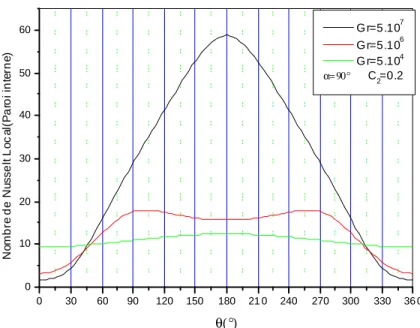
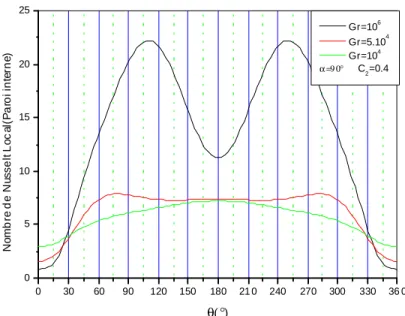
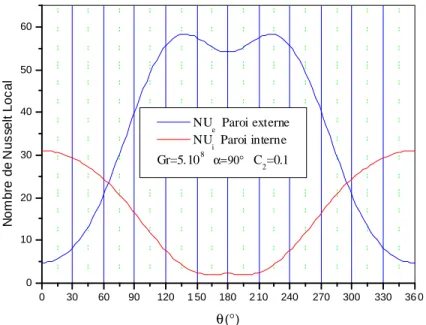
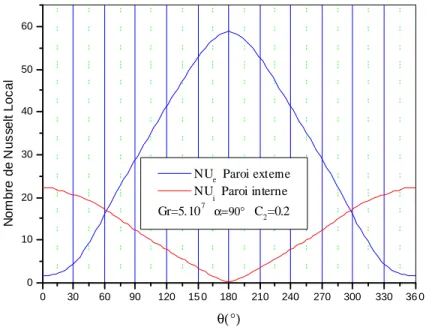
4.4.2.3 Cas où l'angle d'inclinaison α=90° 53

4.4.2.4 Nombre de Nusselt local et moyen 59

4.4.2.5 Nombre de Nusselt moyen 60

4.4.3 Influence de l'excentricité relative 62 4.5 Deuxième condition pariétale thermique : Paroi interne soumise

à une densité de flux de chaleur constante 63

4.5.1 Influence du nombre de Grashof modifié 63

4.5.2 Influence de l'angle d'inclinaison α 67

4.5.3 Variation de la température adimensionnelle sur la paroi interne 67

CONCLUSION 68

ANNEXE : COORDONNEES BICYLINDRIQUES 69

Chapitre 1

Recherche Bibliographique

Une grande variété de corrélations mathématiques servant à la prédiction des transferts

de chaleur est disponible dans la littérature, concernant aussi bien les processus transitoires que permanents.

Parmi les travaux concernant les enceintes fermées la plus grande majorité a été consacrée à la géométrie annulaire, formée par l'espace compris entre deux sphères ou deux cylindres horizontaux de sections droites elliptiques ou circulaires.

Bishop et al. [1,2] ont étudié expérimentalement la convection naturelle entre deux sphères concentriques, chacune étant maintenue à une température constante. Les distributions de température, les données du transfert thermique ainsi que deux corrélations entre le nombre de Grashof et le nombre de Nusselt ont été données par Bishop et al. [3].

Les espaces annulaires formés par des cylindres elliptiques d’axes horizontaux centrés ou excentrés ont aussi donné matière à des travaux, [4-13], citons comme exemple Schreiber et Shingh [5] qui ont fait une étude dans l'espace annulaire entre deux cylindres elliptiques maintenus à des températures constantes, ils ont utilisé la méthode du développement spectral en séries, pour réduire les équations aux dérivées partielles à trois systèmes d'équations différentielles du second ordre. Djezzar et al [10-13] quant à eux, ont étudié numériquement la convection naturelle dans un espace annulaire formé de deux cylindres elliptiques d’axes horizontaux et confocaux en utilisant la formulation en variables primitives, ils ont pu déceler des écoulements multicellulaires, pour certaines géométries quand le nombre de Grashof augmente, ceci pour les trois conditions thermiques pariétales utilisées.

Powe et al. [14] ont mené une étude la convection naturelle dans un espace annulaire cylindrique. Ils ont pu distinguer quatre régimes d'écoulement en utilisant l'air comme fluide

2,6. Ils ont obtenu des résultats en accord avec ceux de l'analyse numérique qu'ils ont réalisée et qui est basée sur la méthode des différences finies et la technique de relaxations successives. Dans un autre travail [16], ils ont introduit le concept de la couche limite pour étudier des écoulements laminaires et turbulents, dans le cas de cylindres horizontaux concentriques ou excentrés et de rangées de cylindres situés à l'intérieur d'une enceinte cylindrique. Les mêmes auteurs [17] ont étudié expérimentalement l'influence de l'excentricité sur le transfert de chaleur. Ils ont présenté des interférogrammes qui permettent de bien visualiser le champ de température et de déterminer les taux de transfert de chaleur. Ils ont mis en évidence un écoulement secondaire localisé au-dessus du cylindre interne quand il est proche du sommet du cylindre externe. Cette structure d'écoulement est confirmée par l'étude numérique de Projahn et al. [18] lorsque les cylindres sont concentriques. Dans leur deuxième étude [19], il semble que ces écoulements persistent même lorsque le nombre de Prandtl est élevé. Quant à Fant et al. [20], ils précisent dans leur étude que le régime bicellulaire n'est obtenu, pour un rapport de rayons de 1.2, que pour des nombres de Rayleigh supérieurs à 2808, alors que pour un rapport de 1.1, c'est un régime tricellulaire qui se développe avec une valeur de transition du nombre de Rayleigh sensiblement plus faible. Naylor et al. [21] ont mené conjointement une étude expérimentale et une étude numérique basée sur une méthode variationnelle d'éléments finis. Ils ont étudié l'effet de l'excentricité du tube interne et de l'angle azimutal sur le champ thermique dans l'espace annulaire pour de faibles nombres de Rayleigh (500-1500). D'autres travaux sur l'effet de l'excentricité sur la convection naturelle entre deux cylindres horizontaux et isothermes, sont disponibles dans la littérature (Rao et al. [22]. Bau [23],...). Prusa et Pao [24] ont examiné l'effet du déplacement vertical du cylindre interne dans un espace annulaire de rapport de rayons 2,6. Ils ont utilisé une transformation radiale pour faciliter l'écriture des conditions aux limites. Malgré les nombreux tests effectués sur l’affinement du maillage, ils n'ont observé aucun écoulement multicellulaire. Kuehn et Goldstein [25] ont mené une étude numérique dans le but de déterminer les effets du nombre de Prandtl et du rapport des rayons sur le transfert de chaleur. Ils ont utilisé la méthode des différences finies et la méthode de relaxations successives pour résoudre les équations de la convection naturelle, laminaire et bidimensionnelle en régime permanent. Pour éliminer les instabilités numériques dues au schéma décentré utilisé dans leur première étude [15], ils ont appliqué une technique hybride lorsque le nombre de Prandtl est faible ou le rapport de rayons est élevé. Ils ont établi une corrélation entre le nombre de Nusselt et deux nombres de Rayleigh basés sur les diamètres des cylindres interne et externe. Mack et Bishop [26] ont étudié la convection naturelle stationnaire entre deux cylindres horizontaux coaxiaux pour de

faibles valeurs du nombre de Rayleigh lorsque les deux cylindres sont maintenus à des températures uniformes et différentes. Ils ont utilisé un développement en séries entières du nombre de Rayleigh. Ils ont donné les champs des vitesses et des températures ainsi que les nombres de Nusselt locaux et moyens. Ils ont également montré que l'influence du nombre de Prandtl est faible dans le cas d'un gaz ou d'un liquide non métallique mais qu'elle est importante pour un liquide métallique. Huetz et al. [27] ont utilisé la même méthode dans le cas où le cylindre interne est soumis à un flux de chaleur alors que le cylindre externe est isotherme. Quant à Abbott [28], il a utilisé la technique d'inversion de matrices pour obtenir des solutions dans des couches de fluide très minces. Une étude plus récente sur la convection naturelle transitoire entre deux cylindres horizontaux, coaxiaux et isothermes a été réalisée par Cheddadi [29]. Il a déterminé les champs de température et de vitesse en utilisant un schéma implicite aux directions alternées. D'autres types de conditions aux limites sont étudiés dans la littérature. Kumar [30] a étudié le cas où le cylindre interne est soumis à un flux de chaleur constant alors que le cylindre externe est isotherme. Les équations de la vorticité et de la chaleur sont résolues par la méthode des différences finies avec un schéma implicite aux directions alternées. Il a étudié l'effet de la variation du rapport de rayons et du nombre de Rayleigh sur la température du cylindre interne. Il a constaté qu'une croissance du nombre de Rayleigh basé sur la même différence de température pour la condition de flux de chaleur constant ou de température uniforme sur le cylindre interne, augmente le transfert de chaleur. Pour des rapports de rayons élevés (supérieurs à 10), les taux de transfert de chaleur sont identiques pour les mêmes types de chauffage. Roschina et al [31] ont étudié la convection naturelle entre deux cylindres concentriques horizontaux avec génération d’énergie à l’intérieur, ils ont considéré un second nombre de Rayleigh thermique concernant le transfert à travers les parois, indépendant du Rayleigh convectif et ils ont pris comme paramètre d’optimisation le champ des températures et non le nombre de Nusselt. Shi et al [32] ont simulé le transfert de chaleur par convection naturelle dans un espace annulaire horizontal concentrique par la méthode des différences finies basée sur le modèle de Lattice Boltzmann pour la résolution des équations de Navier Stockes, les deux parois du système étudié sont portés à deux températures différentes, les champs des vitesses et des températures ont été obtenus pour des nombres de Rayleigh variant de 2.38x103 à 1.02x105 et un nombre de Prandtl de 0.718. Dukaa et al [33] ont étudié la convection naturelle dans un espace annulaire horizontal en utilisant l’approximation non-linéaire de Stockes pour voir le domaine de

Wu [34] ont simulé la convection naturelle dans un espace annulaire excentrique par une méthode de discrétisation n’utilisant pas de transformation de coordonnées rendre le domaine rectangulaire, les nœuds étant pris directement sur l’espace annulaire.

Chapitre2

héorique

T

Analyse

2.1 Description du problème

Considérons un espace annulaire, rempli d'un fluide newtonien en l'occurrence de l'air, situé entre deux cylindres excentriques, horizontaux. La figure (2.1) représente une section droite du système.

Les deux parois cylindriques interne et externe sont isothermes maintenues respectivement aux températures T et ₁ T avec2 T1>T2, dans un premier cas de chauffage,

ensuite la paroi cylindrique interne est soumise à une densité de flux de chaleur constante. Il se produit, dans l’enceinte une convection naturelle que nous nous proposons d'étudier numériquement.

2.2 Hypothèses simplificatrices

Nous posons les hypothèses simplificatrices suivantes :

On considère un écoulement de fluide incompressible, à propriétés physiques constantes et par ailleurs nous supposons être dans le cadre de l'approximation de Boussinesq. Celle-ci consiste à considérer les variations de la masse volumique ρ

Figure 2.1 Section droite du système y T1> T2 T1 T2 α ηe ηi o → g x Horizontale Verticale r1 r2 e

dans le terme de pesanteur dont les variations avec la température, supposées linéaires, engendrent la convection naturelle. Ces variations sont alors traduites par une équation d'état qui relie la masse volumique à la température.

L’équation d’état est donc :

( ) ( )

P,T ρT ρ0

[

1 β

(

T T0

)

]

ρ

ρ= = = − −

(2.1)

où : β est le coefficient d’expansion thermique (constant). ρ0 est la masse volumique de référence (constante).

T0 est la température de référence (constante) associée à ρ0.

Au niveau de tous les autres termes, la masse volumique est constante et égale à ρ0.

La dissipation visqueuse et le travail des forces de pression sont négligeables dans l’équation de la chaleur, le rayonnement n’est pas pris en considération (les propriétés émissives des deux parois étant négligées).

Nous admettons que le problème est bidimensionnel, permanent et laminaire. 2.3 Formulation vectorielle du problème

Les équations de la convection naturelle laminaire, dans le cadre de l'approximation de Boussinesq, s'écrivent sous forme vectorielle :

-équation de continuité : 0 V div→= (2.2) -équation du mouvement : 0 0 g V ) grad . V ( t V ρ ∇ + ρ ρ = + ∂ ∂→ → → → → _P (2.3) -équation de la chaleur : T c T ) grad . V ( t T 2 p ∇ ρλ = + ∂ ∂ → → (2.4) avec : → V : vitesse du fluide. → g : accélération de la pesanteur. P : tenseur des contraintes.

λ : conductivité thermique du fluide. Τ : température du fluide.

p

c : capacité calorifique massique à pression constante du fluide.

t : temps 2.3.1 Formulation indicielle - Equation de continuité:

( )

V 0 x_j j = ∂ ∂ (2.2.a) - Equation du mouvement:

(

)

(

)

0

[

(

0

)

]

i j ij i j i 0 j i 0 1 T T g x x P V V x V t ∂ +ρ −β − ∂ + ∂ ∂ − = ρ ∂ ∂ + ρ ∂ ∂

τ

(2.3.a) - Equation de la temperature:

(

)

(

)

_       ∂ ∂ λ ∂ ∂ = ρ ∂ ∂ + ρ ∂ ∂ j j j j x T x V T x T t Cp Cp (2.4.a) avec : P : pression du fluide.

τ

ij : tenseur des contraintes visqueuses dont les éléments dépendent du

taux de déformation du fluide soumis au champ de vitesse. 2.4 Formulation des équations en coordonnées cartésiennes

Introduisons les coordonnées cartésiennes telles qu’elles sont définies sur la figure (2.1) Le problème étant bidimensionnel et permanent donc les équations (2.2), (2.3) et (2.4) s'écrivent respectivement : 0 y V x U = ∂ ∂ + ∂ ∂ (2.5)

( )

    ∂ ∂ + ∂ ∂ + + ∂ ∂ − = ∂ ∂ + ∂ ∂ y U x U T β α g.sin x P ρ 1 y U V x U U ₂ 2 2 2 d υ

( )

    ∂ ∂ + ∂ ∂ + + ∂ ∂ − = ∂ ∂ + ∂ ∂ y V x V T β α .cos g y P ρ 1 y V V x V U ₂ 2 2 2 d 0 υ (2.6.b)     ∂ ∂ + ∂ ∂ = ∂ ∂ + ∂ ∂ y T x T c ρ λ y T V x T U ₂ 2 2 2 P (2.7)

2.5 Elimination du terme de pression de l'équation du mouvement

En dérivant les équations du mouvement (2.6.a) et (2.6.b) respectivement par rapport à y et à x. il vient :

( )

(

)

    ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ +     ∂ ∂ ∂ ∂ =     ∂ ∂ ∂ ∂ +       ∂ ∂ ∂ ∂ y U x U y α sin T β g y x P ρ 1 y y U V y x U U y 2 2 2 2 d 0 υ (2.8.a)

( )

(

)

    ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ +     ∂ ∂ ∂ ∂ =     ∂ ∂ ∂ ∂ +       ∂ ∂ ∂ ∂ y V x V x α cos T β g x y P ρ 1 x y V V x x V U x 2 2 2 2 d 0 υ (2.8.b)

En soustrayant l'équation (2.8.a) de (2.8.b) et en utilisant l’équation de continuité ainsi que la définition de la fonction de vorticité ω, nous obtenons :

( )

( )

    ∂ ∂ + ∂ ∂ +       ∂ ∂ − ∂ ∂ = ∂ ∂ + ∂ ∂ y ω x ω α sin y T α cos x T β g y ω V x ω U ₂ 2 2 2 υ (2.9) avec : y U -x V ∂ ∂ ∂ ∂ = ω (2.10.a)       ∂ ∂ ∂ − ∂ ∂ = ∂ ω ∂ y x U x V x 2 2 2 (2.10.aa)

      ∂ ∂ ∂ − ∂ ∂ ∂ ∂ = ∂ ω ∂ y x U x V x x 2 2 2 2 2 (2.10.b)     ∂ ∂ − ∂ ∂∂ = ∂ ω ∂ y U y x V y 2 2 2 (2.10.bb)     ∂ ∂ − ∂ ∂∂ ∂ ∂ = ∂ ω ∂ y U y x V y y 2 2 2 2 2 (2.10.c)

2.6 Introduction des coordonnées bicylindriques

Il est commode de définir un référentiel tel que les limites du système se traduisent par des valeurs constantes des coordonnées. Les coordonnées dites « bicylindriques » [38,39], permettent, précisément dans notre cas, d'obtenir ce résultat.

Dans le système de coordonnées

(

η,θ,z

)

, les surfaces η =constante sont des cylindres circulaires avec des axes dans le plan xz, les surfaces θ =constante sont les portions des cylindres circulaires avec des axes dans le plan yz, et les surfaces z=constante sont des plans parallèles.

Le passage des coordonnées cartésiennes aux coordonnées bicylindriques s'effectue à l’aide des relations suivantes (voir annexe) :

( )

( )

( )

( )

( )

( )

         = − = − = z z θ cos η ch θ a.sin y θ cos η ch η a.sh x (2.11)

Les équations (2.5), (2.7), et (2.9) s'écrivent alors respectivement : (hV ) 0 θ ) V h ( η η ∂ θ = ∂ + ∂ ∂ (2.12) θ T η T h 1 c ρ λ θ T V η T V ₂ 2 2 2 p θ η     ∂ ∂ + ∂ ∂ = ∂ ∂ + ∂ ∂ (2.13)

( ) ( )

( ) ( )

[

]

( ) ( ) ( ) ( )

[

]

_ + ∂_{∂ } ∂ ∂ +    ∂ ∂ +    ∂ ∂ + = ∂ ∂ + ∂ ∂ θ ω η ω h ν θ T α cos θ η, G -α sin θ η, F η T α sin θ η, G α cos θ η, F h gβ θ ω h V η ω h V 2 2 2 2 2 θ η (2.14)

( )

1 2

( )

2 1shη rshη r a= =

( )

( )

(

)

( )

₍

_{( )}

( ) ( )

_{( )}

₎

( )

₍

_{( )}

( ) ( )

_{( )}

₎

_       − = − − = − = θ cos η ch η sh θ sin θ η, G θ cos η ch η ch θ cos 1 θ η, F θ cos η ch a h (2.15) Où : θ η,V

V sont les composantes de la vitesse suivant les directions η, θ.

En introduisant la fonction de courant ψ , de façon à vérifier identiquement l'équation de continuité, il vient :        ∂ ∂ − = ∂ ∂ = η ψ h 1 V θ ψ h 1 V θ η (2.16) Nous en déduisons :     ∂ ∂ + ∂ ∂ − = θ ψ η ψ h 1 ω ₂ 2 ₂ 2 ₂ (2.17) 2.7 Adimensionnalisation

L'adimensionnalisation a pour avantage de faciliter la simplification des équations et de généraliser les résultats.

En posant les quantités adimensionnelles suivantes : Dh = a H = h

υ D V Vη+ = η h υ D V V+θ = θ h υ ψ ψ+ = υ 2 h D ω ω+ = Avec:

a : a (distance entre les pôles apparaissant dans la relation des coordonnées (η,θ)) Dh

υ : Vitesse caractéristique. υ

2

Dh : Temps caractéristique.

La température adimensionnelle pour la paroi interne est donnée selon la condition pariétale thermique imposée:

- Cas I « paroi isotherme »: 2 1 2 + T -T T -T =

T donc le nombre de Grashof est : Gr gβD ΔΤ

3 h

υ2

= - Cas II « densité de flux de chaleur constante q »:

(T T ) D q λ = T 2 h +

Et donc le nombre de Grashof modifié est : q λ D β g Gr 4 h m= _υ2

Introduisons aussi le nombre de Prandtl :

λ c ρ Pr = υ p

En portant les quantités adimensionnelles définies précédemment dans les équations (2.12), (2.13) et (2.14), on obtient : 0 ) V H ( ) V H ( = θ ∂ ∂ + η ∂ ∂ + θ + η (2.18) T T P 1 T V H T HV 2 2 2 2 r     θ ∂ ∂ + η ∂ ∂ = θ ∂ ∂ + η ∂ ∂ + + + + θ + + η (2.19)

{

[

( )

( )

( )

( )

]

( )

( )

( )

( )

[

]

}

+

(

)

θ ω + η ω H 1 θ T α cos θ η, G -α sin θ η, F + η T α sin θ η, G + α cos θ η, F H Gr = θ ω H V + η ω H V 2 + 2 2 + 2 2 + + m + + θ + + η ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ (2.20)

- Ou les composantes V_η+,V_θ+de la vitesse et de la vorticité ω adimensionnelles sont + définies par :

θ ψ H 1 Vη ∂ ∂ = + + (2.21.a) η ψ H 1 Vθ ∂ ∂ = + + (2.21.b) _      θ ∂ ψ ∂ + η ∂ ψ ∂ − = ω + + + H 1 ₂ 2 2 2 2 (2.22)

2.8 Formulation des conditions aux limites adimensionnelles

Puisqu'il n'y a pas d'impulsion qui traverse les parois, la fonction de courant s'annule sur celle-ci. Nous déterminons la valeur de la vorticité en appliquant la relation (2.21) directement sur la paroi ou la dérivée de la fonction de courant par rapport à l'azimut θ s'annule.

-Conditions sur la paroi du cylindre intérieur (

η

=

η

_i

=

constant) :

0 η ψ θ ψ V Vη θ = ∂ ∂ = ∂ ∂ = = + + + + (2.23.a) _      θ ∂ ψ ∂ + η ∂ ψ ∂ − = ω + + + H 1 ₂ 2 2 2 2 (2.23.b) i η η constant _η T h 1 λ q = ∂ ∂ − = (2.23.c) - Cas I : T1 =1 + (2.24.a)

- Cas II : le gradient de température peut être déterminé à partir de la définition de la température adimensionnelle, de la façon suivante :

η ∂ ∂ λ = η ∂ ∂ + T H 1 q T h 1 (2.24.b)

En introduisant l'équation (2.24.b) dans l'équation (2.23.c), il vient : 1 T H 1 i − = η ∂ ∂ η = η +

- Conditions sur la paroi du cylindre extérieur (η=ηe=constant) : 0 η ψ θ ψ V Vη θ = ∂ ∂ = ∂ ∂ = = + + + + (2.26.a)       θ ∂ ψ ∂ + η ∂ ψ ∂ − = ω + + + H 1 ₂ 2 2 2 2 (2.26.b) 0 T2+ = (2.26.c)

2.9 Coefficients d’échange de la chaleur 2.9.1 Valeur locale du nombre de Nusselt

La définition générale du nombre de Nusselt est : T qa Nu ∆ λ = (2.27)

q : densité du flux de la chaleur à travers la paroi de l’enceinte.

∆T : écart de température T1-T2. Soit : cste T h 1 q = η η ∂ ∂ λ − = (2.28)

et en utilisant les définitions des températures adimensionnelles dans les deux conditions pariétales thermiques, il vient :

• Cas I : cste T h 1 Nu = η η ∂ ∂ − = ₊ + (2.29) • Cas II : cste T ) , ( T h 1 Nu i ∂η η= ∂ θ η − = _{+ +} + (2.30)

2.9.2 Nombre de Nusselt moyen

Le nombre de Nusselt moyen s’exprime à partir de la relation suivante :

∫

θ θ θ θ − θ = NN 1 Nud 1 Nu 1 NN (2.31)

Chapitre 3

Formulation Numérique

3.1 Introduction

L'examen du système différentiel établi dans le chapitre précédent montre qu'en maintenant le nombre de Prandtl et le rapport des rayons C1=r2/r1=2 constants, trois

paramètres influencent les profils de la fonction de courant et de la température dans l'espace annulaire, ce sont:

-l'angle d'inclinaison α . -le nombre de Grashof Gr.

-l'excentricité relative de l'espace annulaire formé par les deux cylindres excentrés

1 2 r e = C .

Dans notre travail, nous utilisons:

- trois valeurs de l'angle d'inclinaison α : 0°, 45°, 90°. - trois valeurs de l’excentricité relative C2 : 0.1, 0.2 et 0.4

Nous avons utilisés des pas Δη et Δθ constants. Plus précisément, nous posons:

1 NI η η Δη 1 NI -= 1 -θ -θ = Δθ NN 1 NN avec:

NI : le nombre de points suivant η. NN : le nombre de points suivant θ.

3.2 Méthode de résolution numérique

Pour la résolution du système d'équations (2.19), (2.20) et les conditions aux limites associées, nous considérons une solution numérique par la méthode des volumes finis. Alors que pour l'équation (2.22), nous considérons une solution numérique par un développement en série de Taylor. Les deux méthodes sont très utilisées dans la solution numérique des problèmes de

Figure 3.1 Domaine physique et domaine de calcul.

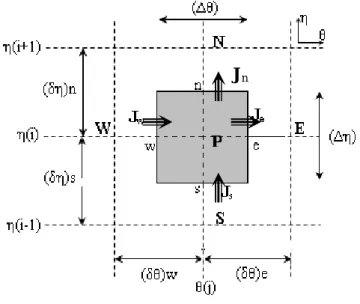
3.2.1 Volume élémentaire d'intégration

On découpe l'espace annulaire selon les directions η et θ en un ensemble de volumes élémentaires ou "volumes de contrôle" égaux à « _H2. ∆η.∆θ .1 _{». (Le problème étant} bidimensionnel, on prend l'unité comme épaisseur dans la direction Z).

Le centre d'un volume fini typique est un point P et ses faces latérales « est », « ouest », « nord » et « sud », sont désignées respectivement, par les lettres e, w, n et s. Chacun des volumes finis intérieurs est entouré de quatre autres volumes finis. Les centres de ces volumes sont les points E, W, N et S. Les variables scalaires (vorticité, température) sont stockées aux points centrés dans les volumes finis. Donc les équations de transfert des variables scalaires sont intégrées dans le volume fini typique. Les nœuds E et N sont pris dans les directions des coordonnées positives de θ et η

respectivement et les nœuds W et S dans les sens contraires. La figure (3.2) représente un volume-fini typique et son voisinage dans un domaine de

calcul.

Chaude Froide

Figure 3.2 Représentation schématique du volume de contrôle sur cette figure, le volume de contrôle entourant le

nœud P est limité par les faces notées w, n, e et s.

3.2.2 Discrétisation de l'équation générale de transfert d'une variable Ф dans le volume de contrôle

Pour illustrer la discrétisation des équations de transfert par la méthode des volumes finis, nous considérons l'équation de transfert sous sa forme générale. Pour bien comprendre cette méthode nous considérons d'abord l'équation de la chaleur

(2.19) et l'équation du mouvement (2.20). Elles s'écrivent, compte tenu de l'équation de continuité (2.18), respectivement :

) 0 θ T Pr 1 T V H ( θ ) η T Pr 1 T V H ( η η θ ∂ = ∂ − ∂ ∂ + ∂ ∂ − ∂ ∂ + + + + + + _(3.1)

( )

( )

[{

( )

( )

]

[

( )

( )

( )

( )

]

}

θ T α cos θ η, G -α sin θ η, F η T α sin θ η, G α cos θ η, F Gr H ) θ ω -ω V H ( θ ) η ω ω V H ( η η θ m + + = + + + + + + + + + ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ -∂ ∂ (3.2) P Jn

Ces deux équations sont de la forme générale: + + = _φ ∂ φ ∂ − φ ∂ ∂ + ∂ φ ∂ − φ ∂ ∂ S ) θ Γ V H ( θ ) η Γ V H ( η η φ θ φ (3.3) avec: Tableau 3.1 équation φ Γ_φ S _φ 3.1 _Τ + _{1Pr 0} 3.2 _{ω 1} +

( )

[{

( )

]

( )

( )

[

]

}

θ Τ cosα θ η, G -sinα θ η, F + η Τ sinα θ η, G + cosα θ η, F HGr + + m ∂ ∂ ∂ ∂

φ : fonction générale (soit_{ω , soit}+ _{Τ ).} +

φ

Γ : coefficient adimensionnel. φ

S : terme de source.

L'équation de discrétisation d'une variable φ est obtenue par l'intégration de son équation de conservation dans un volume fini typique. Ci-après, nous présentons un cas de discrétisation d'une équation de transfert deφ.

∫ ∫

∫ ∫

∫ ∫

η θ= η θ ∂ φ ∂ − φ ∂ ∂ + θ η ∂ φ ∂ − φ ∂ ∂ φ φ + φ + e w n s e w n s θ e w n s η )d d S d d θ Γ V (H θ d d ) η Γ V (H η ou bien :

(

) (

)

43 42 1 4 4 4 4 4 4 3 4 4 4 4 4 4 2 1 4 4 4 4 4 4 3 4 4 4 4 4 4 2 1 3 e w n s 2 e w n s 1 e w n s d d S d d d d V H V H

∫ ∫

∫ ∫

∫ ∫

_ η θ+ η θ            θ ∂ φ ∂ Γ θ ∂ ∂ +     η ∂ φ ∂ Γ η ∂ ∂ = θ η       θ ∂ φ ∂ + η ∂ φ ∂ φ φ φ + θ + η

Les termes 1, 2 et 3 représentent les intégrales doubles dans le volume fini (entre les faces w-e et s-n), des termes de la convection, de la diffusion et de la source deφ. Pour la discrétisation spatiale, nous utilisons le schéma de la loi de puissance (Power Law) pour approcher les variations de φ entre les points du maillage. Ce schéma présente l'avantage d'être inconditionnellement stable.

            θ ∂ φ ∂ Γ − φ =     η ∂ φ ∂ Γ − φ = φ + θ θ φ + η η HV J HV J (3.4) Ou Jη et Jθ sont les flux totaux (convection plus diffusion).

En portant ces valeurs dans l'équation (3.3), on obtient: η θ = _φ θ ∂ ∂ + η ∂ ∂ S J J (3.5) L'intégration de l'équation (3.5) dans volume de contrôle donne:

Jn −Js +Je−Jw =Sφ.∆V (3.6) Je, Jw, Jn et Js sont les valeurs des flux totaux aux interfaces du volume de contrôle.

S est la valeur moyenne de S dans ce volume élémentaire. Ce terme peut généralement φ

être linéarisé en fonction de ΦP (au nœud P) et se mettre sous la forme:

S_φ = S₀+ S_p .φ_p (3.7) avec Sp 〈0

Par suite l'équation (3.7) devient:

Jn− Js+ Je− Jw = (S0 + SP. φP) .∆V (3.8) Si en intègre l'équation de continuité (2.18) dans le volume de contrôle, on obtient: Fn − Fs + Fe − Fw = 0 (3.9) Où F ,n F , s F et e F sont les débits massiques à travers les surfaces de ce volume: w

       η ∆ = η ∆ = θ ∆ = θ ∆ = + θ + θ + η + η . ) V H ( F . ) V H ( F . ) V H ( F . ) V H ( F w w e e s s n n (3.10)

En multipliant l'équation (3.9) par la fonction ΦP et en soustrayant l'équation obtenue de

l'équation (3.8), il vient: V ). . S S ( ) . F J ( ) . F J ( ) . F J ( ) . F J ( p p 0 P W W p e E p s s p n n ∆ φ + = φ − − φ − + φ − − φ − (3.11)

       φ − φ = φ − φ − φ = φ − φ − φ = φ − φ − φ = φ − ) ( a . F J ) ( a . F J ) ( a . F J ) ( a . F J P W W P w w E P E P e e P S S P s s N P N p n n (3.12)

Introduction ces valeurs dans l'équation (3.11) on obtient: V . ) . S S ( ) ( a ) ( a ) ( a ) ( a P P 0 P W W E P E P S S N P N ∆ φ + = φ − φ − φ − φ + φ − φ − φ − φ (3.13)

On obtient donc enfin l'équation de discrétisation :

aPφP =aN φN+aS φS +aE φE +aW φW +b (3.14) avec:

aP =aN +aS +aE +aW -Sp ∆V (3.15) b = S0. Δ V (3.16) D'après PATANKAR [35], la fonctionA

( )

P , est donnée par:

A

( )

P = 0,

(

1−0.1 P

)

5

Le symbole A,B signifie que le maximum entre A et B est choisi.

( )

( )

( )

( )





_









+

=

−

+

=

+

=

−

+

=

0

,

F

P

A

D

a

0

,

F

P

A

D

a

0

,

F

P

A

D

a

0

,

F

P

A

D

a

w w w w e e e E s s s S n n n N (3.17)

Les grandeurs De, Dw, Dn et Ds, sont définies par:

( )

( )

( )

( )

( )

( )

( )

( )

           δθ η ∆ Γ = δθ η ∆ Γ = δη θ ∆ Γ = δη θ ∆ Γ = φ φ φ φ . D . D . D . D w w w e e e s s s n n n (3.18)

           = = = = D F P D F P D F P D F P w w w e e e S s s n n n (3.19)

Les pas d'intégration (δθ)n, (δθ)s, (δη)e et (δη)w peuvent être égaux ou non aux pas de

calcul Δθ et Δη respectivement. Ils sont choisis constants et égaux aux Δθ et Δη. Considérons que les interfaces e, w, s et n sont les milieux des nœuds (P, E), (P, W), (P, N) et (P, S). Dans ces conditions les grandeurs précédentes s'écrivent:

( )

( )

( )

( )

_         θ ∆ η ∆ Γ = θ ∆ η ∆ Γ = η ∆ θ ∆ Γ = η ∆ θ ∆ Γ = φ φ φ φ . D . D . D . D w w e e s s n n (3.20)

Parmi les conditions de convergence et de stabilité exigées par cette méthode, notons que dans l'équation (3.14) tous les coefficients doivent être positifs٫ SP doit être négatif et le

coefficient ap, doit être égal à la somme des autres coefficients et SP∆V.

La discrétisation précédente s'applique aux équations différentielles aux dérivées partielles de toutes les variable dépendantes : Φ est l'une de ces variables T+ et ω+. Pour chaque variable, le coefficient de diffusion ГΦ et la source SΦ sont définis dans le tableau 3.1.

3.3 Discrétisation de l'équation de la chaleur

Réécrivons l'équation (3.14) en remplaçant la fonction générale φ aux nœuds P, E, W, N et S par la température adimensionnelle en ces nœuds, il vient:

aP TP+=aNT+N+aSTS++aETE++aW TW+ +b (3.21) Comme dans l'équation (3.1), le terme de source ST s'annule, le coefficient b s'annule

également et le cœfficient aP figurant dans l'équation (3.15) devient: +

+ + =

Où aN, aS, aE et aW ont respectivement les mêmes expressions que dans le système (3.17).

En introduisant la fonction de courant adimensionnelle ψ+dans le système (3.10), il vient:

                 η ∂ ψ ∂ − η ∆ =     η ∂ ψ ∂ − η ∆ =     θ ∂ ψ ∂ − θ ∆ =     θ ∂ ψ ∂ − θ ∆ = + + + + F F F F w w e e s s n n (3.23)

Dans la suite nous supposons que :

(

)

( )

( )

(

)

(

)

( )

( )

(

)

2 1 j , i j , i 2 j , i 1 j , i 2 j , 1 i j , i 2 j , i j , 1 i w e s n − ψ + ψ = ψ ψ + + ψ = ψ − ψ + ψ = ψ ψ + + ψ = ψ + + + + + + + + + + + +

Le développement du gradient de la fonction de courant à l’interface « e » est établi d’après la démarche de NOGOTOV [36], comme suit : (voir figure 3.3).

Figure 3.3 Représentation schématique des nœuds P, E, W et S dans le maillage

(

)

(

)

η ∆ + − ψ − + + ψ =     η ∂ ψ ∂ + + _{i 1/2, j 1/2} + _{i 1/2 ,j 1/2} e

(

)

(

)

( )

(

)

(

)

(

)

( )

(

)

2 1 j , i j , i 2 j , 1 i 1 j , 1 i 2 1 2 1 j , i j , i 2 j , 1 i 1 j , 1 i 2 1 e      ψ − + +ψ − ₊ψ +ψ + η ∆ −      ψ + + −ψ + ₊ ψ +ψ + η ∆ =     η ∂ ψ ∂ + + + + + + + + +

Par suite la fonction Fe s’écrit :

(

)

(

)

(

)

(

)

[

i 1, j 1 i 1, j - i 1 , j 1 - i 1 , j

]

4 1 Fe= ψ − + +ψ − ψ + + ψ + + + + + (3.24.a) De la même façon, on écrit le gradient à l’interface « w ».

(

)

(

)

(

)

(

)

(

)

(

)

η ∆ − − ψ − ψ − + ψ + + ψ = η ∆ − − ψ − − + ψ =     η ∂ ψ ∂ + + + + + + + 4 1 j , 1 i j , 1 i -1 j , 1 i j , 1 i 2 / 1 j , 2 / 1 i 2 / 1 j , 2 / 1 i w

Et la fonction Fw est donnée par

(

)

(

)

(

)

(

)

[

i 1, j-1 i 1, j - i 1, j-1 - i 1, j

]

4 1 Fw= ψ − +ψ − ψ + ψ + + + + + _(3.24.b)

De la même façon, le gradient à l’interface « n » est défini par :

(

)

(

)

θ ∆ − + ψ − + + ψ =     θ ∂ ψ ∂ + + + 2 / 1 j , 2 / 1 i 2 / 1 j , 2 / 1 i n

(

)

(

)

( )

(

)

(

)

(

)

( )

(

)

2 j , 1 i j , i 2 1 j , i 1 j , 1 i 2 1 2 j , 1 i j , i 2 1 j , i 1 j , 1 i 2 1 n       ψ + − +ψ − ₊ ψ +ψ + θ ∆ −       ψ + + +ψ + ₊ ψ +ψ + θ ∆ =       θ ∂ ψ ∂ + + + + + + + + +

(

)

(

)

(

)

(

)

θ ∆ − ψ − + ψ + ψ + + + ψ =     θ ∂ ψ ∂ + + + + + 4 1 j , i -1 j , 1 i -1 j , i 1 j , 1 i n

(

)

(

)

(

)

(

)

[

i 1, j 1 i,j 1 - i 1, j-1 - i , j 1

]

4 1 Fn= ψ + + +ψ + ψ + ψ − + + + + (3.24.c) Le gradient à l’interface « s » s’exprime par la relation :

(

)

(

)

(

)

(

)

θ ∆ − ψ − + ψ + ψ + + − ψ =     θ ∂ ψ ∂ + + + + + 4 1 j , i -1 j , 1 i -1 j , i 1 j , 1 i s Et l'expression Fs devient :

(

)

(

)

(

)

(

)

[

i-1, j 1 i,j 1 - i-1, j-1 - i,j 1

]

4 1 Fs= ψ + +ψ + ψ ψ − + + + + (3.24.d)

Comme nous l’avons montré précédemment dans le tableau 3.1, le coefficient ΓΦ prend la

valeur(1/Pr).

En portant cette valeur dans le système (3.20), les coefficients De, Dw, Dn et Ds

s’écrivent :       θ ∆ η ∆ = = η ∆ θ ∆ = = P 1 D D P 1 D D r w e r s n (3.25)

Par suite, les nombres de Péclet dans le système (3.19) deviennent

           η ∆ θ ∆ = η ∆ θ ∆ = θ ∆ η ∆ = θ ∆ η ∆ = F P P F P P F P P F P P w r w e r e s r s n r n (3.26)

Pour homogénéiser les notations dans l'équation (3.21), on écrit W, P, E, N et S respectivement

(

i,j-1

)

;

( )

i, ; j

(

i,j+1

)

;

(

i+1,j

)

;

(

i-1,j

)

.

Les coefficients aE, aW, aN et aS sont pris au nœud (i, j).

Ainsi l'équation (3.21) peut s'écrire sous la forme:

( )

i, j a T

(

i ,j 1

)

a T

(

i ,j 1

)

a T

(

i 1, j

)

a T

(

i 1, j

)

T

aP + = E + + + W + − + N + + + S + − (3.27)

3.3.1 Discrétisation des Conditions aux limites

Pour satisfaire les conditions imposées à la température des parois, on doit avoir: § Sur la paroi du cylindre circulaire extérieur (I=NI).

aP = 1

aE = aW = aN = aS = 0 et ST = 0

§ Sur la paroi du cylindre circulaire intérieur (I=1). - Cas I : aP = 1

aE = aW = aN = aS = 0 et ST = 1

- Cas II : aP = 1

aN = 1

aE = aW = aN = aS = 0 et ST = H.∆η

3.4 Discrétisation de l'équation de quantité de mouvement L'équation discrétisée (3.13) peut se mettre sous forme:

a

ω

= a

ω

+ a

ω

+ a

ω

+ a

ω

+ +b W W + E E + S S + N N + P P (3.28)

L'identification coefficient a à celui de l'équation (3.15) donne: _P aP =aN +aS +aE +aW

avec:

SP.∆V = 0

Les coefficientsa ,_S a ,_N a et _E a ont pour expressions celles données par le système _W (3.17).

Lorsque le coefficient ΓΦ est égal à l'unité, comme nous l'avons montré dans le tableau

3.1, aux interfaces e, w, n et s; les coefficients De, Dw, Dn et Ds se déduisent des expressions suivantes:       θ ∆ η ∆ = = η ∆ θ ∆ = = D D D D w e s n (3.31)

Les nombres de Péclet dans le système (3.19) deviennent:

        θ ∆η ∆ θ ∆ = θ ∆ η ∆ = θ ∆ η ∆ = F P F P F P e e s s n n (3.32)

Les coefficientsF ,_e F , w F et n F ont respectivement les mêmes expressions que dans le s

système (3.24.a), (3.24.b), (3.24.c) et (3.24.d).

Dans le tableau 3.1, nous pouvons constater que le terme constant (S0) du terme de source est donnée par:

{

[

( )

( )

]

( )

( )

[

]

}

θ Τ cosα θ η, G -sinα θ η, F + η Τ sinα θ η, G + cosα θ η, F H.Gr = S + + 0 ∂ ∂ ∂ ∂ (3.33)

Par conséquent, le coefficient b devient: b=_S0∆V avec: ∆V= _H2.∆η.∆θ.1 b s'écrit donc:

{

[

( )

( )

]

( )

( )

[

]

}

Δη.Δθ θ Τ cosα θ η, G -sinα θ η, F + η Τ sinα θ η, G + cosα θ η, F .Gr H = b + + m 3 ∂ ∂ ∂ ∂ (3.34) avec:

(

)

(

)

η ∆ − − + = η ∂ ∂ ₊ + + 2 j , 1 i T j , 1 i T T j , i (3.35)

(

)

(

)

θ ∆ − − + = θ ∂ ∂ + + + 2 1 j ,i T 1 j ,i T T j , i (3.36)

Pour homogénéiser on utilise les notations citées au paragraphe précédent, les nœuds W, P, E, N et S deviennent respectivement

(

i,j-1

)

;

( )

i,j ;

(

i,j+1

)

;

(

i+1,j

)

;

(

i-1,j

)

. Les coefficients aN,aS, aE, aW et b sont pris au nœud

( )

i, . j

L'équation du mouvement discrétisée (3.28) s'écrit finalement:

( )

(

)

(

)

(

i , j+1

)

+ a ω

(

i,j-1

)

+ b ω a + j , 1 i ω a + j , 1 + i ω a = j , i ω a + W W + E E + S S + N N + P P

En déterminant la vorticité ω sur les parois, nous utilisons la méthode élaborée par + ROACHE [40], qui a exprimé ω en fonction de + _{ψ et utilisée un développement de Taylor:} +

-condition sur la paroi du cylindre circulaire intérieur (I=1). 1 η η 2 2 2 2 2 1 θ ψ η ψ H 1 ω = + + +       ∂ ∂ + ∂ ∂ − =

Développons en série de Taylor la fonction de courant au voisinage de la paroi interne

(

i=1,j

)

:

( )

( )

( ) ( )

( )

1 , j ... 2! j , 1 1! j , 1 j , 2 ₂ 2 2 + η ∂ ψ ∂ η ∆ + η ∂ ψ ∂ η ∆ + ψ = ψ+ + + +

La vorticité sur cette paroi s'écrit :

( )

( )

(

)

( )

(

)

( )

( )

2

(

(

2, j

)

( )

1 , j

)

1 j , 1 j , 1 2 1 j , 1 1 H 1 j 1, 2 2 2               ψ − ψ η ∆ + θ ∆ − ψ + ψ − + ψ − = ω + + + + + +

• Sur la paroi du cylindre extérieur (I=NI).

2 η η 2 2 2 2 2 2 θ ψ η ψ H 1 ω = + + +       ∂ ∂ + ∂ ∂ − =

La vorticité sur cette paroi s'écrit:

( )

( )

(

)

(

)

(

)

( )

( )

2

(

(

NI-1 , j

)

(

NI, j

)

)

1 j , NI j , NI 2 1 j , NI NI H 1 j NI, 2 2 2               ψ − ψ η ∆ + θ ∆ − ψ + ψ − + ψ − = ω + + + + + +

3.5 Discrétisation de l'équation de la fonction de courant

Réécrivons l'équation adimensionnelle (2.22) sous la forme suivante:

    θ ∂ ψ ∂ θ ∂ ∂ +     η ∂ ψ ∂ η ∂ ∂ = ω − + + + H2 (3.41) Nous remarquons que l'identification de cette équation à l'équation (3.3) est compliquée,

( ) ( )













θ ∂ ψ ∂ + η ∂ ψ ∂ = ω − + + + 2 2 j , i 2 2 j , i 2 j ,i j ,i H Avec: ₂ i+1,j i1,₂j i,j i,j+1 i,j₂1 i,j 2 2 2 Δy 2f -f + f + Δx 2f -f + f = y f + x f - -∂ ∂ ∂ ∂ (3.42) Nous en déduisons:

( ) ( )

(

)

_{( )}

(

)

( )

(

)

(

)

_{( )}

( )

2 ,ij 1 j ,i 1 j ,i j i, 2 j , 1 i j , 1 i j ,i j ,i H 2 2 2     θ ∆ ψ − − ψ + + ψ +     η ∆ ψ − − ψ + + ψ = ω − + + + + + + + (3.43)

La fonction de courant au nœud P sera donc exprimée en fonction de celle aux nœuds W, N, E et S et s'écrit:

( )

_{( ) ( )}

(

_{( )}

)

(

)

(

)

(

)

( )

,ij 1 H

( ) ( )

,ij ,ij 1 j ,i j , 1 i j , 1 i 1 1 2 1 j ,i 2 2 2 -1 2 2    ω + θ ∆ − ψ + + ψ +    η ∆ − ψ + + ψ       θ ∆ + η ∆ = ψ + + + + + + (3.44)

3.5.1 Discrétisation des Conditions aux limites

Les conditions aux limites associées aux parois, que nous avons déterminées dans les équations (2.23.a) et (2.26.a), deviennent:

• Condition sur la paroi du cylindre circulaire intérieur (I=1):

( )

( )

( )

0 2 j , 3 j , 2 4 j , 1 3 j , 1 = η ∆ ψ − ψ + ψ − = η ∂ ψ ∂ + + + +

( )

( )

( )

3 j , 3 j , 2 4 j , 1 = ψ − ψ ψ+ + + (3.45.a)

• Condition sur la paroi du cylindre circulaire extérieur (I=NI):

(

)

(

)

(

)

3 j , 2 NI j , 1 -I N 4 j ,I N = ψ − ψ − ψ+ + + (3.45.b)

Nous obtenons donc un système d'équations linéaires que nous résolvons par la méthode itérative de "relaxations successives".

3.6 Discrétisation des composantes de la vitesse

Les équations (2.21.a) et (2.21.b) nous donnent respectivement les composantes

adimensionnelles V_η+ et V de la vitesse; ROACHE [40], utilise les différences centrées pour _θ+ obtenir une expression discrétisée de ces composantes, ce qui nous donne:

( )

( )

( )

_

(

)

∆θ

(

)

_ − ψ + ψ =   θ ∂ ψ ∂ = + + + + η 2 1 j ,i -1 j ,i j ,i H 1 j ,i H 1 j ,i V j i, (3.46.a)

( )

( )

( )

_

(

)

∆η

(

)

_ − ψ + ψ − =    η ∂ ψ ∂ − = + + + + θ 2 j , 1 i j , 1 i j ,i H 1 j ,i H 1 j ,i V j i, (3.46.b) ∀ (i, j) i ≠ 1 ; i ≠ NI j ≠ 1 ; j ≠ NN 3.7 Processus du calcul

Pour résoudre le système d'équations (3.27), (3.37) et (3.38) nous utilisons la méthode proposée par E.F. NOGOTOV [36].

Ces équations peuvent se mettre sous la forme suivante adaptée précisément à une résolution à l'aide d'une méthode itérative à coefficient de relaxation :

( ) (

) ( )

[

(

)

(

i,j 1

)

_{a T}

(

i 1, j

)

_{a T}

(

i 1, j

)

]

T a 1 j , i T a a G j , i T G 1 j ,i T 1 n S n N 1 n W n E P T n T 1 n − + + + − +     + − = + + + (3.47)

( ) (

) ( )

[

(

)

(

,ij 1

)

_a

(

i 1, j

)

_a

(

i 1, j

) ( )

b ,i j

]

a 1 j ,i a a G j ,i G 1 j ,i 1 n S n N 1 n W n E P W n W 1 n + − ω + + ω + − ω + + ω     + ω − = ω + + + (3.48)

( ) (

) ( )

_{( ) ( )}

(

)

(

)

( )

(

)

( )

(

)

( )

( )

j ,i j ,i H 1 j ,i 1 j ,i j , 1 i j , 1 i 1 1 2 G j ,i G 1 j ,i 1 n 2 2 1 n n 2 1 n n 1 2 2 P n P 1 n             ω + θ ∆ − ψ + + ψ + η ∆ − ψ + + ψ       θ ∆ + η ∆ + ψ − = ψ + + + − + (3.49) n : ordre de l'intégration.

Les paramètres GT, GW et GP sont les "facteurs de relaxation". Leurs valeurs

1/ Initialisation des valeurs de la température, de la vorticité et de la fonction de courant au sein du maillage.

2/ Calcul de la distribution de la température. 3/ Calcul de la vorticité.

4/ Calcul de la distribution de la fonction de courant. 5/ Calcul des composantes des vitesses.

6/ Le processus itératif est répété jusqu'à ce qu'il n'y ait plus de changement significatif de la valeur de ψ par rapport au critère de convergence suivant :

₁₀ max max max 8 1 n n 1 n − + + ≤ ψ ψ − ψ

7/ Le même critère est utilisé pour la température. 8/ Stockage des valeurs de T, ω, ψ.

Début Lecture et écriture Des données Initiation des T, ω, ψ Calcul de la Distribution de T Calcul de la Vorticité ω Calcul de la fonction De courant ψ Calcul de la distribution de

T sur la paroi interne

Calcul des composantes Des vitesses Condition De convergence Sur ψ

(

ψn1+ ψn

)

2 = ψ +

(

_{T T}

)

2 T= n+1+ n Stokage des Valeurs de T, ψ, ω Calcul du nombre De Nusselt local n > nmax Pas de Convergence Fin Condition De convergence Sur T n=0, k=0 n=n+1, k=k+1 oui oui non non non oui

Chapitre 4

Résultats

4.1 Introduction

Nous considérons trois espaces annulaires formés par les deux cylindres excentrés caractérisés respectivement par les excentricités relatives (C2=0.1, 0.2 et 0.4) et le rapport des

rayons C1=2.

Dans notre étude, nous avons utilisé les conditions pariétales thermiques suivantes :

− La paroi cylindrique externe est maintenue isotherme à la température T2.

− La paroi cylindrique interne (est maintenue isotherme à la température T1> T2), dans

un premier cas (puis soumise à une densité de flux chaleur constante) dans un deuxième cas.

4.2 Etude du maillage

Dans cette étude plusieurs maillages ont été utilisés arbitrairement pour la configuration suivante : (α=90° et C2 =0.4. Pour Gr=102, Gr=103, Gr=104, Gr=5.104, Gr=105 et Gr=106),

pour voir leurs effets sur les résultats, le tableau 4.1 nous montre donc, la variation du nombre de Nusselt moyen et de la valeur maximale de la fonction de courant, en fonction du nombre de nœuds, et nous a permis de choisir le maillage (101x111).

4.3 Comparaison des résultats issus de ce code de calcul avec ceux de la littérature T. H. Kuehn et R. J. Goldstein [15] ont élaboré une étude expérimentale et numérique sur la convection naturelle dans l’espace annulaire compris entre deux cylindres concentriques et horizontaux dont le rapport des rayons a été pris égal à 2.6, ils ont calculé une conductivité thermique équivalente locale, définie comme étant le rapport d’un gradient de température lors d’un échange convectif, sur un gradient de température lors d’un échange conductif :

conduction convection éq T T K η ∂ ∂ η ∂ ∂ = ₊ + 111x121 101x111 91x101 81x91 71x81 61x71 51x61 41x51 31x41 21x31 11x21 ηNIxθNN 0.48 0.60 0.62 0.64 0.68 0.87 1.25 1.22 1.68 2.90 Er (%) G r=10 6 32.291 32.449 32.645 32.848 33.060 33.287 33.579 33.998 34.413 34.992 33.975 Ψmax 0.83 0.88 0.92 0.97 1.04 0.94 1.18 0.67 0.66 10.87 Er (%) 13.483 13.595 13.715 13.842 13.977 14.122 14.256 14.425 14.523 14.427 12.858 Num1 0.80 1.07 1.13 1.05 0.88 1.06 1.37 1.12 1.98 11.76 Er (%) Gr =10 5 8.303 8.370 8.460 8.556 8.646 8.722 8.815 8.936 9.036 8.857 7.815 Ψmax 0.38 0.39 0.40 0.43 0.44 0.51 0.38 1.50 2.21 4.52 Er (%) 7.095 7.122 7.150 7.179 7.210 7.242 7.279 7.307 7.417 7.253 6.925 Num1 1.01 1.04 1.11 1.12 1.09 0.96 0.57 0.15 0.90 10.02 Er (%) Gr =5 .10 4 4.935 4.985 5.037 5.093 5.150 5.206 5.256 5.286 5.278 5.229 4.705 Ψmax 0.22 0.25 0.25 0.23 0.29 0.26 0.25 0.09 0.37 2.36 Er (%) 6.324 6.338 6.354 6.370 6.385 6.404 6.421 6.437 6.443 6.419 6.267 Num1 1.05 1.03 1.18 1.17 1.15 1.14 0.90 0.15 1.49 11.58 Er (%) Gr =10 4 1.241 1.254 1.267 1.282 1.297 1.312 1.327 1.339 1.341 1.321 1.168 Ψmax 0.24 0.38 0.09 0.10 0.12 0.16 0.21 0.82 0.27 0.57 Er (%) 5.693 5.679 5.701 5.706 5.712 5.719 5.728 5.740 5.787 5.771 5.804 Num1 0.74 1.48 0.73 1.45 0.71 7.09 9.92 0.00 8.33 14.10 Er (%) Gr =10 3 0.134 0.135 0.137 0.138 0.140 0.141 0.131 0.144 0.144 0.156 0.134 Ψmax 0.05 0.07 0.07 0.10 0.10 0.07 0.34 0.33 0.56 1.12 Er (%) 5.609 5.612 5.616 5.620 5.626 5.632 5.636 5.655 5.674 5.706 5.770 Num1 0.00 0.00 0.00 0.00 0.00 0.00 0.00 7.14 6.66 14.28 Er (%) Gr =10 2 0.014 0.014 0.014 0.014 0.014 0.014 0.014 0.014 0.015 0.014 0.012 Ψmax 0.04 0.05 0.09 0.09 0.12 0.16 0.23 0.35 0.58 1.17 Er (%) 5.607 5.609 5.612 5.617 5.622 5.629 5.638 5.651 5.671 5.704 5.771 Num1

Tableau 4.1 Variation du nombre de Nusselt moyen et de la valeur maximale de la fonction de courant en fonction du nombre de nœuds

illustre bien cette comparaison et nous remarquons que quantitativement nos résultats et les leurs sont en très bon accord.

Etude Numérique Pr 0.7 0.7 0.7 0.7 0.7 Ra 102 103 6x103 104 7x104 Paroi interne Ref. [15] 1.000 1.081 1.736 2.010 3.308 nos calculs 1.000 1.066 1.730 2.068 3.693 |Ecart (%)| 0 1.4 0.3 2.8 10.4 Paroi externe Ref. [15] 1.002 1.084 1.735 2.005 3.226 nos calculs 1.002 1.066 1.736 2.078 3.758 |Ecart (%)| 0 1.7 0.05 3.5 14.1 Etude Expérimentale Pr 0.706 0.706 0.706 0.702 0.702 Ra 2.11x104 3.65x104 5.72x104 7.43x104 9.56x104 Paroi interne Ref. [15] 2.34 2.75 3.09 3.37 3.62 nos calculs 1.95 2.28 2.593 3.755 4.019 |Ecart (%)| 20 20.6 19.16 10.25 9.93

Tableau 4.2 Comparaison du nombre de Nusselt moyen de la référence [15] avec nos résultats

4.4 Première condition pariétale thermique : Paroi interne isotherme 4.4.1 Influence du nombre de Grashof

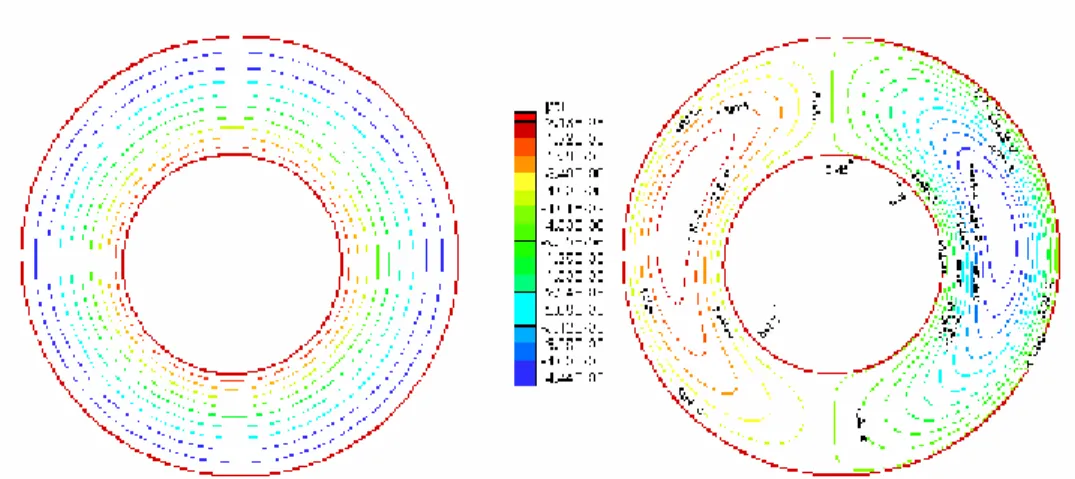
4.4.1.1 Isothermes et lignes de courants

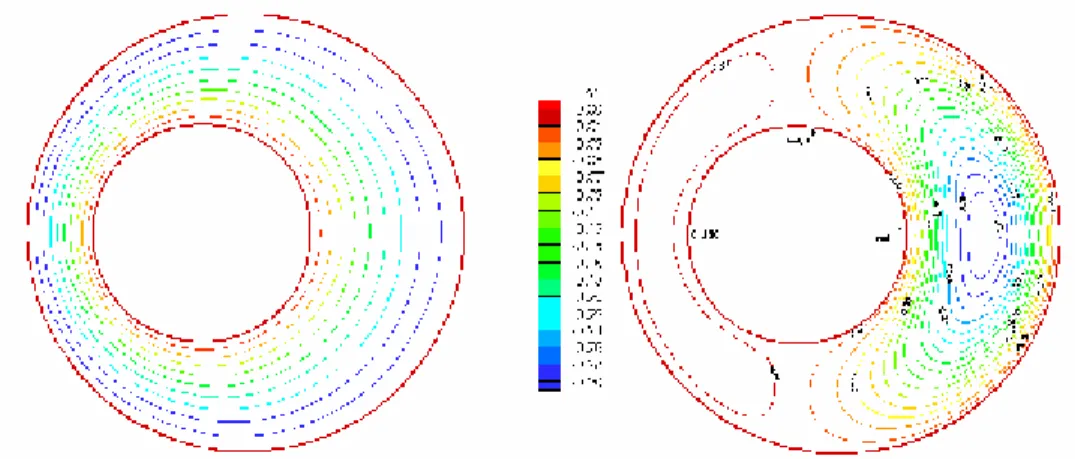
Les figures (4.1-4.15) représentent les isothermes et les lignes de courant pour différentes valeurs du nombre de Grashof Gr quand α=0°.

Ces figures montrent que le régime de l'écoulement est monocellulaire. Du côté gauche, l'écoulement tourne dans le sens trigonométrique et du côté droit, il est de sens contraire (les particules du fluide se déplacent vers le haut sous l'action des forces de la poussée d'Archimède).

Pour Gr=103, Gr=104 et Gr=5.104 les figures (4.1), (4.2), (4.3), (4.7), (4.8) et (4.9) respectivement pour (C2=0.1, 0.2) représentent les lignes de courant du fluide dont

Les isothermes sur ces figures là sont des courbes presque parallèles et épousent assez bien les profils des parois. Dans ce cas la distribution des températures est simplement décroissante de la paroi chaude vers la paroi froide.

On peut dire que les transferts thermiques se font par pseudo conduction au niveau de la paroi chauffée, car les champs des vitesses sont différents de zéro. Les valeurs de la fonction de courant qui sont données sur ces figures sont très petites.

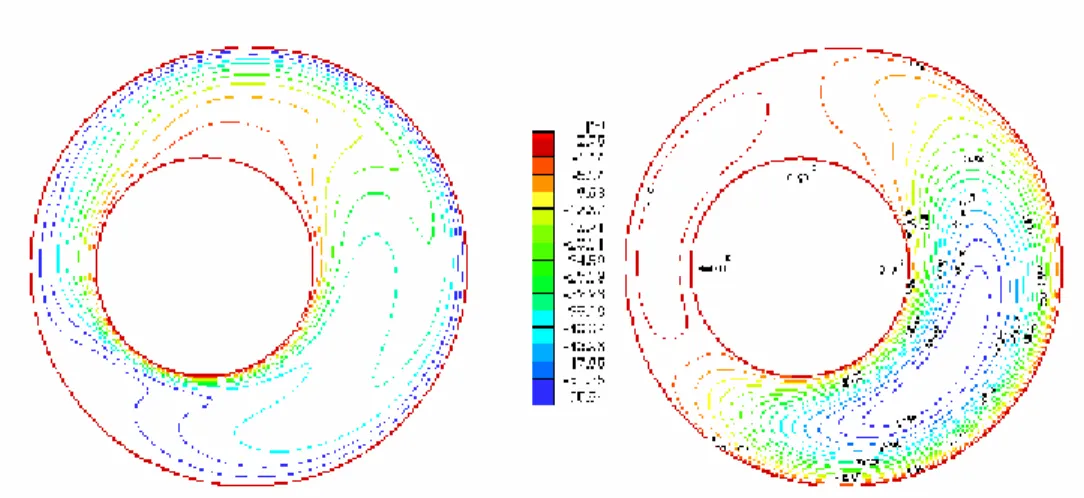
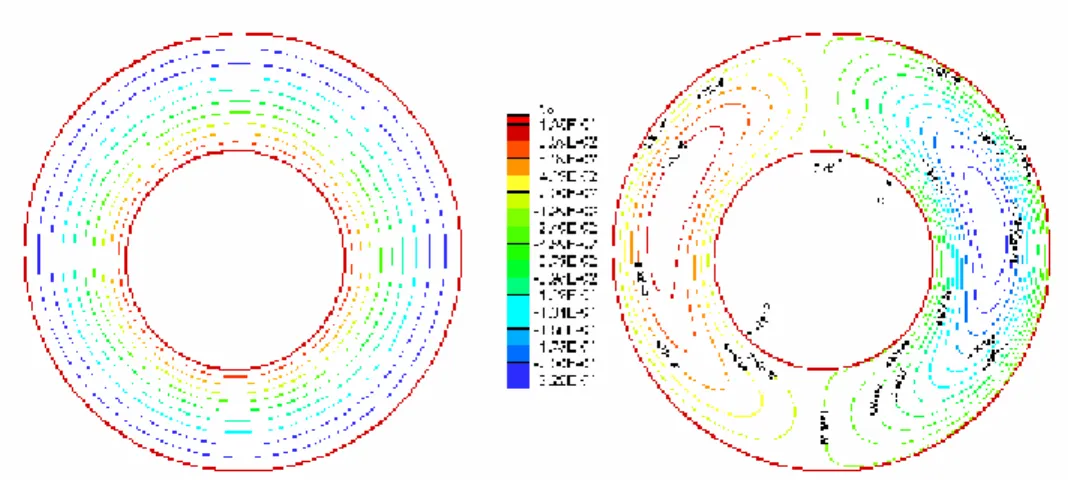
Dans les autres configurations géométriques pour Gr=103, Gr=104 les lignes isothermes des figures (4.12) et (4.13) respectivement pour (C2=0.4) sont des courbes presque parallèles,

les lignes de courant du fluide s'organisent essentiellement dans le coté gauche élargi et tournent très lentement dans le sens horaire, les valeurs de la fonction de courant sont très petites, ce qui traduit une pseudo conduction aussi.

Pour Gr=5.106, Gr=5.104 les lignes isothermes des figures (4.10) et (4.14) respectivement pour (C2=0.2 et 0.4) se modifient sensiblement, et les valeurs de la fonction de

courant mentionnées sur la même figure augmentent aussi sensiblement, ce qui traduit une transformation du transfert conductif au transfert convectif, mais il reste relativement faible, le rétrécissement de l'espace libre favorise le transfert conductif entre les deux surfaces d'échange comme le montre l'allure des lignes isothermes.

Cependant la valeur Gr=5.108 pour (C2=0.1), Gr=5.107 pour (C2=0.2) et Gr=106 pour

(C2=0.4) représentées, respectivement par les figures (4.6), (4.11) et (4.15) montre que les

lignes isothermes se modifient et finissent par adopter la forme d'un champignon. La distribution de la température est décroissante de la paroi chaude vers la paroi froide. Le sens de la déformation des isothermes est conforme au sens de rotation des lignes de courant. En régime laminaire, on peut dire que, sous l'action du mouvement des particules qui décollent de la paroi chaude, les lignes isothermes se « voûtent » et s'éloignent de la paroi à cet endroit. Les valeurs des fonctions de courant augmentent ce qui signifie que la convection s'intensifie.

Notons que les lignes isothermes, de toutes les figures citées plus haut, ont été tracées avec un écart de température adimensionnelle égal à 0.1.

Figure 4.1 Isothermes et lignes de courant pour α=0°, Gr=103 et C2=0.1

Figure 4.2 Isothermes et lignes de courant pour α=0°, Gr=104 et C2=0.1

Figure 4.4 Isothermes et lignes de courant pour α=0°, Gr=5.106 et C2=0.1

Figure 4.5 Isothermes et lignes de courant pour α=0°, Gr=5.107 et C2=0.1

Figure 4.7 Isothermes et lignes de courant pour α=0°, Gr=103 et C2=0.2

Figure 4.8 Isothermes et lignes de courant pour α=0°, Gr=104 et C2=0.2

Figure 4.10 Isothermes et lignes de courant pour α=0°, Gr=5.106 et C2=0.2

Figure 4.12 Isothermes et lignes de courant pour α=0°, Gr=103 et C2=0.4

Figure 4.13 Isothermes et lignes de courant pour α=0°, Gr=104 et C2=0.4

4.4.1.2 Nombre de Nusselt local

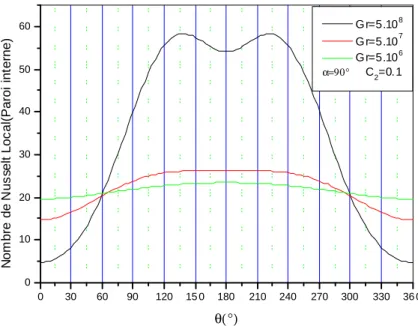
Nous déterminons les nombres de Nusselt locaux dont les variations le long des parois sont étroitement liées aux distributions des isothermes et des isocourants, de sorte que, qualitativement, ces variations et ces distributions peuvent souvent se déduire les unes des autres. Par exemple, si l'on considère un point courant sur une paroi suivant une coordonnée; l'observation d'une diminution monotone du nombre de Nusselt local correspond à un écoulement dirigé suivant cette coordonnée; l'observation d'une augmentation correspond à un écoulement dirigé en sens opposé.

4.4.1.2.1Variation du nombre de Nusselt local sur la paroi du cylindre intérieur et extérieur

Les figures (4.16.a), (4.16.b), (4.17.a) (4.17.b), (4.18.a) et (4.18.b) illustrent la variation du nombre de Nusselt local sur la paroi du cylindre interne et externe, et nous permettent de remarquer qu'avec l'augmentation du nombre de Grashof, la valeur du nombre de Nusselt local augmente, et avec la diminution du nombre de Grashof, le nombre de Nusselt local diminue ce qui est évident.