Best basis algorithm for signal enhancement c H. Krim ... [et al.].

January, 1995

LIDS- P 2284

Research Supported By:

ARO DAAL03-92-G-0115

AFOSR F49620-92-J-2002

NSF MIP-9015281

Best Basis Algorithm for Signal Enhancement*

Krim, H.

Mallat, S.

Donoho, D.

Willsky, A.S.

LIDS-P-2284

January 1995

BEST BASIS ALGORITHM FOR SIGNAL ENHANCEMENT

H. Krim S. Mallatt D. Donoho: and A.S. Willsky

Stochastic Systems Group, LIDS, Room 35-431,

MIT, Cambridge, MA 02139,

e-mail: ahk©mit.edu, tel: 617-258-3370, fax: 617-258-8553, tCourant Institute, NY. NY,

tStanford Univ., CA

This paper appeared in the proceedings of ICASSP'95 bases can approximate it with only a few non-zero co-efficients. It then becomes necessary to adaptively

se-ABSTRACT lect an appropriate "best basis" which provides the best

We propose a Best Basis Algorithm for Signal Enhance- signal estimate by discarding (thresholding) the noisy ment in white gaussian noise. We base our search of coefficients. This approach was first proposed by John-best basis on a criterion of minimal reconstruction er- stone and Donoho [3] who proceed to a best basis search ror of the underlying signal. We subsequently com- in families of orthonormal bases constructed with pare our simple error criterion to the Stein unbiased wavepackets or local cosine bases.

risk estimator, and provide a subtantiating example to This paper focuses on a more precise estimate of the demonstrate its performance. mean-square error introduced by the thresholding algo-rithm, which leads to a new strategy of searching for

1.

Introduction

a best basis. The precision of the estimate is analyzed A universal wavelet basis is more than one could achieve by calculating the exact mean square error with the help of the Stein unbiased risk estimator in a Gaussian given the plethora of classes of signals. Adapted wavelet help of the Stein unbiased risk estimator in a Gaussian bases have consequently been proposed [1,7,9] to alle- setting.

viate this problem. In a sense, an adapted (best) basis Next section gives a brief review of noise removal serhisitmteyte.l(or signal en- .by thresholding and of wavepacket orthonormal bases. search is intimately tied to noise removal In Section 3, we derive the error estimate of our signal To address an inherent variability of thcement).ropy- enhancement procedure. In Section 4, we compare the basedTo address s earch [9] in not variability of the entropy- class optimal best basis search criterion to a suboptimal one, based basis search [9] in noisy scenarios, a new class _{of algorithms have recently been studied in 31} and provide a numerical example of the resulting algo-.and and provide a numerical example of the resulting algo-of algorithms have recently been studied in [3] and rithm to enhance underwater signals (whale signals) in also in [6]. Donoho and Johnstone [3] base their algo- rthm to enhance underwater signals (whale signals) in rithm on the removal of additive noise from

determin-istic signals. The signal is discriminated from the noise 2.

Noise Removal by Thresholding

by choosing an orthogonal basis which efficiently

ap-proximates the signal (with few non-zero coefficients). Let s[m] be a deterministic discrete unknown signal Signal enhancement is achieved by discarding compo- embedded in a discrete white Gaussian noise,

nents below a predetermined threshold. Wavelet or- [m] = sm] + n[m] with n[m] N(O, 2), (1) thonormal bases are particularly well adapted to

ap-proximate piece-wise smooth functions. The non-zero

wavelet coefficients are typically located in the neigh- and m = o . ., N. Let 1 = {WP}1•P•N be a basis

borhood of sharp signal transitions. It was shown in [4] of our observation space. The thresholding procedure that thresholding at a specific level a noisy piece-wise consists of discarding all inner products < x, Wp > smothat thresholdin a wavelet basis, provides a quasi op- above T, in order to reconstruct an estimate s of s. smooth signal in a wavelet basis, provides a quasi op- Let K be the number of inner products such that timal min-max estimator of the signal values. Let K be the number of inner products such that

When a signal includes more complex structures I < , W > I > T. Suppose that < x, Wp > are sorted and in particular high frequency oscillations, wavelet so that I <x, Wp > i decreasing for 1 < p < N,

The work of the first and last authors was supported in K

part by the Army Research Office (DAAL-03-92-G-115), Air S[m] = , < X, Wp > Wp[m].

Force Office of Scientific Research (F49620-92-J-2002) and Na- n=l

tional Science Foundation (MIP-9015281). The second author is

supported by AFOSR grant F49620-93-1-0102 and ONR grant The threshold T is set such that it is unlikely that l < n, Wp > I > T. For a Gaussian white noise

n, Wp > 12}1<p<N is "2o.2logN" w.p.1 [5]. To guar- are above T, the error is antee that the thresholded coefficients always include

some signal information, one chooses T = 2r 2log N. K N

which was shown to be the optimal threshold from a IIS - 112 = E

I

<n, Wp >12+ E

1<s,

Wp> 12 number of perspectives [4,6]. The vectors lopW for p < IK n=l n=K+l

generally have for weights non-zero signal coefficient (2)

l < s, WP > I. Since n[m] is a random process, K is a random variable If the energy of s(n) is concentrated in high ampli- dependent upon n(.). Given that n[m] is a Gaussian tude coefficients, such a representation can provide an white noise of variance c2, < n, Wp > has a variance accurate estimate of s(m). Wavelet bases are known o-2

. To estimate

Ils

-_112, we obtain for a given K, to concentrate the energy of piece-wise smooth signals

into a few high energy coefficients [2]. )

When the signal possesses more complex features, E.{(< n, Wp >)2 I K} . Ka2

one has to search for the basis which would result in n=1

its best compressed representation. In [3] a proposed and to search for a basis, amounted to that which resulted

in the best noise suppression among all wavepacket or N

local cosine bases. E< x, W > 12 K} =

We thus have a collection of orthonormal bases n=K+l

(Bi = {Wp}l<p<N)iEI among which we want to choose N N

the basis which leads to the best thresholded estimate < s, W > 12 + E{(< n, Wp >)2 K}

s. We consider two particular classes of families of or- n=K+l n=K+l

thonormal bases. Trees of wavepacket bases studied

by Coifman and Wickerhauser [9], are constructed by Since the basis includes N vectors

quadrature mirror filter banks and are composed of sig- 2 I K} = -N 2 ± 2Ko2 + nals that are well localized in time and frequency. This EENs _

family of orthonormal bases divides the frequency axis n=K+l < Wp > 2 j K} (3) in intervals of different sizes, varying with the selected

wavepacket basis. Another family of orthonormal bases The estimator e2 can be written as an additive cost studied by Malvar [7] and Coifman and Meyer [1] can function (?). Let us define

be constructed with a tree of window cosine functions.

These orthonormal bases correspond to a division of Cu if

lul

> T the time axis in intervals of varying sizes. For a dis- C(u) = +2 2 if lul < T, crete signal of size N, one can show that a tree of

wavepacket bases or local cosine bases include more N

than 2N bases, and the signal expansion in these bases eX = -No2 + E{ C(I <

x,

Wp> 12)}.

is computed with algorithms that require O(NlogN) n=l

operations, since these bases include many vectors in Among a collection {Bt}2 of orthonormal bases, we pro-common. Wickerhauser and Coifman [9] proved that pose to use this estimated error to search for the best for any signal f and any function C(x), finding the best basis *i3 which minimizes *N C(I < x, W > 2),

basis Bi ° which minimizes an "additive" cost function n=l

~~~~~over

all bases minimize the conditional error estimate. With this

~i.e.

over all bases

cost function, we are able to efficiently compute the

N best basis in wavepacket and local cosine tree bases,

Cost(ft, i) =

ZC(l

< fWi > 12) with O(NlogN) operations.

n=l In the following theorem we show that the

condi-tional estimator e: of Ils - 112 is biased and compute requires O(N log N) operations. the biais by using the Stein unbiased risk estimator [8]. In this paper we derive an expression of C(x) so As will be shown in Section 3, the bias will not, how-that Cost(x, 5i) approximates the mean-square error ever, have a bearing on the optimality of our search, if

Ils

- 112 of the noise removal algorithm. The best noise a threshold T is judiciously chosen. removal basis is then obtained by minimizing this cost

function. Theorem 1 Let {WP}1<p<N be an orthonormal basis

of our observations space. If n[p] is a discrete Gaussian

3.

Error Estimation

white noise of variance oa2, the biais of the estimator is

We first derive with qualitative arguments an estimate N

of the error Ils-sII and then prove that this estimate is a EIlls - s^12] - E[2 = 2TU2 E (q(T-< s, Wp >) +

lower bound of the true error. Since x[m] = s[m]+n[m], p=1

following the thresholding and assuming that K terms P

with 4. Evaluation and Numerical Results

1 2

5(u) = 1e- 2 To analyze the performance of our error-based criterion

for a best basis selection, we first numerically compute

Proof: First define, biais for different classes of signals by using Eq. (4). We then apply this criterion to choose a best basis among

Yt(?7p) = ]P{I%',lI>[T} wavepacket bases, and subsequently to enhance signals

g(77p) = -7rp1

.Z{lhpl<T}, (5) of biological underwater sounds.

Let us consider a class of signals s[p] that are well with rp - N (rsp, a2), with r1sp being the true signal approximated by K coefficients of the orthonormal ba-coefficient, in rp = rsp + rTnp and Z{.} is an indicator sis {WP}1<p<N. We associate to the inner products

function constrained by its argument. We then use < s, Wp > a distribution density given by

7(77) = V~P + 9(7p), N-K 0

to obtain the following, N + Nh(0)

N N This may be interpreted as on average, out of N

coef-E{ZQY(TJp) -~,qP)2} = V'E (Uqp~ - ti}p) + (g(ijp ))2} ficients there are N - K zero-coefficients and K non-zero coefficients whose values are specified by h(O). The

P=i p=' smaller the proportion K/N the better the performance

N of the noise removal algorithm. Fig. 1 shows the mean-=

Z

E{np} + 2E{7,1pg(?1p)} square error EIlls - s§l2] as a function of T, for different

p=l values of K/N. In these numerical computations, we

+E{g92(rp)} . (6) suppose that the signal to noise ratio is of OdB. The parameters of h(O) are adjusted so that the total signal Using the property [8], energy is equal to the total noise energy. The mini-mum expected value of the unbiased risk is obtained

E{r~npg(Op)=} = 7npg('7np + ?7sp) (?np)d7np for a value of T which is close to 2or2 log N'. The value of this optimal T does not remain invariant and is a

_-

]

9(7, +1p)'(71np)dnp function of K/L. Fig. 1 also gives the expected er-ror E[e2 ] computed with our estimator. The precision

012 f ga (,qnp

rof

+ ?7,p)O(?7p, this lower bound increases when the poportion of

- 0.2] g'(?np + s non-zero coefficients K/L decreases. For small values

of T the biais is very large but it is considerably re-and calling upon derivatives in the generalized (distri- duced at T = 2a2 log N which corresponds to the typi-butions) sense, one can write, cal threshold we choose in our pratical algorithm. For

d this threshold, the suboptimal error estimator provides

Z 77p>pO = o0, a resonable estimate of the mean-square error.

dr7p Note that the bias term in Eq. (4 assumes a prior with 60 denoting the Dirac impulse, and which we can knowledge of the signal coefficients, which is clearly not in turn use to derive the case. This difficulty can be partially lifted by ob-taining rather an upper bound of the bias. This is

car-f 9g'(]np + ?7sp)q5(7?np)drlnp = ried out by picking the Maximum Likelihood Estimate, - fI{J?7pl<T}c(?7np)dT7np + T (q(T - rsp) 7 ±+ (-T - r7sp)) namely the observation itself (i.e. the noisy coefficient)

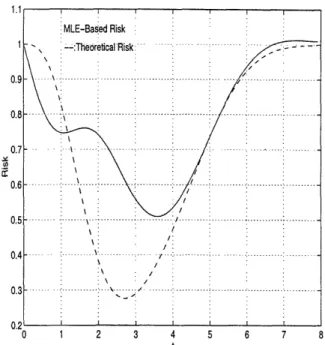
at the given point. We show in Fig. 2 that the effect After susbtitution of the above expressions back into on the risk can be rather drastic in comparison to the

Eq. 6, we obtain, optimal risk.

N N We show in Fig. 3 a noisy whale sound2 with its

EE(Y(

-

p)

2} = e2 + 2Tr72

Z(

O(T - p) + best enhanced representation, using the proposed

algo-p--l p---p1 rithm.

0(-T - rsp)).

5.

References

* [1] R. Coifman and Y. Meyer. Remarques sur l'analyse This theorem proves that the expected value of our de Fourier a fenetre. C. R. Acad. Sci. Serie I, pages conditional estimator e, is a lower bound of the mean- 259-261, 1991.

square error. The biais of the estimator is explained by

the assumpotion that all signal components are always [2] I. Daubechies. Orthonormal bases of compactly above I T I in (2) and (3). We thus did not take into supported wavelets. Com. Pure and Appl. Math., account the errors due to an erroneous decision (i.e. XLI:909996, 1988.

signal + noise component may indeed fall below the 'N=100.

[3] D. Donoho and I. Johnstone. Ideal denoising in an orthogonal basis chosen from a library of bases. Oct. 1994. preprint Dept. Stat., Stanford Univ.

[4] D. L. Donoho and I. M Johnstone. Ideal spatial ,! L s!, adaptation by wavelet shrinkage. preprint Dept. MLE-Saied Risk

_:Theoretcal.Risk... Stat., Stanford Univ., Jun. 1992.

[5] B. Gnedenko. Sur la Distribution Limite du Terme 0.9 ... ... .... Maximum d'une Serie Aleatoire. Annals of

Mathe-m atics, 44(3):423-453, July 1943. 0.8- .\ .... ... ... ...

[6] H. Krim and J.-C. Pesquet. Robust multiscale .7

0.7 . . . ... : ...

representation of processes and optimal signal re-construction. In Time Freq./Time Scale Symp.,

Philadelphia, PA, 1994. 0.6 . ...

[7] H. Malvar. Lapped transforms for efficient trans- 0 . ... ... ... . form subband coding. IEEE Trans. Acoust., Speech,

Signal Processing, ASSP-38:969-978, Jun. 90. 0.4 .

[8] C.M. Stein. Estimation of the Mean of a

Multivari-ate Normal Distribution. The annals of Statistics, 0.3 ... . ... ... ...

9(6):1135-1151, 1981.

0.2

[9] M. V. Wickerhauser. INRIA lectures on wavelet 0 1 2 3 4 5 6 7 8

packet algorithms. In Ondelettes et paquets t

d'ondelettes, pages 31-99, Roquencourt, Jun. 17-21

1991. Figure 2: Comparison of MLE-based Risk and

subop-timal Risk 1.2

..:Unbiased Risk Estimate, 10% of total interval

1 ', .-:Unbiased Risk Estimate, 20% of total inteoyaL N isy Dat

6 ' ,,/<Noisy Datl 0.8 ,. . . , 0.6 / 0.4. 1 0 100 200 300 400 500 600 Time 0.2F 4 Enhancement by Min-Irrror

-:UnbiasdR' Esmate, 10%oftotal interval

0

, ..--:x.. i ed Risk Estimate, 20% of total interval

0 1 2 3 4 5 6 7 8

Figure 1: Risk estimates for various compression ratios 0 100 200 300 400 500 600 Time

Figure 3: Biological Sounds of a whale