Optimal path planning for AUVs in time-varying ocean flows

Publisher’s version / Version de l'éditeur:

16th Annual International Symposium on Unmanned Untethered Submersible

Technology 2009 (UUST 09), 2010-05

READ THESE TERMS AND CONDITIONS CAREFULLY BEFORE USING THIS WEBSITE. https://nrc-publications.canada.ca/eng/copyright

Vous avez des questions? Nous pouvons vous aider. Pour communiquer directement avec un auteur, consultez la première page de la revue dans laquelle son article a été publié afin de trouver ses coordonnées. Si vous n’arrivez pas à les repérer, communiquez avec nous à PublicationsArchive-ArchivesPublications@nrc-cnrc.gc.ca.

Questions? Contact the NRC Publications Archive team at

PublicationsArchive-ArchivesPublications@nrc-cnrc.gc.ca. If you wish to email the authors directly, please see the first page of the publication for their contact information.

NRC Publications Archive

Archives des publications du CNRC

This publication could be one of several versions: author’s original, accepted manuscript or the publisher’s version. / La version de cette publication peut être l’une des suivantes : la version prépublication de l’auteur, la version acceptée du manuscrit ou la version de l’éditeur.

Access and use of this website and the material on it are subject to the Terms and Conditions set forth at

Optimal path planning for AUVs in time-varying ocean flows

Eichhorn, M.

https://publications-cnrc.canada.ca/fra/droits

L’accès à ce site Web et l’utilisation de son contenu sont assujettis aux conditions présentées dans le site

LISEZ CES CONDITIONS ATTENTIVEMENT AVANT D’UTILISER CE SITE WEB.

NRC Publications Record / Notice d'Archives des publications de CNRC:

OPTIMAL

PATH

PLANNING

FOR

AUVS

IN

TIME-VARYING

OCEAN

FLOWS

Mike Eichhorn

Institute for Ocean Technology National Research Council Canada

Arctic Avenue, P.O. Box 12093 St. John's, Newfoundland A1B 3T5, Canada phone + 01 709-772-7986; fax + 01 709-772-2462

e-mail: Mike.Eichhorn@nrc-cnrc.gc.ca

Abstract- This paper presents a new algorithm for path

planning in a time-varying environment based on graphical methods. The methods presented make it possible to find an optimal path using defined requirements in a feasible time. The task of the introduced path planning algorithm using an AUV is to find a time-optimal path from a defined start position to a goal position by evasion of all static as well as dynamic obstacles in the area of operation, with consideration of the dynamic vehicle behaviour and the time-varying ocean current. An additional consideration is to show whether it is feasible to use the algorithms on-line and on-board a Webb “SLOCUM” glider AUV. The presented algorithm is equally applicable to land based or aerial mobile autonomous systems.

I. INTRODUCTION

Path planning represents an important characteristic of autonomous systems. It reflects the possibility for a planned behaviour during a mission using all current and future information about the area of operation. This planning task will be complicated because of the unknown, inaccurate and varying information. That is the result of unpredictable events, restrictions in the sensor quality and range, as well as in the navigation accuracy. The path planning algorithm presented in this paper is designed considering the mission requirements for the AUV “SLOCUM” glider, which is a particular type of autonomous underwater vehicle (AUV). These gliders have a low cruising speed (0.2 to 0.4 m s-1) in a time-varying ocean flow over a long operation range for periods up to 30 days.

There exists a variety of solutions for the path planning in a time-varying environment in the literature, especially for mobile autonomous systems. A generic algorithm was used for an AUV in [1] to find the path with minimum energy cost in a strong, time-varying and space-varying ocean current field. The approach in [1] finds a robust solution which will not necessarily correspond with the optimal solution. A symbolic wave-front expansion technique for an Unmanned Air Vehicle (UAV) in time-varying winds was introduced in [2]. The goal of the approach in [2] was to find the path and additionally the departure time for a minimum travel time between a start point and a goal point. All these approaches need a given, pre-defined mesh structure (see section II.A), unlike the following approaches.

A solution with a non-linear least squares optimization technique for a path planning of an AUV mission through the Hudson River was presented in [3]. The optimization

parame-ters are a series of changeable nodes (xi, yi, zi, Δti), which characterize the route. The inclusion of the time intervals Δti allows a variation of the vehicle speed during the mission. In [4] a solution with optimal control to find the optimal trajec-tory for a glider in a time-varying ocean flow was presented. This approach applied the Nonlinear Trajectory Generation (NTG) algorithm including an ocean current flow B-spline model, a dynamic glider model as well a defined cost function which is a weighted sum of a temporal and an energy cost.

To solve all the requirements which were presented at the beginning of this section a search algorithm in a geometrical graph is preferred. This method makes it possible to find an optimal path using pre-defined criteria in a feasible computing time. The following sections present the algorithm and show the results using practical test scenarios.

II. GEOMETRICAL GRAPH

A. Generation of the geometrical graph

The geometrical graph is a mathematical model for the de-scription of the area of operation with all its characteristics. Therefore defined points (vertices) within the operational area are those passable by the vehicle. The passable connections between these points are recorded as edges in the graph. Every edge has a rating (cost, weight) which can be the length of the connection, the evolving costs for passing the connection or the time required for traversing the connection. There exist many approaches to describe an obstacle scenario with as few of the vertices and edges as possible, and, to decrease the computing time (visibility and quadtree graph [5]). In the case of the inclusion of an ocean current, the mesh structure of the graph will be a determining factor associated with its special change in gradient. In other words, the defined mesh structure should describe the trend of the ocean current flow in the operation area as effectively as possible. A uniform rectangular grid structure is the easiest way to define such a mesh. In the simplest case the edges are the connections between neighbouring obstacle-free sectors; see Figure 1 (a). To achieve a shorter and smoother path for mobile robots additional edges to other sectors are implemented in [6]; see Figure 1(b). The analyses of the found paths in a current field show that is it important to define a great number of edges with different slopes; see Figure 1(c).

a) 8 edges b) 16 edges c) 32 edges Figure 1. Rectangular grid structure a) 1-sector, b) 2-sector, c) 3-sector

A further increase of the number of radiated edges leads to increasing lengths which is not practical to describe the change in gradient of the current flow. Another possibility to define a mesh is presented in [7], which is based on hexagons. The advantages are six direct neighbours with the same dis-tances to their centers; compare Figure 1(a) and Figure 2(a). Figure 2(a) shows the created edges to the direct neighbours using a triangular grid structure. This structure is simpler to handle than the hexagon structure in the programming. Be-cause the hexagon is consisting of six triangles, the created edges are the same in number as using a hexagon structure. Figure 2(b) and (c) shows the defined edges to non neigh-boured sectors in analogue to Figure 1. Both structures, the triangular and the rectangular, will be researched in this work.

a) 6 edges b) 12 edges c) 24 edges Figure 2. Triangular grid structure a) 1-sector, b) 2-sector, c) 3-sector

B. Graph-based Search-Algorithm

The described search method in this section is based on a classical Dijkstra algorithm [8, 9] which solves the single-source shortest-paths problem on a weighted directed graph. The exact solution by using a Dijkstra algorithm in a time-varying environment requires the inclusion of the time information as an additional dimension in the graph. For instance a 2D geometrical graph acquires additional layers for each defined discrete point of time. That will lead to very large graphs with many vertices (nodes) and edges as a result of using small time intervals.

The present algorithm uses the basic idea of the Dijkstra algorithm, to follow the shortest possible paths from a given source vertex and to avoid longer path segments during the updates of the neighbours. The algorithm searches for a path with the smallest travel time. This means the weight w of the individual edges are the necessary time tipath to travel along the path segment. This time depends on the length of the path segment and the speed vpath_ef, with which the vehicle travels along the path in relation to the fixed world coordinate system. A detailed description about these calculations will be presented in section III.

TABLE I shows a comparison between the Dijkstra algorithm (left column) and the new algorithm TVE (time-varying environment) algorithm (right column). The syntax of the pseudo-code is adapted from [9]. The input parameter G contains the graph structure with the vertex list and the edge list (V and E), π is a predecessor list and d is the cost list for each vertex. Q is a priority queue that supports the EXTRACT-MIN and the DECREASE-KEY operations. The color list defines the current state of the vertex in the priority queue Q. The allowable states are WHITE, GRAY and BLACK: WHITE indicates that the vertex has not yet been discovered, GRAY indicates that the vertex is in the priority list, and, BLACK indicates that the vertex was checked. The shaded text fields in TABLE I highlight the differences between the algorithms. There are the following three differences:

1. The new algorithm doesn’t need the weight list w of the edges to begin the search. The algorithm needs a start time to when the vehicle begins the mission.

2. The algorithm calculates the weight for the edge w(u, v) in a function wfunc during the search. This function calcu-lates the travel time to drive along the edge from a start vertex u to an end vertex v using a given start time. The start time to be used will be the current cost value d(u), which describes the travel time from the source vertex s to the start vertex u.

3. A visited vertex v (color[v]=BLACK) can be checked several times and will be again included in the priority queue Q and will be available for further checking.

TABLE I

PSEUDO-CODE OF THE DIJKSTRA AND TVEALGORITHMS

DIJKSTRA(G, s, w) for each vertex u ∈ V d[u] ← ∝ π[u] ← ∝ color[u] ← WHITE color[s] ← GRAY d[s] ← 0 INSERT(Q, s) while (Q≠Ø) u ← EXTRACT-MIN(Q) color[u] ← BLACK

for each v ∈ Adj[u]

dv = w(u, v) + d[u] if (dv < d[v]) d[v] ← dv π[v] ← u if (color[v] = GRAY) DEREASE-KEY(Q, v, dv) else if (color[v] = WHITE)

color[v] ← GRAY

INSERT(Q, v) return (d, π)

TVE(G, s, t0) for each vertex u ∈ V d[u] ← ∝ π[u] ← ∝ color[u] ← WHITE color[s] ← GRAY d[s] ← t0 INSERT(Q, s) while (Q≠Ø) u ← EXTRACT-MIN(Q) color[u] ← BLACK

for each v ∈ Adj[u]

dv = wfunc(u, v, d[u]) + d[u]

if (dv < d[v]) d[v] ← dv π[v] ← u if (color[v] = GRAY) DEREASE-KEY(Q, v, dv) else color[v] ← GRAY INSERT(Q, v) return (d, π)

III. CALCULATION OF THE COST VALUE

This section describes the necessary equations and algorithms to determine the travel time tipath for the several path segments using information about the ocean current. A. Speed calculation

The travel time can be calculated for the ith edge by formation of the quotient of the distance spath and the speed vpath_ef, with which the vehicle travels on the path in relation to a fixed world coordinate system.

_ i path i path i path ef

s

t

v

=

This speed vpath_ef depends on the vehicle speed through the water vveh_bf (cruising speed), the magnitude and the direction of the ocean current vector as well as the direction of the path v0path. This speed can be determined by the intersection point

between a line and a circle (2D) and/or sphere (3D) [10] based on Figure 3 according to the following relation:

(

)

(

)

path current current 0

path current (3)

If the discriminant in equation (3) becomes negative, it means that the vehicle can no longer be held in that path; see Figure 4(a). If the speed vpath_ef is negative the vehicle is still on the path, but moving backwards; see Figure 4(b). Both cases must be considered by setting a large numerical value for the edge weight. Thus such paths are excluded in the search and it does not come to a situation that the vehicle encounters a strong backwards current and leaves the course.

vcur rent x y v veh_b_f Path vpath Intersection point vpath_e fvpat h 0 ϕ

Figure 3. Definition of the velocities

vcu rre nt x y Path vpath |vveh_bf | v_current x y V ve_{h_} bf Path vpath 0 vpath_e fvpath

Figure 4. a) Negative discriminant b) vpath_ef is negative

B. Travel time calculation in time-varying ocean flow The determination of the travel time according to equation (1) works only if the ocean current is constant along the path, appropriate choice of the mesh sizes of the location-varying ocean current. In the case of a

time-va me e used in a conjuncti nt, the al 1. the endpoint n value v . v and the

and t and the

or through an graph for a

rying ocean current or a too coarse sh structur on with a location-varying ocean curre speed vpath_ef will be changed depending on the current vcurrent

ong the path element.

The idea of the algorithm presented below is based on a step size control for efficient calculation of numerical solutions of differential equations. The step size h is here not the time as used in numerical solvers but is a segment of the path element. So the path element will be shared within many segments, for which equation (1) can be solved. The calculation of the travel time for a segment includes the following steps:

Rough approximation of the travel speed vpath_ef on the segment in equation (3) using only the current value vcurrent_start from the start point xstart_local to the time tstart_local.

2. Calculation of the travel time trough_approx using equation (1) with the calculated speed vpath_ef and the length of the segment which correspond with h spath.

3. Determine the ocean current vcurrent_end from xend_local to the time tend_local + trough_approx.

4. Calculation of an average ocean current vcurrent_mean along

the segment by arithmetic mean of the two velocities vcurrent_start and vcurrent_end.

5. Improved approximation of the speed vpath_ef on the seg-ment used in equation (3) using the mea current_mean

6. Calculation of the travel time timproved_approx using equation (1) with the calculated speed path_ef

length of the segment which correspond with h spath. Afterward occurs the calculation of the local error errorlocal between the two times trough_approx improved_approx

determination of the new step size hnew using the equation for an optimal step-size for a second order method [11]:

max , min ,

new min max

local h h h h error ε τ ⎧ ⎧ ⎫⎫ ⎪ ⎪ ⎪⎪ = _{⎨ ⎨ ⎬⎬} ⎪ ⎪ ⎪ ⎩ ⎭⎪ ⎩ ⎭ (4)

The parameter τ is a safety factor (τ∈(0, 1]). Acceptance or rejection of this step will depend on the local error errorlocal, the defined tolerance ε the calculated step size hnew and the minimal step size hmin. TABLE II includes the details of the algorithm.

TABLE II

PSEUDO-CODE OF THE ALGORITHM TO CALCULATE THE TRAVE

CALC-TRAVELTIME(xstart, xend, tstart)

L TIME

defined parameters: vveh_bf, h, hmin, hmax, ε, τ

if ((tstart = ∝) return (ttravel = ∝) tstart_local = tstart

xstart_local = xstart

spath = ||xend - xstart||

0

vpath= (xend - xstart)/lpath stravel ← 0

vcurrent_start = GET-CURRE T(xN start_local, tstart_local) while (stravel < spath)

xend_local = xstart_local + hspathv0path

vpath_ef = CALC-TRAVELVELOCITY(vcurrent_start, v0path, vveh_bf)

if ((vpath_ef = NaN) OR (vpath_ef ≤ 0)) return (ttravel = ∝)

trough_approx=hspath/vpath_ef

vcurrent_end = GET-CURRENT(xstart_local, tstart_local + trough_approx) vcurrent_mean= 0.5(vcurrent_start + vcurrent_end)

vpath_ef = CALC-TRAVELVELOCITY(vcurrent_mean, v0path, vveh_bf) if ((vpath_ef = NaN) OR (vpath_ef ≤ 0))

return (ttravel = ∝) timproved_approx=hspath/vpath_ef

errorlocal = | trough_approx − timproved_approx|

hnew = max(hmin, min(hmax, τ h ε/errorlocal)) if ((errorlocal < ε) OR (hnew = hmin))

vcurrent_start = vcurrent_end xstart_local_ = xend_local

tstart_local = tstart_local + timproved_approx stravel = stravel + h spath

h = hnew

if (stravel+hspath) > spath

h = (spath - stravel)/spath

return (ttravel = tstart_local - tstart)

IV. RESULTS

The llowing tests (sections A and B)

ho influence of the chosen grid structure of the he performance of the developed lgorit g current field. For these tests only

re will be used. The middle part (section C) compares the results using the triangular and the

rectangular mesh st se a numerical

simulation to d t travel time for the

se

first part of the fo s ws the

predicted paths and t a hm in a time-varyin the rectangular grid structu

ructures. All these tests u etermination the exac

veral path elements. There the differential equation solver ode45 from MATLAB will be used to solve the two equations of motion (see equation (9)). The heading angle, ϕ, can be calculated using trigonometric relations in Figure 3. The last part (section D) shows the accuracy of the algorithms used to calculate the travel time using fixed step size and step size control mechanisms in comparison to the numerical simulation.

A. Stationary current field

The first test uses a time-invariant current field without obstacles. The task is to determine a time-optimal path when crossing a river, which possesses the current profile in equation (5).

(

)

current x current y current

current b m b m v s = = 2.2 4 bf s x b x v = − (5)

The time-optimal path for this profile can be confirmed by every swimmer who has crossed a river with a strong current. First one swims against the current, then in the centre of the

ver be carried by the river towards the other bank. The following figures show the paths determine

graph method and for comparison the time-optimal solution by optimal control. The geometrical graphs are produced with different grid sizes, aspect ratio and grid structures. TABLE II 0 v veh m v v = = ri d by the

I contains the travel time s for various paths in a comparison with the best possible solution (optimal control) as well as the number of the vertices and edges of the appropriate geometrical graph.

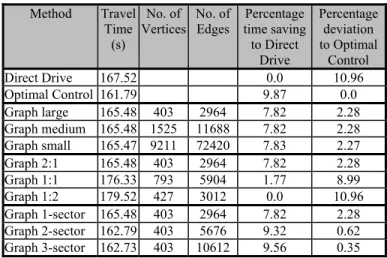
A decrease of the grid size does not bring the desired improvement, as seen in Figure 5. A good choice of the aspect ratio is an important factor in determining the success of the path planning; see Figure 6. In the case of an aspect ratio of 1:2, the slope and the length of the diagonal and vertical edges in relation to the optimal route are so adverse that the predicted solution uses only the horizontal edge elements. The adding of new edges in the grid structure as presented in section II.A, leads to a good approximation of the predicted paths relative to the exact solution.

0 50 100 150 200 250 300 -30 -20 -10 0 10 20 30 x (m) y ( m ) Optimal Control Graphmethod large grid size Graphmethod medium grid size Graphmethod small grid size

Figure 5. Path planning with the same aspect ratio and different grid sizes (large: x=10m, y=5m; medium: x=5m y=2.5m; small x=2m, y=1m)

0 50 100 150 200 250 300 -30 -20 -10 0 10 20 30 x (m) y ( m ) Optimal Control

Graphmethod 2:1 aspect ratio Graphmethod 1:1 aspect ratio Graphmethod 1:2 aspect ratio

Figure 6. Path planning with different aspect ratios for grid structure 1-sector

0 50 100 150 200 250 300 -30 -20 -10 0 10 20 30 x (m) y ( m ) Optimal Control Graphmethod 1-sector Graphmethod 2-sector Graphmethod 3-sector

Figure 7. Path planning with different grid structures (see also Figure 1)

The ad

possibilities to the path search and leads to improvements in comparison to a grid structure with a lesser number of edges.

TABLE III

RESULTS OF THE DIFFERENT GRID STRUCTURES

ding of edges with new slopes gives new variation

Method Travel Time (s) No. of Vertices No. of Edges Percentage time saving to Direct Drive Percentage deviation to Optimal Control Direct Drive 167.52 0.0 10.96 Optimal Control 161.79 9.87 0.0 Graph large 165.48 403 2964 7.82 2.28 Graph medium 165.48 1525 11688 7.82 2.28 Graph small 165.47 9211 72420 7.83 2.27 Graph 2:1 165.48 403 2964 7.82 2.28 Graph 1:1 176.33 793 5904 1.77 8.99 Graph 1:2 179.52 427 3012 0.0 10.96 Graph 1-sector 165.48 403 2964 7.82 2.28

B. Time-Varying Ocean Flow

The function used to represent a time-varying ocean flow describes a meandering jet in the eastward direction, which is a simple mathematical m e Gulf Stream [12]. This

function wa onary path

plan ori v

function is:

odel of th

s applied in [1] to test the evoluti

ning alg thm in a 2D ocean en ironment. The

stream-(

)

(

(

)

(

)

(

)

)

a dimens onless functio i

f a t pende

oscillation e mean er am tude

0 B ( B t)= +εcos(ω θ (7) t+ ) e B .2 0.3, 0.4, 2, o rib oc d:

and the param ter set 0 = 1 , ε = ω = θ = π/ k = 0.84 and c = 0.12 t desc e the vel ity fiel

Graph 2-sector 162.79 403 5676 9.32 0.62 Graph 3-sector 162.73 403 10612 9.56 0.35 ( , , u x y )t , )t x ∂ v x y( , y ∂ ∂ ∂ = − φ = φ (8)

The dimensionless value for the body fixed vehicle velocity vveh_bf is 0.5. The exact solution was founded by solving a boundary value problem (BVP) with a collocation method bvp6c [13] in MATLAB. The three ordinary differential equations (ODEs) include the two equations of motion:

_ _ cos sin veh bf veh bf dx u v dt dy v v dt = + ϕ = + ϕ (9)

and the optimal navigation formula from Zermelo [14]:

(

)

2 2

cos cos sin sin

y x y d u u v v dt ϕ x = − ϕ + − ϕ ϕ + ϕ . (10)

This approach is more robust for solving

rough the me-varying ocean flow found by the TVE al

or grid structure. The determined solu ch

this geometrical graph has the most vertices and edges. Here it is

ecessary to find a compromise betw omputing time. A further increase of t

edges (4…n-sector grid structure) leads to increasing lengths

w of

th ted

aths including stationary obstacles. A compariso sults from all tests is presented in TABLE IV.

this time optimal problem than when trying to solve this same problem using a Hamilton equation.

Figure 8 shows the time sequence of the course th

ti gorithm with a

3-sect tion has the

aracteristic that the vehicle drives in the mainstream of jet. This solution shows a very good agreement with the exact solution by optimal control in Figure 9. This figure contains the paths found by the TVE algorithm using different grid structures. The use of a 3-sector grid structure shows the best approximation with the exact solution but then

n een accuracy and the

c he number of radiated

hich is not practical to describe the change in the gradient e time-varying current flow. Figure 10 shows the predic

p n of the

-5 0 5 -4 -2 0 2 4 t=0.762 x y -5 0 5 -4 -2 0 4 t=6.058 2 x y -5 0 5 -4 -2 0 2 4 x y t=12.160 -5 0 5 -4 -2 0 2 4 x y t=17.719

Figure 8. Time sequence of the predicted paths through the time-varying ocean current field by the TVE algorithm with a 3-sector grid structure

-8 -6 -4 -2 0 2 4 6 8 -4 -3 -2 -1 0 1 2 3 4 x y Optimal Control Graphmethod 1-sector Graphmethod 2-sector Graphmethod 3-sector

Figure 9. Time optimal paths through a time-varying ocean field using an exact numeric solution with Optimal Control and the TVE algorithm

-8 -6 -4 -2 0 2 4 6 8 -4 -3 -2 -1 0 1 2 3 4 x y Optimal Control Graphmethod 1-sector Graphmethod 2-sector Graphmethod 3-sector

Figure 10. Time optimal paths through a time-varying ocean field with obstacles present

TABLE IV

RESULTS OF THE DIFFERENT GRID STRUCTURES IN A TIME-VARYING CURRENT

Method Travel Time No. of Vertices No. of Percentage Edges deviation to Optimal Control Direct Drive ∝ ∝ Optimal Control 17.195 0.0 Graph 1-sector 19.623 861 6520 14.12 Graph 2-sector 17.951 861 12680 4.40 Graph 3-sector 17.719 861 24296 3.05 Graph 1-sector with obstacles 23.094 816 5910 34.31 Graph 2-sector with obstacles 21.319 816 11195 23.99 Graph 3-sector with obstacles 20.903 816 20517 21.57

The two test scenarios used in this section show the perfor-mance of graph-based methods by the search of a path through a

pat l.

If the ocean current is constant as in the first example a classi-cal Dijkstra algorithm can also be used. As the time to travel along an edge is constant, the weights can be calculated before the search begins. However this approach doesn’t perform well in by a time-varying environment. For this set of prob-lems the new TVE algorithm was developed. The algorithm searches for the fastest path through a time-varying environ-ment based on a given start time t0. In this section only the

ocean current parameter is time-variant. By including moving obstacles in the scenario the function wfunc in TABLE I will be expanded with a collision calculation between the edge and the moving obstacles. This is a future research field.

It appears that the main problem associated with using a grid structure based search algorithm in a current field is the right choice of the grid size and the grid pattern. The use of expanded grid structures which were presented in section II.A lead

C. Comparison between d rectangular grid

To rese influenc r s

performance, the test fun i .

Figure 11 shows the determined paths using tri

wi the several sector m he mes as well as the number of vertices and

est cases se in BLE he

vement of a a im to act

the trian r ru ill not

tu per

di-e ur He the

, t be he

pairs of the rectangular grid structure. This shows that an im-pr

complex ocean current field. The accuracy of the predicted hs was compared to the paths predicted by optimal contro

s to an improved approximation of the exact solution. r an

triangula structures

arch the e of the ction i grid st n sectio ucture n B w hape on the ll be used angular and odes. T rectangular grid structures

achieved tra

th vel ti

edges for the t are pre n dte AT T

t x

V. desired impro better pprox ation he e solution using gular g id st cture w be achieved. In fact the triangular grid struc re is a fect ad tion to the rectangle structure (se Fig e 12). re lie pairs of values ([number of edges travel imes]) tween t

oved approximation to the exact solution is only dependant on the number of edges by a constant number of vertices. A further approximation on the exact solution, by increasing the sector mode to four or more is not practical because of the increased lengths of the path elements. The usage of the

D. Comparison between the cost function calculations This section presents the results using the step size control algorithm which is presented in section III.B. Furthermore a comparison between the fixed step size algorithm (FSS) and step size control algorithm (SSC) will be given. Figure 13 shows the paths found using a numerical simulation and the step size control algorithm to calculate the travel time for the several path elements. The paths found using the step size control algorithm are identical to the numerical simulation for the 2 and 3 sector-mode.

TABLE V includes the results of the travel time found for the fixed step size and the step size control algorithm. The parameters for the step size control algorithm are h = 0.2, hmin = 0.1, hmax = 0.9, ε = 0.001, τ = 0.8. To test the fixed step size algorithm the step size control algorithm will be used with th

u

algorithm with a step or less, although the percentage deviation of the travel time of the several path elements is one decade larger.

The percentage deviation of the travel time and of the travel time of the several path elements will be decreased with a decrease of the defined step size using the fixed step size algorithm. The necessary number of current calculations correlates with the percentage deviation. In other words, the highest accuracy will be achieved with the most ocean current calculations which means the largest number of iteration steps. The step size control algorithm cannot demonstrate its full ability in these test cases. One of the reasons is the chosen grid size, which leads to small path elements for which the speed vpath_ef is relatively constant or linearly increasing or decreasing along the elements. Another reason is the coarse step size parameters (h, hmin, hmax) as for which the optimal step size will be achieved at the end of the path element. A

computing time wit e found paths.

triangular grid structure brings a good compromise between computing calculation and accuracy of the results. So the triangular grid structure in 3-sector mode needs 25% fewer edges than the rectangular structure with similar results.

-8 -6 -4 -2 0 2 4 6 8 -5 -4 -3 -2 -1 0 1 2 3 y Optimal Control

Graphmethod Triangle 1-sector Graphmethod Rectangle 1-sector

Graphmethod Triangle 2-sector _{e settings h = hmin = hmax. The paths found are identical when}

sing a step size control algorithm and a fixed step size size of 0.5

Graphmethod Rectangle 2-sector Graphmethod Triangle 3-sector Graphmethod Rectangle 3-sector

x

Figure 11. Time optimal paths through a time-varying ocean field using the TVE algorithm with a triangle and a rectangle grid structure for the

geometrical graph 0.6 0.8 1 1.2 1.4 1.6 1.8 2 2.2 2.4 x 104 17 18 19 20 21 22 23 Number of Edges Ti m e Optimal Control

Graphmethod Triangle 1-sector Graphmethod Rectangle 1-sector Graphmethod Triangle 2-sector Graphmethod Rectangle 2-sector Graphmethod Triangle 3-sector Graphmethod Rectangle 3-sector

Figure 12. Obtained times using the triangle and rectangle grid structure with the individual sector modes

decreasing of these parameters leads to an increase of the hout improvement of th

TABLE V

COMPARISON OF THE TRIANGLE AND THE RECTANGLE GRID STRUCTURE IN A TIME-VARYING CURRENT

Method Travel Time No. of Vertices No. of Edges Percentage deviation to Optimal Control Optimal Control 17.195 0.0

Graph Triangle 1-sector 22.982 850 4858 33.66 Graph Triangle 2-sector 18.234 850 9516 6.04 Graph Triangle 3-sector 17.815 850 18206 3.61 Graph Rectangle 1-sector 19.623 861 6520 14.12 Graph Rectangle 2-sector 17.951 861 12680 4.40 Graph Rectangle 3-sector 17.719 861 24296 3.05

-8 -6 -4 -2 0 2 4 6 8 -5 -4 -3 -2 -1 0 1 2 3 y Optimal Control

Graphmethod (Numerical imulation 1-sectorS ) Graphmethod (Simplified alculatioC n with SSC) 1-sector Graphmethod (Numerical imulationS ) 2-sector Graphmethod (Simplified alculatioC n with SSC) 2-sector Graphmethod (Numerical imulation 3-sectorS ) Graphmethod (Simplified alculatioC n with SSC) 3-sector

x

igure 13. Time optimal paths through a time-varying ocean field using the TVE algorithm with numerical simulation and a simplified calculation with

step size control F

TAB RESULTS OF THE COST FUNCTION CALCU

LE

LA

VI

TIONS FOR A TIME-VARYING CURRENT

Method Travel time using Researched

Method

Travel time of the determined path using Numerical

Simulation Percentage deviation to Numerical Simulation No. of Current Calculations

Average percentage deviation of the determined travel time of the

several path elements to Numerical Simulation Percentage deviation to Optimal Control Optimal Control 17.195 0.0

Numerical Simulation 1-sector 19.623 19.623 0.0 130216 0.0 14.12

Numerical Simulation 2-sector 17.951 17.951 0.0 299684 0.0 4.40

Numerical Simulation 3-sector 17.719 17.719 0.0 724472 0.0 3.05

Fixed Step-Size 1.0 spath 1-sector 19.925 19.983 0.29 11399 0.47 16.22 Fixed Step-Size 1.0 spath 2-sector 17.735 17.951 1.20 22624 1.13 4.40 Fixed Step-Size 1.0 spath 3-sector 17.458 17.759 1.70 43280 1.46 3.28 Fixed Step-Size 0.5 spath 1-sector 19.968 19.983 0.08 16368 0.12 16.22 Fixed Step-Size 0.5 spath 2-sector 17.887 17.951 0.36 32121 0.33 4.40 Fixed Step-Size 0.5 spath 3-sector 17.640 17.719 0.44 60626 0.37 3.05 Fixed Step-Size 0.2 spath 1-sector 19.981 19.983 0.01 31204 0.02 16.22 Fixed Step-Size 0.2 spath 2-sector 19.940 17.951 0.06 60632 0.06 4.40 Fixed Step-Size 0.2 spath 3-sector 17.704 17.719 0.08 114878 0.07 3.05

Fixed Step-Size 0.1 spath 1-sector 19.983 19.983 0.0 56263 0.0 16.22

Fixed Step-Size 0.1 spath 2-sector 17.949 17.951 0.02 108955 0.02 4.40 Fixed Step-Size 0.1 spath 3-sector 17.715 17.719 0.02 204964 0.02 3.05

Step-Size Control 1-sector 19.981 19.983 0.01 34947 0.02 16.22

Step-Size Control 2-sector 17.945 17.951 0.04 78124 0.04 4.40

Step-Size Control 3-sector 17.712 17.719 0.04 160857 0.04 3.05

V. PROGRAMMING AND BENCHMARKS

For futu ori a in

section II and were prog e

Microsoft Visual Studio 2005

(BGL) [9, 16] was used for the nerati path ins a library with te data str

s a, A*) pports

sito of the which

r ow s in isting y lement t TVE gorithm tests se sults, th f the d ill be lo XML te iles (Sc ector f ich will ed in

r in a vector graphic program

C ed

es the foll PUs:

N260 @ Hz (use )

T 2.16 G

Intel Core 2 Extreme CPU Q9300 @ 2.53 GHz Figure 14 and TABLE VII show the computing time for the

gra ocessors.

Th cannot be

used, because the programs are not parallelizable. re work the alg

III

thms which rammed in

re presented C++ using th oost Graph Library

on and the [15]. The B

graph ge

search. It conta comple uctures for

graphs and search algorithm (Dijkstr and su many C++ compilers. The vi r concepts BGL, allow the user to insert thei n operation the ex graph algorithms, make it eas to imp he new algorithm in the Breadth First Search al . For the of the programs and to analy the re e data o generated graphs and the foun paths w gged in files [17]. A converter genera s SVG f alable V Graphics) [18] from the XML

E

iles, wh be view Microsoft Internet xplorer o

is

such as Microsoft V io 2007.

A. Central Processing Units ( PUs) Us

The compiled program was t ted with owing C • Intel Atom CPU 1.60 G in AUV • Intel Core 2 Duo CPU 5850 @ Hz •

ph generation and the path search using several pr e full performance of the multi-core processors

321,2 _104,4 72,5 12.775,3 3.870,8 2.5 0 2000 4000 6000 000 14000   0.4 GS   Duo 0.4 G Qua 5 GS  om 0.05 GS   Duo 0.05 Qu 52,9 8 100 12000 in  ms 00 0.4 GS Atom S  0.0 d At  GS  ad C o mputing  Time  

Generate Graph Path Search Summe

Computing ti he used CPUs TABLE G TIME O PUS USED Figure 14. me of t VII F THE C COMPUTIN Method Processor No. of Vertices/ Computing Tim Edges e in ms Generate Graph Path Total Tim Search e 0.4 Grid s Rectangle N260 861/ 296.5 2 ize Atom 3-sector 24296 24.7 321. Duo T5850 8.7 95.7 104.4 Quad Q9300 7.7 64.8 72.5 0.05 Grid size Rectangle 3-sector Atom N260 51681/ 1627856 1729.3 11046.0 12775.3 Duo T5850 539.2 3331.6 3870.8 Quad Q9300 424.2 2128.6 2552.9

C. Computing time of the several program parts

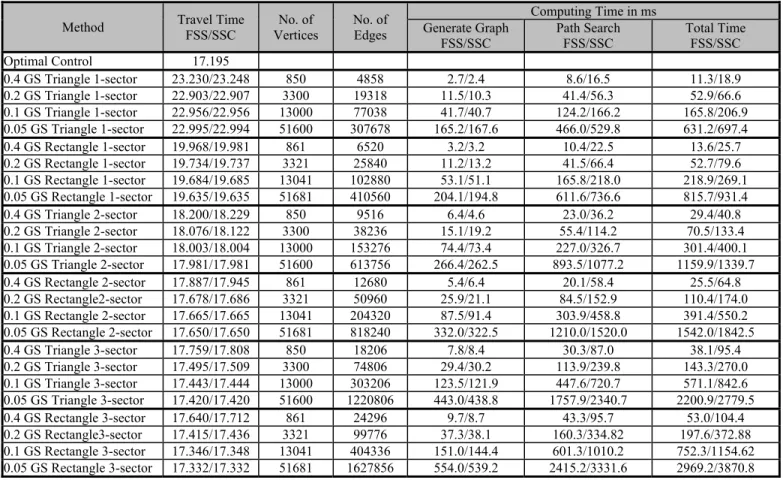
TABLE VIII includes the results of the benchmarks for an Intel Core Duo CPU T5850 using the test function from section IV.B with triangular and rectangular grid structures and using the fixed step size (FSS) and step size control (SSC) algorithms. In order to generate the graph and to search the path for 50000 vertices and 1.6 million edges, the algorithm needs only 3.8 sec.

This is a rea to describe the

area of operation for an ate he

alg ill be used s e-p

situation [19], the graph si b e om g

t tep alg w tep f

0. t e these settin ll b

w s, for wh as

ly fe

listic size for a grid structure underw on-board r glider mission. If t orithm w in a mi e small sion r r. The c lanning ze will putin ime is 3 sec u 5 o

sing fixed s size orithm ith a s size o . It cann

h other

be guarante d that gs wi e work

it cu

control algorit

rrent profile i e

rred.

ch r on the step size hm will like be pre

631,2 500   697,4 815,7 931,4 1.159,9 1.339,7 1000 1500 Time 1.542,1 1.842,4 2.200,9 2.779,5 2.969,2 3.870,8 S    le    r    0 0 2000  in   2500 ms 3000 3500 4000 0.05 GS    Triangle    1‐sector    FSS 0.05 GS    Triangle    1‐sector    SSC 0.05 GS   Rectangle   1‐sector   FSS 0.05 GS   Rectangle   1‐sector   SSC 0.05 GS    Triangle    2‐sector    FSS 0.05 G Triang 2‐secto SSC C o m _.05 GS    Rectangle    2‐sector    FSS 0.05 GS    Rectangle    2‐sector    SSC 0.05 GS    Triangle    3‐sector    FSS 0.05 GS    Triangle    3‐sector    SSC 0.05 GS    Rectangle    3‐sector    FSS 0.05 GS    Rectangle    3‐sector    SSC puting Generate Graph Path Search

ch for the varioius tests using INTEL Core 2 Duo CPU T5850 III

Figure 15. Computing time for the graph generation and path sear TABLE V

COMPUTING TIME USING INTEL CORE 2DUO CPUT5850

Method Travel Time FSS/SSC

No. of Vertices

Computing Time in ms No. of

Edges Generate Graph FSS/SSC

Path Search Total Time

FSS/SSC FSS/SSC Optimal Control 17.195 0.4 GS Triangle 1-sector 23.230/23.248 850 4858 2.7/2.4 8.6/16.5 11.3/18.9 0.2 GS Triangle 1-sector 22.903/22.907 3300 19318 11.5/10.3 41.4/56.3 52.9/66.6 0.1 GS Triangle 1-sector 22.956/22.956 13000 77038 41.7/40.7 124.2/166.2 165.8/206.9 0.05 GS Triangle 1-sector 22.995/22.994 51600 307678 165.2/167.6 466.0/529.8 631.2/697.4 0.4 GS Rectangle 1-sector 19.968/19.981 861 6520 3.2/3.2 10.4/22.5 13.6/25.7 0.2 GS Rectangle 1-sector 19.734/19.737 3321 25840 11.2/13.2 41.5/66.4 52.7/79.6 0.1 GS Rectangle 1-sector 19.684/19.685 13041 102880 53.1/51.1 165.8/218.0 218.9/269.1 0.05 GS Rectangle 1-sector 19.635/19.635 51681 410560 204.1/194.8 611.6/736.6 815.7/931.4 0.4 GS Triangle 2-sector 18.200/18.229 850 9516 6.4/4.6 23.0/36.2 29.4/40.8 0.2 GS Triangle 2-sector 18.076/18.122 3300 38236 15.1/19.2 55.4/114.2 70.5/133.4 0.1 GS Triangle 2-sector 18.003/18.004 13000 153276 74.4/73.4 227.0/326.7 301.4/400.1 0.05 GS Triangle 2-sector 17.981/17.981 51600 613756 266.4/262.5 893.5/1077.2 1159.9/1339.7 0.4 GS Rectangle 2-sector 17.887/17.945 861 12680 5.4/6.4 20.1/58.4 25.5/64.8 0.2 GS Rectangle2-sector 17.678/17.686 3321 50960 25.9/21.1 84.5/152.9 110.4/174.0 0.1 GS Rectangle 2-sector 17.665/17.665 13041 204320 87.5/91.4 303.9/458.8 391.4/550.2 0.05 GS Rectangle 2-sector 17.650/17.650 51681 818240 332.0/322.5 1210.0/1520.0 1542.0/1842.5 0.4 GS Triangle 3-sector 17.759/17.808 850 18206 7.8/8.4 30.3/87.0 38.1/95.4 0.2 GS Triangle 3-sector 17.495/17.509 3300 74806 29.4/30.2 113.9/239.8 143.3/270.0 0.1 GS Triangle 3-sector 17.443/17.444 13000 303206 123.5/121.9 447.6/720.7 571.1/842.6 0.05 GS Triangle 3-sector 17.420/17.420 51600 1220806 443.0/438.8 1757.9/2340.7 2200.9/2779.5 0.4 GS Rectangle 3-sector 17.640/17.712 861 24296 9.7/8.7 43.3/95.7 53.0/104.4 0.2 GS Rectangle3-sector 17.415/17.436 3321 99776 37.3/38.1 160.3/334.82 197.6/372.88 0.1 GS Rectangle 3-sector 17.346/17.348 13041 404336 151.0/144.4 601.3/1010.2 752.3/1154.62 0.05 GS Rectangle 3-sector 17.332/17.332 51681 1627856 554.0/539.2 2415.2/3331.6 2969.2/3870.8

D. Distribution of the program parts

This section shows the distribution of the several program parts using a Dijkstra algorithm and the new TVE algorithm. To compare these two methods is it necessary to use a time– invariant current profile. The current profile used is from section IV.A. The results are included in TABLE IX. The total computing time for both algorithms is similar for several test cases; see Figure 16. Only the distribution of the program parts is different, which is a result of the specific algorithm details; see TABLE I. The Dijkstra Algorithm needs 95% of the time for the graph generation and 5% for the search. The graph generation includes the building of the data structures as well as the calculation of the cost values for the several edges. This second part will be handled in the path search using the TVE algorithm. The analysis shows that the two algorithms need 25% of the time to generate the graph structures, 70% to calculate the weight functions and 5% for the path search.

27,2 25,3 C o 98,5 200 m 90,0 345,8 352,7 1.489,8 1.498,4 1400 1600 .5   E x1.25 jkstra 1x0.5 Dijkstr 0 400 g   600 me   800 ms 1000 1200 10x5   TVE 10x5  Dijkstra 5x2 TV 5x2.5  Dijkstra 2.5x1.25   TVE 2.5 Di   1x0.5 TVE     a putin Ti in   Generate Graph Path Search

Figure 16. Comparison between th TVE m T

PH THE ARCH

A A MS

e Dijkstra and the algorith ABLE IX

COMPUTING TIME FOR THE GRA

DIJKSTR GENERATION AND ND TVE ALGORITH PATH SE USING Method Algo-rithm No. of Vertices/ Edges Computing Time in ms Generate Graph Path Search Total Time 10x5 Grid size TVE

Rectangle 3-sector 10612 403/ 4.3 22.9 27.2 Dijkstra 24.6 0.7 25.3 5x2.5 Grid R size ectangle 3-sector TVE 1525/ 44248 16.0 82.5 98.5 Dijkstra 87.7 2.3 90.0 2.5x1.25 Grid size Rectangle 3-sector TVE 5929/ 180640 72.6 273.2 345.8 Dijkstra 343.1 9.6 352.7 1x0.5 Grid size Rectangle 3-sector TVE 36421/ 1142776 393.3 1096.5 1489.8 Dijkstra 1432.3 66.1 1498.4

Time-Varying Winds," in Proc. The 27th Workshop of the UK

PLANNING AND SCHEDULING Special Interest Group, Heriot-Watt

University, Edinburgh, United Kingdom, December 11-12, 2008. [3] D. Kruger, R. Stolkin, A. Blum and J. Briganti, "Optimal AUV path

planning for extended missions in complex, fast flowing estuarine environments," in Proc. IEEE International Conference on Robotics and

Automation, Rome, Italy, April 10-14 2007.

[4] W. Zhang, T. Inanc, S. Ober-Blöbaum, J.E. Marsden, "Optimal Trajectory Generation for a Glider in Time-Varying 2D Ocean Flows B-spline Model," in Proc. IEEE International Conference on Robotics and

Automation, pp. 1083-1088, Pasadena, CA, USA, May 19-23, 2008.

VI. CONCLUSIONS

In this paper a new algorithm for path planning in a time-varying environment based on graphical methods is presented. The first part of this paper describes the new algorithm in detail, based on a modified Dijkstra Algorithm including the time-variant cost function in the search. Using the ocean current information in a geometrical graph, the position of the vertices and their possible connections (edges) are very important. This choice should consider the trend of the current flow and the possibility of optimal connections from one vertex to another in a given current field. The algorithms of the cost function for every connection are presented in the middle part of this paper. This requires the use of a fast calculation for the precise travel time from one vertex to another with dependence on the start time, the vehicle speed and the time variability of ocean current. The fast calculation ometrical one million. part paper shows some practical scenarios,

e performance of the algorithm in a

time-varying ocean field found with optimal

co lo o so timal

navig oblem us formula melo.

Bench f the al m, which is written in

Micr al Studio g the Boos raries

concl aper.

T ea test plannin will

begi f 2 oal of th s the

valid he offline ission p real

glide for the est area heast

offs sland of nd [20].

AC MENT

Th financed man Res ation

(DF e scop ar rese p. I

would thank the Research anada

Instit cean Tec r its sup this

proje lar D her D. W r the

supp his pro ly ack alf

Bach m the M iversity of and

for hi scussio

[1] A A. Caiti an Evolutiona g for A Underwat Variable urnal

ineering 004, pp.

[2] P. Tail "Path s in

is required because of the number of edges in the ge graph, which range from one hundred thousand to The last of this

which demonstrate th

. The exact paths were

ntrol using the col cation method t lve the op

ation pr ing the from Zer

mark tests o gorith

osoft Visu 2005 usin t C++ Lib

ude this p he first at-s n Fall o of the path 0 g g algorithm i

in the 09. The ese tests

ation of t generated m lan with a

r mission proposed t in the nort

hore of the i Newfoundla

KNOWLEDG

is work is by the Ger earch Found G) within th e of a two-ye arch fellowshi

like to National Council C

ute for O hnology fo port during

ct, in particu r. Christop illiams fo ort during t ject. I grateful nowledge Dr. R

m o s helpful di ayer fr e ns. morial Un Newfoundl REFERENCES . Alvarez, utonomous d " er Vehicles in a

R. Onken, ry Path Plannin Ocean," IEEE Jo

of Oceanic Eng , vol. 29, no. 2, 2 418-428. M. Soulignac, libert, M. Rueher, Planning for UAV

[5] M. Eichhorn, "An Obstacle Avoidance System for an Autonomous Underwater Vehicle," in Proc. Proceedings of 2004 International

Symposium on Underwater Technology, pp. 75-82, Taipei, Taiwan,

20-23 April 2004

[6] T. Ersson and X. Hu, "Path Planning and Navigation of Mobile Robots in Unknown Environments," in Proc. Intelligent Robots and Systems

IEEE/RSJ International Conference, pp. 858-864, Maui, HI, USA, 29

Oct to 03 Nov, 2001.

[7] E.S.H. Hou and D. Zheng, "Hierarchical Path Planning with Hexagonal Decomposition," Systems, Man and Cybernetics, Decision Aiding for

Complex Systems Conference Proceedings, 1991 IEEE International Conference, Charlottesville, VA, USA, 13-16 Oct 1991.

[8] E.W. Dijkstra, "A Note on Two Problems in Connexion with Graphs,"

Numerische Mathematik, no. 1, 1959, pp. 269-271.

[9] J.G. Siek, L. Lee and A. Lumsdaine, The Boost Graph Library, Addison-Wesley, 2002.

[10] P.J. Schneider and D.H. Eberly, Geometric Tools for 3D Graphics, Morgan Kaufmann Publishers, 2003.

[11] W. Hundsdorfer and J. Verwer, Numerical solution of time-dependent

advection-diffusion-reaction equations, Springer Publishers, 2003.

[1

[12] M. Cencini, G. Lacorata, A. Vulpiani and E. Zambianchi, "Mixing in a Meandering Jet: A Markovian Approximation," Journal of Physical

Oceanography, vol. 29, 1999, pp. 2578-2594.

[13] N. Hale and D.R. Moore, A Sixth-Order Extension to the MATLAB

Package bvp4c of J. Kierzenka and L. Shampine, Oxford University

Computing Laboratory, technical report, April 2008.

[14] E. Zermelo, "Über das Navigationsproblem bei ruhender oder veränderlicher Windverteilung," Z. Angew. Math. Mech., vol. 11, no. 2, 1931, pp. 114-124.

[15] Microsoft MSDN, "Visual C++," 2009, http://msdn.mircosoft.com/visualc.

[16] boost, "boost C++ Libraries," 2009, http://boost.org. [17] XERCES, "Xerces WebSite," 2009, http://xerces.apache.org.

[18] W3G, "Scalable Vector Graphics (SVG)," 2009, http://www.w3org/Graphics/SVG.

9] M. Eichhorn, "A New Concept for an Obstacle Avoidance System for the AUV “SLOCUM Glider” Operation under Ice," Oceans '09 IEEE

Bremen, 2009.

[20] NCOG, "Newfoundland Center for Ocean Gliders," 2009, http://www.physics.mun.ca/~glider/.