PGD espace-temps adaptée pour le traitement de problèmes paramétrés

HAL Id: tel-01048636

https://tel.archives-ouvertes.fr/tel-01048636

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

Christophe Heyberger

To cite this version:

Christophe Heyberger. PGD espace-temps adaptée pour le traitement de problèmes paramétrés. Autre. École normale supérieure de Cachan - ENS Cachan, 2014. Français. �NNT : 2014DENS0012�. �tel-01048636�

THÈSE DE DOCTORAT

DE L’ÉCOLE NORMALE SUPÉRIEURE DE CACHAN

Présentée par Christophe Heyberger

pour obtenir le grade de

DOCTEUR DE L’ÉCOLE NORMALE SUPÉRIEURE DE CACHAN

Domaine :

MÉCANIQUE - GÉNIE MÉCANIQUE - GÉNIE CIVIL

Sujet de la thèse :

PGD espace-temps adaptée pour le traitement de

problèmes paramétrés

Soutenue le 1erAvril 2014 à Cachan devant le jury composé de :

Pierre Villon UTC Compiègne Président

David Dureisseix INSA Lyon Rapporteur

Pierre Joyot ESTIA Biarritz Rapporteur

Jayant Sen Gupta Airbus Group Innovations Examinateur Pierre-Alain Boucard ENS Cachan Directeur de thèse

David Néron ENS Cachan Encadrant de thèse

produit une atmosphère de travail idéale durant ces quelques années.

Merci également aux membres de mon jury pour le temps qu’ils ont eu la gtillesse de m’accorder. Vos relectures attentives, vos questions pertinentes et vos en-couragements m’ont permis de préparer au mieux la soutenance.

Je remercie aussi toute l’équipe du LMT, du DGM et du DGC. J’ai énormément ap-pris durant ces années à vos côtés, tant sur le professionnel que sur le plan humain et je ne doute pas que l’ambiance et les personnes qui animent ce lieu feront de nouveaux heureux tout au long des prochaines années.

Je remercie tout particulièrement les personnes qui ont égayé mon quotidien, mes par-tenaires de bureau, tout comme le personnel de l’ENS.

Enfin, je remercie ma famille pour leur support malgré le peu de temps que je pou-vais leur consacrer.

Table des matières i

Introduction 1

1 Contexte de l’étude 7

1 Le projet ANR OMD2 . . . 8

2 Au service des études d’optimisation . . . 9

3 Le problème de référence . . . 13

3.1 Le problème de diffusion . . . 13

3.2 Le problème étudié . . . 14

2 Réduction de modèles 17 1 Méthodes d’approximation . . . 18

1.1 Cadre général des méthodes d’approximation . . . 18

1.2 Proper Orthogonal Decomposition . . . 19

1.3 Proper Generalized Decomposition . . . 22

1.4 Exemples d’application . . . 25

2 Méthodes de réduction de modèle . . . 29

2.1 Méthodes avec apprentissage. . . 30

2.2 Méthodes sans apprentissage . . . 33

2.3 Stratégies d’analyse paramétrique . . . 33

2.4 Exemple d’application numérique . . . 35

3 Stratégie de calcul multiparamétrique 39 1 Notations. . . 40

2 Stratégie de résolution LATIN avec PGD. . . 40

2.1 Stratégie de calcul pour les problèmes non linéaires : la méthode LATIN. . . 40

2.2 Initialisation, convergence et critère d’arrêt de l’algorithme . . . 45

2.3 Développements pratiques par résolution avec la méthode LATIN avec PGD pour un comportement linéaire . . . 46

2.4 Développements pratiques pour un comportement non linéaire . . 54

2.5 Exemple d’application . . . 56

3.1 Stratégie multiparamétrique avec utilisation de la méthode LATIN

sans PGD. . . 57

3.2 Stratégie multiparamétrique avec utilisation de la méthode LATIN avec PGD. . . 63

4 Nature de la base de réinitialisation de la stratégie multiparamétrique 67 1 Avant-propos . . . 68

1.1 Résolution LATIN-PGD vs incrémentale . . . 68

1.2 Etudes paramétriques . . . 68

1.3 « La force brute » . . . 69

2 Processus 1 de réinitialisation. . . 70

2.1 Enrichissement par ROM-PGD : Etude 1 (Variation deλ) . . . 71

2.2 Enrichissement par ROM-PGD : Etude 2 (Variation deρc) . . . 73

3 Extension à d’autres processus de réinitialisation avec PGD . . . 74

3.1 Processus 2 de réinitialisation . . . 74

3.2 Processus 3 de réinitialisation . . . 75

4 Bilan . . . 76

5 Cheminement optimal dans l’espace de conception 79 1 Stratégie multiparamétrique . . . 80

2 Choix d’une erreur en résidu pertinente. . . 80

3 Génération d’une base complète . . . 82

3.1 Existence d’une base complète Bc . . . 82

3.2 Génération d’une base complète à moindre coût . . . 84

4 Exemple numérique . . . 85

4.1 Etudes paramétriques . . . 87

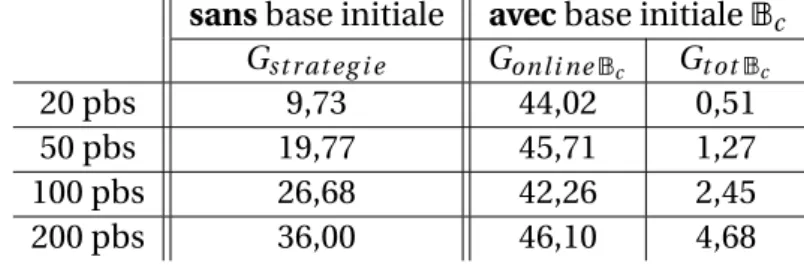
4.2 Génération et utilisation d’une base complète . . . 88

4.3 Application à la résolution d’une étude d’optimisation . . . 90

5 Bilan . . . 93

Conclusion 95

La méthode LATIN sans PGD appliquée au problème de diffusion :

développe-ments pratiques 99

Les campagnes d’essais expérimentaux sont fréquentes dans l’industrie. Elles per-mettent de conforter le dimensionnement par des preuves physiques et sont la conti-nuation d’une culture et d’un savoir-faire d’entreprise. Malheureusement, certains es-sais peuvent se révéler coûteux, complexes à réaliser ou encore nécessiter la destruc-tion de la pièce testée. Le besoin d’être compétitif pousse donc, de plus en plus, les in-dustriels à se tourner vers des outils de simulation numérique. Ces derniers permettent d’obtenir des résultats à coûts et temps réduits et ont donc permis l’accroissement de la fréquence d’utilisation des phases de pré-conception durant lesquelles on simule plusieurs architectures proches, répondant à une même solution technique, afin de déterminer une solution « optimale » au sens d’un objectif donné. C’est ce que l’on peut qualifier d’études d’optimisation.

Chaque technique d’optimisation est développée en correspondance avec la na-ture des modifications opérées durant le processus. Citons par exemple, en se limitant ici au seul cas des problèmes à faible nombre de paramètres, pour des modifications sur l’épaisseur ou la section droite [El-Sayed and Hsiung, 1991,Umesha et al., 2005], sur les propriétés mécaniques du matériau [Theocaris and Stravroulakis, 1998, Bend-soe, 1995], sur la géométrie pour un problème de filet [Borbaru and Mukherjee, 2001] ou pour des problèmes de contact [Li et al., 2005,Pàczelt and Mròz, 2007].

Malgré des méthodes d’optimisation très développées, les temps de calculs restent souvent prohibitifs et l’aspect coût est un véritable verrou pour l’optimisation d’une structure. C’est pourquoi, un certain nombre de techniques d’optimisation consistent à générer, dans un premier temps, un métamodèle à partir du problème mécanique considéré en obtenant les valeurs de la fonction objectif pour plusieurs jeux de pa-ramètres. On cherche ensuite le jeu de paramètres minimisant la fonction objectif à partir du métamodèle (citons, par exemple, les techniques d’optimisation basées sur les surfaces de réponses et autres méthodes d’approximation et de simplification [ Bar-thelemy and Haftka, 1993,Booker et al., 1993,Queipo et al., 2005,Barton and Mecke-sheimer, 2006]).

Toutes les techniques d’optimisation consistent donc à rechercher le jeu de paramètres qui minimise une fonction coût sur un espace de conception, et pour cela, les algo-rithmes de recherche de ce minimum conduisent à résoudre un grand nombre de pro-blèmes similaires (un même problème pour différents jeux de paramètres) : c’est ce que l’on qualifiera de problème paramétré.

Deux voies sont à explorer lorsque l’on souhaite diminuer le coût en calcul d’une étude d’optimisation. Soit on essaye de diminuer l’espace des paramètres d’entrée et de sortie de l’étude (un exemple d’application est donné dans [Raghavan et al., 2013]), soit on essaye réduire le temps de résolution des problèmes successifs. C’est dans ce dernier cas que l’on se place et le but est donc ici de développer une stratégie afin de réduire le temps de calcul associé à la résolution d’un problème paramétré en tirant profit du fait qu’une telle étude amène à traiter une succession de problèmes simi-laires.

On distinguera 2 types d’études parmi celles nécessitant le calcul d’un grand nombre de problèmes similaires :

• Les études ponctuelles, pour lesquelles on ne souhaite résoudre un problème qu’une seule et unique fois et dont le but est de le faire le plus rapidement pos-sible.

• Les études récurrentes, à caractère répétitif, sur un même problème dont les pa-ramètres décrivent un espace de conception. L’objectif est alors d’obtenir une nouvelle solution du problème en quasi-temps réel.

C’est dans ce contexte que le projet OMD2(Optimisation Multi Disciplinaire Distri-buée), financé par l’Agence Nationale pour la Recherche, a vu le jour afin de permettre une intégration industrielle généralisée et plus ambitieuse de l’optimisation. Le travail effectué au cours de cette thèse se situe au sein du Work Package 2.4 d’OMD2et fait suite à celui débuté par le laboratoire LMT dans le cadre d’OMD [Boucard et al., 2009]. Il avait alors été mis en évidence la pertinence des stratégies de calcul spécifiques ar-ticulées autour de la stratégie de calcul multi-échelle LATIN (Large Time INcrement method) [Ladevèze, 1999] ainsi que de l’utilisation d’une stratégie dite « multiparamé-trique » permettant de réduire les coûts de calcul lors du traitement d’un problème paramétré (ce qui est typiquement le cas lors d’un processus d’optimisation).

La méthode itérative LATIN génère une approximation de la solution s du problème sur l’ensemble de l’espace et du temps et en améliore automatiquement la qualité à chaque itération (en apportant des corrections sur l’ensemble du domaine spatio-temporel), quitte à commencer par une approximation très grossière s0. Dans le cadre d’une étude paramétrée et en s’appuyant sur cette technique de résolution, on construit la stratégie multiparamétrique qui consiste à choisir une solution initiale s0 « opti-male » pour la résolution d’un nouveau problème (associé à un nouveau jeu de pa-ramètres) en réutilisant les informations des calculs précédents. On peut ainsi espérer réduire le temps de calcul en initialisant la résolution par une solution initiale « plus proche » de la solution du nouveau problème. Cette technique a initialement été in-troduite dans le cadre de problèmes de contact [Boucard and Champaney, 2003]. La

solution du calcul précédent était alors choisie puis réutilisée en tant que solution ini-tiale s0d’une nouvelle résolution (pour un nouveau jeu de paramètres).

Afin d’améliorer les performances de la stratégie, une idée consiste à utiliser des techniques de réduction de modèle, aussi connues sous le nom de ROM (Reduced-Order Modeling). Ces techniques sont à la base d’un compromis essentiel : réduire le temps de calcul en cherchant une approximation de la solution, sans pour autant dé-grader la qualité du résultat.

Une première possibilité est d’utiliser une technique de réduction de modèle se basant sur la Proper Orthogonal Decomposition (POD, introduite notamment dans le contexte de la turbulence [Lumley, 1967], un exemple d’application général est donné dans [Chatterjee, 2000]) qui a pour but d’approcher une fonction T (t , M) (t étant la variable temporelle, M la variable spatiale) par une décomposition en somme finie à l’ordre K , notée TK, qui minimise la distance à T au sens d’une certaine norme :

T (t , M) ≈ TK(t , M) = K

X

i =1

τi(t )Ti(M) (1)

où l’on impose aux fonctions spatiales d’être orthogonales entres elles lors de la re-cherche de cette décomposition.

La POD est à la base de plusieurs techniques de réduction de modèle, connues sous le nom de techniques a posteriori, qui sont surtout utilisées pour la résolution de problèmes à grand intervalle de temps ou pour la résolution d’une série de pro-blèmes « similaires » [Kunish and Xie, 2005,Lieu et al., 2006,Gunzburger et al., 2007]. Ces techniques nécessitent une phase préliminaire, appelée phase « d’apprentissage », durant laquelle on résout un problème moins coûteux lié au problème à traiter (dis-crétisation grossière ou intervalle de temps réduit) que l’on qualifie de problème de substitution (en anglais, surrogate problem). La solution de ce problème est alors dé-composée par POD et les fonctions (souvent spatiales) sont conservées pour former une base réduite (ROB, Reduced-Order Basis) et sert de base de projection pour tous les autres problèmes, amenant à la résolution de problèmes peu coûteux. L’inconvé-nient majeur de ces techniques est que l’approximation de la solution est extrême-ment dépendante du choix du problème de substitution. Des techniques ont toutefois été introduites pour enrichir la base si elle n’est plus assez représentative de la solu-tion [Ryckelynck, 2005,Ryckelynck et al., 2006]. Une autre technique, appelée Reduced Basis (citons par exemple, [Maday et al., 2002,Maday and Ronquist, 2004,Rozza et al., 2008]), consiste à construire, en amont des évaluations de la solution pour différentes valeurs des jeux de paramètres, une ROB ainsi que l’estimateur qui permettra de quan-tifier l’erreur réalisée en utilisant cette ROB. Cette première phase, offline, est la partie coûteuse de la méthode, mais a le gros avantage de permettre de maîtriser l’erreur. La phase d’approximation de la solution, online, est, pour sa part, très rapide.

A contrario, il existe des techniques de calculs a priori. On introduit ainsi la Pro-per Generalized Decomposition (PGD) qui génère directement une décomposition de type (1) sans forcer l’orthogonalité des fonctions spatiales et surtout sans avoir besoin de la solution d’un problème de substitution mais seulement de l’équation aux déri-vées partielles vérifiée par la solution du problème étudié et donc sans fixer a priori la base des fonctions sur laquelle s’écrit la décomposition. Cette technique ne peut pas être mise en oeuvre avec les méthodes de résolution incrémentales classiques, car chaque sous-résolution à chaque pas de temps reste une vision fractionnée du temps alors que l’on recherche une décomposition à variables séparées dont chaque couple de fonctions doit donner une vision complète du domaine espace-temps. La méthode LATIN [Ladevèze, 1999] caractérisant la solution totalement sur l’ensemble de son do-maine à chaque itération, il est ainsi possible d’y introduire une représentation à va-riables séparées des inconnues afin de diminuer le temps de calcul. La PGD a été ré-cemment utilisée (avec différents algorithmes de génération de l’approximation) pour des problèmes dits « multidimensionnels » [Ammar et al., 2006,Ammar et al., 2007, Chi-nesta et al., 2008], pour la résolution de problèmes stochastiques (dans lequel on parle de « Generalized Spectral Decomposition » [Nouy, 2007, Nouy, 2009]), pour des pro-blèmes multiphysiques [Dureisseix et al., 2003,Néron and Dureisseix, 2008], pour des problèmes multiéchelles [Ladevèze et al., 2010], ou encore couplée avec la BEM (Boun-dary Element Method) pour la résolution de l’équation de la chaleur en linéaire [ Boni-thon et al., 2011] et en non linéaire [Joyot et al., 2011]. Ces travaux conçoivent la PGD comme une décomposition en temps et en espace, mais il est possible de décompo-ser la solution par rapport à des variables supplémentaires, comme les paramètres de l’étude [Ammar et al., 2012] ce qui constitue un bon moyen de résoudre des problèmes paramétrés. Dans le cadre de cette thèse on se limitera à la vision de la PGD en espace-temps, ceci afin de pouvoir réutiliser les résultats sur tous les outils déjà développés dans cette même vision au sein du LMT-Cachan depuis de nombreuses années (calcul multiéchelle, parallélisme ...).

En s’inspirant des techniques de réduction de modèle se basant sur la POD, une première partie des travaux s’est intéressée à l’impact sur les performances de la stra-tégie, de la nature de la base réduite qui sert d’initialisation pour un nouveau calcul. Pour cela, on considère les bases POD et PGD issues d’un même problème (associé à un premier jeu de paramètres) et on utilise la méthode LATIN avec PGD comme mé-thode d’enrichissement de l’une ou l’autre de ces 2 bases réduites pour la résolution d’un nouveau problème (associé à un nouveau jeu de paramètres).

La représentation PGD des solutions permettant d’être sélectif pour le choix des fonc-tions constituant la base réduite, plusieurs méthodes d’enrichissement ou de tri des fonctions de cette base (ce que l’on qualifiera de processus de réinitialisation) peuvent ainsi être envisagées et testées.

• Dans le cadre des études ponctuelles, le choix se porte sur une génération online d’une base réduite adaptée à la représentation de l’ensemble des solutions d’un espace de conception.

• Dans le cadre des études récurrentes, le choix se porte sur une génération offline d’une base réduite par une méthode d’exploration adaptée.

Le thème de la génération online d’une base réduite adaptée a été exploré dans [Relun, 2011, Relun et al., 2013]. L’objectif était la vérification de la tenue en fatigue de pièces aéronautiques constituées d’un matériau élasto-viscoplastique par prise en compte d’incertitudes sur la durée de vie. Cette vérification était à faire une seule fois pour chaque nouvelle pièce et l’intérêt s’est donc porté sur le temps complet de réso-lution de l’étude. Une stratégie dédiée de réutilisation et d’enrichissement de la base réduite a donc été mise en place pour diminuer le temps d’exécution des calculs. Les gains obtenus en termes de coût global de la simulation sont de l’ordre de 30, faisant passer la durée totale d’une étude de plusieurs mois, avec les logiciels commerciaux, à quelques jours.

Le partenariat de Renault avec le projet OMD2 impose à cette thèse le cadre des études récurrentes. Dans un contexte où les pièces à dimensionner peuvent souvent être du même type et les études d’optimisation répétitives, l’objectif est de mettre à disposition, à moindre coût, un outil permettant à l’ingénieur d’obtenir en temps réel la solution d’un nouveau problème. Pour cela, il est nécessaire de construire en amont, durant une phase offline, une base réduite permettant de représenter l’en-semble des solutions dans l’espace de conception (c’est ce que l’on qualifiera de « base complète »). Pour une telle technique, où l’établissement et le stockage d’une base complète est justifié, on différenciera le temps offline de constitution de la base com-plète et le temps online de résolution de l’étude en utilisant cette base en initialisation. Dès lors, la problématique revient à construire une technique de sélection rationnelle, à coût réduit, des jeux de paramètres les plus pertinents à traiter pour enrichir la connais-sance globale de la solution.

Dans le cadre des études récurrentes, des travaux ont montré (par exemple [Buffa et al., 2012]) la possibilité d’obtenir une telle base à l’aide d’algorithmes gloutons. Le problème de ces techniques est qu’elles nécessitent la connaissance d’un grand nombre de solutions sous forme PGD en amont, ce qui les rend très coûteuses en temps de cal-cul. On se propose alors de développer ici une technique de génération de cette base à moindre coût en s’inspirant de la méthode Reduced Basis puis de mettre en oeuvre cette base au sein de la stratégie multiparamétrique.

Cette thèse est divisée en 5 chapitres. Le premier détaille le contexte de l’étude ainsi que le problème de référence. Les exploitations numériques porteront ici sur un pro-blème de diffusion à 1 dimension en linéaire. Le chapitre suivant positionne les travaux

de cette thèse dans le domaine des réductions de modèle. Le troisième chapitre décrit la stratégie multiparamétrique dont la méthode LATIN se trouve au coeur. Le but du quatrième chapitre est de quantifier les impacts de la nature de la base de réinitialisa-tion sur les performances de la stratégie. On s’intéresse tout d’abord au procédé de gé-nération des fonctions de la base en comparant POD et PGD, puis différents processus de réinitialisation sont étudiés. Enfin, le dernier chapitre s’intéressera à la construc-tion et à l’utilisaconstruc-tion d’une base complète. On développera tout d’abord une technique pour trouver une base complète à moindre coût puis on étudiera son efficacité au sein de la stratégie multiparamétrique.

Contexte de l’étude

Ce premier chapitre positionne les travaux de cette thèse dans le cadre du projet ANR OMD2. Le problème de référence

sur lequel s’effectueront toutes les exploitations y est aussi présenté.

Sommaire

1 Le projet ANR OMD2 _{. . . . 8}

2 Au service des études d’optimisation . . . . 9

3 Le problème de référence . . . . 13

3.1 Le problème de diffusion . . . 13

1 Le projet ANR OMD

Profitant du développement de l’ère numérique, les industriels se concentrent de plus en plus sur les phases de pré-conception de produits. Durant ces phases, on es-saye de trouver la « meilleure » solution technique par rapport à un ou plusieurs cri-tères (moins de pollution, plus économique à produire et à utiliser, plus silencieux ...) avec la contrainte du respect d’un cahier des charges fonctionnel. Pour cela, différentes variantes d’une même solution incluses dans un espace de conception sont testées (variation de la géométrie, des matériaux utilisés ...) et une fonction coût est calculée pour chacune des solutions afin de quantifier les performances d’une solution suivant les critères sélectionnés. Une solution « optimale », minimisant la fonction coût sous possiblement certaines contraintes (contraintes géométriques, poids minimal ...) est alors trouvée grâce à des techniques d’optimisation. Ces techniques conduisent donc à résoudre de nombreuses fois des problèmes similaires (pour lesquels seuls certains paramètres de la modélisation ont changé).

Toutefois, dans ce contexte à grand nombre de requêtes, l’important n’est pas d’obte-nir la solution du problème demandé mais d’évaluer le plus rapidement la valeur de la fonction coût associée à ce problème. Ce temps de réponse entre la donnée des pa-ramètres d’entrée de l’étude et les valeurs de sortie de l’étude est appelé le temps de résolution « online ».

Même si de nombreuses techniques d’optimisation existent et sont très perfor-mantes, certaines difficultés persistent. On peut principalement en distinguer deux :

• Le temps de calcul

Ces techniques sont très coûteuses car elles nécessitent de nombreux calculs de la fonction coût pour diverses configurations. Cela incite donc les industriels à limiter le nombre d’études d’optimisation menées dans un contexte où l’on vou-drait toujours que chacune dure moins longtemps.

• Le manque de multidisciplinarité

Dans divers domaines comme l’aéronautique ou l’automobile, différentes dis-ciplines sont présentes au sein d’un même système et il faut être ainsi capable de véhiculer les informations au travers des différents champs disciplinaires. Par exemple, changer la géométrie d’un conduit d’écoulement pourra avoir un im-pact positif sur le coût de fabrication mais pourra avoir un imim-pact négatif sur l’écoulement du fluide à l’intérieur de ce conduit.

D’un point de vue technique, une modification en entraine donc souvent d’autres en cascade au sein de différents champs disciplinaires pilotés par différentes équipes, ce qui est souvent présage de problèmes de communication.

D’un point de vue algorithmique, l’aspect multidisciplinaire amène à considérer plusieurs fonctions coût. Actuellement, pour gérer cet aspect, soit on considère une « super » fonction coût comme étant une somme pondérée des différentes

fonctions coût à considérer, ce qui peut « biaiser » le processus d’optimisation (la solution trouvée ne minimise que rarement l’ensemble des fonctions coût). Soit on établit un front de Pareto pour des solutions difficilement hiérarchisables (performances inégales sur l’ensemble des fonctions coût débouchant sur des compromis).

C’est dans ce contexte que Renault, en coordonnant le projet OMD2, a pris le parti de relever le challenge du développement d’une plateforme d’optimisation multidis-ciplinaire. Pour cela, différentes équipes ont été associées pour partager leurs spé-cialités en CAO paramétrée en web-service (SIREHNA), en modélisation numérique (CD-ADAPCO), en stratégie et puissance de calcul (INRIA, ACTIVEEON), en utilisation d’outils d’optimisation (RENAULT), en langage et outils de programmation (DIGITEO-SCILAB), en mécanique des fluides (Centrale Paris, INRIA) et des solides (LMT CACHAN, IRCCYN, UTC) et en mathématiques appliquées (INRIA, Centrale Paris, ENSM-SE).

2 Au service des études d’optimisation

L’objectif d’une étude d’optimisation est de trouver le jeu de paramètres minimi-sant une fonction coût sur un espace de conception (espace de variation des para-mètres considérés) et pour se faire, il existe 2 familles d’algorithmes d’optimisation : les algorithmes d’optimisation globale et ceux d’optimisation locale.

Ï Algorithmes d’optimisation globale

Ces algorithmes cherchent un minimum global sur l’ensemble de l’espace de concep-tion en s’intéressant aux évaluaconcep-tions de la foncconcep-tion coût associées à différents jeux de paramètres choisis. Ceci rend ces algorithmes plutôt coûteux. Deux différents types de modèles réduits sont donc souvent utilisés pour réduire le temps de calcul :

• Des modèles réduits physiques travaillant sur une approximation plus ou moins fidèle du modèle facilitant les calculs [Engels et al., 2004]. Un exemple de fonc-tionnement est donné sur la figure1.1. La stratégie consiste à réduire la zone de recherche de l’optimum du problème d’optimisation afin de faire le moins de cal-culs possibles avec le modèle le plus complexe et donc le plus coûteux à résoudre, ici le modèle « éléments finis 3D en non-linéaire ». Pour cela, on considère des modèles plus simples et se rapprochant successivement du modèle complexe. On commence ainsi par considérer le modèle « poutre » permettant de réduire le domaine de recherche, puis on recommence une nouvelle étude sur ce do-maine de recherche réduit avec un modèle plus complet, ici le modèle « coque », permettant de réduire à nouveau le domaine sur lequel on recherchera ensuite l’optimum avec le modèle complexe.

Optimisation sur le niveau 1 du modèle

(Modèle «poutre») Optimisation sur

le niveau 2 du modèle

(Modèle «coque») Optimisation sur le niveau 3 du modèle (Modèle «EF 3D NL») espace de conception Réduction de la zone de recherche du minimum optimum trouvé

FIGURE1.1: Modèles réduits physiques

• Des modèles réduits non physiques ou encore métamodèles (aussi appelés mo-dèle de substitution ou « surrogate model »), c’est-à-dire des approximations ou des régressions basées sur quelques évaluations de la fonction coût qui en per-mettent une connaissance globale [Queipo et al., 2005]. Un exemple de construc-tion d’un métamodèle est donné sur la figure1.2suivant la population d’évalua-tions considérée. On remarque sur cet exemple de construction du métamodèle, ici par approximation linéaire entre les évaluations, que plus la population est faible est plus le métamodèle est grossier (le métamodèle lisse la surface de ré-ponse « réelle »). D’autres méthodes de construction du métamodèle sont cepen-dant envisageables suivant les besoins, notamment par krigeage.

0 1 0 1 0 1 fonction coût 0 1 0 1 0 1 fonction coût Approximation de la fonction coût à partir de 16 évaluations

Approximation de la fonction coût à partir de 169 évaluations Variation de la

population

FIGURE1.2: Métamodèle suivant le nombre d’évaluations considérées

Ces modèles réduits permettent de sélectionner une zone d’intérêt dans l’espace de conception pour laquelle des calculs plus fins seront réalisés. L’utilisation de ces 2 mo-dèles réduits peut être regroupée sous le terme d’optimisation multi-niveaux. Deux

visions du niveau, pouvant être complémentaires, sont alors distinguées, que ce soit suivant différents niveaux de fidélité par rapport à un modèle ou que ce soit en terme de différents niveaux de grandeur d’une population de jeux de paramètres à considé-rer.

Les algorithmes d’optimisation globale, souvent inspirés par des phénomènes phy-siques, font appel à la notion de mémoire : l’historique des recherches sur les premières itérations est toujours prise en compte pour une nouvelle itération. Ces algorithmes peuvent se classer en 2 catégories [Goldberg, 1989] : ceux basés sur la notion de par-cours (citons, par exemple, le recuit simulé [Bonomi and Lutton, 1988] et la recherche avec tabou [Glover and Laguna, 1979]) et ceux basés sur la notion de population (ci-tons, par exemple, les algorithmes génétiques [Holland, 1975] et les algorithmes d’op-timisation par essaim [Bonaneau et al., 1999]).

Ï Algorithmes d’optimisation locale

Ces algorithmes permettent de trouver le minimum d’une fonction coût le plus « proche » d’un jeu de paramètres initial. Ils sont très rapides mais peuvent se bloquer sur des mi-nimums locaux et non globaux. Parmi les différentes techniques développées, distin-guons la méthode du simplex [Nelder and Mead, 1965] et les méthodes basées sur des calculs de gradients. La première est une méthode déterministe et n’utilise aucune in-formation sur les dérivées de la fonction coût. Les secondes cherchent à trouver le zéro de la dérivée de la fonction coût. Pour cela, on part d’un point de l’espace de concep-tion, et lorsque les gradients ne sont pas donnés, l’optimiseur demande le calcul de la fonction coût pour des faibles variations des paramètres autour de ce point. Une direc-tion de recherche du minimum sera alors choisie suivant la plus grande pente trouvée. Ces méthodes pouvant se bloquer sur des minimums locaux lorsque la fonction n’est pas convexe, elles sont associées à des stratégies de « restart » s’inspirant des stratégies globales. Ces stratégies, plus exploratoires consistent à regarder la valeur de la fonc-tion coût en plusieurs points de l’espace afin de s’assurer que le minimum trouvé soit global. Des algorithmes globaux peuvent aussi être utilisés durant une première phase afin de sélectionner certaines zones en forme de puits, facilitant le travail des algo-rithmes locaux durant une seconde phase.

En synthèse, une tentative de schématisation du principe d’action de ces 2 familles d’algorithmes d’optimisation (locale et globale) est représentée sur la figure1.3. On y remarque que l’optimisation globale ne peut tomber sur un minimum local car elle commence par tester une très large population sur l’espace de conception avant de partir précisement à la recherche du minimum.

Toutes ces techniques nécessitent donc de nombreux calculs de la fonction coût et donc de nombreux calculs de la solution d’un même problème pour différents jeux de paramètres (c’est ce que l’on qualifiera de problèmes « similaires »). L’élaboration d’un algorithme d’optimisation n’est pas l’objectif de cette thèse. Ainsi, dans un souci

espace de conception fonction

coût

minimum global initialisations

(a) Optimisation globale

espace de conception fonction coût restart minimum global minimum local initialisation (b) Optimisation locale

FIGURE1.3: Principe d’action des 2 familles d’algorithmes d’optimisation

de simplification de certaines exploitations numériques, on se placera dans le cas où seule la contrainte de l’espace de conception est donnée pour la variation des para-mètres et on pourra ainsi simuler une étude d’optimisation par la résolution succes-sive d’un certain nombre de problèmes. L’important ici n’étant pas de trouver la so-lution d’un problème d’optimisation mais plutôt de trouver un moyen de diminuer le temps de résolution d’un tel problème. On distinguera alors la phase de génération d’un métamodèle, des phases de minimisation des algorithmes d’optimisation. Dans le premier cas, le but est d’obtenir les évaluations aux points de la grille de l’espace de conception et l’on pourra ainsi choisir le cheminement dans cet espace pour la résolu-tion successive des problèmes. En revanche, dans le second cas, le cheminement sera imposé par les besoins de l’algorithme durant la minimisation. Pour simuler cela, les jeux de paramètres correspondant aux problèmes à résoudre seront alors successive-ment et aléatoiresuccessive-ment tirés dans l’espace de conception.

Les travaux de cette thèse ont eu pour but de répondre à la problématique posée par la proposition d’une stratégie de calcul dite « multiparamétrique » adaptée à la ré-solution de problèmes similaires. Dans son objectif de réduire considérablement le temps de calcul de ces problèmes, la stratégie multiparamétrique utilise 2 moyens :

• L’approximation spatio-temporelle, sujet du chapitre 2et mise en pratique au sein de la stratégie multiparamétrique au chapitre 3, afin de réduire le coût de résolution d’un problème et de permettre une transmission de l’information per-tinente de calcul en calcul.

• Le choix des informations issues des précédents calculs à transmettre pour la ré-solution de problèmes similaires grâce à un processus de réinitialisation pour les calculs suivants. Cette idée est plus particulièrement décrite dans le chapitre4.

3 Le problème de référence

3.1 Le problème de diffusion

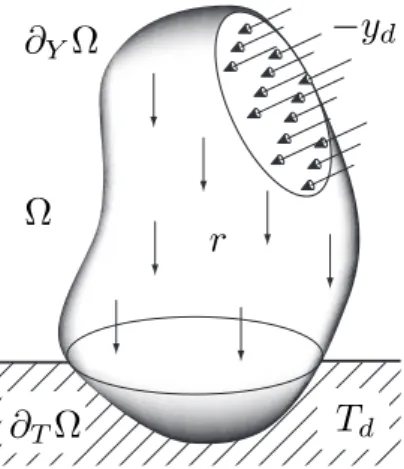
Le problème qui sert d’illustration est celui de diffusion dans un domaine Ω, initia-lement à une température Ti ni t. On s’intéresse à l’évolution de la température T (t , M)

sur ce domaine et au cours d’un intervalle de temps I = [0, tf i nal]. Cette structure (cf.

Figure1.4) est soumise à :

• une production volumique de chaleur propre r sur Ω, • une température Td sur la partie∂TΩ de la frontière,

• une densité de flux de chaleur −yd sur la partie complémentaire∂YΩ.

∂

Ω

∂

Ω

Ω

F

U

f

r

T

∂

Ω

Ω

∂

Ω

−y

FIGURE1.4: Le problème de référence

On désigne la masse volumique par ρ, la capacité thermique massique par c, la conductivité thermique parλ, la densité de flux de chaleur par q (mais on choisit de travailler sur Y = −q pour des raisons qui seront expliquées par la suite).

Le problème de diffusion consiste à trouver s = (T, Y ) définie sur I × Ω qui vérifie : • L’équation de la chaleur : ρc∂T ∂t =r + div Y • La loi de Fourier : Y =λ grad T

• Les conditions aux limites (où n est la normale extérieure à∂YΩ) :

T = Td sur∂TΩ

Y · n = yd sur∂YΩ

• La condition initiale :

T = Ti ni t à t = 0

En notant T = {T | T est suffisamment régulier, T |∂TΩ=Td et T |t =0=Ti ni t} et T ∗ l’espace homogène associé, le problème de diffusion sous forme variationnelle revient à :

Trouver T ∈ T , tel que :

∀T∗∈ T∗, A_{(T, T}∗_{) = L(T}∗_{) (1.1)} avec            A_{(T, T}∗_{) =} Z I_×Ω ρc ∂T ∂t T ∗ dΩ dt + Z I_×Ω grad T∗λ grad T dΩ dt L(T∗) = Z I_×Ω r T∗dΩ dt + Z I×∂YΩ T∗yddS d t

3.2 Le problème étudié

On souhaite étudier la réponse de cette structure lorsque certains paramètres dé-crivent un espace de conception. On peut envisager ici des variations sur différents types de paramètres (chargement (r , yd), conditions aux bords (conditions limites et

initiales), paramètres matériau (ρ, c, λ) et de l’étude (discrétisation, durée, longueur du domaine)), mais on se restreindra ici aux variations des paramètres matériauxλ et

le facteurρc. Dans les études envisagées, on pourra considérer que λ et le facteur ρc seront homogènes ou hétérogènes en espace.

Tous les développements pratiques présents dans les chapitres suivants restent va-lables pour des problèmes à plusieurs dimensions spatiales, mais dans ce travail ex-ploratoire, seul le cas à 1 dimension spatiale a été étudié dans les exploitations numé-riques.

Au cours des différents exemples numériques, on considère le chargement et les conditions limites invariants et comme étant ceux décrits sur la figure1.5. On consi-dère la température comme étant nulle à l’instant initial, la durée de l’étude est fixée à tf i nal=30 s et la longueur du milieu à L = 1 m.

Td(t)

M= 0 M= 1

yd(t)

r(M, t)

1 m

(a) Le problème traité (b) Chargement r (M, t )

0 10 20 30 ï5 0 5 t (s) Td (c) Condition en température Td

dépendante du temps sur le bord M = 0 0 10 20 30 ï4 ï2 0 2 4 t (s) yd (d) Condition en flux yd

dépendante du temps sur le bord M = 1

FIGURE1.5: Le problème traité

Lors de certaines phases d’une étude d’optimisation, comme pour la génération d’un métamodèle, on est amené à explorer l’espace de conception p. Pour ce faire, par exemple lors d’une étude à 2 paramètres (p =©λ, ρcª), on échantillonne les intervalles de variation de ces paramètres, ce qui conduit à déterminer la solution du problème pour N × M jeux de paramètres pi j =©λi,ρcj

ª

avec i = 1, . . . , N et j = 1, . . . , M. C’est à dire à résoudre N × M problèmes similaires.

Réduction de modèles

Ce chapitre expose les bases de différentes méthodes d’approximation. Il s’intéresse ensuite à des techniques adaptées à la résolution de problèmes similaires se basant

sur ces méthodes.

Sommaire

1 Méthodes d’approximation . . . . 18 1.1 Cadre général des méthodes d’approximation . . . 18 1.2 Proper Orthogonal Decomposition . . . 19 1.3 Proper Generalized Decomposition . . . 22 1.4 Exemples d’application . . . 25 2 Méthodes de réduction de modèle . . . . 29 2.1 Méthodes avec apprentissage. . . 30 2.2 Méthodes sans apprentissage. . . 33 2.3 Stratégies d’analyse paramétrique . . . 33 2.4 Exemple d’application numérique. . . 35

1 Méthodes d’approximation

1.1 Cadre général des méthodes d’approximation

Le problème à résoudre peut s’énoncer de la manière suivante ; comment appro-cher une fonction T , dépendante des variables d’espace M (M ∈ Ω) et de temps t (t ∈ I ), par une somme finie à l’ordre N de termes s’écrivant comme un produit de fonctions à variables séparées du type :

T (M, t ) ≃ TN(M, t ) = N

X

i =1

τi(t ) Ti(M) =λN(t ) · ΛN(M)T (2.1)

oùτi(t ) sont les fonctions du temps et Ti(M) les fonctions de l’espace et oùλN(t ) =

[τ1(t ),τ2(t ), . . . ,τN(t )] et ΛN(M) =

£

T₁(M), T2(M), . . . , TN(M)

¤

sont les bases réduites des fonctions temporelles et spatiales.

Une infinité de décomposition sont donc possibles et en pratique 2 voies sont ex-plorées :

• Soit on considère les fonctions Ti comme connues a priori (polynômes de

Le-gendre ou de Chebychev, fonctions trigonométriques, séries de Fourier ...). • Soit on considère des fonctions Ti intrinsèques par nature à la fonction T à

ap-procher. Afin de trouver la meilleure décomposition possible (au regard d’une certaine norme), c’est ce second point qui est le principe de base de la POD. Ï La résolution du problème de minimisation

En choisissant la norme de L2, les fonctions du temps et de l’espace sont solutions du problème suivant : min λN(t ), ΛN(M) kT (M, t ) −λN(t ) ΛN(M)k2 avec k · k2= Z Ω×I ·2_dΩdt (2.2)

oùλN(t ) représente l’ensemble des fonctions du tempsτi et ΛN(M) représente

l’en-semble des fonctions de l’espace Tipour un certain niveau d’approximation de T (M, t ).

En différenciant (2.2) par rapport àλN et ΛN, on trouve que :

∀λ∗_{N, Λ}∗_N Z I λ∗_N Z Ω (T −λNΛN) ΛNdΩ dt + Z ΩΛ ∗ N Z I (T −λNΛN)λNdΩ dt = 0

Ce qui conduit à la résolution du système couplé :          λN(t ) = R ΩT (M,t ) Λ_R N(M) dΩ ΩΛN(M)2dΩ = (T, ΛN) (ΛN, ΛN) ΛN(M) = R IT (M,t )λN(t ) d t R IλN(t )2d t = 〈T,λN〉 〈λN,λN〉 où        ¡ f , g¢=R_{Ωf g dΩ} 〈 f , g 〉 =RI f g d t (2.3)

En substituant, par exemple, la première équation de (2.3) dans la seconde, on trouve alors l’équation en Λ suivante :

〈T , (T, ΛN) (ΛN, ΛN) 〉 = 〈 (T, ΛN) (ΛN, ΛN) , (T, ΛN) (ΛN, ΛN)〉 ΛN

Ce qui peut encore se mettre sous la forme d’un problème aux valeurs propres [ La-devèze, 1985] :

F_{(ΛN) =ω}2_{ΛN (2.4)}

En triant les valeurs propresωi par ordre décroissant, on ordonne ainsi les

fonc-tions propres Ti(M) et on trouve les fonctions du temps associéesτi(t ) à l’aide de (2.3).

Bien souvent, afin de faciliter le calcul des fonctions du tempsτi, on choisit

d’im-poser aux fonctions spatiales Ti d’être orthogonales entre elles et de former une base

orthonormée. Dans ce cas, les fonctions du tempsτi se déduisent simplement de la

décomposition (2.1) : τi(t ) = ¡ T (M, t ), Ti(M) ¢ = Z Ω T (M, t ) Ti(M) dΩ

1.2 Proper Orthogonal Decomposition

On l’a vu, différentes techniques existent pour trouver une décomposition à va-riables séparées de T (M, t ) et peuvent nécessiter un nombre N plus ou moins impor-tant de fonctions pour obtenir une bonne approximation. L’objectif de la POD est de trouver la meilleure décomposition possible de rang N (par rapport à une certaine norme). Pour cela, les fonctions Ti ne sont pas fixées a priori et ce n’est que durant

le processus de génération de la décomposition que les fonctions sont calculées avec la contrainte qu’une nouvelle fonction doit être orthonormale aux autres.

La principale caractéristique de la POD étant son optimalité (meilleure approximation possible au rang N), elle est le moyen le plus efficace de capturer les composantes do-minantes d’un problème en un petit nombre de modes (fonctions Ti) afin d’en avoir

une description à faible dimension [Chatterjee, 2000, Holmes et al., 1996]. Cette dé-composition a été introduite dans le contexte de la turbulence [Lumley, 1967] et est

couramment utilisée pour la compression de données en analyse statistique [ Hotel-ling, 1933, Aubry et al., 1991], le traitement de l’image, l’acoustique, l’ingénierie bio-médicale [Nenadic et al., 2002,Niroomandi et al., 2008].

Sous certaines hypothèses (suivant que la dimension soit finie ou non et suivant le choix de la norme), la POD peut être construite suivant 3 méthodes équivalentes [Liang et al., 2002] : l’analyse en composantes principales (PCA, [Pearson, 1901]), la décomposition de Karhunen-Loeve (KLD, [Karhunen, 1943,Loeve, 1955]) et la décom-position en valeurs singulières (SVD, [Klema and Laub, 1980] pour une revue de cette technique).

Ï PCA et KLD

La PCA peut être vue comme une approximation au sens des moindres carrés. La KLD est similaire à la PCA à la différence près que cette méthode a été introduite plus particulièrement pour le traitement de problèmes à dimension infinie. Ces méthodes consistent à rechercher les valeurs propres de la matrice de covariance du problème.

Ï SVD

En dimension finie et lorsque la norme choisie est celle de L2, la POD est équiva-lente à la SVD. Cette dernière peut être vue comme une extension de la résolution de problèmes aux valeurs propres pour des matrices rectangulaires.

Pour faciliter la compréhension, dans la suite, le domaine spatial est considéré à 1 dimension x et est discrétisé en nx degrés de liberté et le domaine temporel est

discré-tisé en nt pas de temps. La connaissance de T peut ainsi s’écrire sous la forme d’une

matrice des réalisations R :

R =      T (x1, t1) T (x1, t2) . . . T (x1, tnt) T (x2, t1) T (x2, t2) . . . T (x2, tnt) .. . ... ... T (xnx, t1) T (xnx, t2) . . . T (xnx, tnt)     

Le but de la SVD est de décomposer la matrice R en un produit de 3 matrices :

R = UΣVT (2.5)

où U et V sont des matrices orthogonales, respectivement de dimension nx×nx

et nt×nt et où Σ est une matrice diagonale de dimension nx×nt contenant les

gran-deursσi pour i = 1 · · · p , appelées valeurs singulières de R (et de RT), telles queσ1Ê σ2Ê · · · Êσr >σr +1=σr +2= · · · =σp =0 où p = min(nx, nt) et où r est le rang de la

et de U = (u1, u2, · · · , unx) sont dénommées vecteurs singuliers droit et gauche de R. Enfin, puisque les valeurs singulières de R sont rangées en ordre décroissant, l’index i correspondant est appelé numéro d’ordre des valeurs singulières.

D’un point de vue technique, afin de trouver la décomposition SVD ; R = UΣVT, le calcul direct des valeurs singulièresσi et des vecteurs singuliers U et V associés étant

souvent fastidieux, il est préférable de les déterminer par la résolution des problèmes aux valeurs propres équivalents plus simples à résoudre. En effet, les matrices U et V étant orthogonales, si on multiplie la relation (2.5) par sa transposée à droite ou à gauche, on obtient respectivement les 2 équations suivantes :

RRT=_UΣ2UT (2.6)

RTR = V Σ2VT (2.7)

Chercher les valeurs singulières de R revient donc à chercher les valeurs propres de RRTou de RTR. Ainsi, (2.6) amène à résoudre un problème aux valeurs propres de dimension nx et (2.7) un problème aux valeurs propres de dimension nt.

Considérer l’approximation de rang N de T (RN sous forme discrète), amène à ne

regarder plus que les N premières valeurs singulières et N premiers vecteurs singuliers de R. On peut alors écrire :

RN = µ UN 0 ¶ µ ΣN 0 0 0 ¶ µ VN 0 ¶T

où UN est de dimension nx×N, ΣN de dimension N × N, VN de dimension nt×N.

En posant AN = ΣNV_NT, on retrouve alors la décomposition à variables séparées

cher-chée : R ≃ RN= N X i =1 UN(M, i ) AN(i , t ) (2.8)

où les colonnes de la matrice UN représentent les fonctions de l’espace normées Ti et

les lignes de la matrice AN représentent les fonctions du tempsτi.

De plus, on a accès à un indicateur d’erreur d’approximation à l’ordre N avec e_{SV D}N grâce aux valeurs singulières :

e_{SV D}N =1 − N X i =1 σi p X i =1 σi (2.9)

1.3 Proper Generalized Decomposition

Contrairement à la POD, la PGD consiste à trouver une représentation à variables séparées de type (2.1) d’une solution T sans l’avoir calculée a priori (aucune réalisation de T n’est donc connue) mais en utilisant l’équation aux dérivées partielles qui régit T . La PGD génère donc directement la décomposition et la base sur laquelle l’écrire grâce aux équations dont T est solution et non grâce à ses réalisations. La PGD a initiale-ment été introduite sous le nom d’ « approximation radiale » [Ladevèze, 1985, Bussy et al., 1990]. En parcourant les travaux traitant de la PGD, on peut trouver la résolu-tion de problèmes multidimensionnels ou de problèmes inverses, dans lesquels un très grand nombre de variables interagissent [Ammar et al., 2006,Ammar et al., 2007, Chi-nesta et al., 2008], la résolution de problèmes stochastiques [Nouy, 2007,Nouy, 2009], de problèmes multiphysiques [Dureisseix et al., 2003,Néron and Dureisseix, 2008], de problèmes multiéchelles [Ladevèze et al., 2010] ou encore couplée avec la BEM pour la résolution de l’équation de la chaleur en linéaire [Bonithon et al., 2011] et en non linéaire [Joyot et al., 2011]. Une synthèse de cette stratégie et de ses applications est faite dans [Chinesta et al., 2011].

Avec l’hypothèse qu’il est possible de séparer le domaine spatial et le domaine tem-porel, 2 approches sont alors considérées pour la construction de la PGD : l’approche Galerkin progressif et celle de la minimisation du résidu.

1.3.1 Galerkin progressif

En partant de la formulation variationnelle A (T, T∗) = L(T∗) du problème consi-déré (par exemple ici, (1.1) pour le problème de thermique), l’approximation PGD consiste à chercher le champ solution T (M, t ) sous la forme d’une décomposition à variables séparées ainsi que de prendre le champ test adapté T∗(M, t ), avec :

T (M, t ) ≈ TN(M, t ) = N X i =1 τi(t )Ti(M) (2.10) T_N∗(M, t ) = N X i =1 τ∗_i(t )Ti(M) +τi(t )T∗_i(M) (2.11)

Ainsi, en supposant TN−1 connu, le nouveau couple (τN, TN) (que l’on notera par

la suite (τ, T) dans un souci de lisibilité des équations) est solution de :

A_(TN−1+τ T , τ∗T +τ T∗) = L(τ∗T +τ T∗) ∀τ∗, ∀T∗∈ T∗ (2.12) Problème se séparant en 2 problèmes couplés :

( A_{(TN−1+τ T , τ}∗_{T) = L(τ}∗_{T) ∀τ}∗ A_{(TN−1+τ T , τ T}∗_{) = L(τ T}∗_{) ∀ T}∗_{∈ T}∗ ⇔ ( τ = RN(T) T = S_N(τ)

Ces problèmes sont généralement résolus par une méthode du type point fixe dé-crite dans l’algorithme1. En pratique, la boucle While est remplacée par une boucle For sur quelques itérations. En effet, l’algorithme convergeant habituellement rapide-ment, le but ici, afin de gagner du temps de calcul, n’est pas d’arriver à une convergence stricte sur le nouveau couple puisque l’erreur commise sur la génération de ce couple pourra être corrigée par l’ajout du couple suivant.

Algorithme 1 : Recherche du couple d’ordre N par Galerkin progressif Donnée : La décomposition à l’ordre N − 1 : TN−1

Initialisation : τ0_{imposé (par exemple,τ}0_{(t ) = 1);} i = 0;

while critère > seuil do i = i + 1;

τi −1étant fixé, on cherche Ti avec Ti= S_N(τi −1) ; Ti étant fixé, on chercheτi avecτi= RN(Ti) ;

critère =∥τiTi_∥−_ττi_Ti −1i_∥Ti −1∥ ;

On comprend ici le sens du terme « progressif » de cette approche car on recherche successivement chacun des couples. Ceci implique que la décomposition obtenue par l’algorithme1n’est pas optimale au sens de la projection Galerkin. Pour cela, il faudrait chercher l’ensemble des fonctions simultanément. La taille des systèmes à résoudre augmentant proportionnellement au nombre de couples, la génération d’une telle dé-composition devient alors nettement plus coûteuse.

Toutefois, il est possible de rendre la décomposition un peu plus optimale au sens de la projection Galerkin en gardant le caractère progressif de l’algorithme par l’ajout d’une « étape préliminaire ». En effet, dans le cas général, l’application S est coûteuse à ef-fectuer puisque correspondant à la résolution d’un problème global en espace alors que l’application R est relativement peu coûteuse car correspondant à la résolution d’équations différentielles. Un moyen peu coûteux pour se rapprocher de la solution avant d’enrichir la base des fonctions spatiales Λ est alors d’apporter des corrections sur les fonctions du temps (rapides à calculer) en considérant la base des fonctions spatiales fixée. Cela consiste à introduire l’application R qui met à jour l’ensemble des fonctions du tempsλ pour une base des fonctions spatiales fixée Λ (λ = R(Λ)) après la génération d’un nouveau couple (τ, T). Bien que la décomposition obtenue par l’ajout d’une « étape préliminaire » est meilleure que celle obtenue sans cette étape, la dé-composition reste toutefois moins bonne que si on avait fait une SVD de la solution. Cette étape préliminaire sera plus particulièrement décrite dans le chapitre3. Une ap-plication de la réutilisation des bases spatiales est détaillée dans la partie exploitations numériques de ce chapitre.

L’approche galerkin progressive pouvant avoir des problèmes de convergence, une technique plus robuste, s’intéressant à la minimisation du résidu, a été développée [Nouy and Ladevèze, 2004,Ladevèze et al., 2010]. Une revue de tous les types de mé-thodes déjà développés est faite dans [Nouy, 2010].

1.3.2 Minimisation du résidu

On introduit le résidu R(T ) comme étant la quantité vérifiant : ¡

R(T ) , T∗¢=L(T∗) − A (T, T∗) ∀ T∗ (2.13) On considère une nouvelle fois une définition progressive de la décomposition. On suppose donc que la décomposition connue à l’ordre N − 1 et on cherche le nouveau couple (τ, T) comme étant solution du problème de minimisation suivant :

(τ, T) = arg min (τ, T)

∥R (TN−1+τ T) ∥ (2.14)

En pratique, comme pour l’approche précédente, une méthode itérative type point fixe est utilisée pour résoudre ce problème, comme décrit dans l’algorithme2.

Algorithme 2 : Recherche du couple d’ordre N par minimisation du résidu Donnée : La décomposition à l’ordre N − 1 : TN−1

Initialisation : τ0_{(par exemple,τ}0_{(t ) = 1);} i = 0;

while critère > seuil do i = i + 1;

τi −1étant fixé, on cherche Ti minimisant ∥ R¡TN−1+τi −1Ti

¢ ∥; Ti étant fixé, on chercheτi minimisant ∥ R¡TN−1+τiTi

¢ ∥; critère calculé sur la stagnation du résidu;

On montre que cette approche conduit à une construction robuste de la PGD mais peut avoir un taux de convergence faible par rapport à l’approche Galerkin progressive. Il est donc préférable d’opter pour l’approche Galerkin progressive lorsqu’elle fonc-tionne, ce qui sera le cas pour les travaux présentés ici.

Il est à noter qu’il existe aussi d’autres formulations de la PGD particulièrement adaptées au cas où A est une forme bilinéaire non symétrique. Un espace adjoint est alors introduit pour construire la décomposition dans la formulation Petrov-Galerkin de la PGD Minimax [Nouy, 2010]. De plus, pour traiter des problèmes avec un com-portement non linéaire, la PGD peut être associée à la stratégie de résolution LATIN

[Ladevèze, 1985]. Cette façon de faire est le sujet du chapitre3.

Quelle que soit l’approche choisie, la construction itérative de la PGD se génère comme le décrit l’algorithme3.

Algorithme 3 : Construction de la PGD Initialisation : Li ni t i al(T∗) = L(T∗);

T0=0;

for i = 1 to i = N do

Etape 0 : Mise à jour du second membre L(T∗) = Li ni t i al(T∗) − A (Ti −1, T∗);

Etape 1 : Recherche du nouveau couple (τi, Ti)

Utilisation de l’algorithme1ou2; Ajout du couple : Ti =Ti −1+τiTi ;

Etape 2 : Réutilisation de la base spatiale

Mise à jour de fonctions temporelles :λi = R(Λi);

1.4 Exemples d’application

1.4.1 Compression de données par POD

La POD étant une technique d’extraction des modes dominants, on considère un premier exemple visuel sur une photo puis un second exemple sur le problème de dif-fusion pour pouvoir comparer les décompositions POD et PGD.

On choisit de quantifier la qualité de l’approximation d’ordre N (TN) par une erreur

de référence ePODqui compare cette approximation à la solution initiale à compresser :

ePOD=

∥T − TN∥

∥T ∥

où la norme choisie sera la même que celle utilisée pour générer la décomposition. Par défaut, cette norme sera toujours celle de L2avec ∥ · ∥2₂=RI_×Ω·2dΩdt .

Ï Compression d’une image

On considère la photo initiale montrée sur la figure2.1composée de 1000 pixels hori-zontalement et verticalement. Cette photo en noir et blanc peut donc être stockée sous la forme d’une matrice de dimension 1000 × 1000 dont chaque composant représente

un niveau de gris de chacun des pixels de la photo (de 0 si le pixel est blanc à 1 si le pixel est noir).

On observe visuellement qu’un faible nombre de couples suffit à obtenir une bonne approximation de la photo initiale et que les premiers couples contiennent une grande partie de l’information à compresser. La figure2.2montre une dépendance entre l’am-plitude des valeurs singulières et l’erreur. On distingue ainsi une zone d’évolution ra-pide pour les 30 premiers couples puis une zone d’évolution lente pour les couples suivants, ce qui confirme l’observation visuelle précédente.

Pour montrer la dépendance de la POD face au choix de la norme comme expliqué précédemment, l’erreur ePOD en utilisant une norme hilbertienne (on rappelle que

∥ · ∥2

Hi l ber t=

R I_×Ω

³

·2+grad2(·)´dΩdt ) est aussi tracée sur la figure2.2(b). Cette norme est réputée pour mieux capter les différents contrastes d’une image. On remarque tou-tefois que, sur la photo utilisée et pour cette erreur globale choisie, la décomposition est meilleure avec l’utilisation d’une norme L2.

Ï Compression d’une solution du problème de diffusion

On considère le cas d’un milieu ayant les propriétés matériau d’un aluminium don-nées dans le tableau2.1. La discrétisation spatiale tout comme la discrétisation tem-porelle est de 100 éléments (ou pas de temps).

Paramètres Valeur ρal u 2700 kg /m3

cal u 897 J.kg−1.K−1

λal u 237 W.m−1.K−1

Tableau 2.1: Valeurs des paramètres matériau

Pour pouvoir effectuer la décomposition POD de la solution T (x, t ) du problème présenté, la solution a été calculée par des techniques incrémentales classiques. La matrice des réalisations alors connue permet ainsi l’application des techniques pré-sentées au paragraphe1.2.

La figure2.3 montre l’approximation POD, TN, de la solution pour N valant 1, 4

et 10. Les erreurs ainsi que leurs exploitations restent identiques à celle effectuées sur le cas précédent de la photo. Pour pouvoir calculer ePOD, la solution incrémentale est

prise comme solution de référence T . 1.4.2 PGD

Comme le problème choisi au paragraphe précédent est linéaire d’évolution, on peut directement générer la décomposition à variables séparées de la solution sans

Photo initiale

Photos reconstruites

FIGURE2.1: Reconstitution d’une image à l’aide d’un certain nombre de couples POD,

0 100 200 300 400 500 10ï4

10ï2 100

Numéro d’ordre

Amplitude des valeurs singulières

(a) Amplitude normée des valeurs singulières suivant leur numéro ordre

(b) Evolution de l’erreur ePODen fonction de

la norme choisie et du nombre de couples POD gardés

FIGURE2.2: Evolution des valeurs singulières et des différentes erreurs

d’approxima-tion en foncd’approxima-tion du nombre couples gardés pour compresser une photo

(a) 1 couple (b) 4 couples (c) 10 couples

FIGURE2.3: Evolution de l’approximation en fonction du nombre de couples POD

gardés

l’avoir préalablement calculée grâce à l’algorithme3. On choisit ici d’opter pour l’ap-proche Galerkin progressif. La figure2.4montre l’approximation PGD, TN, de la

solu-tion pour N valant 1, 4 et 10.

La figure 2.5se propose de comparer la qualité de la décomposition à variables séparées obtenue par 2 différentes approches :

• La résolution directe du problème par une méthode incrémentale classique avec prise de la POD de la solution obtenue. La qualité de cette décomposition est regardée par rapport à l’erreur ePOD.

• La résolution PGD directe du problème. La qualité de cette décomposition est regardée par rapport à l’erreur ePGD.

Comme on pouvait s’y attendre, cette figure montre que pour un nombre de couple N donné, la POD est toujours meilleure que la PGD au sens d’une erreur de référence.

(a) 1 couple (b) 4 couples (c) 10 couples

FIGURE 2.4: Evolution de l’approximation en fonction du nombre couples PGD

construits

Cela dit, pour obtenir la POD, il a fallut au préalable résoudre le problème considéré pour en obtenir la solution tandis que la PGD a été directement générée à partir des équations caractérisant le problème. Toutefois, il existe des travaux dans la commu-nauté « algèbre tensorielle » qui cherchent à rendre ces 2 courbes identiques. Il est éga-lement prouvé dans [Ammar et al., 2010] que la solution du problème obtenue par PGD convergeait toujours vers la solution du problème obtenue par une méthode de réso-lution classique (éléments finis).

0 10 20 30 10ï5 100 Nombre de couples Erreur e POD e_PGD

FIGURE 2.5: Evolution des erreurs d’approximation POD et PGD en fonction du

nombre couples gardés

2 Méthodes de réduction de modèle

Le but des méthodes de réduction de modèle est d’adapter les principes de l’ap-proximation spatio-temporelle pour la résolution de problèmes similaires ou de sub-stitution. L’idée est de véhiculer une information des calculs précédents pour réduire le temps de calcul des problèmes suivants.

L’information transmise de calculs en calculs est toujours une base réduite des fonc-tions spatiales ou temporelles suivant les problèmes étudiés. Ce qui diffère parmi les différentes techniques existantes réside dans la façon de construire cette base réduite et dans la façon de l’utiliser pour résoudre un nouveau problème. Dans le contexte de cette thèse, les fonctions du temps étant plus rapidement calculables, ce seront les fonctions de l’espace qui seront gardées et transmise par la base réduite.

Les techniques de réduction de modèle se répartissent en 2 catégories :

• Méthode avec apprentissage. Ces méthodes se composent de 2 phases. La pre-mière est une phase d’apprentissage effectuée en offline, durant laquelle une base réduite est construite en résolvant un problème similaire ou de substitu-tion. On obtient ainsi, durant une seconde phase, la solution du problème d’inté-rêt à moindre coût en projetant ses équations sur la base réduite. Ces techniques sont aussi connues sous le nom de méthodes de réduction de modèle a posteriori sous entendant la résolution du problème d’intérêt après avoir résolu un certain nombre de problèmes préalablement.

• Méthode sans apprentissage. A l’opposée des techniques précédentes, cette mé-thode permet de calculer la solution d’un problème d’intérêt sans avoir eu la né-cessité de résoudre des problèmes connexes. Pour cela, cette technique est aussi connue sous le nom de technique de réduction de modèle a priori. La base ré-duite est ainsi construite online durant la résolution des problèmes d’intérêt.

2.1 Méthodes avec apprentissage

On distingue 2 méthodes avec apprentissage. Une se basant sur la résolution d’un problème de substitution, l’autre, sur la résolution de problèmes similaires.

Ï ROM-POD (POD based Reduced-Order Modeling)

La ROM-POD [Kunish and Xie, 2005,Lieu et al., 2006,Gunzburger et al., 2007] est une technique de réduction de modèle basée sur la décomposition POD. Cette mé-thode est particulièrement adaptée au cas où l’on doit obtenir la solution d’un pro-blème trop complexe que l’on ne veut pas résoudre directement. Pour cela, cette mé-thode consiste à résoudre un problème de substitution : un problème plus simple que le problème initial (typiquement, on traite le même problème mais sur un intervalle de temps réduit ou alors sur l’ensemble du temps mais avec une discrétisation plus grossière). La solution obtenue durant cette phase « d’apprentissage » est appelé un « snapshot ». La décomposition POD de ce « snapshot » permet d’obtenir une base ré-duite qui est utilisée pour projeter les équations du problème à traiter initialement. La résolution de ce problème consistera alors à calculer la meilleure combinaison des

vecteurs de la base. Tout cela peut se schématiser comme décrit sur la figure2.6.

Résolution partielle (sur un petit intervalle de temps) ou grossière du problème considéré Snapshot Les fonctions Problème fixées, Ti(M ) Trouverτ_i(t) OFFLINE ONLINE

Problème projeté sur la base réduite Problème réduit Base réduite Λ(M ) POD Apprentissage

Problème long ou difficile à résoudre Problème complexe

FIGURE2.6: ROM-POD pour la résolution d’un problème complexe

Il est aussi à noter que la base réduite peut aussi n’être constituée que des modes dominants de la POD du snapshot. Pour cela, on fixe un pourcentage d’énergie mi-nimale Pe permettant de trouver la dimension N de la base réduite nécessaire pour

arriver à cette qualité d’approximation du snapshot. On peut alors trouver N tel que :

N X i =1 σi p X i =1 σi ÊPe

Dans le cas d’un problème paramétrique, un premier problème (associé à un premier jeu de paramètres) est alors sélectionné et résolu entièrement, puis la solution est dé-composée par POD pour obtenir une base réduite qui servira de base de projection pour les problèmes suivants (associés à d’autres jeux de paramètres).

Bien que cette méthode donne souvent de bons résultats, elle peut parfois être mise en échec. En effet, la base associée à un premier calcul (pour un premier jeu de para-mètres) et qui sert de base de projection pour les calculs suivants, n’est pas forcément représentative de l’ensemble des solutions. Il se peut alors que cette base ne soit pas suffisante pour résoudre un nouveau problème (associé à un nouveau jeu de para-mètres) et la qualité de la solution obtenue peut être médiocre. Des stratégies ont alors été proposées dans [Ryckelynck, 2005,Ryckelynck et al., 2006,Cordier and Bergmann, 2006] pour pallier ce dernier point en enrichissant la base réduite par un contrôle de l’erreur. Ces algorithmes sont appelés par « région de confiance » et permettent un re-tour au modèle pour enrichir la base réduite lorsque la qualité d’approximation des solutions devient trop grossière. Cependant, des problèmes ont été observés dans plu-sieurs cas (en particulier, l’équation d’onde) pour lesquels l’enrichissement de la base