Propriétés combinatoires, ergodiques et arithmétiques de la substitution de Tribonacci

J

OURNAL DE

T

HÉORIE DES

N

OMBRES DE

B

ORDEAUX

N

ATALIYA

C

HEKHOVA

P

ASCAL

H

UBERT

A

LI

M

ESSAOUDI

Propriétés combinatoires, ergodiques et arithmétiques

de la substitution de Tribonacci

Journal de Théorie des Nombres de Bordeaux, tome

13, n

o

_{2 (2001),}

p. 371-394

<http://www.numdam.org/item?id=JTNB_2001__13_2_371_0>

© Université Bordeaux 1, 2001, tous droits réservés.

L’accès aux archives de la revue « Journal de Théorie des Nombres de Bordeaux » (http://jtnb.cedram.org/) implique l’accord avec les condi-tions générales d’utilisation (http://www.numdam.org/conditions). Toute uti-lisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit conte-nir la présente mention de copyright.

Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques

371-Propriétés combinatoires, ergodiques

et

arithmétiques

de la substitution de Tribonacci

par NATALIYA

CHEKHOVA,

PASCAL HUBERT

et ALI MESSAOUDI *

RÉSUMÉ. Nous étudions certaines

_{propriétés combinatoires,}

er-godiques

et

_{arithmétiques}

du _point fixe de la substitution de

Tri-bonacci

_(introduite

par G.

Rauzy)

et de la rotation du tore T2 _qui

lui est associée.

Nous établissons une

_{généralisation géométrique}

du théorème

des trois distances et donnons une formule

_explicite

_{pour la}

fonc-tion de récurrence du

point

fixe. Nous donnons des

_propriétés

d’approximation diophantienne

du vecteur de la rotation de T 2 :

nous _{montrons, que pour} une norme

_adaptée,

la suite de meilleure

approximation de ce vecteur est la suite des nombres de

Tri-bonacci. Nous calculons enfin les invariants

_ergodiques

F et _FC

du

_système

_dynamique

associé à la substitution.

ABSTRACT. We

_{study combinatoric, ergodic}

and arithmetic

prop-erties of the fixed point of Tribonacci substitution

_(first

introduced

by

G.

_Rauzy)

and of the related rotation of the two dimentional

torus.

We

_give

a

_geometric

generalization

of the three distances the-orem and an

_explicit

formula for the recurrence function of the

fixed _point of the substitution. We state

_Diophantine

approxi-mation’s

_properties

of the vector of the rotation of T2: we _prove

that,

for a suitable _norm, the _{sequence of} best

_{approximation}

of

this vector is the _sequence of Tribonacci numbers. We _compute the

_ergodic

invariants F and _FC of the

_symbolic

_system related

to the substitution.

1. Introduction

Les suites sturmiennes constituent une famille

d’exemples

particulière-ment intéressants en

dynamique symbolique

et théorie des

langages.

On

peut

les

_définir,

_par

_exemple,

comme les suites non ultimement

périodiques,

de

_complexité

minimale. Elles ont fait

_l’objet

de très nombreuses

_études,

Manuscrit reçu le 25 octobre 1999.

tant du

_point

de vue combinatoire

(voir

_par

exemple

[5], [6],

[15],

[20],

[36],

[40],

[48])

que pour les

interprétations géométriques

(cf [4], [28],

[47]),

arithmétiques sous-jacentes

(cf

[32],[33], [34],[35], [42], [22])

et

_ergodiques

([3]).

Les suites sturmiennes

_{s’interprètent}

_{géométriquement}

comme les

codages "canoniques"

des rotations irrationnelles du tore

T .

Parmi les nombreuses

_{généralisations}

des suites

_{sturmiennnes,}

G.

_Rauzy

(cf.

[45])

a introduit un

exemple

de

système

symbolique qui

constitue un

"codage

naturel" d’une rotation du tore

1f2.

Le

_{système symbolique}

est le

système

associé à la substitution de Tribonacci Q définie _{par :}

Du

_point

de vue de la théorie

ergodique,

le résultat de G.

Rauzy

signifie

que le

système symbolique

de Tribonacci est

métriquement isomorphe

à

une rotation

Ra

de

La rotation

_Ra

de

T2

s’obtient comme le

quotient

d’un

échange

de

morceaux, dans le

plan complexe,

de domaine fractal

(appelé

fractal de

Rauzy).

Le fractal de

_{Rauzy E possède}

diverses

_propriétés

_{géométriques :}

c’est un

_compact

de

C,

_connexe, à frontière fractale et à intérieur

simple-ment connexe et il induit un _pavage

_périodique

de C modulo un réseau.

Le fractal de

_Rauzy

a fait

l’objet

de

plusieurs

études

(voir

[2], [45], [30],

[37], [38],

[49])

et

_peut

être relié à différents

_{problèmes :}

-

Système

de numération

complexe

[37], [38].

-

Représentation géométrique

des

systèmes dynamiques symboliques

[45],

[30], [37], [38], [49], [50], [51].

- Méthode de

Dekking

pour la construction

d’objets

fractals

[30].

-

Pavages quasi-périodiques

du

_plan

_[30].

- Partitions de Markov

pour les

automorphismes hyperboliques

du tore

’1~3

[2],

&#x3E;

[37].

°

Dans cet

_article,

nous étudions certaines

propriétés

combinatoires et

er-godiques

du

_point

fixe v, de la substitution de Tribonacci

_qui

_{généralisent}

des

_propriétés

connues _pour les suites sturmiennes.

Nous donnons une

_{généralisation}

du théorème des trois distances dû à Sôs

[52],

qui

a été

étudié, récemment,

d’un

point

de vue combinatoire _par

P. Alessandri et V. Berthé

_(cf.

_[1]).

Plus

_{précisément, soit ’0}

la

_conjugaison

entre le

_système

_symbolique

et la rotation

_Ra

et v un mot fini

_apparaissant

dans _u, on

_appelle

v([v]),

_l’image

du

cylindre

[v]

_par

l’application ’lj; ;

étant

donné un nombre entier _n, on l’ensemble formé

où v est un mot de

_{longueur n}

du

_langage

de u. Nous montrons que, pour

tout entier _n, l’ensemble

_e(Ln(u»

est

_constitué,

à translation

_près,

de trois

373

Nous donnons une formule

explicite

_pour la

_fonction

de récurrence R de la

suite de _u,

_qui

mesure la

_longueur

minimale

_qu’il

faut

_prendre

dans la suite

pour être certain de voir tous les mots de

_longueur

n. On

_peut

vérifier,

_par

exemple,

que :

ce

_qui

vérifie,

dans ce cas

_particulier,

la

_conjecture

de

_Rauzy

_[46],

selon

laquelle

cette

_quantité

est

_toujours

_supérieure

à

_{3, 618 ... ,}

valeur atteinte pour la suite de Fibonacci. Cette

conjecture

a été récement résolue _par

J.

_Cassaigne

_[10].

Nous donnons des

_{propriétés d’approximation}

simultanée du

_{vecteur ~}

de la rotation

_{Ra .}

Nous _{remarquons que} le

_{vecteur e}

est mal

_approché

_par les rationnels et nous montrons _{que, pour} une norme

_adaptée,

la suite

de meilleure

_{approximation}

du

_{vecteur e}

_(voir

définition

₆₎

est la suite

numérique

de Tribonacci définie _par la relation de récurrence :

Nous

_{calculons, enfin,}

les nombres de recouvrement

_Fc

et

_{F, qui}

sont des invariants de

_{conjugaison topologique}

du

_{système dynamique symbolique}

associé à la suite de

_{Tribonacci ;}

ils

_mesurent,

_{respectivement,}

la

_proportion

de la suite

_qui

_peut

être recouverte _par des

_apparitions

d’un seul mot dont

toutes les

_apparitions

sont sans

chevauchement,

et la

_proportion

de la suite

qui

peut

être recouverte _par des

_apparitions

sans chevauchement d’un seul

mot,

voir les définitions

_{7, 8,}

_ci-après.

Ces invariants ont été calculés _par

N. Chekhova pour les suites sturmiennes

(cf

[12]).

Ces résultats

_symboliques

ont une

_{interprétation géométrique,}

sous forme

de

_{propriétés ergodiques}

nouvelles de la rotation

Ra :

l’invariant

Fc

que

nous avons calculé se traduit _par l’existence de tours de Rokhlin constituées d’ensembles

_simplement

_connexes, une tour recouvrant

_{0, 618...}

de

_l’espace

et trois tours recouvrant tout

_l’espace,

ce

_{qui améliore,}

dans ce cas

partic-ulier,

certains résultats de Chevallier

_(cf

_[14]).

2. Préliminaires

2.1.

_{Dynamique symbolique}

et

_langages

formels. Soit A un

alphabet

fini ;

on considère les suites unilatérales

(xo, - - - , xn, - - - ),

A.

Un mot de

_longueur

_{l (w) - h}

est une suite finie w =

Wl ... w~ d’éléments de

A. La concaténation de deux mots v et w se note vw. Le mot w = _{Wl ... Wh}

apparaît

au terme i dans une suite

(xn)

ou dans un mot xo - - - xs si zj = _wl,

... , Wh.

Soit z

_appartenant

à le

_langage

de

_longueur

_h,

noté

_Lh(z)

est l’ensemble des mots de

_{longueur h}

_{apparaissant dans z ;}

le

_langage

de z est l’ensemble des mots

_apparaissant

dans z.

On définit le

_décalage

T sur

_l’espace

.A~,

_{pour x} =

(xn, n

_E

N),

_par

(Tx)n

=

Xn+l. Pour une suite _z, on définit l’ensemble

Xz

comme l’adhérence dans

A~

muni de la

_topologie

discrète de l’ensemble

_{(Tnz, n}

_EN).

Un

_{système dynamique symbolique}

est le

_{système dynamique topologique}

(Xz,

T)

pour une suite z sur un

alphabet

A. Le

_{système dynamique}

symbo-lique qu’on

considère ici est minimale

_(toute

orbite est

_dense)

et

_uniquement

ergodique :

il _y a une seule mesure de

_probabilité

invariante _par

_{T ;}

on

_peut

alors définir des

_fréquences.

La

_fréquence

_f(w)

d’un mot est

_limn,

-t-clo

N’ w ,

où

_Nn(w)

est le nombre

d’apparitions

de w dans _{zo - - - zn .}

Dans un

système

dynamique symbolique,

étant donné un _{mot w,} on

appelle

cylindre

associé à _w, noté

_~w~,

l’ensemble des x de

_Xz

tel _{que w}

_apparaît

dans x au terme

_{0 ;}

la hauteur du

_cylindre

_~w~

est la

_longueur

de w. Soit

w un élément de

Ln (z)

et

_{f (w)}

la

_fréquence

_{d’apparition}

du mot v

_{dans z,}

il est connu _que

f (w)

est

_égale

à la mesure du

cylindre

~w~

(voir

[37], [38]).

2.2. La substitution de Tribonacci.

Définition 1. Soit A l’ensemble

_{0,

_1,

_2},

nous

_appelons

substitution de

Tribonacci

_{Inapplication (7}

de A dans A* définie par :

" ,

Nous étendons a en une

_application

de

AN

dans

AN

_par

_{concaténation,}

c’est-à-dire,

pour tout

(an ) n

E

AN,

u est contractante pour la

métrique

naturelle sur elle a donc un seul

point

fixe _que l’on notera u =

(Un)nEN.

A l’instar de la

_{pratique adoptée}

dans le cas de Fibonacci

(substitution

définie _par 0 --~

_01,

_1-~0),

nous

_appelons

suite de Tribonacci

_[9]

la suite On remarque que la

longueur

du mot est

égale

à où

Tn

est le nombre de Tribonacci défini _par la relation de récurrence :

On est amené à considérer le

_polynôme

=

x3 - x2 - ~ -

1. Ce

polynôme

a une racine réelle

{3

=

_{l, 83929 ...}

strictement

supérieure

à 1 et

deux racines

_complexes

_conjuguées

a et ii de module inférieur strictement

à

_1,

on a donc

,Blal2

= 1.

(Dans

tout ce

_{qui suit,}

a est le

_conjugué

de

_partie

_{imaginaire négative,}

cette convention est arbitraire et n’a aucune

influence sur les résultats

_{ci-dessous ;}

a x5 -0.419 -

_0.606i.)

On considère désormais le

_système

_dynamique

_symbolique

_(X~,T)

as-socié

_{à u ;}

il est minimal et

_uniquement

_ergodique

car la substitution est

prirrcitive

[44].

375

FIGURE 1. Fractal de

_Rauzy

2.3. Fractal de

_Rauzy.

Définition 2. Soit 6; = une suite à valeurs dans

{O, 1}.

On dit

que - est une suite admissible

_si,

_pour tout entier naturel

_i,

elle vérifie

= 0. On _note

Nf

l’ensemble des suites admissibles.

Remarque.

Une suite finie - à valeurs dans

_{f 0, 11}

est admissible si la

suite infinie obtenue en

prolongeant -

à

gauche

_par une infinité de 0 est

admissible.

Définition 3. Le fractal de

_Rauzy

est l’ensemble

_{(voir figure 2.3)}

Le fractal de

_Rauzy

est

_partagé

en trois

_régions

similaires

_qui

induisent

un autre _pavage non

_périodique

et auto-similaire du

_plan

_complexe.

Ces

régions

sont :

_So

=

_aS,

_£1

=

a3

₊

a2~

et

~2 = a3

+ a4

₊

a3E.

Conjugaison

entre le

_{système symbolique}

et la rotation. Soit

_Ra

la rotation

_(échange

de trois

_morceaux)

sur définie _par

z+a2

modulo

_{(Z + Za)}

et soit À la mesure de

_Lebesgue

bidimensionnelle. Le

théorème suivant établit le lien entre substitution de Tribonacci et fractal de

_Rauzy

_(voir

_[45],

_[37],

_[38]).

Théorème 1

_(Rauzy).

Soit m

l’unzque

mesure de

_probabilité

invariante

pour l e

système symbolique

(Xu, T).

Le

système d ynamique

(Xu,

T,

m)

est

_{métriquement isomorphe}

au

système dynamique

(E,

Ra,

A)

_par une

ap-plication 0.

En

_{outre 0}

est

_continue,

_surjective

et

_injectzve

sur

Orb(u),

et

pour tout x E

!1,

=

Remarque.

Pour une définition

_{explicite de 0,}

on

_peut

voir

[38]

_page 149.

3.

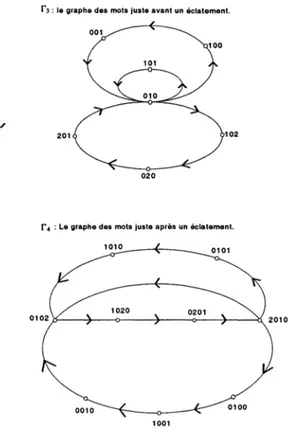
_Graphe

de

_Rauzy

Définition 4. Pour une suite u et un entier

_h,

on définit le

_graphe

de

Rauzy

(ou

graphe

des mots de

_longueur

_h)

_rh

de la manière suivante : les

sommets sont les

_points

de

_Lh(u),

et il _y a une arête de w vers w’ si w et

apparaissent

successivement dans _u, c’est-à-dire si w = av et w’ - vb

pour des lettres a et b et un mot v de on

étiquette

cette arête

par avb E et l’ensemble des arêtes est

Nous étudions ci-dessus la forme des

_graphes

de

_Rauzy

_pour la suite

de Tribonacci u. Pour tout nombre entier

h,

le

graphe

rh

_comporte

un

point unique Dh

triprolongeable

à droite

_(trois

arêtes

_{DhO, Dh1}

et

_Dh2

le

quittent)

et un

_{point unique Gh}

_{triprolongeable}

à

_gauche

_(trois

arêtes

_OGh,

lGh

et

_2Gh

_y

_{arrivent) ;}

_Dh

et

_Gh

_peuvent

être confondus. Pour tout autre

_point,

il _y a une seule arête entrante une seule arête sortante. En

conséquence,

la suite de Tribonacci est une suite

_{d’Arnoux-Rauzy}

et son

graphe

de

_Rauzy

obéit aux

règles

définies dans

[4],

_que nous

explicitons

ci-après :

On

_partitionne

les sommets et les arêtes de

_rh

en

_quatre

branches ;

une branche est un ensemble de sommets et

_d’arêtes,

et sa

_longueur

est le nombre de sommets

_qu’elle

contient.

~ La branche centrale

_comprend

le _sommet

_{Gh, l’unique}

_{arête sortante}

de

_Gh,

le sommet vers

_lequel

va cette

_arête,

_l’unique

arête sortante de

ce

_sommet,

et ainsi de suite

_jusqu’au

sommet

_Dh

_{inclus ;}

si

_Dh

=

Gh,

la branche centrale est réduite au sommet

Dh

=

Gh .

~ _{pour i} =

_{0, 1, 2,}

la branche i

_comprend

l’arête

_Dhi,

le _{sommet vers}

lequel

va cette

_{arête, l’unique}

arête sortante de ce

_sommet,

et ainsi de

suite

_jusqu’au

sommet

_{Gh exclu ;}

si l’arête

_Dhi

va vers

Gh,

la branche

i est réduite à l’arête

_Dhi.

Nous verrons _que, sauf

_{pour h}

=

_1,

les

longueurs

de _ces trois dernières

branches sont

_{toujours différentes,}

et les

_appellerons

_{respectivement}

branche

377

FIGURE 2.

_Graphes

de

_Rauzy

mo yen

Mh

et

long

Lh)

part

de

_Gh

et est

_composé

de la branche centrale

puis

de la branche courte

_(resp.

_moyenne et

_longue).

Les sommets de

_rh+i

sont les arêtes de si

_{Dh ~}

_Gh,

les sommets

d’une branche de

_rh+l

sont les arêtes de la même branche de

_rh

_(il

y a

f ente

d’une

_arête).

De ce

fait,

la

longueur

de la branche centrale diminue

de 1

_quand

on _passe de h à h + 1.

Donc,

pour une infinité de

h,

la branche centrale de

T~

est de

_longueur

1,

par

conséquent

réduite à un

_{sommet ;}

d’où

Gh = Dh :

on dit

qu’il

_y a un éclatement.

Les différents

_types

d’éclatements sont décrits dans

_[4],

mais nous

intro-duisons ici une nouvelle

terminologie ;

nous disons

_qu’il

_y a un éclatement

renversant

_{(noté EL )}

si les sommets de la branche centrale de

_rh+l

sont

les arêtes de la branche

_longue

de

_{rh ;}

il _y a un éclatement _{mo yen}

_(EM)

si les sommets de la branche centrale de sont les arêtes de la branche

moyenne de

Fh ;

il y a un éclatement court

(Ec)

si les sommets de la branche centrale de sont les arêtes de la branche courte de

_{rh ;}

dans les trois

Si l’on énumère successivement les mots de

_{longueur h}

_apparaissant

dans la suite u au terme i pour i =

0, ...

_{n, ... , on} obtient _un chemin infini

rh

dans le

_{graphe rh, composé}

d’une succession de circuits

_courts,

moyens et

longs

(le

premier

étant éventuellement

_tronqué).

Si en h il _y a

_fente,

_rh se déduit de en

remplaçant

_par

Ch,

_par

_Mh

et _par

Lh ;

s’il _y a éclatement

_court,

_rh se déduit de en

remplaçant

_Ch+i

_par

Ch, Mh+I

par

ChMh

et

Lh+l

par

ChLh ;

s’il y a éclatement _{moyen, rh} se

déduit de en

_remplaçant

_par

_Mh,

_Mh+l

_par

_MhCh

et

_Lh+l

par

MhLh ;

s’il _y a éclatement

_renversant,

_rh se déduit de rh+l en

_remplaçant

par

Lh, Mh+l

par

LhCh

et

Lh+l

par

Lhmh.

Dans toute la

_{suite, si,}

par abus de

langage,

nous

_parlons

d’un mot de la branche centrale

_(resp.

_courte,

_moyenne,

_longue),

il

_{s’agira toujours}

d’un

sommet de cette branche. On

_{appelle longueur}

d’une branche son nombre

de sommets.

La méthode de

_[7]

_permet

de calculer de

_proche

en

_proche

les

longueurs

des circuits et les

_fréquences

des mots de

_{chaque branche ;}

le résultat suivant

est à

_rapprocher

du résultat de

_[17]

sur la suite de Fibonacci.

Proposition

1. Pour une valeur de h située entre le n - 2-ème éclatement

(non compris)

et le n - 1-ème éclatement

(compris),

les

longueurs

des

cir-cuits sont

Tous les mots d’une même branche ont la même

_fréquence.

Les

_branches,

centrale,

moyenne et

longue,

contiennent

toujours

des

sommets,

la branche

courte en contient si et seulement s’il _y a

fente

_pour h -

_{1 ;}

donc il _y a

au

_plus

trois ou

_quatre

fréquences différentes.

Les

fréquences

communes

respectives

des mots de la branche

_longue,

moyenne, courte et centrale sont

Preuve. Nous montrons d’abord _que tous les éclatements sont

_{renversants ;}

pour

cela,

nous montrons _par récurrence sur n _{que pour} un h situé

_juste

avant le n-ème éclatement la suite _Th est la suite de Tribonacci

_elle-même,

où on a

_remplacé

0 par

Lh,

1 par

Mh

et 2 par

Ch.

C’est vrai pour n = 1

en choisissant _pour

_Li

le circuit

_comprenant

les sommets 0 et

_1,

_pour

_Ml

les sommets 0 et

_2,

pour

Ci

le sommet

0,

car la

_{décomposition}

de la suite

de Tribonacci en mots

_{01, 02,}

0 est

_unique.

Si c’est vrai pour n, soit h

juste

avant le n-ème

_{éclatement ;}

_{comme -yh} est invariante _{par a} on

_peut

écrire les mots de

_{longueur h}

+ 1

_apparaissant

dans la suite u au terme i pour i =

0,...

n, ... , en tant

_qu’arêtes

de

_rh

ou sommets de

_rh+l,

comme

un chemin infini

_qui

est une concaténation de circuits

_Lh,

et

donc ce chemin ne

_peut

être une concaténation de

Mh, MhCh

et

_MhLh

ou

379

qh+i s’obtient à

partir de qh

en

remplaçant

_Lh

_par

LhCh

_par

_Mh+l,

LhMh

par et

l’hypothèse

de récurrence est vérifiée avant le n + 1-ème

éclatement.

Les

_longueurs

des circuits se calculent donc

_grâce

à l’évolution des

_graphes

indiquée

ci-dessus : _pour h =

1,

_{on a}

si,

pour

h,

il y a

fente,

on a

si,

pour

h,

il y a

éclatement,

on a

Soit V un élément de

Lh (u)

et

_{f (V )}

sa

fréquence,

_{supposons, par}

exemple,

que V

appartienne

à la branche

courte,

soit W l’élément de la branche

courte tel que V = xY _et W = Yz où x _{et z sont} dans

{0,1, 2~.

Comme

V est

_prolongeable

d’une

_{façon unique}

à droite et à

_gauche,

nous avons

f (V)

=

f (Vz)

=

f (Yz).

Par

conséquent

_tous les _mots de la branche _courte

(respectivement

moyenne,

longue)

ont la même

fréquence fc

(resp

et

fL).

De

_même,

les mots de la branche centrale ont la même

_{fréquence f+.}

Par

_ailleurs,

_pour tout entier naturel h non

_nul,

nous avons

Il faut étudier deux cas :

Premier cas : Si

Gh-1

(il

_y a fente

pour h -

1),

Dh-,

a un seul

_prolongement

à

_gauche,

d’où

Il en découle _que

_f+

=

fc

_{+ +}

fL.

Dans _ce

cas,

chaque

branche contient

des

sommets,

et l’ensemble

_{f f (v) ~ v}

E

_Lh(u)}

_prend

au

_plus

_quatre

valeurs.

Deuxième cas : Si =

Gh-i,

alors il existe _x

et y

dans

_{{O, 1, 2}}

tels

que

Gh

=

Gh-lx

_et

Dh

=

yDh-1

=

YGh-1.

Dans _{ce cas,} le

graphe

rh

_{est en}

fente et la branche courte est réduite à une arête. Il _y a

_donc,

au

_plus,

trois

fréquences,

qui

sont

_f+,

_fL

et

_f,yl.

On continuera toutefois à

définir fc

par

fc

=

f+ -

fL - fm,

bien

_qu’à

ce stade ce ne soit la

fréquence

d’aucun mot.

Nous allons maintenant calculer ces

fréquences

_par

récurrence ;

si h = 1

alors

_{f(0) =}

_~,

_{f (1) _ ~}

et

_{f (2) _ ~}

_(voir

_[37]).

Le circuit court est

1

_(le

choix du circuit moyen et du circuit

long

n’est pas

ambigu

en raison

de la suite du _processus,

_{qui impose}

_fL

&#x3E;

_fM),

et on a

On définit

_fc,

sans

objet

à ce

stade, puisqu’il n’y

a _pas de sommet sur la

branche

_courte,

_par

_{f c}

=

f + -

f L - f ~.

Ensuite,

le raisonnement

_ci-dessus,

ou celui de

[7],

_{montrent que} les

fréquences

sont

_inchangées

par une fente

(dans

le cas de la

première

fente

après

un

_éclatement,

la

_{fréquence f c qui}

n’est

_fréquence

d’aucun mot de

rh

devient la

_fréquence

du mot de la branche courte de tandis que,

s’il _y a

_éclatement,

on a

où

_{fc, fL, fm}

sont les

_fréquences

avant l’éclatement et

_f3,

_fL

et les

fréquences après

l’éclatement

_(juste

_{après l’éclatement,}

_fc

n’est la

_fréquence

d’aucun mot mais reste définie _par

_le

=

fL -

On

poursuit

ainsi

la récurrence. D

4. Généralisation du théorème des trois distances

Le théorème ci-dessous est une

généralisation géométrique

du théorème

des trois distances.

Théorème 2. Soit n un entier naturel non

_nul,

l’ensemble

{~((v~) ~ v

E

Ln(u)~

est constitué de trois ou

_quatres

régions

à translations

près

qui

sont

de la

_forme

et

ak+2£

ou bien et

ak+3£

suivant les valeurs de n.

Preuve. Montrons que si

f (v)

=

f (w), v

et _zv dans

Ln(u),

alors les

régions

sont similaires au fractal de

_Rauzy

et sont translatées l’une de l’autre.

Considérons les fonctions de C dans C définies par

Qo :

az,

1/Jl :

z H

a3 -I-

a2z

et

_{1b2 : z}

H

a3

+ a 4

+

az.

Nous _{avons, par}

_{construction,}

Q([1])

pour tout i E

_{{O, 1, 2} ;}

_{plus généralement,}

en vertu du Théorème

_1,

nous avons le résultat suivant

(voir

[38]

_page

151).

Lemme 1. Soit vi ... vn un éléraent de

Ln(u).

Il existe

il, ... , ir

des

élém-ents de

_{{O, 1, 2}}

où r _n, tels _que

~((vl ~ ~ ~

_{= 1/Ji¡}

0 ... _o

(E).

Si,

de

_plus,

vi ... vn est

tri-prolongeable

à

droite,

alors pour

tout j

E

_{{0,1, 2},}

on a

381

Corollaire 1. Pour tout v dans existe une suite E

_~B//

et un entier k &#x3E; N tels _que

Le théorème 2 résulte alors de la

_Proposition

_1,

du Corollaire 1 et du fait

que

f (v)

est

proportionnel

à la mesure de

Lebesgue

de

0 ([v]) ([38]).

D

5. Calcul exact de la fonction de récurrence

Nous

_calculons,

dans ce

_paragraphe,

la fonction de récurrence R de la

suite u. Etant donné _{que u} est le

point

fixe d’une substitution

primitive,

il

était

_déjà

connu

(voir

[44])

_qu’il

existe une constante L telle _{que, pour tout}

entier n,

R(n)

Ln. L’intérêt de notre résultat est de donner une formule

explicite

pour

R(n).

Définition 5. La fonction de récurrence d’une suite z est la

_fonction,

notée

R(n),

qui

à un entier n associe le

_plus

_petit

entier

(fini

ou

non)

r tel _que

tout élément de

_{Ln (z)}

_apparaisse

dans

_LT(z).

On

_appelle

_temps

de

_retour,

noté

_{l (w),}

d’un mot w dans _z, la distance

maximale entre deux occurrences consécutives de w dans _{z, et} on note

_{1 (n)}

le maximum des

_l(w)

pour tous les mots w E

_Ln(z).

On

_appelle

mot

_singulier

de z tout mot w =

xvy

apparaissant

dans z,

tel _{que x}

_{et y}

soient des lettres et

_qu’il

existe

_{x’ 54}

_x,

_{~’ ~}

_y tels que

x’vy

et

_xvy’

_apparaissent

dans z.

Lemme 2. Les

_fonctions

R et 1 sont liées _par

Pour h &#x3E;

_1,

le

_temps

de retour maximal est donné _par

où

_Sh(Z)

est l’ensemble des mots

_singuliers

de z de

_longueur

_inférieure

ou

égal e

à h .

L’article

_[9]

_précise

une méthode

_générale,

essentiellement due à

Hed-lund et Morse

_[28],

pour calculer la fonction de récurrence d’une suite. Le

Lemme 2 est démontré dans

_[9,

_Propositions

2 et

_{3~ .}

Lemme 3. Dans le cas de la suite de

_Tribonacci,

_pour

_{tout n &#x3E;}

_3,

il existe

un

_unique

mot

_singulier

dont la

_longueur

est située entre le n - 3-ème et le

n - 2-ème

éclatement ; il

a _{pour et pour}

_temps

Preuve. Par

_définition,

w est un mot

_singulier

de

_{longueur h}

si et seulement s’il est

_l’unique

arête d’une branche de

_Irh-1,

ce

_qui

ne

_peut

se

produire

_que

juste

après

un éclatement.

On se

_place

au n - 3-ème éclatement. Dans ce _cas, la branche centrale

est réduite à un seul sommet et la

_longueur

_{correspondante h}

est

_égale

à

T+I+Tn-i-3 en

vertu de la

_Proposition

1 et du fait que la

2 2

complexité

p de la suite u

vérifie,

pour tout entier

h,

p(h)

= 2h + 1.

Après

cet éclatement la nouvelle branche courte

_apparaît

et il

_n’y

a

pas de sommets sur cette

_branche,

son

_unique

arète étant le mot

_singulier

w. Le mot

singulier w

apparaît

à

l’étape suivante,

_{gn =} 2 comme sommet dans le circuit court

_C,

et

_{n’apparaît}

dans aucun des autres

circuits,

L et M. Aux

étapes

suivantes,

les circuits restent les mêmes

jusqu’à

l’éclatement

_suivant,

_puis

sont

_remplacés,

au fil des éclatements

ultérieurs,

par des concaténations de ces

_circuits,

_{représentées}

_par le schéma

suivant

_{(1) :}

Le circuit C

_(et

donc le sommet

_w)

_apparaît

dans chacun des trois chemins

LMLC, LMLCLM,

LMLCLML. Comme la suite u est un enchaînement

de ces trois

_chemins,

la distance maximale entre deux

_apparitions

de w est réalisée dans le chemin

_qui

est effectivement autorisé

quand

on _passe à un éclatement de

plus.

Donc

, , , _1_1 _,f;__1 .I - _1- - ,

-Les deux lemmes

_précédents

entraînent immédiatement le résultat

sui-vant.

Proposition

2. La

_fonction

de récurrence de la suite de Tribonacci est

donnée _par

-pour

383

6.

_{Approximation diophantienne}

Soit 11

110

une norme sur

R2 ;

_{pour q E} E

II82

_fixés,

on note

la distance de _qx au

point

entier le

plus

proche

c’est-à-dire

On

_rappelle

que

(Tn )

est la suite des nombres de

Tribonacci,

~3

la racine

réelle de module strictement

_supérieur

à un

de x3 = x2

+ x +

1,

a, a

les deux racines

_complexes

_{conjuguées ;}

on note

,..

Pour tout

_N,

_posons 4 où

1 UN 11

(resp.

est le

nombre de 1

_(resp.

de

₂₎

dans _{UO ...} La matrice

est semblable à et

_vérifie,

_(voir

_[45]),

si

où le vecteur

Nous

_appelons

norme

de

Rauzy

la norme

Il

Il,

telle _{que, pour} tout v E

ÏT&#x26;2

Remarques.

1) l16(1) 11

=

lal4

et

U5(Tn+3)1I =

laln+4.

2)

Il existe deux constantes co et ci telles _{que, pour} tout n E

_N,

Théorème 3

_(Rauzy

_[45]).

Il existe un norrabre strictement

positif

c tel

que, pour tout entier naturel non nul _{q, pour} tout entier naturel m,

Proposition

3. Il existe K tel que pour tout q

Preuve.

_D’après

le théorème

ci-dessus,

Il

1 1

En

_particulier

Prenons

_T~.,2.~2

q

Tm+3 ;

comme _q

_Tm+3,

on a

où K est la constante ce

qui

donne la conclusion de la

propo-sition. D

Ce résultat

_signifie

_{que e}

est mal

_approché

_par les rationnels. En

_effet,,

pour tout vecteur v =

vl ,

il existe _une suite

(qn )

_{et une} constante

Ko

V2

1

tels _{que, pour tout} n,

Ko .

La démonstration élémentaire que nous avons donné de la

_Proposition

3

est

_spécifique

à

_l’exemple

_{étudié ;}

_néanmoins,

cette

_proposition

est une

conséquence

d’un théorème

_classique

_(cf.

Cassels

_{[11]) :}

Théorème 4

_(Cassels).

Soient xl, ... , n nombres réels

_appartenant

à

un _corps de nombres totalement réel de

degré n

+ 1 tel que

1,

xl, ... , xn sont linéairement

_{indépendants}

sur

Q,

alors il existe une constante _’Y telle

que, pour tout entier naturel q non

nul,

on ait

l’inégalité :

Nous

_montrons,

_ci-dessous,

que la suite

(Tn+3)

vérifie la

propriété

En effet

La

_propriété

est

_vérifiée,

vu _{que :}

Remarque.

Les

_inégalités

₍₄₎

et

₍₆₎

sont vraies avec

_{n’importe quelle}

norme

_quitte

à modifier les constantes

_(d’après

_{l’équivalence}

des

_normes).

Nous

_donnons,

_ci-dessous,

une

_{propriété plus}

forte du

vecteur ~

_qui

ex-prime,

elle

_aussi,

_{que e}

est mal

_approché

par les rationnels.

Définition 6. Soit v un vecteur de

1I82

et Il -

Ilo

une _norme, on dit _que la

suite croissante d’entiers

_(qn)

est la suite de meilleure

_{approximation}

de v

pour la norme

Il

.

~~o

si,

pour tout n,

IIlqn+lVlllo

et pour tout

q on a

Proposition

4. Pour toute norme

Il . 110,

la suite

(qn)

des meilleures

385

Preuve.

_{Supposons T~+2}

_qn

_Tk+3.

Pour _{tout q} on

a Iliqelilo

_&#x3E;

i i

-Illqnçlllo.

Or, d’après

(4),

Kq;’2

&#x3E; D’autre

_part,

pour

tout m strictement

positif,

- ", _ 1

v

Comme 0

_1,

il existe _mo tel _que

.8111- -. III. III III. -.... III

C,

par

conséquent

on a

d’où le résultat. D

Théorème 5. Pour la norme de

_Rauzy,

la suite de meilleure

approxima-tion est la suite

_Tn+3.

Pour démontrer ce

_théorème,

on utilise le résultat suivant :

Lemme 4

_(Rauzy).

_(voir

_[45])

Il existe une constante c" telle _{que, pour}

tout q E

N,

pour tout g E

Z2,

Soit no =

8,

= 0.03. Comme

lai

1,

pour tout n &#x3E; no, on a

liâ(Tn+3)11

c" ;

_par

_conséquent,

_pour

_{q &#x3E;}

Tno+3,

d’après

le Lemme

_4,

_pour montrer _que la suite

_(Tn+3)

est la suite

de meilleure

_{approximation,}

il suffit de vérifier _que

Pour _q

_274,

un nombre fini

(273)

de vérifications

_permet

de

conclure,

ces vérifications ont été établies par ordinateur.

Lemme 5. Il exzste A strictement

_{positif explicite}

tel _{que pour toute} suite admissible E = _Eo =

1,

et donc

2-ème cas.

_{Supposons E1}

= 1 et donc _f2 =

_0,

_{on a}

On vérifie

_qu’avec

_{0, 027}

et

_{02 .~}

_{0,037, A}

&#x3E;

lall2 --

_0,025.

D

Soit

maintenant q

=

EkTk+3.

Nous _{supposons que q}

T~+4

ce

qui

est

_équivalent

à d 1~ &#x3E; = 0 . Nous _avons

alors q

=

En 0

EkTk+3’

posons i =

Ek 54

0~, i

est différent de n car on _{suppose que}

q ~

Lemme 6. Si n - i &#x3E; 8 alors

Preuve. Grâce au Lemme

_5,

nous avons

Si maintenant n - i 7

On vérifie aisément

_{que il}

par un

nom-bre fini de vérifications

_{(37 vérifications)}

car n - i

7,

ce

_qui

achève la

démonstration. D

Le Théorème 5 découle de

_façon

immédiate des lemmes

_{précédents. D}

6.1. Calcul de la mesure d’irrationalité. Posons

Ko

=

inf{c,

il existe un infinité de _q tel _que

q2"lIlqçlll

[

c}

La constante

_Ko

est finie car il existe K tel _{que, pour tout q e}

N,

[

&#x3E;

387

Prenons

_{Tn+3 q Z’n+4, d’après}

ce

_qui

précède,

implique

donc

{c,

il existe un infinité de n tels _que

Remarque.

On

_{peut montrer,}

par ces

_méthodes,

_que l’ensemble des

_points

1

d’accumulation de l’ensemble

_{T+3b(T+3 ) n}

E

N}

est une

_ellipse.

7. Nombres de _{recouvrement pour} la suite de Tribonacci Définition 7. Le nombre de recouvrement

_symbolique

F est le

_plus

_grand

réel a tel _{que, pour} tout entier naturel

_ho,

il existe h &#x3E;

_ho,

un mot de

longueur h,

noté _{w, et} une suite d’indices

_{in, n}

E

_N,

vérifiant

~ w

apparaît

dans u à

chaque

terme

in,

~

_{&#x3E; in}

-f- h - 1 pour _{tout n,}

~

#({in

_{+ E}

N,

0 m h -

1 ~

_n

(0, ... ,

N -

1}) ~

aN _pour tout

N assez

_grand.

Définition 8. Le nombre de recouvrement _par

_cylindres

_Fc

est le

_plus

grand

réel a tel _{que, pour} tout entier naturel

_ho,

il existe h &#x3E;

_ho,

un mot

de

_{longueur h,}

noté _{w, et} une suite d’indices

_{in , n}

E

_N,

vérifiant

· w

apparaît

dans u à

chaque

terme

in,

~ w

_{n’apparaît}

dans u à aucun autre terme que les

in,

~

in+l

_&#x3E;

in

-i- tL - 1 pour tout n,

.

N assez

grand.

Ces

_quantités

sont des invariants de

_conjugaison

_topologique

du

_système

dynamique symbolique

associé

_(voir

_[12]).

Pour les

_calculer,

on utilisera

la notion de

_fréquence

sans chevauchement : deux

apparitions

d’un mot z,c~, aux termes i et

_j,

sont sans chevauchement _pose

d(w)

= lim où

_{Mn (w)}

est le nombre maximal

_{d’apparitions}

sans n + 1

chevauchement de w _que l’on

_peut

trouver dans uo ~ ~ ~ un

(cette

limite existe

par

unique

ergodicité).

Calculer F pour un

système symbolique

revient

à

_calculer,

_pour des mots arbitrairement

_longs,

les

_{plus grandes}

valeurs

de la

_quantité

_T(w)

=

l(w)d(w) ;

_nous

appelons

T(w)

le

w. Calculer

Fc

revient à considérer

T(w)

_pour des mots dont toutes les

apparitions

sont sans chevauchement.

Proposition

5. Pour la suite de Tribonacci

2

Preuve.

_Si,

_pour

_h,

il _y a un

éclatement,

la branche centrale est de

_longueur

1,

donc 2h -f-1 =

c’ -I- m’ -~- l’ - 2,

où

c’,

m’ et l’ _sont les

longueurs

des circuits.

On a c’ m’

l’

et c’

-I- m’

&#x3E; l’

_{+ 1,}

si on se

_place

_pour un h assez

_{grand ;}

&#x3E;m’-~.

Juste

_après

cet

_éclatement,

on _passe à h + 1 et aux

_longueurs

c =

l’,

m

= 1’+

c’ et 1

= 1’+

m’ ;

on a h + 1 &#x3E; _{c, et} 1 &#x3E; m &#x3E;

m’ +

c’ &#x3E; h + 1.

On se

_{place après}

_{l’éclatement,}

et on

_{regarde quels}

mots

_peuvent

avoir

toutes leurs

_apparitions

sans chevauchement. Juste

_après

l’éclatement,

la

longueur

des mots est h + 1 et celle du circuit _{court est c,} et h + 1 &#x3E; c ;

ensuite et

_jusqu’à

l’éclatement

_suivant,

la

_longueur

des mots

_augmente

et la

longueur

du circuit court reste c. Si w est sur la branche

centrale,

il

apparaît

sur les trois

_circuits,

et

_{chaque apparition}

sur le circuit court chevauche la

suivante car

lwl

&#x3E; _{c ;} on ne

_peut

utiliser un tel mot _pour calculer

_{FC .}

Si

w est sur la branche

_courte,

ses

_apparitions

sont sans chevauchement car il

n’y a jamais

deux circuits courts

_{consécutifs ;}

on a alors un _pavage

_égal

à

qui

est

_{maximal juste}

à l’éclatement

_suivant,

où

₂

.

Juste

_après

_{l’éclatement,}

la

_longueur

des mots vérifie h + 1 m, par

conséquent,

les mots de la branche _moyenne

_{apparaissent toujours}

sans

chevauchement ;

cette

_propriété

se conserve aux

_étapes

_suivantes,

_jusqu’à

ce _que la

longueur

des mots

_atteigne

_m, ce

_qui

se

_produit

avant l’éclatement

suivant,

celui-ci

_ayant

lieu

_quand

la

_longueur

des mots vaut

On a donc un _pavage

possible égal

à

m f M, lM

étant la

fréquence

du circuit

moyen,

qui

ne

_change

_pas avant l’éclatement suivant.

_Quand

la

_longueur

du

mot

_dépasse

_m, on

_peut

améliorer le _pavage car

_après

l’éclatement suivant

les circuits _moyens sont

_isolés,

et le _pavage est

_optimal

à

_{l’éclatement,}

valant

fM

m l+m+c-3₂ .

Regardons

maintenant les

_apparitions

des mots de la branche

_{longue ;}

juste

après l’éclatement,

comme la

longueur

des mots vérifie h + 1

l,

les mots

_appartenant

à la branche

_longue

_apparaissent

_toujours

sans

chevauchement ;

cette

_propriété

se conserve aux

_{étapes suivantes,}

_jusqu’à

ce _que la

_longueur

des mots

_{atteigne l,}

ce

_qui

se

produit

avant l’éclatement

suivant,

celui-ci

_ayant

lieu

_quand

la

_longueur

des mots vaut l.

On a donc un _pavage

possible égal

à

1 fil, f L

étant la

fréquence

du circuit

long,

qui

ne

_change

_pas avant l’éclatement suivant.

_Quand

la

_longueur

du

mot

_dépasse

_l,

on ne

_peut

_pas améliorer le _{pavage car,}

après

l’éclatement

suivant,

il _y aura deux circuits

_longs

consécutifs et des

_apparitions

avec

389

Entre le n - 2-ème et le n - 1-ème

_{éclatement, 1}

=

Tn+2,

_m =

_Tn

₊

c =

_{f c -}

pnB2.

_{On vérifie facilement que}

le meilleur pavage est donc donné par

l f L,

d’où le

résultat,

sachant que

La ressemblance entre la valeur de

_Fc

et le nombre d’or

_(qui

vaut

1, 61803 ... )

semble

_purement

fortuite. On remarque que

Fc

pour

Tri-bonacci est strictement

_plus

_petit

que le

Fc de

toute suite sturmienne

([12]).

Proposition

6. Pour la suite de Tribonacci

Preuve. Nous devons estimer la

fréquence disjointe

d’un mot w : la

Propo-sition 1 nous

indique

la

fréquence

des

_mots,

mais

aussi,

en

_comparant

leur

longueur

à celle des circuits

_longs

et

_courts,

dans

_quelle

mesure leurs

ap-paritions

sont sans chevauchements.

On remarque tout d’abord que, si

hl

h2

donnent les mêmes

fréquences

et ont les mêmes

_rapports

avec les

longueurs

des circuits

(c’est-à-dire

_que

les

_parties

entières

_supérieures

de

_{I L , hl}

et

_{I C hl}

ont les mêmes valeurs

h

_IMhl

IChi

pour h

=

h 1

et h =

h2 ) ,

la

plus grande fréquence

_sans chevauchement d’un

mot de

_longueur

_hi

est la même _{pour i} = 1 ou 2. Le _pavage

T(w)

sera donc

le meilleur

_{pour h}

=

h2 ;

_on n’a donc à étudier _que les valeurs extrémales de

h,

c’est-à-dire celles

_{correspondant}

à l’éclatemment et celles _pour

_lesquelles

la

_partie

entière

_supérieure

de

_{L ,}

ou

‘C

change

de

valeur ;

en

fait,

h h IChl

les seules valeurs intéressantes ici sont à

_{l’éclatement, qui}

est

_renversant,

pour

lwl

= _{m et pour}

Iwl

= 1

(en

effet,

_{on a}

toujours

_c

lwl

2m

2l ,

et

lwl

= kc _pour k _&#x3E; 1

n’apporte

rien de nouveau car on ne

_{voit jamais}

deux

circuits c

consécutifs).

Pour h

_fixé,

si w est sur la branche courte

_{(resp. longue)}

du

_graphe

il

ne

_peut

_apparaître

_que sur le circuit court

_{(resp. long)}

et sa

fréquence

sans

chevauchement est inférieure à la

_fréquence

sans chevauchement d’un mot

de la branche centrale. En

_revanche,

un mot de la branche centrale

_apparaît

à la fois sur le circuit

_long

et le circuit

_{court ;}

la

_fréquence

et la

_fréquence

sans chevauchement sont donc

_toujours

maximales _pour ces derniers. Nous

prendrons

donc

_toujours

un mot w

_qui

se trouve sur la branche centrale du

graphe ;

une

apparition

de w

_peut

se trouver soit sur le circuit

_court,

C,

de

_rh,

soit sur son circuit _moyen,

_M,

soit sur son circuit

_long,

L.

Pour

_{1 w}

= l : ~

_{1 w}

₁

&#x3E; m &#x3E; _{c, et} la suite est un enchaînement de circuits

_L,

LC et

_{LM ;}

le _pavage

_optimal

s’obtient en ne

_gardant

_que les

_apparitions

Pour

_Iwl

-

m, 1

_&#x3E;

Iwl

_{&#x3E; c ;} le

pavage

optimal

s’obtient en ne

gardant

que les

apparitions

de w sur le circuit _moyen ou

long,

et vaut +

_{f L ) .}

A

_{l’éclatement,}

_Iwl

= donc

Iwl

&#x3E; 1 _{&#x3E; m &#x3E; c} mais

m+c~/+c~~+?7~~2L

On

_peut

donc sélectionner exactement une

apparition

sur deux du mot w de la branche

_centrale,

et sa

fréquence

est

f + =

D’où un _{pavage valant}

(asymptotiquement)

4 (c

+ m +

l

Le calcul

_explicite

montre _que la deuxième formule

_l’emporte.

D On _{remarque que} F _{1 pour}

_Tribonacci,

bien que le

système

associé

soit de _{rang un,} voir Section 8 ci-dessous.

8.

_{Conséquences ergodiques}

de

_{l’approximation}

_{diophantienne}

Dans tout

_système

mesuré

_{apériodique,}

pour tout E &#x3E; 0 et tout h arbi-trairement

_grand,

on

_peut

trouver

(en

vertu du Lemme de

Rokhlin,

voir _par

exemple

[26])

des ensembles

_{disjoints B, TB,}

... , tels que l’union

(appelée

tour de

_Rokhlin)

de ces ensembles ait une mesure

_supérieure

à

1 - e. Un

système

est de _rang au

plus

_r, si r tours de Rokhlin

_permettent

d’approcher

tout ensemble au sens de la _mesure, et le nombre d e

recouvre-ment est la mesure maximale d’une tour de Rokhlin

_permettant

_{d’approcher}

tout

_ensemble,

voir par

exemple

[21]

pour les définitions

complètes

et un

survol de ces notions. Nous nous intéressons à des notions

_{apparentées,}

lorsque

T est la rotation

Ra

sur le tore

’]l’2,

que l’on sait être de rang un

[18],

mais nous allons demander à B d’être mieux

_qu’un

ensemble mesurable.

Proposition

7. La rotation

Ra

a un nombre de _{recouvrement par}

ensem-bl es

_{simpl ement}

connexes d’au moins

a2+,~+1 ;

plus

précisément,

_{pour tout}

ho,

’ pour tout a

2+ +1 _

0, 6184 ... , il

ho et

un ensemble

,Q -2,B-I-3 ’ ° °

° ’

-B

_vérifiant

.

_B,

_RaB,

... ,

l~~-1B

sont des ensembles

simplement

connexes

dis-joints,

·

_{&#x3E; a~}

. _{le diamètre de B est}

_inférieur

_à

10.

Preuve. Le calcul de

_Fc

pour la suite de Tribonacci se traduit

immé-diatement,

dans le

_{système symbolique}

_{(Xu, T),}

avec les notations

ci-dessus,

par l’existence d’un

cylindre

B’,

de hauteur

h,

vérifiant .

B’, T B’,

, ... , sont

disj oints,

° ~.

On

_prend

alors B et on sait _que = sont

simple-ment connexes

_{~45~ .}

Et B est un

cylindre

de hauteur arbitrairement

grande,

391

Proposition

8. La rotation

_{Ra est de}

_"rang

_{exact par} ensembles

simple-ment connexes" au

plus égal

à

_{trois ;}

_{plus précisément, il}

existe trois suites

de

_cylindres

_{Bn,2, Bn,3’}

trois suites d’entiers

_hn,l,

_hn,2,

_hn,3

tendant

vers telles _que

. les

_hn,i

sont des ensembles

_simplement

connexes

_disjoints,

. la réunion des

_1~~~3?1~~~

_{hn,i est}

de mesure

pleine

dans

_1f2,

. le diamètre des

Bn,i

tend vers 0

_{quand n}

tend vers

_l’infinz.

Preuve. On se

_place

_juste

_après

le n-ème

_{éclatement ;}

le

_graphe

_rh

n’a de mots _que sur trois branches

(moyenne,

longue

et

_centrale).

En raison

des

_propriétés

du

_graphe

de

_Rauzy

_(voir

section

_2),

on

_peut

alors recouvrir

complètement

la suite u _par des occurences sans chevauchement de trois

mots dont les

_longueurs

sont les

_longueurs

des trois branches

_(voir

_{[4] ;}

on

prend,

par

exemple,

pour

chaque branche,

le mot formé en concaténant la

première

lettre de

_chaque

mot de la

_branche).

Cette

_propriété

se traduit

par un recouvrement de

_Xu

_par les itérés de trois

_cylindres

_{J3~ ;}

on

prend

ensuite

_Bn,2

Comme toutes les

_longueurs

des branches tendent

vers l’infini avec _n, les

Bn i

sont des

_cylindres

de hauteur arbitrairement

grande,

donc les

_Bn,i

ont un

_petit

diamètre

(ils

sont de la forme

a~E

+

_V,

k étant un entier arbitrairement

grand

et V un

vecteur) ;

les sont

simplement

connexes ; l’union des itérés des étant exactement

Xu,

son

image par yli

est un ensemble de mesure

pleine.

0

Notons

_qu’aucun

des deux résultats ci-dessus

_n’implique

l’autre

_(le

se-cond

_impliquerait

le

_premier

avec nombre de recouvrement au moins

3 ) .

Ces résultats

_{généralisent}

des résultats sur les rotations de

1f1

([19], [12])

et améliorent des résultats de N. Chevallier sur

_{1f2 :}

Définition 9. Soit v un vecteur de

_]R2,

et

_(qn)

la suite de meilleure

ap-proximation

de v _pour la norme

infinie,

on dit _{que v est} à

_quotients

partiels

bornés si la suite

_{( ggn 1 )}

est

_{bornée ;}

on dit _{que v est} à

quotients

partiels

non bornés dans le cas contraire.

N. Chevallier

_[14]

a montré _que toute rotation de

1f2

est de rang fini par ensembles convexes.

Lorsque

le vecteur de la rotation est à

quotients

partiels

non

_bornés,

le résultat est

_{plus précis :}

la rotation est de _rang un

par ensembles convexes ; par

contre,

lorsque

le vecteur de la rotation est

à

_quotients

_partiels

_bornés,

le _{rang par} ensembles convexes est borné par

une

_constante,

en

général grande, dépendant

de M = Pour

un vecteur

_donné,

on ne sait en

général

_{pas si} les

quotients

partiels

sont

bornés ni

_quel

est l’ordre de

_grandeur

de

_{M ;}

_pour

_Ra,

la section 6 nous

permet

de dire _que les

_quotients

_partiels

sont

_bornés,

avec M =

V7J ;