APPLICATION OF THE SCHUR ALGORITHM TO THE INVERSE PROBLEM FOR A LAYERED ACOUSTIC MEDIUM
by
Andrew E. Yagle* and Bernard C. Levy**
Laboratory for Information and Decision Systems Department of Electrical Engineering and Computer Science
Massachusetts Institute of Technology Cambridge, MA 02139
The work of this author was supported by the Exxon Education Foundation.
The work of this author was supported by the Air Force Office of Scientific Research under Grant AFOSR-82-0135.
The Schur algorithm is a signal processing algorithm which works
on a layer-stripping principle. Its time-domain version, the fast Cholesky
recursion, is a fast and efficient algorithm well-suited for high-speed
data processing. In this paper, these algorithms are applied to the
inverse problem for a continuous layered acoustic medium. Three different
excitations of the medium are considered: impulsive plane waves at
normal incidence; impulsive plane waves at oblique incidence; and spherical
waves emanating from an impulsive point source. The fast algorithms
obtained for each of these problems seem to be computationally superior
to past work done on these problems that employed Gelfand-Levitan theory
The one-dimensional inverse acoustic problem consists of probing a
continuous layered medium (e.g. the ocean floor) with impulsive waves,
and determining the profiles of the density p(x) and local speed of
sound c(x) from the reflected waves measured at the surface. The medium
is assumed to be laterally homogeneous, so that material parameters of
the medium vary only with depth. Three different types of excitations
are used to probe the medium: impulsive plane waves at normal incidence
to the medium; impulsive plane waves incident at an angle to the medium;
and spherical waves emanating from an impulsive point source. By measuring
the reflection response of the medium to these waves at the surface,
profiles of the medium parameters are obtained.
Much of the previous work on this problem for the case of plane waves
at normal incidence has consisted of deriving a Schrodinger equation
from the basic acoustic and stress-strain equations, and then reconstructing
the potential appearing in this equation by using the Gelfand-Levitan
1 2 3 4
procedure (Ware and Aki , Newton , Berryman and Greene ). Coen has shown
that the obliquely incident plane wave problem can be transformed into
the normal incidence problem. Coen has also shown that the point source
problem can be reduced to the obliquely incident plane wave problem.
However, all of these approaches involve the Gelfand-Levitan procedure
(Faddeev ), which requires the solution of a Marchenko integral equation.
This is a serious handicap to achieving computational efficiency in
processing data, for reasons to be discussed later.
In this paper the Schur algorithm is used to solve the one-dimensional
inverse acoustic problem for all three excitations, obviating the need
equation. The Schur algorithm is a fast algorithm well-suited, after
transformation to the time domain and after discretization, to high-speed data
processing. Further, the quantities in the Schur algorithm may be
physically interpreted as upgoing and downgoing waves in the sense of
Claerbout. This also happens when the discrete form of this algorithm
is used to solve the discrete layered (,Goupillaud) medium problem for
plane waves at normal incidence, and the resulting "dynamic deconvolution"
procedure is well known (see Berryman and Greene3 and Robinson8). Here, a continuous-parameter dynamic deconvolution procedure is applied not only
to the problem for plane waves at normal incidence, but also for plane
waves at oblique incidence and for an impulsive point source. The latter
two applications are, to our knowledge, new to the literature.
The Schur algorithm is an example of a layer stripping algorithm,
in which an impulse is used to probe a scattering medium, and where the
medium is reconstructed layer by layer. This algorithm works as follows.
The upgoing and downgoing waves at the surface are known (measured), and
the first reflection of the impulse yields information about the medium
immediately beneath the surface (at depth A). This information is then
used to update the waves at this depth. The problem is now the same as
the original problem, except that it starts at depth A instead of at the
surface. Since the impulse continues to propagate down through the
medium, this procedure can be repeated, reconstructing the medium
parameters with increasing depth. The concept of using an impulse to 9
probe the medium in this way has been used by Symes , Santosa and
Schwetlick , and Bube and Burridge ; however their results were limited to
the case of plane waves at normal incidence.
Unless otherwise specified, all quantities in this paper are scalars.
I. THE SCHUR ALGORITHM
The Schur algorithm is a fast algorithm which finds frequent appli-12
cation in solving inverse scattering problems (Yagle and Levy , Dewilde 13
et al. ). In addition to enabling fast data processing, the Schur
algorithm is expressed in terms of quantities having scattering
inter-pretations, such as waves and reflectivity functions. This motivates
the application of the Schur algorithm to the inverse acoustic problem.
The Schur algorithm arises from the study of the two-component wave
12 14
system (Yagle and Levy , Bruckstein et al. )
qlx(x,t) + qlt(xt) = -r(x)q2(x, ) (la)
q2x(xt) - q2t(x't) = -r(x)ql(X,t) (lb)
Note that if r(x) = 0 these equations are simply propagation equations
for up- and down-going waves travelling at unit velocity. The reflectivity
function r(x) represents the effect the scattering medium has on these
waves.
Now, let the downgoing wave ql(x,t) contain a probing impulse,
repre-senting an experiment in which the impulse is used to initiate the waves.
Then, by causality, both the upgoing and downgoing waves must be zero for
t<x, since the impulse will not have had time to reach depth x. Thus,
we may write
ql(x,t) = b6(t-x) + ql(x,t)l(t-x) (2a)
q2(x,t) = q2(x,t)l(t-x) (2b)
r(x) = 2q2(x,x)/b . (3)
The set of equations (1), (3) is the continuous-parameter fast
Cholesky recursion. In Section III it is shown how these equations may
be discretized. The resulting algorithm is quite fast, and consists of
updating ql(x,t) and q2(x,t) in x and t, yielding r(x) by (3). In the
sequel, the impulse scale factor b is dropped for convenience.
We now consider matters in the frequency domain. Taking the Fourier
transform of (1) yields
qlx j- 1(x,w) - r (x) q2(x,) (4a)
q2x = -r(x)ql(x',) + jwqo2(x ,) . (4b)
This is the two-component wave system in the form in which it will be
derived for the various inverse problems considered in this paper. Once
this form has been obtained for a problem, the algorithms discussed in
this section are all immediately applicable, for waves having the form
given by (2).
The wave interpretations for ql(x,w) and q2(x,c) suggests defining
the reflection coefficient representing the medium deeper than depth x:
(x,w) = q2(x,W)l41 (x,W) . (5)
A(x,w) is the transfer function between the downgoing and upgoing waves
at depth x. Substituting (5) in (4) yields the Riccati equation
A = 2jwR(x,w) + r(x) (R(x,W) -1) (6)
and an initial-value theorem argument (see Bruckstein et al.1 4 ) shows that
and an initial-value theorem argument (see Bruckstein et al.
)shows
that
r(x) = lim 2jwR(x,w) . (7)
The set of equations (4), (5), (7) constitutes the Schur algorithm,
and the set of equations (6), (7) constitutes a continuous-parameter
dynamic deconvolution algorithm. The discretized version of the Schur
algorithm is similar to, but not the same as, the recursions given in
Berryman and Greene3 . The discretized dynamic deconvolution algorithm, in which R(x,W) is computed for increasing values of x, starting from
a measured reflection response R(O,w), is comparable to the dynamic
II. PLANE WAVES AT NORMAL INCIDENCE -- PROBLEM SET-UP
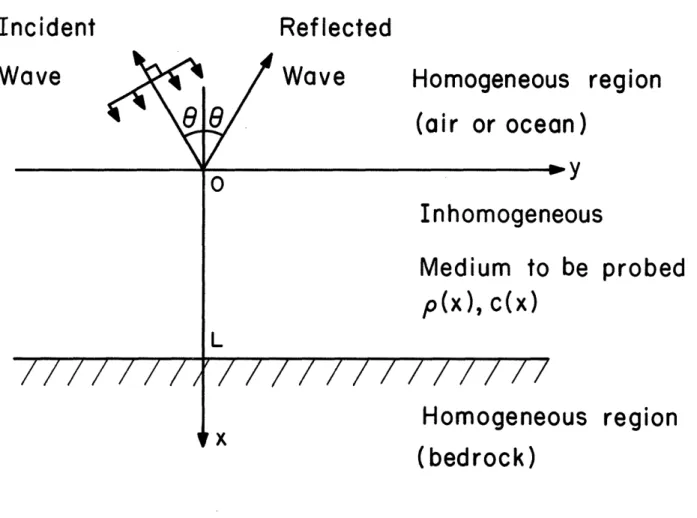
The problem to be considered in this section is illustrated in
Fig. 1 (with 0 set equal to zero). Impulsive planar acoustic waves,
propagating vertically, are incident on a layered medium from a homogeneous
half-space x<O in which the density p0 and local speed of sound co are
known. This half-space could, for example, be the ocean above the ocean
floor. The layered medium is assumed to be laterally homogeneous, so
that material parameters vary only with depth. The reflections or
reverberations making their way back to the surface are measured at the
surface as a function of time. The goal is to obtain profiles of material
parameters as functions of depth x. The actual parameter profiles that
can be reconstructed will be identified shortly. The problem set-up will
follow that of Ware and Aki , Newton , and Berryman and Greene . In this
section, the procedure followed by these authors is quickly reviewed,
for comparison to the Schur algorithm procedure developed in the next
section.
The behavior of the medium subjected to waves is assumed to be
described by the acoustic equation for fluids
p
(x)utt =-- Vp (x,y,z,t)
(8)
and the stress-strain equation
p(x,y,z,t) = -p(x)c(X) V-u(xly.zt) (9)
In these equations u(x,y,z,t) is the (vector) displacement, p(x,y,z,t) is
the pressure or stress, p(x) is density, and c(x) is the local speed of
the problem becomes completely one-dimensional, and (8) and (9) may be
replaced by
P(x)utt- Px (10)
P (x,t)=- p(x)c(x) u (11)
where u(x,t) is now the (scalar) vertical displacement.
We now change variables from depth x to travel time T (x) (Ware and
Aki ), which is the time it takes for a wave, starting at the top of the
medium (x=O), to reach depth x. This is specified by
x
T(X) = J ds/c(s) . (12)
0
We also define the impedance
Z(T) = (p(T)c(T))l/2 (13)
and normalized displacement
f(T,t) = Z(T)u(T,t). (14)
Substituting (11) in (10), using (12) - (14), and taking the Fourier
transform yields the Schrodinger equation (Ware and Aki)1 2^
AUT
2+
WflT,)
=
V(lT)f(TU,)
(15)
where f(T,W) is the Fourier transform of f(T,t) and we have defined the
potential
The term "potential" comes from quantum mechanics, wherein the
Schrodinger equation is often encountered in inverse scattering problems.
The boundary conditions for the Schrodinger equation are
e
+ R(e)ej T < 0 (above surface of medium)
~
(T,e)
-Ii(17) T(e)e je T - T + X (at great depth),
where e represents the source impulsive plane wave and R(')ejOT is
the reflected wave from the medium that is measured at the surface. So
R(U) is the (measured) reflection frequency response. T(w) is the
(un-measured) transmission frequency response; the point here is that there
are no upgoing waves at great depths.
It should be evident from (15) - (17) that the material parameter
profile that may be deduced from R^(e) is precisely Z(T); it is not
possible to recover separate profiles for the density p(x) and local speed
of sound c(x) as functions of depth for the normal incidence problem (Ware
and Aki ). However, it will be possible to recover these separate profiles
as functions of depth for the oblique incidence and point-source problems.
Past procedure at this point (Ware and Aki , Newton , Berryman and
3 6
Greene ) has been to apply the following Gelfand-Levitan procedure (Faddeev ,
Chadan and Sabatier 1 5) to the problems specified by eqns. (15) - (17). The steps are as follows:
(1) Measure R(W) and/or its inverse Fourier transform R(t)
(2) Solve the integral equation
K(t,T) = -R(t+T) -
5
K(z,T)R(z+T)dz, t<T (18) -t(3) Compute from the solution of (18) the Schrodinger potential
:V(T) = 2 dK(T,T)/dT (19)
(4) Using V(T) from (19), solve the differential equation (16) for Z(T), with the initial conditions Z(0) = (p0c0) 1/2
(dZ/dT) (0) = 0.
Berryman and Greene3 have pointed out that steps (3) and (4) may be replaced by the single step
P(T)c(T)/(p(0)c(0)) = 1
+
K(z,T)dz (20)-T
since the differential equation (16) has the same form as the Schrodinger:
equation (15) with w=0.
Note that there are no bound states (see Ware and Aki', Newton )
in this inverse scattering problem. Then, the integral equation (18)
may be discretized and solved by a fast algorithm as in Berryman and 3
Greene . This algorithm has a form similar to the Schur recursions
which will be used below to solve the above inverse scattering problem. 14
However, as noted in Bruckstein et al. , the recursions obtained by
Berryman and Greene correspond to a boundary value problem, whereas the
Schur algorithm is formulated as an initial value problem.
Another difference is that the procedure described above requires
that
I
(l+T)
IV(T)
I dT
<
p
0
This condition is not satisfied when the medium is probed obliquely with
horizontal, as it will in a sufficiently extreme low-velocity zone and
at a turning point, where the ray path is bent back up toward the surface.
In this case the equivalent impedance Z(T) (to be defined by (35)) becomes
infinite, and the reconstruction procedure described above cannot be used.
Since turning points generally occur in real-world experiments, this
limitation is quite restrictive. Note that Coen's procedure for the
non-normal incidence problem requires precritical incidence at all depths
(an unrealistic assumption), while Coen's procedure for the point-source
problem requires separate procedures for the cases of pre-critical and
post-critical incidence. The Schur algorithm solutions to the non-normal
incidence and point-source problems remain valid even in the presence
of turning points, and thus seem to be more general than previous solutions
III. PLANE WAVES AT NORMAL INCIDENCE -- SCHUR SOLUTION
Define the following normalized quantities:
4(T,L~) = Z(T))u(T,L) = normalized displacement (21a)
j4 (T,U) = joZ(T)u(T/,W) = normalized velocity (21b)
W(M,) = p(T,W)/Z(T) = normalized pressure. (21c)
These normalized quantities now have unit energy (Claerbout7 ). As in Claerbout , the following quantities can be interpreted as (respectively)
downgoing and upgoing waves:
q
1(TC)
= f(Tr )
+ jux(T,w)
(22a)
q2(T,L) = (/T,W) - jWf(T,w). (22b)
Taking the Fourier transforms of the acoustic (10) and stress-strain (11)
equations, and making the substitutions (12), (13), (21), and (22) yields
the two-component wave system
qlT= -jwql - r(T)q2(T,c) (23a)
q2 = -r(T)ql(T,') + jwq2
where
r (T) = (l/Z) (dZ/dT) = (d/dT) log Z(T). (24)
Taking the inverse Fourier transforms of (23), and letting ql(T,t) and
q2(T,t) have the forms in equations (2) yields, as before, the fast
Cholesky equations
q2 -2t = -r(T)ql(T,t) (25b)
r(T) = 2q2(T,T) (25c)
which can be propagated recursively, starting from the downgoing and
upgoing waves ql(O,t) and q2(O,t) which are measured on the surface of the
medium. To see this, let the time t and travel time T be discretized by t = nA and T--m, where n and m are positive integers and A is the
discretization time. Then a simple Euler-Cauchy approximation to
the partial derivatives in (24) and (25) yields the following recursive
algorithm:
Z(T+A) = Z(T) (l+r(T'A) (26a)
ql(
T-
+ A,t + A) = ql (T,t) - r(T)q2(T,t)A (26b)q2(T+A, t-A) = q2(T,t) - r(T)ql (T,t) (26c)
r(T+A) = 2q2(T+A,T+A) . (26d)
The recursion patterns for the qi are illustrated in Figs. 2a and
2b. We start off knowing these waves at T for all t, and wish to find
the waves at T+A for all t. Note that by causality there can be no wave
at "depth" T until the initial excitation has had time to reach that far.
Hence, qi (T,t) = 0 for t<T.
The recursions (26) are initialized by measuring the pressure and
velocity of the medium at the surface and using (21) and (22). Often, a
free surface is assumed, in which case the pressure at the surface is
zero. The density p(0) and wave speed c(O) at the surface are assumed
The same approach will also work for the oblique plane wave and
IV. PLANE WAVES AT OBLIQUE INCIDENCE
We now consider the problem in which an impulsive plane wave is
obliquely incident, at an angle 0 to the vertical, on a one-dimensional
layered medium. The reflection frequency response R(W) is now measured
as a function of the horizontal coordinate y (in the normal incidence
problem there is of course no horizontal variation of anything). The
situation is illustrated in Fig. 1. This problem was solved by Coen ,
who showed how this problem could be transformed to the normal incidence
problem and solved using the Gelfand-Levitan procedure. Here, the Schur
algorithm will be shown to solve the problem directly, in terms of
transformed quantities. In addition, it will be shown that running this
experiment twice, at two different angles of incidence, allows the
recovery of the separate profiles p(x) and c(x) as functions of depth
--a signific--ant improvement over the norm--al incidence experiment. Since the
data from the two experiments are processed in parallel, the resulting
algorithm is still quite fast.
An impulsive plane pressure wave incident at angle 0 from the vertical
has the form 6(t-x cos O/c0 - y sin O/c0) in the homogeneous half-space
x<O. In the frequency domain, this is e- j(kx + kyY) where k x = a cos 6/co
and k = X sin O/cO are the vertical and horizontal wave numbers and
cO = c(O). The pressure field for x<O is thus
p(x,y,w,) -j e y (e-kxx + R(w,e)e x) (27) (compare this to the Schrodinger equation boundary condition (17)). This shows that the reflection frequency response R(w,8) in the time domain has
R(t,y;0) = R(t-y sin O/co;
)
(28)
so that theoretically it should only be necessary to measure this response
at a single surface point (e.g. y=0). However, in any real-world
applica-tion it would be a matter of practical necessity to take data for a
range of y and filter or stack it to the form (28). This is because any
real-world impulsive wave could only be locally planar, while the form
of (28) assumes a plane wave of infinite extent.
Taking Fourier transforms of the acoustic (8) and stress-strain (9)
equations, and writing the vector equation (8) as two scalar equations
results in
P(x)2 u (x,y,w) = px (29a)
p(xwu (xy,) = Py (29b)
p(x,y,c)
=
-p(x)c(x) (X
+uy)
(29c)
where ux and uY are the x and y components of the (vector) displacement u(x,y,t).
Since the medium properties vary only with depth x, the horizontal
wavenumber k is preserved, and we may write (following Coen
)
y
-jky
p(x,y,w) = *(x,w)e . (30)
Substituting (30) in (29b), and then substituting the result in (29c)
eliminates uY and yields, after some algebra,
22
2
2^xp(x,y, ) (1-(c(x)
/
)sin)
sin
=-p(x)c(x) u
.(31)
Next, the following substitutions are made:cos (x) 1 - (c(x) /c ) sin20 (32)
(8(x) = local angle ray path makes with vertical)
c'(x) = c (x)/cos e(x) = local vertical wave speed (33)
x
T (x) = I ds/c' (s) = vertical travel time to depth x (34) 0
1/2
Z (T) = (p(T)c' (T)) = effective impedance . (35)
Note that (32) follows from Snell's law (sin O(x)/c(x) is constant along
any ray path), and (33) defines a local vertical wavenumber k (x) = w/c' (x).
Using (32) - (35) in (31) and (29a) yields
Pu = Z / u (T,y,)) (36a)
T
uX=
- (/2)p (T,y,) (36b)and once again defining the downgoing and upgoing waves (as in Claerbout7 )
Vl (T,y,t) = (-T,y,,)/Z + jwZu (CT,y,) (37a)
v
2 (T'YW) = p(T,y,()/Z - jWZu X ( ,y,LW) (37b)yields the two-component wave system
(38a)
v1= -J1 r - (T)v2 38a)
v2-= r (T)V1 + jiv 2 (38b)
with the reflectivity function r(T) defined as
Here y is fixed at whatever value of y R(w,y) is measured at (e.g. y=O),
and 8 is a parameter on which all quantities depend.
Note that once again the quantities in the wave system (38) are the
Fourier transforms of the downgoing and upgoing waves, so that once
again the vertical motion of the medium is decomposed into upgoing and
downgoing waves. Of course, horizontally-travelling waves could not
furnish any information on the vertical variation of material parameters.
Since these waves have the form defined by equations (2), all of the
algorithms specified in Section I can now readily be identified for the
oblique incidence problem.
Now, suppose this oblique incidence experiment were run twice, for
two different angles of incidence 81 and 82' Two different impedances
Zl(T1) and Z2( 2 ), as functions of different vertical travel times T1 and T2, would be obtained. The reconstruction procedure given in Howard
1 6
could then be used to recover the separate profiles p(x) and c(x) from
Z (T ) and Z2(T2 ). However, further consideration of the layer-stripping
idea yields the following procedure for recovering p(x) and c(x) while
the two Schur algorithms are running, obviating the necessity of waiting
for the complete impedances Z (T.). This procedure is also much simpler
than the computationally cumbersome method of Howard1 .
Let ri. (x) be the reflectivity function associated with the experiment
with angle of incidence 8i (i=1,2), and let c'(x) = c(x)/cos .i(x) be
the associated vertical wavespeed. Then
r.(x) = (1/2) (d/dx)log(p(x) c (x)) . (40)
(d/dx)c! (x) = (1/cos 3 (x)) (dc(x)/dx) (41)
Using (41), equation (40) may be rewritten in matrix form as
2 (4)
*1 W-(X)
1l/(2p(x))
1/(2c(x)cos0
1 (x))
(d/dx)p(x)
F2
(x) l1/(2p(x)) 1/(2 c(x)cos 282 (x) (d/dx)c(x) Inverting (42) yields (d/dx)p(x) 1/(2c(x)cos02
(x)) -l/(2c(x)cos1(x))
r1
(X)(d/dx)c(x
-1/(2p(x))
1/(2p(x))
d(x) (43) where d(x) = (cos-2 (x) - cos- 2 (x))/(4p(x)c(x)). (44) 2 1This yields the following recursive algorithm for computing p(x) and
c(x). Discretizing depth as x=nA and time as t. = mA/c (x) (note that
i 1
time is discretized differently at each depth and for the two experiments)
and assuming (for inductive purposes) knowledge of all quantities at
depth x, the update procedure is as follows:
2 2 1/2
cos 1 i.(x) = (l-(c(x) /cO0 )sin 28.) 1 (45)
d(x) = (cos2 2(x) - cos-
02(x))/(4p(x)c(x))
(46)ri(x) = 2v2 (i ,x))cos (x)/c(x) (47)
2 2
p(x+A) = p(x) + (rl(x)/cos
0
2(x) - r (x)cos 02 (x))A(2c(x)d(x)) 1 2(48)2c(x+A) = c(x) + (r
2(x)-r
l(x))A/(2p(x)d(x))
(49)
i
i
v
l (x+A, t+A cosO (x)/c(x)) = v(x,t)
-
riAv2 (x,t)
(50)
i
i
i
v2 (x+A, t-A cos. (x)/c(x)) = v2 (x,t) - riAvl (x,t)
(51)
T.
(x+A) =.(x)
+ AcosO. i(x)/c(x) . (52)At this point all quantities have been updated to depth x+A, so the
recursion is complete. Note that there are two sets of recursions
running in parallel, each one initialized by the data from one of the
two experiments (i=1,2).
The reason that the profiles p(x) and c(x) can be recovered separately
for the oblique incidence problem, but not for the normal incidence
problem, is that by running the oblique experiment twice information has
been gained along two different ray paths. This option is not available
for the normal incidence problem -- there is only one choice for the ray
path, since this problem is completely one-dimensional.
Along any given ray path Snell's law shows that
sin O(x)/c(x) = sin
e0/c
0= ray parameter (constant)
(53)
so that unless
e
is less than the critical anle sin
(c /max c(x))8(x)
will become imaginary at some depth. Physically, this situation results
in evanescent waves, in which the pressure field decays exponentially
instead of propagating as a wave.
The same effect is observed in a
waveguide below cutoff. This causes no problems in the Schur algorithm
until the ray path actually becomes horizontal, prior to turning back up.
When this turning point is reached, [r(x)|
+I. However, since no new
information can be gained beyond the turning point anyway (the upgoing
ray path must be the mirror image of the downgoing path), the Schur
algorithm can simply be terminated when jr(x)
Iexceeds some pre-set
value.
This lack of difficulty with the Schur algorithm when e(x) become
imaginary is in sharp contrast to Coen
4',
in which the cases of
pre-critical (9(x) real) and postpre-critical (e(x) imaginary) incidence must
be treated separately.
V. IMPULSIVE POINT SOURCE
The third and final problem considered is one in which the
one-dimensional layered medium is excited by an impulsive point source.
Such a source, on the surface of a homogeneous medium, would generate
spherical waves within the medium. For the layered inhomogeneous medium,
of course, the waves will only be spherical in the immediate vicinity
of the source.
The situation is illustrated in Fig. 3. Note that since the source
has circular symmetry, the entire problem does also. Hence the reflection
frequency response R(w) is now measured as a function of the distance r
from the impulsive point source.
This problem was solved by Coen , who showed how this problem could
be transformed to the problem with plane waves at oblique incidence by
stacking the data, and then solved as in Coen
.
Here, it will be shown
that a two-component scattering system for the point source problem can
be derived in terms of parametrized Hankel-Fourier transforms of the
up-and downgoing waves. Two different parametrizations up-and the recursive
algorithm of Section IV, starting with suitably transformed data, may then
be used to obtain the separate profiles p(x) and c(x).
The cylindrical symmetry of the problem suggests the use of Hankel
transforms. The n
order Hankel transform is defined as (Papoulis
7 )hnnf~r)} - W f~r)J (ri~rdr = F (5) (54)
0 th
where J (-) is the n order Bessel function. Although Hankel transforms n
of orders zero and one will be used in the derivation, the Schur
algorithm will contain quantities that involve Hankel transforms of order
The signficance of the Hankel transform in problems with circular
symmetry is that the two-dimensional Fourier transform of a function with
circular symmetry is the same as the Hankel transform of order zero of
the function, to a factor of 2f7 (Papoulis 17). Specifically,
f(x,y) = F(u,v) = 27 H {f} ((U2 + v ) (55) It is also true that
H0{f(r)/r + (Da/r)f(r)} = H l{f(r)} (56a)
Hl{(/3r) f (r)} = -H 0
{f(r)}
. (56b)This motivates the use of the Hankel transform in the present problem.
Writing the acoustic (8) and stress-strain (9) equations in cylindrical
coordinates, taking Fourier transforms, and noting the circular symmetry
of the problem (no 6-dependence) yields
2-r p(x)W u (r,x,w) = Pr (57a) p(x)w u (r,x,w) = P (57b) A^~2
Ax
Ar ^ r p(r,x,w) = -p(x)c(x) (u + u /r + u ) (57c) x rwhere u and u are the r and x (depth) components of the (vector)
dis-placement u. Note that the u component of u does not appear.
Taking Hankel transforms of order zero of (57b) and (57c), and
the Hankel transform of order one of (57a) yields
2^x
p(x)W U (g,x,w) = -p(_ x,) (58a)
P(·,x,)
= -p(x)c(x)2(UX +
U
r(,·x,W))
(58c)
where
Ur(E,x ,w) = Hl { ur(rxw) (59a)
bx(Sxw)=
=Hj
(r ,x,) )} (59b)P(·,x,) := H {P(r,x,W)}.
(59c)
Eliminating U from (58) yields
p(x)w U (§,x,O) = P
(60a)
2
2
2
P
(,x,
)
(1
-(2/
2)c
(x))
=
()c(x)
2(60b)
xand defining (compare to (32) -
(35))
c'(X)2
= c(x) /(-(2/ /x2)c(x)
(61)
T(X) = I
ds/c'(s)
(62)
0
1/2
Z(T)
= (p(T)C'(T))l/2
(63)results in the familiar equations (compare to (36))
A 22x P = Z U (,T ,) (64a) T 2^
= -(1/Z )P(,T,o
).
(64b)
TRecalling that the Hankel transform of order zero is the
two-dimen-sional Fourier transform of a circularly symmetric function, we may once
again define the Hankel-Fourier transforms of the downgoing and upgoing
waves (as in Claerbout
7 )Vl(~,Tw) = P(;,T,I)/Z + jcZ6K(g,,)
(65a)
V2(('IT' ) = P('
,T,
' )/Z - jWZUx(,T,W)
(65b) yields the two-component wave systemV1 = -joV l(§,T,w) - r(T) V2 ( ,T) (66a)
V2T = -r(T)V 1 ( ,Tu) + jWV2 (S'T') (66b)
with the reflectivity function r(T) given by
r(T) = (l/Z) (dZ/dT) = (d/d ) log Z(T). (67)
Once again, the waves will have the form defined by equations (2), so
all of the algorithms specified in Section I can now be applied to the point
source problem.
However, it is still necessary to initiate the algorithm using the
given data. One way to do this is to impose the following condition on
the independent variables i and W (Coen 5):
= (w/c0) sin (68)
where
6
is a parameter. Substituting (68) in (61) leads to2 2 22 2 2 2
C'( c (x ) / (1- (c (x) ) sin
6)
=c() /cos (x) (69)which is the same as (32) and (33) in the obliquely incident plane wave
problem. Thus the point source problem has been transformed into an
obliquely incident plane wave problem, which was solved in the previous
To obtain R(w,O), the initial condition for the Schur algorithm for
the oblique plane wave problem, from data measured for an impulsive point
source, it is necessary to use boundary conditions for the impulsive
point source on the oblique plane wave problem solution (27). This is
carried out in detail in Coen5, and we simply repeat the result here:
-k (70)
R(,8) = (l + k0V(w,O))/(l
-k
V(l,))
(70)
where
k = P0c0/b cos 7a)
V(w,e)
= H{v(r,)}Tl
= (w/coj sin
(7
and v(r,w) is the Fourier transform of the vertical particle velocity
measured for an impulsive point source of strength b. It is shown in
Coen5 that the condition (68) amounts to a Radon transform or "slant stack" (Robinson 8 ) on the data v(r,t).
In summary: to use the Schur algorithm to solve the impulsive point
source problem, proceed as follows:
(1) Run the physical experiment, obtaining the data v(r,t):
(2) Using (70) and (71), transform the data v(r,t) to the artifical data R(W,O), for two different values 8l1
e2
of the parameter 6;(3) Run the recursive algorithm specified by equations (45)-(52) to generate the profiles p(x) and c(x).
VI. PERFORMANCE OF THE ALGORITHMS
The basic fast Cholesky algorithm (26) has been proven to be stable by
Bultheel 8 This means that the numerical result of running the algorithm,
starting from a given set of data, is the same result as would be obtained
by running the algorithm, without roundoff errors, on a slight perturbation
of the original data. Since the fast Cholesky algorithm (the time-domain
version of the Schur algorithm) forms the core of the algorithms in
this paper, it can be expected that they too can be proven stable, although
this has not yet been accomplished.
Bube and Burridge have tested the normal-incidence problem algorithm
using numerical simulations, and the results are quite good. The algorithm
does an especially good job of tracking sharp changes in the impedance
profile. The performance of the oblique-incidence and point source
CONCLUSION
The Schur algorithm, a fast algorithm that allows rapid data
processing when discretized, has been applied to the inverse problem
for a> layered acoustic medium. Three different medium excitations were
considered: impulsive plane waves at normal incidence; impulsive plane
waves at oblique incidence; and an impulsive point source. For each
excitation, the Schur algorithm was shown to decompose the pressure
and vertical motion of the medium at each point into upgoing and
down-going waves, yielding the impedance of the medium as a function of travel
time along a given ray path. For the latter two excitations, two Schur
algorithms running in parallel with each other and with differential
up-date equations were used to obtain separate profiles of the density
and local speed of sound as functions of depth.
The use of the Schur algorithm seems to make the procedures of this
paper computationally superior to that of the Gelfand-Levitan procedure 4,5
used by Coen , for reasons explained at the end of Section II. In
any case, the resolution of the medium motion into waves, and the dynamic
deconvolution procedure associated with the Schur algorithm are
interesting. More work needs to be done in testing these algorithms
on actual data. In particular, their performance on noisy data is a
REFERENCES
1. J. Ware and K. Aki, "Continuous and Discrete Inverse-Scattering Problems in a Stratified Elastic Medium, Part I: Plane Waves at Normal Incidence," J. Acoust. Soc. Am. 45, 911-921 (1969).
2. R. Newton, "Inversion of Reflection Data for Layered Media: A Review of Exact Methods," Geophysics J. Royal Astr. Soc. 65, 191-215 (1981).
3. J. Berryman and R. Greene, "Discrete Inverse Methods for Elastic Waves in Layered Media," Geophysics 45(2), 213-233 (1980).
4. S. Coen, "Density and Compressibility Profiles of a Layered Acoustic Medium from Precritical Incidence Data," Geophysics 46(9),
1244-1246 (1981).
5. S. Coen, "Velocity and Density Profiles of a Layered Acoustic Medium from Common Source-Point Data," Geophysics 47(6), 898-905 (1982).
6. L. Faddeev, "Properties of the S-Matrix of the One-Dimensional Schrodinger Equation," Am. Math. Soc. Transl. Ser. 2 65, 139-166
(1967).
7. J. Claerbout, Fundamentals of Geophysical Data Processing, (McGraw-Hill, New York, 1976), p. 146.
8. E. Robinson, "Spectral Approach to Geophysical Inversion by Lorentz, Fourier, and Radon Transforms", Proc. IEEE 70(9), 1039-1054 (1982).
9. W. Symes, "Stable Solution of the Inverse Reflection Problem for a Smoothly Stratified Medium", SIAM J. Math. Anal. 12(3), 421-453 (1981).
10. F. Santosa and H. Schwetlick, "The Inversion of Acoustical Impedance Profile by Method of Characteristics", Wave Motion 4, 99-110 (1982).
11. K.P. Bube and R. Burridge, "The One-Dimensional Inverse Problem of Reflection Seismology", SIAM Review 25(4), 497-559 (1983).
12. A. Yagle and B. Levy, "The Schur Algorithm and its Applications," Tech. Report, Laboratory for Information and Decision Systems,
Massachusetts Institute of Technology, Cambridge,.MA. (November 1983).
13. P. Dewilde, J. Fokkema, and I. Widya, "Inverse Scattering and Linear Prediction, the Time Continuous Case," in Stochastic Systems: The Mathematics of Filtering and Identification and Applications, edited by M. Hazewinkel and J. Willems (D. Reidel, New York, 1981), pp. 351-382.
14. A. Bruckstein, B. Levy, and T. Kailath, "Differential Methods in Inverse Scattering," Tech. Report, Information Systems Laboratory, Stanford University, Stanford, CA. (June 1983), to appear in SIAM J. Applied Math.
15. K. Chadan and P. Sabatier, Inverse Problems in Quantum Scattering Theory (SPringer-Verlag, New York, 1977), p. 307.
16. M. Howard, "Inverse Scattering for a Layered Acoustic Medium using the First-Order Equations of Motion," Geophysics 48(2), 163-170
(1983).
17. A. Papoulis, Systems and Transforms with Applications in Optics, (McGraw-Hill, New York, 1968), p. 141.
18. A. Bultheel, "Towards an Error Analysis of Fast Toeplitz Factorization", Tech. Report No. TW-44, Applied Mathematics and Programming Division, Katholieke Universiteit Leuven, Belgium (May 1979).
FIGURE CAPTIONS
Fig. 1: The incident plane wave problem.
Fig. 2a: Recursion pattern for updating the downgoing waves.
Fig. 2b: Recursion pattern for updating the upgoing waves.