HAL Id: hal-01812890
https://hal.archives-ouvertes.fr/hal-01812890
Submitted on 11 Jun 2018
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of
sci-entific research documents, whether they are
pub-lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diffusion de documents
scientifiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
Public Domain
Calcul de structures en vibrations moyennes fréquences
en présence de liaisons incertaines
Claude Blanzé, Philippe Rouch
To cite this version:
Claude Blanzé, Philippe Rouch. Calcul de structures en vibrations moyennes fréquences en présence
de liaisons incertaines. 7e colloque national en calcul des structures, CSMA, May 2005, Giens, France.
�hal-01812890�
fréquences en présence de liaisons incertaines
Claude Blanzé, Philippe Rouch
LMT Cachan – ENS Cachan 61, av. du Pt Wilson
F-94235 Cachan Cedex
Claude.Blanze@lmt.ens-cachan.fr
RÉSUMÉ.Ce travail propose une approche efficace afin de simuler la réponse stochastique, en moyenne fréquence, d’une structure dont les modèles de liaisons comportent des paramètres aléatoires. Le premier ingrédient est l’utilisation d’un outil dédié à l’analyse des structures dans le domaine des moyennes fréquences : la Théorie Variationnelle des Rayons Complexes (TVRC) [LAD 01, ROU 03] dont les principales caractéristiques sont : l’utilisation de fonctions de base à deux échelles vérifiant la relation de comportement et l’équation de la dynamique, la manipulation de grandeurs effectives au sens moyennes fréquences lors du calcul final (celui-ci ne visant qu’à déterminer la contribution linéaire de chaque mode comportant de façon in-trinsèque une partie fortement oscillante), la gestion indépendante de chaque sous-structure ; les conditions aux limites et aux interfaces sont satisfaites en moyenne de façon automatique à l’aide de la formulation variationnelle. Le second ingrédient est l’utilisation du chaos po-lynomial pour représenter la réponse aléatoire de la structure [GHA 91]. Comme les seuls paramètres incertains sont localisés au niveau des interfaces, on tire parti de la formulation à deux échelles de la TVRC, ce qui conduit à des coûts de calculs très réduits.
ABSTRACT. This paper proposes efficient techniques to obtain effective quantities when con-fronted to complex structures in medium frequency vibrations including stochastic parameters such as interface parameters. The first ingredient is the use of a dedicated approach to com-pute the medium-frequency problem: the Variational Theory of Complex Rays (VTCR). Using two-scale shape functions that satisfy the dynamic equation and the constitutive relation, the VTCR can be seen as a power balance on the different interfaces between sub-structures. The second ingredient is the use of the Polynomial Chaos Expansion (PCE) to compute the random response. Since the only uncertain parameters (in this application: the complex connection stiffness) are those which appear in the interface equations, this approach lead to very small computation cost.
MOTS-CLÉS :Vibrations en Moyennes Fréquences ; Interface aléatoire ; Chaos Polynomial ; TVRC
2 GIENS’05.
1. Introduction
De nombreuses structures industrielles, comme les caisses automobiles, sont au-jourd’hui dimensionnées en fonction de leur comportement vibro-acoustique. Cepen-dant, la modélisation du transfert énergétique en moyennes fréquences ne semble pas résolue aujourd’hui. Les sollicitations rencontrées lors du fonctionnement d’un vé-hicule (rotation du moteur, bruit de roulement, bruit aérodynamique) engendrent des transferts d’énergie le long des longerons de la caisse jusqu’aux panneaux qui la com-posent, générant une ambiance acoustique désagréable pour les passagers. Si ces trans-ferts ne posent pas d’autres problèmes, en basse fréquence, que la modélisation des matériaux ou des assemblages, le domaine des moyennes fréquences ne semble pas résolu aujourd’hui.
En effet, la longueur de variation du phénomène que l’on cherche à décrire est très courte devant la longueur caractéristique de la structure. Il en résulte que les approches traditionnelles basées sur des techniques éléments-finis conduisent à des calculs beau-coup trop lourds tandis que la gamme fréquentielle considérée ne permet pas d’appli-quer avec succès les approches énergétiques de type SEA [LYO 67] utilisées en hautes fréquences. De plus, la solution obtenue est très sensible aux propriétés matériaux et aux conditions aux limites et plus particulièrement à l’amortissement principalement localisé au niveau des liaisons. Son identification est très délicate et la variabilité des résultats obtenus reste très importante.
Ce travail propose une approche efficace afin de simuler la réponse stochastique, en moyennes fréquences, d’une structure dont les modèles de liaisons comportent des paramètres aléatoires. La méthode est illustrée par un exemple de longeron comportant deux liaisons dont les paramètres locaux de rigidité et d’amortissement sont aléatoires. Les résultats sont comparés à la méthode de Monte Carlo.
2. Rappel de la Théorie Variationnelle des Rayons Complexes (TVRC) 2.1. Problème de référence
Dans le but de simplifier la présentation, considérons le problème de vibration en-tretenue, d’un assemblage de deux plaques minces, élastiques, homogènes, isotropes en théorie de Kirchhoff-Love, ceci pouvant être aisément généralisé à un nombre quel-conque de sous-structures. Classiquement, toutes les quantités sont définies dans le plan complexe : l’amplitude Q(X) est associée à Q(X). exp(iωt).
Soient S1et S2 deux plaques, de bords respectifs ∂S1and ∂S2, soumises à une
sollicitation harmonique de fréquence constante ω. L’interface entre S1and S2 sera
notée Γ12. Les quantités d’intérêts sont la déflection wl et le tenseur des moments
Ml. Pour Sl, introduisons l’espace d’admissibilité Sadl du couple déflection-moment
sl∈ Sadl ⇔
sl ∈ U × S (ensembles à énergie finie)
∆∆wl− k4lwl= 0 dans Sl Ml= 2h3l 3 (1 + iηl) KCP lX (wl) pour l = 1, 2 avec kl4=3ρlω 2(1 − ν2 l) (1 + iηl)Elh2l (1)
où klest le nombre d’onde et où ρl, νl, ηl, Elet 2hldésignent respectivement la masse
volumique, le coefficient de Poisson, le coefficient d’amortissement structural, le mo-dule d’Young et l’épaisseur de la plaque Sl. KCP lreprésente le tenseur de Hooke en
contraintes planes et X le tenseur de courbure. Les champs Sadl sont admissibles au sens où ils vérifient à la fois l’équilibre intérieur et la relation de comportement de façon exacte.
2.2. Formulation variationnelle associée à la TVRC
La TVRC est une formulation globale des conditions aux limites et de transmission en termes à la fois de déplacements et d’efforts le long de Γ12[LAD 01, ROU 03].
La méthode comporte en deux étapes : tout d’abord construction des champs ad-missibles, ensuite prise en compte des conditions aux limites à travers la formulation variationnelle associée à un sous ensemble de champs admissibles choisis parmis les éléments de Sad.
Elle utilise une approximation à deux échelles : par exemple, la solution dans la zone intérieure peut s’écrire de la façon suivante :
W (X, P ) = a(P ) exp (η 4
√
ωP · X) exp (i√ωP · X) = a(P )we(X, P ) (2)
où ei√ωP .X représente la partie « rapide »du champ définie explicitement. P désigne
le vecteur caractéristique du mode de vibration local, choisi de sorte que ce mode véri-fie les équations de la dynamique et a(P ) est l’amplitude complexe du rayon complexe élémentaire we(X, P ). Il existe différents choix possibles en fonction de la zone
vi-bratoire étudiée (intérieure, « bord »et « coin »). Afin de prendre en compte la relation d’admissibilité (Eq. (1)), le lieu de l’extrémité du vecteur d’onde admissible P pour la zone intérieure doit appartenir à un cercle C, caractéristique du matériau. Toutes les directions des rayons admissibles sont prises en compte. La solution wsols’ecrit alors :
wsol(X) = Z
C
W (X, P ) ds (3)
Par construction, wsoldépend de l’amplitude généralisée a(P ) définie sur C. Afin de
4 GIENS’05.
finies Slh
adà partir de Sadl . En pratique, on discrétise la courbe C en N éléments de
tailles pouvant être différentes (sur la Fig. 1, C est discrétisée en huit éléments de même taille). L’amplitude a(P ) est considérée commme constante le long de secteurs angulaires ah i. Ainsi : wh(X) = n X i=1 ahi Z Ci we(X, P ) ds = n X i=1 ahiwih(X) (4)
Dans le cas de l’assemblage de deux sous-stuctures S1et S2, la formulation
variation-ah iwe(X, P )
a(P )we(X, P )
Figure 1. Admissible interior modes for a plate
nelle conduit à un système d’équations de dimension finie dans le domaine complexe.
K a = f (5)
K = EhD+ Zh, où EhD est la matrice d’amortissement symétrique, définie positive,
associée à la puissance dissipée, et Zhest la matrice associée à la forme bilinéaire
définie par ZhT ∗= −Zh. f est le vecteur associé à la forme linéaire et a est le vecteur
des amplitudes inconnues.
3. Modélisation des interfaces
La modélisation proposée des assemblages entre ces composants permet de prendre en compte des comportements plus réalistes tels l’amortissement localisé à l’interface de deux sous-structures. Comme les longueurs d’onde des phénomènes vibratoires en moyennes fréquences sont assez grande comparées à la distance entre deux rivets ou deux points de soudure consécutifs, les paramètres d’interface tels l’amortissement ou la raideur seront répartis sur la longueur de la liaison et identifiés sur des assemblages génériques.
3.1. Le modèle d’interface
Chaque interface est une entité mécanique dont le comportement spécifique dé-pend du type de connections ; par exemple, une interface élastique avec amortissement hystérétique est décrite par :
−n1M1n1+ n2M2n2= 0 Equilibre (6)
1
2(n1M1n1+ n2M2n2) = −kc(1 + iηc)(w1,n1+ w2,n2) Comportement (7)
où kcest le coefficient de rigidité à la flexion et ηcle coefficient d’amortissement. Dans
cette application, la nature aléatoire de la réponse provient uniquement du comporte-ment aléatoire des liaisons entre certaines sous-structures. Les paramètres incertains de liaisons sont modélisés par un ensemble de variables aléatoires {α(θ)}, θ apparte-nant à un certain espace des événements Ω.
3.2. Discrétisation dans l’espace aléatoire : le Chaos Polynomial (ECP)
Les paramètres d’interface stochastiques conduisent à un système linéaire similaire à Eq. (5) :
K(θ) a(θ) = f (8)
La variable a(θ) peut se décomposer dans la base du Chaos Polynomial [CAM 47] [GHA 91] : a(θ) = P X i=0 aiΨi(θ) (9)
où {Ψi(θ)} sont des polynomes des variables aléatoires gaussiennes {ξi(θ)}, lesquels
forment une base complète dans l’espace de Hilbert des variables aléatoires du second ordre. Le nombre de polynomes P dépend de l’ordre p de la décomposition Chaos et du nombre L de paramètres stochastiques d’entrée. Supposons que les paramètres ma-tériaux soient constants le long de l’interface. Sinon une décomposition de Karhunen-Loeve peut être utilisée pour représenter la dépendance spatiale et stochastique des caractéristiques d’interface [GHA 96].
Le paramètre stochastique d’interface α(θ) est une variable aléatoire définie par :
α(θ) = α(1 + δg(ξ(θ))) avec g(x) =
2 arcsin(Erf(√x 2))
√
−8 + π2 (10)
où α est l’espérance mathématique de α(θ), δ le coefficient de variation (écart-type divisé par la moyenne), ξ(θ) une variable normale centrée réduite ξ(θ) ∼ N (0, 1) et g une fonction non linéaire telle que la densité de probabilité de α(θ) soit à support borné.
6 GIENS’05.
Le système (Eq. (8)) devient :
P X j=0 L X i=0
cijkKiaj= δ0kf k = 0, 1, . . . P, où les
coefficients cijkreprésentent hg(ξi)Ψj(θ)Ψk(θ)i et ne sont calculés qu’une seule fois.
Les inconnues ajsont obtenues par la résolution de ce système linéaire de taille (P +
1) n × (P + 1) n (n étant le nombre de degrés de liberté) [GHA 91].
4. Exemple : Longeron avec deux assemblages incertains
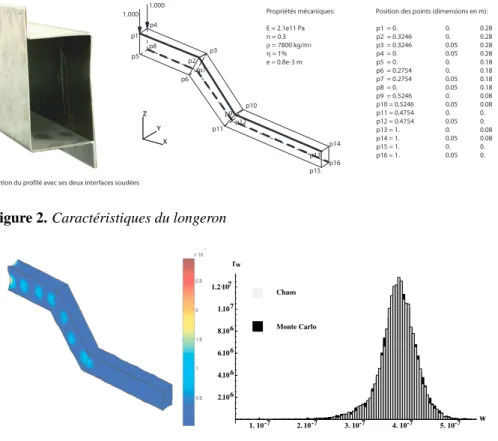
Issu d’un benchmark PSA, l’exemple proposé représente un longeron dont deux liaisons ont été réalisées en soudage par points. Le procédé entraînant des dispersions de fabrication, l’incertitude sur ces deux liaisons sera modélisée par 4 paramètres aléa-toires (2 raideurs et 2 amortissements). Un moment linéique de 1 Nm/m est appliqué sur le coté P1P4. Toutes les autres caractéristiques sont définies Fig. 2.
X Y Z X Y Z p1 = 0. 0. 0.28 p2 = 0.3246 0. 0.28 p3 = 0.3246 0.05 0.28 p4 = 0. 0.05 0.28 p5 = 0. 0. 0.18 p6 = 0.2754 0. 0.18 p7 = 0.2754 0.05 0.18 p8 = 0. 0.05 0.18 p9 = 0.5246 0. 0.08 p10 = 0.5246 0.05 0.08 p11 = 0.4754 0. 0. p12 = 0.4754 0.05 0. p13 = 1. 0. 0.08 p14 = 1. 0.05 0.08 p15 = 1. 0. 0. p16 = 1. 0.05 0. p1 p2 p4 p6 p8 p5 p3 p7
Propriétés mécaniques: Position des points (dimensions en m): E = 2.1e11 Pa n = 0.3 ρ = 7800 kg/m3 η = 1% e = 0.8e-3 m 1.000 1.000 p9 p10 p11 p12 p13 p14 p15 p16 Section du profilé avec ses deux interfaces soudées
Figure 2. Caractéristiques du longeron
1. 10-7 2. 10-7 3. 10-7 4. 10-7 5. 10-7 w 2·106 4·106 6·106 8·106 1·107 1.2·107 f w Monte Carlo Chaos
Figure 3. Amplitude solution déterministe (gauche), comparaison solutions
Chaos/Monte Carlo (droite).
La décomposition dans le Chaos Polynomial d’ordre 2 (n=2) avec 4 paramètres aléatoires d’entrée (L=4) conduit au calcul de 15 coefficients associés au 15
poly-nomes d’Hermite. Les histogrammes du déplacement au centre de la plaque P1P2P3P4 entre la solution « Chaos »et la solution issue d’un tirage de Monte Carlo (10 000 ti-rages) sont très proches et attestent de la bonne réprésentation de la solution par la méthode proposée (Fig. 3).
5. Conclusion
La TVRC est une approche générale de résolution de calcul de structures dans le domaine des vibrations moyennes fréquences. Ces principales caractéristiques sont l’utilisation de fonctions de base dédiées et d’une formulation variationnelle adap-tée permettant l’utilisation d’approximations indépendantes par sous-structures Elle permet également de prendre en compte des liaisons complexes entre les différentes sous-structures, caractérisées par des paramètres aléatoires. Dans ce cas, le bénéfice des fonctions de base à deux échelles est double : d’une part, elles conduisent à un système linéaire global de faible taille, d’autre part, la variation lente des amplitudes généralisées (inconnues du problème) se prête bien à une représentation par des fonc-tions polynomiales de degré peu élevé.
6. Bibliographie
[CAM 47] CAMERONR., MARTINW., « The orthogonal development of non linear functio-nals in series of Fourier-Hermite functiofunctio-nals », Ann. Math., vol. 48, no 16, 1947, p. 385-392.
[GHA 91] GHANEMR., SPANOSP., Stochastic Finite Elements : A Spectral Approach, Sprin-ger, Berlin, 1991.
[GHA 96] GHANEM R., KRUGERR., « Numerical solution of spectral stochastic finite ele-ment systems », Comput. Methods Appl. Mech. Engrg., vol. 129, 1996, p. 289-303. [LAD 01] LADEVÈZEP., ARNAUDL., ROUCHP., BLANZÉC., « The variational theory of
complex rays for the calculation of medium-frequency vibrations », Engineering Compu-tations, vol. 18, no 1/2, 2001, p. 193-214.
[LYO 67] LYONR., MAIDANICK G., « Power flow between linearly coupled oscillators », JASA, vol. 34 (5), 1967, p. 623-639.
[ROU 03] ROUCHP., LADEVÈZEP., « The variational theory of complex rays : a predictive tool for medium-frequency vibrations », Comp. Meth. Appl. Mech. Engrg., vol. 192, 2003, p. 3301–3315.