Very high resolution study of high Rydberg levels of the configurations 4f$^{14}$ 6$sn$d of Yb I

HAL Id: cea-01495020

https://hal-cea.archives-ouvertes.fr/cea-01495020

Submitted on 23 Jun 2020

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Very high resolution study of high Rydberg levels of the

configurations 4f

14

_{6snd of Yb I}

Luc Barbier, René-Jean Champeau

To cite this version:

Luc Barbier, René-Jean Champeau.

Very high resolution study of high Rydberg levels of the

configurations 4f

14

_{6snd of Yb I. Journal de Physique France, 1980, 41 (9), pp.947 - 955.}

Very

high

resolution

_study

of

_high

_Rydberg

levels

of the

_{configurations}

4f14

6snd of Yb I

L. Barbier and R.-J.

_Champeau

Laboratoire Aimé Cotton, C.N.R.S. II _(*), Batiment 505, F 91405 _Orsay Cedex, France

(Reçu le 17 mars _{1980, accepté} le 8 mai 1980)

Résumé. 2014 Les niveaux de

Rydberg élevés de l’ytterbium ont été étudiés sur un _jet d’atomes métastables. Les niveaux de la série 4f14 6snd ont été _peuplés à

_partir

du niveau métastable 4f14 6s _6p

_3P0

grâce à la lumière ultra-violette d’ùn laser à colorant monomode double en

_fréquence

et détectés par la méthode d’ionisation par un

_champ

électrique. Les _{champs critiques} d’ionisation _Fc des niveaux 4f14 6snd

3D1

(24 ~ n ~ 57) ont été mesures; ils obéissent à la loi du

_{col(Fc =}

₍₁₆

_n*4)-1).

Les structures

_hyperfines

des _{isotopes impairs} ont été _analysées; comme

l’interaction

_hyperfine

est du même ordre de _grandeur que les interactions électrostatiques et

_spin-orbite

_(ou même pour les valeurs de n les plus élevées

_{plus importantes}

_que ces _dernières), ces structures ont un _aspect très

_particulier.

Les structures observées ont été _{interprétées théoriquement par la méthode paramétrique} de Slater-Condon. Les influences _respectives de l’électron _optique excité (nd) et de l’électron

_optique

non excité (6s) ont _{ainsi pu être}

étudiées. De

_{plus, l’influence}

d’un niveau de valence _perturbant seulement les composantes des _{isotopes impairs}

a été mise en _{évidence pour le nombre quantique n} = 26.

Abstract. 2014

High Rydberg levels of _ytterbium were studied in a beam of metastable atoms. Levels of the series 4f14 6snd were _populated from the metastable 4f14 6s

_6p

_3Po

level _by means of the U.V. _light of a

frequency-doubled _{single-mode dye} laser and detected _using the field ionization _technique. The critical ionization fields _Fc

of the levels 4f14 6snd

_3D1

_{(24 ~} n ~ 57) were measured and found to obey the _{saddle point} law

_{(Fc =}

₍₁₆

_n*4)-1).

The

_hyperfine

structures of the odd

_isotopes

were _{investigated. They} are _{very peculiar} due to the fact that the

hyperfine

interaction is of the same order of _magnitude as _(or even for the _{highest n} values, much more

_important

than) the _spin-orbit and electrostatic interactions. A theoretical account of the observed structures _using the Slater-Condon _parametric method is _given. The relative influence of the excited _(nd) and of the non-excited (6s) optical electron could thus be studied. Furthermore the influence of a valence level

_perturbing

_only the odd

_isotopes

components for n = 26 _was demonstrated.

Classification Physics Abstracts 32.20J - 32.60

1. Introduction. -

During

the last few _years, the

study of high lying Rydberg

levels of atoms has become

a field of

_increasing

interest in atomic _{spectroscopy.}

The _spectra of one-electron atoms have been the

subject

of a _very

_large

amount of

_experimental

and theoretical work.

_{Comparatively,}

rather few _very

high-resolution

studies have been

_performed

on

many-electron atoms. Technical as well as theoretical difficulties

_easily

_explain

this fact. However the

_study

of

_{high Rydberg}

levels of

_{many-electron}

atoms is

particularly

interesting

because of the

_specific

cha-racteristics

_they

_{possess :}

(i)

their

_properties

are influenced

_by

the _presence

of the non-excited

_optical

electrons ;

(ii)

in the energy range where

high

Rydberg

levels

are located there can also exist levels

_belonging

to

(*) Laboratoire associé à 1Université Paris-Sud.

doubly

excited electronic

_{configurations}

that interact with the usual

_Rydberg

series,

thus

_leading

to the

so-called

_perturbed

series.

The _purpose of this work on the

_ytterbium

atom

was to

_investigate

the two

_foregoing

_phenomena

and more

_precisely

to

_investigate

their influence on the

critical ionization fields and on the

hyperfine

struc-tures of the

_Rydberg

levels.

2.

_Energy

_spectrum

of

_ytterbium

I. - The atomic

number of

_ytterbium

is 70. Ytterbium _possesses seven

stable

_isotopes

with mass numbers

_ranging

from 168

to

_{176 ;}

the

_{corresponding}

natural relative abundances

are

_given

in table I. The nuclear

_spins

of "’ Yb

and of

"3Yb

are

_1/2

and

_{5/2 respectively.}

A _part of the level scheme of Yb 1 is

_given

in

_figure

1.

For some of the levels of Yb 1 located below the first ionization limit

_and,

in

_particular,

for the

_Rydberg

series

_converging

towards this

limit,

the 4f shell is

948

Table 1. -

Isotopic composition

of

natural

_ytterbium.

Fig. 1. - Part of the level-scheme of Yb 1

showing the levels of interest for the _{present experiment.} The metastable 4f " 6s _6p

_3Po

level is populated inside the atomic beam _by means of a _discharge.

High Rydberg levels belonging to the configurations 4f 14 6snd are

excited from this level by the U.V. light of a _{frequency-doubled}

dye-laser. Atoms in the other, higher lying, metastable levels are

directly photoionized by the U.V. beam.

closed : these levels can be considered as

_being

those

of a two-electron atom. The other levels below the first ionization limit are those of a four-electron

spectrum

(in

fact one hole in the 4f shell and three

electrons in other _open

_shells).

3.

_{Expérimental}

_set-up.

- The

_{experimental set-up}

we used for

_{studying high Rydberg}

levels of

_ytterbium

is

_quite

_analogous

to that described

_by

H. T.

_Duong,

S. Liberman and J. Pinard in their work on

rubi-dium

_[1].

The atoms of a beam are excited

_by

a

fre-quency-doubled

single-mode dye

laser

_{[2] (this}

laser is

basically

a CW

_dye

laser but it is

_pumped

simulta-neously by

a CW

_argon-ion

laser and

_by

a

_pulsed

Nd

Yag laser)

providing

U.V.

_pulses

of 50 W

_peak

_power

and 50 ns duration with a

_repetition

rate of

approxi-mately

50 Hz. Atomic - and laser - beams

cross at

right

angle

so as to _get rid of the

_{Doppler broadening}

of the lines.

_By

those means, both very

high

resolution and

_{good efficiency}

can be achieved.

In

fact,

due to the rather

_high

value of the ionization

energy of

ytterbium,

the atoms cannot be excited

directly

from the

_ground

level

_by

the

frequency-doubled laser beam as was done in the rubidium

experiment

[1].

We therefore had to take

_advantage

of the existence of metastable levels

_(Fig.

_1).

These levels can be

efficiently

_populated

inside the atomic

beam itself

_by

means of a

discharge

produced

at the

exit _aperture of the oven

_[3].

The _energy difference

between the

_Rydberg

levels under

_study

and the

metastable level 4f 14 6s

_6p

_3pO

is about 33 000 cm-l.

The

_{corresponding wavelength}

close to 600 nm, before

frequency doubling,

is in the

_spectral

range of Rhoda-mine 6 G

_dye

lasers ;

single-mode

CW

_dye

lasers are

particularly

easy to _operate in this

_{spectral region.}

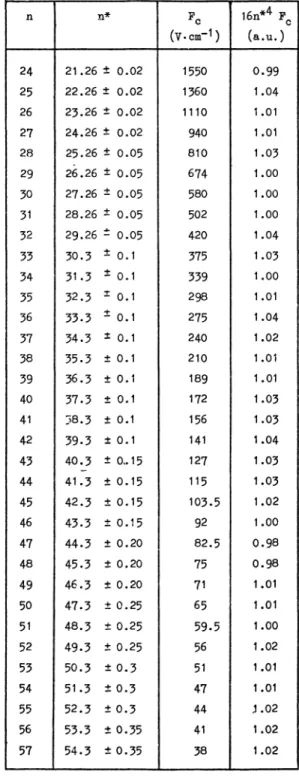
Table II. - Critical ionization

fields

in the series

4f146snd

_3D

1

of

Yb 1. The values

of

the critical

ionization

_fields

_(Fc)

are

_given

as a

function

of

the

principal

quantum number

(n)

or

_of

the

_effective

princi-pal

quantum number

_(n*).

The relative

_uncertainty

on the measured

_Fc

values is about 2

%.

The

_quantity

in the last column

₍₁₆

n*4

_Fe)

is

_expressed

in atomic

units ;

according

to the classical

_{(saddle-point) formula,}

this

_quantity

should be

_equal

to 1.

The excited atoms are detected

_by

the field ioni-zation

_{technique [1, 4].}

The

_positive

ions

_resulting

from the field ionization _process are accelerated

_by

the

_ionizing

field and collected

_by

the first

_dynode

of

an electron

multiplier.

The

_pulses

_provided

_by

the

multiplier

are counted

_during

the _aperture time of a

gate, the

_delay

and duration of which are

_adjusted

so that the ions of interest are all counted whereas the

parasitic

counts are

_rejected

as

_thoroughly

as

_possible.

The excitation _spectrum we have

_investigated

corresponds

to the line series :

4f 14

6s

_6p

3Po-4f14

6snd

F,

F

_being

the total

_angular

momentum of

the atom

_(electrons

+

_nucleus).

4. Critical ionization fields. - The critical

ioniza-tion fields of all levels with n

_ranging

from 24 to 57

have been measured. The results are

_given

in table II.

As is well

known,

in a classical

_picture

the value of

the critical ionization

field,

Fc,

corresponding

to a level with effective

_principal

quantum number n* is

_given

in atomic units

_by

the formula :

_Fc

=

1/16

n*4.

This limit

_corresponds

to the value of the

_potential

energy at the saddle

_point

of the

_potential

_energy

surface of the atom submitted to a static electric

field F.

To check the saddle

_point

formula,

the n* values are

needed. For the lowest n values

_{(24 n 33), they}

were deduced from the measurement of the

wave-length

of the laser in resonance with the transition under

_{study ;}

for

_{higher n}

values

_(n

>

₃₃₎

we used n*

values derived from the work of P.

_Camus,

A. Débarre

and C. Morillon

_[5].

According

to the saddle

_point

formula,

the

_quantity

a =

Fe X 16

n*4

should

equal

1 for

every level.

This was verified

by

plotting

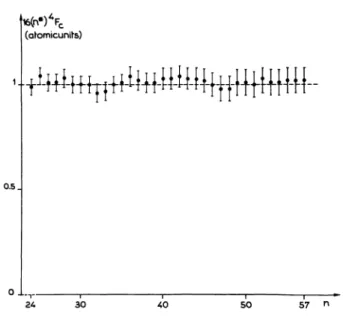
the measured a values versus n in

_figure

2. As can be seen the law is

_obeyed

Fig. 2. - Check of the

saddle-point formula _relating the critical ionization _{field F,} to the effective _{principal quantum} number n* of the level of interest. For every investigated level, the _quantity

16(n*)4 Fc which should _{equal 1 (in} atomic _{units) according} to the classical theory has been plotted versus n.

within the

_experimental

uncertainties for all

investi-gated

levels. This is not too

_surprising

since none of

these levels turned out to be

_perturbed.

In

fact,

as we shall see in

_paragraph

11,

the levels n = 26 _are

slightly perturbed

but

_only

for the odd

_isotopes.

However,

critical field measurements

_performed

on these _components do not _{show any} noticeable

diffe-rence with the values measured on the

_unperturbed

even

isotope

levels

corresponding

to the same value

of n. But it must be

_kept

in mind that first the pertur-bation is

_only

weak and second critical field

measu-rements made on the odd

isotopes

are not _very

_precise

due to the weak

_intensity

of the

_{signal (cf.}

_§"5).

5.

_Hyperfine

structure measurements. -

By

scann-ing continuously

the

_frequency

of the

laser,

one can

record the structure of the transition under

_study.

Figure

3

_{gives typical}

_{recordings corresponding}

to the levels n = 30 and n = 38.

The most intense _components near the centre of

each

_recording

are due to the even

_{isotopes ;}

in the direction of

_increasing

wavenumbers,

one

successively

finds

_17°Yb,

_172Yb,

174Yb

and

176Yb.

The linewidth of a

_single

_component is

_{approximately}

60 MHz due

to the

_spectral

width of the laser

_light

and to the

residual

_Doppler

_{broadening corresponding}

to the

divergence

of the atomic beam. The

_remaining,

less

intense,

components make _{up the} structure of the odd

isotopes.

The

_intensity

of the weakest recorded

component

is less than 1

_%

of the total

_intensity

of the

line.

For

_measuring

the distances between _the compo-nents of the structure, the wavenumber scale of the

recordings

was calibrated

_{by simultaneously}

_recording

the

_fringes

of a

_spherical

_Fabry-Pérot

interferometer

providing

frequency

markers with an interval of

1.5 GHz

_(Fig.

_3).

The

_position

of a

_given

_component

is obtained

_by

a linear

_{interpolation}

between the two

adjacent

reference

_fringes.

The

_position

of all

_compo

nents are referred to the _component of the

_isotope

176Yb

.

The uncertainties in the

_position

measurements

have two

_{origins :}

the noise and other fluctuations

(of

the atomic and

_laser-beams)

and the

_{non-linearity}

of the

_scanning

of the laser

_frequency.

For the odd

isotopes

components the

_uncertainty

is estimated to

be

_{approximately}

3

mK ;

for the _components of the

even

_isotopes

which are more intense and less distant

from one

_another,

the

uncertainty

is

only

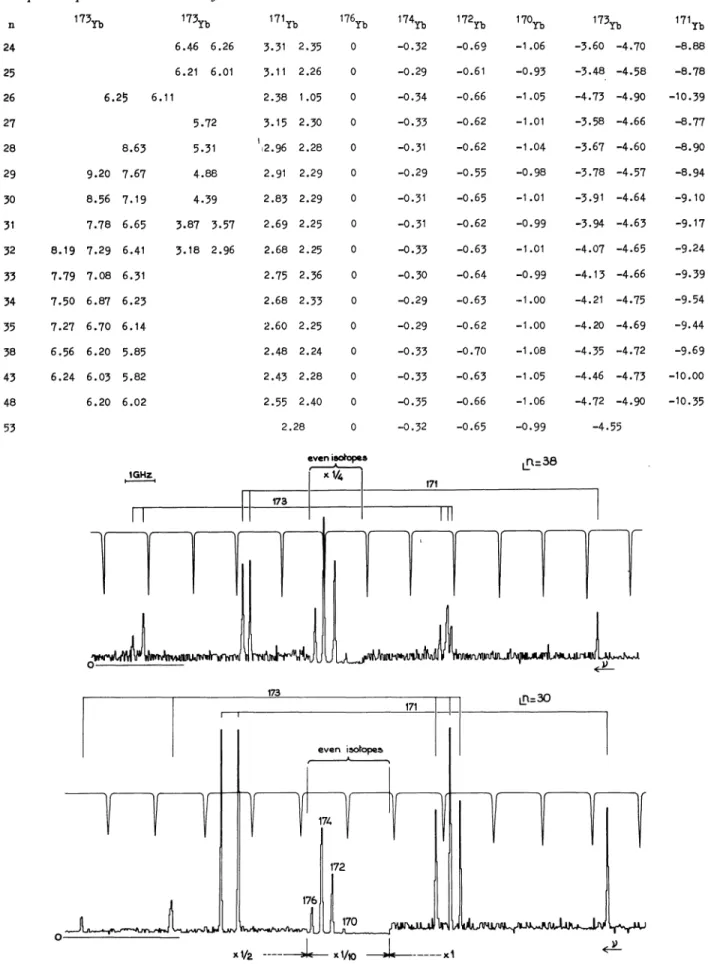
1 mK.

The final results are

given

in table III and a

plot

of

the structures of all recorded transitions is

_given

on

figure

4. The structures of the four even

isotopes

remain

_{remarkably unchanged}

as n

_{varies ;}

in contrast, one observes that those of the odd

_isotopes

_change

considerably

as n is

_{increasing ;}

in

_particular,

the

structures become much

_simpler

for the

_{highest n}

values,

as will be

_explained

in the next section. One should also notice that the structures

_change

_smoothly

950

Table III. - Structures

of Rydberg

levels

_belonging

to the

_{configurations}

4f"

6snd. The

_positions

_of

the recorded components

referred

to

the 176Yb

_component are

_expressed

in GHz. Each line

_of

the table

_corresponds

to a

_given

value

_of

the

_principal

quantum number n. Each column in the table

_corresponds

to a _group

of

_components as it

appears in the

recording (see

Figs.

3 and

4).

The

experimental

uncertainty

is

_{approximately}

0.03 GHz

_for

the even

isotopes

components and 0.1 GHz

for

the odd ones.

Fig. 3. - Recordings of the structures of the transitions 4f14 6s 6p

3Po-4f14

6s 30d and 4fi4 6s 6p

3Po-4f14 bs

38d F. In the region of the

even _isotopes, the ordinates have been divided by 10 in the first _{recording, by} 5 in the second one. In the former _recording the components

Fig. 4. - Plot of the recorded

structures. For the perturbed n-26

level, triangles are used instead of circles for representing the

components of the structure.

this is due to _{the presence} of a

_perturbing

level

_(cf.

§ 11).

6. Interactions

_responsible

for the level structure.

-For the considered

transitions,

4f 14 6s

_6p

3Po-4f 14 6snd,

the structure is

_entirely

due to the _upper

level ; the lower level

_having

J = 0 is

simple

_even in

the case of the odd

_isotopes.

In order to understand the observed structures, it is first _necessary to list the relevant interactions. There are three main

_perturbing

terms in the hamil-tonian :

_(i)

the electrostatic interaction between the

two

_optical

electrons G =

e2/r 12,

where e is the

electron

_charge

and rl2 the relative distance of the

two

_electrons,

_(ii)

the

_spin-orbit

interaction

where

li

and s, are the orbital and

_spin

_angular

momenta of electron i and

_ç(ri)

a scalar function of

the

_{distance r;}

of electron i from the

_origin,

_(iii)

the

magnetic

hyperfine

interaction

_(Fermi

contact

_term)

which can be accounted for

_by

the effective _operator

H.

=

as I.

_ss, where

as is a constant

_{(hyperfine splitting}

factor of the 6s

_electron),

1 the nuclear

_spin

and _ss the

spin

angular

momentum of the 6s electron.

Other

interactions,

e.g. the

magnetic

dipole

and electric

_quadrupole

_hyperfine

interactions associated with the nd electron as well as the

_spin-spin

and

spin-other-orbit interactions are

_supposedly

_negligible.

For each of the

_important

_operators,

_only

one

radial

_integral

_plays

a role in the level structure of the

configuration

4f14 6snd : the Slater

_{integral G2(6s,}

_nd)

for _operator

_G,

the

_spin-orbit

interval

factor

of the nd

electron,

(nd,

for _operator A and the constant _as for

operator

Hm.

The radial function of the nd electron is involved in the first two _{parameters, G2} and

_(,,d,

but not, of

course, in the third one, as. In a

hydrogenic

picture,

it is well known that

(nd

varies as

(n*) - 3

with

_increasing

n ; it can be shown that

G2

also

_obeys

the same law.

In contrast, the parameter a.

only depends

on the

wavefunction of the 6s

electron,

more

_precisely

as is

proportional

to the

_probability

_density

of this electron

at the nucleus. For the values of n that have been

investigated,

the

_probability

_density

of the nd electron near the nucleus is _very

small ;

as a _consequence the

screening

effect

_produced

_by

the nd electron on the 6s

electron is

_{negligible ;}

therefore with _very

_good

accu-racy as has the same value for all

_{investigated high}

Rydberg

lévels and also for the

_ground

level

4f 14 6s

_{2S 1/2}

of Yb II.

7.

_Qualitative

_{interprétation}

of the structures of the

highest

levels. - The

previous

considerations enable

the structures encountered for the

_{highest n}

values

to be understood. For these cases the interactions G and A can be

_neglected

as a first

approximation.

For

each odd

_isotope,

the

_{configuration}

4f14

6snd is thus

split

into two levels whose interval should be

_equal

to as

x

_(I

+

_1/2)

as the

ground configuration

4f14

6s of Yb II, whose

_hyperfine

structure was measured

_by

Chaiko

_[6].

These values are

_compared

in table IV with the

_{corresponding}

values that we have measured

Table IV. -

Comparison

of

the structures

_of

the

Rydberg

levels

4f14

6s 53d and

4f14

6s 48d with the

hyperfine

structure

_of

the

_ground

level

4f14

6s

_2S1/2

of

Yb II. All values are

_given

in GHz.

Hyperfine splitting

(GHz)

in the

_{configurations}

4f14 6s 48d and 4f14 6s 53d.

For each

_isotope,

the values are rather close to one

another,

thus

_giving

a _{strong support} to the

952

8. Theoretical

_{interprétation}

of the

_experimental

results

_by

the

_parametric

method. - To

give

a

quanti-tative theoretical account of all the measurements

we have made use of the

semi-empirical

Slater-Condon

parametric

method.

It must be first recalled that the

_hyperfine

_operator

Hm

does not commute with the total

_angular

momen-tum J of the electrons.

As,

furthermore

Hm

is not

small

_compared

to G and A, none of the usual

_coupling

schemes

_(e.g.

_{Russell-Saunders, jj}

and also J - I

for the

_coupling

between electrons and

nucleus)

corresponds

to the

_physical

_{situation ;}

for the odd

isotopes,

even J is not a

good

_quantum number.

Except

for the

_{highest n}

values

_{(see § 7),}

none of the three

_perturbing

hamiltonians

_G,

A and

_Hm

can be considered as much more

_important

than the other two ; we have therefore to consider the entire

confi-guration

4f14

6snd as the

unperturbed

level and to

handle the total

_perturbation

H’ =

H.

₊ G ₊ A

as a whole.

To

_apply

the

_parametric

method,

the matrix of the hamiltonian H’ is built

_using

the basis set

14f14

6snd(SLJ,

I) FMF >. By diagonalizing

this

matrix,

one obtains the

_perturbed

_{energy levels} that

depends

on

_parameters

_(d,

_G2,

_{as(171), as(173)}

and one additional constant

_(ADD(171)

or

_ADD(173))

for

each odd

_{isotope. Physically}

each of the last two constants determines the

_position

of the structure

of one odd

_isotope

with _respect to the

_{corresponding}

level of

116 Yb

taken as reference.

The

_parameters

are fitted to the

_experimental

values

_by

_comparing

the theoretical and

_experimental

values of the _{energy. In}

_{fact, only G2(6s, nd), ’ncb}

ADD(171)

and

_ADD(173)

were

_free;

the two para-meters

_as(171)

and

_as(173)

were fixed to the values

_they

assume in the

_ground

level of Yb

II,

respectively

12.7 GHz and 3.51 GHz. In the

_{fitting procedure,}

the levels of the two odd

_isotopes

were treated

simul-taneously

so as to avoid that the _parameters

_G2

and

,,d

which have no

_{isotopic dependence}

take different values for the two

_isotopes.

9. Results. - For all

_investigated

levels,

except

n = 26 and n

= 48,

_a

satisfactory

agreement between

experiment

and

_theory

has been achieved since the mean _square difference between

experimental

and theoretical values of the _energy levels is

_{approximately}

equal

to the

_{experimental uncertainty.}

We first comment on the

special

cases. For n =

48,

the

_{fitting procedure}

did not _{converge :} this _may be due to the fact that the values of

G2

and

_’nd

are not

large enough

in

_comparison

to the

_experimental

uncertainties. The case of n = 26 which is

perturbed

will be discussed in

_paragraph

11. For n =

53,

the

observed structure can be

_interpreted

_by

_putting

G2 = (d

= 0

(cf. § 6).

The final values of the _parameters

_G2

and

_’nd

obtained for all the other

investigated n

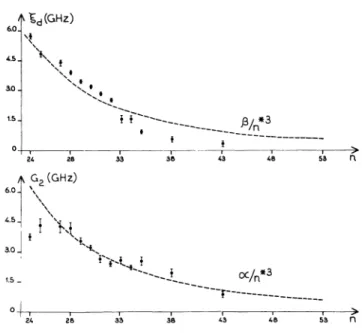
values are

listed in table V. These values are

_plotted

versus n

Table V. - Values

of

the parameters

G2

and

_’d

for

the

_{configurations}

4f14

6snd as a

function of

the

principal

quantum number n. These values are

_given

in

GHz.

in

_figure

5. As can be seen

_they

follow rather

accurately

an

(n*)-3

law,

in agreement with

_{theory (cf. §6).}

However,

a sudden decrease of the values

of (d

and

G2

is observed at n =

33 ;

this is

obviously

related to the

qualitative

change

in the recorded structures

_(in

particular

the

_components

for

173Yb

located on the

large

wavenumbers

_side)

which can be noticed in

Fig. 5. - Evolution with n of the

parameters G2 and ’do In a

hydro-genic scheme, the parameters G2 and ’d should vary like (n*)- 3. To check this, we have drawn on each diagram (dotted line) the

graph of the function (n*)- 3 multiplied by the factor a _{(resp. fui}

which _provides the best agreement with the values obtained for G2

figure

4 for the same value of n but no

_explanation

of

this

_phenomenon

could be found.

For a

given

n, the values obtained for

G2(6s,

nd)

and

₍₀₀

are

approximately

equal.

This is at first rather

surprising

because Hartree-Fock calculations of the ratio

_{(nd/G2 (which}

should be

_independent

of

n*,

as noticed

above)

performed

in the

configuration

4f14

6s 6d

_yield

the value 0.15.

_But,

on the one

_hand,

the

configuration

4f14

6s 6d may be not excited

enough

to fit in the normal characteristics of the

Rydberg

series

and,

on the other

hand,

for the n values we

consider,

the distance between two successive 6snd

_{configurations}

is not much

_larger

than _{the range}

occupied

by

each

_{configuration}

_(for

instance,

the distance between

_{configurations}

6s 38d and 6s 39d

is 5

cm-1,

the overall width of each structure

_being

0.6

_cm-1)

so that

configuration

interaction effects

may be

appreciable.

It is therefore most

_probable

that the values of the _parameters are

_effective

values

taking

into account at least

_partially

the effect of such

interactions. It would be more

appropriate

to treat

together

all

_{configurations}

6snd

_using

the Multi-channel

_{Quantum-Defect}

_{Theory. Unfortunately}

the

application

of the

_MQDT

method to

_hyperfine

sublevels is not

_{straightforward.}

10. Fine structure of the

_{configurations}

4f14

6snd.

-Once the values of the _parameters

_{G2 and (00}

have been obtained for a

_given

n, one can _compute the relative

_energies

of the four levels

_{’D2, 3D1, 3D2}

_and

3D3

without

_hyperfine

structure

_by

_putting

_as = 0

in the energy

matrix,

diagonalizing

it and

_taking

its

eigenvalues.

The

_energies

so obtained are

_plotted

in

_figure

6 with _respect to the _energy of the level

_3D

1

taken as

_origin.

Our measurements allow us to obtain the

_complete

level structure

_resulting

from the electrostatic and

spin-orbit

interactions for all

_investigated

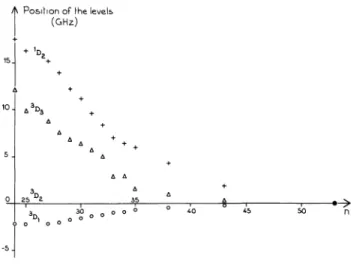
4f " 6snd

Fig. 6. - Level scheme of the

configurations 4f 14 6snd. The relative positions of the four levels of each investigated configuration

4f 14 6snd (without hyperfine structure) have been obtained as a

result of the parametric analysis of the recorded structures (cf. § 10).

These _positions are _plotted versus n _(the level 3D2 is taken as a

reference).

configurations,

in

_spite

of the electric

_dipole

radiation selection rules that _prevent the levels

_{3D2, 3D3}

and

’D2

being

excited from the

_3Po

level. This is

_possible

because,

due to the

_hyperfine

structure

_operator,

the

eigenstates

of several

_hyperfine

levels of the odd

isotopes

contain a

significant

admixture of a state

corresponding

to

_{3D 1.}

Nevertheless,

as the

preceding

results

_rely

on

theoretical

_assumptions

_{(interactions}

have been

neglected),

it would be worthwhile to have a direct

experimental

check of the

_preceding

results

_{by exciting}

the even

_isotopes

levels

ID2,

3D2

and

3D3

and

measuring

their

_energies.

In order to

_perform

those

measurements, it would be

possible

to choose one of

the two metastable levels

_having

J = 2

(Fig. 1)

as

lower level instead of the 6s

_6p

_3Po

level.

11. Perturbation of the

_{configuration}

4f14

6s 26d.

-As was mentioned before

(cf. § 9),

it was not

_possible

to

_give

a theoretical

_{interpretation}

of the structure of

the

_{configuration}

4f14

6s 26d. As can

_clearly

be seen

on the

plot

of

figure

4,

this structure does not follow the normal evolution with n. This is due to _{the presence} of a

_perturbing

level with J = 2

belonging

to the

configuration

4f 13

5d 6s

_6p

_[7]

and located about

5

cm-1

above

the

_{configuration}

4f14

6s 26d. The even

isotopes

levels whose

_eigenstates

are

_purely

J = 1

states are not influenced

_by

this

_perturber,

but the odd ones can be

_perturbed

because their

_eigenstates

contain admixtures of

_3D2

or

1 D 2

states. As

_expected,

the odd levels are shifted

_(with

_respect to the

_unshifted

even

_levels)

towards lower

_frequencies

as a

conse-quence of the

repulsion

of the

perturbing

level. No

further

_analysis

of the

_phenomenon

was

_attempted.

As far as we know this is the first

_reported

evidence of the influence of a

_perturbing

level on the

_hyperfine

structure of a

high

Rydberg

level.

12.

_Isotope

shifts. - The shifts of the

even

_isotopes

are

_given

in table III. Those of the odd

isotopes

can be deduced from the theoretical

_study

of the structures

(cf. § 8)

as

_explained

in

_paragraph

10.

_{By definition,}

the _energy of the

_3Dl

level without

_hyperfine

structure obtained for each

_isotope,

_gives

the shift of that

isotope.

The shifts of both odd

_isotopes

referred to

176Yb

are

given

in table VI.

As can be seen the shift of a

_{given isotope}

does not

depend

on n, at least within the

_experimental

uncer-tainties. This is not

_surprising

because the field effect

as well as the mass effect must have

_{approximately}

constant values for all

_investigated

transitions. The

field effect is determined

_by

the

_probability

_density

at the nucleus of the electrons that should remain constant for all n values

_{(cf. § 5) ;}

the normal mass

effect

_(Bohr

_effect)

_proportional

to the wavenumber of

the considered lines varies

only

by

0.01 mK

_{(0.3 MHz),}

for an

_isotopic

_pair

whose mass numbers difference

is

2,

when n varies from 24 to

_{53 ;}

it is more difficult to

954

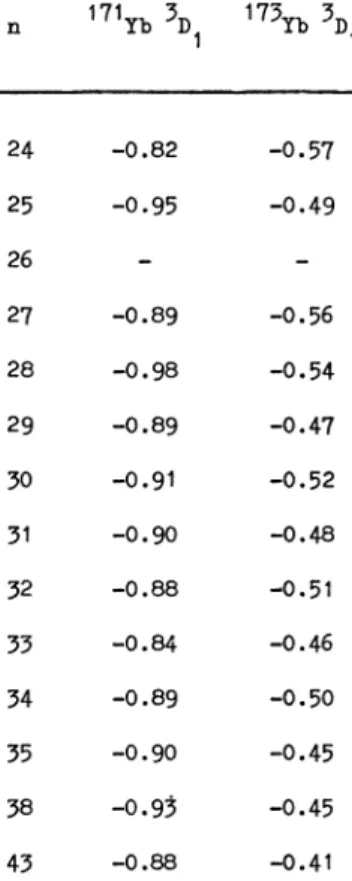
Table VI. -

Isotope

shifts

of

the odd

_isotopes

_of

ytterbium.

In this table are

_given

the _positions the levels

4f14 6snd

_3Dl

_of

the odd

_isotopes

_of

Yb _{would occupy}

if

the

_hyperfine

structure were _{zero ;} these values are

obtained as

explained

in

paragraph

10.

They

are

expressed

in GHz and

_referred

to the

_{corresponding}

component

of 176Yb.

The

uncertainty

is about 0.1 GHz.

but on a theoretical basis this effect is

_expected

to be

small and almost constant for all concerned transi-tions

_[8].

It is therefore

_justified

to take for each

_isotope

the

average values of the shifts of all transitions

(Table VII).

In table VII can also be found the so-called residual shift obtained

_by

_subtracting

the normal mass effect from the total measured shift.

Considering

that the

_isotope

shifts so obtained are dominated

_by

the field

shift,

it is

_interesting

to check if their values

can be

_interpreted

in terms of the

_{empirical screening}

factors well known in the

_analysis

of the field shift

_[8].

The field shift of each

_investigated

transition _is

pro-portional

to the difference of the 6s electron

_probability

densities at the nucleus for _{the upper and lower}

_{levels ;}

it therefore

_directly

reflects the

_screening

effect of the

6p

electron in the level 4f14 6s

_6p

_3Pl

since the nd electron has a

_{negligible screening}

effect. It is known from the

_analysis

of the field

_isotope

shifts in a

_large

variety

of atoms that the _presence of a _np electron decreases the

_{probability density}

at the nucleus of a ns

electron of about 10

_%.

If the residual shifts in table VII

were

_entirely

due to field

_{effects, they}

should thus be

equal

to

_1/10

of the field effect of a 6s electron that is to _say to - 0.10 times the field effect of the resonance lines

4f 14 6s-4f 14

_6p

of Yb II. The shifts of a transition of this _type were measured

_by

Chaiko

_[6]

and the values

can be found in table VII. As can be seen, the ratio of

the residual shifts of the

_Rydberg

lines and of the

resonance line of Yb II is in fact - 0.22 instead of

- 0.1. This

disagreement

should not be taken too

seriously

since we have

_neglected

the

_specific

mass

shifts in the

_Rydberg

as well as in the resonance Yb II

line,

and also because the 10

_{% screening}

factor is

only

an

_approximate

_empirical

_{value ;}

it is

_satisfactory

that the

_signs

and orders of

_magnitude

are in

agree-ment.

13. Conclusion. - The values of the critical

ioniza-tion fields we obtained in this work

_only

lead to the

expected

results that the classical saddle

_point

law is

valid also in the case

_{of many}

electron atoms. In fact

as was discussed

_above,

the series we

_investigated

is

only slightly

and

_indirectly

_perturbed;

the

_problem

of the influence of a

_perturber

on the critical ionization

fields remains therefore an _open one.

The

_analysis

of the structures is much more fruitful.

It

_gives

the

_possibility

of

_describing

the evolution of

the

_hyperfine

structures of

_high

_Rydberg

levels and of

_studying

the relative influence of the excited

_(nd)

and of the non-excited

(6s) optical

electrons on these

structures.

Furthermore,

the influence of a level

perturbing

only

the odd

_isotopes

via the

_hyperfine

interaction has been observed for the first time.

Table VII.

- Average

values

_of

the

_isotope

_{shifts of}

the transitions

4f14 6snd-4fl4

6s

_6p

_of

Yb 1. In the

_first

line

_of

the table are the _average values

_of

the

_{measured position of}

each

_isotope

referred

to l’6Yb

and in the second

line the

_{corresponding}

residual

_shifts.

For

_comparison,

the residual

_{shifts of}

the line  = 369 _nm

of

Yb II _are

_given

in the third line

and,

in the last

line,

the ratios

_for

the residual

_{shifts of}

the

_Rydberg

lines and

_of

the Yb II line. All

shifts

are given in GHz.

Measured shift

_{of Rydberg}

lines

Residual shift of

_Rydberg

lines Residual shift for Yb Il  = 369 _nm

For the

_{highest investigated n}

_values,

we were able

to

reach the limit where all interactions

_responsible

for the structure _except the

_hyperfine

interaction are

negligible.

It would be worthwhile to

_study

the

struc-tures for lower n values in order to reach another

limiting

situation _where, as is the more usual case, the

hyperfine

interaction becomes smaller than the other

interactions ;

in this _way the evolution of the observed

structure between the two

_limiting

_coupling

schemes could be followed

_completely.

Acknowledgments.

- It is

a

pleasure

for the authors

to thank Drs S. Liberman and J. Pinard who

_provided

continuous

_help

and advice

_during

the

_experiment

and Prof. J. Bauche who took a

_leading

_part in the

theo-retical

_analysis.

References

[1] TUAN, D. H., LIBERMAN, S. and PINARD, J., Opt. Commun. 18 (1976) 533.

[2] PINARD, J. and LIBERMAN, S., Opt. Commun. 20 ₍₁₉₇₇₎ 344.

[3] BRINKMANN, U., GOSCHLER, J., STEUDEL, A. and WALTHER, H.,

Z. _Phys. 228 ₍₁₉₆₉₎ 427.

CHILDS, W. J., POULSEN, O. and GOODMAN, L. S., Opt. Lett. 4 (1979) 35.

[4] DUCAS, T. W., LITTMAN, M. G., FREEMAN, R. R. and KLEPPNER,

D., Phys. Rev. Lett. 35 (1975) 366.

AMBARTSUMYAN, R. V., BEKOV, G. I., LETOKHOV, V. S. and

MISHIN, V. I., J.E.T.P. Lett. 21 ₍₁₉₇₅₎ 279.

[5] CAMUS, P., DÉBARRE, A. and MORILLON, C., J. _Phys. B, to be published.

[6] CHAIKO, Y., Opt. Spektr. 20 (1966) 760.

[7] WYART, J.-F. and CAMUS, P., Phys. Scr. 20 (1979) 43. [8] BLAISE, J. and _{STEUDEL, A.,} Z. _Phys. 209 (1968) 311.