HAL Id: hal-02867959
https://hal.archives-ouvertes.fr/hal-02867959
Submitted on 18 Jun 2020
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of
sci-entific research documents, whether they are
pub-lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diffusion de documents
scientifiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
MUSE: une planification d’itinéraires inspirée de
Séparateurs Multimodaux
Amine M. Falek, Cristel Pelsser, Sébastien Julien, Fabrice Theoleyre
To cite this version:
Amine M. Falek, Cristel Pelsser, Sébastien Julien, Fabrice Theoleyre.
MUSE: une planification
d’itinéraires inspirée de Séparateurs Multimodaux. ALGOTEL 2020 – 22èmes Rencontres
Fran-cophones sur les Aspects Algorithmiques des Télécommunications, Sep 2020, Lyon, France.
�hal-02867959�
MUSE: une planification d’itin ´eraires inspir ´ee
de S ´eparateurs Multimodaux
Amine M. Falek
1,2
, Cristel Pelsser
2
, Sebastien Julien
1
, Fabrice Theoleyre
2
1Technology & Strategy group, 4 rue de Dublin, 67300 Schiltigheim, France.
2ICube Lab, CNRS / University of Strasbourg, Pole API, Boulevard Sebastien Brant, 67412 Illkirch Cedex, France.
Le domaine des algorithmes de calcul de plus courts chemins connait un essor important avec le d´eveloppement du cloud. Quelques solutions, dites multimodales, sont conc¸ues pour combiner divers modes de transports, mais au prix d’une augmentation significative de la complexit´e. Nous proposons ici MUSE, un algorithme bas´e sur les s´eparateurs de graphes, mais adapt´e au cas multimodal. Dans une phase de pr´etraitement, nous d´ecoupons tout d’abord le graphe en partitions ind´ependantes (ou cellules), chacune d´ecoup´ee en modes de transport afin de pouvoir plus tard r´epondre `a n’importe quelle requˆete,. Ensuite, nous pr´ecalculons toutes les plus courtes routes, sur ce petit nombre de cellules, en tenant compte des labels (modes) de chaque arˆete. Nous pouvons ainsi r´epondre `a une requˆete tr`es rapidement dans la phase online : l’utilisateur sp´ecifie les s´equences de mode qu’il autorise, et exploite les plus courtes routes pr´e-calcul´ees. Mots-clefs : multimodal algorithm; route planning; graph partitioning; cells;
1
Introduction
Transportation is an intricate network deeply rooted in our society. Thereby, efficient route planning is a pressing necessity to accommodate modern travelers. As a research topic, route planning has tremendously evolved and branched into a myriad of sub-problems. In its purest form, the goal is to identify a shortest route to reach a given destination in the network. Graph separators significantly accelerate queries when ap-plied to road networks [DGPW11]. With independent partitions, the pre-processing becomes parallelizable, and only partitions that have been affected by traffic congestion or delays are ought to be updated.
The multimodal routing problem [ZA08] consists of computing a shortest route constrained by a se-quence of transportation modes. Unfortunately, most of the proposed solutions are tailored for either road networks or public transit networks in isolation. Thereby, to address current limitations, we tackle here the multimodal routing problem using a different approach based on graph separators.
2
Modeling Multimodal Networks
Transportation networks are usually modeled with graphs for their intuitiveness and the extensive algorith-mic toolbox of graph theory. We use a directed Graph model G(V, E) that consists of a set of vertices v ∈ V , and a set of directed edges (v, w) ∈ E connecting vertices v, w ∈ V . The Edge Cost c(v, w, τ) represents the required travel-time to reach vertex w when departing from vertex v at time τ. The cost is given by a periodic positive piece-wise linear function f : Π → R+where Π = [0, p] ⊂ R with a period p ∈ N. A Path P= {v0, v1, .., vk}, also written Pv0vk, is an ordered sequence of vertices vi∈ V .
Road Network: for each segment, we collect a set of speed values over a time window Π sampled at a fine-grained rate ∆t, and we construct its speed profile as a piece-wise linear function fvw.
Foot Network: is a time-independent graph G(V, E), with footpaths including sidewalks and stairs. Bicycle Network: all cycling lanes in addition to rental stations. We insert a vertex v ∈ Vrent⊆ V for each
Amine M. Falek, Cristel Pelsser, Sebastien Julien, Fabrice Theoleyre multi-modal cell road bike public foot w t f t p t f f cut-edges v x y r t r r r r
(a) Cut-edges are shown in bold labeled segments
s1 f p s2 s3 b breturn brent t t s0 c t
(b) NFA combining car, foot, pub-lic transit, and rental bicycles.
Figure 1: Multimodal graph partitioning and NFA
Transit Network: is based on a timetable
T
= (Z
,S
,C
) which consists of a set of shuttle vehiclesZ
, a set of stationsS
, and a set of elementary connectionsC
.The multimodal network combines all of the road, foot, bike, and public transit networks within a single data structure: a labeled directed graph GΣ(V, E, Σ). To distinguish each network, we attach a unique label σ ∈ Σ = {c, f , b, p, t} to each edge, where c, f , b, and p stand for car, foot, bike, and public respectively. Link edges labeled t, are used to transit from the foot network to all other networks. We rely on edge labels to constrain a shortest path by a sequence of acceptable modes.
3
MUSE: Multimodal Separators with Label Constraints
MUSE is a speedup technique to Dijkstra’s algorithm for multimodal route planning inspired by graph separators and label constraints. The user provides a set of transportation modes (e.g., private car/bike, public transit), and MUSE computes a shortest path, restricted to the authorized modes.
The algorithm consists of a preprocessing and a query phase. During the first stage of preprocessing, we execute a graph partitioning algorithm to split the multimodal graph into k−balanced cells {C0,C1, ..,Ck}. Partitioning is run only once, as it solely depends on the topology of the graph. The second stage of the preprocessing consists of computing an overlay graph H: for each cell Ci in the partition, we compute a clique on its boundary vertices, while taking care of the labels (modes of transport) of each edge. We achieve this by running a label constrained Dijkstra DRegLC[BBH+08] from each boundary vertex.
3.1
Preprocessing Phase
Partitioning: Planar graphs can be partitioned in linear time with small separators [Dji82]. The goal is to split the graph into k cells {Ci}i∈[1,k] such that the number of cut-edges linking the boundary vertices of different cells is minimum. Formally, a cut-edge is an edge (v, w) with v ∈ Ci and w ∈ Cj|i 6= j. Road networks, although not planar (due to overpasses and tunnels), can also be efficiently partitioned.
Let us consider a shortest path P and a subpath Pi= {v, .., w} ⊂ P enclosed by the cell Ci(accessing Ci through vertex v and leaving it through vertex w). Using graph partitioning, we can precompute, inside each cell, all the shortest paths between all pairs of its boundary vertices. We propose to apply the same approach to a multimodal network. Computing ideal partitions is NP-hard; thus we use the heuristic METIS [KK98] (Multilevel Graph Partitioning algorithm) adapted to multimodal graphs.
• Coarsening: by repeatedly contracting neighboring vertices in Gi−1(Vi−1, Ei−1) we obtain a graph Gi(Vi, Ei) where |Vi| < |Vi−1|. At each iteration, we compute the maximal matching M and contract in the same cell each pair of vertices v, w|(v, w) ∈ M. Since k is the number of desired cells in the partition, |Vi| ≥ k. • Partitioning: we partition the coarsest graph Gc(Vc, Ec) using Breadth-First-Search (BFS) starting from
a random vertex v ∈ Vcand growing a tree T ⊂ Vcuntil |T | ' 1/2|Vc|. To obtain k partitions, the initial partitions are then recursively partitioned log2(k) times.
• Uncoarsening and Refining: at each iteration i, a less coarse graph Giis obtained by expanding Gi−1 (the pair of vertices that have been merged at the ithstep with coarsening, are here split again).
We have then to process each cell Ci to compute the set of all shortest paths traversing Ci. We have to consider all the paths Pvw, where v, w ∈ Vib⊂ Ci are the boundary vertices. This problem is tractable since the number of boundary vertices is practically small in a cell (by construction). We construct a clique Hi(Vib, Ei) for each cell Ciby creating a virtual edge (v, w) ∈ Ei| v, w ∈ Vibwhose cost c(v, w) = c(Pvw). It is worth noting that we can easily reconstruct a shortest path during the query phase since we have its cost. In essence, we construct the complete graph induced by boundary vertices whose edge costs correspond to the shortest paths. Combining all cliques, we build an overlay H(V, E) whose vertex-set V = ∪ki=1Vib contains all boundary vertices, and edge-set E = Ec∪ki=1Eiconsists of all edge-cuts and clique edges. Label Constrained Cliques: For a multimodal network, however, we must ensure that the cliques im-plement modes that are allowed by the user. Figure 1a illustrates a multimodal partition where each cell Ci spans across all layers of uni-modal networks with, possibly, boundary vertices at each level. Since a user can specify the accepted sequence of modes, we must solve the Label Constrained Shortest Path Problem (LCSPP). An edge may or may not be considered, depending on where the user comes from: we must verify the acceptability of the sequence of modes.
We model the user’s constraint with a regular expression, accepted by a Non-deterministic Finite State Automata (NFA). Conveniently, an NFA denoted
A
, can be implemented as a directed labeled graph GA. Thus, we can solve the LCSPP with a Dijkstra variant DRegLC, deployed on the product graph G×= GΣ⊕GA merging the underlying graph GΣand the automaton graph GA. A vertex hv, si ∈ V×is a combination of a vertex v ∈ V and a state s ∈ S. An edge (hv, sii, hw, sji) ∈ E×is added iff there exists an edge (v, w) ∈ E such that si× label(v, w) → sjis a valid transition of δ ∈A
. The space complexity of DRegLCisO
(V × S) but we implement an improved version reducing the complexity toO
(V + S).Furthermore, to avoid computing large cliques, we construct the NFA such that each state corresponds to a unique transportation layer in the multimodal graph (Figure 1b). Thereby, each boundary vertex is potentially combined to only a subset of states sharing the same label.
3.2
Query
During the query phase, we run DRegLCon the graph Gq= Gr∪ H ∪ Gt, where H is the overlay graph, and Cr and Ct are the root and target cells respectively (i.e., the cells that contain the point of departure and arrival). Therefore, we achieve a significant speedup by skipping most of the underlying graph GΣas most of the computational effort is spent exploring Grand Gt.
4
Experimental Evaluation
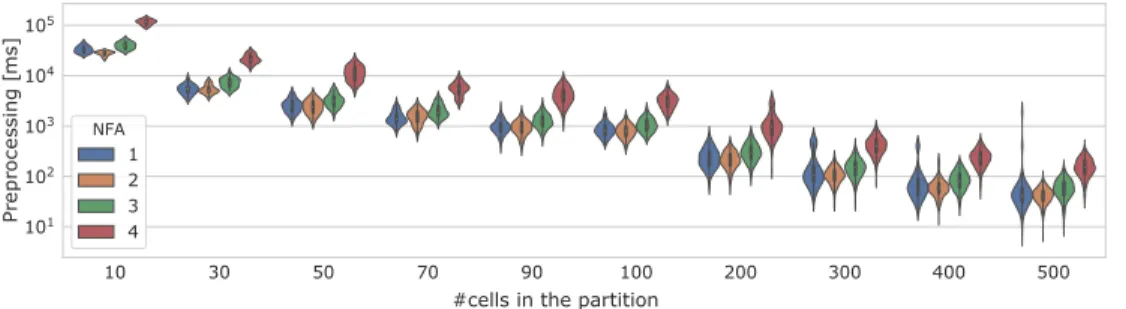
We construct a multimodal graph with 1,444,634 vertices and 4,630,315 edges for the Ile-de-France re-gion. The dataset was obtained with OpenstreetMap [MM+17] to model the road, cycling and pedestrian networks. The public transit network was built from GTFS timetables combining train, RER, subway, tramways, and bus transportation from the Ile-de-France mobilit´es open dataset. We evaluate the algo-rithm on four Non-deterministic Finite Automata (NFA): 1) Foot-Transit consists of two states combining walking and public transportation; 2) Car-Foot: private car is used initially, followed by walking; 3) Foot-Transit + rental Bicycle: similar to the Foot-Foot-Transit NFA with the addition of rental bicycles for faster transfers in the city center. 4) Bicycle-Foot-Transit-Car combines all modes. The private bike is used ini-tially, then followed by any combination involving walking, public transportation, or taxi and uber services. The experiments were run on an Intel Cascade Lake CPU with 24 cores and 128GB of memory, using Java JRE 1.8. Figure 2 reports the preprocessing time for each NFA and partition size, parallelized on the 24 cores. Preprocessing requires less time with a larger number of partitions: we have smaller cells, and fewer border vertices; thus, the algorithm computes the label constrained cliques faster. Total preprocessing time is reduced from 17 minutes (10 cells) to less than 2 minutes for partitions with 100 cells or more. The NFA impacts only slightly the preprocessing time: the partitions are the same (with a different number of modes), but the number of border vertices remains comparable. We ran 1000 queries for each partition size
Amine M. Falek, Cristel Pelsser, Sebastien Julien, Fabrice Theoleyre
10 30 50 70 90 100 200 300 400 500
#cells in the partition
101 102 103 104 105 Pr e p ro ce ssi ng [ ms] NFA 1 2 3 4
Figure 2: Preprocessing time to compute the constrained cliques for different graph partitions and NFA.
#cells in the partition
Figure 3: Query time for 1000 queries using DRegLCand MUSE constrained by the NFA in figure 1b. using both MUSE and DRegLC (constrained by the NFA in figure 1b). As shown in figure 3, query-time depends on the partition size, mainly, we achieve a significant speedup over DRegLCwith a partition of 100 cells which offers an excellent computational trade-off between preprocessing and query.
5
Conclusion and Future Work
We presented a multimodal shortest path algorithm based on graph separators. Using partitions, we can parallelize preprocessing to accommodate large graphs, and pre-compute a set of shortest paths, through each possible pair of cells. That way, we can retrieve very fast a shortest path during the query phase, for any sequence of modes. We are currently running further experiments involving much larger graphs (France and Europe) as well as exploring multi-level partitions combined with a bidirectional search during query-time for even better speedups. Moreover, we are investigating how to exploit this multimodal partition based solution with dynamic graphs, where only a subset of the modes have time-dependent travel times. The objective consists in re-running only one part of the preprocessing, to make the solution scalable.
References
[BBH+08] Chris Barrett, Keith Bisset, Martin Holzer, Goran Konjevod, Madhav Marathe, and Dorothea Wagner. Engineering label-constrained shortest-path algorithms. In Algorithmic Aspects in Information and Management, pages 27–37, 2008. [DGPW11] Daniel Delling, Andrew V Goldberg, Thomas Pajor, and Renato F Werneck. Customizable route planning. In
Interna-tional Symposium on Experimental Algorithms, pages 376–387. Springer, 2011.
[Dji82] Hristo Nicolov Djidjev. On the problem of partitioning planar graphs. SIAM Journal on Algebraic Discrete Methods, 3(2):229–240, 1982.
[KK98] George Karypis and Vipin Kumar. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM Journal on scientific Computing, 20(1):359–392, 1998.
[MM+17] Peter Mooney, Marco Minghini, et al. A review of openstreetmap data. In Mapping and the Citizen Sensor. Ubiquity Press, 2017.
[ZA08] K. G. Zografos and K. N. Androutsopoulos. Algorithms for itinerary planning in multimodal transportation networks. IEEE Transactions on Intelligent Transportation Systems, 9(1):175–184, 2008.