Contribution à la modélisation des structures mécaniques sous sollicitations sévères

(1)

RÉPUBLIQUE ALGÉRIENNE DÉMOCRATIQUE ET POPULAIRE

MINISTÈRE DE L’ENSEIGNEMENT SUPÉRIEUR

ET DE LA RECHERCHE SCIENTIFIQUE

Mémoire

Présenté

AU DÉPARTEMENT DE MÉCANIQUE

FACULTÉ DES SCIENCES DE L’INGÉNIEUR

UNIVERSITÉ DE BATNA

Pour obtenir le titre de

MAGISTÈRE EN GÉNIE MÉCANIQUE

Option : Construction Mécanique

Par

Riad Abdenouri

Contribution à la modélisation des structures

mécaniques sous sollicitations sévères

Soutenu publiquement le : 30/01/2007, devant le jury composé de :

Dr. A. DJEBAILI M.C. Centre Universitaire O. El Bouaghi Président Dr. K. ZIDANI M.C. Université de Batna Rapporteur

Dr. R. BENBOUTA M.C. Université de Batna Examinateur

Dr. M. BRIOUA M.C. Université de Batna Examinateur

(2)

Remerciement

Ce travail a été effectué dans le département de mécanique. Je remercie le bon DIEU, mes parents, mes frères et toutes les personnes qui me sont proches.

J’exprime ma sincère reconnaissance envers mon encadreur Dr.

K

AMEL

ZIDANI

pour m’avoir encadré, soutenu et conseillé tout au long de ce travail.

Je remercie également tous les enseignants du

(3)

Table des matières

CHAPITRE I NOTIONS DE LA MECANIQUE DES MILIEUX CONTINUS ... 7

I. Référentiel et repère ... 8

I.2. Déformation ... 9

I.2.1. Etat de déformation sphérique et état de déformation déviatorique ... 9

I.3. Contraintes ... 9

I.4. Equation d’équilibre ... 10

I.5. Comportement élastique ... 10

I.6 . le comportement élasto-plastique ... 10

I.6. 1. L’expérience de traction simple ; limites d’élasticité ... 11

Remarque ... 13

1.7. Cas d'une sollicitation uniaxiale ... 15

1.7. 1. Matériau écrouissable ... 15

1.7.2. Matériau parfaitement plastique ... 17

1.7.3. Sollicitation multiaxiale en domaines d’élasticité ... 18

CHAPITRE II MODELES ANALYTIQUES D’ETUDE DU COMPORTEMENT ELASTO- .

PLASTIQUE ... 20

Introduction ... 21

II.1. Les critères de plasticité ... 21

II.1.1. Critère de von mises ... 22

II.1.1. Frontière d’écoulement ... 22

II.1.2. Critère de Tresca ... 23

II.1.2.1. Frontière d’écoulement ... 23

II.1.3. Le critère de hill ... 24

II.2. Hypothèse de la théorie de plasticité ... 24

II.2.1. Règle de normalité. « plasticite associée » ... 24

II.2.2. Règle d’écoulement ... 25

II.2.2.1. Sollicitation uniaxiale pour un matériau écrouissable ... 26

II.2.2.2. Sollicitation multiaxiale pour le materiau ecrouissable ... 28

II.2.3. Evolution de la surface de charge ... 30

II.2.3.1. L’écrouissage isotrope ... 30

II.2.3.2. L’écrouissage cinématique ... 30

II.2.3.3. L’écrouissage mixte ... 31

II.3. Déduction de la matrice élasto-plastique par la mécanique des milieux continus ... 31

II.3. Mesure de l’endommagement ... 33

II.3. 1. Méthodes statique ... 33

II.3. 2. Méthode dynamique par ultra-sons ... 34

CHAPITRE IV RAPPEL SUR LA MECANIQUE DE LA RUPTURE ... 40

IV.1. Historique ... 41

IV.1.2. Hypothèses et cadre de l’étude ... 42

IV.1.2.1. Endommagement et mécanique de la rupture ... 42

IV.1.2.2. Fissures statiques, quasi-statiques, dynamiques ... 42

IV.1.2.3. Modes de rupture ... 43

IV.1.2.4. Mécanique linéaire, et non-linéaire de la rupture ... 43

• Etude d’un milieu élastique fissuré ... 44

• Plasticité confinée ... 45

• Plasticité étendue ... 45

(4)

IV.1.3.1. Facteurs d’intensité des contraintes ... 46

IV.1.3.2. Calcul des facteurs d’intensité des contraintes ... 46

• Eléments singuliers ... 47

• Méthode des fonctions de poids ... 47

• Calcul par extrapolation ... 47

IV.1.4. Approche Globale ou Energétique ... 48

IV.1.4.1. Le taux de restitution d’énergie ... 48

VI.1.4.2. Intégrales de contour ... 49

VI.1.4.3. Calcul du taux de restitution d’énergie ... 50

• Calcul par avancée réelle de fissure... 51

• Méthode de l’intégrale J ... 51

• Calcul par avancée virtuelle de fissure ... 52

• Méthode Gθ ... 53

- La variation d’énergie potentielle totale Wp ... 53

- Propriétés du champ θ ... 54

- Expression du taux de restitution d’énergie ... 55

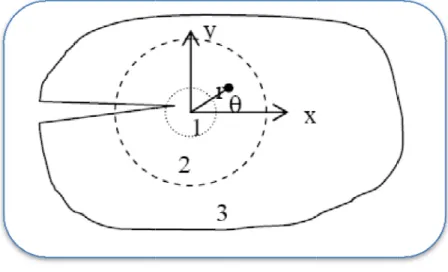
VI.1.4.4. Maillage Concentrique ... 55

CHAPITRE V SIMULATION NUMERIQUES PAR LE CODE CASTEM2000 ... 57

Introduction ... 58

V.1. Dimension de la structure ... 58

V.2. Modélisation numérique ... 59

V.3. Distribution des contraintes et des déformations ... 59

V.4. Géométrie maillée ... 60

V.5. Charge appliquée ... 60

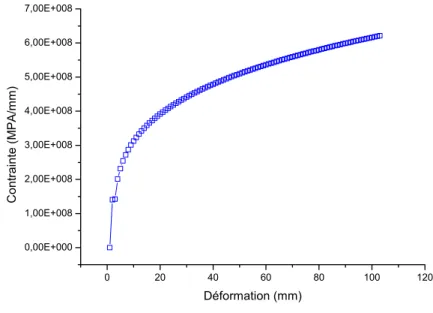
V.6. Courbe de traction ... 61

V.7. Courbe de temps pour la manipulation de la procédure pas à pas ... 61

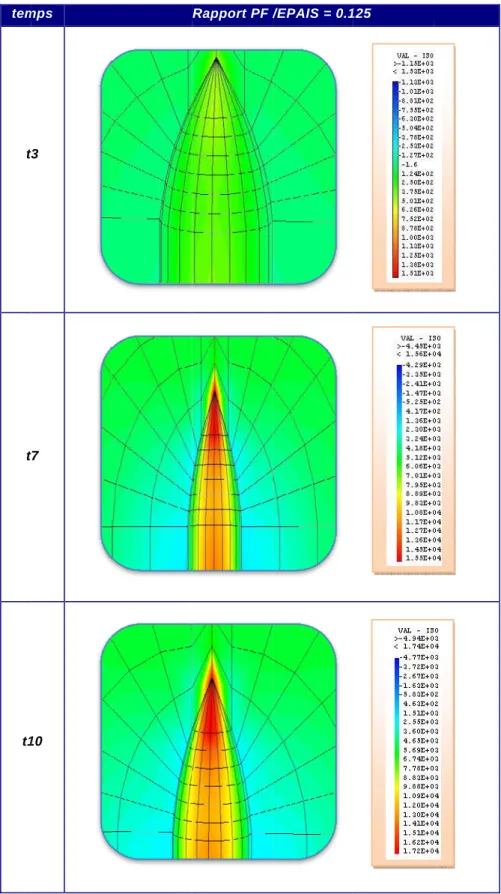
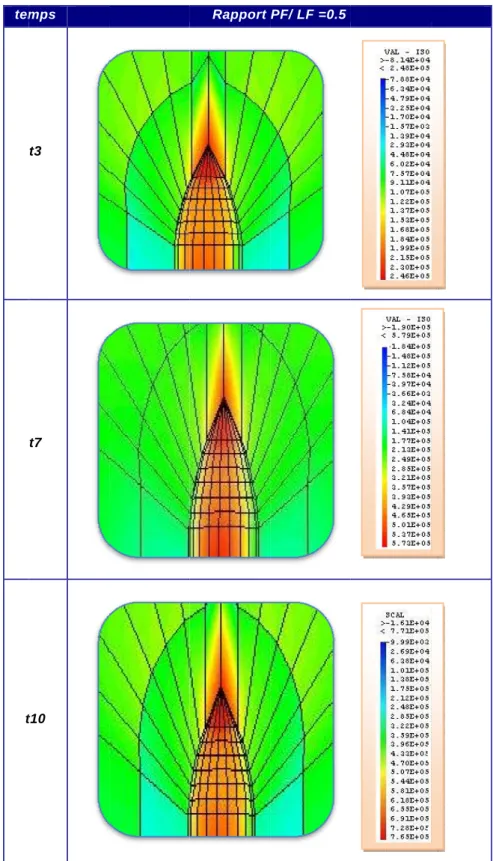
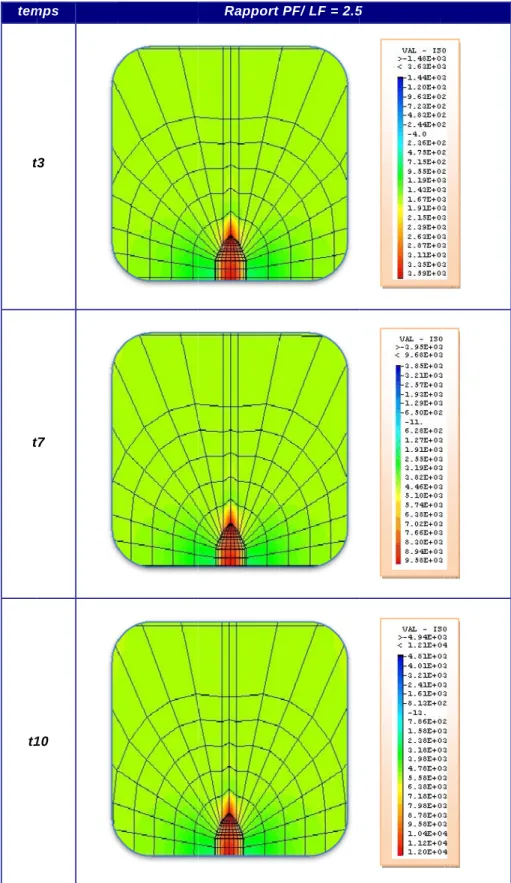
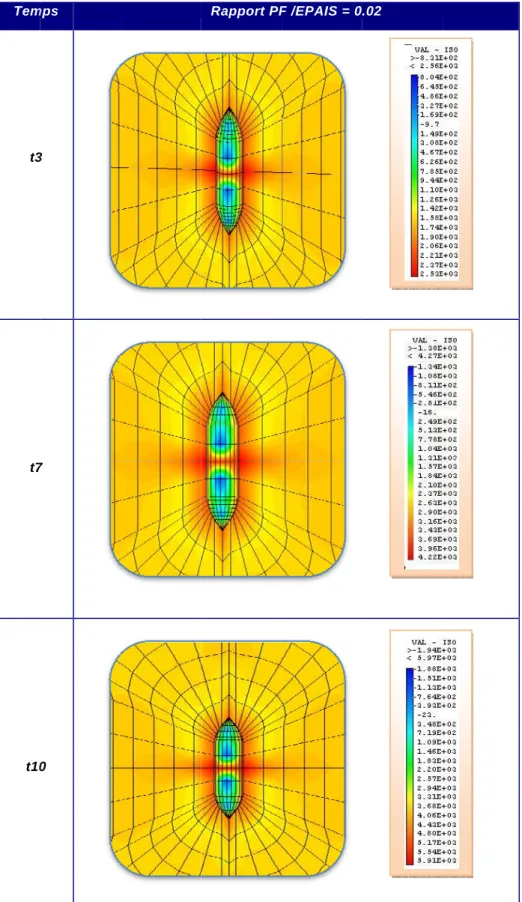
V.8. Résultats des contraintes de Von Mises ... 62

V.8.1. Interprétation des résultats des contraintes de Von Mises ... 74

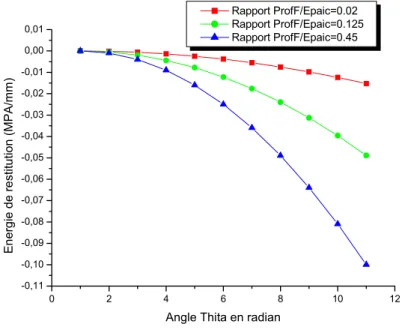
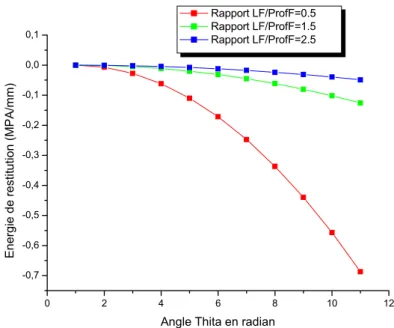
V.9. Les résultats du calcul de l’énergies de restitution pour les diférentes géométries ... 74

V.9.1. Interprétation des résultats relatifs à l’énergie de restitution ... 76

V.10. Le facteur d'intensité des contraintes ... 77

V.10.1. Interprétation des résultats des facteurs d'intensité des contraintes ... 79

V.11. Interprétation globale des résultats ... 80

BIBLIOGRAPHIE ... 83

(5)

Introduction générale

Le travail entrepris est une contribution à l’analyse de la réponse d’une structure mécanique soumise à des sollicitations mécaniques complexes. La structure en question est une conduite utilisée dans le transport sous des pressions et des gradients de température importants de fluides. La conduite en question, présente une fissure initiée sur sa face interne. L’étude présente des intérêts aussi bien techniques qu’économique. L’intérêt technique réside dans la mise en place d’un outil fiable de prédiction du comportement et de la stabilité et permettant la modélisation et la conception de ces structures mécaniques. L’intérêt économique réside dans le fait de pouvoir éviter les conséquences désastreuses relatives à la rupture ou la ruine de ces structures. La littérature traitant de la mécanique élastique linéaire de la rupture, nous renseigne que pour ce type de problèmes mécaniques, la région critique se situe généralement en pointe de fissure. Il est par conséquent important de pouvoir disposer des outils mathématiques permettant la modélisation des divers comportements mécaniques, en particulier, ceux régissant les comportements plastiques et élasto-plastiques des matériaux utilisés dans la conception de ce type de structures.

Le cylindre présentant une fissure interne initiée est sujet à une pression de service relativement importante, il s’agit de pouvoir faire une étude paramétrique incluant les différents paramètres aussi bien géométriques que de chargement qui influent directement sur la stabilité de la fissure. La littérature nous informe qu’en pointe de fissure se localise généralement une zone plastifiée dont il convient de prendre compte lors de toute étude. En relation avec l’importance de cette zone, plusieurs modèles ont été proposés pour l’approche des champs de déplacement et de contraintes. Dans notre étude, nous nous intéressons particulièrement aux comportements élasto-plastique et plastiques des matériaux.

Notre objectif principal est d’étudier et de montrer, par une simulation numérique en élasto-plastique utilisant le code de calcul Castem2000, l’influence des paramètres : effort appliqué, facteur de plasticité, la géométrie du cylindre et la géométrie de fissure.

Un des aspects principaux de ce travail consiste à établir une étude de sensibilités des principaux paramètres qui influent directement sur stabilité de la fissure. Le plan de rédaction de la thèse est le suivant :

• Nous commençons par un premier chapitre présentant un rappel de la mécanique des milieux continus avec une description sur l’élasticité linéaire.

(6)

• Le deuxième chapitre est consacré à une bibliographie en relation avec les différentes lois de comportement en particulier, les comportements élasto-plastique et plastique.

• Le troisième chapitre est consacré aux différentes notions de la mécanique de la rupture (énergie de restitution, facteurs d’intensité de contraintes :KI, KII, KIII, KIC) ainsi que les méthodes de leurs calcul.

• Le quatrième chapitre est consacré à l’étude par éléments finis d’un cylindre fissuré à l’aide du code de calcul Castem2000.

(7)

CHAPITRE I

NOTIONS DE LA MECANIQUE DES

MILIEUX CONTINUS

(8)

I. Référe

La repérag plan ini de Kirc exprimé Où moyenn Soit points Où ; L’invers Ainsi le

entiel et repè

formulatio ge du systè tial et la hhoff, les v ées par rap

{ } {

X

q

=

est le vec ne en , , , et q par

{ }

dX_q =[F₀]−

{ }

dxq =[Fz] e se du tense

[F] e tenseur de

[B]

ère

n mathém ème étudié a forme 3D vectrices po pport au po

} {

z

0

n

0

X

p

+

cteur de d est la coo Fig I.1 : le repère rapport à P

{ }

[ 1 _dx _où _F −

{ }

[ ] dx où st l’élongat eur gradien 1 0 1 _[ _] _[ ]− ₌ _F − _F e Cauchy– 1 _[ _] _[ ]− ₌ _F −T _F atique néc é tout au lo D de la pièc ositions ini oint P situé

}

{ } {

0

=

x

p

−

déplacemen ordonnée à : Cinématiqu e local orth P est donné [ ]1 _, 0 F − = x_p_x− [ ] [Fz = xp,x+ tion d’épais nt de déform 1 ]− z F

Green gau 1 ]− F

cessite que ong de son ce finale so tiales et fin sur la surfa

} {

z

0

n

0

u

p

+

nt du poin à travers l’é ue d’un élém hogonal. Le é par : , _, ,x py p p x u u − ,n,x xp,y z + sseur (sup mation en q

che entre q

e l'on proc évolution nt considé nales d’un ace moyen

}

0

ntp , es épaisseur in ment en défor e tenseur ] / , ₀ ₃ ,y n λ

] ,n,y n z

posée con q est obten

q et peu

cède à la au cours d rées. En ut point maté ne de C (v

st la norm nitiale. rmation. gradient de

stante à tra u par form

ut être défin

description du temps. S tilisant l’hy riel q peuv .1) :

ale de la e déformat

avers l’épa mule (I.2) et

ni par :

n et au Seuls le pothèse vent être

(I.1)

surface tion aux

(I.1)

(I.2)

aisseur). t (I.3) :

(I.3)

(I.4)

(9)

Chapitre Le calc λ , λ e l’hypoth I.2.

Défo

Il co Il existe d’usage représe I.2.1.

Eta

Il e d’un te T = S + D volume volume I.3.

Cont

Les une rép contrain On a do en M d projecti le vecte représe IJ ε = I

cul des vale et leur mat hèse.

rmation

onvient de e des cham e de dire q enté par le

at de déforma

st toujours nseur sphé D, Dans le sans cha constant.

traintes

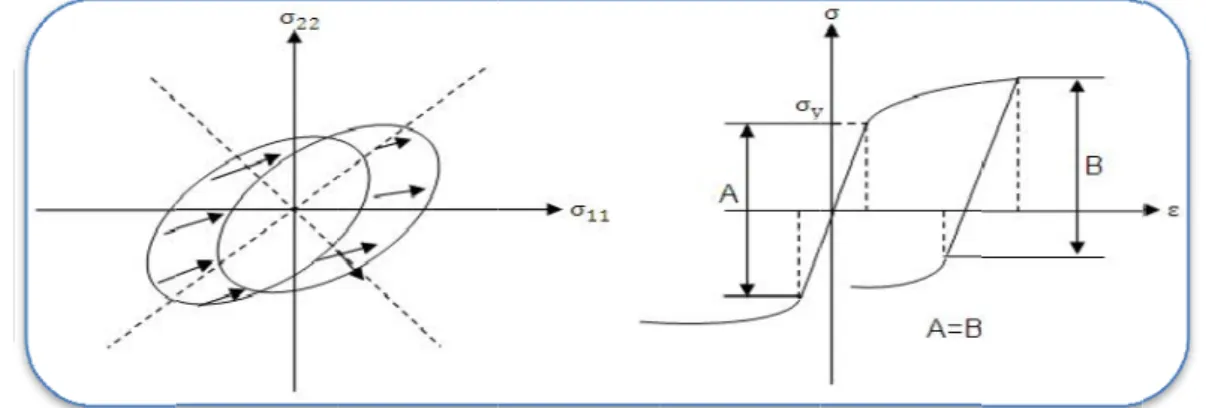
s efforts ex partition su nte en un p onc une re ans la dire on sur la d eur contrai ente le vect 1 2 I J u u X X ∂ ∂ ∂ ∂ ⎛ = _⎜ + ⎝ eurs propre trice de tra bien différe mps vectorie que, dans tenseur de

ation sphériq

s possible érique S et cas du tens anger la fo ercés sur u urfacique d point matér Fig I.2 eprésentatio ection . On direction de inte tangen teur contra 1 2 J I I J u u X x ∂ ∂ ⎞ ⎛ = + ⎟ ⎜ ⎠ ⎝ es de ansformatio encier la no els de dép le cas de es déformat

que et état de

de décomp t tenseurs seur de dé orme alors une facette de forces. iel est sché 2 : État de co on par un v n peut alor e la normal ntielle (a inte projeté J I u x ∂ ∂ ⎞ + _⎟ ⎠ donne deu on M. L’élo otion de dé lacement q e petites p tions linéai

e déformation

poser un te déviatoriqu formation, que le te e d'un milie La représe ématisée s ontrainte en vecteur du rs définir la le du vec appelé ciss é dans le p ux élongati ongation d’ éplacement qui ne crée perturbation res défi

n déviatoriqu

enseur de ue D. Les f le tenseur nseur dév eu continu p entation la ur la figure un point ma type , a contrainte cteur contra sion ou co lan de la fa Mécanique ons princip épaisseur t de la notio nt aucune ns, l'état d ni par :

ue :

deuxième formules so sphérique iateur D c peuvent êtr plus fréqu e ci-dessou atériel. appelé e normale ainte , ontrainte de acette on a e des milieux pales dans est calculé on de défor déformatio e déforma ordre sou ont les sui associé ch hange la f re représen uente de l s. vecteur co comme . De mêm e cisaillem : x continus le plan ée avec rmation. on. Il est tion est

(I.6) s forme vantes : hange le forme à ntés par 'état de ontrainte étant la me on a ent) qui

(10)

(

)

(

)

(

)

,

.

,

n n n

T M n n

n T M n

n

σ

τ

σ

=

= ∧

∧ =

−

r

_{r r}

r

(I.7) I.4.

Equation d’équilibre

À partir des expressions des puissances virtuelles des efforts extérieurs et des efforts intérieurs, on obtient les équations de la statique :

g

(M t R, / ) div f M t( , )

ρ γr = → σ +ρ r (I.8) I.5.

Comportement élastique

Selon le dictionnaire du groupe français de rhéologie de 1988: L’élasticité exprime la « tendance d’un corps à reprendre la forme et les dimensions qu’il avait avant une sollicitation, lorsqu’on supprime cette sollicitation ». Un corps est idéalement élastique lorsqu’il évolue de manière totalement réversible (sans déformation permanente), et que toute transformation subie produit une dissipation nulle. Elle s’écrit par une relation inversible entre la contrainte et la déformation. Par exemple, lorsque cette relation est linéaire et isotrope, la loi de l’élasticité de Hooke (17ème_{siècle) est la plus simple (1.5):}

_E

T

)

E

(I.10)

Où : , , sont respectivement les composantes des tenseurs des contraintes, des déformations et de la tenseur unitaire. T ) Est la trace du tenseur des déformations. Enfin λ, sont les coefficients de Lamé.

E,

ν

sont le module d’Young et le coefficient de

Poisson.

I.6 . le comportement élasto-plastique

Le schéma élasto-plastique pour le comportement des matériaux, a été élaboré à partir de constatations expérimentales relatives au comportement tridimensionnel des métaux. Actuellement, on résout par voies analytiques ou numériques, des problèmes d’élastoplasticité en calcul des structures (structures réticulées, structures à barres fléchies), des plaques et coques métalliques, et l’on utilise aussi ce modèle pour l’analyse de structures en béton [01].

Le modèle de comportement élasto-plastique classique ne tient pas compte de tout effet de vieillissement et de viscosité du matériau. Du point de vue des formules mathématiques par lesquelles on représente le comportement plastique, cela implique :

1. en conséquence de l’absence de vieillissement, l’invariance par translation sur la variable temps ;

2. en conséquence de l’absence de viscosité, la réponse (déformation) du matériau à la variation élémentaire de sollicitation (contrainte) effectuée à un instant donné, se produit en totalité simultanément à cette variation et est indépendante de la vitesse avec laquelle celle-ci est effectuée.

(11)

Chapitre Le mod suivant 1. le é e 2. la m

I.6. 1. L

On con compor I dèle de co s: es domaine évidence d exemple) et a règle d’ multiaxiales

L’expérience

Fig I nstate, l'ex rtement du mportemen es d’élastic ans les ex t qui sont é ’écoulemen s, la façon d

de traction s

.3 : Expérien xistence d matériau d nt élasto-pl cité, qui gé xpériences étroitement nt plastiqu dont évolue

simple ; limit

nce de tracti (vitesse d 'un seuil devient irré Fig I.4 : lastique s'a énéralisent en sollici liés au phé ue qui déf e la déform

tes d’élasticit

on simple po de déformati pour la co versible Fig Limite d’élas appuie sur la notion d tations un énomène e finit, dans mation plast

té

our un matér ion fixée). ontrainte, g I.4. sticité . Mécanique les conce de limites d iaxiales (tr essentiel d’ le cas d tique. riau écrouiss soit σ , à

e des milieux epts fondam d’élasticité, raction sim écrouissag des sollic sable à partir du x continus mentaux , mis en mple par ge ; citations uquel le

(12)

On cha décharg Après représe plastiqu On pro celle-ci décrit lo Quand monoto Ainsi lo ( ) ap de cont représe forme arge l'épro ge. La déc décharge entée par ( ue ( ). cède alors s'effectue ors de la d la contrain one. ors de la no paraît com trainte et d entation du d’un diagr ouvette au charge suit totale, il (OC) sur la Fig I.5 : C à une nou en suivant décharge; te (σ) dépa Fig ouvelle cha mme le nouv e la déform u modèle d ramme rel u-delà du sur le diag subsiste a Fig I.5: c Charge et dé uvelle char t le trajet ( le comport asse ( ), l g I.6: Courbe rge effectu veau seuil mation dans de compor iant la co point (A) gramme le une défo cette défor écharge "ma rge: tant qu CB), identi tement dem e point rep e de chargem uée à partir en traction s la partie rtement co ontrainte σ jusqu'en chemin (B ormation p rmation per atériau écrou ue la contr que, au se meure réve présentatif s ment monoto r du point (C n. En suppo utile de l’é rrespondan σ à la déf (B), puis, BC) et non permanente rmanente e uissable". rainte reste ens de parc ersible tout suit la cour one. C), La vale osant l’hom prouvette, nt pour le formation on effect le chemin e de l'épr est la défo e inférieure cours près, t au long d rbe de char eur de la co mogénéité d la Fig I.6 d matériau ε selon l’ tue une n (BAO). rouvette ormation e à ( ), , à celui de (CB). rgement ontrainte de l’état donne la sous la ’axe de

(13)

Chapitre l’éprouv plasticit de plas déforma

Remarq

Pour ce irrévers en part Le mod viscopla alors sc Le phén de ( ), cas « m une fon Ce phé plastiqu traction présent tel com illimité Ainsi, p valeur ( I vette. Sur té. Après c sticité est é ation perm

que

ertains ma sible, c'est-iculier, pou dèle de co asticité et d chématisé nomène ob , correspon matériau à nction crois énomène, ue. Ainsi la n simple ef te un palier portement et l’on dit q pour le mod (σ ) et, lors ce diagram charge jusq égale à : anente apr tériaux, le -à-dire inéla ur l'aluminiu Fig I.7 : Ex d’alumin omporteme de vieillisse par la cour bservé à la nd au cas d écrouissag sante de ( quoique le Fig I.8 rep ffectuée su r pour des est modéli que le mat dèle élastiq squ’elle atte mme, σ e qu’au nivea ce résulta rès décharg diagramm astique, de um comme xpérience en nium : Influen ent élasto-p ement : le rbe unique

Fig I.6, où du matériau ge positif » ). e plus rép présente le ur une épr déformatio isé selon le tériau corre que-parfaite eint cette v est la limite au , la lim at est parfo ge est la dé e contraint e la vitesse montrée s traction sim nce de la vit plastique c comportem de la Fig I. ù la limite a u dit écroui » pour tradu pandu, n’es diagramm rouvette d’ ons allant d e diagramm espondant ement plas valeur il y a e initiale d mite actuel ois appelé « éformation te-déforma e de déform ur la Fig I.7

mple sur une esse de défo classique l ment du ma 6. actuelle d’é ssable; on uire le fait st pas gén e relevé da ’acier doux e 10 à 10 me de la Fig est élastiq tique, la co possibilité Mécanique d’élasticité lle d’élastic « Principe plastique ation, dépe mation ε ad 7. éprouvette ormation. aisse de c atériau en t lasticité ( précise m que le seu néral pour ans le cas x : on con 0 (ordres g I.9 avec ue et parfa ontrainte ne d’allongem e des milieux ou seuil in cité ou seu de Coulom . nd, dans l optée; c'es côté tout e traction sim ) est une ême dans uil de plast le compo de l’expérie nstate que s de grande un palier p aitement pl e peut dép ment illimité x continus nitial de il actuel mb ». La a partie st le cas effet de mple est fonction certains icité est ortement ence de celui-ci eur). Un plastique astique. asser la é.

(14)

Fig . On revi Après la On con trouve l’écroui traction compre segmen compre après é Pour l’a déforma décharg compre (algébr compre phénom g I.8 : Expéri . ient à la F a décharge Fig I state alors ramenée à ssage en n, s’accomp ession. Ce nt [-σ ,σ ] ession simp écrouissage acier doux, ation plast ge de la ession est iquement) ession, la c mène n’est ence de trac un matéria ig I.6 de la e suivant (B I.10 : Expérie s que la lim à la valeur traction qu pagne d’un phénomèn définit le ple tandis q e en tractio , si l’on eff ique sous traction e égalemen et que, s contrainte t pas pris ction simple au a courbe d BC) on soll ence de trac ite d’élastic r (σ ), sup ui correspo ne diminutio ne est con e domaine que le segm on simple ju fectue une contrainte et charge t ramenée si l’on pou rejoint rap en comp pour . de charge-d icite la mêm ction-compre cité en com périeure (a ond à un on (en vale nnu sous e initial d ment [-σB,σ usqu’à la va première constante en compr e à une va ursuit la c pidement u te dans la Fig I.9 : Re élastique décharge d me éprouve ession: effet mpression, lgébriquem relèvement eur absolue le nom d’ d’élasticité σB] définit l aleurσB. charge en égale à σ ression, q aleurσ_B, lé harge ave un palier à a modélisa eprésentatio e parfaiteme d'un matéri ette en com de Bauschin initialemen ment) à (-σ t de la lim e) de la lim effet Baus du maté le domaine traction ju on const ue la limi égèrement ec déforma la valeur ation du m n schématiq ent plastique au "écroui mpression F nger. nt égale à ( σ ). Autrem mite d’élast mite d’élast schinger [ ériau en t e actuel d’é usqu’à obte ate ensuite ite d’élasti supérieure ation plasti -σ , Fig I matériau é que. e. ssable". Fig I.10 (-σ ), se ment dit, ticité en ticité en [02]. Le traction-élasticité enir une e, après icité en e à -σ ique en .10. Ce lastique

(15)

Chapitre parfaite compre

1.7. Cas

1.7. 1. M

Au cou d’élasti comme plus à d Si l’on l’atteind suffit à compor En se r indé bien ide que l’o matéria les circ I ement plas ession sont

d'une sollici

Matériau écro

urs de l’hi cité initiale e en élastic définir σ et connaît à dre à partir à détermin rtement est reportant au pendante d entifiées, o n connait au et donc onstances stique qui des consta Fig I.11 : Ex

itation uniax

ouissable

stoire de e, l’apparit cité, corresp vice-versa la fois la de l’état in ner la var t alors dite u diagramm de la vitess on voit plus σ et ε qui la position suivantes: F pose que antes Fig I xpérience de

xiale

chargeme tion des d pondance a. contrainte nitial nature riation corr de type inc me de la Fi se de char s préciséme suffit, ave de σ par Fig I.12 : la li les valeur .11 e traction-co nt du mat déformation biunivoque actuelle σ el, alors la d respondant crémental. g I.7 où la rge et le ent que dε ec ε, à dét rapport à l imite d’élast s limites d ompression: tériau, dès ns perman e entre σ et σ et tout le donnée d’u te de la a courbe de es droites d

ε est déterm

terminer l’é a limite d’é icité actuelle Mécanique d’élasticité acier doux. s que l'on nentes fait t ε : la don e trajet de une variatio déformatio e première de décharg minée en f état d’écro élasticité a e. e des milieux en tractio n franchi l qu’il n’y nnée de σ n charge su on de contra on dε. La charge est ge élastique onction de uissage ac ctuelle. On x continus n et en a limite a plus, ne suffit uivi pour ainte dσ loi de t unique e toutes dσ dès ctuel du n a ainsi

(16)

1. Si σ réve 2. Si σ déc (c'e défo 3. S c q

d

σ est inférie ersible, don σ est éga harge: la st-à-dire q ormation à e

d

ε

=

ε

Si σ est é charge: la partie réve que l'on ré irréversible e

d

ε

=

ε

+

eure à la lim nc puremen le à la lim variation qu'une déc sa valeur a Si

d

σ

égale à la variation ersible et d' écupère en e est le com p

d

ε

+

mite d’élast nt élastique Fig I.13 : la mite d'élas de déform charge (–d antérieure)

0 <

Fig I.14 : se limite d'éla de déform 'une partie effectuant mplément p Si

d

σ

icité actuel e : dε = dε a variation d ticité actue mation est dσ) effectu , alors:

euil d'élastic asticité act ation est d irréversibl t, après la pour obtenir

0 >

le: la varia ∀ le signe e la charge elle et dσ réversible uée après

cité actuelle. uelle et dσ décomposé e. La parti charge dσ r la variatio

tion de déf e de dσ. < 0, corr e, donc pu s la charg

σ 0, cor ée, comme e réversibl σ, la décha on de défor

formation e respondant urement é ge dσ ram

rrespondan e la somm e est la pa arge -dσ. L rmation tota

est alors t à une lastique mène la

(I.11)

nt à une e d'une artie d a partie ale:

(I.12)

(17)

Chapitre Le mod E= Dans le tangent E_t Le mod Μ D'où: = 1 Et Le mo corresp au cas alors né

1.7.2. M

Pour le uniaxia I dule d'élast e d d ε σ =

e cas où le t" par la rel

ε

σ

d d = dule d'écrou p d d

ε

σ

= Μ Μ + =1 1 E

dule d’écr pondant au où la cour égatifs [03]

Matériau parfa

e matériau le se prése Fig icité E est d

point de ch ation:

0 >

σ

d

uissage du

d

σ

>

0

rouissage diagramm rbe de char ].

faitement pla

parfaitem entent com I.15 : la vari défini dans

harge est à

matériau é

M est po e de la Fig rge, après

astique

ent plastiq me indiqué iation de déf chaque ét

à la limite d

étant:

ositif pour g I.3 le mat avoir crû j que, les ré és sur la Fig formation tot at (ε, σ) pa

d'élasticité

le matér tériau à écr usqu’à un sultats de g I.16 Mécanique tale. ar:

actuelle on

iau écroui rouissage n maximum, l’expérien e des milieux

n définit le "

issable cla négatif corr décroît E ce en soll x continus

(I.13)

"module

(I.14)

(I.15)

(I.16)

assique, respond , M sont icitation

(18)

Si σ es élastiqu

d

ε

Si σ es variatio

d

ε

Si σ est entièrem

d

ε

La défin tangent

1.7.3. So

L’ex sollicita général tenseur compte évidenc tout tra entièrem réversib rapport tracé s l’interse st inférieure ue e

d

ε

=

t égale à la on de déform e

d

ε

=

_si t égale à la ment irréve

0 ≥

=

_d

_ε

p

ε

nition du m t comme le

ollicitation m

xpérience m ations que

le, une sol r des contra e des symé ce l’existen ajet de ch ment à l’in bles). Ce d à la sollic ur l’axe de ection du Fig e à la limi

∀

d

σ

a limite d’é mation est

d

σ

<

0

a limité d’él ersible

module d’él e module d’

multiaxiale en

monoaxiale peut subir llicitation q aintes σ (te étries nce d’un do harge de ntérieur de domaine no itation unia es σ à la domaine d g I.16 : Matér te d’élastic

élasticité σ purement

asticité σ

asticité est écrouissag

n domaines d

e évoquée un élémen quelconque enseur de C , i, j 1, omaine d’é l’élément ce domain oté C est a axiale, il ap Fig I.17. O d’élasticité riau parfaitem cité σ : la

σ et si dσ < élastique

et si dσ =

t évidemme ge sont éga

d’élasticité

ci-dessus nt de milie e de l’élém Cauchy), é , 2, 3 . Par élasticité in de matièr ne, les déf ainsi défini pparaît com On peut dir initial ave ment plastiq variation d

< 0, corres

0 : la varia

ent inchang aux à zéro. ne représe u continu t ent de ma élément de les résulta itial conten re, partant formations dans l’esp mme l’homo re aussi qu ec la droite que. de déforma

spondant à

ation de déf

gée. En rev ente qu’un tridimensio atière est c l’espace ats expérim nant l’origin t de l’état sont élast pace R de ologue du s ue le segm e « sollicit ation est pu

une décha

formation e

vanche, le cas particu onnel. D’un caractérisée (ou en mentaux on ne, et tel q t naturel e tiques (c’es es tenseurs segment

[

ment [− , tation en t urement

(I.17)

arge : la

(I.18)

est alors

(I.19)

module ulier des ne façon e par le n tenant met en ue pour et situé st-à-dire s σ. Par

σ , ]

] est

(19)

traction-Chapitre compre réalisée 1970), contrain de l’aut défini d I ession ». D e dans l’ex où les se nte normale tre Fig I.17 dans l’espa -dire le plan Fi et to De même, d xpérience eules comp e σ et la 7, on obtien ace 6_avec n d’équatio ig I.17 : Epro orsion d’un t déter dans le cas de traction posantes n contrainte nt un doma c le sous-e ons = ouvette pour tube mince miné expérim s d’une so n-compress non nulles de cisaillem aine d’élas espace cor = = r l’expérience ; exemple d mentalemen llicitation p sion et tor s du tense ment σ va sticité qui e rrespondan = 0. e de traction de domaine i t (H. D. Bui, Mécanique plus comple rsion de tu eur des co ariant indé est l’interse nt à la soll n-compressio nitial d’élast 1970). e des milieux exe telle q ubes mince ontraintes pendamme ection du d icitation ap on ticité x continus ue celle es (Bui, sont la ent l’une domaine ppliquée

(20)

CHAPITRE II

MODELES ANALYTIQUES D’ETUDE

DU COMPORTEMENT ELASTO-

PLASTIQUE

(21)

Chapitre II Modélisation du comportement élasto-plastique

Introduction

La construction des modèles de comportement non linéaire des matériaux comporte deux volets : l’étude des propriétés rhéologiques et la définition de la forme des équations pour un chargement tridimensionnel. La rhéologie, étude des écoulements, permet de relier les contraintes, les déformations, et leurs dérivées, et caractérise la nature des comportements. On va voir dans ce chapitre que les comportements les plus complexes se bâtissent à partir de briques élémentaires.

a. Le ressort, qui symbolise l’élasticité linéaire parfaite, pour laquelle la déformation est

entièrement réversible lors d’une décharge, et où il existe une relation biunivoque entre les paramètres de charge et de déformation Fig II.1.a.

b. L’amortisseur, qui schématise la viscosité, linéaire Fig II.1.b ou non linéaire Fig II.1.c. La viscosité est dite pure s’il existe une relation biunivoque entre la charge et la vitesse de chargement. Si cette relation est linéaire, le modèle correspond à la loi de Newton.

c.

Patin représenté la plasticité Fig II.1.d.

Ces éléments peuvent être combinés entre eux pour former des modèles rhéologiques.

a) σ=

E ε

b)

σ=

η

_{c) =}

_η

_σ

d)-σ

_y

σ

_y

Fig II.1 : Les « briques de base » pour la représentation des comportements. II.1.

Les critères de plasticité

Lorsqu’un solide est soumis à un champ de contraintes σ, celui-ci se déforme avec un champ de déformation ε. Ce dernier peut être décomposé en la somme de deux déformations :

ε ε

_e

ε

_p

(II.1)

Avec

:

est la déformation élastique, proportionnelle à σ selon la loi de Hooke:

ε = K σ

(II. 2)

:

est la déformation plastique. Celle-ci n’apparaît que lorsque le champ σ dépasse un certain état de contrainte. La variation de cette « limite élastique », fonction de , définit l’écrouissage. Comme nous venons de le voir, le solide rentre en plasticité pour un certain champ de contrainte. Plusieurs critères ont été mis en place pour caractériser cette limite. Ils se présentent en général comme une relation de la forme :

f(σ) < 0 avec : f(σ) =

σ

eq

-

(II. 3)

Où , est la contrainte équivalente, est la limite élastique. La « zone limite de contrainte » pour laquelle cette relation est respectée s’appelle la surface de charge. Le modèle « plan orthotrope » possède quelques points remarquables qui peuvent être déterminés en trouvant la

(22)

limite élas dans les d - les points - les points - les points Différentes II.1.1.

Critèr

La forme l égale :

= ∑

II.1.1.

Fronti

la sur révolution indépenda génératric Chemin de Déformatio Début de stique de d directions d s de cisaill s de tractio s de tractio s lois ont é

re de von mis

a plus simp

∑

_,

∑

tière d’écoule

rface d’éc de géné ante de ces parallèl e chargement. on élastique. la déformation Fig divers essa e contraint ement pur on biaxiale ons larges. Fig II.2 été élaborée

ses

ple pour le

∑

ement

oulement ératrice pa la pr es à l’axe plastique. II.3 : schéma ais. On peu te principa ; ; : Points rem es pour déf critère de

est représ arallèle pl ression (1, 1,1). a représenta ut notamme ales : marquables d finir ce critè Von Mises

sentée da an (1,1,1), hydrostatiq ant la Frontiè ent noter de la surface ère. f ( ₂ ) = 0,

ns le rep , voir la que, la fro ère d’écoulem les deux p de charge.

tel que ₂ a

père princi Fig II.3 ontière d’é ment de Von oints de tr atteint une pal par u La plastif coulement n Mises. raction sim valeur (II un cylindre fication éta a donc d ple I.4) de ant des

(23)

Chapitre II II.1.2.

Critèr

La pla provoqué lorsque la matériau i premier, le Où et II.1.2.1.

Fron

La sur le critère d la surface droite un n’étant pri Von Mises intermédia

re de Tresca

asticité inte par les co cission ap isotrope, le e critère de

=

: sont r

ntière d’écou

rface d’éco de Von Mis Fig II e d’écoulem hexagone ivilégié, on s, le critère aire n’in Fig ervient par ntraintes d ppliquée da es plans su e plasticité

espectivem

ulement

oulement es ses comme I.4 : schéma ment est u régulier de retrouve l de Tresca ntervient pa II.5 : schém glissemen de cisaillem ans un plan ubissant le de Tresca

ment la con st un hexag le montre représentan n prisme d e côté 0 a symétrie a est défini as, car elle

a représenta nt des plan ment le long n atteindra e cisailleme s’écrit :

trainte de gone inscr la Fig II.4. nt la Frontièr de générat 2/3, inscri e d’ordre 3 à l’aide d’u n’influe pa ant le critère Modélis ns atomiqu g de ces p une valeur ent maxima

cisaillemen

rit dans l’el

re d’écoulem rices paral t dans le c autour de un seul par as sur la va e de Tresca e sation du com es les uns plans. La p r critique k al atteindro

nt et contra lipse précé ment plane de llèles à l’a cylindre de l’axe (1,1, amètre . leur du cis en trois dime mportement é s sur les a lasticité se k. Dans l’hy ont la valeu

ainte princip édemment e Tresca. xe (1,1,1) Von Mise 1). Comme La contrai aillement m ensions. élasto-plastiqu autres qui e déclenche ypothèse d ur critique

(II pale. obtenue po et de sect s. Aucun a e le critère nte princip maximal. ue est era ’un en I.5) our ion axe de ale

(24)

II.1.3.

Le crit

On pa un incrém maximal é de contrai celui dont contrainte Prenons [ L’expressi ∑ On peut d

d

Où

dλ : es II.2.

Hypoth

II.2.1.

Règle

La rè maximal dp(σ, , le cas où

itère de hill

art d’un éta ent de défo énonce que nte situés t le travail [σ ] admis σ*] = [σ] + ion du trava

∑ onc écrire

=

st un scalai

hèse de la thé

de normalit

ègle de n implique est dirigé ù σ est un t de déform ormation no e pour un in à l’intérieu est maxim ssible que + [dσ] un te ail étant δ

:

ire multiplic Fig

éorie de plast

té. « plasticit

ormalité c la convex suivant la n point rég mation plas ormal à la s ncrément d ur ou sur la mal. C’est à le tenseur enseur sur δW=∑

cateur. II.6 : L’incré est normal

ticité

ite associée »

concerne la xité du do a normale gulier de la stique [εp] e surface d’é de déforma a surface d’ à dire que réel [σ], le la surface le princip

ément de déf à la surface

»

a règle d’é omaine C(E extérieure a frontière et on appliq écoulement ation plastiq ’écoulemen si on asso e travail de d’écoulem pe de Hill s

formation pla d’écouleme écoulement E). Le ta e à C(E) a de C(E), o que des co t [dεp] Fig II que donné, nt, le cham ocie à [d ] e [σ*] sera ment ([σ*] n ’écrit :

astique ent. t. Le princ ux de u point de on a sur la f ntraintes [σ .6. Le princ , parmi tou mp de contr tout autre inférieur à ne peut être

cipe du trav déformatio e charge σ figure Fig I σ] provoqua cipe du trav s les cham rainte réel e tenseur d à celui de [ e en dehor

(II

vail plastiq on plastiq σ. Ainsi, da I.7: ant vail mps est des [σ]. rs). I.6) I.7) que que ans

(25)

Chapitre II • L'incrém puisqu'ils

• La surfa

• L'incrém et est don

=

On dit alor II.2.2.

Règle

La déf deux ques QUAND ? et de règle COMMENT ment de co sont perpe ace de plas ment de dé c parallèle

=

λ

rs que la lo

d’écoulemen

finition du stions suiva (y-a-t-il dé es d’écroui T ? (s’effect Fig ntrainte n ndiculaires stification φ éformation et proporti

oi d'écoulem

nt

comportem antes : éformation p ssage, obje tue la défor II.7 : Princip rè ne fournit a s Fig II.8. φ (σ_i)

est tou

plastique onnel à ∂φ

ment est as Fig II.8 : S ment plastiq plastique). et de la sec rmation pla pe du travail ègle de norm aucun trava ujours conv est perpe φ/∂σ, ce qui

ssociée (à l Surfaces de p que se com Ce sont le ction précé astique). C’ Modélis plastique ma malité.

ail sur l'incr

vexe. endiculaire i détermine

la surface d plastification mpose sc s notions d édente. est la règle sation du com aximal : rément de d e à la surfa e une loi d'é

de rupture) n. hématique de seuils, d e d’écoulem mportement é déformatio ce de plas écoulemen

). ment de l e domaine ment plastiq élasto-plastiqu n plastique tification φ t de la form

(II a réponse s, de critèr que. ue e (σi) me: I.8) e à res

(26)

Quand on même co déformatio En d’autre déformatio chemin pa s’occupe permettan élémentair II.2.2.1.

Solli

Il est l’histoire d comme en définir ε et tout le tr variation d On dit la fig II.9, les droite est déter l’état d’écr actuelle. O réalise un ntrainte co on peut cor es termes on suivi. Po as à pas, c plus de l t de relier res.

icitation uni

clair que de charge d n élasticité t vice-versa rajet de ch de contraint que la loi où la courb es de décha minée en rouissage a On a ainsi l n essai de orrespond rrespondre Fig II.9 : L l’état de c our connaît c’est à dire a partie é [σ], [d ] et [

iaxiale pour u

e, dès que du matéria , correspo a. En revan harge suivi te dσ suffit de compor be de prem arge élastiq fonction actuel du m es circonst traction in à plusieur à plusieurs a contrainte contrainte tre l’état de e regarder élastique q [d ]. La dé

un matériau

e la limite u, l’apparit ndance biu nche, si l’o i pour l’att à détermin rtement est mière charg que toutes de dσ dès matériau et tances suiv terrompu p rs déforma s contrainte dépend du c pour une e contrainte à chaque que l’on c formation t

u écrouissab

e d’élastic tion des dé univoque e on connait eindre à p ner la varia t de type in ge est uniq bien iden que l’on c t donc la po vantes, rep par plusieu ations et d es. chemin de la déformatio e ou de dé instant la onnaît). La totale étant

ble

cité initiale éformations entre σ et ε non seulem partir de l’é tion corres crémental. ue indépen ntifiées, o connait σ e osition de σ résentées rs décharg de la mêm a déformatio on donnée formation, variation d a loi d’éc t alors la so e a été f s permanen ε, la donné ment la co état initial, pondante d En se rep ndante de n voit plu t ε qui suff σ par rappo sur la Fig I ges, on con me manière on. dépend d il faudra d de [ε ] et d oulement omme des franchie, a ntes fait qu ée de σ ne ontrainte ac alors la d de la déform ortant au d la vitesse us précisém ffit avec σ, ort à la limi I.10. nstate qu’u e, une mê du chemin onc suivre de [σ], (on sera une déformatio au cours u’il n’y a pl e suffit plus ctuelle σ m donnée d’u mation dε. diagramme de charge ment que à détermin ite d’élastic une me de ce ne loi ons de us, s à ais une de e et dε ner cité

(27)

Chapitre II • Si σ est La variatio de dσ : • Si σ est la variation (−dσ) effec

dε =

• Si σ est variation d partie irrév après la c variation d

dε =

Le module E

= dσ

Dans les e un métal d charge est 1

₌

1 , E et M M est pos II.10, le m crû jusqu’à t inférieure on de défo

d

égale à la n de déform ctuée après

d si

égale à la de déforma versible, la charge dσ, de déforma

d +d

e d’élasticit

σ/d

expérience donné (deu t à la limite

+

1

sont des g itif pour l atériau à é à un maxim Fig II.10 : So à la limite rmation es

a limite d’él mation est s la déchar

dσ < 0.

limite d’éla ation est d a partie rév la décharg tion totale:

si ; dσ

té E est déf

s effectuée uxième pro e d’élasticité

grandeurs e matéria écrouissage mum, décro ollicitation u irréversi d’élasticité t alors réve

lasticité act t réversible rge dσ ramè

asticité ac décomposé ersible est ge (−dσ), la

σ > 0.

fini dans ch

es sur les m oposition du é actuelle o

ayant la d u écrouiss e négatif c oît et M uniaxiale pou ibilité du com é actuelle: ersible, do

tuelle et dσ e, donc pu ène la défo

tuelle et dσ ée, comme la partie é a partie irr

haque état

métaux il a u « princip on définit le

dimension able classi correspond sont alors Modélis ur le matéria mportement. nc pureme

σ est négat rement éla ormation à

σ est posit la somme élastique d réversible e

(σ, ε) par :

pparaît com e de Coulo e « module

d’une con ique, corre au cas où négatifs. sation du com u écrouissab . nt élastiqu

if, correspo astique (c’e sa valeur a

if, correspo e d’une pa que l’on est le com

mme indép omb ». Dan e tangent »

trainte. Le spondant a ù la courbe mportement é ble, e quel que

ondant à un est-à-dire q antérieure)

ondant à u artie révers récupère e plément po

pendant de ns le cas o par la rela

e module d au diagram de charge élasto-plastiqu e soit le sig

II.1 ne décharg qu’une char :

(II.1

une charge sible et d’u en effectua our obtenir

(II.1

σ et d po où le point tion :

(II.1 d’écrouissa mme de la e, après av ue gne 10 ge, rge 11) , la une ant, r la 12) 13) our de 14) age Fig voir

(28)

II.2.2.2.

Solli

Dans qu’au par représenta C(E) et à s Conna situations • Si σ paragraph • Si f • Si σ le compor du domain (II.5), il y a

f (σ,

E E

(σ,

Ainsi, de disting L’arc de tr formulatio par exem E

(σ,

il y a déch

icitation mul

le cas gén ragraphe p ant le tens sa frontière Fig II.11 aissant σ e suivantes. σ est inté he précéden (σ, E) < 0, a est à la fro tement de ne d’élastic a charge si E

) = 0

E

, ) =

lorsque σ guer la ch rajet de cha n précéden ple, critère E,

) = su

harge si:

ltiaxiale pou

néral de la précédent, seur σ dans e Fig II.11. : Comportem et l’état d’ rieur au d nte II.2.2.1. alors la var ontière du définir les cité est rég i :

,

_:

< 0

est à la fro harge et la arge neutre nte, le cas e de Tresca

up {y : σ | y

ur le materi

sollicitatio mais on s l’espace ment incréme ’écrouissag domaine d iation de dé domaine d notions de ulière, et e

0

ontière de décharge e e correspon où la front a, on écrira

y

E

∂

f

(σ,

iau ecrouiss

on multiaxia doit dés e , et on ental élasto-ge actuel s d’élasticité éformation d’élasticité e charge e en définissa

C(E), c’est et de défi nd à E (σ, E tière du do a: E

)}

sable

ale, le prob ormais rai doit se réfé -plastique éc symbolisé actuel c’e est purem actuel, il es t de décha ant celui-ci

t le signe d inir les ar E, ) = 0. L omaine d’é

blème se p isonner su érer au dom crouissable e par E on est-à-dire, ent élastiq st nécessa rge. En su par une fo

du scalaire rcs de traje es caractèr élasticité pr

pose de la ur le poin maine d’éla en décharge a l’une o avec les ue. aire pour po pposant qu onction de

E (σ, E, ) et de charg res, pour in résente des

même faç nt de char asticité act . u l’autre d notations ouvoir décr ue la frontiè charge se (II.1

(II.1 ) qui perm ge croissan nclure dans s singularit

(II.1 çon rge uel des du rire ère lon 15) 16) met nts. s la tés 17)

(29)

Chapitre II

f (σ,

E

(σ,

et l’on po sollicitatio • Si σ déformatio élastiques

dε =

• Si σ est est décom partie réve partie irré

dε = d

D’une faço de l’histoir trajet de c de déform charge σ e La déform à travers c

d (σ

E

) = 0

E

, ) =

oursuit la d n uniaxiale Fig II .12 est à la f on est pure s, la formule

d = Λ :

à la frontiè mposé com ersible est éversible es

d + d =

on générale re de σ. La harge crois mation plas et l’état d’é mation plast celle de l’hi

σ

, E

,

)= 0

,

_{: < 0}

description e. 2 : Comporte frontière du ement élas e (II.11).s’e

ère du dom mme la so la partie é st le comp

= Λ : + d

e on peut d a fonctionn ssants, qui tique e crouissage tique ét istoire de σ

si

E

(σ

0

du comp ement incrém u domaine tique Fig I xplicite sou

maine d’élas omme d’un élastique, r lément néc

d

dire que la nelle εp

ne r

définit aus engendré à e E, corresp tant une fon σ entre les i

σ,

E

,

) < 0

ortement é mental élasto e d’élasticit I.12. En dé us la formu

sticité actu ne partie récupérable cessaire po

déformatio retient, de ssi l’état d’é à l’instant pond à la d nctionnelle instants t e

Modélis

élasto-plas o-plastique é té actuel, ésignant pa le II.21:

el et s’il y a réversible e par déc our obtenir

on plastique l’histoire d écrouissage t par le ta dérivation d e de l’histoi et t +dt.

sation du com

tique, com écrouissable et s’il y a ar Λ le tens

a charge, l et d’une charge de ( le taux de

e à l’instan e σ, que la e actuel, re ux de cont e

ε

p par ra re de σ, ce

mportement é

mme dans e en charge. a décharge seur des co

e taux de partie irr (− ), soit : déformatio

nt t est une a séquence eprésenté p trainte , d pport à l’ins ette dérivat

élasto-plastiqu

(II.1

(II.2 le cas de e, le taux omplaisanc

(II.2 e déformat réversible.

:

dε = Λ:σ, n total, soi

(II.2

fonctionne e des arcs par E. Le ta dans l’état stant actue ion s’effect

(II.2

ue 18) 20)

la de ces 21) ion La La t: 22) elle de aux de el t. tue 23)

(30)

d (σ

, De plus, c l’échelle d de εp _sur résulte qu

α >

Enfin, la est différe

d (

II.2.3.

Evolu

L’évolu élémentair II.2.3.1.

L’éc

Ce mo manière u compressi Fig . II.2.3.2.

L’éc

Dans même tail dimension cours de la

σ

, E

,

) = 0

comme le du temps (f la même e dp (σ, E, )

> 0, d (σ

relation en ntiable, elle

(σ,

E

, ) = P

ution de la su

ution de la res.

crouissage iso

ode d’écrou uniforme, m ion simple, g II.13 : Ecrou

crouissage cin

le cas de l le. Seul so n une, l’éca a déformat

si

E

(σ

rappellent facteur d’é période s ) est posit

σ,

E

, α) = α

ntre d (σ, e se met so

P (σ,

E

) :

urface de cha

a surface

otrope

uissage est mais la for cela se tra uissage isot

nématique

’écrouissag on centre e art entre les

tion.

σ,

E,

) > 0

t les terme chelle pos subit le mê ivement ho

α d (σ,

E

,

E, σ) et σ,

s

ous la form

arge

de charge t une homo rme et le aduit par un opique dans ge cinémat est déplacé s limites éla

es « séque itif quelcon ême facteu omogène d

)

si

E (σ, E, ) me :

est très othétie de l centre res ne évolutio s le plan. tique, la su . Il y a une astique de

ence » et « nque) d’une ur d’échelle de degré u

) >

0,

est li

complexe. a surface d stent les m n symétriq Fig II.14 : E es urface de c e « translat traction et

« trajet de e histoire d e sans au un en σ, c’e

néaire lors

Toutefois, de charge, mêmes. Po ue des limi crouissage i ssai de tracti charge gard tion » de la de compre

charge », s de σ donn utre modif st-à-dire qu

sque la fonc

, il existe la surface our un test ites élastiq isotopique a ion-compres de la même a surface d ession reste

(II.2

si l’on mod née, l’histo fication. Il ue :

(II.2

ctionnelle ε

(II.2 des modè s’agrandit t de tractio ues. avec un ssion. e forme, et de charge. e le même 24) ifie oire en 25)

ε

p

26) les de on- t la En au

(31)

Chapitre II Fig II II.2.3.3.

L’éc

Comm Concrètem rayons au II.3.

Déducti

L'écro détermine dissipé pa

f (

,

L’incrémen

=

On peut é .15 : Ecrouis .

crouissage m

me son no ment, cela gmentent p

tion de la ma

uissage pe la positio ar l'incréme

,

E

) = 0

nt de défor

crire:

+

ssage ciném

mixte

om l’indiqu veut dire proportionn F

atrice élasto-p

eut être int n de la su nt de défor

rmation pla

0

atique dans ue, c’est que le cen nellement le

Fig II.17 : Ecr

plastique par

troduit, dan urface de rmation pla

stique: le plan à la fois ntre de la es uns par rouissage m

r la mécaniq

ns la loi de plastificatio astique:

Modélis Fig II.16 : E e un écrou surface de rapport au ixte dans le

que des milieu

e plastificat on à un ce

sation du com Ecrouissage essai de trac uissage iso e charge s x autres. plan.

ux continus

tion, par u ertain mom

mportement é cinématique ction simple. otrope et se déplace ne variable ment et au

élasto-plastiqu e pour un cinématiqu e, et que s e d'état E ssi, le trav

(II.2

(II.2 (II.2 ue ue. ses qui vail 27) 28) 29)

(32)

On pose:

q

ij

(II.30)

Nous savons déjà que:

=

.

)

(II.31)

: Matrice d'élasticité.

En combinant (II.27), (II.28) et (II.29) on peut calculer:

. .

. . .

(II.32)

En remplaçant λ dans (II.28) et (II.30):

. (II.33)

. _. . . _. _. (II.34)

DEP : est la matrice élasto-plastique.

Dans le cas de la loi de plastification de Von Mises qui peut s'écrire:

f

0

(II.35)

R = 2 2 : variable d'état,

: cohésion apparente

E E

E

)

(II.36)

qui implique :

=

(II.37)

Pour :

=

et

avec H =

.

(II.38)

E : est le module de Young,

: Le module d'écrouissage définit graphiquement sur la Fig II.18, on peut appeler

(33)

Chapitre II II.3.

Mesure

L’endo quantitativ choisie po contrainte découlent la modifica II.3. 1.

Métho

Repre précédent Ou : E : étant l être interp est connu D 1 σ/ soit : 1 Toute me petites. L’e très faible Pour toute 1. Uti l’en

e de l’endom

ommageme ve, comme our représe effective, sont esse ation des c

odes statique

nons la loi t, qui sera j 1 le module prété comm , toute mes E ε , et av 1

sure de m endommag de l’ordre es ces raiso lisation d ndommage Fig II.18 :

magement

ent n’est e celle de t nter le phé associé a entiellement aractéristiq

e

i d’élasticit ustifiée pa d’élasticité me le modu sure de raid vec

module d’él gement est de 0.5 à 5m ons nous p des éprou ment, un e Essai de tra pas direc toute gran énomène [0 au principe t liées au ques méca té endomm r: é du matér ule d’élastic deur élastiq

asticité im le plus so mm. réconisons uvettes à exemple est action uniax ctement deur physi 01]. Ayant c e d’équivale couplage d nique des m magée unid riau vièrge cité du mat que permet

mpose une uvent très s la procédu section t donné su Modélis iale, loi de P accessible ique, est li choisi une d ence en déformation matériaux e imensionne de tout en tériau endo t d’atteindre

bonne pré localisé, c ure suivant centrale r la Fig II.1 sation du com Prandtl-Reus e à la m iée à la d définition fo déformatio n-endomma engendrée elle, déjà é ndommage ommagé. S e l’endomm

écision sur e qui impo te : affaiblie 9 à droite. mportement é s. mesure. S définition d ondée sur on, les me agement, c par l’endo évoquée au ement, 1 Si le modul magement p

r des défo se une bas pour bi élasto-plastiqu on évolut de la varia le concept sures qui c'est-à-dire mmageme u paragrap (II.3 (II.4 pe le d’Young par: