Mouvement d'une corde vibrante en présence d'un obstacle rectiligne fixe. Il

HAL Id: hal-01527107

https://hal.archives-ouvertes.fr/hal-01527107

Submitted on 23 May 2017

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Distributed under a Creative Commons Attribution| 4.0 International License

Mouvement d’une corde vibrante en présence d’un

obstacle rectiligne fixe. Il

Henri Cabannes

To cite this version:

Henri Cabannes. Mouvement d’une corde vibrante en présence d’un obstacle rectiligne fixe. Il.

Comptes rendus de l’Académie des sciences. Série IIb, Mécanique, Elsevier, 1983, 296, pp.1367-1371.

�hal-01527107�

· VIBRATIONS. - Mouvement d'une corde vibrante en présence cfun obstacle rectiligne fixe. Il. Note(*) de Henri Cabannes, Correspondant de l'Académie.

Une corde vibrante fixée à ses deux extrémités oscille dans un plan en présence d'un obstacle parallèle à la position

d'équilibre-de la corde. La corde étant initialement au repos dans une position quelconque, on démontre que, si

l'obstacle est suffisamment proche de la position d'équilibre de la corde, Je mouvement est une fonction

presque-périodique du temps.

VIBRATIONS. - Motion of a String Vibrating Against a Straight Fixed Obstacle.

ri.

A vibrati11g strlng·fixed at both eiUis moves in a plane in the presence of a straigltt fixed obstacle pa~·allel to the equilibrium position of the string. The string being inilially at rest with an arbitrary shape, we prove that,

if

the obstacle is near enough to the equilüJrùun position of the string, the motion is an almost-periodicfunction of the ti1ne. 1. PosmoN ou PROliL~ME. - Dans un plan rap.Porté à un repère orthonormé 0 xu, on considère les petits mouvements d'une corde vibrante fixée à ses deux extrémités

(x=

±

1 /~, u=O). La corde oscille en présence d'un obstacle rectiligne fixe d'équation u

= -

H(H~O) sur lequel elle rebondit suivant une loi qui assure la conservation de l'énergie. La fonction u(x, t)

qui représente, à l'instant t, la position du point d'abscisse x ~atisfait les conditions suivantes : (1) (2) (3) (4) ô2 _{u ô}2_u 7fj'ï - ôx2

=

0 si u(x,t)>-I-I,

au

au

Ft(x, t+O) = -Ft(x, t- 0) si u(x, t)= -H, ( 1 ) . u

+-

_{- 2'} t

=0

i

u(x, O)~«(x)<lO pour

ôu ôt(x, O)=p(x) pour pour t;;;;O,

lxi~~.

~( ±~)=o,

1 lxl~2'

~(

±4)=0

.

.

Dans la suite nous supposerons toujours que la cÇ>rde est initialement au repos dans une position quelconque, donc ~(x)=O. Dans l'intervalle -1/2~x~1/2. la fonction~(x) possède n maximums relatifs M; atteints potJI:

x=a; (

-~-~a

1

<

a;2

< ...

<a,.<~)

et n- 1 minimums relatifs rn; atteints pour

x=b,

(a;<b;<ai+l).

li est connu [3] que, si Ü(x, t) désigne une soiution(avec ~

=0)

du problème (1)-(4), il en est de même de la fonction : (5) . avec:

(6)

u(x~·t)=Ü(X., T), { 2X=F(x+ t)+F(x- t), 2T=F(x+ t)- F(x-t),

la fonction F(y), non décroissante, satisfaisant les conditions suivantes :

(7) F(y+1)=1-F(~y), F(y+2)=2+F(y).

Les instants initiaux t =0, T=O se correspondent, mais naturellement les conditions initiales pour les fonctions u(x, t) et Ü(X, T) ne sont pas les mêmes; on a :

(8)

l

u(x, O)=Ü{F(x),û},

au

, aü

Ft(x, 0) = F (x) ôt ( F(x), 0}.

Les deux dérivées (ôu/ôt)(x, 0) et (ôÜ/ôf)(X, 0) sont nulles en même temps et les fonctions u(x,

0)

et u(X,

0)

possèdent dans les. . intervalles

-1

/2

. ~x~

1/2, -

. 1/2 . ~X~

1

/

2

. les mêmes maximumsM1 et les mêmes minimums m1• La fonctionu(x, O)=œ(x)· étant

donnée satisfaisant

la

première des relations (4), il est toujours possible de choisir la fonction F de façon que la fonction

ïi(X,

0) soit affine par morceaux, les différents morceaux ayant pour pente ±k(Jç>O). Il suffit de choisir pour Fla fonction défmie dans l'intervalle

-1/2 ~y~

1/2

par les relatio.ns :

(9) . F(y)~ - -1 +~ l

f

'

1 -ôu (x, y) 1 dx, 2 le -(1/2) ôx avec : (10) _k=

_f

l/2

l

ÔU

1

{

n n- 1 }

8

cx, 0) dx=2

LM;-

L

m1 .• - (1/2) x . Ï"'l 1=1

Cette remarque permet de ramener 1 'étude du cas générl!l( avec ~ = 0 naturellement) au cas où

le graphe de la foncti?nœ(x) est une ligne polygonale(&) dont les segments ont pour pente

±k.

Nous désignerons par ii(x) la fonctionœ(x) correspondante.

2. ÛBSTACLE SUR lA POSITION D'ÉQUILIBRE : H = Û.

THÉORÈME.l. - .Si la corde est initialement au repos dans une position quelconque, le

mouvement en présence d'un obstacle rectiligne placé sur la position d'équilibre est un mouvement périodique dont la période a la même valeur que dans l'oscillation libre.

L'oscillation libre défmie par les équations (1), (3) et(4) ayant pour période 2, nous devons démontrer que le mouvement défmi par les équations(1)-(4), avec H=O et ~=0, possède aussi la période 2; Il résulte des relations (5), (6) et (7) que, si la fonction ii(X, T) est une fonction périodique du temps T dont la période est un nombre entier pair, la fonction u(x, t)

est une fonction périodique du temps t de même période. Il suffit donc, ce que nous allons faire, de démontrer le théorème 1 pour a.{x)=n(x).

Au début du mouvement, avant tout contact, le mouvement de la corde est l'oscillation

libre Ü(x, t) = w(x, t) :

(11) w -( x, t )-- ii(x+ t)+2 ii(x- t)

et, dans le plan

x

-

t, on a, suivant les régions,

w(x,

t)= ±kx+Cte ou ±kt+Cte. Les lignes w(x, t)=O sont formées de segments parallèles à l'axe des temps ou

à

l'axe des abscisses, et la solution u(x, t) = w(x, t) est valable jusqu'à la première ligne d'influence (L. Amerio et G. Pro use [1]) formée ici de segments t

=

Cte et de caractéristiques issues de certains points anguleux de la ligne

w=O

:

fl~re

1.

A partir de la ligne

w=O

on peut construire (cf. fig. 1) un régionnement du plan

x-

t (plus exactement de la bande 1

x

1 ~ 1/2,

t~O) qui comprend des rectangles(~) dont les côtés sont des caractéristiques et dont un sommet est le point

x

=

- 1/2, t= 1/2+b₁ (ou le point x= 1/2, t = 1/2 -b1), les trois autres

sommets étant situés sur la ligne

w

=

0; ce régionnement comprend aussi des régions(~ ₁₎ et 2

(91!2 ) adjacentes à l'lm des axes x=± 1/2, limitées par des côtés des rectangles(9l!) et par des

segments t

=

1/2 ±ai suivant que ces régions sont adjacentes à

1

'axe x== -1 /2 ou à l'axe

x=l/2. . Les régions (!H1) sont .celles qui touchent l'axe x=-e/2 (E=±l) . pour

-1/2+sb₁~t~l/2+eai+l; les régions(9!!₂₎ sont les autres.

Il est possible d'exprimer la fonction ïi(x, t) qui représente le mouvement de la corde en présence de l'obstacle u=H=O, à l'aide de la fonction w(x, t) et de la fonction associée: (12) -

_{v x,}

( _t )_ëi(x+t)_- -₂ <i(x-t)_-( _{. - w t}

₊

_2'

1 l)

_x

_-

₂

_.

. . .

Dans les rectangles(Bl) ayant un sommet surl'axe x= -(1/2), on a Ü(x, t)=v(x, t)-v3 ,

v

₈

étant la valeur de ven 1 'un quelconque des sommets; dans les r~tangles(~) ayant un sommet sur l'axe x=l/2, on a u=vs- v. On a en fait ïis=m₁ pour les rectangles touchant l'axe

x

=

-e/2 au point t= l/2+eb1• Dans les régions(~

1

), on a ïi=w, et dans les régions(~

2

),

ü

=-w. Avec les expressions précédentes de la fonction ïi(x, t), on satisfait toutes les

·conditions du problème ( 1) :équation (1), conditions de réflexion sur l'obstacle, positivité de

ïi(x, t). En particulier on obtient :

(13)

·

1

ïi(x~

~)=

-w(x, !)=w(-x,

O~=ii(

-

x,

O),

· ôu

ôw

ôw

·

-8

t (x, 1)=- -

8

t (x, 1)=- -

8

t (x, 0)=0., ce qui démontre le théorème 1.

~-~.s---~0---~.s~ x

Fig. L - Régions dans le plan x-1.

Fig .. l. - Regions in the x-t plane.

3. EXTENSION DES RÉSULTATS : H;fü.

THÉORÈME 2. - La solution du problème (1)-(4) correspondant aux conditions initiales

œ(x) =<i(x), B(x)

=

0, lorsque la distance H de l'obstacle à la position d'équilibre de la corde est

suffisamment petite, est une fonction périodique du temps dont la période Test donnée par la

formule (14) : 2H (14) T

=

2

+-,.----

--

,.

-::-

₁ -LM;-

L

m1 i=! i=l 3

Avec les conditions initiales œ(x)=ii(x), ~(x)=O, la fonction u(x. t) qui représente le mouvement de la corde en présence de

1

'obstacle u = H (H

<

M,

= sup M 1) peut être construite de proche en proche et vérifJe, comme l'oscillation libre w(x, t), l'es relations suivantes :

(15) ôÜ ôü - 0

ôx

.

ôt- '

(ôÜ)

2

(ÔÜ)

2 12

-

+

--

=tC

ôx

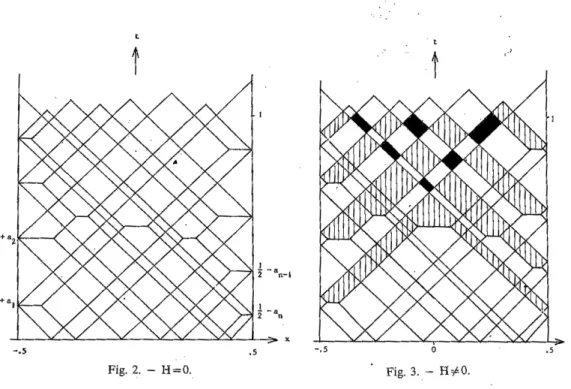
Ôt .

A partir des-caractéristiques issues des points x=.a; ou -,.=b .• , t=O et des caractéristiques réfléchies soit sur les droites x=± 1/2, soit sur les segments( <a}, t=-Cte, qui correspondent au contact de la corde avec l'obstacle, on peut construire un régionnement de la bande lxl~l/2, t~O: fi,gure 2 pour H=O, frgure 3 .. p,our R;o:O. Si H est sufftsamment petit

(2H/k~inf(M₁-m

₁

,

m

1

-

m

₁)), à tout contact, pour H=O correspond un contact pour H#O,

et on passe du régionnement p.our H=O à celui pour H?';O en faisant subir à tous les segments_(~) (plus exactement aux droites qui' \c;:s contiennent) la translation !!ï(x=O,

t = H/ k) et à toutes les caractéristiques issues de ces segments la translation 2 f!ï. Comme conséquence des formules (13) le régionnement de la flgure 2 est symétrique par rapport au point A (x= 0, t = 1 /2), donc celui de la f1gure 3 est symétrlquy par rapport au point

(x=O, t=1!2+H!k). ·. :.

t

_t

l -· 2 n-1 l 2 -· n - . ) .5 -.5 0

Fig. 2. - H =0._ Fig. 3. - H~O.

Si on désigne par _Ü0 l'expression de la fonction Ü(x, t) dans une région de la figure' 2, et par

ÜH l'expression de la fonction Ü(x, t) dans ta région correspondante de la f1gure 3, on a :

UH=u0+2H dans les régions sombres,

uH = _{u 0} - 2 H dans les régions hachurées,

uH = _{u 0} dans les régions claires. 4

Il faut ajouter U=k( -1/2

±x)

dans les petites régions triangulaires qui ont un côté sur les

axes

x=

±1/2. Avec ces expressions de la fonction

u(x,

t) on satisfait en effet toutes les

conditions du problème pour H c;6 0 et, à l'instant t

=

t1

=

1

+

2 H/k, on a :

(16)

l

ii(x,

t₁

)=ii(

-x, 0),

aii

aii

al(x,

t,)=

at(x,

0)=0,

ce qui démontre le théorème 2.

A partir de ce théorème, de la transformation (5)-(6) et des propriétés de la fonction F(y),

on démontre alors, en raisonnant com1ne pour le cas d'une position initiale unimodale

([2], [3], [4]), le résultat annoncé :

THÉORÈME 3. - Une corde vibrante fixée à ses deux extrémités oscille dans un plan en

présence d:un obstacle rectiligne parallèle, à /a distance H, à la position d'équilibre de la corde. La corde étant initialement au repos dans une position arbitraire, si H est suffisamment petit, le

mouvement est une fonction presque-périodique du temps.

Dans le cas où la période T défmie par la formule (14) est un nombre rationnel p

1

q(p et q

entiers premiers entre eux), le 1nouvement est même périodique avec la période psi pest Pair,

2 p si p est impair.

(Ï) Une démonstration détaillée de ces résultats sera donnée dans une publication ultérieure.

(*) Remise le 2 mai 1983.

[1] L. ÀMERIO ct G. PROUSE, Rendiconti di Matematica, 8, 1975, p. 563-581.

(2] H. CABANNES et A. HARAUX, Comptes rendus, 291, série A, 1980, p. 563.

[3] H. CADAt:!NES et A. HARAUX, Int. J. Non-linear Mechantes, 16, 1981, p. 449-458.

[4] A. HARAUX ct H. CABANNES, J. Non-linear Analysis, 7, 1983, p. 129-141.

Laboratoire de Mécanique théorique, assocM au C.N.]J..S., Université Pierre-et-Marie-Curie, 4, piace Jussieu, 75005 Paris.