*Corresponding author: Dieter Schwarzenbach, Ecole Polytechnique Fédérale de Lausanne, IPSB–Cristallographie, Le Cubotron (BSP), CH-1015 Lausanne, Switzerland, E-mail: dieter.schwarzenbach@epfl.ch
Dieter Schwarzenbach*
La coupe du roi and other methods to halve
objects
DOI 10.1515/zkri-2015-1863
Received May 26, 2015; accepted August 12, 2015; published online October 31, 2015
Abstract: The symmetry theory of halving objects into two
identical fragments is developed and illustrated by exam-ples. La coupe du roi is a fascinating way to slice an apple into chiral fragments with the same handedness. It may be applied to any object with point group symmetry 2 or 222 and their supergroups, e.g. to cones, cylinders or spheres. Variants of coupes du roi are presented and applied to a cube. An object is divided into halves by a number of cuts. The important cuts extend to the centre of the object, and these must form a single closed loop. The symmetry of the division into two fragments is given by the point group of the decorated object, i.e. the object including all the cuts. Point groups comprising only rotations result in chiral frag-ments with the same handedness. Such divisions may illus-trate the reaction path for changing the sense of chirality of molecules via a dimeric achiral transition state rather than by deformation. Non-trivial divisions of objects into achi-ral fragments or into racemic chiachi-ral fragments are obtained with point groups, again of the decorated object, compris-ing roto-inversions X̅, exceptcompris-ing X = 4n + 2. All other point groups either do not lead to half-objects, or they result in a trivial single planar cut parallel to a mirror plane.
Keywords: chirality; identical half-objects; symmetry of
fragmentation.
In memoriam Hans Wondratschek
Introduction
La coupe du roi, the royal division, is a peculiar way to slice
an apple into two identical halves. It got its name from being a party trick much loved by the French aristocracy
(Figure 1). To describe it in crystallographic language, we define an orthonormal coordinate system with c through the apple's core and the peduncle. The apple is supposed to possess conical symmetry ∞m, the origin of the coordi-nate system being chosen on the rotation axis. The follow-ing cuts are applied: (1) parallel to the plane (100) from above (i.e. the peduncle) down to the origin; (2) paral-lel to the plane (010) from below to the origin; (3) in the plane (001) through two non-adjacent sectors of 90° again reaching the origin. At first sight maybe surprisingly, the resulting two fragments are chiral with the same chiral-ity. However, the cuts, in the following called decoration, reduce the symmetry of the apple from achiral ∞m to chiral 2, where the twofold axis (parallel to c) transforms the two halves into each other. Cutting the other two 90°-sectors in step (3) creates the opposite chirality.
I have been told that in the region of lake Geneva in Switzerland and France some 50 years ago, la coupe du
roi was known as la coupe de l’école, the slicing for the
school breaks. Mothers would slice apples for their chil-dren in this way, remove the core and maybe fill the void with dried raisins. Putting the parts back in place made the sliced apple quite stable for transport. In European tradition, apples have a mystic significance, as exempli-fied by Adam and Eve's apple in Eden, or the poisoning of Snow White by the queen using an apple. In accordance,
la coupe du roi is used in occult rituals of Roma or Sinti
[1]. La coupe du roi has also fascinated the artist, architect and designer Max Bill [2] who has sculpted a family of five half-spheres, one of them being a coupe du roi.
The designation coupe du roi is not restricted to apples. Idealizing the apple to become a sphere whose symmetry including the cuts is 222, the half-spheres possess symme-try 2, and are again related by a twofold axis. La coupe
du roi may be applied to any polyhedron with symmetry
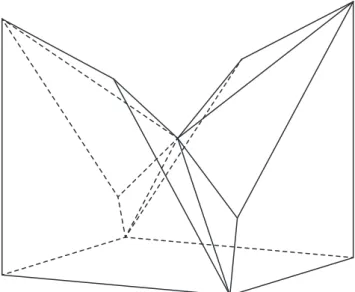
higher than or equal to point group 2. In Figures 2–4, we show a cube sliced in this way. The complete symmetry theory is presented below.
La coupe du roi has a chemical application, as
rec-ognized by Anet et al. [3]. While these authors discuss real-world segmentations of achiral molecules into chiral fragments and the reverse process, we present here a simple formal example showing the essence of the argu-ment. An achiral molecule A4B4 is defined on adjacent
edges of the cube of Figure 2(i). Its symmetry (without decorating cuts) is mmm with the twofold axes along [110], [ 1̅10] and [001]. The coupe du roi cuts the bonds A – B′ and A′ – B, and results in the chiral molecules B – A – A – B of Figure 2(ii) and Figure 2(iii), symmetry 2[110]. Inversely, when the two half-cubes are joined, intra- and intermolec-ular A – B distances become equal and the achiral dimer A4B4 of Figure 2(i) is formed. This may be split by a coupe
du roi cutting the bonds A – B and A′ – B′ to obtain
frag-ments of the opposite chirality. This method to change the chirality of B – A – A – B works for any bond lengths, bond angles and torsion angle, and also for more general molecules of composition A – B – C – D. The achiral dimer may then have symmetry mm2.
We restrict the designation coupe du roi to divisions of objects of the type presented above and in Figures 1–4: one cut from above, one cut from below and two cuts connect-ing these, resultconnect-ing in fragments of the same chirality. The symmetry of the objects including the cuts is always 222 or 2. However, there exist other methods to divide objects into equal fragments, of which we present examples in the following. The number of such segmentations is of course infinite, but their symmetries can be enumerated exhaus-tively. We present in the following the symmetry theory underlying the segmentation of objects into identical halves, discuss variants of the coupe du roi, and derive the point groups enabling the division of objects into identi-cal achiral halves, or a racemate of chiral halves, or chiral halves of the same handedness.
Symmetry theory for halving
objects
We consider any object characterized by its point sym-metry such as sphere, cylinder, cone, polyhedron, or
a
c
Fig. 1: La coupe du roi of an apple, c is along the rotation axis.
(i) (ii) (iii)
A A B B A A B B A′ A′ B′ B′ A′ A′ B′ B′ a b c
Fig. 2: Coupe du roi of a cube. (i) The complete cube decorated with the cuts has point group G = 222; bold lines define a molecule A4B4 with symmetry mmm on the edges of the cube. (ii) and (iii) are the chiral half-cubes; the coupe du roi splits the bonds A – B′ and A′ – B resulting in two molecules B – A – A – B with symmetry 2[110] and the same chirality.
(i) (ii) (iii)
a b c
Fig. 3: Variant of the coupe du roi. The vertical cuts are along the planes (120) and (210) and thus not perpendicular to each other. (i) the decorated cube with G = 222. (ii) and (iii) the fragments with H = 2[110].
(i) (ii) (iii)
a b c d a b c
Fig. 4: Variant of the coupe du roi. The vertical cuts extend to the points a, b and c, d. They are continued to the centre by the inter-sections with the oblique cuts through a, c and b, d; a, b, c, d are the corners of a tetragonal bisphenoid. (i) the decorated cube with G = 222. (ii) and (iii) the fragments with H = 2[110].
(idealized) apple. In order to slice it into fragments, we need consecutive cuts through the centre of the object. Polar point groups have a floating centre not defined by the symmetry elements, to be chosen on the rotation axis wherever convenient. We assume these cuts to be planar. They may be represented by great-circles on a circum-sphere centred on the object. Since the two fragments are to be completely separable and are of equal volume, these great-circles must form a single closed loop mean-dering around an average plane we call equator. For example, the equator of the coupe du roi of Figures 2–4 is the plane (110).
The loop of cuts may be embellished with additional cuts not passing through the centre, or cuts may be non-planar and warped (examples are found in [2]). In this way, highly complicated divisions may be imagined. However, such complications do not create any additions to, or modifications of the classification of the symme-tries derived with simple loops of planar cuts. The theory developed in the following is completely general.
We call the cuts applied to an object decoration. Figures 2–4 show decorated cubes and the corresponding individual fragments We designate the point group sym-metry of the decorated object by G. The symsym-metry of the undecorated object is a proper or improper supergroup of
G, i.e. the decoration usually reduces the symmetry of the
object. The symmetry of a single fragment is designated by the point group H, a subgroup of G of index 2. The two fragments are identical and therefore related by a sym-metry operation t, and by all operations in the coset t of t relative to H, consisting of all operations in G not in H; t is akin to a twinning operation.
The group H is necessarily polar, i.e. one of the groups 1, 2, 3, … or m, mm2, 3m, …, since its operations image the equator plane onto itself and do not flip it over. The corresponding symmetry elements are perpendicular to the equator plane. The symmetry operations t in t image the equator plane onto itself, but also flip it over. The cor-responding admissible symmetry elements are a mirror plane or a twofold axis in the equator plane, or a roto-inversion axis perpendicular to the equator plane. Odd powers of roto-inversions belong to t, even powers belong to H. The roto-inversions X̅ with X = 2n + 1 include an inver-sion, those with X = 4n + 2 a mirror reflection. The mirror plane results in a simple planar cut of the object, e.g. in the usual trivial half-apple with G = mm2 and H = m (see also [2]). The decorated object may have the symmetry G of any point group, except the polar groups 1, 3, 4, … and 3m, 4mm, 5m …, and the cubic, icosahedral and spheri-cal groups; the former do not comprise an operation t, the latter possess no polar subgroups of index 2. However, the
polar point groups 2, m and mm2 are admissible, with the twofold rotation and/or a mirror serving as operation t.
The family of coupes du roi
The classical coupe du roi as presented in the Introduc-tion may serve as a nice example of various related divi-sions with the same symmetry. The apple is supposed to have the symmetry of a cone ∞m, the decorated apple has the symmetry G = 2, the equator plane is (110) or ( 1̅10) depending on the cuts applied in the plane (001), the frag-ments are asymmetric H = 1, and t is a twofold rotation about [001]. For slicing a sphere, cylinder or the cube as in Figures 2–4, G = 222, the equator plane is (110), H = 2 with the twofold axis along [110], and the operations t are twofold rotations about [001] and [ 1̅10].
A first type of variant of this classical coupe du roi is obtained by realizing that the vertical cuts, perpendicular to a and b in Figure 2, need not be perpendicular to each other and may indeed intersect at any angle. In Figure 3, these cuts are chosen symmetrically relative to the faces of the cube. The group G is still 222, H is still 2, and the equator plane and operations t remain unchanged. However, the vertical cuts may be chosen along any planes (hk0), oblique to the directions a and b. The upper and lower parts of the cube are then in general no longer equivalent, and the type of symmetry is the one found for the division of the apple, G = 2.
A second type of variant arises when the vertical cuts extend initially only to the points a, b and c, d in Figure 4 If these cuts are perpendicular and of equal depth as in Figure 4, the points a, b, c, d form the summits of a tetragonal bis-phenoid. The required loop of cuts through the centre of the cube is along four of the edges of the bisphenoid, specifically the two apical edges (a, b) and (c, d), and two of the equa-torial edges (a, c) and (b, d) as in Figure 4, or (a, d) and (b,
c) to obtain the opposite handedness of the segments. The
cuts from the apical edges to the centre complete the vertical cuts. The symmetry properties of this division are the same as those of the classical coupe du roi. The symmetry may be reduced to the one of the apple by extending the initial verti-cal cuts from above and below to different depths. A wide variety of shapes is obtained by combining the two variants: the vertical cuts may have any direction with respect to the edges of the cube, intersect at any angle and extend to any depth. The bisphenoid is in general orthorhombic, but the symmetries discussed above are preserved.
In the classical coupe du roi, the points a, b, c, d are coplanar. Starting from a coupe du roi with the vertical
cuts along the diagonal planes (110) and ( 1̅10), another limiting case with higher symmetry is obtained when the bisphenoid becomes a tetrahedron inscribed in the cube. All loops through four of its edges become equivalent. The group G is now 4̅2m, H is mm2, and the segments are achiral (Figure 5).
Systematics of achiral and chiral
divisions
The fragments of an object sliced into two identical parts may be achiral, racemic chiral with different chirali-ties and enantiopure chiral with the same chirality. We present here the symmetry classes G of decorated objects for all admissible point groups. Figures 2–8 give exam-ples of dividing a cube into two identical fragments with various symmetries. We denote the symmetry of a division by (G, H). The coset t relating the two fragments consists of all the operations of G not in H. Remember that the polar groups 1, 3, 4, …, 3m, 4mm, 5m …, and the cubic, icosahedral and spherical groups cannot serve as group
G. For completeness, we include in the systematics the
somewhat trivial single planar cuts along a mirror plane with fragments either achiral or racemic.
(A) Achiral fragments (i) Planar divisions
G = X/mmm, X = 2n: (mmm, mm2), (4/mmm, 4mm),
(6/mmm, 6mm)
G = X̅m2, X = 4n + 2: (mm2 = 2̅m2, m), (6̅m2, 3m), (10̅m2, 5m)
(ii) Non-trivial divisions
G = X̅2m, X = 4n: (4̅2m, mm2) see Figure 5, (8̅2m, 4mm) G = X̅m, X = 2n + 1: (2/m = 1̅m, m), (3̅m, 3m) see Figure 6,
(5̅m, 5m)
(B) Fragments have opposite chiralities (i) Planar divisions
G = X/m, X = 2n: (2/m, 2), (4/m, 4), (6/m, 6) G = X̅, X = 4n + 2: (m = 2̅, 1), (6̅, 3), ( 1 ̅0̅, 5)
(ii) Non-trivial divisions
G = X̅, X = 4n: (4̅, 2) see Figure 7, (8̅, 4). The fragments are
related by a roto-inversion. a+b+c
a-b b-c
Fig. 6: Half-cube obtained with symmetry G = 3̅m, H = 3m, t is the inversion 1̅. The cuts are defined by six of the twelve edges of an octahedron inscribed in the cube. A similar half-sphere has been sculpted by Max Bill [2].
Fig. 7: Half-cube obtained with symmetry G = 4̅, H = 2, t = 4̅. The coordinate system is given in Figure 5. The figure is obtained by desym-metrizing Figure 5, by adding the corners of a second bisphenoid.
a
b c
Fig. 8: Half-cube obtained with symmetry G = 422, H = 4, t one of the twofold rotations about a or b or a ± b. The cuts are defined by the edges of a trapezohedron inscribed in the cube.
a c
b
Fig. 5: Two half-cubes obtained with symmetry G = 4̅2m, H = mm2, for t the 4̅ operation about the c-axis may be chosen, see also [2]. The cuts are defined by four of the six edges of a tetrahedron inscribed in the cube.
G = X̅, X = 2n + 1: ( 1̅, 1), ( 3̅, 3), ( 5̅, 5). The fragments are
related by a centre of symmetry. (C) Fragments have the same chirality
G = X22: (2, 1) as in coupe du roi of apple Figure 1, (222,
2) as in Figures 2–4, (32, 3), (422, 4) see Figure 8, (52, 5), (622, 6)
Conclusions
Dividing an apple according to la coupe du roi is a curios-ity probably known since a long time as a surprising trick. We have shown that la coupe du roi is a family of divisions of many kinds of objects comprising many variants and resulting in many shapes. The decorated object including the cuts possesses point group symmetry 2 or 222. Thus, the symmetry of the undecorated object without the cuts must comprise at least a twofold axis, and two of the cuts are parallel to this axis. The minimal symmetry of an achiral undecorated object is therefore 2/m or mm2. This is the minimal symmetry of a transition state when chang-ing the sense of chirality of chiral objects via formation of an achiral dimer, rather than by deformation [4].
If an object is to be divided into two equal fragments with the same chirality, admissible symmetries G of the decorated object consist, not really surprisingly, exclu-sively of rotation operations, groups X2. Non-trivial divi-sions resulting in fragments with opposite chirality arise with groups G = X̅, (X ≠ 4n + 2). Non-trivial achiral frag-ments are produced with G = X̅m, (X ≠ 4n + 2). All other point groups G admit only the trivial planar cut.
Acknowledgments: I am grateful to H. D. Flack for his
encoragement and advice.
References
[1] P. Derlon, in Les enigmes de l'univers. Editions Robert Laffont, Paris, p. 187, 1975.
[2] M. Bill, Familie von fünf halben Kugeln vor dem Mathematischen Institut der Universität Karlsruhe. http://de.wikipedia.org/wiki/ Max_Bill.
[3] F. A. L. Anet, S. S. Miura, J. Siegel, K. Mislow, La coupe du roi and its relevance to stereochemistry. Combination of two homochiral molecules to give an achiral product. J. Am. Chem.
Soc. 1983, 105, 1419.
[4] A. Rassat, P. W. Fowler, Is there a “Most chiral tetrahedron”?