Discrete-continuous optimization for robot perception via semidefinite relaxation

Discrete-Continuous Optimization for Robot

Perception via Semidefinite Relaxation

by

Siyi

Hu

Submitted to the Department of Aeronautics and Astronautics

in partial fulfillment of the requirements for the degree of

Master of Science

at the

MASSACHUSETTS INSTITUTE OF TECHNOLOGY

June 2019

Massachusetts Institute of Technology 2019. All rights reserved.

Signature redacted

A uthor ...

....

...

Department of Aeronautics and Astronautics

May 18, 2019

Certified by ...

Signature redacted...

Luca Carlone

Charles Stark Draper Assistant Professor

of Aeronautics and Astronautics

Thesis Supervisor

Signature redacted

A ccepted by ...

...

...

Sertac

Karaman

MASSACHUSETTS INSTITUTE

OF TECHNOLOGY

Associate Professor of Aeronautics and Astronautics

Chair, Graduate Program Committee

JUL

0

1201

9

Discrete-Continuous Optimization for Robot Perception via

Semidefinite Relaxation

by

Siyi Hu

Submitted to the Department of Aeronautics and Astronautics on May 18, 2019, in partial fulfillment of the

requirements for the degree of Master of Science

Abstract

In this thesis, we propose polynomial-time algorithms based on semidefinite program-ming (SDP) relaxation to find approximate solutions to nonconvex problems arising in two fields of robot perception, semantic segmentation and robust pose graph opti-mization. Compared with other inference techniques, SDP relaxation have shown to provide accurate estimate with provable sub-optimality guarantees without relying on an initial guess for optimization. On the downside, general SDP solvers scale poorly in terms of time and memory with the problem size. However, for problems admitting low-rank solutions, low-rank solvers and smooth Riemannian optimization can speed up computation significantly.

Along this direction, the first contribution is two fast and scalable techniques for inference in Markov Random Fields (MRFs). MRFs are a popular model for several pattern recognition and reconstruction problems in robotics and computer vision, but are intractable to solve in general. The first technique, named Dual Ascent

Rieman-nian Staircase (DARS), is able to solve large problem instances in seconds. The second

technique, named Fast Unconstrained SEmidefinite Solver (FUSES), utilizes a novel

SDP relaxation and is able to solve similar problems in milliseconds. We benchmark

both techniques in multi-class image segmentation problems against state-of-the-art MRF solvers and show that both techniques achieves comparable accuracy with the best existing solver while FUSES is much faster. Building on top of MRF models, our second contribution is a Discrete-Continuous Graphical Model (DC-GM) that combines discrete binary labeling with standard least-square pose graph optimization to iden-tify and reject spurious measurements for Simultaneous Localization and Mapping

(SLAM). We then perform inference in the DC-GM via semidefinite relaxation.

Exper-iment results on synthetic and real benchmarking datasets show that the proposed approach compares favorably with state-of-the-art methods.

Thesis Supervisor: Luca Carlone

Acknowledgments

I would like to thank my advisor Luca Carlone for incredible guidance in research. I would also like to thank Spark Lab members and friends for wonderful friendship

Contents

1 Introduction

1.1 Motivations for Semidefinite Relaxation in Robot Perception

1.1.1 Inference in M RF . . . .

1.1.2 Robust SLAM . . . .

1.2 Contributions . . . .

1.3 Preliminaries on MRF . . . .

1.3.1 M RF M odels . . . .

1.3.2 MRF Inference and Applications . . . .

1.4 Preliminaries on Robust SLAM . . . . 1.4.1 Pose Graph Optimization . . . .

1.4.2 Robust PGO . . . .

2 Accelerated Inference on MRF

2.1 Preliminaries: Semidefinite Relaxations . . . .

2.2 DARS: Dual Ascent Riemannian Staircase . . . .

2.2.1 Dual Ascent Approach . . . . 2.2.2 A Riemannian Staircase for the Dual Ascent Iterations 2.2.3 DARS: Summary, Convergence, and Guarantees . . . . .

2.3 FUSES: Fast Unconstrained SEmidefinite Solver . . . . 2.3.1 Matrix Formulation . . . .

2.3.2 Novel Semidefinite Relaxation . . . .

2.3.3 Accelerated Inference via the Riemannian Staircase . . 2.3.4 FUSES: Summary, Convergence, and Guarantees . . . .

13 14 14 15 . . . . 16 . . . . 17 . . . . 17 19 . . . . 20 . . . . 21 . . . . 22 23 . . . . 26 . . . . 27 . . . . 28 . . . . 29 . . . . 31 . . . . 32 . . . . 32 . . . . 33 . . . . 34 . . . . 36

2.4 Experim ents . . . . 36

2.4.1 FUSES and DARS: Implementation Details . . . . 37

2.4.2 Setup, Compared Techniques, and Performance Metrics . . . . 38

2.4.3 Semantic Segmentation Results . . . . 39

2.4.4 Semantic Segmentation: Results with Enhanced MRFs . . . . 42

2.5 Sum m ary . . . . 46

3 Robust Pose Graph Optimization 47 3.1 Discrete-continuous Graphical Models for Robust Pose Graph Opti-m ization . . . . 49

3.1.1 A Unified View of Robust PGO . . . . 49

3.1.2 Modeling Outlier Correlation and Perceptual Aliasing . . . . . 51

3.2 Inference in DC-GM via Convex Relaxation . . . . 53

3.3 DC-GM solver: Riemannian Optimization . . . . 56

3.4 Experim ents . . . . 58

3.4.1 Experiments On Synthetic Dataset . . . . 58

3.4.2 Experiments On Real Datasets . . . . 63

3.5 Sum m ary . . . . 65

4 Conclusion and Future Work 67 A Proof of Propositions 69 A.1 Equivalence between Problems (2.1) and (PO) . . . . 69

A.2 Proof of Proposition 2 . . . . 71

A.3 Proof of Proposition 3 . . . . 73

A.4 Proof of Proposition 8 . . . . 73

B Additional experiments 77 B.1 Effect of threshold . . . . 77

B.1.1 Effect of the Maximum Admissible Residual Threshold eI . . . 77

B.1.2 Effect of the Correlation Terms a ) on the Objective Function 80 B.2 Effect of heterogeneous groups of loop closures . . . . 82

List of Figures

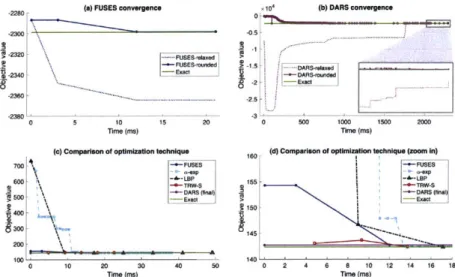
2-1 Snapshots of the multi-label semantic segmentation computed by the proposed MRF solvers (a) FUSES and (b) DARS on the Cityscapes dataset. FUSES is able to segment an image in 16ms (1000 superpixels). 23

2-2 Convergence results for a single test image: objective value over time (in milliseconds) for all the compared techniques. (a) Objective vs.

time for (P2); (b) Objective vs. time for (P1); (c)-(d) Objective vs. tim e for (PO). . . . . 40

2-3 Relaxation gap for FUSES and DARS for (a) increasing number of nodes and (b) increasing number of labels. The shaded area describes the 1-sigma standard deviation. . . . . 42

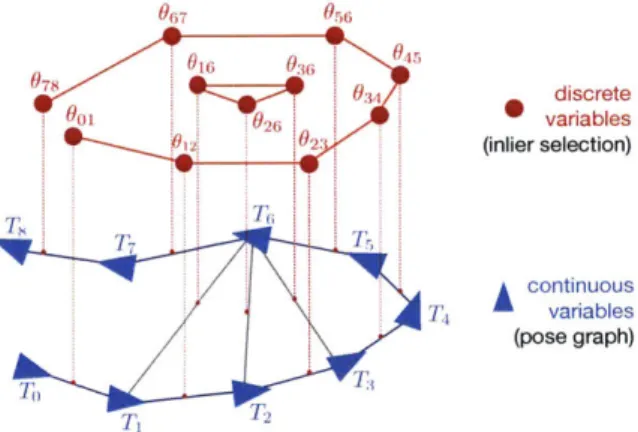
3-1 We introduce a Discrete-Continuous Graphical Model (DC-GM) to model perceptual aliasing in SLAM. The model describes the inter-actions between continuous variables (e.g., robot poses) and discrete variables (e.g., the binary selection of inliers and outliers), and captures the correlation between the discrete variables (e.g., due to perceptual

aliasing). . . . . 47

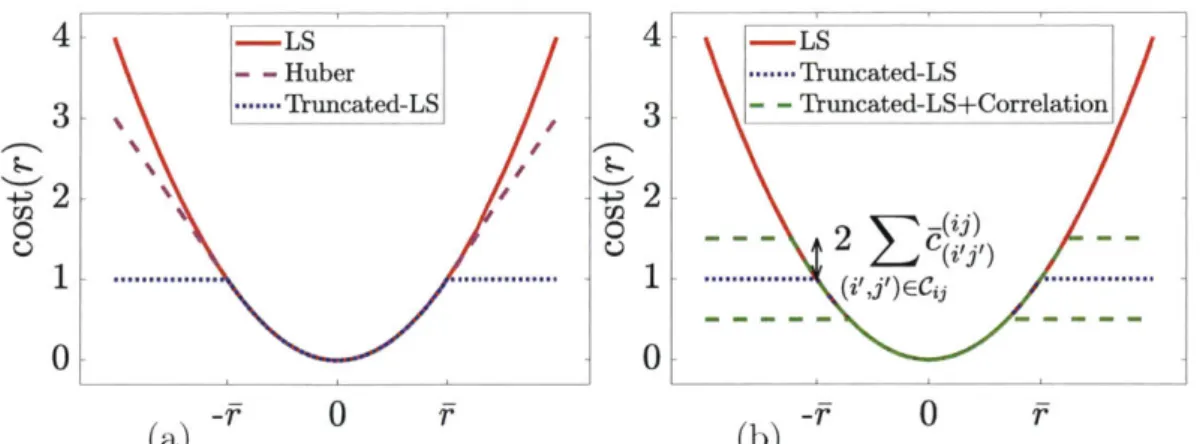
3-2 (a) Cost associated to each residual error in the least squares (LS),

~(ij)

Huber, and truncated LS estimators. (b) The correlation terms c (,/3 ) in

eq. (3.6) have the effect of altering the error threshold in the truncated

3-3 Trajectory estimates computed by the proposed techniques (black, overlay of 5 runs) versus ground truth (green) for the simulated grid dataset. . . . . 60

3-4 Average translation error of all approaches on a synthetic grid graph . 60 3-5 Percentage of rejected outliers for the proposed techniques on a

syn-thetic grid graph. . . . . 61

3-6 Ground truth (green) overlaid on the DC-GM solution (black, indistin-guishable from the ground truth), and outlier loop closures (red). . . 62 3-7 Average translation error of all approaches on a Manhattan World graph. 62 3-8 Percentage of rejected outliers for the proposed techniques on a

Man-hattan W orld graph. . . . . 63 3-9 Trajectory estimates computed by DC-GM (black) versus ground truth

(green) for the real datasets CSAIL, FR079, and FRH. . . . . 64 B-i Results on the simulated grid graph with maximum admissible

resid-uals of 0.Olu. (a) average translation error of the DC-GM and DC-GMd solutions compared with the odometric estimate; (b) rank of Z*, (c)

percentage of rejected inliers, and (d) percentage of rejected outliers for DC-GM and DC-GMd. . . . . 78

B-2 Results on the simulated grid graph with maximum admissible

residu-als of 1o-. . . . . 79

B-3 Results on the simulated grid graph with maximum admissible

residu-als of 2a-. . . . .

.79

B-4 Effect of the correlation terms on the robust cost function. . . . . 81

B-5 Results on the simulated grid graph with heterogeneous groups of loop closures and correlation terms 6 ) equal to 0.1M. (left) Percentage of rejected inliers; (right) Percentage of rejected outliers. . . . . 82

B-6 Results on the simulated grid graph with heterogeneous groups of loop closures and correlation terms 5 ) equal to 0.01. .. . . . . 82 B-7 Results on the simulated grid graph with heterogeneous groups of loop

(is)

List of Tables

2.1 Parameters used in DARS and FUSES. . . . . 38

2.2 Performance on the Cityscapes dataset (1000 superpixels). . . . . 41

2.3 Performance on the Cityscapes dataset (2000 superpixels). . . . . 41 2.4 Performance on the Cityscapes dataset (1000 superpixels, Bonnet 1024x

512 m odel). . . . . 43

2.5 Performance on the Cityscapes dataset (2000 superpixels, Bonnet 1024x

512 m odel). . . . . 43

2.6 Performance on the Cityscapes dataset (1000 superpixels, Bonnet 1024x

512 model, improved binary). . . . . 44

2.7 Performance on the Cityscapes dataset (2000 superpixels, Bonnet 1024x

512 model, improved binary). . . . . 44

2.8 Performance on the Cityscapes dataset (1000 superpixels, Bonnet 1024x

512 model, improved binary and superpixel). . . . . 45

2.9 Performance on the Cityscapes dataset (2000 superpixels, Bonnet 1024x

512 model, improved binary and superpixel). . . . . 45

Chapter 1

Introduction

This chapter begins with motivations of applying semidefinite program (SDP) relax-ation to inference in Markov Random Fields (MRFs), and Simultaneous Localizrelax-ation

and Mapping (SLAM) problems with spurious measurements. Then section 1.2 lists

the contributions of this thesis and provides a layout of the following chapters. Sec-tion 1.3 provides a brief introducSec-tion of MRF as well as a review of related inference techniques and applications. Section 1.4 reviews standard and robust Pose Graph Optimization (PGO), which is one of the most popular models for SLAM. Most of the materials covered in this thesis can be found in

142]

1.1

Motivations for Semidefinite Relaxation in Robot

Perception

Many optimization problems in robot perception are nonconvex and hence NP-hard to solve. Existing literature tends to favor local search methods to compute approximate solutions. These methods are generally fast, but usually require a good initial guess to find a solution close to the global optimum. Semidefinite programming (SDP) relaxation has the advantage of being a global method, where the solution does not rely on an initial guess, while providing a sub-optimality guarantee.

The drawback is that general-purpose SDP solvers scale poorly in terms of time and memory with the problem size. For some problems where we expect low-rank solutions, it is possible to leverage the geometric structure of the problem to speed up the computation. For this reason, we developed two fast inference algorithms in Markov Random Fields (MRFs) via smooth Riemannian optimization. Section 1.1.1 explains the motivations and challenges of SDP based methods for inference in MRF. On the other hand, SDP has shown to result in fast and accurate solvers for some robotics application, such as Simultaneous Localization and Mapping (SLAM). However, existing SDP based methods assumes there are no spurious measurements, or outliers. Section 1.1.2 explains challenges in SLAM with the presence of outliers.

1.1.1

Inference in MRF

Markov Random Fields (MRFs) are a popular graphical model for reconstruction and recognition problems in computer vision and robotics, including 2D and 3D semantic segmentation, stereo reconstruction, image restoration and denoising, texture synthe-sis, object detection, and panorama stitching [56, 4, 361. An MRF can be understood as a factor graph including only unary and binary factors, and where node variables are discrete labels. The discrete nature of the variables makes maximum a

posteri-or (MAP) inference in MRFs intractable in general, and this clashes with the need

understanding, mapping).

The literature on MRFs (reviewed in Section 1.3) is vast and includes methods based on graph cuts, message passing techniques, greedy methods, and convex relax-ations, to mention a few. These approaches are typically approximation techniques, in the sense that they attempt to compute near-optimal MAP estimates efficiently (the problem is NP-hard in general, hence we do not expect to compute exact solu-tions in polynomial time). Among those, semidefinite programming (SDP) relaxasolu-tions have been recognized to produce accurate approximations [41]. On the other hand, the computational cost of general-purpose SDP solvers prevented widespread use of this technique beyond problems with few hundred variables [38] (semantic segmenta-tion typically involves thousands to millions of variables), and SDPs lost popularity in favor of computationally cheaper alternatives including move-making algorithms (based on graph cut) and message passing. Move-making methods [9] require spe-cific assumptions on the MRF and their performance typically degrades when these assumptions are not satisfied. Message passing methods [60, 63], on the other hand, may not even converge, even though they are observed to work very well in practice. The challenge of SDP based approach is to couple with a fast and scalable solver while keeping relaxation tight.

1.1.2

Robust SLAM

Simultaneous Localization and Mapping (SLAM) is the backbone of several robotics applications. SLAM is already widely adopted in consumer applications (e.g., robot vacuum cleaning, warehouse maintenance, virtual/augmented reality), and is a key enabler for truly autonomous systems operating in the wild, ranging from unmanned aerial vehicles operating in GPS-denied scenarios, to self-driving cars.

Despite the remarkable advances in SLAM, both researchers and practitioners are well aware of the brittleness of current SLAM systems. While SLAM failures are a tolerable price to pay in some consumer applications, they may put human life at risk in several safety-critical applications. For this reason, SLAM is often avoided in those applications (e.g., self-driving cars) in favor of alternative solutions where the

map is built beforehand in an offline (and typically human-supervised) manner, even though this implies extra setup costs.

Arguably, the main cause of SLAM failure is the presence of incorrect data associ-ation and outliers [12]. Incorrect data associassoci-ation is caused by perceptual aliasing, the phenomenon where different places generate a similar visual (or, in general, percep-tual) footprint. Perceptual aliasing leads to incorrectly associating the measurements taken by the robot to the wrong portion of the map, which may lead to map deforma-tions and potentially to catastrophic failure of the mapping process. The problem is exacerbated by the fact that those outliers are highly correlated: due to the temporal nature of the data collection, perceptual aliasing creates a large number of mutually-consistent outliers. This correlation makes it even harder to judge if a measurement is an outlier, contributing to the brittleness of the resulting pipeline. Surprisingly, while the SLAM literature extensively focused 6n mitigating the effects of perceptual aliasing, none of the existing approaches attempt to explicitly model positive cor-relation between outliers. In addition, the local search methods relies on an initial guess, typically through odometry measurements, so that the optimization is likely to stop at local minima when odometry measurements are off. Previous SDP-based approach on provably-correct SLAM [52, 17] are susceptible to outliers. The challenge is to incorporate outlier identifications into the model.

1.2

Contributions

As a first contribution, discussed in Chapter two, we propose two fast and scalable techniques for inference in MRFs. The first technique is a dual ascent method to solve standard SDP relaxations that takes advantage of the geometric structure of the problem to speed up computation to address the scalability issue of general purpose

SDP solvers. This technique, named Dual Ascent Riemannian Staircase (DARS), is

able to solve large problem instances in seconds. We also develop a second and faster technique, named Fast Unconstrained SEmidefinite Solver (FUSES). The backbone of this approach is a novel SDP relaxation combined with a fast and scalable solver

based on smooth Riemannian optimization. We show that this approach can solve large problems in milliseconds. We demonstrate the proposed approaches in multi-class image segmentation problems. Extensive experimental evidence shows that (i)

FUSES and DARS produce near-optimal solutions, attaining an objective within 0.1% of the optimum, (ii) FUSES and DARS are remarkably faster than general-purpose SDP solvers, and FUSES is more than two orders of magnitude faster than DARS while

attaining similar solution quality, (iii) FUSES is faster than local search methods while

being a global solver.

Chapter three presents our second contribution, a Discrete-Continuous Graphical

Model (DC-GM) that provides a unified framework to model perceptual aliasing in

SLAM and provides practical algorithms that can cope with outliers without relying

on any initial guess. This model combines standard PGO with discrete binary MRF to identify and reject spurious measurements. The continuous portion of the

DC-GM captures the standard SLAM problem, while the discrete portion describes the

selection of the outliers and explicitly models their correlation. To perform inference in the DC-GM, we propose a SDP relaxation that returns estimates with provable sub-optimality guarantees. Experimental results on synthetic datasets as well as standard benchmarking datasets show that the proposed technique compares favorably with state-of-the- art methods while not relying on an initial guess for optimization.

Chapter four concludes this thesis with a discussion and future work.

1.3

Preliminaries on MRF

This section explains common setup of a MRF and a short review of MRF inference and semantic segmentation. The reader can find a more comprehensive review in the supplemental material of [311.

1.3.1

MRF Models

A Markov Random Field (MRF) is a graphical model in which nodes are associated

probabilistic constraints relating the labels of a subset of nodes. Formally, for each node i in the node set V = {1,... , N} (where N is the number of nodes), we need to assign a label xi E L, where L {1, .. . , K} is the set of K possible labels. If K = 2 (i.e., nodes are classified into two classes) the corresponding model is called a

binary MRF. Here we consider K > 2 possible labels, a setup generally referred to as

a multi-label MRF.

Maximum a posteriori (MAP) inference. The MAP estimate is the most

likely assignment of labels, i.e., the assignment of the node labels that attains the maximum of the posterior distribution of an MRF, or, equivalently, the minimum of the negative log-posterior. MAP estimation can be formulated as a discrete optimiza-tion problem over the labels xi E L with i = 1, ... , N [56]:

min Ei(xi) + E Ei (xi, x) (PO)

Xi EC:

i=1,...,N iEU (ij)EB

where U C V is the set of unary potentials (probabilistic constraints involving a single node), B C V x V is the set of binary potentials (involving a pair of nodes), and E(-) and Eg3(-) represent the negative log-distribution for each unary and binary potential,

respectively (described below). For instance, in semantic segmentation each node in the MRF corresponds to a pixel (or superpixel) in the image, the unary potentials are dictated by pixel-wise classification from a classifier applied to the image, and the binary potentials enforce smoothness of the resulting segmentation [64]. The binary potentials (often referred to as smoothness priors) are typically enforced between nearby (adjacent) pixels.

MRF Potentials. A typical form for the unary and binary potentials is:

Ei(xi) = 0 if Xi = xi

ci otherwise

(1.1)

i , 0 if Xi = Xj

where 2, is a data-driven noisy measurement of the label of node i (typically from a classifier), and ci and 6ij are given scalars. Typically, it is assumed ei > 0, i.e., choosing a label different from the measured one incurs a cost ci in (P0). Similarly, for the binary potentials Eij(.) it is typically assumed 6ij > 0, i.e., label mismatch

(xi =, xj) incurs a cost of 6ij in the objective (PO). In this case the binary potentials

are called attractive, while they are referred to as repulsive when 6ij < 0 (i.e., the potentials encourage label mismatches) [23].

The MRF resulting from the choice of potentials in eq. (1.1) is known as the Potts

model [50], which was first proposed in statistical mechanics to model interacting

spins in ferromagnetic materials. When K =2 (binary MRFs) the resulting model is known as the Ising model [4, Section 1.4.11.

1.3.2

MRF Inference and Applications

Exact MRF inference. Inference in MRFs is intractable in general. However,

par-ticular instances of the problem are solvable in polynomial time, e.g., binary MRF such as the Ising model [27]. For multi-label MRFs, exact solutions exist for the case when the binary terms are convex functions of the labels [35] or when the binary terms are linear and the unary terms are convex [30]. These assumptions are unrealistic in semantic segmentation and do not apply to the Potts model of Section 2.1. When polynomial-time methods are not applicable, (PO) can be solved using integer pro-gramming (e.g., CPLEX [34]) for moderate-sized problems, although this approach does not scale to large instances.

Approximate and local MRF inference. When MRF inference is NP-hard,

one has to resort to approximation techniques. Move-making algorithms [40, 9],

at each inner iteration, solve a binary MRF using graph cut, while the outer loop attempts to reconcile the binary results into a coherent multi-class segmentation.

Message-passing techniques adjust the MAP estimate at each node in the MRF via

local information exchange between neighboring nodes. Popular message passing tech-niques are Loopy Belief Propagation [63] (LBP) and Tree-Reweighted Message

MRFs and may oscillate. Linear Programming Relaxations relax MRF inference to work on continuous labels 60, 39, 19]. Spectral and semidefinite relaxations rephrase MRF inference in terms of a binary (pseudo-boolean) quadratic optimization

153,

Application to semantic segmentation. Semantic segmentation methods

as-sign a semantic label to each "region" in an RBG image, RBG-D image, or 3D model. Traditional approaches for semantic segmentation work by extracting and classify-ing features in the input image, and then enforcclassify-ing consistency of the classification across pixels, using MRFs or other models. Common features include pixel color, his-togram of oriented gradients, SIFT, or textons, to mention a few [64]. More recently, deep convolutional neural networks (CNNs) have become a popular segmentation ap-proach, see [24]. State-of-the-art methods, such as DeepLab [20], refine the results of a deep convolutional network with a fully-connected conditional random field in

order to improve the localization accuracy of object boundaries.

1.4

Preliminaries on Robust SLAM

This section reviews basic concepts about Pose Graph Optimization (PGO) for SLAM problems as well as existing literature coping with outliers.

1.4.1

Pose Graph Optimization

Pose Graph Optimization (PGO) is one of the most popular models for SLAM. PGO consists in the estimation of a set of poses (i.e., rotations and translations) from pairwise relative pose measurements. In computer vision a similar problem (typically involving only rotation) is used as a preprocessing step for bundle adjustment in Structure from Motion (SfM) [28].

PGO estimates n poses from m relative pose measurements. Each to-be-estimated

pose T = [R, ti], i = 1, . . ., n, comprises a translation vector ti E Rd and a rotation

matrix Ri E SO(d), where d = 2 in planar problems or d = 3 in three-dimensional

problems. For a pair of poses (i, j), a relative pose measurement [Ij fiJ, with

eij

c Rd and RI3 E SO(d), describes a noisy measurement of the relative pose between

Ti and T. Each measurement is assumed to be sampled from the following generative

model:

fi- = R (tj - ti) + tE, RnK = RTRjRE (1.2)

where t' E Rd and Ric E SO(d) represent translation and rotation measurement

noise, respectively. PGO can be thought as an MRF with variables living on mani-fold: we need to assign a pose to each node in a graph, given relative measurements associated to edges S of the graph. The resulting graph is usually referred to as a

pose graph.

Assuming the translation noise is Normally distributed with zero mean and in-formation matrix WtId and the rotation noise follows a Langevin distribution [17, 14] with concentration parameter wr, the MAP estimate for the unknown poses can be

computed by solving the following optimization problem:

min

ZWtI|tj-ti-Rizfij|

tiER2

RiES0(d)('J)E-where 11-JIF denotes the Frobenius norm. The derivation of (1.3) is given in [14, Proposition 1]. The estimator (1.3) involves solving a nonconvex optimization, due

to the nonconvexity of the set SO(d). Recent results [14, 52] show that one can still compute a globally-optimal solution to (1.3), when the measurement noise is reasonable, using convex relaxations.

Unfortunately, the minimization (1.3) follows from the assumption that the mea-surement noise is light-tailed (e.g., Normally distributed translation noise) and it is known to produce completely wrong pose estimates when this assumption is violated, i.e., in presence of outlying measurements.

1.4.2

Robust PGO

The sensitivity to outliers of the formulation (1.3) is due to the fact that we minimize the squares of the residual errors (quantities appearing in the squared terms): this implies that large residuals corresponding to spurious measurements dominate the cost. Robust estimators reduce the impact of outliers by adopting cost functions that grow slowly (i.e., less than quadratically) when the residual exceeds a given upper bound. This is the idea behind robust M-estimators, see [33].

Traditionally, outlier mitigation in SLAM and SfM relied on the use of robust M-estimators, see [5, 28]. Agarwal et al. [1] propose Dynamic Covariance Scaling (DCS), which dynamically adjusts the measurement covariances to reduce the influence of outliers. Olson and Agarwal [471 use a max-mixture distribution to accommodate multiple hypotheses on the noise distribution of a measurement. Casafranca et al. [18] minimize the fl-norm of the residual errors. Lee et al. [44] use expectation maximiza-tion. Pfingsthorn and Birk [491 model ambiguous measurements using a mixture of

Gaussians.

An alternative set of approaches attempts to explicitly identify and reject outliers.

A popular technique is RANSAC, see [22], in which subsets of the measurements are

sampled in order to identify an outlier-free set. Si nderhauf and Protzel [54, 55] propose Vertigo, which augments the PGO problem with latent binary variables (then relaxed to continuous variables) that are responsible for deactivating outliers. Latif

et al. [43], Carlone et al. [15], Graham et al. [251, Mangelson et al. [45] look for large

Chapter 2

Accelerated Inference on MRF

Contribution. This chapter covers the first contribution, two fast and scalable

techniques for inference in MRFs.

The first technique is a dual ascent method to solve standard SDP relaxations that

takes advantage of the geometric structure of the problem to speed up computation to

address the scalability issue of general purpose SDP solvers. This technique, named

Dual Ascent Riemannian Staircase (DARS), is able to solve large problem instances in

seconds. We also develop a second and faster technique, named Fast Unconstrained

SEnidefinite Solver (FUSES). The backbone of this approach is a novel SDP relaxation

combined with a fast and scalable solver based on smooth Riemannian optimization.

We show that this approach can solve large problems in milliseconds.

The first technique, presented in Section 2.2, is a dual-ascent-based method to

(a) FUSES (b) DARS

Figure 2-1: Snapshots of the multi-label semantic segmentation computed by the proposed MRF solvers

(a)

(b)

solve standard SDP relaxations that takes advantage of the geometric structure of the problem to speed up computation. In particular, we show that each dual ascent iteration can be solved using a fast low-rank SDP solver known as the Riemannian

Staircase [6]. This technique, named Dual Ascent Riemannian Staircase (DARS), is able to solve MRF instances with thousands of variables in seconds, while general-purpose SDP solvers (e.g., cvx [26]) are not able to provide an answer in reasonable time (hours) at that scale.

The second technique, presented in Section 2.3, is a Fast Unconstrained

SEmidef-inite Solver (FUSES) that can solve large problems in milliseconds. The backbone of

this second approach is a novel SDP relaxation combined with the Riemannian Stair-case method [6]. The novel formulation uses a more intuitive binary matrix (with entries in {0, 1}), contrarily to related work that parametrizes the problem using a vector with entries in {-1, +1}. FUSES does not require an initial guess for optimiza-tion (i.e., it is a global solver) and provides per-instance sub-optimality guarantees.

We also provide an extensive experimental evaluation in 2.4. We test the proposed

SDP solvers in semantic image segmentation problems and evaluate the corresponding

results in terms of accuracy and runtime. We compare the proposed techniques against several related approaches, including move-making methods (a-expansion [9]) and message passing (Loopy Belief Propagation [631 and Tree-Reweighted Message

Passing [60]). Upon convergence, DARS attains the same solution of standard SDP relaxations. FUSES, on the other hand, trades-off inference time for a mild loss in accuracy. More specifically, our results show that (i) FUSES and DARS produce near-optimal solutions, attaining an objective within 0.1% of the optimum, (ii) FUSES and DARS are remarkably faster than general-purpose SDP solvers (e.g., CVX [261), and

FUSES is more than two orders of magnitude faster than DARS while attaining similar

solution quality, (iii) FUSES is more than 2x faster than local search methods while being a global solver.

While the evaluation in this contribution focuses on the MRF solver (rather than attempting to outperform state-of-the-art deep learning methods for semantic segmen-tation), we believe FUSES can be used in conjunction with existing deep learning

meth-ods, as done in

120],

Before delving into the contribution, Section 2.1 provides preliminary on standard

2.1

Preliminaries: Semidefinite Relaxations

The MAP estimation of an MRF can be written as an optimization problem, (P0) in Section 1.3.1. For this problem, semidefinite programming (SDP) relaxation has been shown to provide an effective approach to compute a good approximation of the global minimizer 138, 37, 481. In this section we introduce a standard approach to obtain an SDP relaxation, for which we design a fast solver in Section 2.2.

In order to obtain an SDP relaxation, related works rewrite each node variable

xi E L f{1, ... , K} as a vector wi E {-1, +1}K, such that wi has a single entry equal

to +1 (all the others are -1), and if the j-th entry of wi is +1, then the corresponding node has label

j.

min, wTAw + 2bTw

subject to diag (wwT) - 1NK, (2.1)

iw =2-K, i=1,...,N

where A and b are a suitable symmetric matrix and a suitable vector collecting the coefficients of the binary terms and the unary terms in (1.1), respectively; diag (wwT)

is the diagonal of the matrix wwT, and ui = eT o 1 T where ei is an N-vector which

is all zero, except the i-th entry which is one, 1K is a K-vector of ones, and 0 is the Kronecker product. Intuitively, diag (wwT) contains the square of each entry of w, hence diag (wwT) = 1N imposes that every entry of w has norm 1, i.e., it belongs to {-1,

+1};

enforces each node to have a unique label (i.e., a single entry in wi can be +1, while all the others are -1).

Before relaxing problem (2.1), it is convenient to homogenize the objective by reparametrizing the problem in terms of an extended vector y [wTl]T, where an

entry equal to 1 is concatenated to w. We can now rewrite (2.1) in terms of y:

miny tr (LyyT)

subject to diag (yyT) = 1NK+1 (P1)

tr

(UyyT)

where L

[

[

],

(UgyyT)

So far we have only reparametrized problem (PO), hence (P1) is still a MAP estimator. We can now introduce the SDP relaxation: problem (P1) only includes terms in the form yy , hence we can reparametrize it using a matrix Y - yy . Moreover, we note that the set of matrices Y that satisfy Y _ yyT is the set of positive semidefinite (Y - 0) rank-1 matrices (rank (Y) = 1). Rewriting (P1) using Y and dropping the non-convex rank-1 constraint, we obtain:

miny tr (LY)

subject to diag (Y) = 1NK+1 (Si)

tr (UY) =2 - K, Z= 1, . .. , N

Y >_ 0

which is a (convex) semidefinite program and can be solved globally in polynomial time using interior-point methods [8]. While the SDP relaxation (Si) is known to provide near-optimal approximations of the MAP estimate, interior-point methods are typically slow in practice and cannot solve problems with more than few hundred nodes in a reasonable time.

2.2

DARS:

Dual Ascent Riemannian Staircase

This section presents the first optimization technique: a dual ascent approach to efficiently solve large instances of the standard SDP relaxation (Si).

2.2.1

Dual Ascent Approach

The main goal of this section is to design a dual ascent method, where the subproblem to be solved at each iteration has a more favorable geometry, and can be solved quickly using the Riemannian Staircase method introduced in Section 2.2.2. Towards this goal, we rewrite (Si) equivalently as:

miny g(Y)

(2.2)

subject to tr (UY) 2 - K, i = 1,..., N

where the objective function is now g(Y) tr (LY)

+I(diag

>_-0), where

I(.)

Under constraints qualification (e.g., the Slater's condition for convex programs [59, Theorem 3.11), we can obtain an optimal solution to (2.2) by computing a saddle-point of the Lagrangian function L(Y, A):

max inf L(Y, A) = max inf g(Y) + E_1 Ai(tr (UgY) + K - 2) (2.3)

A Y A Y

where A E RN is the vector of dual variables and Y is the primal variable.

The basic idea behind dual ascent [7, Section 2.1] is to solve the saddle-point problem (2.3) by alternating maximization steps with respect to the dual variables A and minimization steps with respect to the primal variable Y.

Dual Maximization. The maximization of the dual variable is carried out via

gradient ascent. In particular, at each iteration t = 1,... , T (T is the maximum number of iterations), the dual ascent method fixes the primal variable and updates the dual variable A as:

A(t)

where VLA(Y(t1), A(t-1)) is the gradient of the Lagrangian with respect to the dual

and a is a suitable stepsize. It is straightforward to compute the gradient with respect to the i-th dual variable as VLsx (Y, A) = tr (UY) + K - 2. Intuitively, the second summand in (2.3) penalizes the violation of the constraint tr (UgY) = 2 - K (for all i). Moreover, since the gradient in (2.4) grows with the amount of violation tr (UiY) - K + 2, the dual update (2.4) increases the penalty for constraints with

large violation.

Primal Minimization. The minimization step fixes the dual variable to the

latest estimate A('-) and minimizes (2.3) with respect to the primal variable Y:

min g(Y) + EN A(-) (tr (UY) + K - 2) (2.5)

Y i

where we substituted "inf" for "min" since the objective cannot drift to minus infinity due to the implicit constraints imposed by the indicator functions in g(Y). Recalling the expression of g(Y), defining LA = L +

Z:N

Y() = arg miny tr (LAY)

subject to diag (Y) = 1NK+1 (2.6) Y >- 0

where we dropped the constant terms E1 l(K - 2) from the objective since

they are irrelevant for the optimization. The minimization step in the dual ascent is again an SDP, but contrarily to the standard SDP (Si), problem (2.6) can be solved quickly using the Riemannian Staircase, as discussed in the following.

2.2.2

A Riemannian Staircase for the Dual Ascent Iterations

This section provides a fast solver to compute a solution for the SDP (2.6), that needs to be solved at each iteration of the dual ascent method of Section 2.2.1.

R(NK+1)x(NK+1) in (2.6) with a rank-v product RRT with R E C (NK+1)xr.

minR tr (LARRT) (2.7)

subject to diag (RRT) = 1NK+1

Note that the constraint Y >- 0 in (2.6) becomes redundant after the substitution,

since RRT is always positive semidefinite, hence it is dropped.

Following Boumal et al.

16]

St(d, p) = {M E RdxP: MMT = d} (2.8)

Then, we observe that diag (RRT) = 1NK+1 can be written as RiRT = 1, i

1, ... , NK

+1

min tr (LxRRT

)

RESt(1,r)NK+l

The formulation (RI) is convex (the product of Stiefel manifolds describes a non-convex set), but one can find local minima efficiently using iterative methods [6, 521. While it might seem that little was gained (we started with an intractable problem and we ended up with another non-convex problem), the following remarkable result from Boumal et al. [6] ties back local solutions of (RI) to globally optimal solutions

of the SDP (2.6).

Proposition 1 (Optimality Conditions for (R1), Corollary 8 in [6])

If R G St(1, r)NK+l is a (column) rank-deficient second-order critical point of prob-lem (R1), then R is a global optimizer of (RI), and Y* RRT is a solution of the

The previous proposition ensures that when local solutions (second-order critical points) of (RI) are rank deficient, then they can be mapped back to global solutions of (2.6), hence providing a way to solve (2.6) efficiently via (RI).

The catch is that one has to choose the rank r large enough to obtain rank-deficient solutions. Related work [61 therefore proposes the Riemannian staircase method, where one solves (RI) for increasing values of r till a rank-deficient solution is found. Boumal et al. [61 also provide theoretical results ensuring that rank-deficient solutions are found for small r (more details in Section 2.4).

2.2.3

DARS:

Summary, Convergence, and Guarantees

We name DARS (Dual Ascent Riemannian Staircase) the approach resulting from the combination of dual ascent and the Riemannian Staircase. DARS starts with an initial guess for the dual variables (we use A = ON), and then alternates two steps: (i) the primal minimization where a solution for (2.6) is obtained using the Riemannian Staircase (Ri) (in practice this is solved using iterative methods, such as the Truncated Newton method); (ii) the dual maximization were the dual variables are updated using the gradient ascent update (2.4).

- Rounding. Upon convergence, DARS produces a matrix Y* = RRT. When deriving the standard SDP relaxation (Si) we dropped the rank-1 constraint, hence Y* cannot be written in general as Y* = . The process of computing a feasible

solution 0 for the original problem (P1) is called rounding. A standard approach for rounding consists in computing a rank-i approximation of Y (which can be done via singular value decomposition) and rounding the entries of the resulting vector in

{-1; +1}. We refer to as the rounded estimate and we call fsi the objective value

attained by

y

Convergence. While dual ascent is a popular optimization technique, few con-vergence results are available in the literature. For instance, dual ascent is known to converge when the original objective is strictly convex [58]. Currently, we observe that DARS converges when the stepsize a in (2.4) is sufficiently small. We prove the following per-instance performance guarantees.

Proposition 2 (Guarantees in DARS) If the dual ascent iterations converge to a

value A* (i.e., the dual iterations reach a solution where the gradient in (2.4) is zero) then the following properties hold:

" let R* be a (column) rank-deficient second-order critical point of problem (RI)

with LA L + ZN XU, then the matrix Y* (R*)(R*)T is an optimal

solution for the standard SDP relaxation (Si);

* let

fi

relaxation (Si), f;1 be the optimal objective of (P1), and

fs1

attained by the rounded solution , then it holds isi - f1 fs1 -

fsi-The proof of Proposition 2 is given in Appendix A.2. fsi-The first claim in Proposition 2 ensures that when the dual ascent method converges, it produces an optimal solution for the standard SDP relaxation (Si). The second claim states that we can compute an upper-bound on how far the DARS' solution is from optimality (fsi -

f

the rounded objective fsi and the relaxed objective

f

2.3

FUSES:

Fast Unconstrained SEmidefinite Solver

In this section we propose a more direct way to obtain a semidefinite relaxation and a remarkably faster solver. While DARS is already able to compute an approximate MAP estimate in seconds for large problems, the approach presented in this section requires two orders of magnitude less time to compute a solution of comparable (but slightly inferior) quality. We first present a binary {0, 1} (rather than {-1, +1}) matrix formulation (Section 2.3.1) and derive an SDP relaxation (Section 2.3.2). We then present a Riemannian staircase approach to solve the resulting SDP in real time

(Section 2.3.3) and discuss performance guarantees (Section 2.3.4).

2.3.1

Matrix Formulation

In this section we rewrite the node variables xi {1,. .. , K} as an N x K binary

node i has label

j

j,

j

Proposition 3 (Binary Matrix Formulation of MAP-MRF) Let G E RNxK

and H

e

G = G = -e if i G U G =OT, otherwise (2.9) H = H = -Bij, if (i,j) E 13 H = 0, otherwise

where Gi is the i-th row of G, H j is the entry of H in row i and column

j,

(i

minx tr (XT H X)

+

subject to diag (XXT) = 1N (2.10)

X E

{0,

1JNxK

The equivalence between (PO) and (2.10) is proven in Appendix A.3. We note that the constraint diag (XXT) = 1N in (2.10) (contrarily to the diag

()

in (2.1)) imposes that each node has a unique label when X E {0, 1}NxK.

2.3.2

Novel Semidefinite Relaxation

This section presents a semidefinite relaxation of (2.10). Towards this goal, we first homogenize the cost by lifting the problem to work on a larger variable:

V

[

where IK is the KxK identity matrix. The reparametrization is given as follows.

Proposition 4 (Homogenized Binary Matrix Formulation) Let us define

Q

S

0G

]

E

Then the MAP estimator (2.10) can be rewritten as:

f

{0,

where [VVT]tl denotes the (N x N) top-left block of the matrix VVT, Cf. (2.11), (the

corresponding constraint rewrites the first constraint in (2.10)), and where [VVT b,

denotes the (K x K) bottom-right block of VVT, Cf. (2.11).

At this point it is straightforward to derive a semidefinite relaxation, by noting

that tr (VTQV) = tr (QVVT) and by observing that VVT is a (N+K) x (N+K)

symmetric positive semidefinite matrix of rank K.

Proposition 5 (Semidefinite Relaxation) The following SDP is a convex

relax-ation of the MAP estimator (P2):

fs2 a minz subject to tr (QZ) diag ([Z]ti) = 1N [Zlbr = 1K Z >_ 0 (S2)

where [Z]ti and [Z|b, are the (N x N) top-left block and the (K x K) bottom-right block of the matrix Z, respectively, and we dropped the rank-K constraint for Z.

2.3.3

Accelerated Inference via the Riemannian Staircase

We now present a fast specialized solver to solve the SDP (S2) in real time and for large problem instances. Similarly to Section 2.2.2, we use the Burer-Monteiro

method [11], which replaces the matrix Z in (S2) with a rank-r product RRT:

minR tr

(QRRT)

subject to diag ([RRT]ti) =N (2.12)

[RRT]br = IK

where R E RNxr (for a suitable rank r), and where the constraint Z & 0 in (S2) becomes redundant after the substitution, and is dropped.

Similarly to Section 2.2.2, we note that the constraint set in (2.12) describes a smooth manifold, and in particular a product of Stiefel manifolds. Specifically, we observe that diag

([RRT~t1)

N can be written as RiR[ = 1, i = 1,. . ., N, which is equivalent to saying that RI E St(1, r) for i = 1, ... , N. Moreover, denoting with

Rb the block matrix including the last K rows of R, the constraint [RRT br = IK

can be written as RbR[ = 'K, which is equivalent to saying that Rb E St(K, r). The

two observations above allow concluding that the matrix R belongs to the product manifold St(1, r)N x St(K, r). Therefore, we can rewrite (2.12) as an unconstrained

optimization on manifold:

min tr (QRRT) (R2)

RE St (1,r)N x St(K,r)

The formulation (R2) is non-convex but one can find local minima efficiently using iterative methods [6, 52]. We can again adapt the result from Boumal et al. [61 to conclude that rank-deficient local solutions of (R2) can be mapped back to global solutions of the semidefinite relaxation (S2).

Proposition 6 (Optimality Conditions for (R2), Corollary 8 in [6])

If R

C St(1,

the semidefinite relaxation (S2).

Similarly to Section 2.2.2, we can adopt a Riemannian staircase method, where one solves (R2) for increasing values of r till a rank-deficient solution is found. In all

tests we performed, at most two steps of the staircase (initialized at r = K + 1) were

sufficient to find a rank-deficient solution.

2.3.4

FUSES:

Summary, Convergence, and Guarantees

We name FUSES (Fast Unconstrained SEmidefinite Solver) the approach presented in

this section. Contrarily to DARS, FUSES is extremely simple and only requires solving the rank-restricted problem (R2), which can be solved using iterative methods, such as the Truncated Newton method. Besides its simplicity, FUSES is guaranteed to converge to the solution of the SDP (S2) for increasing values of the rank r (Proposition 6).

Rounding. Upon convergence, FUSES produces a matrix Z*. Similarly to DARS,

we obtain a rounded solution by computing a rank-K approximation of Z* and round-ing the correspondround-ing matrix in {0, 1} (i.e., we assign the largest element in each row to 1 and we zero out all the others). We denote with X the resulting estimate and we call fS2 the objective value attained by X in (2.10).

Since the SDP (S2) is a relaxation of the MAP estimator (P2), it is straightforward to prove the following proposition.

Proposition 7 (Guarantees in FUSES) Let f 2 be the optimal objective attained by

Z* = (R)(R)T in (S2), f 2 be the optimal objective of (P2), and !s2 be the objective

attained by the rounded solution X, then

fs

fs2-Again, we can use Proposition 7 to compute how far the solution computed by

FUSES is from the optimal objective attained by the MAP estimator.

2.4

Experiments

This section evaluates the proposed approaches, FUSES and DARS, on semantic segmen-tation problems, comparing their performance against several state-of-the-art MRF solvers.

2.4.1

FUSES

and DARS: Implementation Details

We implemented FUSES and DARS in C++ using Eigen's sparse matrix manipulation and leveraging the optimization suite developed in [52]. Sparse matrix manipulation is crucial for speed and memory reasons, since the involved matrices are very large. For instance in DARS, the matrix LA in (R1) has size (NK +1) x (NK +1) where typically

N > 103 and K > 20. We initialize the rank r of the Riemannian Staircase to be

r = 2 for DARS and r = K + 1 for FUSES (this is the smallest rank for which we expect

a rank-deficient solution). The Riemannian optimization problems (RI) and (R2) are solved iteratively using the truncated-Newton trust-region (TNT) method. We refer the reader to [511 for a description of the implementation of a truncated-Newton trust-region method. As in [51], we use the Lanczos algorithm to check that (RI) and (R2) converged to rank-deficient second-order critical points, which are optimal according to Proposition 1 and Proposition 6, respectively. If the optimality condition is not met, the algorithm proceeds to the next step of the Riemannian staircase, repeating the optimization with the rank r increased by 1. In all experiments, FUSES found an optimal solution within the first two iterations of the staircase, while we observed that the rank in DARS (initially r = 2) sometimes increases to 6 - 8.

Parameter Choice. The proposed techniques are based in the Riemannian staircase method and they look for rank-deficient solutions for increasing values of the rank r. As mentioned above, we use the initial value of r = 2 for DARS and

r = K+1 for FUSES. After solving the rank-constrained SDP for a given value of r, each

technique checks if the resulting solution is rank deficient (in which case an optimal solution is found), or the techniques moves to the next step of the staircase (r <--r + 1). The th<--resholds used to check that the Riemannian optimization conve<--rged

(gradient norm and relative decrease in the objective) and that the resulting solution is rank deficient (eigenvalue tolerance) are given in Table 2.1. The table also reports parameters governing the trust-region method (maximum number of iterations, initial radius and parameters a, and a2 the decide how to change the radius), as well as the Conjugate Gradient (CG) solver used within TNT. In DARS, we also limit the

maximum number of dual ascent iterations to T = 1000, and we terminate iterations when the gradient in (2.4) has norm smaller than 0.5. We adopted a stepsize a 0.005 for the dual ascent iterations.

Parameters DARS FUSES

Initial rank 2 K+ 1

Gradient norm tolerance le-3 le-2 Eigenvalue tolerance le-2 Relative decrease in function value tolerance le-5 Max TNT iterations 500

Initial trust-region radius (o) 1

Trust region decrease factor (ai) 0.25

Trust region increase factor (a2) 2.5

Max GC iterations 2000 Successful CG step (77) 0.9 Max dual ascent iterations (T) 1000

-Dual ascent gradient tolerance 0.5

-Dual ascent gradient stepsize 0.005

-Table 2.1: Parameters used in DARS and FUSES.

2.4.2

Setup, Compared Techniques, and Performance Metrics

Setup. We evaluate FUSES and DARS using the Cityscapes dataset [21], which contains a large collection of images of urban scenes with pixel-wise semantic annotations. The annotations include 30 semantic classes (e.g., road, sidewalk, person, car, building, vegetation). We first extract superpixels from the images using OpenCV (we obtain around 1000 superpixels per image, unless specified otherwise). Then, the unary terms are obtained using the 512 x 256 pretrained model from Bonnet

1461,