A Rough-Cut Capacity Planning Model with Overlapping

A Rough-Cut Capacity Planning Model with

Overlapping

Baydoun G.1_{, Haït A.}2 _{and Pellerin R.}1

1 _{École Polytechnique de Montréal, Montréal, Canada}

georges.baydoun, robert.pellerin@polymlt.ca

2 _{University of Toulouse, Institut Supérieur de l’Aéronautique et de l’Espace, Toulouse, France}

alain.hait@isae.fr

Keywords: Rough-Cut Capacity Planning, Concurrent Engineering, Overlapping. 1 Introduction

The overlapping of activities is a common practice to accelerate the execution of engi-neering projects. This technique consists in executing in parallel two sequential activities by allowing a downstream activity to start before the end of an upstream activity based on preliminary information. However, the overlapping of activities can entail rework tasks and modifications further to the transmission of complementary information after the start of the downstream activity (Grèze et. al. 2012). Activity overlapping thus allows reducing the total duration of project execution, at the expense of additional workload and execution cost associated to rework tasks. In this paper, we propose a Rough-Cut Capacity Planning (RCCP) model that determines the order of execution in time of a set of work packages (WPs) so as to minimize the total project duration and/or project cost, while respecting precedence relations, resource constraints and considering overlapping possibilities. The model was developed for supporting the project planning function in the early phases of projects by considering variable activity intensities, and aggregate resource capacities. The reminder of the paper is organized as follow. We first give a brief state of the art of existing RCCP and Resource-Constrained Project Scheduling Problem (RCPSP) models and over-lapping models. We then introduce our RCCP model with multiple overover-lapping modes. In section 4, we present preliminary results before concluding the paper in section 5.

2 Related work

Several authors have studied the relation between rework and the amount of overlap in project conducted in a concurrent engineering context but only few papers have incorpo-rated overlapping in the RCPSP. For instance, Gerk and Qassim (2008) proposed a linear model for project acceleration using crashing, overlapping and activity substitution. This model assumes that the relation between overlap amount and rework is continuous and linear. Grèze et. al. (2012) proposed a more realistic approach by restricting overlapping possibilities to a set of feasible overlap durations for each couple of overlappable activities, instead of considering a continuous and linear relation between overlap amount and rework. This assumption is more realistic as scheduling is performed in practice on a period-by-period basis (i.e. resource availabilities and allocations are determined per period-by-period). Also, overlapping points between activities is defined through clear document or information exchange in a concurrent engineering context, which limits the overlapping modes to a reduced and discrete set of possibilities.

However, these RCPSP models are not suited for planners in the early phases of projects as detailed activity content and resources are not known with precision and as work in-tensity is assumed to be constant over execution time. Indeed, planners tend to adopt an

ning horizon into time buckets (or periods) used to evaluate critical resource usage and by allowing resource allocation to WP to vary from one period to another (De Boer 1998). As such, a WP may start or end during a period; it is therefore possible to plan a WP and its successor within the same period.

Among existing RCCP models, Hans (2001) proposed an exact approach that consists in determining the periods where each job can be executed, and then specifying the fractions of the WP contents that are actually executed in each period. Several heuristic approaches have also been proposed to solve the RCCP problem including constructive heuristics (De Boer 1998) and linear-programming based heuristics (Gademann and Schutten 2005). How-ever, none of these models considers overlapping and rework. To fill this gap, we propose a mixed integer linear-programming model, that is an extension of the RCCP model proposed by Haït and Baydoun (2012), where predecessor-successor WPs can overlap according to multiple overlapping modes. This extended model assumes that each overlapping mode can be defined by the percentage of execution of predecessor WP that needs to be reached in order to start the successor, as well as the amount of reworks on both WPs. The model is further explained in the following section.

3 RCCP model with overlapping

The model of Haït and Baydoun (2012) combines a continuous time representation of events and a discrete time evaluation of resources. A set of binary variables ensures the relation between starting time, ending time and durations over periods. These durations give minimum and maximum workload that can be assigned to the period. Our new model is based on the same representation of time and events of WP start and WP end, but adds a third type of events: intermediate milestone attainment.

An overlapping mode between a WP i and its successor j is defined regarding the attainment – in terms of workload – of a milestone within WP i; the successor can start once the milestone is reached. Each WP i is therefore divided into Ci+ 1 parts, the end of each part matching the time when a milestone of i is reached. Each part has its own set of durations over the periods, denoted dc

ip, and assigned workload during the periods, lc

ip. Variables dcip are used to guarantee that workloads lipc always respect the minimum and maximum intensities. Constraints (1) ensure that the required workload is attained for each part of WP i according to the selected mode.

X

p∈P

l_ipc ≥ Lc

im· eim ∀i ∈ I, c ∈ {1..Ci+ 1}, m ∈ Mi (1)

The end of each part gives the time tc

i when a successor in Succ1ican start. Constraints (2) ensure that successor j begins after the correct milestone of i. For successors in Succ0i that cannot overlap on i, a classical end-to-start constraint is defined in constraints (3).

t0_j ≥ tc

i− H · (1 − eim) ∀i ∈ I, m ∈ Mi, j ∈ Succ1i, c ∈ {1..Ci+ 1|c = P osijm} (2) t0_j ≥ tCi+1

i ∀i ∈ I, j ∈ Succ0i (3)

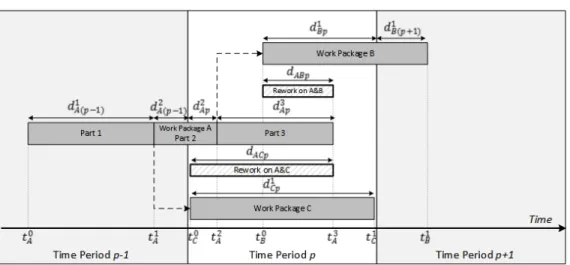
Figure 1 presents an example of a WP (A) with two successors (B, C) that can overlap. A is therefore divided into three parts. In the depicted mode, the milestone corresponding to C comes before the one corresponding to B. Consequently C can start after the end of the first part of A, while B can start after the end of the second part of A.

Table 1. Nomenclature : sets & parameters / variables

P, D, H Set of time periods (p ∈ P ), duration of a period, time horizon H = D · |P | I Set of work packages (i ∈ I)

RDi, DDi Ready date (respectively due date) of i (t0i ≥ RDi; tC_ii+1≤ DDi ∀i ∈ I)

R Set of resources (r ∈ R)

Krpint Available regular capacity of resource r during period p

Air Percentage of consumption of resource r by WP i

BJimin, BJ max

i Minimum and maximum workload that can be assigned for i during a duration of D

Succ0i Set of successors of i that cannot overlap on i (j ∈ Succ0i)

Succ1i, Ci Set of successors of i that can overlap on i (j ∈ Succ1i), Ci= |Succ1i|

P red1i Set of predecessors of i that can overlap on i (i0∈ P redi)

Mi Set of overlapping modes between i and its direct successors (m ∈ Mi)

P osijm Position of j among the successors of i according to mode m ∈ Mi

Chijm Binary parameter that equals 1 if WPs i and j overlap in mode m ∈ Mi

Lcim Required workload of part c of WP i in mode m

Lpredijm, L succ

ijm Required rework on i (respectively on j) in mode m ∈ Midue to overlapping

between i and j

Cext, Crwk Unitary cost of non-regular capacity and rework (respectively)

t0i, t Ci+1

i Starting time and ending time of i

tci For c ∈ 1..Ci: ending time of part c of i (tc+1i ≥ t c

i ∀i ∈ I, c ∈ {0..Ci})

zcip For c ∈ 0..Ci+ 1 : binary variable that equals 1 if tci is in period p or before

eim Binary variable that equals 1 if mode m is chosen for i ( P m∈Mi

eim= 1)

dcip Duration of part c of i within period p

dijp Duration of overlapping between i and j within period p

lipc Workload of part c of i during period p

l_ijppred, lsucc

ijp Rework on i (resp. j) during p due to overlapping between i and j

yint

rp, yrpext Regular and non-regular required capacity of resource of resource r in period p

rwk Total amount of rework in the project f Project makespan (f ≥ tCi+1

i ∀i ∈ I)

Fig. 1. A work package (A) with two successors (B, C) that can overlap.

In addition to initial workloads, reworks are required on predecessors and successors that overlap. The reworks should be executed during the overlapping time between predecessors and successors. Constraints (4) and (5) make sure that the total executed reworks match the required reworks in selected modes.

X

p∈P

lpred_ijp ≥ Lpred_ijm · eim ∀i ∈ I, m ∈ Mi, j ∈ Succ1i (4) X

p∈P

lsucc_ijp ≥ Lsucc

ijm · eim ∀i ∈ I, m ∈ Mi, j ∈ Succ1i (5)

Workload variables lc_ip, l_ijppred, and l_ijpsuccare linked to durations dijpand dcipto ensure the respect of minimum and maximum allowed intensities. Constraints (6) and (7) guarantee that total assigned workload for WP i in period p stays in the allowed workload window for the total duration dc

ip in period p. Constraints (8), (9), and (10) ensure that maximum intensity is respected for initial workload as well as for reworks.

Ci+1 X c=1 l_ipc + X j∈Succ1i lpred_ijp + X i0∈P red1i lsucc_i0ip ≤ BJmax i · Ci+1 P c=1 dc_ip D ∀i ∈ J, p ∈ P (6) Ci+1 X c=1 lipc + X j∈Succ1i lpred_ijp + X i0∈P red1i lsucci0ip ≥ BJ min i · Ci+1 P c=1 dc ip D ∀i ∈ J, p ∈ P (7) lcip≤ BJimax· dc ip D ∀i ∈ J, c ∈ {1..Ci+ 1}, p ∈ P (8)

lpred_ijp ≤ BJmax

i ·

dijp

D ∀i ∈ J, j ∈ Succ1i, p ∈ P (9)

lsucc_ijp ≤ BJmax

j ·

dijp

D ∀i ∈ J, j ∈ Succ1i, p ∈ P (10)

tc_i ≥ D · p · (1 − zc

ip) ∀i ∈ J, c ∈ {0..Ci+ 1}, p ∈ P (11)

tc_i ≤ D · p + H · (1 − zc

ip) ∀i ∈ J, c ∈ {0..Ci+ 1}, p ∈ P (12)

zip+1c ≥ zipc ∀i ∈ J, c ∈ {0..Ci+ 1}, p ∈ {1..|P | − 1} (13) Constraints (14) to (18) provide the link between durations per periods dc

ipand variables tc

i and zipc. Inequalities (14) force dcip to 0 if the corresponding part of the WP is finished before period p or is started after p and give upper-bound for other cases. Inequalities (15) give dc_ip lower-bounds if the correspond part of WP begins before period p and is not completed during p. Constraints (16) (respectively(17)) provide lower-bounds for dc_ip when the corresponding part of WP is finished (respectively started) in period p. Finally, constraints (18) provide global coherence between starting and ending times, and durations per periods. dc_ip ≤ D · (zc−1_ip − zip−1c ) ∀i ∈ J, c ∈ 1..Ci+ 1, p ∈ 1..|P | (14) dcip ≥ D · (z c−1 ip−1− z c ip) ∀i ∈ J, c ∈ 1..Ci+ 1, p ∈ 1..|P | (15) dc_ip ≥ tc i− D · p + D · z c−1 ip−1− H · (1 − z c ip) ∀i ∈ J, c ∈ 1..Ci+ 1, p ∈ 1..|P | (16) dc_ip ≥ D · p · (1 − zc−1 ip−1) − t c−1 i − D · z c ip ∀i ∈ J, c ∈ 1..Ci+ 1, p ∈ 1..|P | (17) |P | X p=1 dc_ip= tc_i − tc−1 i ∀i ∈ J, c ∈ {1..Ci+ 1} (18)

Constraints (19) to (21) give upper-bound for overlapping durations within periods dijp. Constraints (19) and (20) make sure that overlapping durations within periods never exceed durations within periods of both predecessor i and successor j. Constraints (21) ensure that overlapping durations do not surpass the span between the starting time of j and ending time of i.

dijp≤d1jp ∀i ∈ J, j ∈ Succ1i, p ∈ P (19)

dijp≤ Ci+1 X c=1 dc_ip ∀i ∈ J, j ∈ Succ1i, p ∈ P (20) dijp≤tCii+1− t 0 j+ H · (1 − eim) ∀i ∈ J, j ∈ Succ1i, m ∈ {Mi|chjim= 1}, p ∈ P (21) The following constraints are straight-forward results of the definition of variables yint_rp, y_rpext, rwk and c. yintrp + yextrp ≥ X i∈I Air· ( Ci+1 X c=1 lcip+ X j∈Succ1i l_ijppred+ X i0∈P red1i lisucc0ip) ∀r ∈ R, p ∈ P (22) yint_rp ≤ Kint rp ∀r ∈ R, p ∈ P (23) rwk = X i∈I,p∈P X j∈Succ1i lpred_ijp + X i0∈P red1i lsucci0ip (24) c = Crwk· rwk + Cext· X r∈R,p∈P yrpext (25)

Possible objective functions are project delivery time f , project cost c or a trade-off between delivery time and cost.

and that are commonly used to test RCCP models. These instances were modified in order to handle overlapping. Half of predecessor-successor couples were randomly selected and were allowed to overlap. Each selected couple has a maximum of two overlapping modes (80% and/or 60% of the workload of predecessors) and reworks were fixed proportionally (factor of 0.4) to the maximum workload that can be overlapped. We tested our model using CPLEX 12.5 on instances, with and without overlapping. We solved the problem with two objective functions: project cost (cost of using external resources and adding reworks), and project delivery time. The results for one instance of 10 WPs (table 2) show that overlapping is beneficial in both cases. Note that the objective can easily be adapted in order to make a trade-off between project cost and delivery time.

Table 2. Results for instance RCCP 125

Without overlapping With overlapping

Cost Makespan CPU time Cost Makespan Total rework CPU time Minimise cost 3269.9 31 1.75 s 3261.5 30.313 33.84 5 s Minimise delivery time 3540.2 29 1.5 s 3673.4 27.54 119.04 2.57 s Minimise delivery time with a target cost of 3540.2 3540.2 28.031 119.04 4.28

5 Conclusion

In conclusion, we proposed an interesting extension of the RCCP that allows overlapping of work packages. Preliminary results show that overlapping adds a flexibility in distributing the workload for earlier delivery date or smaller cost of project.

Future work will focus on improving the performance of our model, and conduct an extended analysis on the benefits of overlapping, over a sufficient number of instances. References

Cherkaoui, K., Pellerin, R., Baptiste, P. and Perrier, N., 2013 "Planification hiérarchique de projets EPCM", 10ème Conférence Internationale de Génie Industriel 2013, June 12-14, La Rochelle, France.

De Boer, R. 1998, "Resource-constrained multi-project management : a hierarchical decision sup-port system", PhD thesis, University of Twente, Enschede, Netherlands.

Gademann, N. and Schutten, J.M.J. 2005, "Linear-programming-based heuristics for project ca-pacity planning", IIE Transactions, Vol 37(2), pp. 153-165.

Gerk, J. and Qassim, R. 2008, "Project Acceleration via Activity Crashing, Overlapping, and Substitution", IEEE Transactions on engineering management, Vol. 55(4).

Grèze, L., Pellerin, R., Leclaire, P. and Perrier, N., 2012, "A heuristic method for resource-constraint project scheduling with activity overlapping", to appear in Journal of Intelligent Manufacturing, DOI 10.1007/s10845-012-0719-5.

Haït, A. and Baydoun, G. 2012, "A new event-based MILP model for the resource-constrained project scheduling problem with variable intensity activities", The IEEE International Con-ference on Industrial Engineering and Engineering Management 2012, Hong Kong, 10-13 De-cember.

Hans, E. 2001, "Resource loading by Branch-and-Price techniques", PhD thesis, University of Twente, Enschede, Netherlands.