NOOMEN BEN GHORBAL
ETUDE DE CERTAINES MESURES
D'ASSOCIATION MULTIVARIÉES ET D'UN
TEST DE D É P E N D A N C E EXTRÉMALE
FONDÉS SUR LES RANGS
Thèse présentée
à la Faculté des études supérieures de l'Université Laval
dans le cadre du programme de doctorat en mathématiques
pour l'obtention du grade de PhilosophiaeDoctor (Ph.D.)
DEPARTEMENT DE MATHEMATIQUES ET DE STATISTIQUE
FACULTÉ DES SCIENCES ET DE GÉNIE
UNIVERSITÉ LAVAL
QUÉBEC
2010
Cette thèse contribue à la modélisation de la dépendance stochastique par la théorie des copules et la statistique non paramétrique. Elle s'appuie sur trois articles rédigés avec mes directeurs de thèse, M. Christian Genest et Mme Johanna Neslehovâ.
Le premier article, intitulé « On the Ghoudi, Khoudraji, and Rivest test for extreme-value dependence, » a été publié en 2009 dans La revue canadienne de statistique, vol. 37, no 4, pp. 534-552.
Le second article, intitulé « Spearman's footrule and Gini's gamma : A review with complements, » paraîtra sous peu dans le Journal of Nonparametric Statistics.
Le troisième article, intitulé « Estimators based on Kendall's tau in multivariate copula models, » est en cours d'évaluation.
Abstract
This thesis contributes to the modeling of stochastic dependence using the theory of copulas and nonparametric statistics. It is based on three papers written with my Ph.D. supervisors, Professors Christian Genest and Johanna Neslehovâ.
The first paper, entitled "On the Ghoudi, Khoudraji, and Rivest test for extreme-value dependence," was published in 2009 in The Canadian Journal of Statistics, vol. 37, no 4, pp. 534-552.
The second paper, entitled "Spearman's footrule and Gini's gamma : A review with complements," will appear soon in the Journal of Nonparametric Statistics.
The third paper, entitled "Estimators based on Kendall's tau in multivariate copula models," is currently under review.
Avant tout, je remercie Dieu le tout-puissant de m'avoir accordé son infinie bonté, ainsi que le courage, la force et la patience pour réaliser cet humble travail.
Je tiens ensuite à remercier sincèrement mes codirecteurs de thèse, M. Christian Genest et Mme Johanna Neslehovâ, d'avoir accepté de diriger mes travaux. Je leur suis reconnaissant de la confiance qu'ils m'ont accordée et du soutien dont ils m'ont gratifié. Leurs encouragements, leurs précieux conseils et leur disponibilité m'ont permis d'élargir mes connaissances et d'avancer considérablement mes recherches.
Je dois ma première expérience d'enseignement au directeur du département, M. Roger Pierre. M. Jean-Pierre Carmichael, M. Gaétan Daigle, Mme Hélène Crépeau ont participé à ma formation au Service de consultation statistique. M. Thierry Duchesne, M. Rachid Kandri-Rody et Mme Emmanuelle Reny-Nolin m'ont soutenu au long de ma formation comme chargé de cours. À vous tous, mes salutations les plus distinguées.
Ma gratitude va aussi à tous les professeurs du département, qui m'ont procuré l'occasion d'aiguiser mes compétences en mathématiques et en statistique. Je remercie tout spécialement M. Lajmi Lakhal Chaieb pour son soutien et pour m'avoir aidé à intégrer le milieu étudiant.
Je tiens à exprimer la profonde gratitude que j'ai envers mes parents bien aimés, El Béji et Fathia, ma chère épouse Jihène, mon grand frère Walid, mes deux sœurs Elham et Henda, et enfin à tous mes neveux et nièces, pour le support moral, la compréhension et l'encouragement qu'ils m'ont offerts. Je remercie enfin tous mes amis intimes et tous mes collègues, grâce auxquels ces quatre années de travail ont été agréables.
Merci enfin aux organismes suivants pour leur soutien financier (par l'intermédiaire d'octrois accordés à mes directeurs) : le Conseil de recherches en sciences naturelles et en génie du Canada, le Fonds québécois de la recherche sur la nature et les technologies, l'Institut des sciences mathématiques et l'Institut de finance mathématique de Montréal.
J'exprime aussi ma gratitude envers les membres du jury, M. Christian Genest, Mme Johanna Neslehovâ, M. Louis-Paul Rivest, M. Thierry Duchesne et M. Friedrich Schmid, qui ont accepté de lire et d'évaluer cette thèse. Leurs commentaires judicieux ont permis d'améliorer sa version finale. Finalement, un remerciement va à Mme Line Baribeau pour avoir accepté d'agir à titre de président lors de la soutenance.
Lis au nom de ton Seigneur qui a tout créé, qui a créé l'homme d'une adhérence! Lis, car la bonté de ton Seigneur est infinie ! C'est Lui qui a
fait de la plume un moyen du savoir et qui a enseigné à l'homme ce qu'il ignorait. ]
[Ce sont les cinq premiers versets de Sourate Al-Alaq du Saint Coran. La grande majorité des savants musulmans affirment qu'elles constituent la toute première révélation descendue sur le Saint Prophète Mohammad—paix et bénédiction de Dieu soient sur lui.]
Table des matières
R é s u m é ii A b s t r a c t iii A v a n t - P r o p o s iv Table des m a t i è r e s viii
Liste des t a b l e a u x ix Table des figures xi
1 I n t r o d u c t i o n 1 2 Préliminaires 4
2.1 Définition d'une copule 4 2.1.1 Une copule de type extrême 5
2.1.2 Inference basée sur les rangs 6 2.2 Quelques mesures d'association 6
2.2.1 Axiomes de Scarsini 7 3 S p e a r m a n ' s footrule a n d Gini's g a m m a : A review with c o m p l e m e n t s 9
3.1 Introduction 10 3.2 Definitions and basic properties 12
3.3 Distribution under independence 13 3.4 Distribution in the case of dependence 14
3.5 Asymptotic relative efficiency 15 3.6 Estimation of the asymptotic variance 18
3.7 Extensions 19 3.8 Sample properties in the multivariate case 21
3.9 Conclusion 23 3.10 Appendix 24
3.10.1 Proof of Proposition 3.1 24 3.10.2 Proof of Proposition 3.3 25
3.10.3 Moments of <p„ at independence 27
3.10.4 Computation of of, 28
3.11 Acknowledgements 30 4 E s t i m a t o r s based on K e n d a l l ' s t a u in multivariate copula models 32
4.1 Introduction 34 4.2 Properties of r^ and examples of calculation 30
4.2.1 Meta-elliptical copulas 4.2.2 Archimedean copulas
4.2.3 Farlie-Gumbel-Morgenstern copulas 39
4.3 Properties of T<Jn 40
4.4 Properties of the coefficient of agreement 43
4.4.1 Bounds 43 4.4.2 Sampling properties 44
4.5 Comparison of the estimators 45
4.6 Conclusion 49 4.7 Appendix 50 4.8 Acknowledgements 55
5 O n t h e G h o u d i , Khoudraji a n d Rivest test for extreme-value
depen-dence 57 5.1 Introduction 58
5.2 Description of the test statistic 59
5.3 Finite- and large-sample variance of Sn 61
5.4 Estimators of the finite- and large- sample variance 64
5.5 Finite-sample power of the test 67 5.6 Large-sample power of the test 69 5.7 Illustrations and discussion 72
5.8 Appendix 75 5.8.1 Proof of proposition 1 75
5.8.2 An algorithm for computing the variance of Sn 77
5.9 Acknowledgements 79
6 Conclusion 80 Bibliographie 82
Liste des tableaux
4.1 Seven expectations needed to compute var(fn) 52
5.1 Fifteen indicator random variables whose expectations appear in the
va-riance of Sn 64
5.2 Rejection rate (in percent) of the null hypothesis for the test based on the jackknife and the plug-in variance estimates, as observed in 100,000 random samples of size n = 50, 100 and 200 from the Cuadras-Augé (CA), Galambos (GA), Gumbel-Hougaard (GH), Clayton (C), Frank (F), Normal (N), Plackett (P) and Student copula (t4) when r = 1/4,
1/2, 3/4 68 5.3 P-values (in percentage) for the test of extremeness based on b \ (upper
triangular part) and for the Cramer von Mises goodness-of-fit test that the copula is Gumbel-Hougaard (lower triangular part) for the 21 pairs
of variables in the uranium exploration data set 74
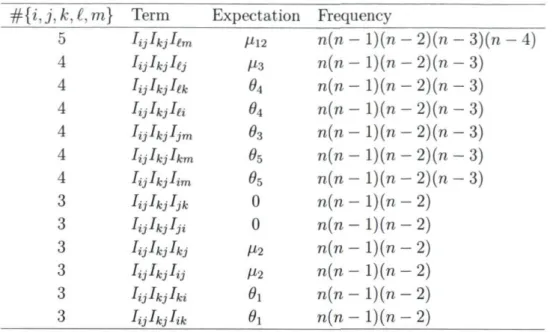
5.4 Seven expectation terms for calculating An 70
5.5 Thirteen expectation terms for calculating Bn 77
3.1 Relative efficiency of ipn versus pn (left) and 7n versus pn (right) as a
function of parameter m ^ 1 in the Woodworth alternatives of Example
3.4 17
3.2 Dispersion of the asymptotic variance estimate of Spearman's footrule (left) and Gini's gamma (right), based on 100 random samples of size n = 50,100,250 and 500 from the Farlie-Gumbel-Morgenstern copula
with parameter 9 = 1/2 20 4.1 Dispersion of estimators #2,n> ®T,n, &T,n and ffyn around the percent relative
bias, based on 5000 random samples of size 100 from two 5-dimensional Ar-chimedean copulas, the Clayton (top) and the Gumbel-Hougaard (bottom),
when r2 = 3/10 (left), 5/10 (center), and 7/10 (right) 47
4.2 Dispersion of the estimators 02,n, ®T,n, #r,n and 6(<n around the percent relative
bias, based on 5000 random samples of size 100 from three 5-dimensional ex-changeable meta-elliptical copulas, the Normal (top), the Student £5 (middle), and the Student £2 (bottom), when r2 = 3/10 (left), 5/10 (center), and 7/10
(right) 48 4.3 Dispersion of estimators QT,U^ &T,TI a nd dt,n around the percent relative bias,
based on 5000 random samples of size 100 from two Archimedean copulas in dimensions 5 and 10, the Clayton (top) and the Gumbel-Hougaard (bottom),
when r2 = 3/10 (left), 5/10 (center), and 7/10 (right) 49
5.1 Finite-sample (left) and limiting (right) variance of \ / n Sn, as a function
of 8 G [0,1] in the Cuadras-Augé family of extreme-value copulas. In the left panel, the curves are for n = 10, 25, 50, 100 and 1000, from top to
bottom 63 5.2 Eight panels showing the observed variation in the plug-in and jackknife
variance estimators of Sn, based on 1000 samples of size n = 50 (left)
and 100 (right) of the Cuadras-Augé copula with r = 0, 1/4, 1/2, 3/4 (from top to bottom). Each panel shows, from left to right, the boxplots of o ^ , à\ and <3j. The horizontal lines represent the true value of the
XI
5.3 Asymptotic local power of the test of level 5% when C0 is the
indepen-dence copula and C\ is the Plackett with r = 1/4,1/2,3/4 (from bottom
to top) in the mixture model (5.6) 71 5.4 Asymptotic local power of the test of level 5% when C0 is the
Cuadras-Augé with r = 1/4,1/2,3/4 (from bottom to top) and C\ is the Farlie-Gumbel-Morgenstern copula with 7 = 1/2 (left) and 7 = 1 (right) in
the mixture model (5.6) 72 5.5 Graph connecting the pairs of variables in the uranium exploration data
set which could be modelled adequately by an extreme-value copula. The two edges surmounted by an asterisk are those for which a
Introduction
On peut faire remonter la théorie des copules aux travaux de Sklar (1959). Depuis, son application ne cesse de s'étendre à tous les domaines scientifiques et économiques, conséquence de la flexibilité et de la robustesse qu'elle procure dans la modélisation de la structure de dépendance entre les composantes d'un vecteur aléatoire X = { X \ , . . . , Xd)
indépendamment de ses marges.
Selon le théorème de décomposition de Sklar, on peut exprimer la fonction de ré-partition du vecteur X sous la forme
H ( x1, . . . , xd) = P ( X i ^ xu. . . , Xd ^ xd) = C { Fl( x i ) , . . . , Fd( xd) } ,
où F i , . . . , Fd sont les fonctions de répartition des variables X i , . . . , Xd et C est une
copule, c'est-à-dire une fonction de répartition de marges uniformes sur [0,1].
La structure de dépendance caractérisant les variables à étudier est complètement déterminée par la copule sous-jacente. Puisque cette dernière est invariante par transfor-mations continues et croissantes des marges, l'inférence concernant C ou les paramètres qui en dépendent peut être limitée aux rangs des observations. Ceci permet en outre d'éviter qu'une mauvaise spécification des marges affecte l'inférence.
La théorie des copules est un outil privilégié pour l'étude des mesures de dépendance non paramétriques. Les plus connues sont certainement le rho de Spearman et le tau de Kendall. Mais ces dernières années, deux mesures d'association anciennes ont refait surface dans la littérature scientifique : la règle de Spearman et l'indice gamma de Gini. En raison de sa simplicité, de sa robustesse et de son interprétation naturelle, la règle de Spearman a de fait été redécouverte et utilisée dans divers contextes depuis
Chapitre 1. Introduction
l'an 2000, notamment en génomique, en bioinformatique et dans les expériences de puces à ADN. Plus populaire dans les cercles mathématiques, l'indice gamma de Gini pourrait lui aussi gagner en faveur populaire, notamment en raison de sa relation avec la règle de Spearman (Nelsen & Ubeda-Flores 2004).
À l'appui de ces développements récents, l'article présenté au chapitre 3 vise à conso-lider les connaissances basées sur la règle de Spearman et l'indice gamma de Gini. La littérature sur le sujet y est rassemblée et organisée de façon structurée. La théorie des copules y sert de cadre unificateur. Ceci conduit à plusieurs résultats nouveaux, qui sont démontrés et illustrés. Après avoir examiné les propriétés de base et les relations entre la règle de Spearman et l'indice gamma de Gini, on décrit leurs lois sous l'indépendance et sous des contre-hypothèses générales. Divers résultats concernant des tests d'indé-pendance basés sur ces deux coefficients sont ensuite présentés. Puis, une procédure jackknife est détaillée pour l'estimation de la variance asymptotique de ces statistiques sous une structure de dépendance quelconque. Enfin, des généralisations multidimen-sionnelles de ces deux mesures sont considérées et leur comportement stochastique est étudié. Quelques recommandations pratiques sont formulées en conclusion.
Récemment, les modèles de copule ont été favorisés par un nombre croissant de chercheurs dans des domaines tels que l'assurance, la finance, la gestion des risques et l'hydrologie. Dans ces domaines d'application, le nombre de variables considérées est parfois très grand mais par souci de simplicité, on suppose souvent que la copule sous-jacente provient d'une classe (Ce) dont le paramètre 9 est unidimensionnel.
Le projet d'article présenté au chapitre 4 a pour objectif d'examiner l'estimation de 9 basée sur l'inversion du tau de Kendall dans un modèle multidimensionnel de copules et de comparer cette solution à l'approche standard, qui consiste à maximiser la pseudo-vraisemblance, telle que discutée par Genest, Ghoudi & Rivest (1995) et Shih & Louis
(1995). Deux généralisations du tau de Kendall sont considérées. La première option est due à Joe (1990), qui définit le tau de Kendall en dimension d par
^
x
)=^M-
i
+
2
'
J
(
0
,
I
]'
c ( u ) d c ( u )
}-Beaucoup plus ancienne, la deuxième option remonte aux travaux de Kendall &: Ba-bington Smith (1940). Ce tau de Kendall d-varié est défini comme la valeur moyenne des taus de Kendall calculés sur toutes les paires possibles (Xr, Xs) avec r ^ s, à savoir
T
d(X) = —^—S2MX
r,X
s).
d(d - 1) ^
Au chapitre 4, on fournit des propriétés de base de rd et quelques exemples de calculs
ensuite décrites ; les résultats s'avèrent très similaires à ceux qui sont déjà connus dans le cas bivarié. En particulier, l'inversion de rd conduit à un estimateur convergent de
9 sous des conditions de régularité minimales. Puisque l'évaluation numérique de rd
est parfois difficile, il est tentant de fonder l'estimation du paramètre de dépendance sur l'inversion de Td. En vue de comparer ces deux approches, les propriétés de la
version empirique Td n de Td sont d'abord présentées. Les résultats d'une étude de
Monte-Carlo sont ensuite rapportés. Il appert que pour les diverses familles de copules multidimensionnelles utilisées, les deux stratégies sont presque équivalentes.
Le dernier chapitre de la thèse concerne la modélisation d'une paire (X, Y) de va-riables aléatoires dans le cas où l'on soupçonne que leur structure de dépendance est de type extrême. Avant de sélectionner un modèle de copule paramétrique pour une telle paire, il est nécessaire de vérifier que la copule sous-jacente C est bel et bien extrémale. D'après Pickands (1981), les copules de ce type s'expriment sous la forme
C(u,v) = exp ln(uv)A ' ln(uv)
en terme d'une application convexe A : [0,1] —» [1/2,1] telle que max(£, 1— t) ^ A(t) ^ 1 pour tout t G [0,1]. Le seul test de dépendance extrémale actuellement disponible a été proposé par Ghoudi, Khoudraji & Rivest (1998). Toutefois, ses propriétés n'ont encore jamais été étudiées à ce jour. Le but de l'article contenu dans le chapitre 5 est de combler cette lacune. Ce test s'appuie sur une [/-statistique dont on détermine la varian-ce asymptotique et à taille finie. On propose en outre des estimations de varian-cette varianvarian-ce qu'on compare à l'estimateur jackknife de Ghoudi, Khoudraji & Rivest (1998) à l'aide de simulations. Par la suite, on évalue le seuil, la puissance et l'efficacité asymptotique de ce test sous diverses contre-hypothèses, tant par des calculs théoriques qu'à l'aide de simulations. Finalement, on illustre le propos au moyen de données financières et géologiques.
Chapitre 2
Préliminaires
Au cours des dernières années, la popularité des copules n'a cessé de croître. Ce concept est un outil intéressant qui permet de modéliser la dépendance entre les com-posantes d'un vecteur aléatoire X = ( X i , . . . ,Xd). En effet, selon le théorème de Sklar
(1959), la fonction de répartition conjointe du vecteur X peut s'exprimer sous la forme H { xx, . . . , xd) =PLYi ^ X i , . . . , Xd^ xd) = C { F1( x1) , . . . , Fd( xd) } ,
en terme d'une copule C et des fonctions de répartition marginales F i , . . . , Fd des
va-riables X \ , . . . , Xd. De plus si les marges sont continues, alors C est unique.
Pour alléger la compréhension du concept de modélisation par copule, nous allons dorénavant nous limiter au cas bidimensionnel.
2.1 Définition d'une copule
Une fonction C : [0, l]2 —> [0,1] est une copule si elle satisfait les conditions
sui-vantes :
(i) C(u, 0) = C(0, v) = 0 pour tous u, v G [0,1] ; (ii) C(u, 1) = u et C(l, v) = v pour tous u, v E [0,1] ;
(iii) Pour tous ui,U2,Vi,V2 G [0,1] tels que u\ ^ «2 et v\ ^ t>2, on a C(u2,v2) - C ( u2, v i ) - C(ui,v2) + C(ui,vi) ^ 0.
Un modèle de copule pour la paire (X, Y) consiste à supposer que l'on peut écrire H(x,y) = P ( X ^ x , Y ^ y ) = C{F(x),G(y)}
pour tous x,y Ç. R, où par hypothèse C G (Ce). En d'autres termes, on suppose que la copule liant les marges dépend d'un paramètre d'association 9. Ces modèles offrent une entière flexibilité dans le choix des marges de X et Y, qui peuvent être supposées connues ou appartenir à des familles paramétriques (Fa) et (Gp).
Toute copule C est bornée par les copules W(u, v) = rnax(« + v — 1,0) et M(u, v) = min(u,v), appelées les bornes de Fréchet-Hoeffding. En d'autres termes, les inégalités
W(u,v) < Ce(u,v) ^ M(u,v),
sont valides pour tous u,v G [0,1]. Si les variables X et Y sont continues et indépen-dantes, alors la copule les liant est définie en tous u, v G [0,1] par
C(u, v) = U(u,v) = uv.
On dit qu'une copule C\ est plus petite qu'une copule C2 si Ci(u, v) ^ C2(u, v) pour tous u,v G [0,1]. On note alors C\ -< CV
2.1.1 Une copule de type extrême
Une façon commode d'appréhender le comportement extremal commun de X et Y consiste à modéliser leur fonction de répartition conjointe sous la forme
H(x, y) = P ( X ^ x , Y ^ y ) = C{F(x),G(y)}, x,y e R où F(x) = P ( X ^ x), G(y) = P(Y ^ y) et C est une copule de type extrême.
Cette approche est motivée par le fait que les copules de ce type caractérisent les structures de dépendance extrémale asymptotique. D'après Pickands (1981), les élé-ments de cette classe c(o de copules s'expriment en tous u,v G (0,1) sous la forme
ln(t C(u,v) = e x p ln(uv)A
M
y
uv) J \n(uv)
en terme d'une application convexe A : [0,1] —» [1/2,1] telle que max(t, 1—t) ^ A(t) < 1 pour tout t G [0,1].
Chapitre 2. Préliminaires 6
2.1.2 Inference basée sur les rangs
La dépendance entre deux variables X et Y est toujours caractérisée par une copule. Puisqu'une copule C est invariante par transformation croissante des marges
(X,Y)r+(<f>(X),tb(Y)),
toute l'information concernant la dépendance dans un échantillon (X\, Y i ) , . . . , (Xn, Yn)
est contenue dans les couples de rangs notés par (Ri, S i ) , . . . , (Rn, Sn) qui sont associés
aux observations.
Les paires (Rt/n, Si/ri) peuvent être considérées comme des pseudo-observations de la copule sous-jacente qui caractérise la structure de dépendance. Comme Rùschendorf (1976) et Deheuvels (1979) l'ont montré, une estimation convergente de C est fournie par la copule « empirique, » définie en tous u,v E [0,1] par
C
n(u,v) = - £ l ( — — r < « , — ~ < v)
n r ^ V n + l n + 1 /où 1(E) dénote l'indicateur de l'ensemble E. Toute mesure de dépendance fondée sur les rangs peut s'exprimer en terme de Cn et le pendant théorique de la même mesure
s'exprime en fonction de la copule.
2.2 Quelques mesures d'association
Plusieurs mesures d'association classiques peuvent être exprimées en fonction de la notion de « concordance. » D'un point de vue intuitif, on dit qu'une paire de variables aléatoires est concordante (discordante) si une valeur élevée d'une des variables s'associe généralement avec une valeur élevée (faible) de l'autre variable.
De façon plus formelle, soit (Xi,Yi) un couple aléatoire de copule Ci et ( À ^ , ^ ) un autre couple de copule CY La différence Q entre la probabilité de concordance et la probabilité de discordance des couples est alors définie par
Q = Q(Ci,C2)
= p{(Xi - x2) (y, - Y2) > 0} - P{(X, - X2) (Y, - Y2) < 0}
= - 1 + 4 [ f C2(u,v)dCi(u,v).
On peut aisément évaluer Q pour les trois copules repères W, M et II. On trouve Q ( M , M ) = 1, Q ( W , W ) = - 1 , Q(M,W) = 0,
Q ( M , n) = 1/3, Q ( W , n ) = - 1/3, Q(U, U) = 0.
Tel que montré entre autres dans le livre de Nelsen (2006), plusieurs mesures de dépendance non paramétriques classiques peuvent s'exprimer en terme de Q. Ainsi si X et Y sont des variables aléatoires continues dont la copule est C, on peut montrer que la valeur théorique du tau de Kendall entre X et Y est donnée par
rx,Y = rc = Q(C, C) = - 1 + 4 / / C(u, v) dC(u, v).
De même, la valeur théorique du rho de Spearman entre X et Y est donnée par
P X Y = P C = 3Q(C, n) = - 3 + 12 / / uvdC(u, v). JJ[0,1}2
Un troisième exemple est fourni par la mesure d'association de Gini entre X et Y, laquelle est donnée par
1X,Y = 1 C = Q(C,M) + Q ( C , W )
= 2 ff (\u + v - l \ - \ u - v \ ) d C ( u , v ) .
JJ[0,1}2
Ces mesures d'association sont souvent appelées des mesures de concordance, dû au fait qu'elles répondent à un ensemble d'axiomes proposé par Scarsini (1984).
2.2.1 Axiomes de Scarsini
Une mesure d'association KX,Y = «c entre deux variables aléatoires continues X et Y de copule C est une mesure de concordance si et seulement si les conditions suivantes sont vérifiées :
1. La mesure K est définie pour toute paire (X, Y) de variables aléatoires continues. 2. Il faut que - 1 ^ KX,Y < L *x,x = L «x,-x = - L
«y,x-Chapitre 2. Préliminaires 8
4. Si X et Y sont indépendantes, alors Kxy = Kn = 0.
5. Il faut que K_X,K = « x - y = —Kxy-6. Si Ci -< C2, alors «Ci ^ Kc2
-7. Si {(Xn, Y„)} est une suite de variables aléatoires continues issue de la copule C„
et si C„(u, v) —> C(u, v) en tous u,v G [0,1], alors lim^oo Kcn =
KQ-On se convainc facilement que les valeurs théoriques du tau de Kendall, du rho de Spearman et du gamma de Gini sont des mesures de concordance au sens de Scarsini (1984). Notons cependant que toutes les mesures d'association provenant de la fonc-tion Q ne sont pas nécessairement des mesures de concordance. Par exemple, la valeur théorique de la règle de Spearman, définie par
<PX,Y = <Pc = \ {3Q(C,M) - 1} = 1 - 3 ( f \ u - v\dC(u,v),
Spearman's footrule and Gini's
gamma : A review with
complements
R é s u m é
La littérature éparse sur la règle de Spearman et l'indice gamma de Gini est colligée. Les sujets suivants sont abordés : moments à taille finie et loi limite sous l'indépendance ; loi asymptotique sous des contre-hypothèses arbitraires ; efficacité relative asymptotique pour tester l'indépendance ; estimateur jackknife convergent de la variance asympto-tique ; généralisations multivariées et applications. Des résultats complémentaires et une vaste bibliographie sont présentés, ainsi que plusieurs illustrations originales.
Abstract
The scattered literature on Spearman's footrule and Gini's gamma is surveyed. The following topics are covered : finite-sample moments and asymptotic distribution under independence ; large-sample distribution under arbitrary alternatives ; asymptotic relative efficiency for testing independence ; consistent asymptotic variance estimation through the jackknife ; multivariate generalisations and uses. Complementary results and an extensive bibliography are provided, along with several original illustrations.
Spearman's footrule and Gini's gamma 10
3.1 Introduction
Spearman's footrule is a nonparametric measure of association. It was introduced by the British psychologist Charles Spearman as an alternative to the correlation in the pairs (Ri, S i ) , . . . , (Rn, Sn) of ranks associated with a random sample ( X i , Y i ) , . . . ,
(Xn,Yn) from some continuous bivariate distribution H(x,y) = P ( X ^ x, Y ^ y).
Spearman's footrule usually refers to the statistic
<fn = I ~ ^ r ÊlRiSil (3.1) although other normalisations have been used, even by Spearman himself (cf. Spearman
1904, 1906; Dinneen and Blakesley 1971). This coefficient is closely related to the indice de cograduazione semplice introduced by the Italian statistician, demographer and sociologist Corrado Gini (1914), viz.
7n =
R / 2 ] Ê {K»+ ! " * ) SI U* " Sl> ■ (
3
2)
where [^J denotes the integer part of arbitrary m > 0.Spearman's footrule and Gini's gamma remained largely neglected until fairly re cently. In the 4th edition of his book on rank correlation methods, Kendall (1970) discussed the footrule as a nonparametric measure of association but dismissed it be cause of a lack of statistical properties. Prior to 1980, the main sources of information on Gini's gamma were in Italian (Savorgnan 1915 ; Salvemini 1951 ; Amato 1954; Cucconi 1964).
Interest in Spearman's footrule was apparently revived by Diaconis and Graham (1977), who highlighted its natural interpretation in terms of the Manhattan (or city block) distance between two sets of ranks. They derived its asymptotic distribution under independence and noted that in small samples, it is less variable than Spearman's rho, which is based on the Euclidean metric. Extensions have since been proposed to handle data that are incomplete (Alvo and Charbonneau 1977), multivariate (Ubeda Flores 2005), and censored (Sen, Salama, and Quade 2003; Salama and Quade 2004; Quade and Salama 2006).
Because of its simplicity, robustness and natural interpretation, the footrule has since been rediscovered and used in various contexts. For instance, motivated by litigation about a scoring procedure for civil service examinations, Berman (1996) proposed the statistic Mn = XXR* — Si)l(Ri > Si) as a measure of "unfairness" when the results of
an exam leading to ranks R i , . . . , Rn are replaced by scores leading to ranks S i , . . . , Sn.
However, Berman did not notice that Mn — (n2 — 1)(1 — <^n)/6.
In the field of genomics, a simple function of <çn was advocated a few years ago
by Kim, Rha, Cho, and Chung (2004) to measure reproducibility among replicates in microarray experiments, which are likely to produce outliers due to a low signal-to-noise ratio. In the field of information retrieval, Spearman's footrule distance has also been used to measure the discrepancy between rank lists (Fagin, Kumar, and Sivakumar 2003; Mikki 2010). The same idea was used very recently in gene expression profiling and in bioinformatics by Iorio, Tagliaferri, and di Bernardo (2009) and by Lin and Ding (2009), respectively.
In comparison with Spearman's footrule, Gini's gamma seems to be used rather rarely in practice. This may well change in the years to come, however, as a strong connection between the two coefficients was recently uncovered by Nelsen and Ubeda-Flores (2004). They observed that 7„ is in fact an extension of ipn which Salama and
Quade (2001) introduced to remedy its asymmetry, already noted by Spearman (1904). In support of these recent developments, this paper aims to consolidate the know-ledge base on Spearman's footrule and Gini's gamma. The scattered literature on the subject is collected and organised in a structured way using the theory of copulas as a unifying framework. This leads to several new results, proofs and illustrations.
Section 3.2 reviews basic properties and relations between Spearman's footrule and Gini's gamma. Sections 3.3 and 3. 1 describe their distributions under independence and under general alternatives, respectively. Section 3.5 collects results on tests of indepen-dence based on the two coefficients.
A jackknife procedure is detailed in Section 3.6 for the estimation of the statistics' asymptotic variance under any dependence structure. Finally, multivariate extensions of ipn and 7n are considered in Section 3.7, and their sampling properties are studied
in Section 3.8. Practical recommendations are summarised in the Conclusion.
Various Appendices contain the technical arguments, including new, simpler proofs of known results based on the asymptotic behaviour of the empirical copula process.
Spearman's footrule and Gini's gamma 12
3.2 Definitions and basic properties
It is clear that the statistic <pn defined in Equation (3.1) equals 1 when Ri = Si for
allz G { 1 , . . . , n}. It takes its smallest value when the two sets of ranks are antithetic, that is, when Ri = n + 1 — 5, for every i G { 1 , . . . , n}. A simple calculation shows that
£ | n +
l - 2 i |
= i
1 = 1
n2/2 when n is even,
(n2 — l)/2 when n is odd.
Therefore, v?n varies in [—1/2,1] when n is odd but it can go as low as — (n2 + 2)/{2(n2 —
1)} G [ - 1 , - 1 / 2 ) for n even.
In order to span the entire interval [—1,1], one can replace 3/(n2 — 1) by 2/[n2/2j
in Equation (3.1). Even if this is done, the statistic tpn may still be regarded as
unsa-tisfactory in some applications. This is because it generally assigns different degrees of dependence (in absolute value) to the samples ( X i , Y i ) , . . . , (Xn, Yn) and (—Xi,Yi),...,
( - Xn, Yn) . For example, if {XuYi) = (10,20), (X2,Y2) = (20,30) and {X3,Y3) =
(30,10), then <pn = - 1 while <pn = 0 for the sample (-10,20), (-20,30) and (-30,10).
As explained by Salama and Quade (2001), this problem can be solved by making (pn symmetric with respect to the rank transformation R t-> n + 1 — R. Nelsen and
Ubeda-Flores (2004) pointed out that the resulting coefficient is the right-hand side of Equation (3.2), that is, Gini's 7„.
Many properties of tpn and 7n stem from their representation as linear rank statistics.
From the identity \u — v\ = u + v — 2 min(u, v) valid for all u,v Ç.R, one gets 1 « / Ri Si \ 2 n + l
¥n = r 2 ^ J* — — , ——" r- , (3.3)
n - l ~ [ \ n + l n + U n —
\
where Jtp(u,v) = 6min(u,v). Similarly, one can use the identity \(n + 1) — u — v\ = 2max{0,it + v — (n + 1)} — u — v + (n + 1) to see that
2 [ n y 2 \ ^
l J l{ n - r l
,n + l ) [n
2/2\ ' ^
4 j3.3 Distribution under independence
The behaviour of ipn, 7„ and variants thereof has been extensively studied under the
assumption that the variables X and Y are independent. From results which Spearman (1904) attributed to Felix Hausdorff (see, for example, Kleinecke, Ury, and Wagner 1962 for a derivation), one gets
E(ifn) = 0 and var ((/?„) =
5(n + l ) ( n - l )
2'
Tables of the null distribution of tpn were produced by Ury and Kleinecke (1979).
They were later expanded by Franklin (1988) and Salama and Quade (1990) ; see also Salama and Quade (2002). Diaconis and Graham (1977) were apparently the first to show that under independence,
n1/2^ - ^ ( 0 , 2 / 5 ) ,
where ~> denotes convergence in distribution as n —> oo. See Sen and Salama (1983) for an alternative proof.
For Gini's gamma, Amato (1954) and Cucconi (1964) obtained independently
f 2(n
2+ 2)
E(7n) = 0 and var(7„) = <3(n - l)n2
2(n2 + 3)
{ 3 ( n - l ) ( n2- l )
when n is even;
when n is odd.
A third derivation was provided by Salama and Quade (2001) but note the typo in their final formula for n even.
The exact null distribution of Gini's gamma was given by Savorgnan (1915) for n ^ 5 ; these tables were later extended by Salvemini (1951) and Cifarelli and Regazzini (1977). In addition, Rizzi (1971) used simulations to approximate the null distribution of 7„ up to n = 30. Betrô (1993) later showed how the exact distribution can be derived numerically. Other approximations were designed by Landenna and Scagni (1989), and by Vittadini (1991). It was suspected for a long time (Salvemini 1951 ; Amato 1954; Cucconi 1964 ; Herzel 1972) that under independence,
n1 / 27 n - ^ ( 0 , 2 / 3 )
Spearman's footrule and Gini s gamma 14
3.4 Distribution in the case of dependence
The asymptotic distribution of Gini's gamma was given by Cifarelli, Conti, and Regazzini (1996) in the general case where the pair (X, Y) has a bivariate distribution H(x, y) = P(X < x,Y < y) with continuous margins F(x) = P(X ^ x) and G(y) = P(Y ^ y). The parallel result for Spearman's footrule is reported below, seemingly for the first time.
As it turns out, the large-sample distributions of (pn and 7n depend on H only
through the function C implicitly defined by
H(x, y) = P(X < x, Y < y) = C{F(x), G(y)}
for all x,y G R. The so-called copula C, which is unique, is a bivariate distribution function with uniform margins on the interval (0,1) (Nelsen 2006, Chap. 2).
The following proposition, whose proof is in Appendix 3.10.1, shows that ipn and 7„
are asymptotically unbiased estimators of
(fc = 1 - 3 f \ u - v \ d C ( u , v ) = - 2 + 6 / C ( t , t ) d i
y(o,i)2 Jo
and
7c = 2 / {\u + v - l \ - \ u - v \ } d C ( u , v ) = - 2 + 4 f {C(t,t) + C(t, 1 - t)}dt,
J{0,1)2 Jo
respectively. From these definitions, reported by Nelsen (1998), it is clear that (pc and 7c depend only on the copula's main and secondary diagonal sections, defined for all t G [0,1] by C(t,t) and C(t, 1 - t), respectively.
P r o p o s i t i o n 3 . 1 . Suppose that a bivariate copula C admits continuous partial deriva-tives Ci(u,v) = dC(u,v)/du and C2(u,v) = dC(u,v)/dv on (0,1). Then as n —» oo,
n1'2 (<pn - <pc) - ^ ( 0 , a2 ), n1/2 (7 n - 7c ) - ^ ( 0 , < r2 ), tt&hrteft i n fTnimtirfn i
with o2 and oi defined in Equations (Al) and (A2), respectively.
When C(u, v) = U(u, v) = uv is the independence copula, one gets o ^ = 2/5 and <r2c = 2/3. Additional examples of explicit calculations are given below.
E x a m p l e 3.1. Let C(u,v) = uv + 9uv(\ — u)(l — v) be the Farlie-Gumbel-Morgenstern copula with parameter 9 G [—1,1]. Routine calculations yield <pc — 0/5, 7c = 45/15,
2 2 3 . 11 .o , o 2 88 ^9
CT2 = - H 9 9l and a2 = 9 .
E x a m p l e 3.2. Given 9 G [1,1], let A(v) = 9sin(2Kv)/(2it) and C(u,v) = uv + u(l -u)A(v) for all u, v G (0,1). These are examples of copulas with quadratic sections, as defined by Quesada-Molina and Rodriguez-Lallena (1995). Interestingly, <pc = 7c = 0
for all 9 G [—1,1]. This is in fact the case for any measure of concordance à la Scarsini (1984), because C(u,v) + C(u, 1 — v) = u for all u,v G (0,1), so that all members of this family are "indifferent," in the sense given to that term by Gini ; see Conti (1994). With the help of Maple, one finds
2 1080 92 + 72 flV + 225 0 V + 64 TT6
a*c ~ 160 7T6
and
2 _ 330 92 + 24 0 V + 95 0 V + 20 TT6
° ^c ~~ 3 0 ^ "
3.5 Asymptotic relative efficiency
Spearman's footrule and Gini's gamma are natural statistics for testing indepen-dence. Cifarelli and Regazzini (1977) compared the merits of the test based on j n in
terms of Pitman's asymptotic relative efficiency in a Gaussian model. More recently, Conti and Nikitin (1999a) computed the local Bahadur efficiency of <pn and 7„ for a
large class of alternatives. As the test statistics are rank-based, the calculations rely only on the dependence structure under the alternative, that is, the copula.
In their work, Conti and Nikitin (1999a) considered copula alternatives defined for each u, v G (0,1) by Ce(u,v) = uv + 9Qe(u,v), where 0 ^ 0 and Qe is a non-negative function whose mixed partial derivative satisfies mild conditions. They showed that for such alternatives, Bahadur's and Pitman's efficiencies coincide.
Using results of Genest et al. (2006b), one can extend these comparisons to other copula families (Ce) in which independence occurs when, say, 9 = 0. Indeed, note that by Equations (3.3) and (3.4), ipn and 7„ are asymptotically equivalent to statistics of
the form
*-kp(£î-&)-*Zptà-viàïY
(35)
Here, J = J^ and J' = J7, respectively. Many classical nonparametric tests of
indepen-dence are based on statistics of the form (3.5) for some score function J.
Given right-continuous, square-integrable, quasi-monotone score functions Jj and J2, it is shown by Genest et al. (2006b) that Pitman's asymptotic relative efficiency
Spearman's footrule and Gini's gamma 16
(ARE) equals
A R E ( 5B^ , S * ) = f ^ ^ ) ,
provided that the family (Ce) of copula alternatives meets mild regularity conditions concerning mainly the existence and properties of the function Co, defined as dCe(u, v)/ 89 evaluated at 9 = 0. Here, p ji is the derivative with respect to 0 of the asymptotic
mean of S£ under Ce, evaluated at 0 = 0, that is,
PJi = / C0(u,v)dJi(u,v).
.7(0,1)2
Furthermore, o2 stands for the asymptotic variance of S„* at independence.
Given below are applications of this result when J\, J2 G {J^,,/^ Jp} with Jp(u,v)
= 12uv for all u,v & (0,1), which corresponds to Spearman's rho.
E x a m p l e 3.3. If Ce is the Gaussian copula and $ denotes the cumulative distribution function of a <yV(0,1) random variable, one finds C0(u, v) = $ ' { $- 1( u ) } $ ' { $_ 1( v ) } for
all « , » E (0,1). Thus, p jv = \/3//T, p j1 = 4/(\/3TT) and p jp = 3/#T. Hence
A R E ( S ^ , Sfr) = - w 0.83 and A R E ( 5 ^ , S%>) = - « 0.89.
These calculations are in accordance with the findings of Cifarelli and Regazzini (1977). For this class of alternatives, both Spearman's footrule and Gini's gamma are less efficient than Spearman's rho. The Pitman efficiency of the latter is 9//T2 ~ 0.91 as
compared to the van der Waerden statistic, which is locally optimal for such alternatives (Genest and Verret 2005).
E x a m p l e 3.4. Suppose that the family (Ce) is such that for all u,v ÇL (0,1), C0(u, v) =
kuv(um — l)(vm — 1) for some k > 0 and m ^ 1. The Farlie-Gumbel-Morgenstern,
Dabrowska, Plackett and Frank families of copulas fall in this category when m = 1. The alternatives of Woodworth (1970) illustrate the case m > 1. Simple calculations yield
4A:m2 3fcm2
^
=( m + 3)(2m + 3) *
M^
=JÏ+^mJ
2'
A complex but explicit expression is also available for p ^ ; it reduces to 4fc/15 if m = 1. Using op = 1, one recovers the results of Conti and Nikitin (1999a) for m = 1,
viz.
A R E ( S ; S ^ ) = - = 0 . 9 0 and ARE(SnJ\SnJ") = - = 0.96.
1U 25
Spearman's footrule and Gini's gamma are thus somewhat less efficient than Spear-man's rho, which is the locally optimal test statistic for this class of models (Genest and
Verret 2005). As shown in Figure 3.1, however, <pn eventually becomes more efficient
than pn as m —> oo, while 7„ gradually looses ground when m ^ 2. In fact,
10 2 lim AKE(SJn^SJn") = — ~ 1.11 and lim ARE(5^,5^") = - .67.
F I G U R E 3.1 - Relative efficiency of ipn versus pn (left) and 7„ versus pn (right) as a
function of parameter m ^ 1 in the Woodworth alternatives of Example 3.4.
E x a m p l e 3.5. Suppose that the family (Ce) is such that for all u, v G (0,1), CQ(U, V) = kuv \n(u) \n(v) for some k > 0. The Clayton/Cook Johnson and Gumbel-Barnett fa-milies fall in this category, as well as Model 4.2.10 of Nelsen (2006). Here, p jv = Ak/9,
p j1 = /c(15 — 7r2)/9 and p jp = 3k/4. Consequently,
A R E ( # , # ) - | § * . 8 8 and ARE(S„\<#>) = ~ ^ « -87. The tests based on <pn and 7„ thus have similar efficiencies. For this class of alternatives,
however, neither they nor the test based on pn can be recommended. Indeed, the Pitman
efficiency of Spearman's rho is only 9/16 ~ .563 compared to Savage's log-rank test, which is the locally most powerful test statistic in this case (Genest and Verret 2005).
The final example, adapted from Conti and Nikitin (1999a), exhibits dependence models for which Spearman's footrule and Gini's gamma are the locally most powerful test statistics.
Spearman's footrule and Gini's gamma 18
and
Q ( u , , ) = u,+ ^ l' - " - "| 3 +' " - 1' '3 -3 ( t t 2 + " ' - " - ) - 1 > .
6
Both of them lie in the class of cubic-section copulas introduced by Nelsen, Quesada-Molina, and Rodriguez-Lallena (1997). As shown by Conti and Nikitin (1999a), tests of independence based on ipn and ~yn are locally most powerful for the classes of alternatives
Cg and Cg, respectively. For the family Cg, one gets pj^ = 2/5, pJ y = 1/2 and
PJP = 3/5. Thus,
ARE(SJn-,SJn") = l ^ \ . l l and ARE(SJ n\ S^") = | j « 1.04.
For Cg, one finds p jv = 1/2, /xj7 = 2/3 and p jp — 4/5. Hence,
125 25 A R E ( < ^ , < ^ ) = — « 0 . 9 8 and A R E ( S £ , S £ ) = - * 1 M .
3.6 Estimation of the asymptotic variance
An alternative derivation of the limiting distributions of <pn and 7„ was given by
Conti (1994) using an asymptotically equivalent (/-statistic (see also Cifarelli et al. 1996). His approach leads to a consistent estimate of their large-sample variances. Given u,v, s,t G R, let
ipi(u,v;s,t) = \u — v\ +sign(u — v){l(s < u) - l(t < v) — u + v},
tb2(u,v;s,t) = \u + v — 1| + sign(w + v — l){l(s ^ u) + l ( t ^ v) — u — v},
with the convention sign(0) = —1. For k = 1,2, define ^ ( u , v;s,t) = xjjk{u,v;s,t) + ijjk(s,t;u,v) as well as
^ = ( 2 ) E^iUuVi^Vj),
where Ui = F(Xi), Vi = G(Yi) for i G { 1 , . . . , n). Conti's result is as follows (see Conti 1994 for a proof).
P r o p o s i t i o n 3.2. If the conditions of Proposition 3.1 hold, then as n —> oo, n1 / 2( Tl n- ^ c ) - ^ ( 0 , < T2 C) and nl'2( T2 n - Tl B - 7c ) - ^ ( 0 , a2 c) .
Let <r2c and d2 c be the delete-one jackknife variance estimators based on Tl n and
T2 n — Ti„, respectively. The theory of (/-statistics (Lee 1990, Chap. 5) implies that o2 c
is a consistent estimate of cr2c ; similarly, o2 c estimates o2 c consistently. In his work,
Conti (1994) used slight variants based on the work of Sen (1960). Specifically, let
TfeM = - \ f; MUuVi,Uj,Vj)
n
-
1i-ti*
for A; = 1,2 and i G { 1 , . . . , n}. Conti's estimators of o ^ and o2 c are then given by A2 — ST'f'r v \2 — (n ~ *> ~i
and
*2 4 » 2 (n ~ 2)2 2
respectively. In this fashion, var(<r2c) < var(à2 c) and var(â2 c) < var (cr2c).
As shown by Conti (1994), the delete-one jackknife remains consistent when Ut
and V{ are replaced by Fn(Xi) = Ri/n and Gn(Yi) = Si/n, where Fn and Gn are the
empirical versions of F and G, respectively.
The procedure can be implemented more easily upon noting that ^ i ( u v s t)
—^—-— = 1 {u ^ min(u, s), t < min(v, 5)} + 1 {s ^ min(i, u), v < min(£, u)} and
^ 2 { u , v ; s , t )
= 1 {s ^ min(w, 1 —t),v > max(£, 1 — u)\
+ 1 {u ^ min(s, 1 — v),t > max(v, 1 — 5)} . The behaviour of <72c and o2 c is illustrated in Figure 3.2 using random samples of
size n = 50,100,250 and 500 from the Farlie-Gumbel-Morgenstern copula with para-meter 0 = 1/2. As can be seen, the convergence is fairly rapid. The same phenomenon was observed for several other classes of copulas [results not shown].
3.7 Extensions
In recent years, various generalisations of Spearman's footrule and Gini's gamma have been proposed. In particular, Cifarelli et al. (1996) considered
Spearman's footrule and Gini's gamma 20 1 1 1 — ' ■ — 1 .. - —1 , 1—1 1 I 1 1— o o ) n=250 n=500
F I G U R E 3.2 - Dispersion of the asymptotic variance estimate of Spearman's footrule
(left) and Gini's gamma (right), based on 100 random samples of size n = 50,100,250 and 500 from the Farlie-Gumbel-Morgenstern copula with parameter 0 = 1/2.
and
79,c
/ {g(\u + v - l \ ) - g ( \ u - v \ ) } d C ( u , v )
•'(0,1)where g : [0,1] —¥ [0,1] is a strictly increasing, continuous function. If in addition g is convex and satisfies g(0) = 0, 73;c is a measure of concordance in the sense of Scarsini
(1984) ; the cases g(t) = t and g(t) = t2 correspond to Gini's gamma and Spearman's
rho, respectively. Cifarelli et al. (1996) identified the asymptotic distribution of the empirical version of 7ffic and showed how to estimate its variance consistently by the
jackknife. See Conti and Nikitin (1999b) for additional limiting results. However, it is not clear how g should be chosen in practice.
More recently, multivariate versions of Spearman's footrule and Gini's gamma were proposed by Ubeda-Flores (2005) and by Behboodian, Dolati, and Ubeda-Flores (2007), respectively. The d-variate version of ipc is
<Pc = P ~ ^ f \ c ( t , . . . , t ) + C ( t , . . . , t ) } d t
-d — 1 Jo d - 1
where C is the distribution function of 1 — U with U = ( U i , . . . , Ud) distributed as
C. Ubeda-Flores (2005) showed that ipc = 0 at independence and <pc = 1 at the Fréchet-Hoeffding upper bound, defined for every u \ , . . . , ud € (0,1) by
In addition, he proved that the inequality <fc ^ — 1/d always holds and that if Ci2,Ci3,C23 are the bivariate margins of a trivariate copula C, then
Pc = g {feu + VcX3 + Vc23)- (3.6)
This property, which does not extend to higher dimensions, is shared by the multi-variate extension of Gini's gamma proposed by Behboodian et al. (2007). The latter is defined as a linear transformation of
7c = l \ c ( t , . . . , t ) + C(t,...,t)}dt+ E l - l )
1 4 1/ MiM)dC(u),
Jo X QD Ao,i)d
where |A| denotes the cardinality of the set A Ç D = { 1 , . . . , d} and u^ is the vector derived from u = ( i t i , . . . , ud) G (0, l )d by replacing its £th coordinate by 1 if and only
if t £ A. The expression for 7C also involves the multivariate Fréchet-Hoeffding lower
bound, defined for every i t i , . . . ,ud G (0,1) by
W ( u i , . . . , ltd) = max(0, Ui + (- ud + 1 — d).
More specifically, Behboodian et al. (2007) defined 7c = (7c — 2ad + l)/(2&d — 2ad)
with
chosen in such a way that 7c = 0 at independence and 7c = 1 at M.
3.8 Sample properties in the multivariate case
Given a random sample ( X n , . . . , X id) , . . . , ( Xni , . . . , Xn d) from some continuous
d-variate distribution, and ( R u , . . . , R id) , . . . , (i2»»i, • • •, Rnd) the associated vectors of
componentwise ranks, Ubeda-Flores (2005) defined the empirical version of <pc by , d + 1 " Li
where for each i G { 1 , . . . , n } , Lt = max(i?ji,..., Rid) — m i n ( R n , . . . , Rid). The
follo-wing proposition, whose proof is in Appendix 3.10.2, implies that ipn is asymptotically
Spearman's footrule and Gini's gamma 22
P r o p o s i t i o n 3.3. Suppose that a d-variate copula C admits continuous partial deriva-tives C \ ( « i , . . . , ud) = d C ( u i , . . . , ud) / d u i , . . . , Cd( u i , . . . , ltd) = d C ( ux, . . . , ud)/dud on
(0, l)d. Then as n —> oo,
n1/2(<pn-<Pc) - ^ ( 0 , a jc) ,
where a2 c is defined in Equation (A5).
It is checked readily that Equation (A5) reduces to Equation (Al) when d = 2, and that Property (3.6) continues to hold for the empirical version of ipc- Although a closed-form expression is available for o2 , its computation can be tedious. Here is a
simple example in dimension d = 3.
E x a m p l e 3.7. Given 0i2,0i3,023,0m G ( — 1,1) and u, v,w G (0,1), the expression C(it, v, w) = uvw{l + 012(1 - it)(l - v ) + 013(1 - it)(l - w)+
023(1 - V)(l - W ) + 0123(1 - U)(l - V)(l - W)}
defines a trivariate version of the Farlie—Gumbel-Morgenstern copula when the para-meters meet suitable conditions. Simple algebra yields tpc = (0i2 + 013 + 023)/15 and
^ 5 Ô(^2 + ^3 + ^2 3 )" Î 3 5
Note that 0123 is absent from the formulas, as might be expected from Property (3.6) PC = Tg + ^q (#12 + #13 + #23) — Ï35Ô (é'l2+013 + 6 ,23)_ Y ^ (012^13+ 012023+ 013023) •
One possible use of the extended version of ipn is as a test statistic for multivariate
independence. It is shown in Appendix 3.10.3 that under the null hypothesis,
w x , d + 1 n f 2 " fk\d) ,n„,
Observe that while it vanishes when d = 2 or 3, this expectation is only 0 ( l / n2) in
general and, for example, equals l/(9n2) when d = 4. A closed-form expression for the
finite-sample variance of <pn is also given in Equation (A6), but it is cumbersome.
In view of Proposition 3.3, a more practical solution is to reject the null hypothesis at asymptotic level a if \(pn\/on is larger than the quantile of level 1 — a / 2 of the jV(t), 1)
distribution. Here, o \ stands for the large-sample variance of ipn under H0, that is,
when the underlying copula is U.(ui,..., ud) = iti x • • • x ud for all Ui,... ,ud € (0,1).
As shown in Appendix 3.10.4,
/ d + l \2f 2 + 4 d - d2 + d3 âë(d,d + 2)
where Se denotes the Beta function. In particular, o \ = 2/5, 2/15 and 149/2268 when d = 2, 3 and 4, respectively.
Behboodian et al. (2007) defined the empirical version of 7c by _ Y n - C n
l n ~ d - c
for appropriate normalising constants c„, dn and a function 7* of the vectors R i , . . . , R„
of normalised ranks given for each i G {!,...,ri) by R = {Ru,...,Rid) /(n + 1).
Specifically,
1 "
Af(Ri) + W(R,) + £ ( - 1 ) W { M ( R M ) + W ( R M ) }
ACD
where for each i G { 1 , . . . , n}, Rj^ is the vector obtained from R G (0, l )d by replacing
its £th coordinate by 1 if and only if £ £ A.
It may be conjectured that j n is an unbiased, asymptotically normal estimator of
7c in arbitrary dimension d ^ 3. It will be a challenge to determine its large-sample variance, however, even under independence. This may be the object of future work.
3.9 Conclusion
This paper reviewed and complemented the properties of Spearman's footrule and Gini's gamma. As mentioned in the Introduction, Spearman's footrule, cpn, is quickly
gaining popularity in applications, mainly due to its interpretation as a Manhattan distance between two sets of ranks. As such, it is more robust than, for example, Spear-man's rho which is based on the Euclidean distance. However, it suffers from one major drawback, namely its asymmetry. Gini's statistic, 7„, corrects this defect while maintai-ning the interpretation as a distance. From this point of view, it thus seems preferable.
Furthermore, <pn and 7„ may be regarded as measures of non-linear association.
Ho-wever, only 7„ satisfies the axiomatic definition of such a measure proposed by Scarsini (1984). Nonetheless, both statistics can be used for testing independence. In most cases considered here, they turned out to be less efficient than the classical Spearman's rho. A general recommendation cannot be made, however, as both <pn and 7„ are locally
optimal for specific classes of alternatives. For additional discussion on rank-based tests of independence and efficiency considerations, see, for example, Genest and Rémillard (2004), Genest and Verret (2005) and Genest et al. (2006b).
Spearman's footrule and Gini's gamma 24
At present, standard errors for ipn and 7„ are rarely found in applications, if ever.
Asymptotic confidence intervals for both statistics can be derived readily from Propo-sition 3.1 using the simpler form of Conti's variance estimator given in Section 3.6.
Results in Sections 3.7 and 3.8 make it possible to use the multivariate version of Spearman's footrule proposed by Ubeda-Flores (2005) for the comparison of d ^ 3 sets of ranks. It was shown that ipn is again asymptotically normal, but that it is generally
biased in finite samples if d ^ 4. The asymptotic variance under independence was com-puted and can be used to construct tests for multivariate independence. Similar results concerning the multivariate extension of Gini's gamma are still under development.
3.10 Appendix
3.10.1 Proof of Proposition 3.1
First define a variant of the empirical copula of Deheuvels (1979) by Cn(u,v) = - J 2n r - J V n + 1 n + 1 / 1{ — T T ^u- — T T ^ v)
for every u,v G (0,1). Observe that for any score function J : (0, l )2 —> M, one has
n fj-J \ n + l n + 1 J J(o,i)2
If in addition J itself is a copula, up to a multiplicative constant, Fubini's theorem yields
/ J(u,v)dCn(u,v) = Cn(u,v)dJ(u,v).
7(0,1)2 7(0,1)2
When these identities are used with J = J^, Equation (3.3) becomes 6n /* , . , 2n + 1
V n = 7 / Cn(t,t)
n — 1 Jo
dt
n - 1 '
which shows that n1//2 (<pn — ipc) has the same asymptotic behaviour as
Z
c,
n= 6Jc
n(t,t)dt,
where Cn = n1'2 (Cn — C) is the empirical copula process. Similarly, n1 / 2 (7„ — 7c)
Now it has been known since the work of Riischendorf (1976) that when C admits continuous partial derivatives, Cn converges weakly as n —> oo to a continuous centred
Gaussian process C of the form C(u,v) = Uc(u, v) — Ci(u, v)Vc(u, l) — C2(u,v)Wc(l,v)
for all u, v G (0,1). Here, Uc denotes a pinned C-Brownian sheet, that is, a cen-tred Gaussian random field whose covariance function at u , v , s , t G (0,1) is given by cov{Uc(u, v),Uc{s, t)} = C{min(u,s),mm(v,t)}—C(u,v)C(s,t). See, for example, Fer-manian, Radulovic, and Wegkamp (2004), Stute (1984), Tsukahara (2005) for further discussion.
Because Zc,n is a continuous linear functional of Cn, it converges weakly as n —> oo
to the centred Gaussian random variable ZQ = 6 / C(i, t) dt with variance
o%c = 3 6 £ fQ cov{C(s, s),C(t, t)} dsdt. (Al)
Similarly, the weak limit of Zc as n —> oo is the centred Gaussian random variable
Z*c = 4 f{C(t, t) + C(t, 1 - t)} dt with variance
o2 c = 16 f j cov{C(s, s) + C(s, 1 - s),C(t, t) + C(t, 1 - t)} ds dt. (A2)
The latter limit corresponds to the case g(t) = t in Cifarelli et al. (1996, Theorem 4.1).
3.10.2 Proof of Proposition 3.3
For arbitrary u = ( u i , . . . ,ud) G (0, l)d, let
1 A , / #U ^ Rid
i - 1
be the d-variate empirical copula. One then has d + 1 n
1(0,1)*
and the factor n/(n — 1) can be ignored asymptotically.
c„(u) = - £ i ( — - V ^ «i,...,—TT ^
u<n
n f ^ K n + 1 n + 1 J pirical copula. One then has
<Pn = 1 ~ - , — 7 7 / {max(u) - min(u)}dC„(u), (A3) d — 1 n — 1 J(o,i)d
Now if ( U i , . . . , Ud) has distribution Cn and U is an independent uniform random
variable on (0,1), then / max(u)dCn(u) = 1 - P(f/ > Uu. . . , U > Ud) = 1 - / C„(t, ...,*)d< J(0,l)d Jo and / min(u)dC„(u) = P(U < f/j,... ,U ^ Ud) = / ' P(f/j > t , . . . , Ud> t ) J(o,i)d Jo dt.
Spearman's footrule and Gini's gamma 26
The latter expression can be formulated alternatively in terms of C
nby means of
the inclusion-exclusion formula. To this end, let |A| denote the cardinality of any set
A Ç D = { 1 , . . . , d}, and denote by t
Athe vector (ti,
.
.., t
d) such that t
e= tl(£ G
A) + 1(£ $ A) for all £ G ( 1 , . . . , d} so that, for example, t
D= (t,..., t). Then
p(Ui > t , . . . , u
d> t ) = Y , (~
l)
lA]p( r \ i
ui < *}) = E (-i)
|i4|Cn(t,0,
AÇD \içA J AÇDwhere an intersection over the empty set is to be interpreted as the sure event.
Similarly, one has
f
1c(t,...,t)dt= f
1c ( i - t , . . . , i - t ) d t = £ ( - i )
, A |fc(t
A)dt.
Jo Jo £~D Jo
Consequently, w}l2(ipn — </?c) has the same asymptotic behaviour as d +
\\£c
n(t
D)dt+ Y, (-i)
141f*c
n(t
A)dt\,
ZC,n = d
which is a continuous linear functional of the process C
n. From the work of Riischendorf
(1976), the limit of the latter is of the form
C(u) = Uc(u) - D Q f u J U c N (A4)
j = i
for arbitrary u = (iti,... ,itd), where Uj represents a d-dimensional vector with Uj in
its jth coordinate and 1 everywhere else. Here, Uc is a d-variate centred Gaussian
field with covariance given by cov{Uc(u),Uc(v)} = C(u A v) — C(u)C(v), where for
all u, v G (0, l)
d, u A v represents the componentwise minimum. Thus Zc,
nconverges
weakly as n —> oo to a centered Gaussian random variable
^c =
dT^\fc(t
D)dt+ £(-l)
|A|/ ' c ^ d t l .
d - 1 j^O Xçjj JO J
Hence if s
Ais defined as t
Amutatis mutandis, the variance of Zc is given by
<c = {jz\) lr(D,D) + 2^-l)Wr(A,D) + r(D,D)\, (A5)
where for arbitrary A, B Ç D, one has
T(A,B)= f l\ov{C(s
A),C(t
B)}dsdt
Jo Jo
and
T(D,D)= Y, E ( - l )
| 4 | + | B |r ( A , B ) = f f* cov{C(3
D),C(t
D)}dsdt.
AÇDBÇD ° °
Here, the process C is defined in Equation (A4), with C replaced by C everywhere.
Thus when C is radially symmetric, that is, C = C, one gets T(D, D) — T(D, D).
3.10.3 M o m e n t s of tp
nat independence
For arbitrary integers k ^ n, let k / n ^ denote the vector ( k i , . . . , k
d)/(n + 1), where
k
t= kl(£ G A) + ( n + 1)1(£ £ A) for all £ G { l , . . . , d } . Using results stated on
p. 59 of Hâjek and Sidâk (1967), one can see easily that E{C
n(k/n^)} = ( k / n ) ^ at
independence. Thus if t^ is defined as in Appendix 3.10.2, one gets
E
{/„' ° ^ *} =Ti £ ■ W*fcd> ^ g g
W
It then follows from the identities proven in Appendix 3.10.2 that
E { f max(u)dC
n(u)l = 1 E { f C
n(t
D) d t ) = 1 ± £ ( )
and that
E i f min(u)dC
n(u)} = V ^ ( l ) ^ E { /
1C
r !( t ^ ) d A
The latter sum can be simplified further using the binomial theorem, viz.
£é^3(9'=ÈH)'=ê(f
Taking expectations on both sides of Equation (A3) and making the appropriate sub
stitutions, one gets Formula (3.7), as stated.
Turning to the computation of va,r(ip
n), one can immediately deduce from first prin
ciples and the above expression for E(<p
n) that
1»).(|i!)'(
i
^,)
,
U»(.,*.JÊ(
3'
where
M(n,d) = (n + 1)
2f l { C
n( s
D) C
n( t
D) + C
n(s
D) £ ( l ) ^ C
n( t
A) \ dsdt.
Spearman's footrule and Gini's gamma
28
Now at independence, one has E { C „ ( j / nD) C „ ( k / n , ) } =
n2 \ n j n [ nl — n
for arbitrary j , fc G { 0 , . . . , n} and A Ç £). Thus if
I.-» I
'* j = 0 fc=0 v " '
for all £ G { 0 , . . . , d}, one gets
•1 /•!
minfj, A;)
n - r ( n - l )
jA: - min(j, A;) nz — n
E{/
o
7
o
'
C
„(s
D
)C„(
W
d
S
d
(
}=^)
Upon substitution and an application of the binomial identity, one finds
d
E{M(n,d)} = A
n(d,d) + £ ( - l )
€^ W / , d ) = A„(d,d) + A
n(d),
where i n n*n(d)
=
i - E E
Uj = 0 k = 0 j min(j, k) ) f j jfc - min(J, fc) V n « n n" — nCollecting terms, one finds
var((^„) = 2
d+1
n
d - 1 ) \ n 2- l
A
n(d,d) + A
n( d ) - 2 { Y [ -
(A6)3.10.4 Computation of G\
Because the independence copula is radially symmetric, Formula (A5) reduces to
< c =
2(^{rwnz^rw)}
To compute <r2c, one must evaluate 2d covariances of the form cov{C(s,i),C(to)} for
some A Ç D. In view of Equation (A4), any such covariance may be expressed as
d d
cov{Uc(s/ 1),Uc(tD)} + E E Cj(sA)Ck(tD) cov{Uc(sAn{j}),Uc(tDn{fc})} } = \ fc=l
d d
- V2C,(syi)cov{Uc(s4nO}),Uc(tJr?)} - 2ZCk(tD)cov{Vc(sA),Vc(tD n { k })}.
Simplifications occur when C = TI because Cj(s
A) = «MWI, C
k(t
B) = *
|BX{fc}land
for arbitrary A , B C D ,
JIT f H I r t U J ^ 1 ( ^ 1 - ^ 1 ) if » < * ,
cov{Uc(s^),Uc(t
B)} = |
t l B | ( V s | A N B |_
s | A 1 ) ] £ s > tThus if s < t and A Ç D , one finds
cov{C(
S/4),C(t
D)} =
S^ ( i l
D^ - t l
Dl ) + £ s ^ t ^ - ^ l - t )
j=fc£j4
- £ «WtM-^i - *) - £ s
| y t |^
l _ 1(i - *).
which reduces to
s\A\{t\D\A\ _ t\D{ ) _ | ^ | s\ A \t\ D \ - l{ 1 _f ) = s\ A \{ t\ D \ A \{ 1 _ ^ |} _ | ^ | , m | - l( 1 _ t ) }
Similarly if s > t, one gets
t\D\{ s\A\D\ _ JA{ ) _ |A| ^ |S| A | -1 ( 1 _ s ) = , | D |{ ( 1 _ 8|A|J _ j i 4| S\ A \ - 1{ 1 _ g ) }
Consequently, for any A C D with |A| = A;,
r ( A , D ) = / / cov{C(s
A),C(t
D)}dsdt = Ai(fc,d)-l-A
2(fc,d),
Jo Jo
where for arbitrary fc € { 1 , . . . , d},
Ai(k,d)= f' [
ts
k{ t
d-
k( l - i * ) - H
d-
1( l - t ) } d s d t ,
Jo Jo
a n d ,i , iA
2(k,d)= f I i
d{ ( l - s
f c) - f c s
f e-
1( l - s ) } d s d t .
Jo Jt
Consequently,
"^
2
(^)
2
g{
A
'(«»
+
£(-l)'(")A,(M)}.
Now observe that in view of the binomial identity,
= t f \ ( t - s )
d- { l - s)
dt
d+ d s ( l - s)
d-
lt
d-
1- d s ( l - s)
d-H
d} ds dt.
Jo Jo
Similarly,
£(-i)*(fW
2(M) = £ £ -t
d{(i -
s)
d- (i - sy-'d + ds(i -
s)
d-
i}dsdt.
Spearman's footrule and Gini's gamma 30
3.11 Acknowledgements
Funding in support of this work was provided by the Natural Sciences and Enginee-ring Research Council of Canada, the Fonds québécois de la recherche sur la nature et les technologies, and the Institut de finance mathématique de Montréal.
Le chapitre 3 a présenté les propriétés stochastiques et différentes relations entre la règle de Spearman et la mesure d'association de Gini. Bien qu'elles se soient révélées moins efficaces que le rho de Spearman, ces deux statistiques sont localement optimales pour certaines classes de contre-hypothèses. Les résultats obtenus permettent d'évaluer l'emploi de la règle de Spearman et de la mesure d'association de Gini pour tester l'indépendance dans le cas bidimensionnel. De plus, la variance asymptotique de la version multidimensionnelle de la règle de Spearman proposée par Ubeda-Flores (2005) a été calculée sous l'indépendance, ce qui permet son emploi pour effectuer des tests d'indépendance multidimensionnelle.
Des résultats similaires concernant une extension multidimensionnelle de deux autres mesures d'association sont élaborés dans le chapitre suivant. Il s'agit en l'occurrence de deux généralisations du tau de Kendall dues respectivement à Kendall & Smith Ba-bington (1940) et à Joe (1990). Ces résultats sont ensuite utilisés pour comparer deux méthodes non paramétriques d'estimation d'un paramètre de dépendance à valeurs réelles dans un modèle de copules multidimensionnelles. On montre par voie de simu-lation que l'inversion des deux généralisations multidimensionnelles du tau de Kendall conduit à des estimateurs à peu près équivalents, qui peuvent servir de bonne valeur de départ pour la maximisation de la pseudo-vraisemblance, au sens de Genest, Ghoudi & Rivest (1995) ou de Shih & Louis (1995).
Chapitre 4
Estimators based on Kendall's tau
in multivariate copula models
R é s u m é
Les auteurs considèrent l'estimation d'un paramètre de dépendance à valeurs réelles dans un modèle de copules multivariées. Des procédures basées sur les rangs sont souvent employées dans ce contexte pour se prémunir contre une spécification éventuellement erronée des lois marginales. Une approche standard consiste à maximiser la pseudo-vraisemblance, comme le proposent Genest et coll. (1995) et Shih & Louis (1995). Les auteurs étudient deux autres approches possibles fondées sur l'inversion de versions multivariées du tau de Kendall respectivement dues à Kendall & Babington Smith (1940) et à Joe (1990). La plus ancienne, qui revient à prendre la moyenne des taus sur toutes les paires de variables, est souvent appelée le coefficient de concordance. Les auteurs rappellent les résultats déjà connus sur les propriétés asymptotiques et à taille finie de ce coefficient et présentent de nouveaux résultats analogues pour la version due à Joe, ainsi que des illustrations. Ils comparent les performances des estimateurs résultant de l'inversion de ces deux versions du tau de Kendall dans le cadre de modèles de copules. Des simulations sont utilisées à cette fin.
A b s t r a c t
The authors consider the estimation of a real-valued dependence parameter in a multivariate copula model. Rank-based procedures are often used in this context to guard against possible misspecification of the marginal distributions. A standard ap-proach consists of maximizing the pseudo-likelihood, as discussed in Genest et al. (1995) and Shih &: Louis (1995). The authors investigate alternative estimators based on the inversion of two multivariate extensions of Kendall's tau due to Kendall & Babington Smith (1940) and Joe (1990). The former, which amounts to the average value of tau over all pairs of variables, is often referred to as the coefficient of agreement. The au-thors summarize existing results concerning the finite- and large-sample properties of this coefficient and provide new, parallel findings for the multivariate version of tau due to Joe, along with illustrations. They compare the performance of the estimators resulting from the inversion of these two versions of Kendall's tau in the context of copula models. Simulations are used to this end.



![FIGURE 5.1 - Finite-sample (left) and limiting (right) variance of y/nS n , as a function of 0 G [0,1] in the Cuadras-Augé family of extreme-value copulas](https://thumb-eu.123doks.com/thumbv2/123doknet/5603002.134849/74.898.203.734.695.962/figure-finite-limiting-variance-function-cuadras-extreme-copulas.webp)