Sur la taille finale des épidémies dans un environnement périodique

(1)

HAL Id: hal-02123093

https://hal.archives-ouvertes.fr/hal-02123093v4

Submitted on 25 May 2020

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

Sur la taille finale des épidémies dans un environnement

périodique

Nicolas Bacaër

To cite this version:

Nicolas Bacaër. Sur la taille finale des épidémies dans un environnement périodique. Comptes Rendus

Biologies, Elsevier Masson, 2019, 342, pp.119 - 123. �10.1016/j.crvi.2019.07.001�. �hal-02123093v4�

(2)

Sur la taille finale des ´epid´emies dans un

environnement p´eriodique

Nicolas Baca¨er

∗

Comptes Rendus Biologies 342 (2019) 119-123

doi:10.1016/j.crvi.2019.07.001

Traductions : [ar, de, es, it, ja, nl, pt, ru, zh], [html]

R´esum´e

Il est difficile de prédire la taille finale d’une épidémie comme celle de dengue qui sévit actuellement à La Réunion, d’autant qu’il faut tenir compte de la sai-sonnalité. Dans cet article, on se propose d’étudier d’un point de vue théorique comment, dans le cadre d’un modèle très simple de type S-I-R pour une maladie à transmission directe, un environnement saisonnier périodique peut modifier la taille finale d’une épidémie. On obtient des résultats analytiques en supposant que l’amplitude de la saisonnalité est faible.

1 Introduction

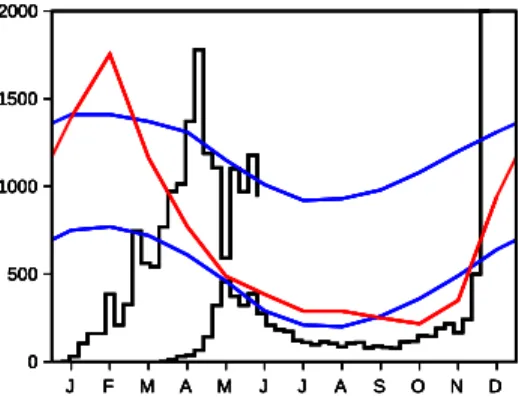
Une épidémie de dengue sévit actuellement sur l’ˆıle de La Réunion, dans l’océan Indien. Plus de 5 000 cas ont été confirmés biologiquement entre jan-vier et juin 2018, et plus de 16 000 cas évocateurs de la dengue ont été si-gnalés (figure 1). Fin juin, du fait de l’arrivée de l’hiver austral mais aussi de la lutte antivectorielle, l’épidémie recule. Cependant il est difficile de prévoir si le nombre d’infections diminuera suffisamment pour empêcher une seconde vague épidémique à la fin 2018, lorsque les conditions climatiques seront plus favorables aux moustiques vecteurs de la maladie. C’est cette deuxième vague qui en 2006 avait infecté presque un tiers de la population avec le chikungunya. Il serait tentant de modéliser mathématiquement la propagation de la dengue de manière réaliste tout en limitant la complexité du modèle pour n’avoir que quelques paramètres inconnus, comme on a essayé de le faire pour le chikun-gunya dans (Bacaër, 2007). Mais les incertitudes qui pèsent sur ces paramètres et sur leur dépendance par rapport aux variables climatiques sont si grandes

∗_{Institut de Recherche pour le D´}_{eveloppement, Les Cordeliers, Paris, France,}

(3)

J F M A M J J A S O N D 0 500 1000 1500 2000 J F M A M J J A S O N D 0 500 1000 1500 2000 J F M A M J J A S O N D 0 500 1000 1500 2000 J F M A M J J A S O N D 0 500 1000 1500 2000 J F M A M J J A S O N D 0 500 1000 1500 2000

Figure_{1 – Courbe en noir du haut (échelle sur l’axe vertical de gauche) :} esti-mation du nombre de cas hebdomadaires évocateurs de la dengue à La Réunion entre janvier et juin 2018, d’après Santé publique France (2018). Courbe en noir du bas (même échelle) : cas hebdomadaires de chikungunya en 2005, avant le grand pic de la fin 2005 et du début de 2006 (Bacaër, 2007). Données clima-tiques à la station de l’aéroport de La Réunion, d’après Météo France : en bleu, température minimale (de 18,0 à 23,7o_{C) et température maximale (de 25,2 à}

30,1o_{C) ; en rouge, pr´ecipitations mensuelles (de 43 `}_{a 351 mm).}

que les résultats numériques risquent fort d’être assez douteux (Raoult, 2016). On se contentera ci-dessous d’un modèle épidémique extrêmement simplifié à transmission directe et non vectorielle, qui ne prétend donc pas pouvoir être appliqué au cas de la dengue à La Réunion. Cela n’aurait pas vraiment de sens de vouloir ajuster ses paramètres aux données épidémiques. L’objectif est plutôt d’attirer l’attention sur la question de la taille finale d’une épidémie dans un environnement saisonnier périodique, qui a été peu étudiée d’un point de vue théorique.

Même les modèles mathématiques les plus simples qui tiennent compte de la saisonnalité présentent de nombreuses difficultés. On sait depuis longtemps que pour les modèles de maladies endémiques, un coefficient périodique peut engen-drer des oscillations avec une période différente, voire des oscillations chaotiques (Choisy et Cazelles, 2009). Dans l’étude (Bacaër, 2007) inspirée de l’épidémie de chikungunya à La Réunion, on a vu par ailleurs que même la notion clas-sique de reproductivité, notée R0 à la suite de Lotka (1939), dans les modèles

périodiques devait être définie avec quelques précautions pour que l’inégalité R0 > 1 traduise bien l’instabilité de la situation sans épidémie ; la difficulté

apparaˆıt notamment pour les mod`eles avec au moins deux compartiments d’in-fect´es.

Dans (Bacaër et Gomes, 2009), on a abordé le modèle S-I-R périodique, simple généralisation du modèle classique de Kermack et McKendrick (Hillion,

(4)

1986, p. 75) : dS dt = −a(t) S I/N, dI dt = a(t) S I/N − b I, dR dt = b I, (1) où N est la taille de la population, S(t) le nombre de personnes susceptibles d’être infectées, I(t) le nombre de personnes infectées, R(t) le nombre de per-sonnes guéries, a(t) le taux de contact infectieux, b le taux de guérison. Les conditions initiales sont S(t0) = s = N − i avec 0 < i < N , I(t0) = i et

R(t0) = 0. La fonction a(t) est périodique de période T . Après avoir posé

R0= 1 bT Z T 0 a(t) dt,

on a montré que la propriété de seuil épidémique se traduisait de la manière suivante : si R0 < 1, alors la taille finale R(∞) de l’épidémie tend vers 0 si i

tend vers 0 ; si au contraire R0> 1, alors

R(∞) > N (1 − 1/R0),

quel que soit 0 < i < N . Cette propriété s’étend d’ailleurs des modèles avec une transmission directe comme le système (1) aux modèles avec une transmission vectorielle comme pour la dengue. Dans (Bacaër et Ait Dads, 2011, figure 1), on a étudié numériquement comment la taille finale R(∞) de l’épidémie dépend de l’instant initial t0 et de l’amplitude du taux de contact infectieux a(t). On

a observé que R(∞) pouvait varier du simple au double pour une même valeur de la reproductivité R0.

En combinant méthodes numériques et méthodes analytiques, on étudie ici plus attentivement la taille finale de l’épidémie dans le cas particulier où

a(t) = ¯a(1 + ε φ(t))

avec une fonction φ(t) (disons continue par morceaux) qui est périodique de période T et de moyenne nulle, et avec un paramètre ε qui est petit de sorte que l’environnement n’est que faiblement saisonnier. Notons Sε(t), Iε(t) et Rε(t) les

solutions correspondantes mais avec toujours la mˆeme condition initiale (N − i, i, 0). On montre dans la section 2 que

Rε(∞) = R0(∞) + N c ε + o(ε)

quand ε → 0, où R0(∞) est la taille finale de l’épidémie dans un environnement

constant. Le coefficient correcteur c peut ˆetre positif ou n´egatif.

Si φ(t) = cos(ωt), si le nombre de personnes infect´ees au d´epart est petit devant la taille de la population (i ≪ N ), si R0 = ¯a/b > 1 avec R0 proche

de 1, et si i/N ≪ (R0−1)2, alors on d´etermine analytiquement le coefficient

correcteur c en fonction des param`etres N , i, ¯a, b, t0et ω du mod`ele. On trouve

que l’environnement périodique augmente la taille finale de l’épidémie (c > 0) si le taux de contact infectieux vérifie a(t0+ τ ) > ¯a, où t0+ τ est le moment où

(5)

2 Formule exacte pour le coefficient correcteur

Rappelons tout d’abord qu’à partir du système différentiel (1), on montre que : Sε(t) + Iε(t) + Rε(t) = N pour tout t ≥ t0; Sε(t) > 0, Iε(t) > 0 et

Rε(t) ≥ 0 pour tout t ≥ t0; Sε(t) est une fonction d´ecroissante qui tend vers

une limite Sε(∞) ; Rε(t) est une fonction croissante qui tend vers une limite

Rε(∞) ; Iε(t) tend vers une limite qui ne peut ˆetre que 0 (Baca¨er et Gomes,

2009). Intégrons la troisième équation différentielle de t0 à l’infini : cela donne

Rε(∞) = bR ∞

t0 Iε(t) dt. Par ailleurs, la première équation différentielle s’écrit

1 Sε

dSε

dt = −a(t)Iε(t)/N . Int´egrons de mˆeme pour obtenir

logSε(∞) N − i = − ¯ a N Z ∞ t0 Iε(t) dt − ¯ a N ε Z ∞ t0 Iε(t) φ(t) dt .

On peut remplacer la premi`ere int´egrale et tenir compte de ce que Sε(∞) =

N − Rε(∞) pour obtenir l’´equation implicite

logN − Rε(∞) N − i + ¯ a b Rε(∞) N + ¯ a N ε Z ∞ t0 Iε(t) φ(t) dt = 0 , (2)

qui est de la forme F (Rε(∞), ε) = 0. Lorsque ε = 0, le dernier terme `a droite

disparaˆıt et on reconnaˆıt l’équation classique pour la taille finale de l’épidémie dans un environnement constant (Hillion, 1986, p. 76). D’après le théorème des fonctions implicites (Deschamps et Warusfel, 2001, p. 892), la fonction qui à ε associe Rε(∞) est continûment dérivable au voisinage de ε = 0, de sorte que

Rε(∞) = R0(∞) + N c ε + o(ε) pour ǫ → 0, avec

N c = −∂F ∂ε(R0(∞), 0) / ∂F ∂R(R0(∞), 0) . On trouve ainsi c = _Na/N¯ N −R0(∞) − ¯ a b Z ∞ t0 I0(t) φ(t) dt . (3)

Rappelons comme dans l’introduction que R0(∞) > N (1−b/¯a). Donc le d´enominateur

de la formule (3) est strictement positif et en particulier non nul. Le coefficient c a le mˆeme signe que l’int´egraleR∞

t0 I0(t) φ(t) dt.

On peut évaluer numériquement cette intégrale. On utilise d’abord un logiciel de calcul numérique (tel que Scilab et sa fonction≪ode≫, voir www.scilab.org/fr)

pour résoudre le système différentiel (1) avec ε = 0. On obtient ainsi (S0(t), I0(t), R0(t))

pour un ensemble discret de valeurs de t, avec un petit pas de temps. On en déduit en particulier la valeur R0(∞). Puis on calcule l’intégrale avec cette même

discr´etisation du temps. On en d´eduit la valeur du coefficient c.

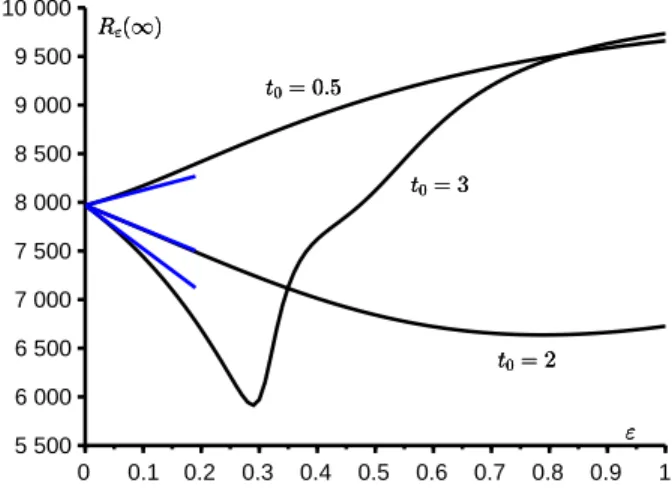
Prenons un exemple. Supposons que φ(t) = cos(ωt) avec ω = 2π/T , N = 10 000, i = 1, T = 12 mois, ¯a = 10/mois et b = 5/mois. Alors la reproductivité est R0 = 2 ; la taille finale de l’épidémie dans un environnement constant est

R0(∞) ≃ 7 968. La figure 2 montre comment Rε(∞) varie en fonction de ε

(6)

moments diff´erents d’introduction du premier cas infect´e dans la population : 0,5 mois, 2 mois ou 3 mois. La figure montre aussi l’approximation R0(∞) + N c ε

pour ε petit, avec le coefficient correcteur c calculé selon la formule (3). On observe que le coefficient c peut être positif ou négatif, de sorte que la taille finale de l’épidémie peut être plus grande ou plus petite que dans un environnement constant. On observe aussi que pour t0 = 3 mois, la fonction Rε(∞) varie en

fonction de ε de manière plus compliquée que pour les deux autres valeurs de t0 : en particulier, cette fonction n’est décroissante que tant que ε < 0,3.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 10 000 6 000 8 000 7 000 9 000 5 500 6 500 7 500 8 500 9 500

Figure _{2 – La taille finale de l’épidémie en fonction de ε pour trois valeurs} différentes de t0. En bleu : l’approximation R0(∞) + N c ε.

3 Formules approch´

ees

Kermack et McKendrick ont trouvé — voir par exemple (Bacaër, 2012, §2) ou (Gani et Badrikian, 1975, p. 235) — une approximation pour I0(t) à partir

de l’équation exacte dR0/dt = b(N − s e−¯aR0/(N b)−R0) vérifiée par R0(t). Un

développement limité de l’exponentielle e−x_{= 1 − x + x}2_{/2 + o(x}2_{) tronqué à}

l’ordre 2 conduit à une équation de Ricatti résoluble pour R0(t) et à une courbe

en cloche sym´etrique pour I0(t),

I0(t) ≃ N X ch2(Y (t − t0) − Z) pour tout t > t0, o`u X = b 2_{N W}2 2 ¯a2_s , Y = b W 2 , th(Z) = ¯ a s b N −1 W ,

(7)

et W = ( [a s¯ b N −1] 2_{+ 2} s i N2 ¯ a2 b2 ) 1/2_.

Ici, ch(·) et th(·) d´esignent le cosinus et la tangente hyperboliques. Rappe-lons que s = N − i. L’approximation pour I0(t) est d’autant meilleure que

¯

aR0(∞)/(N b), la valeur maximale du terme dans l’exponentielle, est petit

de-vant 1. Alors c ≃ _N¯aX N −R0(∞)− ¯ a b Z ∞ t0 φ(t) ch2(Y (t − t0) − Z) dt . (4)

Supposons plus pr´ecis´ement que R0 = ¯a/b → 1 avec R0 > 1 et que

(i/N )/(R0−1)2→0 ; autrement dit, R0est proche de 1 et i/N ≪ (R0−1)2.

Alors i → 0 et on a bien R0(∞) → 0 d’apr`es l’´equation (2) avec ε = 0. Comme

on a aussi i/N ≪ (R0−1), on trouve que

W ∼ ¯a b −1, X ∼ (1 − b/¯a)2 2 , Y ∼ ¯ a − b 2 et 1 − th(Z) ∼ _(b/¯i/N_a−1)2. Donc Z → +∞ et 1 − th(Z) ∼ 2 e

−2Z , ce qui donne Z ∼ 1 2log 2(b/¯a − 1)2 i/N .

Posons τ = Z/Y ; c’est en t = t0+ τ que l’approximation de I0(t) atteint son

pic. Notons que Y → 0 et que τ → +∞. Apr`es le changement de variable t = t0+ τ + u, on remarque que la fonction 1/ch2(Y u) est presque nulle en

dehors du voisinage de u = 0, de sorte que Z ∞ −τ φ(t0+ τ + u) ch2(Y u) du ≃ Z ∞ −∞ φ(t0+ τ + u) ch2(Y u) du .

Cette derni`ere int´egrale se calcule explicitement lorsque φ(t) = cos(ωt). En effet, Z ∞ −∞ cos(ω(t0+ τ + u)) ch2(Y u) du = cos(ω(t0+ τ )) Z ∞ −∞ cos(ωu) ch2(Y u)du

puisque l’intégrale avec la fonction impaire sin(ωu) s’annule. D’après la formule dans l’appendice de (Bacaër, 2015), on a

Z ∞ −∞ cos(ωu) ch2(Y u)du = πω Y2 sh(πω_2Y),

où sh(·) désigne le sinus hyperbolique. Avec les équivalents de X et Y déjà obtenus, on arrive finalement à

c ≃ cos(ω(t_N 0+ τ )) N −R0(∞)− ¯ a b 2πω ¯ a sh(πω ¯ a−b) . (5)

(8)

On voit que le signe de c est le mˆeme que celui de cos(ω(t0+ τ )). Donc

l’envi-ronnement périodique augmente la taille finale de l’épidémie si a(t0+ τ ) > ¯a, où

t0+ τ est le moment où l’épidémie atteindrait son pic dans un environnement

constant.

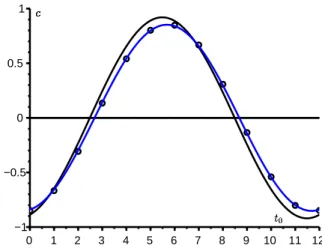
Comme exemple, prenons les mˆemes valeurs des param`etres que dans la figure 2 sauf que ¯a = 6/mois pour avoir R0 = 1,2 plus proche de 1 ; [8,

p. 240] indique d’ailleurs que l’approximation en cloche sym´etrique de Kermack et McKendrick n’est satisfaisante que pour R0< 1,5. La figure 3 compare

l’ex-pression exacte (3) du coefficient correcteur c avec les approximations (4) et (5). Avec nos valeurs num´eriques, ces deux derni`eres approximations sont indiscer-nables. Elles sont d’autant plus proches de la valeur exacte que R0 est proche

de 1. Notons qu’ici i/N = 10−4

≪(R0−1)2= 0,04. La figure s’interpr`ete comme

ceci : si l’épidémie démarrait à t0= 0, les valeurs des paramètres conduiraient

`

a un pic de l’épidémie environ τ ≃ 6,3 mois plus tard dans un environnement constant ; or l’environnement périodique sera défavorable à ce moment (on sera dans le creux du facteur cos ωt) ; donc la taille finale de l’épidémie sera moindre et c < 0. 0 1 2 3 4 5 6 7 8 9 10 11 12 0 −1 1 −0.5 0.5

Figure _{3 – Le coefficient correcteur c pour la taille finale de l’épidémie en} fonction de t0, l’instant du début de l’épidémie. Comparaison de l’expression

exacte (3) [en noir] avec les approximations (4) [points] et (5) [en bleu].

4 Remarque

On peut adapter la formule exacte (3) pour le coefficient correcteur c à des modèles plus complexes. Supposons par exemple que l’épidémie se propage entre deux populations (comme des hommes et des vecteurs) suivant le schéma S-I-R,

(9)

avec N1= S1(t) + I1(t) + R1(t) et N2= S2(t) + I2(t) + R2(t) : dS1 dt = −a(t)S1 I2 N2, dI1 dt = a(t)S1 I2 N2 −b1I1, dR1 dt = b1I1, dS2 dt = −a(t)I1 S2 N2 , dI2 dt = a(t)I1 S2 N2 −b2I2, dR2 dt = b2I2.

Supposons aussi que a(t) = ¯a(1 + ε φ(t)) comme pr´ec´edemment. Notons S1,ε(t),

I1,ε(t), etc., les solutions. Posons i1= I1(t0) et i2= I2(t0). On trouve facilement

l’équivalent de l’équation (2), qui est un système :

logN1−R1,ε(∞) N1−i1 + ¯ a b2 R2,ε(∞) N2 + ¯ a N2ε Z ∞ t0 I2,ε(t) φ(t) dt = 0 logN2−R2,ε(∞) N2−i2 + ¯a b1 R1,ε(∞) N2 + a¯ N2 ε Z ∞ t0 I1,ε(t) φ(t) dt = 0.

Ce syst`eme a des solutions de la forme Rk,ε(∞) = Rk,0(∞) + Nkckε + o(ε) pour

k = 1 ou 2. Avec le th´eor`eme des fonctions implicites, on trouve que   N1c1 N2c2  =   1 N1−R1,0(∞) − ¯ a b2N2 −_b¯a 1N2 1 N2−R2,0(∞)   −1   ¯ a N2 R∞ t0 I2,0(t) φ(t) dt ¯ a N2 R∞ t0 I1,0(t) φ(t) dt  .

Il n’est cependant pas possible de poursuivre comme dans la section 3 car on ne dispose pas de formules approch´ees explicites pour I1,0(t) et I2,0(t).

5 Conclusion

On a déterminé de manière analytique comment la taille finale de l’épidémie était influencée par un taux de contact infectieux périodique de faible ampli-tude, lorsque la reproductivité R0reste proche de 1. Il s’agit d’un petit progrès

par rapport aux études précédentes qui étaient soient qualitatives comme dans (Bacaër et Gomes, 2009), soit purement numériques comme dans (Bacaër et Ait Dads, 2011, figure 1). Les hypothèses sont néanmoins assez restrictives. Elles évitent en particulier les cas où plusieurs pics épidémiques se produisent, puisque l’on reste proche de la situation à un seul pic des environnements constants. Or ce sont justement ces cas qui risquent de se présenter avec l’épidémie de dengue à La Réunion.

R´

ef´

erences

[1] N. Baca¨er (2007), Approximation de la reproductivit´e nette R0 pour

les maladies `a vecteurs avec une population p´eriodique de vecteurs, https://hal.archives-ouvertes.fr/hal-01291211.

(10)

[2] N. Bacaër, M.G.M. Gomes (2009), Sur la taille finale des épidémies avec saisonnalité, https://hal.archives-ouvertes.fr/hal-01299608. [3] N. Bacaër, E. H. Ait Dads (2011), Les généalogies avec

sai-sonnalité, la reproductivité nette et la pandémie de grippe, https://hal.archives-ouvertes.fr/hal-01274025.

[4] N. Bacaër (2012), Le modèle de Kermack et McKendrick pour la peste à Bombay et la reproductivité nette d’un type avec saisonnalité, https://hal.archives-ouvertes.fr/hal-01340008.

[5] N. Bacaër (2015), Sur le modèle stochastique SIS pour une épidémie dans un environnement périodique, https://hal.archives-ouvertes.fr/hal-01265563.

[6] M. Choisy, B. Cazelles (2009), Conséquences des dynamiques épidémiques en santé publique : rôle des modèles mathématiques, in : J.-F. Guégan, M. Choisy (éd.), Introduction à l’épidémiologie intégrative des maladies infectieuses et parasitaires, De Boeck, Bruxelles, p. 3-39.

[7] C. Deschamps, A. Warusfel (2001), Math´ematiques 2e_{ann´ee, Dunod, Paris.}

[8] J. Gani, J. Badrikian (1975), Processus stochastiques de population, in : P.-L. Hennequin (éd.), École d’été de probabilités de Saint-Flour IV-1974, Springer, Berlin, p. 188-293.

[9] A. Hillion (1986), Les th´eories math´ematiques des populations, Presses Uni-versitaires de France, Paris.

[10] A.J. Lotka (1939), Th´eorie analytique des associations biologiques, 2e

par-tie, Hermann, Paris.

[11] Météo France, Données climatiques de la station de Gillot-aéroport, www.meteofrance.re/climat/reunion/gillot-aeroport/97418110/normales. [12] D. Raoult (2016), Les modèles prédictifs sont des prophéties modernes, in :

D. Raoult, Arrˆetons d’avoir peur, Michel Lafon, Neuilly-sur-Seine.

[13] Santé publique France (2018), Épidémie de dengue à la Réunion – Point épidémiologique au 19 juin 2018, www.santepubliquefrance.fr.