Méthode vectorielle d'analyse de la texture

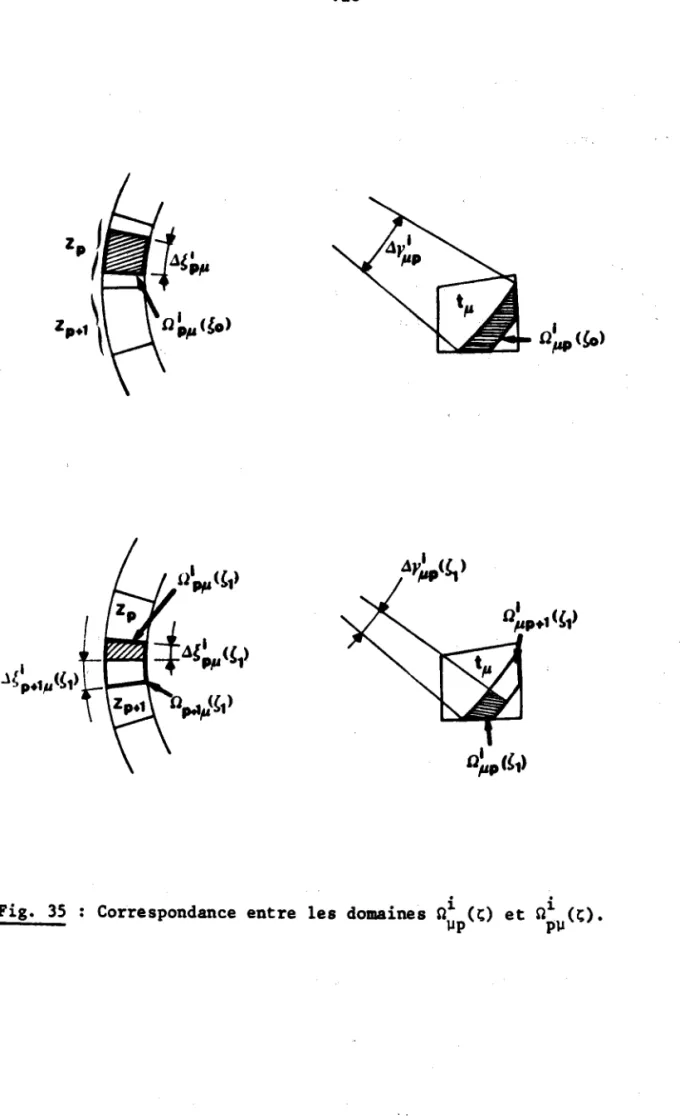
HAL Id: tel-01775584

https://hal.univ-lorraine.fr/tel-01775584

Submitted on 24 Apr 2018

HAL is a multi-disciplinary open access archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.

To cite this version:

Daniel Ruer. Méthode vectorielle d’analyse de la texture. Cristallographie. Université Paul Verlaine - Metz, 1976. Français. �NNT : 1976METZ002S�. �tel-01775584�

AVERTISSEMENT

Ce document est le fruit d'un long travail approuvé par le jury de

soutenance et mis à disposition de l'ensemble de la

communauté universitaire élargie.

Il est soumis à la propriété intellectuelle de l'auteur. Ceci

implique une obligation de citation et de référencement lors de

l’utilisation de ce document.

D'autre part, toute contrefaçon, plagiat, reproduction illicite

encourt une poursuite pénale.

Contact : ddoc-theses-contact@univ-lorraine.fr

LIENS

Code de la Propriété Intellectuelle. articles L 122. 4

Code de la Propriété Intellectuelle. articles L 335.2- L 335.10

http://www.cfcopies.com/V2/leg/leg_droi.php

THÈSE

; présentée

A I'U.E.R. "SCIENCES

_EXACTES

_{ET NATURELLES"}

DE I'UNIVERSITÉ

DE METZ

pour obtenir le grade de

DOCTEUR

ÈS SCteruces

par

Daniel RUER

Maître-Assistant

l'!NSTITUT UN|VERS|TA|RE de TECHNOLOGTE_{de METZ}

MÉTHODE VECTORIELLE

D'ANALYSE DE LA TEXTURE

soutenue le 2l octobre 19z6 devant la commission d,Examen Monsieur le Doyen A. GUINIER

Monsieur le Professeur p. COULOMB Monsieur le Professeur H.J. BUNGE Monsieur le Professeur B. SCHMITT Monsieur le Professeur R. BARO Président :

M e m b r e s :

B I BLrorrËeue ur.r rvensrra _rnÊ

47+( oo3

_S

5/r,ts

_{7[ lL}

U . E . R . ' ' S C I E N C E S _{E X A C T E S} DirecÈeur : M. REIN ET !{ATURELLES'' Georges

P R O F E S S E U R S

M. LONCHÂMP M. BARO :'tme CAGNIAI{T M. LEMY M. BTOCH M . K L E I M },1. CIIARLIER M. TAVARD M. IIENDLING M. BAUDELET Jean-Pierre Raymond D e n i s e J o s e p h Jean-Miche 1 Roland r . l p h o n s e Claude Edgar Bernard Physique Physique Chirnie Physique Chimie Physique Physique Physique Chinie Physique

M A Î T R E S

D E C O N F E R E N C E S

M. CERTIER M. IÆBER M. CARABAÎOS M. FALLER M. RHIN ltne SEC M. DAX M. SCHUITT M. PLWINAGE M. HEIZMANN M. ROIIX Miche I Jean-Danie I Cons tant in P i e r r e Georges Antoinette Jean-Pierre Bruno Guy Jean-Julien André Physique Mécanique Physique Chinie Mathénatiques Mathématiques M a t h é m a t i q u e s Mathénatiques Phys ique Physique l.lathématiques

j o u r s gardé son enÈière confiance malglé les réactions diverses que le t r a v a i l _{q u e j t a v a i s e n t r e p r i s a p a r f o i s s u s c i t é e s . Je lui sais gré, en} p a r t i c u l i e r , _{d e m ' a v o i r d o n n é l a p o s s i b i l i t é d r e x p o s e r p o u r l a p r e n i è r e} f o i s m e s idées à la dernière Conférence Annuelle de 1'Université de

D e n v e r ( C o l o r a d o ) e t d ' a v o i r s u , p o u r j u g e r le trevail décrit dans le pré-s e n t ouvrage, réunir un jury aupré-spré-si prepré-stigieux.

Que Monsïeuz, Le Dogen A. GllrNrER, professeur à l runiversiré d r 0 r s a y , dont les travaux et les inventions dans le domaine de Ia cristal-l o g r a p h i e sont de renorrnée universecristal-lcristal-le, _{t r o u v e ici Itexpression de ma} d é f é r e n t e gratitude _{p o u r avoir accepté la présidence de ce jury.}

$te Monsieur Le Professeur P. COUL)MB de l tUniversité paul

S a b a t i e r de Toulouse, auteur du seul ouvrage édité en France dans le domaine d e s t e x t u r e s , v e u i L l e b i e n a c c e p t e r q u e j e l u i renouvelle mes plus sincères r e m e r c i e m e n t s p o u r l t e s t i m e q u t i l n e t é n o i g n e e n p a r t i c i p a n t pour la secon-d e f o i s à l r u n secon-d e m e s j u r y s .

Que Monsiew Le Doeteu.r H.J. BUNGE, professeur à la Technische U n i v e r s i t â t , d e C L a u s t h a l - Z e l l e r f e l d ( n . r . R . ; , _{p r e m i e r s p é c i a l i s t e u r o n d i a l} d e l r a n a l y s e m a t h é m a t i q u e d e s t e x t u r e s , v e u i l l e bien agréer mes plus vifs e t p l u s s i n c è r e s r e m e r c i e m e n t s p o u r f i n c é r ê t e t la considération qu'il m t a m a n i f e s t é s t p o u r l e s c o n s e i l s e t l e s c r i t i q u e s q u t i l a f o r u u l é s e t p o u r sa participation à m o n j u r y .

Q u e M o n t i e u r B . s c 4 V r r r , p r o f e s s e u r à ltuniversité d e M e È 2 , t r o u v e é g a l e m e n t ici l texpression de mes plus sincères remerciements pour a v o i r accepté de participer _{à uron jury en tant que spécialiste d a n s l e} d o m a i n e des nathénatiques et de ltinformatique.

I 1 m r e s t êgalernent Èrès agréable de remercier toutes les person-n e s q u i m r o person-n t p u i s s a t t r person-n t e person-n t _{a i d é d a n s m o n e n t r e p r i s e e t p l u s p a r t i e u l i è r e m e n t}

l'Iessieu.ts P. EMERY _{et P. VAySSIERE, Directeurs successifs de la} S t a t i o n d r E s s a i s d e l r l n s t i t u t _{d e R e c h e r c h e s d e l a S i d é r u r g i e q u i m r o n t}

C a l c u l q u i , q u e l l e s q u e s o i e n È l e u r s f o n c Ë i o n s , m r o n t t o u s a i d é à r é s o u d r e l e s n o m b r e u x p r o b l è n e s q u i s e s o n t p o s é s l o r s d e I a m i s e a u p o i n t d e s P r o g r a r m e s ,

Monsieut J. f . WRDEJA, professeur à la Escuela Îécnica Superior d e I n g e n i e r o s d e M i n a s d r O v i e d o ( E s p a g n e ) q u i n t a p e r m i s d r u t i l i s e r l a m é c h o d e d e I ' I i l l i a n s ,

Messieurs C. ESLING et F. t'lAGI,lER qui mtont aimablenent cornmuniqué l e s r é s u l t a t s o b t e n u s p a r l a r n é t h o d e d e B u n g e ,

Monsieur J.J. HEIZMANN à qui revient le rnérite dravoir été le p r e m i e r à monÈrer les modifications d e t e x t u r e i n t e r v e n a n t l o r s d e l a r é d u c t i o n d e s o x y d e s d e f e r r g u i s t e s t c o n s t a @ n t i n t é r e s s é à l r a v a n c e -m e n t d e -m e s t r a v a u x e t . d o n t l e s r e -m â r q u e s p e r t i n e n È e s -m t o n t c o n s i d é r a b l e -m e n t

a i d é à r e n d r e m o n l e x t e p l u s c l a i r e t , d a n s l a t r E s u r e d u p o s s i b l e , p l u s f a c i l e à l i r e .

Je terninerai en exprimant ma satisfaction sans réserve à

M o n s i e u r A . T H T L , r e s p o n s a b l e d e l a r é a l i s a t i o n d e s f i g u r e s e t d e s t i r a g e s photographiques, ainsi qu'à MademoiseLLe F. KRAFFTT chargée de la présenta-t i o n d u È e x présenta-t e , p o u r l a n a n i è r e d i g n e d e présenta-t o u s é l o g e s d o n présenta-t i l s s e s o n présenta-t

I N T R O D u c r l O N _{! . r . r r r r | | ! r . r r . I r r r r | | r ' r r r r r . . r .} I r r . r . . r I r r !

I I - n É s u t q É

D E s P R I N C T P A L E S

M É T H ' D E S

_{A c r u E L L E s}

_{r , , , , . , , r , , , . . , ,}

_r

₇

I - L a m é t h o d g d e B u n g e _{r r r r . r r . r r r r r . . r . , r r r r r r r . . r r r r r r r r r . . r g} 2 ' L a m é t h o d g d e R o e . r r r r , . r r r r r r r r . r . r . ! r r . r . r . r r r . . r r r r r r r , t l 3 - L a m é t h o d e d e w i l l i a n s _{r r r r r r r . r r r r r r r r r r r r r r r r . r . ! . . r r r . . ,} 1 5 l l r l l l - T H E O R I E DE LA MÉTHODE _{V E C T o R I E L L E rr , r . , , r , r , , . . , , , . r r r . . . . ,} r 9 I I - P r i n c i p e s g é n é r a u x . r r r r . r r r . r r r r . r !r r.r rrrr _{r r r r r r r r . r r t . r r r} ? . 1 2 - c h o i x d e s p a r a m è t r e s . a n g u l a i r e s , , r r ! r , r r . r r r r r r r ! . r . _{r . r I r r r ,} 2 4 3 - P a r t i t i o n _{d e l . r e n s e m b l e G d e s o r i e n t a t i o n s} r r r r r r . r , t l r r r r . r r r t r r 2 7 4 - D é f i n i t i o n _{d u v e c t e u r È e x t u r e r r r r r r . . r r r r r r r r . . r . r r r . r . r r . r} , 3 4 5 - P o u v o i r d e r é s o l u t i o n d e l a n é t h o d e _{r . r r r . . . r . . . r r r r . . r r t r . r r , 3 5} 6 - P a r t i t i o n _{d e l a d e m i - s p h è r e d e s p ô l e s} r r r r r , r r r r r r . . r . r r . r r r r r 3 5 7 - P r i n c i p e f o n d a m e n t a l d e l a n é c h o d e r r r r . r . . r r . r r r r . r r r r r r r r t ! r _{3 7} 8 - R e l a t i o n s _{g é o m é t r i q u e s e n t r e l e s c o o r d o n n é e s de lraxe oN et celles} d t u n p ô l e ( h k l ) _{. r . r . . ! r r r r l . r . r r r r r r . . r r r r r . . r r r r r . . . r r} 3 B 9 - R e l a t i o n s _{g é o u r é t r i q u e s existant} e n t r e t r n e c a s e zn et uilê câsê Ëu _{r r 4 2} l o - E x p r e s s i o n d e 1 a d e n s i t é d e p ô l e s d a n s u n e " r " " f ^ r . r r r . . . . r r r r 4 s I | - D é f i n i t i o n _{d t u n e f i g u r e d e p ô I e s é l é m e n È a i r e , , ,} l , | | | | . . | . . . | . | 4 g 1 2 - R e l a t i o n s e x i s t a n t _{e n c r e l e s d e n s i t é s d e p ô l e s e t l e vecËeur texture 49} 1 1 ,

I t l - M E T H O D E

_{D E c A L c u L D U v E c r E U R}

_{T E X T U R E}

, : , r , , , , , , , . , , , , . , . . . . 55

| - A v g r È i s s g m g n t t t ' . . r r . r r r . r . r r r r r r r _{r r r . r r r r} r r r . r r r r r r r r r _{r r} 5 7 2 - D é f i n i t i o n _{d u v e c t e u r e x p é r i m e n t a l} I r r r r r | | r . I r r r . | ! . ! . r . r . | | | 5 7 3 - E x i s t e n c e e t u n i c i e é d e l a s o l u t i o n r | | r r . | | r I r i r r r r . | | | r . . r | , 5 g 4 - c h o i x d e l a s o l u t i o n , r . . | | | | r.r . | | r | . | | _{| | | | | | | r I r r l | | . r r | | . r} 6 t 5 - U t i l i s a t i o n _{d e f i g u r e s d e p ô l e s i n c o m p l è t e s , r r r r r r r . r r r , . r r . r r} 6 3 6 - U t i l i s a t i o n _{d e f i g u r e s d e p ô t e s n o n n o r m a l i s é ê s , r . . r r r . r . . r . r . r} 6 5 7 - C a l c u l d r u n e f i g u r e d e p ô l e s i n v e r s e _{r . r r r r . r r r . r r r . r r . r r ! . r r r} , 6 6 8 - D é f i n i t i o n _{d u d e g r é d r a n i s o t r o p i e} i . r r r r r r r r r , r r , r . r . . r r . r r . . . _{6 g}

I-2 - C a l c u l d e l a s o l u t i o n _{, : , : , : : , : : : : : : , : : : : , : : : : : : , , : : : : : : : : :} " )

VI

VII

P R É c I s I o N C o M P A R É E

D E S D I F F É . R E N T E S

M É T H O D E S

I I . . . . I . I . . I . . .

8 3

t - B u È d e I a e o m p a r a i s o n . r r . r r r r r r r r r r r r r r r . r . r r r . r r r . . r r t . . . 8 5 2 - D o n n é e s e x p é r i m e n t a l e s _{. . . r . . r r . r r t . r . r . . . r . r . . I r . r .} r ! r r . r , 8 5 3 - C a l c u l s , , . . I r I r r r . | | | | r r . . | | | r | | ! | r ! r r . r . . | | | r . r . r l ! | . . . 8 7 4 - C o n p a r a i s o n d g s r é s u l t a t s _{I r . | ! r | | | r r I r I r I r r . r . r .} r . . r . . r . . . . 9 0 P R I N C T P A U X A V A N T A G E S D E L A M É T H O D E V E C T O R I E L L E I I I ' I ' I " . . ' I O I | - S i g n i f i c a t i o n p h y s i q u e d u r é s u l t ê t , , , r r . . . . r . . . r . . . . r . . . r . . . . 1 0 3 2 - D e s c r i p t i o n d e s n o d i f i c a t i o n s d e l a t e x Ë u r e r . , . . r . r r . . . r r . . . 1 0 9 3 - G é n é r a l i s a t i o n _{d e l a r n é t h o d e . . r r . . . I r . | | | r . r . . . .} ! . r | | r . . . l l I V I I I - c o N c L u s t o N | | . . . I r I r . | | r r r r | | r r . r | . r . r : r t | | r | | | | . r . . r . . . . | . I 1 3

ANNIXES

I-

C A L C U L

D E S L I M I T E S D E S C A S E S

D U T R I A N G L E

S P H É R I Q U E S T A N D A R D r r . r r . r r . r . . . r . r . I r . . . . r . r . I t r r . r . . l 1 9

C A L C U L

D E S

D E N S I T É S

D E P O L E S

" l n ( h k l

) . , . , . . , . , r . . , . . r r 1 2 5

M I S E E N M É M o l R E

D ' u N E M A T R I C E

[ o o n ( h k l ) J

. . , , , . . , . , . .

r 1 3 3

AMÉLIORATION

DE LA CONVERGENCE

DE LA MÉTHODE

D E C A L C U L D U V E C T E U R T E X T U R E . . t t r . t r r r . . r . r r . . r . r r r . , 1 3 9 f * , r , t r ' ' l M A T R I C E S L o k p ( n K l ) J _{I r . r r I r r . . r | | r . . r . I r . . . r r r . . r I r . . .} 1 4 5

C A L C U L

D E S F I G U R E S

D E P ô L E S

D , A X E

P A R A L L È L E

A U

P L A N D E t ' É C t t l t t t t l L L O N . . . . r r r r r . I r r r r r r r r . . . . r r . . r . r . . t 5 t

II

III

IV

V-VI

BIBLIOGRAPHIE

L a r é p a r t i t i o n _{d e s o r i e n t a t i o n s} r i a u p o l y c r i s t a l l i n _{c o n s t i t u e c e q u e l r o n} g r a p h i q u e d e c e t é c h a n t i l l o n .

d e s cristallites _{d a n s un} naté-a p p e l l e lnaté-a texture cristnaté-allo- cristallo-La néthode la plus simple pour rettre en évidence la texture

à lraide de la diffraction _{d e s rayons x est la néthode de DEByE-SCHERRER.} L e diagrame de diffraction _{s e p r é s e n t e dans ee cas sous ra foræ}

d ' a n n e a u x dont Itintensité _{n r e s t pas r:niforme, indiquant par conséquent} I ' e x i s t e n c e d r o r i e n t a t i o n s p r é f é r e n t i e l l e s .

p o u r déterniner les orientations préférentier.les u n é c h a n t i l l o n , _{l e s chercheurs ont inaginé des dispositifs} d o n t le plus utilisé _{e s t l e g o n i o r n è t r e de scHItLz, associé à} é l e c t r o n i q u e d ' i m p u l s i o n s .

présentes dans expérinentaux

un compÈeur La technique de scHIILz permet drexplorer complèterent l-féchan-t i l l o n _{à c o n d i t i o n d ' u t i l i s e r s u c c e s s i v e n e n t l a d i f f r a c t i ô n}

d e s R . x . e n r e E o u r et en transmission. Le résultat expérinental se présente alors sous la forme dtun diagrarme linéaire dont les points ont pour ordormée l r i n t e n s i t é _{d i f f r a c t é e}

e t p o u r a b s c i s s e un couple de deux paramètres _{r e p é _} r a n t dans I rêchantilron la position de la normale au plan (hkl) diffrac_ t a n t .

L a déÈermination des orientations p r é f é r e n t i e l l e s _{à p a r t i r d e} c e diagranme est souvent très difficile. _{r r e s t g é n é r a l e m e n t nécessaire} d e Ie reporter sur une projection stéréographique. 0n obtient alors ,,,re f i g u r e de pôles' Le travail fastidieux qui consiste à transcrire l e d i a -graræ _linéaire

en figure de pôres a été suppriné grâce à ra mise au p o i n t d e t r a c e u r s automatiques (l). Crâce à lfutilisation _{d e c a n e v a s ( 2 )} ( 3 ) ' il esr possible en mesurant les angles entre Les maxina d r u n e figure d e p ô l e s de réaliser une anaryse qualitative _{d e r a texture.}

L e s orientations p r ê f é r e n t i e l l e s _{m i s e s en évidence ne sonË} gé-n é r a l e gé-n e gé-n t qurapproxigé-nativeægé-nt _{d é f i n i e s .}

c e l a a amené les chercheurs à r e m p l a c e r la noËion dtorientation _{p r é f é r e n t i e l L e p a r ce1le plus théorique} d r o r i e n t a t i o n _{i d é a l e autour de laquelle lee orientations préférentielles} se répartissent _{plus ou noins uniforménent pour forner rm domaine de} dis-p e r s i o n .

Dans le but de décrire de façon plus complète la texture dttrr é c h a n t i l l o n , l a n o t i o n d e f i b r e p a r t i e l l e q u i a été introduite p a r

G R E I I E N - T I A S S E R M A N N a é t . é r e p r i s e r é c e m e n t ( 4 ) , ( 5 ) , ( 6 ) . L e s descriptions o b È . e n u e s g r â c e au concept de fibre partielle s o n t c e r t a i n e m e n t p 1 - u s f i n e s m a i s restenÈ du domaine qualitatif. D e p l u s , un Ëel Èype de description e s t s o u v e n È t r è s d i f f i c i l e à u t i l i s e r .

C r e s t à p a r t i r d e 1 9 5 2 e n v i r o n , q u e l e s p r e m i è r e s t e n t a Ë i v e s d ' a n a l y s e q u a n t i t a t i v e d e l a t e x t u r e s o n t a p p a r u e s . A u d é b u t , e n r a i s o n d e l a d i f f i c u l t é d u p r o b l è m e p o s é , l e s chercheurs se sont limités aux t e x t u r e s d r é c h a n t i l l o n s p r é s e n t a n t une synétrie axiale, crest-à-dire a u x f i l s m é t a l 1 i q u e s . D a n s c e t y p e d ' é c h a n t i l l o n s , l e s o r i e n t a t i o n s s e m b l e n t a p p r o x i n a E i v e n e n t réparties sous forme de fibres complètes dont lfaxe est p a r a l l è l e à l r a x e d u f i l . . D a n s ce casr la texture se réduit alors à La f o n c t i o n d o n n a n t l a d i s t r i b u t i o n d e s d e n s i t é s de directions < u \ n r > paral-l è paral-l e s à paral-l r a x e du fiparal-l. D a n s l e c a s p a r t i c u l i e r d u s y s Ë è m e c r i s t - a l I i n

c u b i q u e , l a représentation de cette fonction densité peut se faire à lrin-E é r i e u r d ' r - r r triangle s p h é r i q u e r e p r é s e n t a n t l / 4 8 è n e d e l - a s p h è r e d e s p ô 1 e s . Cette forme de représentation esË appelée selon les auteurs, fi-g u r e de pôles inverse ou fifi-gure axiale

La relation fondamentale définissant une figure de pôles inverse a ê t ê é t a b l i e p a r G . B . I I A R R I S (7 ) . E l l e a é t é r e p r i s e , c o r r i g é e e t g é n é -r a l i s é e p a -r d i f f é -r e n t s c h e r c h e u r s , t e l s C . M . M I T C I I E L L e t J . F . R O W L Æ . I D ( 8 ) , L . K . JETTER, C.J. Mc IIARGUE e t R . 0 . I ^ I I L L I A U S (9 ) , H . J . B U N G E ( 1 0 ) et

R . J . R O E ( l l ) q u i ont développé successivement et séparément leur néthode p e r s o n n e 1 le.

P a r l a s u i t e , a u c o u r s d e s d e r n i è r e s a n n é e s , c e r t a i n s d e . e e s auteurs ont étendu leur analyse aux textures de ptus en plus complexes et de nouveaux chercheurs, tel K. f,ÛCrC (12) ont également proposé de nouvel-les méthodes. On trouvera dans Les ouvrages écrits par J. GREIIEN

-G . I , I A S S E R I . { A N N ( 1 3 ) , c.S. BARRET ( 1 4 ) , H.J. BITNGE ( t 5 ) et P. COULOI{B ( 1 6 )

a i n s i q u e d a n s l e s r a p p o r t s e t p u b l i c a t i o n s d e P . PARNIERE ( 1 7 ) l e s p r i n c i p a l e s r é a l i s a t i o n s _{e t 1 e s p r i n à i p a u x r é s u l t a t s o b t e n u s j u s q u t i c i d a n s le domaine des} È e x t u r e s

D e p u i s 1 9 6 9 , d e s c o l L o q u e s internationaux biannuels font le point sur lrévolution de l-a recherehe dans ce domaine encore en pleine

La seule néthode dranalyse des textures vraiment t a n È aujourdrhui est cerle développée dfune part par BUNGE p a r È , par ROE (22).

g é n é r a l e exis-e t , d t a u t r exis-e Les néthodes de BITNGE _{et de RoE ne sont en fait}

v a r i a n . e s drune seule et même méthode. Les différences qui p o r È e n t pas sur le principe de la néthode mais uniquement p r o c é d é s d e c a l c u l s .

que deux e x i s Ë e n t n e s u r certains s i l r o n se restreint _{à lranalyse des matériaux de réseau} eubi-9uê, Ia nérhode dranalyse linéaire _{développée par ItrLLrAMs (23) permer} d t o b t e n i r des résultats comparables à ceux obtenus avec la néthode d e BUNGE-ROE' _{La néthode de lÛcrc est spécialemenr adaprée à la déreruination} d e l a Ë e x t u r e à p a r t i r ' d ' o b s e r v a t i o n s _{f a i t e s e n m i c r o s c o p i e é l e c t r o n i q u e .} c e Ë t e procédure très longue et fastidieuse exclut donc cette néthode d e I ' e n s e u b l e d e s m é È h o d e s usuelLes dranalyse.

o n p e u t donc considérer qu'ir nrexiste aujourdrhui que deux g r a n d e s méthodes usuelles dtanalyse de la Ëexture des natériaux _{d e réseau} c u b i q u e , drune partr celle de BIINGE-ROE _{e t , drauËre parË, cerre de}

l I r L L r A l I s ' Bien que différenÈes dans leur principe, les méthodes a c t u e r l e s ont cependanÈ rm point cottrnun important. _{Quelle gue soit La néthode} uti-l i s é e , _{i l e s t nécessaire de réaliser plusieurs figures de pôles pour} o b t e n i r un résultat satisfaisant. _{r l e s t de plus généralement admis quril} n f e s t pas possible de calculer avec une précision suffisante _{l a fonction} d e disÈribution _{d e s orientations à p a r t i r}

d r u n e seure figure de pôres. La p l u p a r t des auteurs aduettent en effet qutune seule figure de pôles n r e s t q u t u n e représentation inconplète de la texture et que Les renseignenents q u ' e 1 l e contient sont théoriquemenÈ insuffisants pour pornroir _{c a r c u l e r la} f o n c t i o n d è d i s t r i b u t i o n d e s o r i e n t a t i o n s , _{c r e s t - à - d i r e , l a t e x t u r e ( 2 4 ) .}

Nous nous proposons de montrer que, contraire'ent _{à lropinion} g é n é r a L e n e n t admise, dans le cas particulier _{d u systèue cubique, une} seule figure de pôles est suffisante _{pour analyser la texture avec une} a i r p r o x i n a t i o n satisfaisante.

Avant de présenter la rnêthode gue nous avons inaginêe à cet effet, nous rappellerons pour conmencer les principales caractéristiques des méthodes de BTNGE-ROE et de $IfLLIAlfS. Nous comparerons ensuite les résultats obtenus avee chacune des principal-es méthodes eÈ Rous essaierons de dégager les avantages que présente la nouvelle oéthode proposée.

. II

-RESUI'|E.

DES PRINCIPALES

I - LA rÉftoæ rE BtficE

Dans ra méthode de Bunge, ra texture est représentée par une f o n c t i o n conÈinue f(91, 0, 9) appelée fonction de distribution _{d e s} orien-t a orien-t i o n s . L e s p a r a m è orien-t r e s g l , 0 eorien-t _{e , s o n t r e s a n g l e s d r E u r e r c l a s s i g u e s} q u i définissent l r o r i e n t a t i o n _{d ' u n repère orthonormal K, associé au} ré-s e a u criré-stallin _{d ' ' n g r a i n par rapport à un autre repère Ko fixe par} r a p p o r t à 1 ' é c h a n t i l l o n ( f i g . la). cette foncËion est généraleuent notée f ( g ) où la variable g représente syrnboliquemenr le tripLet (gt, _{6 , g Z ) .} L a fonetion f(g) se présente sous la forue d'un déveLoppenent en série de Ia forme : I +9, +1, _{[rr nrn}

r(s) =.

_{1 I}

_i

_{C;' T; (e)}

0=O m=-C n=_.0 k ,. ( 2 - t ) (2-3)

( 2 - + 1

s u r Ia base des harrnoniques sphériques généralisés définis par :

f i cr> = .i^92 pf (ù .iogr

Q - 2 ) polynônes de Legendre qui ol les Pfl @) sont des polynômes associés

peuvenË _{êÈre calculês par La relation :}

+9,

( 6 ) = I

_{" f t}

. i s O

s = - C

Ies coeff icienrs afls érrnc définis par :

" f t

= ( - r l 9 f + n pns

c e q u i petinet de sinpl.ifier _{l e calcul}

tanÈes

_{parriculières Pfl}

Ç) a6rini""

irFn

P o * ( g t =

-

( - t ) s * t

29'

ry

q P;"

e?

D - D t 9.+m) ;;\ !.-d,

e n utilisant _{r m i q u e m e n t les cons_}

: r=&-n

I

c-r

_{l' C' çca-r}

rao l-n 0+n P a r

l"'

(2-s

₎

partir _{de données} expé-f o r n e de plusieurs

I æ calcul de la fonction f(g) s,opère à r i n e n t a l e s

figures de pôles. Chaque figure de pôles est tout drabord développée en série sur 1a base des trarmniques sphériques simples kf, (t,n)' ti 4

représenre la norrnale à un plan (hrkili), la figure de pôles Pfrfe,l) est définie par :

Pfit, tE,n) =

Fr' tilr>

r! (e,n)

(2-6)

où (E,q) repèrent la direction { attt" le repère KO solidaire de lréehan-ritlon er où Ff tÈrl sont les coefficients du développement' Les coeffi-cients Fgt

"oot, dans le cas général, des nombres complexes'

Ils sont de p1us, pour une figure de pôles Pn+ donnêe' reliés aux coefficients f,fl du dévelopPemenÈ ae f(g) par une *elation de la forme :

+1,

T

n--1,

Ci rl* to, ,Q1)

= (?â*) Fi (tr)

(2-7) o + 1 ,

TI

9,=O F{ _ *

o ù k i ( o i , 9 i ) e s t l e

ot (oi,9i) rePèrent la

ionj ugué

direction f,l

( o r , 9 i ) e t

dans le rePère KU.

ae tf,

I l v a d e s o i q u e , d a n s d é f i n i p a r l a r e l a t i o n ( 2 - l ) d o i t c h o i s i r a 1 e p l u s é l - e v é p o s s i b L e '

la pratique, le développenent de f(g) être linité à un rang 9' = L que lron

D r a u t r e p a r t , l a r e l a t i o n ( 2 - 7 ) montre al.ors querdans ce cas' pour un nême couple (&rrn) donné, à tout FitÇt corresPondent 2L+l coef-f i c i e n t s d t

" n . " n v a r i a n t d e - L à + L ' ' 9 .

La relation (2-7) est donc une équation à 2L+l inconnues' Pour déterminer ces inconnues, il est donc indispensable de pouvoir écrire au noins 2L équations supplémentaires pour ce même couple dtindices (9,n)

donné. Gela signifie qut il faudra au minimun réaLiser expérimentalement 2 L f i g u r e s d e p ô l e s s u p p l é n e n t a i r e s . C o r r m e l t a p p r o x i n a t i o n a e f ( g ) s e r a drautant neilleure que le rang L du dêveloPpement sera plus êlevé' on voit gue, par son principe même, cette néthode donne tm résultat dont la

précision dépend du nombre de figlres de pôles erpérirnentales gue lton p e u t r é a l i s e r .

Ileureusenent, Iorsque le système cristallin auquel appartient I r é c h a a E i l l o n p o s s è d e d e s é l é m e n t s d e s 5 r u r é t r i e , l e n o n b r e d e c o e f f i c i e n t s Cm indépendants non nuls est sensiblement réduit. Ctest ainsi que dans

l e eas Ie plus favorable c u l e r le développenent de d e p ô l e s , j u s q u ' a u rang L a v e c t r o i s f i g u r e s .

q u i est celui du systèæ cubique, on peut f ( g ) j u s q u t a u rang L = lO avec une seule = 22 avec deux figures et jusqutau rang L

cal-figure

= 3 4

L o r s q u e , cottme crest le d e p ô l e s expériæntales _{p o s s è d e n t} s i m p l i f i e _{e n c o r e car le nombre des}

t i t e r , de plus, les Cfl

" t

f e s Ff,

c a s d e s produits larninés, Les figures é g a l e æ n t des symétries, le calcul se

'.Illn

V L r n d e p e n d a n t s e s t encore plus pe_ s o n t alors des nombres réels.

L t équation

@

r(e) = I

l=o - ï'uv

o u I _{L ( g ) sont les harmoniques sphériques} E r o u v e r a Ie détail du calcul dans I rouvrage q u e d a n s 1 e s articles que lui consacrent _{C .} C . E s l i n g , E . B e c h l e r er R. Baro (26),

généralisés synétrisés dont on p u b l i é p a r Bunge (t969), ainsi E s l i n g e r C. Tavard, (2S) et

( 2 - l ) s r é c r i t a l o r s :

I't(r) 111

s1

_{: .}

u=i,

J, cl' Îi'

(e)

( 2-8)

2 - [Â lÉTHoDE

_{E RoE}

Le principe _{de ra néthode de Roe est absolument identique à} c e l u i de la néthode de Bunge. Les différences entre ces deux n é t h o d e s a p p a r a i s s e n t d f u n e p a r t , au niveau des noËations, et drautre part, a u n i v e a u d e s E e c h n i q u e s de calcul utilisées.

2 . I , - N O T A T I O N S

Dans la néthode de Roe, La È a È i o n s s t é c r i t , :

f o n c t i o n de distribution _{d e s} orien-+9, +9,

J-, J-,

w.c*,

zr*r(e)"

i'Û" - i"o

! r ( { r , e r 0 ) =

_I

9.=o

(z-g)

Les l e s

p a r a m è t r e s û, 0 , 6 Gig. lb) sont Liés aux paranètres _{d e} r e l a t i o n s :

F i g . l a : Définition des pararnètres dans la rnéthode de H.J. BIINGE L e r e p è r e f i x e K O s o l i d a i r e d e 1 r ê c h a n t i l l o n e s t n o t é O L T N . L a r o t a t i o n ( 0 N , 9 1 ) arnène le repère mobile KB lié a u c r i s t a l d e l a p o s i t i o n O X Y Z à l a p o s i t i o n O X r Y r Z . L a s e c o n d e r o t a t i o n ( O X t r0) amène K, dans La position

O X r Y r f Z f e t l a t r o i s i è m e r o t a t i o n ( O Z ' , 9 2 ) a m è n e K , d a n s l a p o s i t i o n O x " Y " ' z r q u i d é f i n i t l r o r i e n t a t i o o ( 9 t , 6 , 9 2 ) d u c r i s t a l .

7

KN

s

xttt

F i g . l b : Définition d e s p a r a m è r r e s dans la méthode de R.J. ROE L e s t r o i s r o t a t i o n s s u c c e s s i v e s s o n t ( o N r { r ) , ( o y l r 0 ) e t

( O Z ' ,q). On remprque que seule la seconde roÈation est d i f f é r e n t e d e c e l l e urilisée p a r BUNGB.

= 9 1

g = 0

o R o " = 9 2

TI 2 Bunge 1T + . ; z

( 2 - l o )

Si deux Èriplets (,1.,,0, 0*o")

"t (9t,6yunee, QZ) se

correspon-d e n È s e l o n l e s é g a l i t é s ( 2 - 1 0 ) , l e s r e l a t i o n s ( 2 - l ) e t ( 2 - 9 ) s o n t é q u i v a l e n t e s .

2 . 2 . - C A L C I ' L D E S C O E F F I C I E N T S

D a n s l e eas général, il nty a aucune différence entre les deux m é t h o d e s . P a r c o n t r e , d a n s l e cas où lton tient compte des synétries é v e n È u e l I e s , l e p r i n c i p e du calcul de Roe est différent d e c e l u i d e B u n g e .

Pour tenir conpte des éIêments de synêtrie, Br.rnge a calculé de n o u v e l l e s b a s e s s y m é t r i s é e s de 1'espace des harnoniques sphériques géné-r a l i s é s , _{n o t é s Ï[" <tl dans le cas de la symétrie cubique du cristaL er} d e l a syrnétrie orÈhorhombique de Lréchantillon. L e c a l c u l c o n s i s t e a l o r s à n e calculer que fes f,lv qui sont les coefficients d u d é v e l o p p e m e n t s u r c e t t e n o u v e l l e b a s e , e n résolvant le systène dréquations (2-7).

Dans la néthode de Roe, au contraire, on montre que, dans le c a s d e I t e x i s È e n c e d ' é l é n e n t s d e s y n é t r i e , s e u l s c e r t a i n s c o e f f i c i e n t s l"lu,',,r,

"oot linéairement indépendants. On ne calcule donc que les llgnn linéairement indépendants à parÈir (aux notations près) du nâne systène d ' é q u a t i o n s ( 2 - 7 ) . 11 suffit _{e n s u i t e d e c a l c u l e r l e s Wg-n mnguants par} leurs relations de dêpendance linéaire en fonction _{deb |l|O-,., choisis corme} é t a n r i n d é p e n d a n t s . A titre d r e x e m p l e , o n a l a r e l a t i o n d e d é p e n d a n c e l i -n é a i r e suiva-nte :

W , r r , = 0 , 8 1 4 9 1 5 1 4

W , r r o ' t , 4 4 z i g z z W , r r o

( 2 - l l ) d a n s l e c a s d ' u n r é s e a u c r i s t a l l i n c u b i q u e .

L e d é t a i l d u calcul de f(g) par la néthode de Roe esË explicité d a n s l e s p u b l i c a t i o n s d e R o e ( 2 2 ) , M o r r i s et llecklex (27).

C e t È e néthode c u b i q u e s p r é s e n t a n t soi r h o n b i q u e ( f i l s o u r ô l e s ê t r e u È i l i s é e , d a n s s o n p ô l e s ( l o O ) e È ( l l t ) .

3 - ua pÉrxom E l,lILLIAt',ts

n e p e u Ë a c t u e l l e n e n t s r a p p l i q u e r q u r à des matériaux t une synétrie axiale, soit une symétrie ortho_

n é t a l l i q u e s ) . _{D e p 1 u s , c e t t e m é t h o d e n e p e u t} é t a t actuel, qutavec les deux seules figures de

L a m é t h o d e de Williams est Erès différente de celle de Bunge-R o e . Elle se caractérise en premier lieu par une représenËation inverse d e s o r i e n t a t i o n s ( r i g ; 2 ) . L e r e p è r e K A lié à 1réchantillon est repéré p a r Erois paramètres angulaires à ltintérieur d u repère K, représentant l e sysÈème cristallin _{c u b i q u e . L e s axes oN et oL du repère Ko} représen-E e n t respectivement, par exempLe, la normale au plan de laninage et la d i r e c t i o n _{d e l a m i n a g e dtune tôre. Lraxe oN est repéré pa= ae,rxt angres} p e t a à l r i n t é r i e u r _{d u r r i a n g l e s p h é r i q u e d e s o n r n e t r [roo],[rlr] e t}

[ r r o ] . L a v a l e u r d e l f a n g l e p r e p r é s e n t e l t a m p l i t u d e d e l a r o t a t i o n a u -Ë o u r de 1'axe oN qui amène l'axe oL dans le plan (ooty. Le repère Ko é t a n t trirectangle, _{l a p o s i t i o n du troisiène axe oT se déduit} imédia-t e m e n imédia-t . des posiimédia-tions occupées par les axes ON eimédia-t OL.

E n résumé, dans la méthode de williams, une orientation est d é f i n i e par la position de deux axes mâcroscopiques reccangulaires à I ' i n t é r i e u r _{d u r e p è r e m i c r o s c o p i q u e a s s o c i é a u c r i s t a l . p o u r c e t t e raison,} l r a u t e u r définit _{s a n é t h o d e conne étant r:ne méthode biaxiale.}

L e p r i n c i p e de cette néthode consiste à calculer la fonction de d i s t r i b u t i o n _{d e s o r i e n t a t i o n s T ( p rcrB) pour 1296 oti,entations (oloir Br)} d i s t i n c t e s _{e t supposées uniformément réparEies.}

A chaque point (6,'r> drune figure de pôles (hkl) correspond'ne d e n s i t é de nornales aux plans (hkl) proportionnelle _{à l r i n t e n s i t é r ( 6 ; y )} d u rayonneænÈ diffracté. _{C e t t e intensité I e s t liée à la fonction T par} l a relation :

r(o'Y

_)rucr

=

T

a

to

[ttt]

ê,\

\

[ro

pl

\

L

'ol

_[tto]

[oo

i

b

a)

b)

2 : D é f i n i r i o n d e s p a r a m è t r e s u t i l i s é s d a n s l a s r é t h o d e d e R . 0 . I ^ I I L L I A I ' { S a ) D a n s c e t t e n é t h o d e , c r e s t l e r e p è r e K O = O L T N q u i e s t r n o b i l e , l e r e p è r e K B l i é a u c r i s t a l é t a n t f i x e . L e s p a r a m è t r e s p e t o r e p è r e n t l a p o s i t i o n d e l a n o r m a l e O N a u p l a n d e 1 ' é c h a n t i l l o n d a n s l e t r i a n g l e s t a n d a r d

[ r o o ] - [ r ' o ] - [ r r r ] .

o n r e p è r e l ' a x e O L à l t a i d e d e l r a n g l e $ r e p r é s e n t a n t l f a n p l i -t u d e d e l a r o -t a È i o n a u -t o u r d e 0 N q u i a n è n e o L d a n s l a p o s i -t i o n O L ' c o n t e n u e d a n s l e P l a n ( O O l ) . b ) R e p r é s e n t a t i o n d e l f e n s e m b l e d e s o r i e n t a t i o n s ( p ' a ' B ) s o u s for.me dtun prisme désigné dans la néthode de IÛILLIAMS sous n o m d e "volume biaxial". F i g . 1 a 1 e

(p,u,F)

.,---n

ou de 1 e . m?T A = f r , m é t a n t , l a m u l t i p l i c i t é d u p l a n ( h k l ) e t o ù Ê est ra mesure l r a r c d é c r i t p a r l r a x e o N d a n s l e r r i a n g l e [roo]-[r r r] - [t to] ror"q,r. P o i n t ( 6 ' v ) 6 1 1 e s t s u P P o s é f i x e .

L e s v a r i a b l e s e t ô s o n t l i é e s p a r l a r e l a t i o n : = ô 1 Y + n n

o ù n = - 1 , O o u l , d e n a n i è r e q u e B e t ô s o i e n t t o u j o u r s c o m p r i s entre O o e t l 8 O o .

L e c a l c u l du paramètre ô pour une figure (hkl) autre que la f i g u r e ( l o o ) n t a , à n o t r e c o n n a i s s a n c e , p a s é t é p u b l i é . D ' a u t r e p a r È , l e s p a r a m è t r e s 6 , p e t o , n e s o n t p a s i n d é p e n d a n t s et les relations liant ces t r o i s p a r a m è t r e s ne semblent pas non plus avoir été publiées.

L e p r i n c i p e d u c a l c u l e m p l o y é p a r W i l l i a m s c o n s i s È e ' à r e m p l a c e r l ' é q u a t i o r l ( 2 - 1 2 ) p a r l a s o m r e d i s c r è È e :

B

I i = *

r ( O j y 5 ) n t r = *

, l ;

T ( p , o , B ) A e i D a n s c e t t e d e r n i è r e e x p r e s s i o n , h k l = l o o o u I I I e t l e s p a r a -m è t r e s p et a sont constanEs pour chaque point (Q, t;) de chaque figure d e p ô l e s . L r e x p r e s s i o n ( z - 1 3 ) p e u t s r é c r i r e ,

" o , r r ' r o r * " " o o d " o " é " :

( 2 - r 3 )

( 2 - t 4 )

r = [n] r

o f I n] es! une matrice rectangulaire non négative, r étant le vecteur c o l o n n e r e p r é s e n r a n t l e s i n t e n s i Ê é s e x p é r i m e n t a l e s I(Aj, tj)nnf supposées c o r r i g é e s e t n o r m é e s ' e È T l e v e c L e u r r e p r ê s e n t a n t l e s densités drorien-t a È i o n s T ( g i , c i , B i ) a v e c i = 1 , . . , . , 1 2 9 6 .

L a soluËion du systène dréquation (2-14) est obtenue par une méthode itérative désignée par l.Iillians sous le nom de ntEthode prLS

( P o s i t i v e I t e r a t i v e L e a s t Squares Method).

C e t E e néthode consiste à séLectionner un certain nosibre d'orien-t a d'orien-t i o n s ( o i , a i , Ê i ) e d'orien-t à é d'orien-t a b l i r l e s c o r r e s p o n d a n c e s exisd'orien-tand'orien-t end'orien-tre les

7 i n c e n s i t é s l ( 6 3 r v 5 ) i j = 1 1 . " , 7 a s s o c i é e s à u n m ê n e

r^ ^ Q. \

\ " i r * i t " i / .

On calcule tout dtabord une valeur approchée Tr du vecteur I à I ' a i d e d u p r o d u i t : 7

r, - r fI rl (hkl)

(2-15)

i = l r C e p r o d u i t P o r t e s u r l e s T v a l e u r s l , c o r r e s p o n d a n È a P p r o x i n a -E i v e m e n r a u x 7 p ô l e s ( 3 p ô I e s ( l O O ) e t 4 p ô l e s ( l l l ) ) r e p r ê s e n t â n È u n e r n ê m e o r i e n t a t i o n ( 9 i , a i r B i ) . L e s v a l e u r s d u c o e f f i c i e n t k e t d e l f e x p o -s a n t n -s o n È c h o i " i e e a l r a i d e d t u n p r o c é d é e n p i r i q u e q u i n f e s È p a s p r é c i a é . P a r t r r e n é t h o d e d e n o i n d r e s c a r r é s , o n a n é l i o r e e n s o i t e l e r é s r r l Ë a t È o u t e n é l i r n i n a n t s y s t ê m a t i q u e n e n g l e s v a l e u r s n é g a t i v e s d e ! f n , a y a n t a u c u n s e n s p h y s i q u e e t c e , i u e q u ' à o b t e n i r u n e v a r i a n c e m i n i n a t e d e T t . N o u s r e n v o y o n g l e l e c t e u r ' P o u r p l u s d e p r é c i s i o n s a u x e r t i c l e s d a n s l e s q u e l s W i l l i a m s e x p o s e 8 8 r n é t h o d e ( 9 ) , ( 2 3 ) .

on remarquera que ta &éthode de I'rilliams possède certaine avantages p a r É a p p o r t s u x d e u x m é t h o d e s p r ê c é d e n t e e . E n p a r t i c u l i e r , c e t t e u é t h o d e c o n d u i t à u n r é s u l t a t d o n t l e e é l é n e n È e o n t t o u E u n s e n o p h y s i q u e ' D r a u È r e p a r t , , l e g d o n n é e s e x p é r i n e n t a l e s ' u n e f o i s c o r r i g é e s ' 8 o n È u c i l i s é e s d i r e c t e -m e n t d a n o l e e c a l C u l s e Ë n r o n t p a g b ê g o i n ' c o r n m e d a n s l a n é U h o d e d e B u n g e - R o e ' d r ê t r e m i c e g c o u t l a f o r m e d r u n d é v e l o p p e m e n t e n s é r l e ' C e t t e t r a n s f o r n â t i o n m a t h é m a t i q u e l u p o a é e a u x d o n n É e e e x p é r i m e n t a l e s e n t r a l n e , e n e f f e t ' d e s e r r e u r s ( 2 E ) q u i e t a j o u t e n t a u x e r r e u r s e x p é r i m e n È ê l e s d ê j à e x i s t a n t e s '

1 - pnlncrpes

eÉruÉnar-lx

L a r o é t h o d e vectorielle _{e s t basée sur les relations géométriques} e x r s t a n t entre une figure de pôles directe et la figure de pôles i n v e r s e s e l o n la normale au plan de Lféchantillon. _{c e È È e rnéthode s,apparente donc,} d u moins dans son principe général, à celle de l,rilliams. EIle en diffère t o u E e f o i s s u r d e n o m b r e u x poinÈs essentiels :

l e s p a r a m è t r e s définissant _{l e s o r i e n t a t i o n s s o n t indépendants,} - I'ensemble des orientations esË divisé en sous-ensembles

é g a u x ,

- les êquations nécessaires au calcur sont générales _{e t} rigou-r e u s e s ,

- la méthode itérative utilisée est systénacique e t n , u t i l i s e pas de paramètres décerminés de façon enpirique,

- aucune hypothèse restrictive _{concernant la s5iuétrie} r1acros-c o p i q u e d e 1 t é r1acros-c h a n t i l l o n n'est nér1acros-cessaire,

- une seur.e figure de pôles incomprète obtenue par la méthode d e schulz en réflexion peut suffire pour res applications. s i I t o n s t e n t i e n t a u x g r a n d e s lignes, la méthode vectorierle p e u c se résumer par les étapes suivântes :

a) on repère chaque grouPe de 24 orientations _{physiquement équivalentes} d u systène cubique par un seul triplet _{( r l i r o r r E ) de paramètres angulaires} i n d é p e n d a n t s .

b ) on réalise une partition _{f i n i e d e l'ensernble G de ces groupes en N} c l a s s e s d t é q u i v a l e n c e d e fibres partierres Grr, n = te,..eN. chaque c l a s s e G1 contient le même nombre infini d'orientations. L r e n s e m b l e G c o r r e s p o n d au double du "volume biaxial" défini par wirrians.

c) 0n associe à chaque classe Go le volune partiel de mesure yrrr occupé d a n s l f é c h a n t i l l o n p o l y c r i s t a l l i n _{p a r l e s g r a i n s d o n t l e s orientations}

appartiennenE à cette même classe Grr. Chaque nombre Y' vérifie les d e u x r e l a t i o n s : N ! n ' . O e t I l o = t ' n = l N d ) O n r e p r é s e n È e a l o r s l a t e x t u r e P a r l e v e c t e u r d e _{$ '} : N - > n - ) Y = T _{I O " "} n = l D a n s l e c a s o ù l ' ê c h a n t i l l o n e s t i s o È r o p e ' o n P o s e Y r , = Y l = l , q u e l g u e soiÈ n. La texture dtun échanÈiLlon isotrope est donc représentée p a r I e vecteur :

= ( l r l r . . . r l )

donc conrme 1r niè* comporsante T o u t v e c È e u r d e b a s e Ë o a p p a r a Î t v e c t o r i e l l e d u v e c t e u r I o . I i h k l ) d e N

rË

t r l t n e ) o n r e p r é s e n t e u n e f i g u r e d e p ô l e s 1 ' e s p a c e v e c t o r i e l R P t e l q u e : P

i i n n ] =

_{[ r}

P = t P I - { h k l } ê t a n t l a æ s u r e e x p é r i m e n t a l - e d e f i n t e n s i t é d i f f r a c t é e D .

( s u p p o s e e corrigée et nornée) sur la pleme ease Cn de la figure de p ô l e s

P o u r u n é c h a n t i l l o n i s o t , r o P e , o n p o s e l - { h k l } _{' p '} - = l, pour tout {hkl} e t q u e l q u e s o i t p , d e s o r t e q u e , d a n s c e c a s , L o u t e f i g u r e d e p ô l e s e s t r e p r é s e n t é e p a r l e v e c t e u r I o = ( 1 r t r . . . ' l ) d e R P .

f ) O n c a l c u l e p o u r c h a q u e c a s e C O d r u n e f i g u r e d e p ô L e s { h k l } , l a d e n -s i t é o _ _ d e -s p ô l e -s thkl) de-s grain-s dont le-s orientation-s a p p a r t i e n

-Pn n e n t à r r n e c l a s s e G o , l t é c h a n t i l l o n é t a n t s u p p o s é i s o t r o p e . 0 n a s s o c i e a i n s i à t o u c v e c t e u r È n a " R N , , r t v e c t e u r Û r r { h k r } d " n P t . l gue : Û r , { t t t } = ( o l o , o 2 n , . . . . , o p o . . . r o r r ) = f ( È r r ) { h k l } p a r l e v e c t e u r { h k l } È P > N P

C h a q u e v e c t e u r

{ O n t } r e p r é s e n r e une figure de pôles appelée f i g u r e de pôles élérnentaire. une telle figure représente en quelgue s o r t e une texÈure équivalente à une orientaÈion idéale. La superposition d e toutes les figures de pôles élémentaires est égale au vecteut il. on a donc : - ) N J

ro = I É_ft,n)

n j t n 8 ) o n m o n E r e q u ' u n v e c E e u r i { n t r } d o n n é e t l e v e c t e u r i q , r i 1 u i c o r r e s p o n d s o n t l i é s p a r I a r e l a t i o n :

i r n u r i = T vn*tmr]

_{' n n} l a q u e l l e p e u t s ! é c r i r e é g a l e m e n t : o ù [o*-{hkl}l

" " r u n e m a r r i c e non négarive de dimension p x N.

L p n J

h ) on utilise' _{P o u r t r o u v e r u n e s o l u t i o n a p p r o c h é e d e ce système linéaire,} une méEhode de réduction systématique de la norme du vecteur résidu qui e s t t o u j o u r s c o n v e r g e n t e e t q u i e x c l u t la possibilité de trouver des ' r o l u m e s yo négatifs. Pour les applications, on a choisi p = 3240 et N = 2 5 9 2 .

Le fait de choisir _{une dimension de nP supérieure à celle de RN, pernet} d e câlcul"t f à p a r t i r _{d ! u n e seule figure de pôles inconplète obtenue} u n i q u e m e n t en réflexion.

L e d é t a i l e t I a j u s t i f i c a t i o n _{d e s c a l c u l s f o n t l f o b j e t d e s} p a r a g r a p h e s suivants du présent chapitre.

2 - cFrorx

IES pAml4Èrres

Æ'rGUtâtREs

L ' é c h a n t i l l o n e s È s u p p o s é s o l i d a i r e d r u n r e p è r e

\ t r i r e c t a n -g l e d i r e c t d ' a x e s O L , O T , O N . C h a q u e c r i s t a l l i t e e s t s o l i d a i r e d f u n a u t r e r e p è r e t r i r e c t a n g l e d i r e c t R ç r de mêne origine O, dont les axes OA, OB et o c s o n t respectivement parallèles _{a u x r a n g é e s [roo], [cro]}

" t [ o o t ] . r , " s e n s p o s i t i f d e s r o È a t i o n s e s t c e l u i d é f i n i p a r l e s e n s i n v e r s e d e s a i -g u i l l e s d r u n e m o n t r e . L e s r e p è r e s R " " a R a s o n t r a u x n o t a t i o n s p r è s , c e u x c h o i s i s j u s q u ' i c i _{p a r t o u s l e s a u t e u r s . D a n s l e c a s p a r t i c u l i e r d u s y s t è n e c u b i} -q u e , n o u s avons préféré au repère Ra le repère obli-que direct

\ d é f i n i p a r l e s r a n g é e s [oor], . [ïïr] et [rTr] (f ig.3). ce repère peur',êrre consi-déré corme forrné de la rér:nion de deux repères obliques voisins _\, et R r ^ , l e p r e m i e r é t a n t d é f i n i p a r l e s r a n g é e s [oor], [oTl] et [rîl]'er l e

t a

s e â o n d p a r l e s r a n g é e s [oor] , [oTr]

" t [ t f r ] . ' L e s r r i è d r e s R r . " . \ , d é c o u p e n t respectivement sur la sphère des pôles les triangfËl

" p n e r i q r . r e s s t a n d a r d s T , e t T 2 .

E n raison de la synétrie cubique, iL existe 24 repères \ m a t h é n a c i q u e n e n t d i s t i n c t s m a i s p h y s i q u e æ n t é q u i v a l e n t s . _{Q u e l l e q u e s o i t}

1 ' o r i e n t , a t i o n d f u n c r i s t a l l i t e , l r a x e O N d u r e p è r e

\ e s t t o u j o u r s s i t u é à l f i n t é r i e u r d u t r i è d r e d é f i n i p a r lrun des 24 repères équivalents à

\ . C o n m e c e s r e p è r e s sont physiqueneut indiscernables, o n p e u t t o u j o u r s c o n s i d é r e r q u e l r a x e O N e s t s i t u é d a n s l e seul repèr. \ q u e n o u s avons d é f i n i . D é f i n i r u n e o r i e n t a È i o n r e v i e n t a l o r s à d é f i n i r I t o r i e n t a t i o n d u r e p è r e \ e . . r a p p o r t a u r e p è r e \. L r a v a n t a g e de l'ernploi du repère \ e s t d e p e r m e t t r e la repré-s e n È a t i o n d e repré-s 2 4 o r i e n t a t i o n repré-s é q u i v a l e n t e s d r u n cristal c u b i q u e p a r u n e s e u l e e t r : n i g u e o r i e n t a t i o n . P o u r d é f i n i r u n e o r i e n t a t i o n , o n r e p è r e e n p r e m i e r l a p o s i t i o n d e I ' a x e O N d a n s le repère

\ p " t 1es deux paramètres indépendanÈs t et r , r ( f i g . 3 ) .

L

A

a

1 \

- " 4

\

T +

-tgr't = tg "À cos /

F i g . 3 : P r o j e c t i o n s t é r é o g r a p h i q u e d e s r e p è r e s o b l i q u e s é g u i v a l e n t s a u r e p è r e _\ = ( [ o o t , _{L Î T l ] , [ i l ] ) P o u r u n c r i s t a l d ' o r i e n} -t a È i o n ( , r -t Q , 0 r O ) .

v

qn

\ \ \ \

o n c o n v i e n t d e d o n n e r u n e v a l e u r p o s i t i v e a u ParanèËre'D ,i O N e s t d a n s l e r e p è r e R 1 , , c e t t e v a l e u r é t a n t n é g a t i v e s i O N e s t d a n s * t r . L ' e n s e m b l e d e t o u E e s l e s p o s i t i o n s p o s s i b l e s d e l f a x e 0 N e s t o b t e n u e n f a i s a n t v a r i e r ù e n È r e - r / 4 e t + r / 4 e t o e n t r e o e t t / 4 . T o u L c o u p l e ( Ù r o ) d é f i n i t I ' a x e c r i s t a l l o g r a p h i q u e d ' t r n e f i b r e , c e t a x e é t a n t n o r m a l a u p l a n d e 1 t é c h a n t i l l o n . L e s o r i e n t a t i o n s a p p a r Ë e n a n Ê à u n e m ê m e f i b r e d ' _ a 1 e ( û r u r ) p e u v e n t s e d é d u i r e 1 ' u n e d e I ' a u E r e p a r u n e r o È a t i o n a u t o u r d e l r a x e O N .

D é s i g n o n s p t t q 1 a p o s i t i o n d u r e p è r e \ lorsque les rangées [ i o o ] , [ r , o ] e t [ o o r ] s o n t c o n f o n d u e s r e s p e c t i v e m e n t a v e c l e s a x e s o L , O T , o N d u r e p è r e _{\ .} L f o r i e n Ë a t i o n d é f i n i e p a r { _{" s t} l r o r i e n t a t i o n ( 0 , 0 , 0 ) . D é s i g n o n s p " r R + l a p o s i t i o n d u r e p è r e \ c o r r e s p o n d a n t à u n e o r i e n t a t i o n ( r l . , r r r l _{, O ) a r b i t r a i r e .} L f o r i e n t a t i o n ( ù , o , 0 ) e s t d é f i n i e p a r l a p l u s p e t i t e r o t a t i o n q u i f a i t p a s s e r h d " l a p o s i t i o n n ! à l a p o s i t i o n R | . L r a x e d e c e t t e p l u s p e t i t e r o t a t i o n e s t t a n o r m a l e O D a u p l a n ( [ o o t ] , o N ) . t r a x e O D e s t s i r u é d a n s l e p l a n ( O L , O T ) e t l r a n g l e q u e f a i t c e t a x e a v e c l a d i r e c -t i o n o L e s -t é g a l à r f . P o u r a r n e n e r l e r e p è r e R , d e l a p o s i -t i o -t -t { a f" I p o s i t i o n R i c o r r e s p o n d a n t à l r o r i e n t a t i o n ( û , o , 0 ) , i l s u f f i t d e E o u r n e r a u t o u r d e O D , d a n s l e s e n s n é g a t i f , d r u n a n g l e I é g a l à l ' a n g l e _{t [OOl, Onl} d o n E l a v a l e u r e s t donnée par : i t g À cosrlr = tg,r)\ ( 3 - t ) U n e o r i e n t a t i o n ( û r o : r E ) a r b i t r a i r e e s t d é f i n i e c o n m e 1 ' o r i e n t a t i o n a p p a r t e n a n t à l a f i b r e d ' a x e ( ù r u r ) e t q u i s e d é d u i t d e l t o r i e n -t a È i o n ( U r , . ^ l r O ) p a r l a r o t a t i o n d t a n p l i t u c l e Ç a u t o u r d e O N . L r e n s e m b l e d e t o u t e s l e s o r i e n t a t i o n s d t u n e f i b r e e o m p l è Ë e c o r r e s p o n d à u n e v a r i a t i o n d e 0 à 2 n d u p a r a m è t r e q . N o u s c o n v i e n d r o n s d e f a i r e v a r i e r Ç de 0 à 2n s i 0 N e s t d a n s l e r e p è r e \ , e t d e O à - 2 r . s i O N e s t d a n s l e r e p è r e R r , C e t t e convenÈion n'est pas ârbitraire. O n r e m e r q u e r a , e n e f f e t . , q u e d e u i o r i e n È a È i o n s ( û r u r r E ) e t ( - r l r r , r , - E ) s o n t s 5 m é t r i q u e s p a r r a p p o r t a u p l a n

s o n t s y o é t r i q u e s p a r r a p p o r t à I ' a x e O N e t d e u x o r i e n t a t i o n s ( r f r u i , Ç ) e t ( V r o , 4 n ) s o n E s y m é t r i q u e s p a r r a p p o r t a u p l a n ( O N ' O L ) . L e s p a r a -m è È r e s q u e nous avons choisis pernettent donc de regrouper facilerænt l e s o r i e n t a t i o n s e n f o n c t i o n d e s s y m é t r i e s q u e p e u t p r ê s e n t e r l a t e x t u r e d ' u n é c h a n t i l l o n . L e s p a r a m è t r e s p e r d u t i l i s é s p a r W i l l i a m s s o n È i d e n t i q u e s a u x p a r a m è t r e s d é s i g n é s i c i p a r À e t r l . L a r e l a t i o n ( 3 - l ) m o n t r e q u e t g À v a r i e d e 0 à l / c o s r l . L a l i m i t e s u p é r i e u r e d e I d é p e n d d o n c d e { i . L e n o u v e a u p a r a n è t r e o q u e n o u s a v o n s c h o i s i a l t a v a n t a g e d e p o ' u v o i r v a r i e r e n t r e l e s l i m i t e s f i x e s O e t r l 4 . L ' e n s e m b l e G d e s o r i e n t a t i o n s e s t d o n c d é f i n i p a r : ( 3 - 2 ) t l r > 0

r l r < o

S i I ' o n r e p r é s e n t e g r a p h i q u e n e n t u n e o r i e n t a t i o n ( û r o r E ) p a r u n p o i n t d e c o o r d o n n é e s û, o, 6 dans un repère orEhogonal direct 0 Û tl 6t I ' e n s e m b l e G d e t o u t e s l e s o r i e n t a t i o n s e s E r e p r é s e n t ê p a r u n d o u b l e p r i s -n e d r o i È ( f i g . 5 ) . D a n s c e t t e r e p r é s e n t a t i o n s y n b o l i q u e , l e s t r i a n g l e s T t e t T 2 sont représentés par deux carrés du plan V 0 rrl.

3 - pARTITtoN

DE L'ENSEItsLE

G Es oRIENTATIoNS

o n r é a l i s e tou! d'abord une partition d e c h a c u n d e s t r i a n g L e s s p h é r i q u e s T , e t T z e n 3 6 c a s e s a u d ' a i r e é g a l e ( f i g . 4 ) . L e s l i m i t e s u r . e t ûij des cases tu sont indiquées dans le tableau I. Les cases de T, c o r r e s p o n d e n t à d e s i n d i c e s g p o s i t i f s _{e t c e l l e s d e T , à d e s i n d i c e s n é} -g a t i f s . _{D e u x cases drindiees opposés sont symétrigues par rapport au plan} ( t O O ) . L e c a l c u l d e c e s l i m i t e s e s t explicité en annexe I. G = { ( r l , o , Ç ) }

* . f î,* i]

., .f o,

_{+ Ël}

ç € [ o , + z d s i

c e l ' 0 , - 2 C s i

. t \

a{",u \

'

indices

_/

indices i

₎

F i g . 4 : P a r t i r i o n d u t r i a n g l e s p h é r i q u e T , e n 3 6 c a s e s t . . ( u = I , . . . , 3 6 )_u j . d ' a i r e é g a l e . L ' i n d i c e t r e s t é g a l à i ( i - l ) / Z +

ttt .-(') 5 C! 5 ? .çf (7) È N Oi (.) rn tî, (f, o, (Y1 r^ .if .t .t (1 t\ N € o, q, (\ O) @ (1 æ (1 (Y') c! (f) .if (Y) (Y't |\ o Or (r) (1 N .û rn N N N @ Or Cî o\ (n o C1 @ t\ È (n o .t l\ o c\ rô N t\ \o t\ co @ o |rl .dF ôl t..l o\ o\ tn Ot N c.l ôl o\ \o (f) .t o(\

I

Cî (1 .f .d-.+ o ôl a^ N \o rô (! ôl t\ .il æ rn o\ ôl t\ \o \o cl o ,\ o .t È .t o \0 rô (f) (tl r^ rn o |\ \o @ Cî \o ôl c! rn N N N rô lô o (\ @ o F o N (1 (\ (\ o rrl rn N (') c1

-29-É o o OE o \oÊ Éo É .'1 orJ €.J .o lrÉ Éo oc) a ,o .F{ N È t-, oo) 'q Fl ot rrÉ oro .il tr 3P oo 'dÊ Of. trj oo. F{ (Éu >É q) utÊ oo Fl Fl .. è0 _ro tsl l(,' q, l o -ll t{ ôcl ! Él qt Ol F{ .Fil d t{l ut lu al É .n "ol o ...1 'f,è rJl o ot llr1' rhl a ol o o Ol ,{É (ul rË èt (,,1 > ..{ | .l) crrl o ol o o !l o I ol . tl CJ | (Dr OJ !l tol èc .F{| t É El ô0 (É .Hl o .c FJI'O U

t e s s o u s - e n s e m b l e s d e f i b r e s s a n t c h a q u e p r i s m e C f e n 3 6 p r i s r n e s p l u s m ê m e h a u È e u r A Ç u = r / 1 8 c o n s t i t u e n t u n e s o u s - e n s e m b l e s G u u é e i a u x . o n d é s i g n e p a r C l I e p r i s r n e d r o i t d e b a s e t u e È d e h a u t e u r é g a l e à 2 n d a n s l e v o l u m e s y r n b o l i q u e G ( f i g . 5 ) . O n r é a l i s e a i n s i u n e p a r t i t i o n d e I t e n s e n b l e G e n 7 2 s o u s - e n s e r r b l e s G j ._{t l} L f e n s e m b l e d e s o r i e n t a È i o n s r e p r é s e n t é e s p a r l e s p o i n t s d t u n s e g m e n t t e l q u e N N t c o n s t i t u e r : n e f i b r e c o m p l è t e d o n t l t a x e , q u i e s t n o r -m a l a u p l a n d e l r é c h a n t i l l o n , e s t r e p é r é d a n s l e c r i s t a l p a r l e s coordonnées û*

"t \ du poinÈ N. Chaque sous-ensemble Cj comprend donc a u t a n È d e f i b r e s c o m p l è t e s q u t i l y a d e p o i n t s d a n s l a c a s e t u . C o r n r n e l e s a i r e s d e t o u t e s l e s c a s e s t u s o n t é g a l e s r o n e n d é d u i t q u e l e n o m b r e i n -f i n i d e f i b r e s e o m p l è Ë e s c o n t e n u e s d a n s c h a q u e s o u s - e n s e n b l e C f , e s t c o n s t a n t e t p r o p o r t i o n n e l à l r a n g l e s o l i d e f l r = r / 4 3 2 q u i c o r r e s p o n d à c h a q u e c a s e t u . C r e s t e n c e s e n s q u e , p o u r s i m p l i f i e r ' n o u s d i r o n s g u e l e s s o u s - e n s e m b l e s d e f i b r e s c o m p l è E e s C l s o n t é g a u x . p a r t i e l L e " G u u o b t e n u s e n d i v i -p e t i t s d e m ê n e b a s e t u e t d e n o u v e l l e p a r t i t i o n d e G e n 2 5 9 2 0 n a d r n e t q u e , p a r h y p o t h è s e , l e s f i b r e s p a r t i e l l e s a i n s i d é f i n i e s v é r i f i e n t 1 a r e l a t i o n : ' r d e u x f i b r e s p a r t i e l l e s s o n t i n d i s c e r -n a b l e s s i , e t s e u l e m e -n t s i r e l l e s a p p a r t i e n n e n t à u n m ê m e s o u s - e n s e m b l e G u u " . C r e s t d a n s l e b u t d e r a p p e l e r c e t t e h y p o t h è s e f o n d a m e n t a l e q u e n o u s d i r o n s d r u n s o u s - e n s e n b l e G u u g u t i l c o n s t i t u e u n e c l a s s e d t é q u i v a l e n c e d e f i b r e s p a r t i e l l e s . C o n m e d e u x o r i e n t a t i o n s a p p a r t e n a n t à r n e m ê m e f i b r e p a r t i e l l e s o n t , p a r v o i e d e c o n s é q u e n c e , é g a l e m e n t i n d i s c e r n a b l e s , nous pouvons également considérer Eout sous-ensemble Guu

"o* une classe d t é q u i v a l e n c e d t o r i e n t a È i o n s .

C h a q u e c l a s s e d r é q u i v a l e n c e G p v p e u t ê t r e d é f i n i e s o i t p a r u n t r i p l e t o r d o n n é d ' i n t e r v a l l e s ( A û u r A r u , Â E v ) , s o i t p a r r m c o u p l e ( t r , a 6 u ) o u , p l u s s i n p l e n e n t e n c o r e , FâE un couple (uru). Lorsqufune n o t a È i o n à u n s e u l i n d i e e e s t p r é f é r a b l e , u r l e c l a s s e d r é q u i v a l e n c e ( u r v ) s e r a n o t é ê G r r , l r i n d i c e n é t a n t d é f i n i p a r . 3

n = 7 2 ( l u l - l ) + n

e t m = 3 6 - v s i v c O . a v e c m = v s i v > O

(q-3)

2 n

Fig. 5 : ReprésentaËion syubolique de la partition de l r e n s e n b l e G de toutes tes orientationg

physiquenent distinctes. Le segment NNt une fibre _{cornplète dont ltaxe (rf ,to) est} p l a n de Iréchantillou.

( û , r o , E ) repréceote norrnal au

O n n o t e r a q u e l e s r e l a t i o n s d e s y u r é t r i e e x i s t a n t e n t r e l e s o r i e n t a t i o n s s o n t c o n s e r v é e s e . t q u e , p a r e x e m p l e , l e s o r i e n t a t i o n s d e d e u x c l a s s e s ( u r v ) e t ( - u r - v ) s o n t d e u x à d e u x s y m é t r i q u e s p a r r a p p o r t a u p l a n ( O N , O T ) . O n v é r i f i e r a é g a l e m e n t q u e l r e n s e m b l e G r e p r é s e n t é p a r l a f i g u r e 5 c o m p r e n d e f f e c t i v e m e n Ë l f e n s e m b l e d e t o u t e s l e s o r i e n t a t i o n s p h y s i q u e n e n È d i s t i n c t e s . O n s a i t , e n e f f e t , _{{ u ' à c h a q u e o r i e n t a t i o n} d t u n c r i s t a l c u b i q u e , o n p e u t a s s o c i e r 2 4 t o t a t . i o n s d i s t i n c t e s a u t o u r d t u n a x e p a s s a n t p a r O , r o t a t i o n s q u i amènent le repère RE lié à lréchantillon e n c o i n c i d e n c e a v e c l e r e p è r e R C l i ê a u cristal. C h a c r l n e d e c e s r o t a t i o n s p e u c ê t r e c o n s i d é r é e c o u r n e u n p o i n t d e L a s p h è r e u n i t é d e l r e s p a c e v e c

-t.

t o r i e l R ' ( 2 9 ) . L t e n s e r o b l e G d o i t d o n c c o r r e s p o n d r e à l l 2 4 d , e " l t a i r e t t t , ,

de la sphère r:nité de R-, laquelle est êgale à n'. "Ltaire'l A regæéocar t , é e p a r l r e n s e m b l e G e s t é g a l e à : [ = 2592

I'u"u'

l.u'=

e x p r e s s i o n d a n s l a q u e l l e 1 1 é l é o e n t s p h è r e u n i t é d e n 3 e s t , é g a l à : d i f f é r e n t i e l d g i n v a r i a n t s u r l a sintr dû dI dE O n e n d é d u i t : sinl dÀ dtl, e x p r e s s i o n d a n s l a q u e l l e t r ' i n t é g r a l e d o u b l e r q u i r e p r é s e n t e l t a i r e d t u n e c a s e t r r a p o u r v a l e u r 1 1 1 4 3 2 " L t a i r e t ' A e s t d o n c b i e n é g a l e a 1 2 / 2 4

O n r e m a r q u e r a enfin quiil e x i s t e 4 8 f i b r e s complètes oathéma-tiquement distinctes mais physiquement iadiscernabl-es et non 24, cornme d a n s l e c a s d e s o r i e n È a t , i o n s . 11 est, en effet, i n p o s s i b l e d e distinguer s u r u n e f i g u r e d e p ô l e s directe guelconque une fibre conplète dtaxe (ùro) d e l a f i b r e c o m p L è t e d ' a x e ( û r u r ) ( f i g . 6 ) . C e l a s i g n i f i e q u ' u n s o u s -a e n s e m b l e G [ e s t indiscernable d u s o u s - e n s e n b l e G*.

d s = *

L

ds=

*'it

rr

(,rru

₎

J ^<uil

uv

I \ ' \ ,

ô1

\,t

\

(roo)

F i g . 6 : _{D i f f é r e n c e d e m u l È i p r i c i t é des orientations eÈ des fibres} c o n p l è t e s .

^

æ s P o f _{\ ! r e p r é s e n t e n t u n e o r i e n r a r i o n (Uro,O) et Les} p ô l e s ( ! t ' o r i e n t a t i o n _{( - r l , o r O ) . Alors que deux orienra_} t i o n s ( û r r l , Er) et (-û,o, E2) ne peuvent coÏncider, les f i b r e s complètes (û,r,r) et (-û,,) auxquetles ces orienta_ t i o n s appartiennent sont confondues puisgurelles _{s o n t} r e p r é s e n t é e s sur cette figure de pôles (tOO) par les trois m ê æ s cercles concentriques.