Geometric study of a 2D tiling related to the octagonal quasiperiodic tiling

HAL Id: hal-02382037

https://hal.archives-ouvertes.fr/hal-02382037

Submitted on 27 Nov 2019

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Geometric study of a 2D tiling related to the octagonal

quasiperiodic tiling

Clément Sire, Rémy Mosseri, Jean-François Sadoc

To cite this version:

Clément Sire, Rémy Mosseri, Jean-François Sadoc. Geometric study of a 2D tiling related to the

octagonal quasiperiodic tiling. Journal de Physique IV Proceedings, EDP Sciences, 1989, 50 (24),

pp.3463-3476. �10.1051/jphys:0198900500240346300�. �hal-02382037�

Cl´

ement Sire, R´

emy Mosseri, Jean-Fran¸cois Sadoc. Geometric study of a 2D tiling related

to the octagonal quasiperiodic tiling.

Journal de Physique, 1989, 50 (24), pp.3463-3476.

<10.1051/jphys:0198900500240346300>. <jpa-00211156>

HAL Id: jpa-00211156

https://hal.archives-ouvertes.fr/jpa-00211156

Submitted on 1 Jan 1989

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not.

The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destin´

ee au d´

epˆ

ot et `

a la diffusion de documents

scientifiques de niveau recherche, publi´

es ou non,

´

emanant des ´

etablissements d’enseignement et de

recherche fran¸

cais ou ´

etrangers, des laboratoires

publics ou priv´

es.

Geometric

_study

of

a

2D

tiling

related

to

the

_octagonal

quasiperiodic tiling

Clément Sire

_(1),

_Rémy

Mosseri

₍₁₎

and

Jean-François

Sadoc

₍₂₎

(1)

Laboratoire de

_Physique

des Solides de Bellevue,

C.N.R.S.,

1

_place

Aristide Briand, 92195

Meudon, France

(2)

Laboratoire de

_Physique

des Solides, Université Paris-Sud, 91405

_Orsay,

France

(Reçu

le 31 mai 1989, révisé le 19

_juillet

1989,

accepté

le 6

_septembre

₁₉₈₉₎

Résumé. 2014

Au moyen de trois tuiles, nous construisons un _pavage

_{quasipériodique}

du

_plan,

_que

nous relions au

_quasicristal

_octogonal.

Ainsi, nous montrons _{que les coordonnées des n0153uds}

peuvent être obtenues de deux manières différentes. Le facteur de structure est calculé

exactement. _{Ce pavage}

_qui

_possède

« _presque » une

_symétrie

d’ordre huit, soulève la difficulté de la détermination

_pratique

de la

_symétrie

d’un

_{quasicristal.}

Finalement, nous montrons comment

construire une

_large

_{classe de pavage du type} de

_{l’octogonal,}

à

_partir

de ce nouveau _pavage.

Abstract. 2014 A

quasicrystal

built with three _types of tiles is related to the well-known

_octagonal

tiling.

The

_{relationships}

between both

_tilings

are

_{investigated.}

More

_precisely,

we show that the coordinates of the vertices can be obtained in two different but

_equivalent

ways. The structure

factor is calculated

_exactly.

We

_emphazise

the

_difficulty

one can have to define the order of the

symmetry of a

_{quasicrystal,}

from a

_{practical point}

of view,

exhibiting

a

_{quasiperiodic}

_tiling

whose

spectrum has a «

_{quasi »}

_eigth-fold

_symmetry.

_Finally,

we show how to recover

_easily

a class of

octagonal-like

quasicrystals.

Classification

Physics

Abstracts 61.50E

1. Introduction.

Since the

_discovery

of

_alloys

with

_{quasiperiodic}

structure

_by

Shechtman et al.

_[1],

many cares

have been devoted in the

_experimental

domain,

to the determination of atomic

_positions.

This is a

_prerequisite

to a better

_{understanding}

of

_{physical properties.}

At the

_theory

level,

a

parallel

effort has been done _{with many} new results

_concerning

the

_geometry

of the

quasiperiodic

structures and their diffraction

_patterns.

_Concerning

the

_{physical properties,}

however,

the field is still in its

_infancy.

This is

_mainly

due to the lack of

_appropriate

tools,

the

analogues

for

_instance,

of Bloch sums, or Brillouin zones of

crystal physics. Only

in one

dimension do we have a rather

precise

_knowledge

of the

_quasicrystal

excitation

spectrum.

This is

_why

we found

interesting

to look to extensions to

_higher

dimensions of these 1 D

quasicrystals.

In the case of the 1D structure related to the irrational number 1 +

B/2,

we have

discovered a more

_{interesting tiling,}

the «

labyrinth

», which is a subset of order two of the euclidian

_product.

As will be shown

_below,

the

_labyrinth

_{is very}

_closely

related to the standard

octagonal

[5,

6] quasiperiodic

tiling.

However,

it is much

_simpler

to _{many respects.} For

example,

its coordinates can be

_given

_explicitely,

which is a non trivial

_property

for

quasiperiodic

tilings

of dimension

_greater

than 1. This

_tiling

has a _very

_simple

_average

_lattice,

and their mutual

_{correspondence}

is derived in a

_{straightforward}

_{way from the}

_expression

of the site coordinates.

2. The recursive method.

We shall consider a _{sequence of letters A} and B

_describing

the alternation of

_segments

of two

different

_lengths.

Let us call

_Se

the sequence obtained

_according

to the

_following

rule :

where * is a

_symbol

for

_string

concatenation. This sequence is of the same kind as the well-known Fibonacci sequence studied in a _very exhaustive _way

_by

_{many authors. This sequence,}

which we shall call the « Octonacci » sequence, is related to 4Y = 1 +

J2

in the

_following

way : if

Fl

is defined as the

length of Se

then

Fl obeys

the same recursion formula as

Se

with

_Fo

=

F

= 1.

Then,

it is easy to see that

Fe + 1 IFi --+ 0

when

i --* + oo.

Moreover,

Se +

1 can be obtained

from Se

by applying

the

following

rule due to the

self-similarity

of

S

.

It is well-known that

_S.

is nor

_periodic

neither random but

_{quasiperiodic.}

Then,

a _sequence

of

_{arbitrarily length}

in

_Soo

can be found an infinite number of times.

Now,

after

_having

associated a

_length

f A

to an A and a

_length

f B

to each

B,

let us define the

«

labyrinth » tiling by

selecting

_{among the} set of

_points

of the Euclidian

_product

Se

x

_Se,

those sites which can be linked to their

_neighboring

sites

_by

a

_path

of non vertical nor

horizontal

bonds,

starting

the process at the

_origin

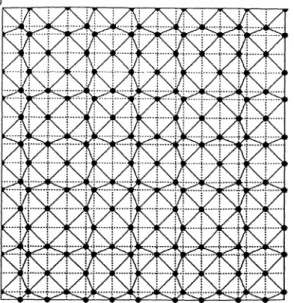
_{(Fig. 1).}

More

_precisely,

we see that this

tiling

consists of half the whole

_product

set.

_Finally,

if we

_join

the nearest

_{neighbors by}

Fig.

1. -

The

labyrinth

is obtained

_starting

from the euclidian

_{product Sp}

x

_Se

_{(dotted lines)}

_{by linking}

points

with

diagonal

bonds.

«

_{diagonal »}

bonds,

we obtain a

_tiling

of one

_quarter

of the

_plane.

In order to obtain a

_tiling

of

the whole

_plane,

we tile the three other

_quarters

in the same _way as the first one. The infinite

tiling

we obtain is of course

_{quasiperiodic}

and consists in the

_assembly

of three

_elementary

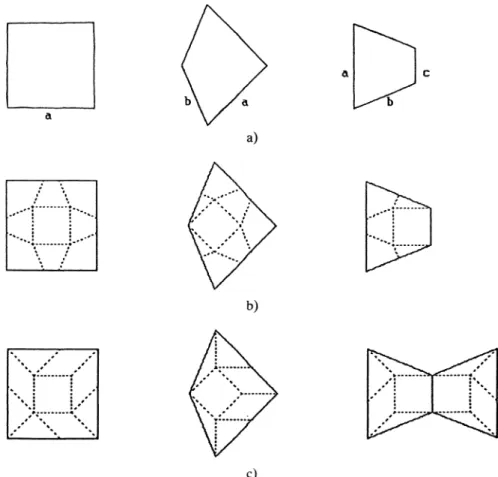
tiles whose exact

_{shapes depend}

on the ratio r =

f A/fB.

We

always

obtain _a

square, a

trapezoid

and a kite whose sides are

_given

on

_figure

2. If we colour each

_elementary

tile in a

different way, the reason for

_calling

this

_tiling,

the «

labyrinth

_», becomes manifest. We show

on

_figure

3 the

_labyrinth

for r «-- 1 and r :::&#x3E; 1. We can even consider the limit case

r =

1,

and obtain a

_{quasiperiodically}

_{coloured square lattice}

_ressemling

a

_labyrinth

(Fig. 3).

If we follow one of those

_paths,

we can see that it can be

arbitrarily long.

Indeed,

since

SOC)

is self-similar we

_expect

the

_{« labyrinth »}

to be self-similar too. We found inflation-deflation rules for this

_{quasiperiodic}

_tiling

which we have summarized in

_figure

2 The

_shapes

of the inflated tiles are the same as those of the

_{original tiling}

if and

_only

if r = 1 ₊

-.J2 =

0.

It is

_possible

to do the same

_{procedure starting}

with _{the Fibonacci sequence} or _{any other}

sequence not related to 4l. Note that the two 1D

_{quasicrystals,}

are not

_necessarily

the same,

neither at

_{right angle.}

In _{this paper,} we focus

however,

on the structure based on the Octonacci sequence, and first describe another construction of the

labyrinth.

Fig.

2. -

(a)

The

_labyrinth

is made of three

_elementary

tiles : a s uare, a kite, and a

_trapezoid.

The

lengths a, b,

c, are

_{respectively equal}

to

#,

F

and

#.

Here we took

r =

f AI f B

= 1 ₊

h.

(b)

Deflation rules for the

labyrinth.

(c)

The decorations of the three tiles

_leading

3. Another dérivation of the

_labyrinth.

The

_labyrinth

structure _{appears very}

_simply

out of a new construction of

quasiperiodic tilings

[2],

derived from the cut and

_project

method

_[4].

This method is rather

_general

but we shall focus on the

_{octagonal tiling}

case. Vertices of the

_hypercubic

lattice

Z4

are selected and

mapped

onto a 2D

_physical

_space

E,

whenever their

_projection

onto _{the 2D space E’}

(orthogonal

to

_E)

falls inside a window W. The window is the convex hull of the

_projection

onto E’ of the standard

_hypercube

of

Z4.

Now,

let us view

Z4

as a stratified structure : a 2D square lattice

(the base)

of 2D square lattices

(the fibres),

associated to each

_point

of the base.

The

_acceptance

_region

can be drawn on each fibre as the

_{projection, parallel}

to

_E,

of the unit

hypercube.

The

_{octagonal tiling}

vertices can then be selected. The

procedure

can be done

directly

on E

_{by mapping}

these

_acceptance

_regions,

one for each fibre. The

_projection

onto E of the base

_gives

a _{square lattice B. The}

_acceptance

_regions

are

_regular

_octogons

O lm,

centered on a sublattice of order 4 of B. To each

_{point B l+m,}

the

_{corresponding}

afm

is centered on the line from the

_origine

to

_Bem,

at twice the distance. Each fibre

_projects

onto E as another square lattice

_{Fe, m,}

identical to

_B,

but rotated

_by

_{7T /4.}

The vertices are

selected as follows. To each

_{point Bem,}

one attaches a _{square lattice}

_Fe,m,

from which we

select those vertices which fall inside the

_octogon

_Oem.

An

_{octagonal tiling}

is thus recovered. But

_instead,

if in each

_octogon

one

_{only keeps}

the vertex of F closest to the

_aem

center, which

we call

_Qem,

then,

the

_labyrinth

is obtained. The coordinates can be

easily

obtained. Let us

derive them in the B-basis with unit

_edge.

We have

Let A be the rotation matrix

_by

ir

/4

So,

the lattice F is obtained

_{by applying}

A to each vertex of B. In the F

_basis,

the

_point

Bem

has coordinates

_{given by}

A -

_{1 (Bem).}

In order to attach a F lattice to

_Blm,

one should shift

it

_by

a vector

_Sem

where frac

_{(x )}

is the fractional

_part

of the coordinates of x. In the shifted F

_basis,

the

_point

Qem

has coordinates

_equal

to

A -l(Qem) -

_Sem.

The

_point

of the shifted F closest to

Qem

is

where

_{F (x )}

is the closest

_integer

to x. In the

_B-basis,

the coordinates are

This can be written

These above relations form what is called

_explicit

coordinates for the

_tiling

vertices. It is a one

to one relation between a

_couple

of

_integers

_{(f, m)}

which takes all

_possible

values,

and the

corresponding pair

of real coordinates. This is not the case for

_{tilings generated by}

the standard cut and

_project

method. In that case, the vertex coordinates can be written as a

linear combination

_(with

_{integer coefficients)}

of a set of n « star » vectors. _{But among all}

possible n-uplets, only

a few are

_kept

after a selection

_procedure

in the

_orthogonal

_{space. It is}

precisely

this

_algorithmic

_step

_(the

most time

_consuming)

which is

_bypassed

when

_explicit

coordinates are

_given.

Now,

consider a non

_periodic

_{array of}

_points.

It is said to _possess an _average

_(periodic)

lattice if there exists a one-to-one relation between the former

_points

and the lattice

points,

and if their distance remains bounded. With this

_definition,

the

_labyrinth

has an _average

square

lattice,

the

_acceptance

_region

_lattice,

_{which shows up}

_{simply by replacing}

F (x )

by

an

_identity

_operator.

This is not

_surprising

since the

_octagonal

_tiling

itself was found

to have an _{average lattice}

_[3].

This

_question

of non

_{periodic tilings having}

or not an _average

lattice is a difficult one and is in fact two fold. First is the existence

_problem.

A

_surprising

result comes from the

_study

of 1D

_tilings

_generated

_by

_{the circle map}

_[7].

As a _{consequence of} a theorem

_by

Kesten,

it is found that for a

_large

class of such

_tilings,

the fluctuation of the site

coordinates _{from their average}

_position

_(the

lattice defined

_by

the

_density)

is unbounded.

Other

results,

in the context of the cut and

_project

method,

have been obtained

_[8]

which show that it is a subtle

_question.

The second

_point

is,

whenever an _{average lattice}

_exists,

to

find the

_explicit

one-to-one relation. In the case of the

_octogonal

_tiling,

this is a difficult task. In the

_present

_labyrinth

_case, both the existence and the

_explicit

relation can be very

_simply

read from the above

_expressions.

From the more

_{physical point}

_{of view,}

it may be

_argued

that

viewing

a

_quasicrystal

as a

_suitably

distorted

_crystal

can _open new field of

_{investigations.}

As

an indication among

_others,

the

_Hume-Rothery

_type

of

_arguments

to

_explain

their relative

stability

[9]

can then be studied. For

_example

in

_1D,

it has been shown that the Fibonacci

chain

_might

be stabilized with

_respect

to the

_periodic

chain for some electron densities

_[10].

4. Proof of the

equivalence

of the two methods.

In the

_following,

we show that the

_preceding

definition of the

_labyrinth

is

_equivalent

to the

one

_given

in section 2. Let us define

We notice

_{that p and q}

have the same

_parity.

_Therefore,

it is

_equivalent

to define the

_labyrinth

by

the

_points

whose coordinates are

and

With this new definition and since

_{Up - Up - e}

takes

_only

two values 1/2 and 1/2 + a, in order to show that both definitions are

_equivalent,

we

_only

need to _{prove that the sequence of 0 and}

1 defined

_by

where

_Re(p)

is the

_{p th}

term _{of the sequence of}

_{length Fe,}

is

equal

to Se

with the

correspondence

First of

_all,

we define a _{sequence of rational}

approximants

for a,

pe/qe f

E N. _pp and q p

verify

the

following

recursion formulas

since all the terms in the continued fraction

_{representing a}

are

_equal

to 2. The first

step

of the

proof

consists in

_showing

that for 5 small

enough,

F(qpe/qe

+

₅₎

=

F(qpe/qe).

For any

integers p

and q, and for 9 = _±

1,

we have 2 qpf -

(2 p + 0 )

_{qe =1= 0,}

since for

any f,

it is easy

This last

_inequality

shows that

since

Now,

using

this last

_result,

_{it becomes easy} to see that

_{F (aq )}

=

F (qpf , 21qf -, 2) for

any

q = 1, ... , q P + 2 by recalling

that,

according

to the definition

_{of pe + 2}

_{and qf , 2,} we have

1 a -

pe

+ 21qi , 21

-

1 lqe

+ 2 qf

+ 3 . We can therefore rewrite

We deduce that

_{Re (q)}

=

Re (qf , 2 - q

₊

1 )

and

thus,

that

Rl

is

symmetric.

Since

Rl + 2

is

beginning

in the same _way as

_{Rl + 1}

we have shown that

where

_Wl

is a _{sequence of}

_{length qe}

=

Fe.

We end this

proof by showing

that

WQ

=

Rl.

For q

=

1, 2,

..., ql we have to show that

This is a _{consequence of the first lemma} we

_proved

in the

_beginning

of this section and the

following

property

verified

_by

_{pp/qe :}

where we used the fact that

and

Moreover,

since

_Ro

=

So, R1

=

S,

and

Rp

and Se obey

the _same recursion formula _we conclude

that

_they

are

_equal,

and

thus,

that both definitions for the coordinates of the vertices of the

labyrinth

are

_{completely equivalent.}

Let us show now, two _{other ways} to build the

_labyrinth.

The first one consists in

_starting

from an

_octagonal

_{quasicrystal.}

But instead of

_applying

_{the process described in section}

3,

we

take as the vertices of the

_labyrinth,

the vertices of the

_octagonal

_{tiling, plus}

some new

_points

choosen in the

_following

_{way. Each horizontal square of the}

_octagonal

_tiling

is surrounded at

least

_by

two

_rhombi,

and forms an

_hexagon

with them. We add a vertex and two bonds in each such

_{hexagon, symmetric}

to the

_{already existing}

vertex and

_bonds,

with

_respect

to the center

of the

_hexagon.

In the

_{octagonal tiling,}

each

_hexagon

contains one vertex taken from a

« flipping pair

», the

flipping occuring

under an infinitesimal shift of the band in

Z4

_(in

the cut and

_project

method

_{[4] language).}

_Then,

in the

_octagonal

_tiling,

we

_only

_keep

vertical and horizontal

_bonds,

_put

bonds on the shorter

_diagonal

of the thin

rhombi,

and link

together

two vertices in the same

_hexagon.

The «

labyrinth »

is then obtained.

We _{found the last way} to build the

_labyrinth

in our

_attempt

to find local

_growth

rules for

_it,

i. e. some rules

_allowing

one two

_put

a tile of the

_{labyrinth, knowing}

the tiles in a circle of finite constant radius around it. Even if the

_labyrinth

cannot be built

_by

means of local

growth

rules,

we can construct it with some local rules and

_only

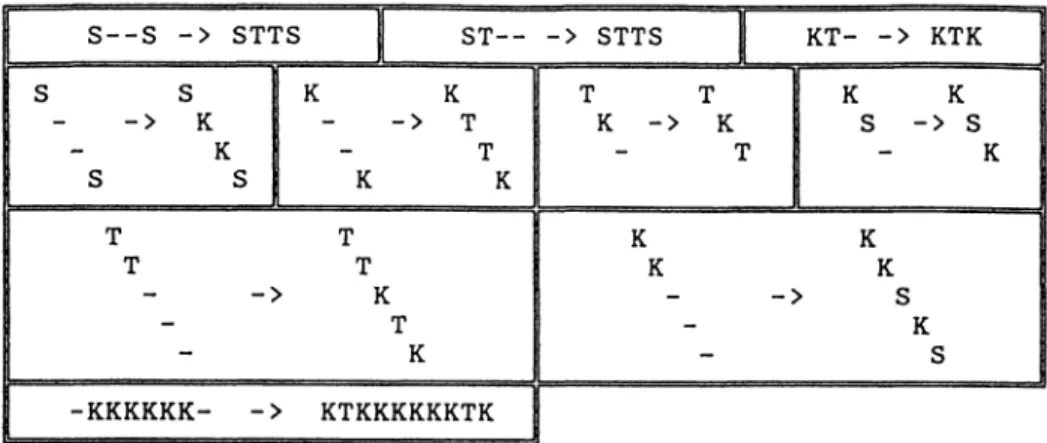
one non local rule. Let us start from four kites.

_Then,

_enumerating

the

_possible

local

_arrangements

in the

_labyrinth,

deduced from the

_properties

_{of the Octonacci sequence,} we found the local rules showed in

_figure

4. We write K for a

_kite,

S for a _{square and T for} a

_trapezoid,

and build the

_labyrinth

for

r =

1,

_even if those rules _are correct for any r

(with

few modifications since the three tiles are

then

_différent).

_They

have to be read in the

_following

_{way : if we find} one of the

_arrangements

quoted

in

_figure

4

_(or

this

_arrangement

rotated

_by

a

_multiple

of

_{’TT’ /2),}

add

_letter(s)

_according

to the rule

_{corresponding}

to this

_arrangement.

The

_procedure

has to be carried out until it is

no

_{longer possible}

to

_{put any other tile.}

_Then,

we

_apply

the

_only

non local rule needed : we

add one tile on the closest free

_place

to the x

and y

axes, and to the

_origin.

There are

_eight

such

_points.

The tile is the same for those

_points,

_{and is choosen in order that the sequence of}

large

and short bonds between groups of four kites

along

the x axis follows

_Soo

_(because

of the

self-similarity

of the

_labyrinth).

We show the first iterations of this method in

_figure

5. Of

course, instead of

_applying

this non local

_rule,

we can decide to

_put

a tile on a random free

place,

preserving

the four-fold

_symmetry

or not.

_Then,

we obtain a

_{labyrinth-like}

quasiper-iodic

_tiling.

In that case, some

_arrangements

_{appear that} cannot be found in the

_{real labyrinth}

(Fig. 5).

Moreover,

in the random case, and

when r =A 1,

there are some

_defects,

since the K and the T are not _{squares any}

_longer.

Fig.

4. - Local rules for the

labyrinth

on a _{square lattice}

_(r

=

1 ). « »

represents a free

_place,

« K » a

kite, « T » a

_trapezoid,

and « S » a _square.

5.

_Reciprocal

_space.

In this section we are interested in the

_k-space

of the

labyrinth

and

especially

to its

symmetries.

A well-known result

_concerning

quasicrystals

like the

_{quasiperiodic}

_octagonal

tiling,

is that their

_spectrum

is dense.

Moreover,

in a bounded

part

of the

_reciprocal

space, and for any

7o &#x3E;

0,

one can find

_only

a finite number of

peaks

whose

intensity

exceed

Io.

Thus,

experimentally,

for real

_{quasicrystal,}

one can

_only

observe a

_point

_spectrum

whose

symmetries give

us some informations about the structure _{into the real space.}

We show below

_that,even

if the

_labyrinth

has

_only

a true four-fold

_symmetry,

it would have been very difficult to

_distinguish

«

experimentally »

its

_spectrum

from the

spectrum

of the

octagonal tiling,

which has a

_eight-fold

_symmetry.

Let us now

_proceed

to the calculation of the

spectrum

of the

_labyrinth.

We showed in sections 2 and 3 that the

_points

of the

_labyrinth

are

Fig.

5. -

(a)-(c)

The first iterations of the

_procedure

described in section 4.

_(d)

An

_example,

where the

non local rule has been

_{replaced by}

a random choice.

_(With

the

_{correspondence,}

_square = black,

kite =

grey and

trapezoid

=

stripes).

located at the nodes of the

_product

of two Octonacci linear chains whose coordinates have the

same

_parity.

_Thus,

we define

I (q)

and

J(q),

the Fourier transforms of both chains

With this

normalization,

the

_intensity

of the

_peak

at k = 0 is

equal

to 1. We _now derive the

exact form of I

_{(q )}

and

_{J(q ),}

_by

the mean of the cut and

_project

method

_[4],

which

_easily

leads

to the

_spectrum.

From the form of

_Up

we see that

_Si

can be obtained

_by

the

projection

of the

points

of

Z2 belonging

to a

_strip

of

_{slope 0}

obtained

_by

the translation of the unit _square on a

line of the same

_slope.

Furthermore,

since

_Up

= -

U-,,

we deduce that the center of the unit square must be on vertex _{of the square lattice for the chain} to be

_symmetric.

In order to

evaluate

_{I(q) (and J(q )) ,}

we sum the contributions of

_points,

which are the

_projections

of

vertices in

Z2

whose coordinates have the same

_parity

_{(respectively,}

of the

_opposite

parity).

A

straightforward

calculation

_gives

the intensities of the

_peaks

of both even and odd chains :

and

where H = 7r

(cos (0)

+ sin

_{( 0 »,}

and 0 is defined

_by

tan

_{( 0 )}

= 0. Now _{we can} deduce the

intensity

of the diffraction

_peaks

of the

_labyrinth

_{W (k) =}

_{|S (k ) | 2}

_by

_using

₍₅₎

and

_(6).

It

_gives

the diffraction

_pattern

of

_figure

6. At first

sight,

it seems to have the

_eight-fold

_symmetry.

We show in the

_following

that it is not true,

by studying

the

_spectrum

on the two axes

kz

= 0 and

kl = k2,

for which the calculations _are

quite

easy.

First,

we show the

_following

result : if k =

(k, 0)

is in the

_spectrum,

then k’ =

(k/

J2,

k/

-N,/2-)

which is the _vector k

rotated

_by

_ir/4,

is also in the

spectrum. Indeed,

if k =

(k, 0)

is in the

_spectrum

of the

labyrinth,

then it _{is easy} to show that the

_{integers m}

and n in

₍₆₎

must be even.

_{Thus, k}

can be

written k = m cos

(0)

+ n sin

(0)

and we have to

_verify

that

_k/

J2

can be written in the same way as in

(6).

It is a _{consequence of the}

_equality

Fig.

6. -

Diffraction pattern of the

_labyrinth.

The area of a _spot is

proportional

to _{the square of}

S (k ).

We have

_only

considered

peaks

whose

_intensity

were _greater than

_Io,

with the convention that the

intensity

at k = 0 is

equal

to 1. For

Io,

_we have taken,

(a)

Io

= 0.06,

(b)

Moreover,

this

_property

is not

_only

true for k on the x

axis,

but for every k in the

spectrum,

what can be seen

_by

a calculation of the same kind as above. The strict four-fold

symmetry

of the Fourier

_spectrum

was

_expected

since in the cut and

_project

method,

the

_labyrinth

acceptance

region

is a _{square tangent} to the

_{octagonal region corresponding}

to the

_octagonal

tiling

[11].

We have to notice that it can

_happen

that the

_peak

at k’

vanishes,

it the

_phase

in the sine in

₍₆₎

is a

_multiple

of 2 7T. We find that it occurs when k is of the form k =

2 n (cos ( 0

₊ sin

( e ) ) = n (4 + 2

h)

where n is an

_integer.

But for those values of

k,

we shall see that the

_intensity

in k is

_only

4.7/n 2

_percent

of the

intensity

at

k = 0. This

property

of invariance

by

_a rotation of

ir/4

(even

if the intensities are not the

same)

is shared

by

the

_{quasiperiodic}

_tilings

built from an Octonacci like sequence but no other

sequence. For

example,

the 2D

quasicrystal

built with the Fibonacci sequence does not show the same

_property.

_Being

the

_product

of two linear

chains,

its

spectrum

has of course the

four-fold

_{symmetry. But,}

if k is in the

_spectrum,

then the vector k rotated

_by

_-U/4

never

_belongs

to

it.

_Now,

_going

back to the

_labyrinth,

we can _{compare the} two intensities at k and k’. Let us

define

where we _{define pk} = n cos

_{( 0 ) -}

m sin

( 9 )

for k = m

cos ( 0 )

+ n cos

_{( 0 ) -}

If we look for

Rmax

the absolute maximum

_of

_{| R (k) |}

_|

we find

So,

the maximum

_disagreement

between both

_spectra

arises for the value

where

_{W (k ) ---}

0.047 and

_{W (k’ )}

= 0. This value is easy to understand : since the

labyrinth

is

obtained

_{by adding}

vertices to the

_{octagonal quasiperiodic tiling}

we

_expect

its

_spectrum

to

ressemble that of the

_{octagonal tiling.}

More

_precisely

we

_expect

the maximum

_disagreement

to be _{about the square of the number of}

_points

we _{add per} « atom » of the

_{octagonal tilling,}

that is

(1 /2 - 1 / B/2-)2 -.

_0.043,

which is

_quite

close to the value

_effectively

obtained. Moreover if the

_intensity

_W(k)

is

_{quite large}

then

_{W (k’ )}

_{will be very close} to

_W(k).

This

explains

the

_{« quasi » eight-fold}

_symmetry

of the

_labyrinth.

For

_example,

for k = _cos

(0)

₊ 3 sin

(0),

we have

_{W(k) --}

0.748 and

_W(k’);.--

0.751,

and for k = _cos

(0)

₊ 2 sin

(0),

we find

_{W (k ) .-}

0.8667 and

_{W (k’ )}

= 0.8674. If we do the _same

study

with k not on the x

_axis,

we _{obtain very similar results}

_(compare

_Figs.

6a and

_b).

Thus,

in this section we have shown an

_{explicit example}

of a

_{quasiperiodic}

_tiling,

whose

spectrum

seems at first

_sight

to have the

_eight-fold

_symmetry,

without

having

it

_perfectly.

Furthermore,

the «

_experimental

»

_spectrum

of the

_labyrinth

_{would have been said} to have the

_eight-fold

_symmetry,

if the resolution were at best 5 %. This raises the

_question

of whether or not it is

_{really possible}

to

_specify

at the

_experimental

_level,

the real

_symmetries

of

a

_{quasicrystal.}

The

_problems

encountered at the moment, to _{propose icosahedral}

quasiper-iodic structures which fit

_exactly

the

_experimental

diffraction

_patterns,

are

_perhaps

linked to

the

_{problem developed}

in this section. Can we find modelized

_{quasicrystals}

which have not

the

_{icosahedral _}

_symmetry,

but whose

_spectrum

fits the

_experimental

_patterns

at _{the accuracy}

description

of the

_{experimental aperiodic phases,}

either as

_{quasicrystals,}

or

_crystals

with

_large

unit cell.

Indeed,

while in that case the diffraction

_spectrum

sit at different

_points

_(even

_very

close),

in our case, the locations of

_points

are the same,

only

do the intensities

_slightly

_vary.

6.

Recovering

the

octogonal

quasicrystal.

Now,

we show the way to recover the

_{octagonal quasiperiodic tiling}

from the

_labyrinth

whereas,

in section

_3,

we have shown how to build the

_labyrinth

from the standard

octagonal

quasiperiodic

tiling.

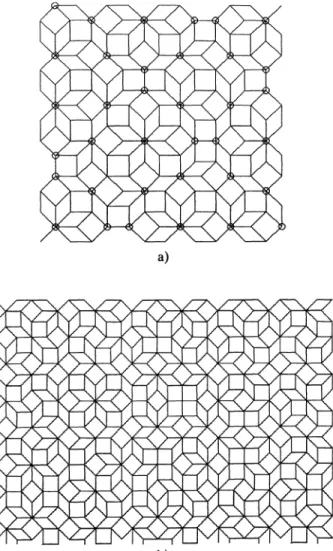
If we look for the

_possible

decorations of each tile of the

_labyrinth

(Fig. 7),

we

_only

find one decoration for the kite and the square, and two

_possible

decorations for the

_trapezoid,

which are

_{always coupled}

(Fig. 2).

Moreover, since the square

can have four

_{orientations,}

we have to show that the

_degrees

of freedom due to the two

_possible

decorations of the

_trapezoid,

and the four

_possible

_{orientations of the square} are

_only

apparent.

In order to recover the

_octagonal

_tiling,

we first decorate every kite of the

labyrinth

in the way shown in

figure

2. We have

_already

_{noted that every}

_path

of kites is closed. At each

Fig.

7. -

(a)

The

_labyrinth

as obtained

_by

the method of section 3.

(b)

An

octogonal-like

quasiperiodic

tiling generated by

means of the random

_procedure

described in section 6.

corner of those

_paths,

there is

_only

one _way to decorate a _square.

_Following

the

_path

of kites

there is

_only

one _way to decorate the

_trapezoid

_{after the square. The} next

_trapezoid

is choosen

symmetric

to the last one.

_Then,

there is

only

one _way to decorate the next _{square with}

respect

to the decorations of the last

_trapezoid

and the border of kite

_except

if the _square is

surrounded

_by

four

_trapezoids.

In that case we have to wait until we know the decoration of a

trapezoid

perpendicular

to the direction of the

_{trapezoid preceding}

_{the square, that} we

already

know. We carry on the process until we find another corner, and so on.

_Thus,

we find

only

one _way to _{decorate the squares and}

_trapezoids

between two closed

_paths

of kites in order to obtain the

_octagonal

_tiling.

However,

if we do not want to recover the exact

octagonal tiling,

but

_only

a

_quasicrystal

built with the same two tiles

_(the

_{square and the}

rhombus),

we can

_apply

the

_following

rules.

_Starting

from the

_labytinth,

remove one of the vertices of the shortest side of each

_trapezoid,

and link the

_{remaining points}

with bonds of the

same

_length

as the square side in the

_labyrinth.

One can choose the

_point

to remove,

randomly

or with any other rules. For

_example,

_{among the} two

_points,

for a

_{given trapezoid,}

we can remove the left-hand vertex, for horizontal

bonds,

and the bottom vertex, for vertical bonds. In the random case we

_expect

the diffraction

pattern

to have a

_eight-fold

_symmetry,

whereas in the second case the

_spectrum

has

_only

a four fold

_symmetry.

_Moreover,

in

_general,

we obtain

_tilings

with certain local

configurations

that cannot be found in the real

_octagonal

tiling

(Fig. 7).

7. Conclusion.

In _{this paper,} we have studied the

_{geometric properties}

of a new

_{quasiperiodic tiling,}

the

«

labyrinth

»,

closely

related to the well-known

octagonal tiling.

We showed a _{recursive way}

to build the

_labyrinth,

and

_then,

_gave

_explicit

coordinates for its vertices. The

_labyrinth

has an

average

lattice,

which is a _{square lattice. It is self-similar but} cannot be built

_by

means of local

growth

rules.

Moreover,

its diffraction

_pattern

exhibits an

_interesting

_property.

_Although

it

has

_{strictly speaking, only}

the four-fold

_symmetry,

its

_spectrum

has «

nearly

» the

eight-fold

symmetry.

Consequently,

it would have been very difficult to make the difference

«

experimentally »

(if

we have not known its

_spectrum

_{analytically).}

In a

_forthcoming

_{paper, the excitation spectrum} of the

_labyrinth,

which possesses very

interesting properties,

will be

_presented

_[12].

Acknowledgements.

We are indebted to M. Duneau and C.

_Oguey

for

_stimulating

conversations.

References

[1]

SHECHTMAN I., BLECH _I., GRATIAS D., CAHN J. W.,

Phys.

Rev. Lett. 53

₍₁₉₈₄₎

1951.

[2]

SADOC J. F. and MOSSERI R., to be

_published

in J.

_Phys.

France.

[3]

DUNEAU M. and OGUEY C., Number

Theory

and

Physics,

Les

Houches,

March 1989

_(Springer),

to

be

_published.

[4]

DUNEAU M. and KATZ A.,

Phys.

Rev. Lett. 54

_{(1985) ;}

KALUGIN P. A., Yu KITAEV A. and LEVITOV L. S., Pis’ma Zh.

Eksp.

Teor. Fiz. 41

₍₁₉₈₅₎

_{119 ;} ELSER _V.,

_Phys.

Rev. Lett. 54

₍₁₉₈₅₎

1730.

[5]

BEENKER F. P. M., report 82-WSK-04,

Sept.

82,

Dept.

of Math.

_(Un.

of

Technology,

Eindhoven).

[6]

SOCOLAR J. E. S.,

Phys.

Rev. B 39

₍₁₉₈₉₎

10519, for recent _aspects.

[8]

OGUEY C., DUNEAU M., to be

_published.

[9]

FRIEDEL _J., DENOYER _F., C. R. Acad. Sc. Paris 305

₍₂₇₎

171.

[10]

MAKLER S. S., GASPARD J. P., to be

published.

[11]

DUNEAU M.,

private

communication.