HAL Id: tel-00011775
https://tel.archives-ouvertes.fr/tel-00011775
Submitted on 7 Mar 2006
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-entific research documents, whether they are pub-lished or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d’enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
To cite this version:
Hichem Eleuch. Etude théorique des fluctuations quantiques dans la lumière sortant d’une microcavité semiconductrice. Physique Atomique [physics.atom-ph]. Université Pierre et Marie Curie - Paris VI, 1998. Français. �tel-00011775�
DE L’ECOLE NORMALE SUPERIEURE
LABORATOIRE
KASTLER BROSSEL
Thèse de doctorat de l’Université Pierre et Marie Curie
Spécialité
: Physique Quantique
présandee par
Hleboma HLERICH
Pour obtenir le orade de DOCTEUR de l’UNVERSITE PIERRE ET MARIE CURUS,
ET
DES
FLUCTUATIONS QUANTIQUES
UDE THE
ORIQUE
DANS
LA LUMIERE SORTANTDNE
MICROCAVTIE
SEMICONDOCTRICE
A Seioterice 26 olis 1998 devasle janry composede
M. L ABRAM Rappersur
M. G. BASTARD Rapporeus
M. R. BENNACHUR
M. C. FABRE
LABORATOIRE
ARIS
6KASTLER BROSSEL
Thèse
dedoctorat
del’Université Pierre
et MarieCurie
Spécialité : Physique Quantique
présentée par
Hichem
ELEUCH
Pour obtenir le
grade
de DOCTEUR de l’UNIVERSITE PIERRE ET MARIE CURIESujet .
ETUDE
THEORIQUE
DES FLUCTUATIONS
QUANTIQUES
DANS
LA
LUMIERE SORTANT
D’UNE
MICROCAVITE SEMICONDUCTRICE
A Soutenir le 26
juin
1998 devant le jurycomposé
de :M. I. ABRAM
Rapporteur
M. G. BASTARDRapporteur
M. R. BENNACEURM. C. FABRE
Table des
matières
1 Introduction 3
2 Notions de base 5
2.1 Atomes dans une cavité ... 5
2.1.1
Régime
decouplage
faible ... 52.1.2
Régime
decouplage
fort ... 62.2 Microcavité semi-conductrice ... 14
2.2.1 Exciton dans un semi-conducteur libre ... 14
2.2.2 Exciton dans une cavité à
puits quantiques
... 162.2.3 Polariton... 18
2.2.4 Interaction non linéaire
exciton-photon
... 223 Fonction d’autocorrélation et états
comprimés
27 3.1 Fonction d’autocorrélation ... 273.1.1 Définition
classique
deg
(2)
... 283.1.2 Définition
quantique
deg
(2)
:
... 303.2
Spectre
de bruit ... 323.2.1 Définition des états
comprimés
... 323.2.2
Spectre
de bruit ... 364 Calcul de la fonction d’autocorrélation dans le cas linéaire 39 4.1
Pompage
cohérent ... 404.2
Pompage
incohérent ... 474.3 Conclusion ... 56
5 Valeurs moyennes et intensités intracavité 57 5.1 Non-linéarité
excitonique
... 585.2
Couplage
non-linéaire ... 665.3 Cas non-linéaire :
couplage
non-linéaire + non-linéaritéexcitonique
.. 705.4 Non-linéarité
optique ...
735.5 Conclusion ... 74
6
Spectres
de Bruit 75 6.1 Non-linéaritéexcitonique
... 756.2
Couplage
non-linéaire ... 846.3 Interaction non-linéaire:
couplage
non-linéaire + non-linéaritéexcitonique
: ... 886.4 Non-linéarité
optique ...
927.1.1 Recherches des
pôles
... 997.1.2 Etude
numérique
de la fonction d’autocorrélation ... 1057.1.3 Traitement
analytique
... 1097.2
Couplage
non-linéaire ... 1147.3 Interaction
non-linéaire:couplage
non linéaire + non-linéaritéexcitonique :
115 7.4 Non-linéaritéoptique ...
1157.5 Conclusion ... 117
8 L’effet du
couplage
avec lesphonons
119 9 Conclusion 141 10Annexe 143 10.1 Annexe A :Expression
de la fonction d’autocorrélation àl’approximation
gaussienne
... 14310.2 Annexe B: ... 145
10.2.1 Calcul
de I
ij
(t,t’) :
... 14610.2.2 Calcul de
N
ij
(t, t’) :
... 14710.2.3 Calcul de
E
ij
(t, t’) :
... 14810.3 Annexe C :
Quelques
propriétés
utiles de la transformation de Fourier et de la transformation deLaplace
bilatérale ... 14810.3.1 Définition de la transformation de Fourier et de la transformation de
Laplace
bilatérale ... 14910.3.2
Propriétés
de la transformation de Fourier et de la transformation deLaplace
bilatérale ... 14910.4 Annexe D : ... 151
10.5 Annexe E ... 152
10.6 Annexe F: Relation entre les fonctions d’autocorrélation intra- et extra-cavité : ... 153
10.6.1
Système
en transmission ... 15310.6.2
Système en
réflexion ... 16410.6.3 Relation entre
l’amplitude
duchamp
pompe intra- et extracavité . 165 10.6.4 Relation entre les fonctions d’autocorrélation intra- et extracavité 1661
Introduction
L’étude du
couplage
matière-rayonnement,
dans le cas où lechamp
est confiné dans une cavité degrande
finesse et ou la matièreprésente
une résonanceproche
de lafréquence
de lacavité,
est un domaine enpleine
activité. L’intérêt de ces recherchesest à la fois
fondamental,
pour une meilleurecompréhension
ducouplage
matière-rayonnement
et une vérification despostulats
de lamécanique quantique,
etappliqué,
car onespère
obtenir dessystèmes optiques présentant
despropriétés exceptionnelles,
comme parexemple
une luminescence monomode à hautgain,
permettant
d’envisager
la réalisation d’un laser sans seuil.
Jusqu’à
unepériode
récente,
ces études se divisaient en deux domaines biensé-parés :
l’optique
quantique
d’atomes en milieu très dilués(qualifié
d’électrodynamique
quantique
encavité)
et laphysique
des solides(semiconducteur
enmicrocavité).
Maisrécemment,
desphénomènes
connus reliés àl’électrodynamique quantique
encavité,
comme laséparation
de Rabi du vide ou la réduction de bruitquantique,
ont étéob-servés dans des milieux
solides,
notamment dans les semiconducteurs. A la suite deces découvertes des recherches se sont
engagées
pour essayer d’obtenir avec lessemi-conducteurs des effets
d’électrodynamique
quantique
analogues
à ceuxqui
avaientdéjà
été mis en évidence dans des
expériences
dephysique atomique.
Les semiconducteursprésentent
en effetl’avantage
d’êtrebeaucoup
plus
faciles à manier que les atomesfroids ou en
jet, qui
nécessitent undispositif
expérimental
assez lourd.Un effet très intéressant observé en
physique
atomique
est la modification despropriétés
quantiques
duchamp électromagnétique
sortant de la cavité contenant desatomes : il a été
prévu théoriquement
et observéexpérimentalement
que cechamp
pos-sédait des
propriétés non-classiques
dégroupement
dephoton
(antibunching)
etcom-pression
des fluctuationsquantiques
(squeezing).
Les études initiées dans le grouped’Optique Quantique
du Laboratoire Kastler Brossel visent à obtenir des effetsana-logues
dans des microcavitéssemiconductrices,
où lesystème
actif n’estplus
constitué d’atomes mais depuits quantiques
dans un milieu semiconducteur.Ce mémoire traite l’étude des fluctuations du
champ
sortant de lamicrocavité,
etplus précisément
de sonspectre
de bruit et de sa fonction de corrélation du second ordre àpartir
d’un hamiltonien modèleprenant
encompte
les non-linéarités dusystème.
Lescalculs
présentés
iciprévoient
une réduction de bruit parrapport
au bruitquantique
cavité.
Lorsque
lecouplage
avec les fluctuationsthermiques
du réseauintervient,
les effetsnon-classiques disparaissent;
cependant
l’étude des fluctuations de la lumière sortantde la microcavité
apporte
aussi desrenseignements précieux
sur ladynamique
desphénomènes qui
seproduisent
lors ducouplage
entre lechamp
et les excitons.Nous
présentons
tout d’abord dans lechapitre
2 un aperçurapide
surl’electrodynamique
quantique
en cavité. Ensuite nous introduisons les excitons et lespolaritons
tout enremarquant
l’analogie
avec l’atome habillé. A la fin de ce deuxièmechapitre
nous don-nons lesgrandes lignes
de la démarche menant à l’hamiltonien non-linéaire modèle dusystème photon-exciton
que nous utilisons par la suite.Dans le
chapitre
3 nous introduisons la fonction d’autocorrélationg
(2)
d’unpoint
de vue
classique
etquantique
et nousrappelons
la définition des étatscomprimés
etdu
spectre
de bruit.Le
chapitre
4 contient l’étude de la fonction d’autocorrélation dans le cas d’uneinteraction
exciton-photon
purement
linéaire pour un pompage cohérent et pour un pompage incohérent. Nousprésentons
la méthode établie dans cette thèse pour le calcul de la fonction d’autocorrélation et nous donnons lespropriétés
de celle-ci pourles deux
types
de pompage.Dans le
cinquième chapitre
nous calculons les intensitésexcitonique
etphotonique
intracavité pour des
paramètres
réalistesexpérimentalement .
Ces intensités sontin-dispensables
pour le calcul de la fonction d’autocorrélation et duspectre
de bruit deschapitres
suivants.Le
spectre
de bruit est étudié dans lechapitre
6 dans le cas où l’interaction avecles
phonons
estnégligée.
Cetteapproximation
est valable à faibletempérature.
Notre modèle nouspermet
deprévoir
un effet desqueezing
dans les microcavitéssemicon-ductrices en
régime
decouplage
fort.Le
chapitre
7 est consacré à l’étude de la fonction d’autocorrélation. Enplus
des résultatsnumériques,
uneexpression analytique
de la fonction d’autocorrélation estétablie.
L’effet du
couplage
dusystème
avec lesphonons
du réseau estpris
en considérationet étudié dans le
chapitre
8. Nous étudions dansquelle
mesurel’augmentation
de la2
Notions
de base
2.1 Atomes
dans
unecavité
Au cours des
années1940,
les étudesthéoriques
de Purcell et de Casimir([Purcell
46], [Casimir 48])
ont montré que le taux d’émissionspontanée
de l’atomepeut
être modifié si onplace
celui-ci àproximité
de miroirs ou deparois
diélectriques.
Desexpériences
menées dans les années 70 et 80 ont montréqu’on
peut
augmenter,
diminuerl’émission
spontanée
[Drexhage
74], [Goy
83], [Heizen 87], [DE
Martini87]
ou même larendre réversible
[Rempe
87]
en mettant l’atome dans une cavité dont lalongueur
estde l’ordre de la
longueur
d’onde.L’émission
spontanée
dans le vide secomprend
par l’effet ducouplage
de l’atome avec le continuum des modes duchamp
électromagnétique.
Laprésence
d’une cavitémodifie le continuum de modes du
champ
et lecouplage
de l’atome avec ces derniers.Lorsque
l’on met l’atome dans unecavité,
deuxrégimes
sontsusceptibles
d’apparaître
suivant la finesse F de la cavité. Pour une faible valeur de
F,
l’atomepeut
interagir
avec ungrand
nombre demodes,
et lesparois
ont pour effetprincipal
de modifier la structuredu
champ
parrapport
à cellequ’il
a dans le vide. Dans cerégime
que l’onpeut
traiterperturbativement
(appelé
régime
decouplage
faible),
le taux d’émissionspontanée
etles
déplacements
radiatifs des niveaux sont modifiés dans certaines conditions.Quand
onaugmente
la finesseF,
l’interaction entre atome et cavité devient trèsimportant
et le traitementperturbatif
n’estplus
valable: un deuxièmerégime
apparaît,
appelé
régime
decouplage
fort. Dans ce cas, l’atomeéchange
del’énergie
avec la cavité surplusieurs
cycles
(oscillations
deRabi)
et l’émissionspontanée
devient réversible[Rempe 87].
2.1.1
Régime
decouplage
faible
Dans une
première approche
lerégime
decouplage
faible se caractérise par unefaible valeur de la finesse F de la cavité. On traite ce cas dans un cadre
pertubatif,
oùl’on suppose que la modification du
dipôle
par lechamp
de la cavité est assez faiblepour que l’on
puisse
lanégliger
dans le calcul de cechamp.
Pour un
dipôle atomique qui
oscilleparallèlement
auplan
des miroirs(classique-ment,
l’orbite de l’électron estparallèle
auplan
desmiroirs),
on trouve que l’onpeut
à 03BB 2
(L
= 03BB 2
Dans le cas
contraire,
ledipôle
atomique qui
oscilleperpendiculairement
auplan
des miroirs a un taux d’émission
spontanée
considérablementaugmenté
pour L inférieurà 03BB 2
et
modifié d’une valeurnégligeable
pour Lsupérieur
ouégale
à 03BB 2 .
On note aussi que, pour des
longueurs
L trèsgrandes
devant 03BB 2
etindépendamment
de la
polarisation,
iln’y
aplus
de modification de l’émissionspontanée
[Haroche 92].
Fig.
1: le rapport de l’émission spontanée dans la cavité et le vide en fonction de la longueur de lacavité
2.1.2
Régime
decouplage
fort
Lorsque
la cavité a une trésgrande
finesseF,
le traitementpertubatif
n’estplus
valable. Un autre
régime,
nonperturbatif appelé régime
decouplage
fort,
apparaît.
L’atome est
couplé
à un seul mode de lacavité, qui
est résonnant ouquasi
résonnant avec l’une de ses transitions : lesystème
global
(atome
+mode)
est décrit par un atome à deux niveaux(caractérisé
par un niveau fondamental|g>
et un niveau excité|e>)
en interaction avec le mode de la cavité. Nous supposerons par ailleurs que lacavité est ouverte et ne modifie
qu’une
faibleportion
des modes du vide. De ce faitla relaxation
atomique
estprincipalement
due à l’émission dephotons
dans des modes vides del’espace
libre et sontaux 03B3 2
n’est pas modifié.Si on
néglige
la relaxation dans unpremier
temps,
lesystème
constitué par l’atomeet le
champ
peut
alors être décrit par l’hamiltonien deJaynes
Cummings
[Jaynes 63] :
qui
estcomposé
de troistermes;
lepremier
décritl’atome,
lesecond,
le mode et ledernier,
l’interaction entre l’atome et lechamp.
Fig.
2: Interaction entre l’atome et le champ du mode de la cavitéL’hamiltonien de l’atome s’écrit :
où 03C9at
désigne
lafréquence
de l’atome etD
z
l’opérateur
d’inversion défini par :L’hamiltonien du
champ
a pourexpression :
où 03C9ph
désigne
lafréquence
de la cavité et lesopérateurs
a eta
~
sont lesopérateurs
d’annihilation et de création d’unphoton
dans le mode duchamp.
Ils vérifient la relation de commutation :L’hamiltonien d’interaction s’écrit : où g est la constante de
couplage
définie par :d est le moment
dipolaire
del’atome,
Vdésigne
le volume de la cavité etE
0
,
lechamp
électrique
parphoton
(amplitude
des fluctuations duvide) :
Les
opérateurs atomiques
et
changent
l’étatatomique,
D
~
étantl’opérateur
qui
transforme l’état|g>
vers l’état|e>
etD de l’état
|e>
vers l’état|g>.
L’interaction entre le
champ
et l’atome se traduit par unéchange
simultané dephoton
et d’état tout en conservant le nombre d’excitation. Le termeaD
~
décritl’absorption
d’unphoton
et l’excitation de l’atome et le termea
~
D
décrit l’émission d’unphoton
et la désexcitation de l’atome.Les états du
système
atomechamp
(H
at
+H
F
)
noncouplés
s’expriment
par :Le
système
couplé atome-champ
connu sous le nom d’atome habillé[Cohen-Tannoudji
L’état fondamental habillé est :
L’angle
decouplage
est défini par :où 0394
présente
le désaccord entre atome et cavité03B8
n
vaut 03C0 4
àrésonance,
0 pour 0394 << -get 03C0 2
pour
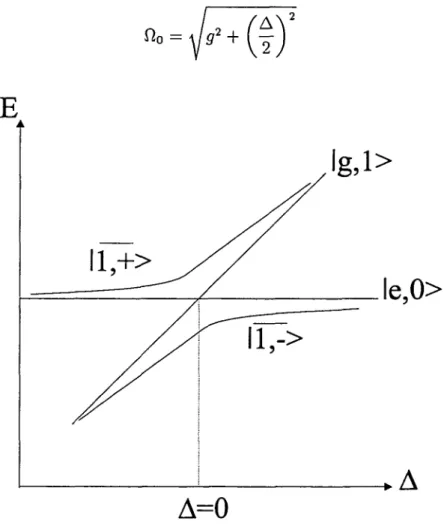
0394 » g.Ces états habillés ont pour
énergie :
où
03A9
n
est lafréquence
de Rabi pour nphotons
dans le mode.dans la
cavité),
secouplent
pour donner deux états habillés|+, 1>
et|-, 1>
définie par :avec
Ils sont
séparés
par une différenceénergétique équivalente
à203A9
0
,
où03A9
0
est lafréquence
de Rabi du vide(nommée
encore le dédoublement de Rabi du vide "vacuumRabi
splitting"):
La
Figure
4 montre que lafréquence
de Rabi dans le vide est minimale pour la résonance cavité-atome. Les niveaux noncouplés
se croisent et les niveaux habillés s’anticroisent et ils tendent vers des états noncouplés
pour un fort désaccord.2.1.2.1
Largeurs
despremiers
états habillésDans une situation
réelle,
l’atome et lechamp
ont uncouplage
dissipatif
avecleur environnement. Le processus
dissipatif
est bien décrit parl’équation pilote
del’opérateur
densité dusystème atome-champ
[Carmicheal 89] [Haroche 92] :
où
~
0393
p et~
at
p décrivent la relaxation duchamp
dans une cavité et la relaxationatomique, qui
sont données par lesexpressions
suivantes dans le cas d’une cavité à latempérature
T=0 :où 03B3 2
est le taux dedissipation atomique
(taux
de désexcitation de l’état|e>
vers l’état|g>)
dans le vide(on
suppose que l’émissionspontanée
n’a pas été modifiée par lacavité)
et 03BA, le taux d’amortissement duchamp
dephotons
dans la cavité. 03BA est relié au coefficient dequalité Q
de la cavité par :Les calculs de
<1,
+
| (~
F
+~
at
)
03C1|f >et
<1, -
|(~
F
+~
at
)
03C1|f>
fontapparaître
lestaux d’amortissement 03B3+ et
03B3
-
des
états habillés|+, 1>
et|-, 1>.
Ils ont pour expres-sion :Ils sont
égaux
à résonance(0394
=0)
à lamoyenne des
dissipations atomiques
etphotoniques.
On a défini le
régime
decouplage
fort comme étant lerégime
nonpertubatif
où lacavité
possède
une trèsgrande
finesse F. Cette définitionqui
a été donnée par Haroche[Haroche 92]
s’applique
bien au cas où le taux d’émissionspontanée
de l’atome estnégligable.
Cependant
dans le casqui
va nous intéresserici,
les constantes detemps
du milieu émetteur et de la cavité seront du même ordre degrandeur.
Il est doncplus
entre l’atome et le
champ
de la cavité est trèsgrand
devant ladissipation
dudipôle
atomique 03B3 2
et ladissipation
duchamp
de la cavité 03BA :2.1.2.2 Plusieurs atomes dans une cavité
Le traitement
précédent
de l’atome habillé s’est limité au cas d’un seul atome dansune cavité. On étudie maintenant le cas de N atomes
identiques
en interaction avec lechamp
de la cavité ensupposant
que les atomes ont la même constante decouplage
get la même
fréquence
03C9at. L’hamiltonien de cesystème
s’écrit :où les
opérateurs atomiques D
i
,
D
~
i
etD
zi
de l’atome i sont donnés par lesexpressions
suivantes :et
L’état fondamental des N atomes non excités est : et le
premier
état excité est :Ces états se
couplent
avec lechamp
de la cavité pour donner les états habillés à N atomes.Les deux
premiers
états habillés sont :où
Ils ont pour
énergies :
avec
03A9
(N)
est lafréquence
de Rabi du vide(pour
Natomes) :
A
résonance,
la structure des deuxpremiers
états habillés(à
Natomes)
estiden-tique
à celle d’un seul atome avec unefréquence
de Rabi du videmultipliée
parN.
Des
expériences
menées dans les années 80 et au début des années 90 ont mis en évidence l’oscillation de Rabi du vide pour un[Thompson
92],
[Bernardot
92]
etplusieurs
atomes[Brecha
86a],
[Raizen 89]
par l’observation duspectre
d’émission ou par lecomportement
temporel
de l’intensité de fluorescence[Brecha
86a,b],
[Orozco
87].
2.2
Microcavité semi-conductrice
Le traitement
précédent
apermis
decomprendre
que la cavité modifie l’émissionspontanée
etpermet
l’apparition
d’oscillation de Rabi pour des atomes. Desexpériences
au début des années
90,
ont montré des effetsanalogues
dans les semi-conducteurs.Elles ont mis en évidence une modification de l’émission
spontanée
[Yokoyama 90],
[Yamaguchi 91],
et aussil’apparition
d’un doublepic,
dans lespectre,
caractéristique
durégime
d’oscillation de Rabi[Weisbuch 92].
Dans ce casl’échange
énergétique
périodique
seproduit
entre exciton etphoton.
On se limite dans ce
qui
suit aurégime
decouplage
fort et on suppose deplus
quel’émission
spontané
n’est pas modifiée par la cavité.2.2.1
Exciton dans
unsemi-conducteur libre
L’émission et
l’absorption
durayonnement
dans un semi-conducteur sontrégies
par le passage des électrons entre la bande de valence et la bande de conduction
(de
différenceénergétique
E
g
)
qui
sontséparées
par une bande interdite(gap)
où latransi-tion
électronique
est nonpermise.
L’observation duspectre
d’absorption
[Baumeister
61]
a montré l’existence depics
étroitsd’énergie
inférieure àE
g
.
Ces résonances sontattribuées à des états liés électron-trou résultant de l’attraction colombienne entre un
électron et un trou. Ces états sont semblables à des états de l’atome
d’hydrogène.
Ils sontappelés
étatsexcitoniques
ousimplement
excitons[Frenkel
31],
[Wannier 37],
[Knox 63], [Haug 90].
Fig. 7: les états excitoniques
Les excitons sont des états propres de
l’hamiltonien[Haug 90], [Dimmock 67] :
où 03B5 est la constante
diélectrique
du milieu et mr la masse réduite définie par :dont
m*
e
etm*
h
sont les masses effectives de l’électron et du trou. Dans l’arseniure degallium
(GaAs)
où ont été faitesbeaucoup d’expériences,
ces masses effectives sontde l’ordre de
m*
e
~
0.069 m0 et~
h
m*
0.35 m0(m
0
étant la masse libre del’électron)
[Miller 95] .
Les
énergies
de liaisonexcitonique
ont une valeur de l’ordre de10
-4
fois celle del’atome
d’hydrogène
(E
ex
n
~
10
-4
E
at
n
) :
où
R
ex
est la constante deRydberg
excitonique qui
définiel’énergie
de liaison dupremier
étatexcitonique
(exciton
1s) :
A titre indicatif la
figure
8 donne pour différents semi-conducteurs la valeur de laFig.
8: Valeur de Rex etEg
pour différents semi-conducteursLe rayon de Bohr
excitonique :
est de l’ordre de 150
A
0
(dans
Ga As massif[Miller 95]).
La fonction d’onde de l’exciton
peut
êtreexprimée
en fonction despolynômes
deLaguerre
L
l
n
et
de la fonctionharmonique sphérique
Y
lm
:
avec
2.2.2
Exciton
dans unecavité
àpuits
quantiques
Une cavité à
puits quantiques
est constituée de couches trés minces desemicon-ducteur de
dopages
différents insérées entre deux miroirs deBragg
formés de couchesmultidiélectriques
d’indices différents(figure 9).
Dans de telles structures les étatsélectroniques
sont confinés dans une directionperpendiculaire
auplan
despuits
et lemouvement est
quantifié
dans cette direction. Dans leplan
des couches les électrons sontlibres,
et onpeut
parler
de mouvement à deux dimensions.Fig.
9: Microcavité à puits quantiquesDans cette
configuration
l’énergie
de liaison des excitons dans lespuits quantiques
est donnée par
[Haug
90] :
Dans ce cas les excitons ont un
Rayon
de Bohr : et une fonction d’onde :avec
Notons que le confinement
augmente
l’énergie
de liaison(d’un
facteurquatre
pour lepremier
étatexcité)
et diminue le rayon de Bohr de l’exciton d’unfacteur 1 2.
Leconfinement
permet
aussid’augmenter
la force d’oscillateur de l’exciton[Miller 85],
[Bastard 82]
conduisant à uneaugmentation
ducouplage
entre exciton etphoton.
Pour de très faibles densités
excitoniques
(très
faiblepompage),
les excitonsn’interagissent
2.2.3
Polariton.
Dans le
régime
decouplage
fort,
où la constante decouplage
g estgrande
devant lesdissipations
excitoniques 03B3 2
et
photoniques 03BA :
L’exciton se
couple
à un modeunique
de la cavité pour donner naissance à unpolariton.
L’hamiltonien du
système couplé
estcomposé
de trois termes :Le
premier
terme décrit lesphotons
du mode de lacavité,
le second le modeexcitonique
et le dernier l’interaction entre exciton et
photon.
L’hamiltonien
photonique
s’écrit :où 03C9ph
désigne
lafréquence
de ce mode eta,a
~
lesopérateurs
d’annihilation et decréation de
photon
vérifiant la relation de commutation :L’hamiltonien
excitonique
s’écrit :où 03C9ex est la
fréquence
de l’exciton etb,b
~
lesopérateurs
d’annihilation et de créationexcitonique
vérifiant la relation de commutation :Ces deux oscillateurs
harmoniques
sontcouplés
par l’hamiltonien d’interaction : où la constante decouplage
g est une fonction du nombre depuits
N
QW
,
de la forced’oscillateur par unité de
surface(f S),
de lalongueur
effective de la cavitéL
c
,
de laL’interaction entre le mode de la cavité et l’exciton se traduit par
échange
d’excitation :le terme
a
~
b
décrit la création d’unphoton
et l’annihilation d’un exciton et le termeab
~
décrit la création d’un exciton et l’annihilation d’unphoton.
On considère tout d’abord le cas le
plus simple
où l’exciton et la cavité sont enrésonance
(03C9
=03C9 ex =
03C9
ph
).
L’hamiltonien H est
diagonalisable
avec desopérateurs
a1, a2 définis par :Ces
opérateurs
sont les modes propres dusystème couplé.
Ils commutent entre eux et conservent les relations de commutations :L’hamiltonien s’écrit alors :
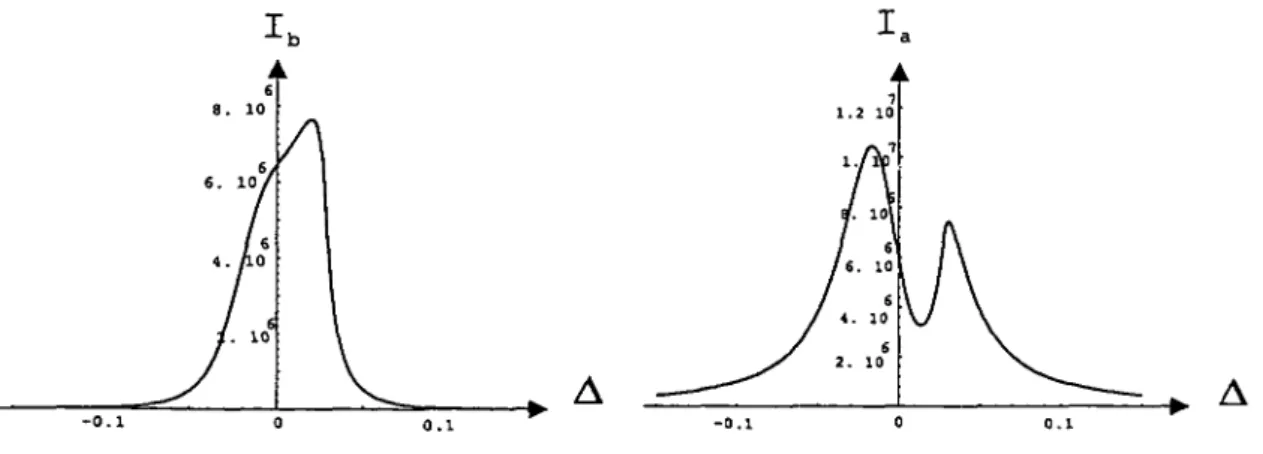
avec
On constate que l’hamiltonien H est une somme de deux nouveaux oscillateurs
Fig.
10: Les polaritonsLes deux
premiers
états excités|n
1
=1, n
2
=0)
et|n
1
=0, n
2
=1)
ont pouréner-gies
03C9
1
et03C9
2
,
séparées
par laquantité 2g.
Ils vont donner naissance à unspectre
d’émission ou
d’absorption
qui
présente
deuxpics
defréquence
03C91et 03C92séparés
par unefréquence
de valeur2g
(fréquence
deRabi).
On retrouve ici le mêmespectre
que dans le cas de l’atome à deux niveaux.Fig.
11: Spectre d’émission en tenant compte des dissipationsCe
phénomène
estanalogue
aucouplage
de deux oscillateursclassiques couplés
où on observel’apparition
de deux modes propres : lepremier
se manifestelorsque
lesdeux oscillateurs oscillent ensemble en
phase
(mode
a
1
)
et le deuxièmelorsque
les deuxFig. 12: Les modes de deux oscillateurs classiques couplés
D’une manière
générale,
lorsque
le désaccord defréquence
entre exciton et cavitéest non nul. les deux
premiers
états excités de l’hamiltonien(polaritons)
sont donnéspar les
expressions
suivantes :où
l’angle
decouplage 03B8
est défini par :et 0394
désigne
le désaccord exciton-cavité :Ces deux
polaritons
sont dessuperpositions
des deux états noncouplés
|1, 0> (un
exciton et zérophoton
dans lacavité)
et|0, 1> (zéro
exciton et unphoton
dans lacavité)
analogue
à ceux définis dans le cas de l’atome(2.18).
Ils sontséparés
par unedifférence
énergétique
égale
à203A9,
où 03A9 est lafréquence
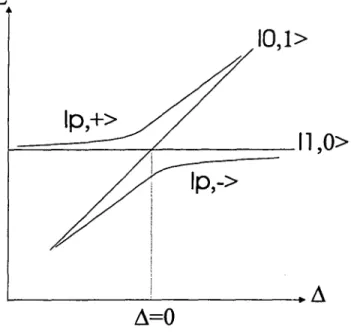
de Rabi du vide :La
figure
13 montre la variation de lafréquence
de Rabi du vide 03A9 en fonctionde désaccord cavité-exciton. On constate que cette
quantité
est minimale pour la résonance exciton-cavité. Les états propres décrivant lespolaritons
sont alors lescom-binaisons
1 2(|1,0) ±
|0,1>) .
Lorsque
0394varie,
les deux branches depolaritons
s’anticroisent. Les états proprescorrespondants
tendent vers les étatsexcitoniques
etphotoniques
(|1,0>
et|0,1>)
pourFig.
13: variation del’énergie
en fonction de désaccord cavité-excitonOn
peut
montrer que les taux d’amortissements despolaritons
sont[Sermage
96] :
Ils sont
égaux
à résonance à la moyenne desdissipations excitoniques
etpho-toniques
(03B3±
= 03B3 2+03BA 2).
L’analogie
de cesystème
avec l’atome habillé estfrappante.
Pour cette raison lespolaritons
sontappelés
dans certains articles " exciton habillé ".2.2.4
Interaction
nonlinéaire
exciton-photon
L’image
simplifiée
de l’exciton considéré comme un oscillateurharmonique
(linéaire)
apermis
d’expliquer
plusieurs phénomènes
(spectre
d’émission,
oscillation de Rabi ....).
Elle est valable dans la limite de très faible densitéexcitonique
(très
faiblepompage).
Si onaugmente
la densitéexcitonique,
la distancequi sépare
les excitonsdevient de
plus
enplus petite
et l’exciton ne secomporte
plus
comme uneparticule
libre. Les
composantes
électron et trou d’un excitoninteragissent
avec lescomposantes
d’un
autre,
à cause de l’interaction colombienne et de larépulsion
dePauli,
le modèleNous
présentons
dans cettepartie
et d’une manièrerapide,
la démarche[Steyn 83],
[Hanamura 74]
menant à l’hamiltonien non linéaire dusystème photon-exciton
ainsique les
approximations
utilisées.On se limite au cas du semi-conducteur à deux bandes directes
(bande
de valenceet bande de
conduction).
L’hamiltonien du
système
couplé photon
et semi-conducteur s’écrit :Il est
composé
de troistermes,
lepremier
décrit le semi-conducteur(système
deplusieurs
fermions),
le second lesphotons
de la cavité et le dernier l’interaction entresemi-conducteur et
photon.
L’hamiltonien
H
sm
dusystème
deplusieurs
fermions s’écrit[Hanamura77] :
où
H
p
est l’hamiltonien d’une seuleparticule placée en x
etV
p
représente
l’interaction colombienne entre uneparticule
enposition
x
1
et une deuxième enposition
x
2
.
Lafonction d’onde 03A8 s’écrit dans le formalisme de la seconde
quantification
en fonctionde la fonction d’onde d’une seule
particule 03A6
(état
propre de l’hamiltonienHp
),
del’opérateur
ck de destruction d’un électron de la bande de conduction avec une impul-sionk
et del’opérateur
d
k’
opérateur
de destruction d’un trou de la bande de valenceavec une
impulsion k
:Dans ce cas, on
exprime
l’hamiltonienH
sm
dansl’espace
desimpulsions
[Hanamura
E
v
estl’énergie
de la bande de valence :et le
potentiel
d’interaction colombienne dansl’espace
réciproque
est :Les deux
premiers
termes de(2.66)
donnentl’énergie
totale des électrons et destrous considérés comme libre et le troisième terme de l’hamiltonien décrit l’interaction
entre électrons et trous : la
première partie
décrit l’interactionélectron-électron,
ladeuxième l’interaction trou-trou et la troisième l’interaction électron-trou.
Revenons
maintenant sur le deuxième et troisième termes(H
int
etH
ph
)
de l’hamiltonientotal
H.
L’hamiltonien d’interaction entre
champ
et semi-conducteur a la formegénérale
suivante :
où A
est le vecteurpotentiel
quantifié
en termed’opérateurs
bosoniques
â. Oncon-sidère
qu’un
seul mode duchamp interagit
avec le semi-conducteur. En utilisant uneprocédure
analogue
à celleprésentée
ci-dessus et en faisantl’approximation
duchamp
tournant,
on trouve :g’
c
étant la constante decouplage.
L’hamiltonien duchamp
s’écrit :k :
Dans la
suite,
on introduitl’opérateur
de création d’un exciton de vecteur d’ondeL’opérateur
excitonique
vérifie la relation de commutation[Keldysh
68] :
avec est la densité
excitonique
et aex le rayon de Bohrexcitonique.
Pour une faible densité
excitonique
a
ex
<< 1 l’excitonpeut
donc être considérécomme étant un boson.
On passe de
l’espace
desopérateurs
fermionique
(décrivant
les électrons et lestrous)
versl’espace
desopérateurs bosoniques
(décrivant
lesexcitons)
soit par latransforma-tion de Marmori modifiée
[Steyn 83]
ou bien par la transformation de Usi[Hanamura
74].
On obtient un nouveau hamiltonien :où U est
l’opérateur
de transformation.On considère dans la suite le cas de faible densité
excitonique,où l’opérateur
ex-citonique
vérifie la relation de commutation desbosons,
mais où certains effets nonlinéaires venant du troisième terme de
(2.66)
sont nonnégligables
et on se limite au casdes excitons
d’impulsion
nulle(dans
leplan
descouches).
On ne tiendracompte
que del’état
excitonique
1S de l’exciton(la
force d’oscillateur est trèsgrande
pour l’exciton1S par
rapport
à la force d’oscillateur des autres étatsexcitoniques).
Dans ce cas on montre
([Hanamura 74])
que l’hamiltonien H dusystème
totalexciton-photon prend
la forme suivante :H est la somme de l’hamiltonien
excitonique,
de l’hamiltonienphotonique et de
l’hamiltonien d’interaction
qui
sontrespectivement
les transformés desm
,
ph
etint
par U.
L’hamiltonien d’interaction s’écrit :
Il est
composé
de deux termes: lepremier
terme est lecouplage
linéaire et le secondun terme de
couplage
non-linéaire. Celui-cis’explique
qualitativement
par un effet duremplissage
del’espace
dephases : plus
il ad’excitons, plus
il est difficile de créerd’autres en
plus.
Il est caractérisé par la constante ducouplage
non-linéairer’.
La constanter’
dépend
du volume dusystème
V et du rayon de Bohr de l’exciton aex parl’expression approché
suivante:avec:
Il contient un terme de non-linéarité
excitonique
03B1’
~~
décrivant l’interaction Colombienne entre deux excitons(non-linéarité excitonique).
L’effet de ce terme esten
général
assez nettementsupérieur
à celui du terme non linéaire de(2.77).
Nouscalculerons
séparément
l’effet de ces différents termes non linéairespuis
l’effet total3
Fonction d’autocorrélation
et
états
comprimés
3.1
Fonction d’autocorrélation
L’étude des corrélations d’intensité de la lumière émise par un
système physique
constitue un outilpuissant
pour étudier cesystème.
Par
exemple, jusqu’au
début des années50,
lesastrophysiciens
utilisaient l’interférométriede Michelson pour mesurer les distances
angulaires
des étoiles[Pease
31].
En1956,
Hanbury
Brown et Twiss ontproposé
une nouvelle méthode basée sur l’utilisation descorrélations d’intensité
[Hanbury
Brown56].
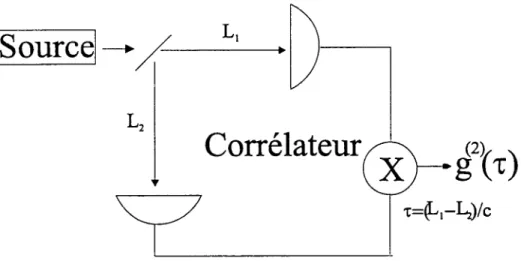
Fig. 14: Principe de corrélation d’intensité de Hany Brown et Twiss
Grâce à cette
méthode,
ils sont parvenus, d’unepart,
à améliorer laprécision
deces mesures, et d’autre
part,
à mesurer des distancesbeaucoup plus petites.
Au fil dutemps,
la mesure des corrélations d’intensité apris
uneampleur
deplus
enplus
grande.
Elle est devenue un outil
puissant
pourexplorer
ladynamique
interne d’unsystème
donné à
partir
de l’étude de lastatistique
deschamps
émis par celui ci. Enparticulier
elles ontpermis
de mettre en évidenceexpérimentalement
la naturenon-classique
deNous nous limiterons tout au
long
de cette thèse aurégime
stationnaire. Dans cerégime
la fonction d’autocorrélation d’intensité est alors définieclassiquement
par : où la valeur moyenne"()"
correspond
à la moyenne d’ensemblestatistique.
La fonction d’autocorrélation
g
(2)
présente
un certains nombres depropriétés
qui
sontprésentées
dans la suite.Les
systèmes
étudiés sontsupposés ergodiques,
c’est-à-dire que la valeur moyenne d’état et la valeur moyennetemporelle
sontégales
pourn’importe quel
opérateur
dusystème.
On montre que[Mandel 95]
de cetteergodicité
découle lapremière propriété
deg
(2)
:
Ce
qui
nouspermet
de définir letemps
de cohérence c comme letemps
caractéristique
au delàduquel
g
(2)
() ~
1. Dès que est trèssupérieur
autemps
de cohérencec
(
c
),
les valeurs moyennes de l’intensité mesurées à des instants distants de sont non corrélés(voir
fig explicatif).
Fig.
15: Temps de cohérenceDans ce
régime
(
régime
stationnaire)
une deuxièmepropriété
deg
(2)
est l’invariance par renversement dutemps
(Symétrie T) :
En
effet,
àpartir
de la définition deg
(2)
stationnaire
onpeut
écrire :ensuite,
la stationnarité donne :et
enfin,
on obtient àpartir
de ces deux dernières relations :Une troisième
propriété
marquante
deg
(2)
est :Elle découle directement de
l’inégalité
de Schwarz. En effetquelque
soit t et , on a :ce
qui
donne :vu la stationnarité on obtient :
qui
estéquivalent
à :La
quatrième propriété
deg
(2)
est :
De
plus
la fonction d’autocorrélation est une fonction continue[
Mandel95].
Si en même
temps
l’intensité I estcontinue,
alorsg
(2)
possède
un extremum à =0 :3.1.2
Définition
quantique
de
g
(2)
:
La
quatrième propriété
de la fonction d’autocorrélationclassique
indique
queg
(2)
(0)
nepeut
être quesupérieur
ouégale
à 1. Or il a été démontréexpérimentalement,
quecette
propriété
n’est pasrespectée
pour la lumière de fluorescence d’un atome[Kim-ble
77].
Enfait,
au niveauquantique,
l’expression
de la fonction d’autocorrélationd’intensité
g
(2)
tellequ’elle
est mesurée par les détecteurs n’est pas donnée par(3.1).
Quantiquement
la fonction d’autocorrélation d’intensitég
(2)
est définie dans le cas d’unchamp
monomode[Glauber 63]
par :où ’:’
désigne
l’ordre normal etâ,
â
~
lesopérateurs
de création et d’annihilation d’unphoton
dans ce mode.g
(2)
est doncproportionnel
à laprobabilité
de détecter unphoton
à l’instant t etun autre à l’instant t+
(qui
n’est pasobligatoirement
celuiqui
est émisjuste
après).
En utilisant la distribution de
quasiprobabilité
P(03B1)
de Glauber-Sudarshan[Glauber
63][Sudarshan 63],
onpeut
écrire[Cohen-Tannoudji
80] :
ce
qui
ne donneg
(2)
(0)
1 que pour desquasiprobabilités
P(03B1)
qui
peuvent
prendre
des valeurs
négatives.
Le fait queg
(2)
(0)
est inférieur à 1 est donccaractéristique
d’unchamp non-classique.
La fonction d’autocorrélation
g
(2)
est reliée directement à lastatistique
duchamp,
En effetg
(2)
est lié au facteur de MandelQ
M
par[
Teich88] :
où
(n)
est le nombre dephotons
moyen et0394n
2
=<n
2
> -
<n>
2
l’écartquadratique
moyendans le
champ.
Le facteur de
Mandel ieprésente
l’écart parrapport
à lastatistique poissonienne.
Ainsi
Q
M
estnégatif
pour unchamp
subpoissonien,
nul pour unchamp poissonien
etpositif
pour unchamp superpoissonien.
Ceci nouspermet
de déduire que l’effet dedégroupement
(g
(2)
(0)
<1)
est une manifestation de lastatistique subpoissonienne
du
champ
tandis que l’effet degroupement
(g
(2)
(0)
>1)
est une manifestation de lastatistique superpoissonienne
duchamp.
Enfin onpeut
dire que lechamp poissonien
neprésente
ni d’effet degroupement
ni d’effet dedégroupement
(g
(2)
(0)
= 1).
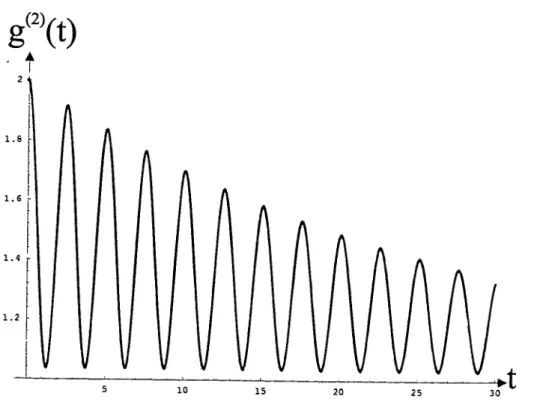
Fig.
16: Fonction d’autocorrélationg
(2)
en fonction du temps t pour·(a)champ
classique(effet
degroupement),(b)champ
cohérentet(c)champ
non-classique(effet
dedégroupement)
En 1977 Kimble
Dagenais
et Mandel ont mesuré la corrélation d’intensité dans la lumière de fluorescence d’un atome[Kimble
77],
et ont mis en évidence pour lapremière
fois l’effet de
dégroupement
et donc l’existence d’étatsnon-classiques
duchamp.
L’effet dedégroupement s’explique
dans ce cas de lafaçon
suivante :après
l’émissiond’un
photon,
l’atome retourne dans l’état fondamental et nepeut
reémettre un secondphoton
au même instant.La mesure de la fonction d’autocorrélation
g
(2)
révèle des effets nonclassiques
surl’intensité. De
plus
elle est bienadapté
à deschamps
àpetit
nombre dephotons.
Pour caractériser les effetsnon-classique
de manièreplus
générale,
enparticulier
les effets sur les diversescomposantes
duchamp
il est utile d’introduire la notion despectre
de bruit.Fig.
17: Fonction de corrélation d’intensité de la lumiére de fluorescence d’un atome(
experience de KimbleDagnois
et Mandel1977)
3.2
Spectre
de
bruit
La
précision
des mesures enoptique
alongtemps
été considérée comme limitéepar le bruit de
photon
ou bruitquantique
standard(Shot noise).
Dans les années 70 et80,
des étudesthéoriques
[Stoler 70],
[Stoler 71], [Yuen 76]
suivies par des étudesexpérimentales
[Slusher 85], [Wu 86]
ont montré lapossibilité
dedépasser
cettelimite,
ouvrant lapossibilité
de nombreusesapplications,
comme l’amélioration des mesuresinterférométriques
(
enparticulier
dans le but de détecter les ondesgravita-tionnelles)
[Grishuck
77],
[Jaekel
90],
les mesuresspectroscopiques
[Zhang
95],
[Marin
97],
[Polzik 92], [Souto
Ribeiro97]
et l’utilisation dessignaux
de télécommunication moins bruités[Yuen 76].
3.2.1
Définition des états
comprimés
Un
champ classique
monomodeE(t)
est défini par safréquence
03C9, sonamplitude
E et sa
phase
~0 :où
E
1
etE
2
sont lescomposantes
dequadratures
duchamp.
Lechamp
E (t)
estreprésenté
dans leplan
de Fresnel par unpoint
de coordonnées cartésiennes(E
1
,
E
2
)
oupolaires
(E, ~
0
) .
Fig.
18: Représentation du champ E dans le plan de FresnelEn
optique
quantique
lesquadratures
duchamp
sont desopérateurs, qui
peuvent
ètre
exprimés
en fonction desopérateurs photoniques
d’annihilation et de création â etâ
~
et en fonction duchamp
d’un seulphoton
E
0
:
De la
relation â, â
~
=
1 pour
lesopérateurs â,
â
~
,
découle la relation de commutation pourÊ
1
etÊ
2
:
Les
quadratures
Ê
1
etÊ
2
sont alors des observablesconjuguées
qui
ne commutent pas. Parconséquent,
elles obéissent àl’inégalité
deHeisenberg, qui impose
une limitecorrespond
dispersion
pourétats cohérents.
La relation d’incertitude n’interdit pas que l’un des facteurs
(0394
Ê
1
ou 0394Ê
2
)
soitinférieur au shot noise
(E
0
)
pourvu que lagrandeur conjuguée
soitsupérieure
àE
0
.
Lesétats
qui
ont cetype
depropriété
sontappelés
des étatscomprimés.
Dans
l’espace
desphases
( espace
décrit par les deuxquadratures
Ê
1
etÊ
2
qui
correspond classiquement
auplan
de Fresnel),
lechamp
estreprésenté
par sa valeur moyenneclassique,
àlaquelle
sontsuperposées
ses fluctuationsquantiques.
A cause dela relation d’incertitude de
Heisenberg,
l’extrémité du vecteurchamp
dansl’espace
desphases
n’est pas unpoint.
Lechamp
est alors décrit par une distribution dansl’espace
des
phases.
Les fluctuations du vide ou d’un état cohérent
correspondent
dansl’espace
desphases
à un cercle dont la surface estégale
à la surface minimale(03C0E
2
0
)
[Reynaud
90],
[Reynaud
92],
et à une distributiongaussienne
des fluctuations pour les deuxquadratures.
Un état
comprimé
(qui
a unedispersion
plus
faible sur l’une descomposantes )
estreprésenté
dansl’espace
desphases
par uneellipse.
La
représentation
d’unchamp
monomode encomposantes
dequadrature
n’est pasunique.
Eneffet,
onpeut
changer l’origine
desphases
dansl’équation
(3.15).
Ainsi lareprésentation
générale
d’unchamp
peut
s’écrire :avec
Les états
comprimés
sont définis de manièregénérale
comme
lesétats
ayant
unbruit réduit au dessous de shot noise sur l’une des
quadratures Ê
1,~
ouÊ
2,~
,
pour uneFig. 19: Allure de la dépendence spatiale du champ électrique et représentation de Fresnel pour différents états du champ