ةــــــــيبعشــلا ةـــيطارـــــقميدــلا ةـــــــيرئازـــــــــجـلا ةـــــــيروهـــمــــــجـلا People's Democratic Republic of Algeria
يــمـــــــلـعــلا ثــحبـلا و يــلاـعــلا مــــــــيلــعــتـلا ةرازو
Ministry of Higher Education and Scientific Research دــــــيمحلا دـبع ةـــــــــعـماــــــــج
ــــــــيااا ــاا –
مــــــــــناغـتسم
Abdelhamid Ibn Badis University of Mostaganem اــيــــــــــجوـــــلونكتــلا و موــــــــــلـعـلا ةــــــــــــيلـك
Faculty of Sciences and Technology ةيكيناكيملا ةسدنهلا مسق
Department of Mechanical Engineering
Flexion thermomécanique avec effet stretching de plaques FGM
sandwich en utilisant la théorie raffinée de déformation par
cisaillement (HSDT)
N° d’ordre: M………/10/2020
MEMOIRE DE FIN D’ETUDE
MASTER ACADEMIQUE
Filière: Génie Mécanique
Spécialité: Construction Mécanique
Présenté par:
BELKHODJA Mohamed
BENGUELLA Sidahmed
Soutenu le 30/09/2020 devant le jury composé de :
Président Dr. M. Sahnoun M.C.A. Université de Mostaganem Examinateur Mme. A. Belhachemi M.A.A. Université de Mostaganem
Encadreur Pr. D.Ouinas Université de Mostaganem
i
ii
RÉSUMÉ
Le présent travail apporte aux lecteurs une étude des comportements mécanique des structures plaques sandwich, isotropes et en matériaux fonctionnellement graduées, soumissent à l’effet de la flexion thermomécanique, ou l'objectif majeur de cette analyse est de développer des nouvelles théories raffinée 2D, quasi-3D et 3D de la déformation de cisaillement d’ordre élevé qui considère l’effet d’étirement de l’épaisseur dans une seule formulation théorique ainsi que de démontrer la capacité de ces modèles. Les équations du mouvement sont dérivées en utilisant le principe d’Hamilton et les solutions analytiques sont trouvées à partir de la technique de Navier, appliqués à des plaques simplement appuyées. Les résultats numériques obtenus expriment l’effet de différents paramètres non dimensionnels et prédisent des réponses appropriées en comparaison avec des solutions existantes des autres théories trouvée dans littérature.
Mots clés: Matériaux fonctionnellement graduées; Théorie 2D, quasi-3D et 3D de déformation de cisaillement d’ordre élevée; L’effet d’étirement; Plaque sandwich; Flexion thermomécanique.
ABSTRACT
This work provides readers with a study of the mechanical behaviors of sandwich plate structures, isotropic and on functionally graded materials, subjected to the effect of thermo-mechanical bending, where the major objective of this analysis is to develop new refined 2D, quasi-3D and quasi-3D high order shear deformation theories, which consider the thickness stretching effect in a single theoretical formulation as well as to demonstrate the capability of these models. Equations of motion are derived using the Hamilton’s principle and analytical solutions are found using Navier's technique, applied to simply supported plates. The obtained numerical results express the effect of various non-dimensional parameters and predict appropriate responses in comparison with existing solutions of other theories found in the literature.
Keywords: Functionally graduated materials; 2D, quasi-3D and 3D higher order shear deformation
theories; Stretching effect; Sandwich plates; Thermo-mechanical bending.
صخلملا
دٔزٚ ازْ مًعنا ءاشقنا تساسذب اٛكٕهسنا ث تٛكَٛاكًٛنا ذإنلأ مكاٛٓب ةشٛطش ، تخسذتي صإخنا اًٛفٛظٔ ٔ ،تهثاًتي تضشعي شٛثأتن ءاُحَلاا ٙكَٛاكًٛنا ٘ساشحنا ، ثٛح مثًتٚ فذٓنا ٙسٛئشنا ازٓن مٛهحتنا ٙف شٕٚطت ثاٚشظَ تٛئاُث ،داعبلأا ّبش تٛثلاث داعبلأا تٛثلاثٔ داعبلأا ثار دآخإ ضق ٙناع تخسذنا ٘زنأ زخأٚ ٙف سابتعلاا شٛثأت دذًت تكاًسنا ٙف تغٛط تٚشظَ ،ةذحأ اًك شٓظٚٔ ةسذق ِزْ جراًُنا . قتشُت ثلاداعي تكشحنا واذختساب أذبي ٌٕتهياْ ىتٚٔ سٕثعنا ٗهع لٕهحنا تٛهٛهحتنا واذختساب تُٛقت ّٛٛفاَ ، تقبطًنا ٗهع ثاحٕهنا تيٕعذًنا تطاسبب . حئاتُنا تٚدذعنا ٙتنا ىت لٕظحنا آٛهع شبعت ٍع شٛثأت ذٚذعنا ٍي ثاشٛغتًنا تٚذعبلانا أبُتتٔ ثابادتسلااب تبساًُنا تَساقي لٕهحب ثاٚشظُنا ٖشخلأا . تاملكلا ةيحاتفملا : دإًنا تخسذتًنا اٛفٛظٔ ؛ ثاٚشظَ تٛئاُث ،داعبلأا ّبش تٛثلاث داعبلأا تٛثلاثٔ داعبلأا ثار دآخإ ضق ٙناع تخسذنا شٛثأت؛ دذًتنا ؛ تحٕن ةشٛطش ؛ ءاُحَا ٙكَٛاكٛي ٘ساشح .iii
TABLE DES MATIÈRE
RÉSUMÉ
TABLE DES MATIÈRE LISTE DES TABLEAUX LISTE DES FIGURES LISTE DES SYMBOLES LISTE DES ABREVIATIONS
INTRODUCTION GÉNÉRALE
CHAPITRE 01: LES MATÉRIAUX FGM.
1.1. Historique et concept des FGM 1.2. Les champs d’utilisation des FGM 1.3. Propriété des FGM.
Les métaux. Les céramiques.
1.4. Processus et technique de fabrication des FGM. 1.5. Modèle et mécanique des structures en FGM
1.5.1. Les théories des plaques FGM
1.5.1.1. Théorie d’ordre supérieur (HSDT- High order shear deformation theory) 1.5.1.1.1. Théories de plaques bidimensionnelles (2D)
1.5.1.1.2. Approches quasi-tridimensionnelles 1.5.1.1.3. Théorie tridimensionnelle
1.6. Structures sandwiches en FGM
CHAPITRE 02: FORMULATION THÉORIQUE.
2. 1. Propriétés matérielles 2. 2. Champ des déplacements 2. 3. Principe d’Hamilton
2. 3.1. L'énergie de déformation :
2.3.2. Le travail effectué par des charges externes 2. 4. Les équations du mouvement
2. 5. Solution analytique de Navier
CHAPITRE 03: ANALYSE THERMO-MÉCANIQUE DES PLAQUES SANDWICH EN FGM EN UTILISANT DES NOUVELLES THÉORIES 2D, QUASI-3D ET 3D
3.1. Résultats numériques et discussions
3.1.1. La flèche centrale adimensionnelle 3.1.2. Contraintes axiale 3.1.3. Contraintes transversales CONCLUSION GÉNÉRALE Références bibliographique ii iii iv v vi viii 1 3 3 4 4 4 4 5 5 5 6 7 7 7 8 9 9 10 14 14 15 15 19 22 22 23 33 37 42 43
iv
LISTE DES TABLEAUX
CHAPITRE 2: FORMULATIONS THÉORIQUES DE L’ANALYSE THERMOMÉCANIQUE DES PLAQUES SANDWICH EN FGM
Tableau 2.1: Les fonctions de forme pour différentes théories de déformation par cisaillement. CHAPITRE 3: ANALYSE THERMOMÉCANIQUE DES PLAQUES SANDWICH EN FGM EN UTILISANT DES NOUVELLES THÉORIES 2D, QUASI-3D ET 3D.
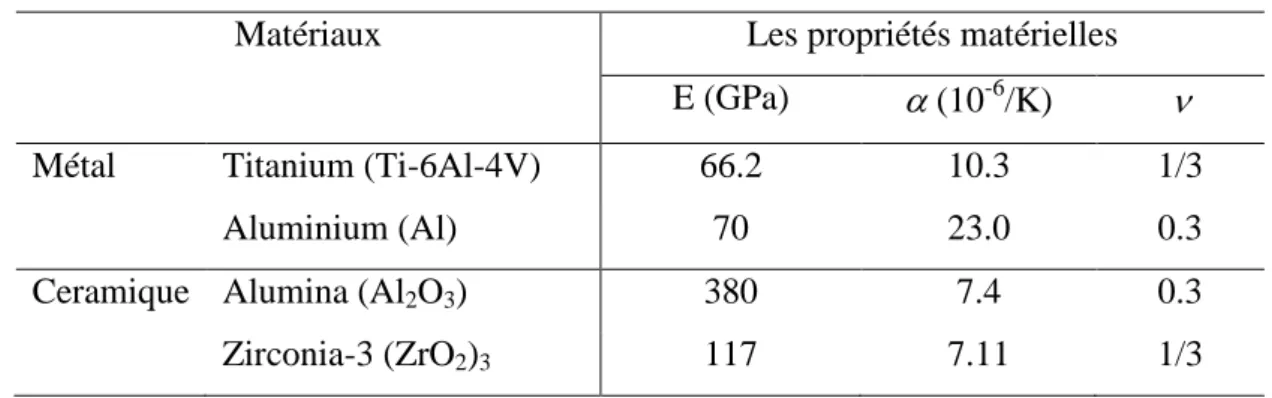
Tableau 3.1. Propriétés matérielles du métal et de la céramique.
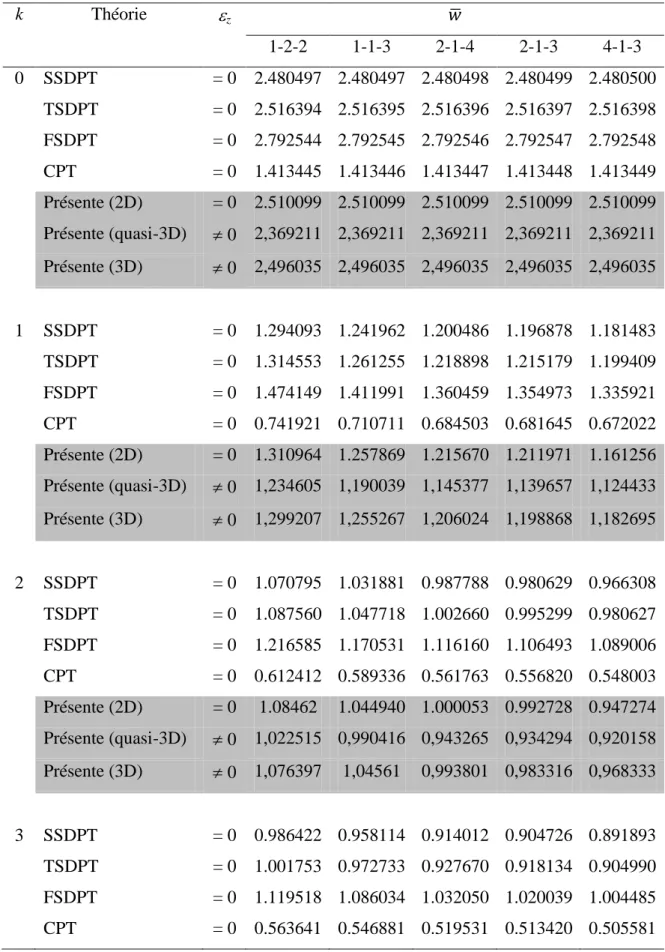
Tableau 3.2. Comparaison entre les résultats du modèle (2D), (quasi-3D) et (3D) de la flèche adimensionnelle
(w̅ ) pour différents types des plaques sandwiches asymétriques en FGM ((Al)1/ZrO2)1 avec soft âme en métal.
Tableau 3.3. Comparaison entre les résultats du modèle (2D), (quasi-3D) et (3D) de la flèche adimensionnelle
(w̅ ) pour différents types des plaques sandwiches symétrique en FGM (Ti-6Al-4V/ (ZrO2)3) avec dure-âme en céramique.
Tableau 3.4. L’effet du rapport d’aspect géométrique (a/b) sur les résultats du modèle (quasi-3D) de la flèche
adimensionnel (w̅ ) pour différents types des plaques sandwiches avec (k=3).
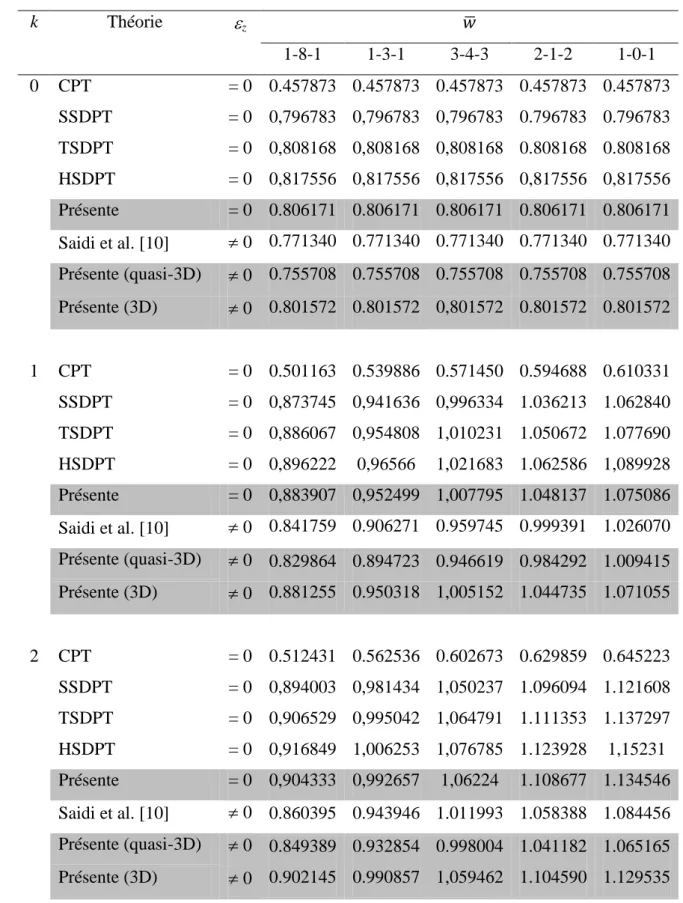
Tableau 3.5. Comparaison entre les résultats du modèle (2D) et (3D) de la flèche adimensionnelle (w̅ ) pour
différents types des plaques sandwiches en FGM ((Al)1/ZrO2)1 avec dure-âme en céramique avec (t1 = t2 = t3 =
0, q0 =1 et (a/h)=10).
Tableau 3.6. Comparaison entre les résultats du modèle (2D), (quasi-3D) et (3D) de la contrainte
adimensionnelle (𝜎 𝑥) pour différents types des plaques sandwiches en FGM.
Tableau 3.7. Comparaison entre les résultats du modèle (2D), (quasi-3D) et (3D) de la contrainte
adimensionnelle ( 𝜏 𝑥𝑧) pour différents types des plaques sandwiches en FGM.
11 23 24 26 28 29 33 37
v
LISTE DES FIGURES
CHAPITRE 1: GÉNÉRALITÉ SUR LES MATÉRIAUX FGM Figure 1.1.a. Graduation par tranche [3].
Figure 1.1.b : Graduation continue [3].
Figure 1.2. Domaines d'application des matériaux a gradient de propriété [3]. Figure 1.3. Schéma de dimension et de géométrie d'une plaque rectangulaire. Figure 1.4. Modèle de la cinématique de l’ordre supérieur.
Figure 1.5. Schématisation de l'effet de l'étirement à travers l'épaisseur de la plaque.
CHAPITRE 2: FORMULATIONS THÉORIQUES DE L’ANALYSE THERMOMÉCANIQUE DES PLAQUES SANDWICH EN FGM
Figure 2.1. Modèle géométrique de la plaque sandwich FGM.
Figure 2.3. La fonction de forme f(z) et sa dérivation de f’(z) pour différentes théories de déformation par
cisaillement.
Chapitre 3: ANALYSE THERMO-MÉCANIQUE DES PLAQUES SANDWICH EN FGM EN UTILISANT DES NOUVELLES THÉORIES 2D, QUASI-3D ET 3D.
Figure 3.1. Variation de la flèche adimensionnelle en fonction de rapport largeur/épaisseur (a/h) pour deux
types de plaques sandwich en FGM: (a) la plaque (1-3-1). (b) la plaque (2-1-2).
Figure 3.2. Variation de la flèche adimensionnelle en fonction de rapport largeur/épaisseur (a/h) pour deux
types de plaques sandwich en FGM: (a) la plaque (1-3-1). (b) la plaque (2-1-2).
Figure 3.3. Variation de la flèche adimensionnelle en fonction de rapport d’aspect géométrique (a/b) pour
deux types de plaques sandwich en FGM: (a) la plaque (1-3-1). (b) la plaque (2-1-2).
Figure 3.4. La variation de la flèche adimensionnelle en fonction de rapport d’aspect géométrique (a/b) et
l’influence des charges mécaniques, thermiques et thermomécanique sur une plaque sandwich en FGM de type (1-3-1).
Figure 3.5. Variation de la contrainte axiale adimensionnelle à travers l’épaisseur des deux types de plaques
sandwich en FGM: (a) la plaque (1-3-1). (b) la plaque (2-1-2).
Figure 3.6. Variation de la contrainte axiale adimensionnelle à travers l’épaisseur des deux types de plaques
sandwich en FGM: (a) la plaque (1-3-1). (b) la plaque (2-1-2).
Figure 3.7. Variation de la contrainte axiale adimensionnelle à travers l’épaisseur d’une plaque sandwich en
FGM de type (1-3-1) soumise à l’influence des charges mécanique, thermique et thermomécanique.
Figure 3.8: La variation de la contrainte transversale adimensionnelle à travers l’épaisseur des deux types de
plaques sandwich en FGM: (a) la plaque (1-3-1). (b) la plaque (2-1-2).
Figure 3.9. Variation de la contrainte transversale adimensionnelle à travers l’épaisseur des deux types de
plaques sandwich en FGM: (a) la plaque (1-3-1). (b) la plaque (2-1-2).
Figure 3.10. Variation de la contrainte transversale adimensionnelle à travers l’épaisseur d’une plaque
sandwich en FGM de type (1-3-1) soumise à l’influence des charges mécaniques, thermiques et thermomécanique. 3 3 4 6 6 7 9 11 31 32 32 33 36 36 37 40 40 41
vi
LISTE DES SYMBOLES
x coordonnées axiale dans le plan horizontal de la plaque y coordonnées axiale dans le plan horizontal de la plaque
z Coordonnée axiale dans le plan transversale et verticale de la plaque
(x, y, 0) le plan médian de la plaque
t de temps
a Longueur de la plaque
b Largeur de la plaque
h Épaisseur de la plaque
k l’indice de puissance (l’indice matérielle), Paramètre du matériau (Exposant
de la loi du la fraction volumique)
E (z) Module de Young en fonction de « z »
V (z) Fraction volumique
Vc La fraction volumique du matériau céramique par la loi de puissance
(z) Coefficient de Poisson en fonction de « z »
u, v, w Les déplacements selon les directions x, y et z, respectivement.
u0, v0, w0 Les composantes du champ de déplacement sur le plan moyen de la plaque Dérivée partielle
f (z) Fonction de gauchissement (fonction de cisaillement transverse), fonction de
forme
f’(z) La première dérivée de la fonction de gauchissement par rapport à z
f’’(z) La deuxième dérivée de la fonction de gauchissement par rapport à z
x, y, z Les rotations autour des axes x, y et z,
une composante supplémentaire de déplacement transversal, prend en compte l’effet de contrainte normale (effet d'étirement),
G(z) Module de cisaillement en fonction de « z » dans le plan transversale
x, y Contraintes axiale dans le plan horizontal de la plaque
z la contrainte normale transversale
xz Contrainte de cisaillement
x, y, z Déformation dans la direction x, y et z
xy Déformations dans le plan
xz, yz Déformations de distorsion
Champ virtuel
U Travail virtuel intérieur = L’énergie de déformation
A, la section
V le volume
xyz Champ de déformation longitudinal virtuel
xz, yz Champ de déformation transversal virtuel
Nx, Ny, Nz, Nxy Efforts normaux = les résultantes de contraintes
Mbx, Mby, Mbxy Moments de flexion = les résultantes de contraintes
Msx, Msy, Msxy Moment supplémentaire du au cisaillement transverse = les résultantes de contraintes
vii
Ssyz, Ssxz Effort de cisaillement = les résultantes de contraintes
V Le travail effectué par des charges externes Travail virtuel extérieur
q Force extérieure (N) charge transversale
K L’énergie cénitique
u0, v0, w0 et Champ virtuel de déplacement
Aij Termes de rigidité en membrane de la plaque
Bij Termes de rigidité de couplage de la plaque
Dij Termes de rigidité de flexion de la plaque
Bsij Termes de rigidité de la plaque en cisaillement
Dsij Termes de rigidité de la plaque en cisaillement
Hsij Termes de rigidité de la plaque en cisaillement
Asij Termes de rigidité de la plaque en cisaillement
Qmn un coefficient donné pour deux charges typiques
T(x, y, z) Chargement thermique (K)
Le vecteur des déplacements généralisés
F Le vecteur des efforts généralisés
Vecteur colonne
viii
LISTE DES ABREVIATIONS
FGM Matériaux Fonctionnellement Graduée CPT Théorie Classique des Plaques
FSDT Théories de la Déformation de Cisaillement de Premier Ordre TSDT Théories de la Déformation de Cisaillement de troisième Ordre HSDT Théories de la Déformation de Cisaillement D’ordre Élevé SSDT Théories de la Déformation de Cisaillement Sinusoïdale 2D Deux dimensionnelles
Quasi-3D Quasi Trois dimensionnelles 3D Trois dimensionnelles
1
INTRODUCTION GÉNÉRALE
Depuis le premier homme sur Terre; les matériaux ont un rôle important de tout temps, parce qu’ils définissent le niveau du développement et le progrès de la civilisation à chaque époques. Au première développement, les humains utilisaient les matériaux simples, naturellement disponibles sur la surface de Terre, grâce à leur faciliter d’utilisation dans différente applications, comme la pierre, le silex, le bois, les peaux, les coquillages, diverses fibres, l'argile et la boue.
Avec le temps jusqu’à l’arriver à la technologie moderne, la nécessité à la découverte des nouveaux matériaux est devenir inévitable (en utilisant obligatoirement des techniques de production), la seule solution était des matériaux hybride qui combinent non seulement des matériaux simple mais permet aussi d’avoir des propriétés matérielles plus élevés, allient par exemple la rigidité, la résistance mécanique et la ténacité élevée avec une grande légèreté.
Les matériaux composites (conventionnels) a atteint cet objective, mais ils restent encore incapables de résister à des conditions de travail extrêmes correspond à une différence de température très élevée qui conduit à une défaillance des composants par le processus de délaminage, à cause d’une transition brusque des propriétés à la jonction des matériaux.
Alors, pour surmonter ce problème, la transition nette des propriétés est remplacer par des propriétés variables lisses et continues du matériau dans une direction spatiale souhaitée telles que la résistivité à la corrosion, la conductivité thermique, la chaleur spécifique, la dureté et le rapport de rigidité, dans des nouvelles matériaux composites (avancés), nommés matériaux fonctionnellement graduée (FGM). En raison des caractéristiques importantes et tous ses avantages, les FGMs devenu bien meilleures que les matériaux composites conventionnels à utiliser dans de multiples applications.
Par la suite, plusieurs efforts ont été déployés dans les recherches pour améliorer encore plus les propriétés des FGM, et dans notre travail, une nouvelle solution analytique est développé dont l’objectif est de analyser le comportement statique des plaque sandwich FGM soumissent à des charges due à la flexion thermomécanique, en utilisant une nouvelle théorie de la déformation par cisaillement hybride (Trigonométrique et polynomiale), en utilisant trois modèles mathématiques 2D, ainsi que Quasi-3D et 3D qui prennent en considération l’effet d’étirement de l’épaisseur. Cette étude est basée sur les effets du champ de température sur la flèche ainsi que les contraintes de cisaillement axiales et transversales adimensionnelles de la plaque sandwich FGM. Les résultats numériques du déplacement et des contraintes sont étudiés. Le présent mémoire est organisé en trois chapitres :
2
Le premier chapitre présente un aperçu sur l’historique des matériaux FGM, définir leur concept, leurs principaux domaines d’application, leur propriétés effectives, ainsi que leurs différentes méthodes d’élaboration. Ensuite les théories et les modèles des plaques utilisés pour l’analyse du comportement mécanique ont été rappelés, suivie par une définition sur les structures sandwiches et leurs types.
Le deuxième chapitre est consacré à la mise en œuvre du modèle mathématique, de la théorie de déformation de cisaillement d’ordre élevée, qui tient en compte la déformation normale, pour analyser le comportement statique des plaques sandwiches FGM reposant sur des appuis simples, et est soumise à des charges mécanique, thermique et thermomécanique, en utilisant une nouvelle fonction de forme de déformation de cisaillement.
3
1. CHAPITRE 01: LES MATÉRIAUX FGM.
1.1. Historique et concept des FGM
La création des FGM est apparue au Japon au début des années 1980, lorsque les chercheurs ont été confrontés à un problème nécessitant un type de matériau composite capable de résister à une différence de température très élevée dans un projet aérospatial [1]. Ils ont d'abord été conçus d’abord comme matériaux de barrière thermique pour les réacteurs de fusion [2].
Les FGM sont une nouvelle classe de matériaux composites, fabriqués d'une manière spéciale, qui garantissait un changement graduée, varier d’un matériau à l’autres soit en continue ou discontinue par étape (Figure 1.1) des constituants à l'intérieur, souvent de la céramique aux métaux dans un seul corps (matériaux microscopiquement inhomogènes) des FGM les plus connu, à travers la direction de l'épaisseur selon des fonctions mathématiques. Et par conséquent, une modification correspondante des propriétés mécaniques effectives et des caractéristiques du matériau apparaît, en font une solution non seulement au problème thermique (supporter des niveaux de température élevés) bien connus en premier lieu dans les industries aérospatiales, mais aussi à certains problèmes des matériaux composites classiques, tels que la discontinuité des matériaux qui génèrent des niveaux de concentration de contraintes élevés, et donc des problèmes d'interface (la rupture de délaminage) ainsi que des déformations, De plus, les FGM supportent également les charges mécaniques appliquées et offrent de bonnes performances dans des conditions d’utilisation dure et exigeante. En conséquence, les FGM ont attirés plusieurs industries à utiliser leurs composants structurels, et donc beaucoup de domaine de l'ingénierie les étudient de manière approfondie afin de prédire leurs comportements et leurs réponses.
4 1.2. Les champs d’utilisation des FGM
Grace à leurs importantes propriétés, les FGM sont devenu un choix favorable dans la plupart des domaines d’ingénierie et d’industrie. Cela inclus une application dans le domaine aérospatial, automobile, biomédical, électrique, énergétique, et maritime
Figure 1.2. Domaines d'application des matériaux a gradient de propriété [3].
1.3. Propriété des FGM
Les FGM peuvent incorporer des fonctions incompatibles telles que la résistance à la chaleur, à l'usure et à l'oxydation des céramiques avec la ténacité élevée, la résistance élevée, l'usinabilité et la capacité de liaison des métaux sans contrainte thermique interne sévère [1], souvent constitués de deux types de matériaux de base, céramique et métal, choisie en fonction des propriétés physiques de chaque composant [4].
Les métaux
Lorsque la majorité des éléments chimiques dans le tableau de Mendeleïev sont les métaux, ils possèdent plusieurs avantages :
très bons conducteurs de chaleur,
très bons conducteurs d’électricité,
plus souvent durs et rigides,
déformables plastiquement,
un nombre important possèdent une température de fusion très élevée.
Les métaux les plus souvent utilisés sont le fer, le nickel, le tungstène, le titane, le magnésium et l'aluminium [4].
Les céramiques
Les céramiques sont en général, des matériaux très durs, résultent de la combinaison des éléments métalliques (Al, Ni, Ti, Zr…) et non métalliques dont le plus courant est l’oxygène.
Ils sont largement utilisés comme abrasifs et typiquement dans les régions ou les environnements extrêmes (hautes températures, etc.), caractérisés par leurs comportements
5
réfractaires schématisés par leurs résistances mécaniques et thermiques très élevées [4]. Alors qu’ils ont généralement un comportement fragile ce qui réduit leurs emplois pour des applications où les chocs mécaniques et thermiques importants. Ce matériau est choisi grâce à ses caractéristiques exceptionnelles qui sont énumérées comme suit [1]:
Faible réactivité chimique, bonne tenue à la corrosion,
Haute température de fusion ou de décomposition,
Haut module d’élasticité et haute dureté,
Charge à la rupture élevée,
Bas coefficient de frottement, bonne résistance à l’usure.
1.4. Processus et technique de fabrication des FGM
Une variété des méthodes de production des FGM ont été créé, basée souvent sur une variation des méthodes de traitement des différente processus d’élaboration conventionnelles bien établis, des procédés qui sont capables de s'adapter à une étape de gradation, ou on peut citer [2] :
La compaction sèche des poudres,
La stratification des feuilles
Les méthodes de dépôt chimique en phase vapeur.
Le coulage centrifuge
Coulage séquentiel en barbotine
Coulage en bande
Projection thermique (plasma)
1.5. Modèle et mécanique des structures en FGM
Depuis l’apparition des FGM, les théories particularisées à analyser les structures isotropes ou composites sont établies à nouveau, diverses théories ont été proposées et développer, et plus particulièrement qui sont concernée aux structures plaques, qu’ils ont acquis un intérêt appréciable [5].
1.5.1. Les théories des plaques FGM
Notre recherches est basé sur des structures plaques, employées par exemple en aéronautique, aérospatial, constructions navale, automobile et nucléaire. À cet axe, qui prennent une importance dans la mécanique des structures, diverses théories ont été proposées sur les plaques en FGM qui peuvent les regroupées selon l’approche adoptée [5] aux:
6
Théories du premier ordre des plaques (FSDT),
Théories de déformation de cisaillement d’ordre élevée des plaques (HSDT).
Figure 1.3. Schéma de dimension et de géométrie d'une plaque rectangulaire.
1.5.1.1. Théorie d’ordre supérieur (HSDT- High order shear deformation theory)
Une théorie fiable, précise et preuve des performances appréciables même pour une étude des plaques épaisses par rapport à la théorie classique de Love-Kirchhoff qui est limitée à l’étude des plaques minces, sans pris en compte de la déformation normale, sachant que les résultats obtenues ne sont pas fiable ainsi que les théories de premier ordre qui s'étend à des plaques modérément épaisses ou les résultats obtenue sont globalement satisfaisants et imparfaite pour les cas des plaques épaisses, et elle nécessite toujours un facteur de correction de contrainte pour satisfaire les conditions de nullités de contraintes de cisaillement tangentielles sur les surfaces supérieur et inférieur de la plaque. Le facteur de classification de ces théories est l’importance de l’épaisseur par rapport aux autres dimensions, cette particularité conduit à l’effet de la déformation par cisaillement transversal à travers l’épaisseur qui est tenu en considération, une théorie intéressantes soit pour une présentation correcte de la cinématique ou pour les contraintes de cisaillement à travers l’épaisseur, classé selon l’approche adoptée à l’étude aux:
Théories des plaques FGM bidimensionnelles (2D),
Approches Quasi-dimensionnelles des plaques FGM (Quasi-3D),
Théories des plaques FGM tridimensionnelles (3D).
7 1.5.1.1.1. Théories de plaques bidimensionnelles (2D)
Ces Théories appropriées pour les plaques en FGMs minces à modérément épaisses, et non recommandé pour les plaques épaisses [6]. L’ensemble de ces théories sont basées sur l’état de contraintes planes (la déformation normale est négligée (z=0)) qui cause la négligence ainsi de
l’effet de l’étirement de l’épaisseur [7].
1.5.1.1.2. Approches quasi-tridimensionnelles
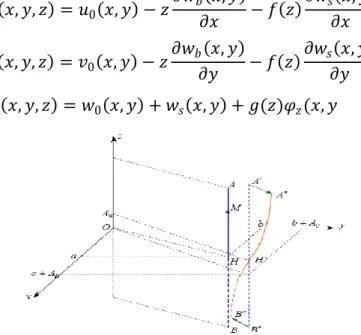
Dans la recherche à formuler une théorie efficace pour pouvoir analyser des plaques, en statique et dynamique d’une façon générale, ces théories de déformation par cisaillement d’ordre élevé concédèrent l’effet de l’étirement de l’épaisseur. Pour éviter de recourir à une analyse tridimensionnelle, cette particularité utilise un état de contraintes de la théorie bidimensionnelle, le déplacement transversal est exprimé et dépend d’une variation non linéaire à travers l’épaisseur de la plaque. Le champ de la cinématique est basé sur la théorie d’ordre élevée, une spécification est donc introduite à la composante de déplacement transversal pour le rendre variable à travers l’épaisseur, on injecte une fonction non-linéaire en fonction de la coordonné transversale (z), alors la cinématique devient : 𝑢 𝑥, 𝑦, 𝑧 = 𝑢0 𝑥, 𝑦 − 𝑧 𝜕𝑤𝑏 𝑥, 𝑦 𝜕𝑥 − 𝑓 𝑧 𝜕𝑤𝑠 𝑥, 𝑦 𝜕𝑥 𝑣 𝑥, 𝑦, 𝑧 = 𝑣0 𝑥, 𝑦 − 𝑧 𝜕𝑤𝑏 𝑥, 𝑦 𝜕𝑦 − 𝑓 𝑧 𝜕𝑤𝑠 𝑥, 𝑦 𝜕𝑦 𝑤 𝑥, 𝑦, 𝑧 = 𝑤0 𝑥, 𝑦 + 𝑤𝑠 𝑥, 𝑦 + 𝑔(𝑧)𝜑𝑧(𝑥, 𝑦
Figure 1.5. Schématisation de l'effet de l'étirement à travers l'épaisseur de la plaque.
1.5.1.1.3. Théorie tridimensionnelle
Une théorie efficace formulée pour analyser des plaques en statique et dynamique, une nouvelle stratégie qui prise en considération l’effet de l’étirement de l’épaisseur, cet effet a un
8
impact important dans l’évaluation exact du comportement pour des plaques en FGMs épaisses, qui parmi ainsi une description précise des champs de contraintes à travers l’épaisseur, surtout les contraintes de cisaillement, il est pertinent de mentionner que les coefficients de rigidité sont différentes a celles de la théorie bidimensionnelle, qui sont les mêmes de l’approche quasi-3D, ainsi qu’elle comporte le même champ de la cinématique de l’approche quasi-3D. Et donc le recours à l’élasticité tridimensionnelle est nécessaire pour résoudre de façon fiable les problèmes traité pour obtenir des résultats à précision forte et satisfaisante.
1.6. Structures sandwiches en FGM
La structure sandwiche est composée de deux revêtements, et situé entre elle un noyau qui sont réalisées directement de manière continue avec une nature différente des deux composantes entre les céramique ou le FGM, un matériau résultant ayant de très bonnes caractéristiques, permettant de concilier la légèreté et la rigidité. L'utilisation de telle structure aide à éliminer mécaniquement et thermiquement les contraintes induites par la distribution non graduelle des propriétés matérielles (changements brusques de propriétés) et à améliorer l’adhérence, elles peuvent être divisées en trois types:
Type-A, plaques sandwich avec peau en FGM et noyau homogène;
Type B, plaques sandwich avec des feuilles de face homogènes et un noyau FGM;
Type C, plaques sandwich avec une couche Supérieure homogènes et les couches centrale et inférieure en FGM [3].
9
2. CHAPITRE 02: FORMULATION THÉORIQUE.
2.1. Propriétés matérielles
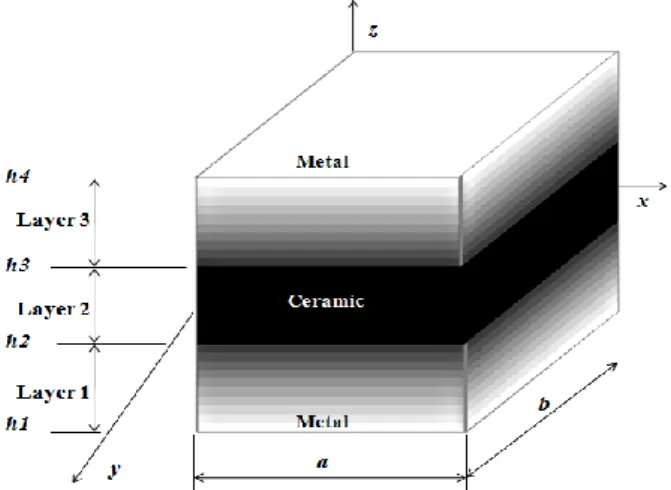
On considère une plaque sandwich plate simplement appuyée, composée de trois couches (métal-céramique, céramique, céramique-métal) ayant l'épaisseur h, la longueur a et la largeur b, et les limites avec une régularité convenable, évoluée selon les coordonnés de l'axe z perpendiculaire au plan médian de la plaque, défini par le système de coordonnées cartésienne (x, y, z), comme représenter sur la figure 2.1.
Figure 2.1. Modèle géométrique de la plaque sandwich FGM.
Le plan médian est défini par z = 0 et ses plans de délimitation externes sont définis par z =
± h/2. Les couches de face de la plaque sandwich sont constituées d'un matériau isotrope dont les
propriétés du matériau varient doucement dans la direction z uniquement. La couche centrale est constituée d'un matériau homogène isotrope. Les positions verticales de la surface inférieure, des deux interfaces entre les couches de noyau et de faces et la surface supérieure sont désignées respectivement par h1 = - h/2, h2, h3, h4 = h/2. Les propriétés matérielles effectives de chaque couche, comme le module de Young, le coefficient de Poisson et le coefficient de dilatation thermique, peuvent être exprimées comme
m n m c P V P P z P ( ) (2.1)Où P et c P désignent respectivement les propriétés correspondantes de la céramique et du m
métal de la plaque sandwich FGM, et désignent aussi les propriétés des faces inférieure et supérieure de la couche 1 et vice-versa pour la couche 3 en fonction de la fraction volumique V(n)
10
(n= 1, 2, 3). La fraction volumique à travers l'épaisseur des faces de la plaque sandwich suit une simple loi de puissance alors qu'elle est égale à l'unité dans la couche centrale [8].
k h h h z V 0 1 0 ) 1 ( , z
h1, h2
, (2.2.a) 1 ) 2 ( V , z
h2, h3
, (2.2.b) k h h h z V 3 2 3 ) 3 ( , z
h3, h4
, (2.2.c) Où k est l'exposant de la fraction volumique, qui prend des valeurs supérieures ou égales à zéro. La couche centrale est indépendante de la valeur de k qui est une couche entièrement céramique. Cependant, la valeur de k égale à zéro représente une plaque entièrement céramique. Notez que la fraction volumique du métal est élevée près des surfaces inférieure et supérieure de la plaque, et celle de la céramique est élevée près des interfaces [8].Nous signalons qu’il y a des rapports importants caractérisant les plaques sont engendrés comme le rapport entre le côté à épaisseur (a/h), (qui définie une plaque épaisse, modérément épaisse et mince, respectivement aux rapports de valeurs plus élevée, modérément élevée et faible) et le rapport d'aspect (a/b), (qui définie une plaque carrée et rectangulaire respectivement aux rapports de valeurs (ab) et (a/b1)).
2.2. Champ des déplacements
Sur la base de la théorie de la plaque épaisse et incluant l'effet de la déformation normale transversale (effet d'étirement de l'épaisseur), les hypothèses de base pour le champ de déplacement de la plaque peuvent être décrites comme suit [9] :
f
z x y x w z y x u z y x u , , 0 , 0 x , (2.3.a)
f
z x y y w z y x v z y x v , , 0 , 0 y , (2.3.b)
x y z
w
x y f
z x y w , , 0 , z , (2.3.c)11
Où u, v, w sont des déplacements dans les directions x, y, z, u0, v0 et w0 sont des
déplacements dans le plan médian, x, y et z les rotations des plans yz, xz et xy dues à la flexion,
respectivement. f(z) représente la fonction de forme déterminant la distribution des déformations et contraintes de cisaillement transversale le long de l'épaisseur. Notez que f ′′(z) =0 pour l’analyse 2D [10].
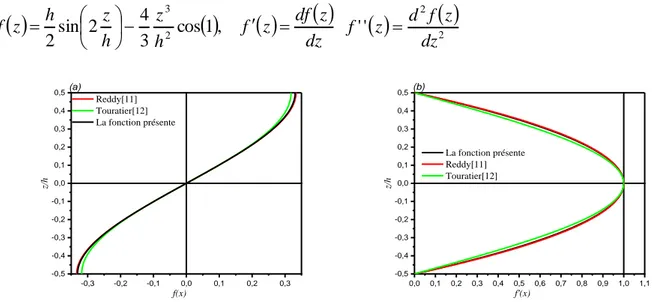
Dans cette étude, une nouvelle fonction de forme de déformation par cisaillement f (z) est développée comme indiqué dans l’équation. (2.4) et illustré sur la figure 2.3 avec d’autre modèles dans le tableau 2.1. Ce nouveau modèle assure une distribution précise de la déformation de cisaillement en fonction de l'épaisseur de la plaque et considère les contraintes de cisaillement transversales paraboliques sur l'épaisseur comme satisfaisant les conditions de surface sans contrainte de cisaillement sans y compris les facteurs de correction de cisaillement.
dz z df z f h z h z h z f cos1, 3 4 2 sin 2 2 3
2
2 ' ' dz z f d z f (2.4) -0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 (a) f(x) z/h Reddy[11] Touratier[12] La fonction présente -0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 (b) f'(x) z/h La fonction présente Reddy[11] Touratier[12]Figure 2.3. La fonction de forme f(z) et sa dérivation de f’(z) pour différentes théories de déformation par
cisaillement.
Tableau 2.1: Les fonctions de forme pour différentes théories de déformation par cisaillement.
Modèle Fonctions de forme f (z) de la déformation par cisaillement
Reddy (TSDT) [11] 22 3 4 1 h z z Touratier (SSDT) [12] z h h sin
12 Atmane et al (HSDT) [13]
cosh /2 1
sinh 1 2 / cosh 2 / cosh h h z z Zaoui et al. (HSDT) [15] 4 4 3 2 2 4 4 sin cos h h h z h h z e h z hzLa présente théorie cos
13 4 2 sin 2 2 3 h z h z h
Sur la base des hypothèses de l’équation. (2.3), les déformations peuvent être liées au champ de déplacement comme x y z f x z f y z f z f y z f x z f y x w y w x w z x v y u y v x u y x x z y z z y x xy xz yz z y x ) ( ) ( ) ( ) ( ) ( ) ( 2 0 0 0 0 0 0 0 2 2 0 2 2 0 2 0 0 0 0 (2.5)
Il peut être observé à partir de l’équation. (2.5) que les déformations de cisaillement transversal (xz, yz) sont nulles aux surfaces supérieure (z = h/2) et inférieure (z = -h/2) de la plaque.
Par conséquent, les conditions aux limites sans contrainte sur les surfaces de la plaque sont satisfaites.
Les relations contrainte-déformation tenant compte de la déformation de cisaillement transverse et des effets thermiques pour la nième couche peuvent être exprimées comme les relations constitutives du comportement linéaire d’une plaque FGM, regroupant les contraintes et les déformations via la matrice de rigidité, s’écrivent [15] :
13 xy xz yz n z n y n x xy xz yz z y x T T T C C C C C C C C C C C C 66 55 44 33 23 13 23 22 12 13 12 11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 (2.6)
Où (x, y, z, yz, xz, xy) et (x, y, z, yz, xz, xy) sont respectivement les composantes de
contrainte et de déformation. (n) est le coefficient de dilatation thermique, et T est la distribution de la charge thermique.
Sans l’effet d’étirement:
Les coefficients de rigidité, définis pour 2D (z = 0) sont:
2 22 11 1 ) ( ) ( C z E z z C n , (2.7.a) ) ( ) ( 11 12 z C z C , (2.7.b) 0 ) ( ) ( 23 13 z C z C (2.7.c)
) ( 2 1 ) ( ) ( ) ( ) (z C44 z C55 z C66 z C11 z G (2.7.d)Avec l’effet d’étirement:
Les coefficients de rigidité, définis pour le modèle quasi-3D (z 0) sont :
2 22 11 1 ) ( ) ( C z E z z C n , (2.8.a) ) ( ) ( ) ( ) ( 13 23 11 12 z C z C z C z C , (2.8.b)
) ( 2 1 ) ( ) ( ) ( ) (z C44 z C55 z C66 z C11 z G (2.8.c)Les coefficients de rigidité, définis pour le modèle 3D (z 0) sont :
1 2 1 1 ) ( ) ( ) ( 22 33 11 z E z C z C z C n , (2.8.d)14 ) ( ) 1 ( ) ( ) ( ) ( 13 23 11 12 z C z C z C z C , (2.8.e)
( ) 1 2 2 1 ) ( ) ( ) ( ) (z C44 z C55 z C66 z C11 z G , (2.8.f)Où E(n)(z) et (n)(z) sont le module d’Young et le coefficient de Poisson caractérisant les
propriétés élastiques dans le plan d’isotropie de la nième couche.
2. 3. Principe d’Hamilton
Pour déterminer les équations du mouvement d’un solide déformable on utilise le principe d’Hamilton. Ce dernier peut être formulé analytiquement sous la forme suivante :
U V
dt T
0 0
(2.9)Où T désigne une période de temps et U, V sont respectivement, la variation d’énergie de déformation et le travail effectué par les charges externes de la plaque FGM.
2.3.1. L'énergie de déformation :
V xz xz yz yz xy xy z z y y x x dV U ( ) (2.10.a) dA x y M y x w M x v y u N y Q x Q N y M y w M y v N x M x w M x u N U y x s xy b xy xy y z yz x z xz z z y s y b y y A x s x b x x
0 2 0 0 2 0 2 0 2 0 2 0 2 (2.10.b)Où A, V, N, M et S désignent la section, le volume et les résultantes de contraintes définies comme suit:
15
3 1 1 , , , , n n h h xy yy xx xy yy xx N N dz N n n (2.11.a)
3 1 1 , ) ( ' , n n h h yz xz y x Q f z dz Q n n (2.11.b)
3 1 1 , , , , n n h h xy yy xx s xy s yy s xx M M f dz M n n (2.11.c)
3 1 1 , , , , n n h h xy yy xx b xy b yy b xx M M z dz M n n (2.11.d)Où hn et hn+1 sont les coordonnées z du haut et du bas de la nième couche,
2.3.2. Le travail effectué par des charges externes
La variation de l’énergie potentielle des charges externes dans les directions horizontale et transversale peut être exprimée par :
dA z f w q V dA w q V A z A 0 (2.12)Où q est la charge transversale.
2.4. Les équations du mouvement
Les équations de mouvement appropriées aux six inconnues du champ de déplacement et des équations du mouvement sont obtenues en substituant les équations des énergies (2.10 et 2.13) dans l'équation (2.9). En regroupant tous les coefficients u0, v0, w0, x, y et z après
intégration par partie, le système d’équations s’écrit comme suit:
0 : 0 y N x N u x xy (2.13.a) 0 : 0 y N x N v xy y (2.13.b)
16 0 2 : 2 2 2 2 2 q y M y x M x M w b y b xy b x b (2.13.c) 0 : y M x Mxs xys x (2.13.d) 0 : x M y Msy xys y (2.13.e)
0 : z f q N y Q x Q z yz xz z (2.13.f)Les contraintes résultantes sont obtenues par substitution de l'équation (2.6) dans (2.10), il vient : z T s y T s x T b y T b x T y T x T z x z y z y x y x a a a s s s s s s s s s s s s s s s s s s a s s a s s s s s s s z xz yz s xy s y s x b xy b y b x xy y x N M M M M N N x y x y y x y x w y w x w x v y u y v x u R R R L L L L A A H D B R H H D D B B R H H D D B B D D B L D D D D B B L D D D D B B B B A L B B B B A A L B B B B A A N Q Q M M M M M M N N N 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 0 2 2 0 2 0 0 0 0 55 44 66 66 66 22 12 22 12 22 12 12 11 12 11 12 11 66 66 66 22 12 22 12 22 12 12 11 12 11 12 11 66 66 66 22 12 22 12 22 12 12 11 12 11 12 11 (2.14)
17
3 1 12 11 2 2 66 66 66 66 66 66 12 12 12 12 12 12 11 11 11 11 11 11 , ) ( ) ( ) ( ) ( ), ( ), ( , , , 1 1 n n h h s s s s s s s s s dz z G z C z C z f z zf z f z z H D B D B A H D B D B A H D B D B A n n (2.15.a)
s s s
s s s
H
D
B
D
B
A
H
D
B
D
B
A
22,
22,
22,
22,
22,
22
11,
11,
11,
11,
11,
11 (2.15.b)
3 1 2 55 44 1 ) ( ) ( n n h h s s n n dz z G z f A A (2.15.c)Pour le modèle quasi-3D :
3 1 11 2 1 ) ( ) ( ), ( ) ( ), ( ), ( n n h h a a dz z C z f z f z f z f z z f R R L L n n (2.15.d) Pour le modèle 3D :
3 1 11 2 1 ) ( ) ( 1 ), ( ) ( 1 ), ( 1 ), ( 1 n n h h a a dz z C z f z f z f z f z z f R R L L n n (2.15.e)Les résultantes de contrainte et de moment, T y T x N N , T y T x M M , sTy T x s M M et NTz dues au chargement thermique sont définies par :
Pour le modèle 2D:
dz z f z f z T z z E z N M M N n h h n n n n T z T x s T x T x n n
3 1 2 1 1 1 1 (2.16.a)Pour le modèle quasi-3D
dz z f z f z T z z E z N M M N n h h n n n n T z T x s T x T x n n
3 1 2 1 1 1 2 1 (2.16.b)18 Pour le modèle 3D :
dz z f z f z T z z E N M M N n h h n n n T z T x s T x T x n n
3 1 1 1 2 1 (2.16.c)La variation du champ de température à travers l'épaisseur est supposée être comme suit [15] :
T x y z
h z f z y x T h z z y x T z y x T , , 1 , , 2 , , 3 , , (2.17)Où T1, T2 et T3 sont des charges thermiques.
En remplaçant l’équation. (2.14) dans l'équation. (2.13), on obtient,
1 2 2 2 66 2 0 3 66 0 2 2 0 2 66 2 12 2 0 3 12 0 2 12 2 2 11 3 0 3 11 2 0 2 11 2 f y x y B y x w B y x v y u A x L y x B y x w B y x v A x B x w B x u A y x s z y s x s (2.18.a) 2 2 2 2 66 2 0 3 66 2 0 2 0 2 66 2 2 22 3 0 3 22 2 0 2 22 2 12 2 0 3 12 0 2 12 2 f x y x B y x w B x v y x u A y L y B y w B y v A y x B y x w B y x u A y x s z y s x s (2.18.b) q f y x y x D y x w D y x v y x u B y L y D x w D y v B y x B y x u B x L y x D y x w D y x v B x D x w D x u B y x s z a y s x s z a y s x s 3 2 3 2 3 66 2 2 0 4 66 2 0 3 2 0 3 66 2 2 3 3 22 4 0 4 22 3 0 3 22 2 3 12 2 0 3 12 2 2 2 3 12 2 2 0 4 12 2 0 3 12 3 3 11 4 0 4 11 3 0 3 11 2 4 2 2 (2.18.c)
19 4 55 2 2 2 66 2 0 3 66 0 2 2 0 2 66 2 12 2 0 3 12 0 2 12 2 2 11 3 0 3 11 2 0 2 11 2 f x A y x y H y x w D y x v y u B x R y x H y x w D y x v B x H x w D x u B z x s y x s s s z y s s x s s s (2.18.d) 5 44 2 2 2 66 2 0 3 66 2 0 2 0 2 66 2 2 22 3 0 3 22 2 0 2 22 2 12 2 0 3 12 0 2 12 2 f y A x y x H y x w D x v y x u B x R y H y w D y v B y x H y x w D y x u B z y s y x s s s z y s s s x s s s (2.18.e)
z f q f y y A x x A R y R y w L y v L x R x w L x u L z y s z x s z a y a x a 6 2 2 44 2 2 55 2 0 2 0 2 0 2 0 (2.18.f)Où {f} = {f1, f2, f3, f4, f5, f6}t est un vecteur de force généralisé.
Les composantes du vecteur de force généralisé {f} sont données par
x N f T x 1 , y N f T y 2 , 2 2 2 2 3 y M x M f T y T x , x M f T x s 4 , y M f T y s 5 , T z N f6 . (2.19)
2.5. Solution analytique de Navier
Considérons une plaque rectangulaire simplement appuyée avec une longueur a et une largeur b sous une charge thermomécanique. Pour résoudre ce problème, nous utilisons la solution de Navier, les charges mécanique et de température sous la forme suivante :
x y t t t q T T T q sin sin 0 3 2 1 3 2 1 (2.20)Où q0, t1, t2 et t3 sont des constantes,
et
sont déterminées comme suit :a m
20
Sur la base de l’approche Navier, la solution des variables de déplacement satisfaisant les conditions aux limites d’une plaque simplement appuyée sont comme suit :
y x Z y x Y y x X y x W y x V y x U w v u z y x sin sin cos sin sin cos sin sin cos sin sin cos 0 0 0 (2.21)Avec (U, V, W, X, Y, Z) sont des fonctions inconnues à déterminer, En considérant les équations (2.15) et (2.19), on obtient l'équation d’opérateur suivante :
A
F (2.22)21
, , , , , , , , 2 , 2 , 2 2 , 2 2 , , , 2 , , , , , 2 , , 55 2 44 2 66 55 56 55 66 2 22 2 55 44 46 66 12 45 44 66 2 11 2 44 2 2 36 66 12 2 22 3 35 66 12 2 11 3 34 2 2 22 4 66 12 2 2 11 3 34 22 4 66 12 2 2 11 4 33 26 22 2 66 2 25 66 12 24 66 12 2 22 3 23 22 2 66 2 22 16 66 12 15 66 2 11 2 14 66 12 2 11 3 13 66 12 12 66 2 11 2 11 a s s s s s s s s s s s s a s s s s s s s w s s s s s s s s s s s R A A a A R a A H H a A R a H H a A H H a L a D D D a D D D a K K D D D D a D D D D a L a B B a B B a B B B a A A a L a B B a B B a B B B a A A a A A a (2.23)Les composantes du vecteur de force généralisé {F} = {F1, F2, F3, F4, F5, F6}t sont données
par
, , , , , , 3 2 1 6 3 2 1 5 3 2 1 4 3 2 1 2 2 3 3 2 1 2 3 2 1 1 t R t L t L h F t F t D t B h F t F t D t B h F t D t D t B h F t B t B t A F t B t B t A F T T a T T a T a T a T a T a T a T a T T T a T T T a T T (2.24) Telle que22
![Figure 1.a. Graduation par tranche [3]. Figure 1.b : Graduation continue [3].](https://thumb-eu.123doks.com/thumbv2/123doknet/13197444.392312/12.892.103.789.793.1013/figure-graduation-tranche-figure-graduation-continue.webp)
![Figure 1.2. Domaines d'application des matériaux a gradient de propriété [3].](https://thumb-eu.123doks.com/thumbv2/123doknet/13197444.392312/13.892.112.782.228.431/figure-domaines-application-matériaux-gradient-propriété.webp)