Impurity scattering in 1D ring of interacting electrons

HAL Id: jpa-00247022

https://hal.archives-ouvertes.fr/jpa-00247022

Submitted on 1 Jan 1994

HAL is a multi-disciplinary open access

archive for the deposit and dissemination of

sci-entific research documents, whether they are

pub-lished or not. The documents may come from

teaching and research institutions in France or

abroad, or from public or private research centers.

L’archive ouverte pluridisciplinaire HAL, est

destinée au dépôt et à la diffusion de documents

scientifiques de niveau recherche, publiés ou non,

émanant des établissements d’enseignement et de

recherche français ou étrangers, des laboratoires

publics ou privés.

Impurity scattering in 1D ring of interacting electrons

Georges Bouzerar, Didier Poilblanc

To cite this version:

Georges Bouzerar, Didier Poilblanc. Impurity scattering in 1D ring of interacting electrons. Journal

de Physique I, EDP Sciences, 1994, 4 (11), pp.1699-1703. �10.1051/jp1:1994215�. �jpa-00247022�

Classification

Physics

Abstracts

72,10 71.27 72.15

Impurity

scattering

in

lD

ring

ofinteracting

electrons

Georges

Bouzerar

(*)

and Didier Poilblanc

_(**)

Groupe

de

Physique

Théorique,

Laboratoire de

Physique

Quantique,

Université Paul

Sabatier,

31062

Toulouse,

France

(Received

18 May 1994,

accepted

28

July 1994)

Abstract. The

stability

of the lD

Luttinger

hquid

phase of

interacting

spinless

particles

(t

V

mortel)

to an on-site

diagonal

disorder is studied

by

exact

diagonalization

of small ID

rings

_up to 22 sites. We discuss _our numencal results _m the

light

of the

phase diagram

predicted

by

the Renormalization

Group

analysis.

In _a finite _range of attractive interactions

(around

V/t

+~

-0.5)

the metallic

phase

(with

superconducting

fluctuations)

seems to be stable up to

some small value of the disorder parameter. On the other

hand,

m the

repulsive

case, the

impurity

potential

clearly

leads to _a strong localization of the

particles.

Tl~e aim of tl~is _paper is to

study

the

interplay

between interactions and disorder in _a lD

Luttinger liquid.

For lattice models of

spinless

fermions witl~ short _range

repulsiue

interactions

on-site

diagonal

disorder is believed to

produce

localization of tl~e

partiales.

However,

for an

attractive

interaction,

superconducting

critical fluctuations _appear and tl~e influence of tl~e

disorder is net so dear.

To be more

specific

we consider tl~e

following

Hamiltonian

describing

a N-site cl~ain of

spinless

fermions in tl~e _presence of disorder:

7i

=

-t/2

~(exp

(2ix4l/N)

c)

c~+i +

h-c-)

+ V

~j

_{n~ n~+i} +

~j

w~ n~

(1)

~ ~ ~

wl~ere _w~ are on-site

energies

cl~osen

randomly

between

-W/2

and

W/2,

V is tl~e nearest

neigl~bour

interaction and 4l is a

magnetic

flux

througl~

tl~e

ring

(measured

in units of flux

quantum

4lo =

hle).

So for we set t = 1. Tl~e

magnetic

flux will be useful later on to test tl~e

sensitivity

of tl~e

system

to a

change

in tl~e

boundary

conditions.

In tl~e absence of disorder

(W

= l~) the model is

integrable.

At

l~alf-filling,

for

repulsive

interaction

(V

>

0),

Umklapp

scattering

dommates and a metal-insulator transition occurs

at V = 1 witl~ a

charge

gap

opening

up for V > 1.

Away

from

commensurability

(1.e.

away

(*)

E-mail:

georges@sibena.ups-tlse.fr.

1700 JOURNAL DE

PHYSIQUE

I N°11

from

half-filling),

tl~e system remains metallic even for V > 1. For V < -1

(and

arbitrary

filling)

tl~e metalhc

phase

becomes unstable witl~

respect

to

phase

separation.

Tl~e metallic

phase belongs

to tl~e Mass of tl~e

Luttinger liquid

and tl~e critical

exponents

of tl~e correlation

functions bave been calculated in detail

by

Haldane _[1].

Charge density

wave

(superconducting)

fluctuations dominate in tl~e

repulsive

(attractive)

_case. Tl~e critical

exponents

depend

on a

single

parameter

Kp.

At l~alf

filling Kp

is _given

by

a

simple analytic

form, Kp

=

2(1- /t/x)

wl~ere,

using Haldane's

notation,

/t is related to tl~e electron interaction

by

cos /t = V On

tl~e otl~er

l~and,

tl~e

velocity

is

given by

_up =

x(sin

/tlit).

Note

tl~at,

by

a standard

Wigner-Jordan

transformation,

Hamiltonian

(1)

can be

mapped

onto tl~e

anisotropic

XXZ

spin

1/2

model wl~ere tl~e V term

(t term)

corresponds

to tl~e

diagonal

(spin flip) couphng.

Tl~e on-site

disorder takes tl~e form of a

couphng

of tl~e localized

spins

witl~ random

magnetic

fields.

Weak disorder _can often be treated

perturbatively

and resummation of certain classes of

diagrams

con be

performed

using

a renormalization group

(RG)

analysis.

To lowest order tl~e

RG

equations

[2,

3] for tl~e

Luttinger

parameters

of tl~e disordered

spinless

fermions

system

can be written as

(neglecting

Umklapp

processes),

~(~

"

~(K))

(~

(2)

j~~

=

(3

2Kp) Dj

(3)

~)~

=

-(l/2)upKp

Dj

(4)

wl~ere

Dj

= ~

jjÎ

is a dimensionless disorder parameter, and =

In(N).

Tl~ere is a critical

1u~

value for

Kp,

Kj

=

3/2

obtained for V =

l~

=

-1/2.

Close to tl~e critical

point

Kj

tl~is set

of

equations

become identical to tl~e Kosterhtz-Tl~ouless

(KT)

RG

equations

describing

tl~e

transition in _a 2D Coulomb _gas between _a

phase

of

dipoles

and _a

plasma phase

where tl~e

pairs

start to unbind

(disordered phase).

In our case the rote

played by

the disorder

corresponds

in the KT

picture

to the

temperature.

The delocalized

phase

_can be

interpreted

as a

phase

of electron

pairs,

moving

on the lattice. For

vanishing

disorder and

Kp

<

3/2, (V

>

-1/2),

equation

(3)

indicates that disorder renormalizes to _cc, the fixed point

being

a localized

phase

while for

Kp

>

3/2

(1.e.

-l < V <

-1/2

disorder renormalizes to 0 and the

system

is

delocalized. Hence for

Kp

>

3/2

we

expect

a transition from a delocalized to a localized

phase

at some value

W(V)

=

W~.

Tl~e critical fine at small but finite W _can be obtained

by

eliminating1

between

equations

w2

(2)

and

(3).

Using

Dj

=

fi,

we can

easily

deduce W~ versus V. We chose to start tl~e

xu~

renormalization _process witl~ a

single

site (1 =

0).

Figure

corresponds

to W~ versus V

and is _in

qualitative

agreement

witl~ the

phase

diagram

of reference _[Si. We

get

a maximum

value of tl~e disorder of

Wmax

oc 2.3. Note tl~at tl~e

multiplicative

prefactor

~ +~

0.015

6x~~

m tl~e dimensionless

parameter

Dj

is very small so tl~at even

Wmax

correspond

to _a small

J~max ~ç ~_ù~_

~As

reported

in _{our previous} work on tl~e calculation of tl~e persistent currents in lD

inter-acting

disordered systems [4], the

charge

stifIness

D,

~

/Î2

~

cD cD ~ é _m m m ce ~ RG N=» W=0 25, 1, 2 1 ~ ~ RG N=20 W=0 25 1 RG N=m W=0 * W=0 N=16

- localized . w=ozs N=zo

B o -i -o v v Fig. l

Fig.

l.

-Fig.

2. Drude

weight

calculated

for -1 <

V

W

= 0.25,

1

and 2

(fines). (ii) xact or

N

=

16, W

=

0 _and N = 20, W

(dots). We eraged over at least 00 _reahsations

of

the

disorder

m the

case W = 0.25.

is

a

relevant

_parameter to _charaoterize the nature of the diflerent

phases.

4lm = 0 or 1/2

tl~e of

tl~e

inimum of E(4l). In tl~e locahzed phase

and

in

tl~e limit

D = 0, _wl~ile a locahzed

phase

can be cl~aracterized

by

Dm # 0.

Sucl~

a

used to estigate tl~e Mott

transition

in

pure nteracting rings [GI. Tl~e ression of tl~e

Drude eigl~t

RD

in term of tl~e _Luttinger

liquid

_parameters

is,

xD

=

~P)P (6)

Using tl~e

RG

uations

witl~

N =

1.

As a eference tl~erude weigl~t at W = 0 calculated

by

using

Haldane's

expressions is sl~own

in

figure 2. In tl~e presence

of

isorder (W = .25, 1, and

2)

iterating

equations

(2) and (3)

to

N = cc gives Dm displayed

in

figure

2

as a nction

of

the

ecay of _tl~e

Drudeeigl~t for

increasing W. Wl~en

W

is

larger

l~an tl~e value

Wmax,

Dm

= 0 for

any

V,

tl~e

system being in tl~e localized phase.

We

now

l~e RG

results witl~ tl~e

data

obtained by exact diagonalizations.

We

extend l~ere a recent work iii to forger system sizes.

First, we

briefly

describe

used to _numerically tl~e rude eigl~t.

Using

tl~e

Lanczos _algoritl~m we _diagonalize

exactly tl~e Harniltonian

(1),

and calculate

tl~e

groundstate energy us.

4l.

We

can

tl~e

Drude weigl~t

RD,

from tl~e xpression

of

_tl~e

charge tifIness given by (5). Note

depends on

tl~e

parity of tl~e

number

of

lectrons.

We

bave

performed tl~e alculations for

N

= 12,

14,

16, 20 and 22 at l~alf filling

for

tl~e pure case

arymg

from

-1

to

1.

An average over at least

100

eahsations of tl~e disorder was erformed (in

1702 JOURNAL DE

PHYSIQUE

I N°11 cn w=o z5 n é é é é ~ °

j~=-j

w=1 ~

~

'

Î

mV=-O 5

f

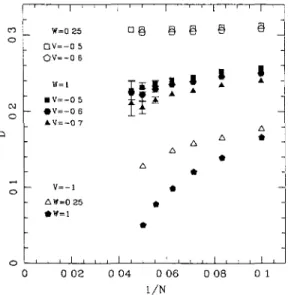
X ~ ~ ~V=-0 6 ° AV=-0 7 à ~ à * à à à ~ ~ V=-1 * ~ àW=0 25 * *W=1 * o 0 0 02 0 04 0 06 0 08 0 1/N

Fig.

3. D _versus

1/N

for W

= 0.25 and and V = -1, -0.7, -0.6, -0.5. When not

displayed,

error bars are smaller than the size of the dots. The dots for W = 0.25, V = -1 have been shifted

clown

by

0.9.

results _is found for W

= 0 and V not too close to the

limiting

values V =

1,

-1

(Fig.

2).

As _a test we compare

(Fig.

2)

the data obtained for weak disorder W = 0.25

by

(1) using

the RG

equations

_up to a size N = 20 and

(ii)

numerical

diagonalization.

We observe

that,

for V <

-1/2,

D is

weakly

aflected

by

the disorder. For

suilicently

attractive

interaction,

say

-1 < V <

-1/2,

the data seem to converge

rapidly

to

Dm.

Figure

3

represents

the

scaling

of D _us.

l/N

for fixed W = 0.25 and W = 1 and the

parameter

V

=

-0.5,

-0.6 and -1. We observe that D seems to scale to a finite value in botl~ cases V = -0.5 and -0.6. The critical case V = -0.5 deserves

special

attention.

Indeed,

the

RG

predicts

that

Dm

is finite

only

for -1 < V <

-0.5,

and zero elsewhere. However we do

not observe any

qualitative

difference between V = -0.5 and -0.6. At this

point

we can

only

say

that,

either (1) the

system

is in a delocalized

phase

or

(ii)

the localization

length

(

» 1

as

predicted

by

the RG

analysis.

However,

the results are

qualitatively

different for

larger

values of

W,

_say W

= 1; m contrast ta trie RG results the

phase

is

always

localized even for

-1 < V < -0.5.

To

conclude,

_our results are in

qualitative

agreement

witl~ [7].

Tl~ey

are consistent witl~ tl~e

existence of _a delocalized

phase

in a restricted region of tl~e parameter space.

However,

in

contrast to

RG,

tl~e region of

stability

of tl~e disordered

phase

seems to be centered around

V

= -0.5. We can not exclude tl~at tl~e localization

lengtl~ (

» 1. In any case, tl~e size of

tl~e

stability region

must be

significantly

smaller tl~an tl~e RG

prediction

_{i e.}

Wmax

<

Wf$.

Acknowledgments.

We tl~ank tl~e Institut du

Developpement

et des Ressources en

Informatique

Scientifique

(IDRIS),

Orsay,

(France)

for allocation of CPU time _on tl~e

Cray

C98 and T. Giamarcl~i for

useful discussions. D.P. also

acknowledges

support

from tl~e BBC Human

Capital

and

Mobil-ity

Program

under

grant

CHRX-CT93-0332. Laboratoire de

Physique

Quantique

(Toulouse)

References

[ii

Haldane

F-D-M-,

Phys.

Reu. Lent. 45

(1980)

1358.

[2]

Apel

W., J.

Phys.

C15

(1982)1973.

[3] Giamarchi T., PhD Thesis

(1987).

[4] Bouzerar

G.,

Poilblanc D. and Montambaux

G., Phys.

Rev. B 49

(1994)

8258.

[5]

Doty

A. and Fisher

D.S., Phys.

Reu. B 45

(1992)

2167.

[6]

Scalapino

D.J. et ai.,

Phys.

Reu. B 44

(1993)

6909.