Detuning effects in the one-photon mazer

Detuning effects in the one-photon mazer

Thierry Bastin*and John Martin†

Institut de Physique Nucle´aire, Atomique et de Spectroscopie, Universite´ de Lie`ge au Sart Tilman, Baˆtiment B15, B-4000 Lie`ge, Belgium

共Received 26 December 2002; published 27 May 2003兲

The quantum theory of the mazer in the nonresonant case共a detuning between the cavity mode and the atomic transition frequencies is present兲 is described. The generalization from the resonant case is far from being direct. Interesting effects of the mazer physics are pointed out. In particular, it is shown that the cavity may slow down or speed up the atoms according to the sign of the detuning and that the induced emission process may be completely blocked by use of a positive detuning. It is also shown that the detuning adds a potential step effect not present at resonance and that the use of positive detunings defines a well-controlled cooling mechanism. In the special case of a mesa cavity mode function, generalized expressions for the reflection and transmission coefficients have been obtained. The general properties of the induced emission probability are finally discussed in the hot, intermediate, and cold atom regimes. Comparison with the resonant case is given.

DOI: 10.1103/PhysRevA.67.053804 PACS number共s兲: 42.50.Pq, 42.50.Ct, 42.50.Vk, 32.80.Lg

I. INTRODUCTION

The interaction of cold atoms with microwave high-Q cavities共a cold atom micromaser兲 has recently attracted in-creasing interest since it was demonstrated by Scully et al. 关1兴 that this interaction leads to a new type of induced emis-sion inside the cavity. The new emisemis-sion properties arise from the necessity to treat quantum mechanically the center-of-mass motion of the atoms interacting with the cavity. To insist on the importance of this quantization, usually defined along the z axis, the system was called a mazer 共for micro-wave amplification via z-motion-induced emission of radia-tion兲. The complete quantum theory of the mazer was de-scribed in a series of three papers by Scully and co-workers 关2–4兴. The theory was written for two-level atoms interact-ing with a sinteract-ingle mode of the high-Q cavity via a one-photon transition. In particular, it was shown that the induced emis-sion properties are strongly dependent on the cavity mode profile. Results were presented for the mesa, sech2, and sinu-soidal modes. Retamal et al.关5兴 later refined these results in the special case of the sinusoidal mode, and a numerical method was proposed by Bastin and Solano 关6兴 for effi-ciently computing the mazer properties with arbitrary cavity field modes. Lo¨ffler et al. 关7兴 showed also that the mazer may be used as a velocity selection device for an atomic beam. The mazer concept was extended by Zhang et al. 关8–10兴, who considered two-photon transitions 关8兴, and three-level atoms interacting with a single cavity 关9兴 and with two cavities关10兴. Collapse and revival patterns with a mazer have been computed by Du et al. 关11兴. Arun et al. 关12,13兴 studied the mazer with bimodal cavities and Agarwal and Arun 关14兴 demonstrated resonant tunneling of cold at-oms through two mazer cavities.

In all these previous studies, the mazer properties were always presented in the resonant case where the cavity mode frequency␻ is equal to the atomic transition frequency␻0.

When three-level atoms were considered, a generalized reso-nant condition was assumed 关9,10,12兴. In this paper, we re-move this restriction and establish the theory of the mazer in the nonresonant case (␻⫽␻0) for two-level atoms.

The paper is organized as follows. In Sec. II, the Hamil-tonian modeling the mazer in the nonresonant case is pre-sented. The wave functions of the system are described and generalized expressions for the reflection and transmission coefficients in the special case of the mesa mode function are derived. The properties of the induced emission probability when a detuning is present are then discussed in Sec. III. Three regimes of the mazer are considered 共hot, intermedi-ate, and cold兲. A brief summary of our results is finally given in Sec. IV.

II. MODEL A. The Hamiltonian

We consider a two-level atom moving along the z direc-tion on the way to a cavity of length L. The atom is coupled unresonantly to a single mode of the quantized field present in the cavity. The atomic center-of-mass motion is described quantum mechanically and the usual rotating-wave approxi-mation is made. We thus consider the Hamiltonian

H⫽ប␻0␴†␴⫹ប␻a†a⫹ p 2

2m⫹បgu共z兲共a

†_␴⫹a␴†_{兲, 共1兲}

where p is the atomic center-of-mass momentum along the z axis, m is the atomic mass, ␻0 is the atomic transition fre-quency,␻ is the cavity field mode frequency,␴⫽兩b

典具

a兩 (兩a

典

and 兩b

典

are, respectively, the upper and lower levels of the two-level atom兲, a and a† are, respectively, the annihilation and creation operators of the cavity radiation field, g is the atom-field coupling strength, and u(z) is the cavity field mode function. We denote in the following the detuning ␻ ⫺␻0by␦, the cavity field eigenstates by兩n

典

, and the global state of the atom-field system by兩␺(t)

典

.

*Electronic address: T.Bastin@ulg.ac.be

B. The wave functions We introduce the orthonormal basis

兩⌫n⫹共␪兲

典

⫽cos␪兩a,n

典

⫹sin␪兩b,n⫹1

典

,

兩⌫n⫺共␪兲

典

⫽⫺sin␪兩a,n

典

⫹cos␪兩b,n⫹1

典

, 共2兲 with ␪ an arbitrary parameter. The兩⌫_n⫾(␪)

典

states coincide with the noncoupled states 兩a,n

典

and兩b,n⫹1

典

when ␪⫽0 and with the dressed states when␪⫽␪n given by

cot 2␪n⫽⫺ ␦ ⍀n , 共3兲 with ⍀n⫽2g

冑

n⫹1. 共4兲

We denote as 兩⫾,n

典

the dressed states 兩⌫_n⫾(␪n)

典

. The Schro¨dinger equation reads in the z representation and in the basis共2兲 iប ⳵ ⳵t␺n,␪ ⫹ _共z,t兲⫽

冋

_⫺ ប2 2m ⳵2 ⳵z2⫹共n⫹1兲ប␻⫺ប␦cos 2_␪ ⫹បgu共z兲

冑

n⫹1 sin 2␪

册

␺n,⫹_␪共z,t兲 ⫹

冋

បgu共z兲

冑

n⫹1 cos 2␪ ⫹1 2␪ប␦sin 2

册

␺n,␪ ⫺ _{共z,t兲, 共5a兲} iប ⳵ ⳵t␺n,␪ ⫺ _共z,t兲⫽

冋

_⫺ ប2 2m ⳵2 ⳵z2⫹共n⫹1兲ប␻⫺ប␦ sin 2_␪ ⫺បgu共z兲

冑

n⫹1 sin 2␪

册

␺n,⫺_␪共z,t兲 ⫹

冋

បgu共z兲

冑

n⫹1 cos 2␪ ⫹1 2ប␦ sin 2␪

册

␺n,␪ ⫹ _{共z,t兲, 共5b兲} with ␺n,⫾␪共z,t兲⫽

具

z,⌫⫾n共␪兲兩␺共t兲

典

. 共6兲 We get for each n two coupled partial differential equa-tions. In the resonant case (␦⫽0), these equations may be decoupled over the entire z axis when working in the dressed state basis and the atom-field interaction reduces to an el-ementary scattering problem over a potential barrier and a potential well defined by the cavity 共see Ref. 关2兴兲. In the presence of detuning, this is no longer the case: there is no basis where Eqs.共5兲 would separate over the entire z axis and

the interpretation of the atomic interaction with the cavity as a scattering problem over two potentials is less evident.

Outside the cavity 共which we define to be located in the range 0⬍z⬍L), the mode function u(z) vanishes and Eqs. 共5兲 become in the noncoupled state basis (␪⫽0)

iប ⳵ ⳵t␺n a_共z,t兲⫽

冋

_⫺ ប 2 2m ⳵2 ⳵z2

册

␺n a_{共z,t兲, 共7a兲} iប ⳵ ⳵t␺n⫹1 b _共z,t兲⫽

冋

_⫺ ប 2 2m ⳵2 ⳵z2⫹ប␦

册

␺n⫹1 b _{共z,t兲, 共7b兲} with ␺n

a_{共z,t兲⫽e}i(␻₀⫹n␻)t

_具

_{z,a,n兩␺共t兲}

_典

_{, 共8a兲} ␺nb⫹1共z,t兲⫽ei(␻0⫹n␻)t

具

z,b,n⫹1兩␺共t兲

典

. 共8b兲 In Eq. 共8兲, we have introduced the exponential factor ei(␻0⫹n␻)t _{in order to define the energy scale origin at the}

兩a,n

典

level. The solutions to Eqs.共7兲 are obviously given by linear combinations of plane wave functions. If we assume initially a monokinetic atom 共with momentum បk) coming upon the cavity from the left side共negative z values兲 in the excited state兩a

典

and the cavity field in the number state兩n

典

, the atom-field system is described outside the cavity by the wave function components 共which correspond to the eigen-state 兩␾_k

典

of energy E_k⫽ប2_k2_/2m)

␺na_{共z,t兲⫽e⫺i(បk}2/2m)t_␸na_{共z兲, 共9a兲} ␺nb_{⫹1共z,t兲⫽e⫺i(បk}2/2m)t_␸n ⫹1 b _{共z兲, 共9b兲} with ␸n a_共z兲⫽

再

e ikz_⫹␳ n a e⫺ikz, z⬍0, ␶na_eik(z⫺L)_{, z⬎L,} 共10兲 ␸nb⫹1共z兲⫽

再

␳nb_⫹1 e⫺ikbz_{, z}⬍0, ␶nb⫹1eikb(z⫺L), z⬎L, 共11兲 and k_b2⫽k2⫺2m␦ ប . 共12兲 Introducing ␬2_⫽2mg ប 共13兲 we may write k_b2⫽k2⫺␬2␦ g. 共14兲

The solutions共9兲 must be interpreted as follows: The ex-cited atom coming upon the cavity will be found reflected in the upper state or in the lower state with the amplitude ␳na and␳n_⫹1

b

, respectively, or transmitted with the amplitude␶na or␶nb_⫹1. However, in contrast to the resonant case, the atom reflected or transmitted in the lower state兩b

典

will be found to propagate with a momentum បkb different from its initial value បk. The atomic transition 兩a

典

→兩b

典

induced by the cavity is responsible for a change of the atomic kinetic en-ergy. According to the sign of the detuning关see Eq. 共14兲兴, the cavity will either speed up the atom 共for ␦⬍0) or slow it down共for␦⬎0). This results merely from energy conserva-tion. When, after leaving the cavity region, the atom is passed from the excited state兩a

典

to the lower state兩b

典

, the photon number has increased by one unit in the cavity and the internal energy of the atom-field system has varied by the quantity ប␻⫺ប␻0⫽ប␦. This variation needs to be exactly counterbalanced by the external energy of the system, i.e., the atomic kinetic energy. In this sense, when a photon is emitted inside the cavity by the atom, the cavity acts as a potential step ប␦ 共see Fig. 1兲, and the atom experiences an attractive or a repulsive force according to the sign of the detuning. Similar共although not identical兲 mechanical effects are obtained under the adiabatic approximation关15兴 共requir-ing no quantum treatment of the atomic center-of-mass mo-tion兲. In this case the dressed levels may also decelerate or accelerate the atoms. However, in this regime and contrary to what is described here, the atom always leaves the cavity with the same kinetic energy 共if no dissipation process is considered兲 and the mechanical effects are not related to the emission of a photon inside the cavity.

Presently the use of positive detunings in the atom-field interaction defines a well-controlled cooling mechanism. A single excitation exchange between the atom and the field inside the cavity is sufficient to cool the atom to a desired temperature T⫽ប2k_b2/2mkB (kB is the Boltzmann constant兲 which may in principle be as low as imaginable. However, if the initial atomic kinetic energy ប2k2/2m is lower thanប␦ 共i.e., if k/␬⬍

冑

␦/g), the transition 兩a,n

典

→兩b,n⫹1

典

cannot take place共as it would remove ប␦ from the kinetic energy兲 and no photon can be emitted inside the cavity. In this case the emission process is completely blocked.

Due to this change in the kinetic energy when a photon is emitted, the reflection and transmission probabilities of the atom in the lower state 兩b

典

are given, respectively, by 共for ប2_k2_{/2m⬎ប␦)} R_nb_⫹1⫽kb k 兩␳n⫹1 b _兩2_{, 共15a兲} T_nb_⫹1⫽kb k 兩␶n⫹1 b _兩2_{. 共15b兲}

These probabilities vanish for ប2k2/2m⭐ប␦. When the atom remains in the excited state兩a

典

after having interacted with the cavity, there is no change in the atomic kinetic en-ergy and the reflection and transmission probabilities are di-rectly given by

R_na⫽兩␳na兩2, 共16a兲 T_na⫽兩␶na兩2_{. 共16b兲} To calculate any quantity related to the reflection and transmission coefficients, we must solve the Schro¨dinger equation over the entire z axis. Inside the cavity, the problem is much more complex since we have two coupled partial differential equations. In the special case of the mesa mode function关u(z)⫽1 inside the cavity, 0 elsewhere兴, the prob-lem is, however, greatly simplified. In the dressed state basis (␪⫽␪n), the Schro¨dinger equations 共5兲 take the following form inside the cavity:

iប ⳵ ⳵t␺n ⫾_共z,t兲⫽

冋

_⫺ ប2 2m ⳵2 ⳵z2⫹Vn ⫾

册

_␺ n ⫾_{共z,t兲 共17兲} with ␺n⫾_{共z,t兲⫽e}i(␻₀⫹n␻)t

_具

_{z,⫾,n兩␺共t兲}

_典

_共18兲 and

Vn⫹⫽sin2␪nប␦⫹បg

冑

n⫹1 sin 2␪n, 共19a兲

V_n⫺⫽ប␦⫺V_n⫹. 共19b兲

V_n⫹ and V_n⫺ represent the internal energies of the 兩⫹,n

典

and兩⫺,n

典

components, respectively. Except for the resonant case, they cannot be strictly interpreted as a potential barrier and a potential well as Eq.共17兲 holds only inside the cavity.

Using Eq. 共3兲, we have the well-known relations

sin␪n⫽

冑

⌳n⫹␦

冑

2⌳n , tan␪n⫽

冑

⌳n⫹␦ ⌳n⫺␦ , cos␪_n⫽

冑

⌳n⫺␦

冑

2⌳n , cot␪_n⫽

冑

⌳n⫺␦ ⌳n⫹␦ , 共20兲 with ⌳n⫽

冑

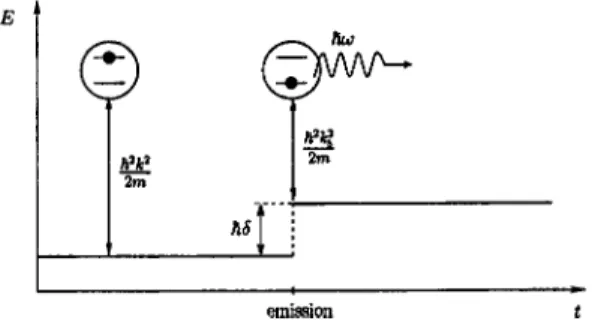
␦2⫹⍀n 2 . 共21兲

FIG. 1. Potential step effect of the cavity when a photon is emitted by the atom. E represents the total energy of the atom-field system.

We thus have

V_n⫹⫽បg

冑

n⫹1 tan␪n, 共22a兲 V_n⫺⫽⫺បg

冑

n⫹1 cot␪n. 共22b兲 The exponential factor ei(␻0⫹n␻)t _{has been introduced as}

well in Eq. 共18兲 in order to define the same energy scale inside and outside the cavity. Figure 2 illustrates the internal energies of the atom-field system over the whole z axis. The positive internal energy V_n⫹increases with positive detunings and vice versa with negative ones. For a fixed value of the incident kinetic energy Ek⫽ប2k2/2m, Vn⫹ may be switched in this way from a higher value than Ek to a lower one. For large positive 共negative兲 detunings, V_n⫹ tends to the 兩b,n⫹1

典

(兩a,n

典

) state energy.

The most general solution of Eqs. 共17兲 corresponding to the eigenstate兩␾k

典

is given by

␺n⫾共z,t兲⫽e⫺i(បk 2_/2m)t ␸n⫾共z兲 共23兲 with ␸n⫾_共z兲⫽A n ⫾_eik_n⫾z_⫹B n ⫾_e⫺ikn⫾z_, 共24兲

where A_n⫾ and B_n⫾are complex coefficients and

kn⫾2⫽k2⫺ 2m ប2 Vn ⫾_{. 共25兲} Defining ␬n⫽␬

冑

4 n⫹1, 共26兲 we have k_n⫹2⫽k2⫺␬_n2 tan␪n, 共27a兲 k_n⫺2⫽k2⫹␬_n2 cot␪n. 共27b兲

Using Eq. 共19b兲, we may also write

k_n⫺2⫽k_b2⫹␬_n2 tan␪n. 共28兲

From Eq.共2兲, we may express the wave function compo-nents of the atom-field state inside the cavity over the non-coupled state basis. We have

␺n

a_{共z,t兲⫽cos␪n␺n}⫹_{共z,t兲⫺sin␪n␺n}⫺_{共z,t兲, 共29a兲} ␺nb_{⫹1共z,t兲⫽sin␪n␺n}⫹_{共z,t兲⫹cos␪n␺n}⫺_{共z,t兲. 共29b兲} This allows us to find the wave function components of the eigenstate兩␾k

典

over the entire z axis. The relations共9兲 hold with ␸na_共z兲⫽

再

eikz_⫹␳na_{e⫺ikz, z⬍0,} ␸na_共z兲兩 C, 0⬍z⬍L, ␶na_eik(z_{⫺L), z⬎L,} 共30兲 ␸nb⫹1共z兲⫽

再

␳n⫹1 b e⫺ikbz_{, z}⬍0, ␸nb⫹1共z兲兩C, 0⬍z⬍L, ␶nb_⫹1 eikb(z⫺L)_{, z}⬎L, 共31兲 and ␸na_共z兲兩 C⫽cos␪n共An⫹e ik n ⫹_z ⫹Bn⫹e⫺ikn ⫹_z 兲 ⫺sin␪n共An⫺e ik_n⫺z_⫹B n ⫺_e⫺ikn⫺z兲, 共32a兲 ␸n⫹1 b _共z兲兩 C⫽sin␪n共An⫹e ik_n⫹z_⫹B n ⫹_e⫺ikn⫹z兲 ⫹cos␪n共An⫺eikn ⫺_z ⫹Bn⫺e⫺ikn ⫺_z 兲. 共32b兲 The coefficients␳_na,␳_nb_⫹1,␶na,␶nb_⫹1, A_n⫹, A_n⫺, B_n⫹, and B_n⫺in expressions共30兲–共32兲 are found by imposing the con-tinuity conditions on the wave function and its first deriva-tive at the cavity interfaces. A tedious calculation yields

FIG. 2. Schematic energy diagram of the atom-field system in-side and outin-side the cavity, for␦⬎0 共a兲 and␦⬍0 共b兲.

␶na_⫽ 共cos 2_␪ n兲␶n⫺共k兲/␶n⫺共kb兲␶n⫹共kb兲⫹sin2␪n␶n⫺共k兲 关共cos2_{␪n兲共k⫺k} b兲/kn c 共L兲⫺1兴关共cos2_{␪n兲共k⫺k} b兲/kn t 共L兲⫺1兴, 共33兲 ␳n a_⫽ 共cos2_␪n兲 ␶n ⫺_共k兲 ␶n

⬘

⫺_共k,k b兲 ⌬n⫹共k兲 ⌬n⫹共kb兲 ␳n⫹_共k b兲⫹

冉

1⫺共cos2␪n兲 ␶n⫹_共k b兲 ␶n

⬙

⫹共k,kb兲

冊

␳n⫺_共k兲⫹cos2␪n 4

冉

kb k⫺ k kb

冊

u_n共k兲␳n ⫺_共k兲␳ n ⫹_共k b兲 ⌬n⫺共k兲⌬n⫹共kb兲

冉

cos2_␪ n k⫺kb kn c_共L兲⫺1

冊冉

cos2␪n k⫺kb kn t_共L兲⫺1

冊

, 共34兲 ␶nb_⫹1⫽sin 2␪n 4

冉

1⫹ k kb

冊

关␶n⫺_共k兲/˜_␶ n ⫺_共k,k b兲兴␶n⫹共kb兲⫺关␶n⫹共kb兲/˜␶n⫹共k,kb兲兴␶n⫺共k兲 关共cos2_␪ n兲共k⫺kb兲/kn c_{共L兲⫺1兴关共cos}2_␪ n兲共k⫺kb兲/kn t_{共L兲⫺1兴}, 共35兲 ␳n⫹1 b _{⫽sin 2␪} n 1 2关␶n⫺共k兲/¯␶n⫺共k,kb兲兴关⌬n⫹共k兲/⌬n⫹共kb兲兴␳n⫹共kb兲⫺ 1 2关␶n⫹共kb兲/¯␶n⫹共k,kb兲兴␳n⫺共k兲⫹ 1 4共k/kb⫺1兲vn共k兲␶n⫺共k兲␶n⫹共kb兲 关共cos2_␪ n兲共k⫺kb兲/kn c_{共L兲⫺1兴关共cos}2_{␪n兲共k⫺k} b兲/kn t_{共L兲⫺1兴} , 共36兲 with un共k兲⫽sin2␪n Sn⫹⫺ sin共k_n⫹L兲sin共k_n⫺L兲⫹

冉

kn⫺kn⫹ k2 ⫺ k2 k_n⫺k_n⫹

冊

, 共37兲 vn共k兲⫽i

冉

k_n⫹ k sin共kn⫹L兲cos共kn⫺L兲 ⫺kn⫺ k sin共kn ⫺_L兲cos共k n ⫹_L兲

冊

_⫺cos 2␪n 2 Sn ⫹⫺_, 共38兲 S_n⫹⫺⫽sin共k_n⫹L兲sin共k_n⫺L兲

冉

kn ⫺ k_n⫹⫹ k_n⫹ k_n⫺

冊

⫹2关cos共kn⫺L兲cos共kn⫹L兲⫺1兴, 共39兲 and ␳n⫾_{共k兲⫽i⌬} n ⫾_{共k兲sin共k} n ⫾_L兲␶n⫾_{共k兲, 共40兲} ␶n⫾_{共k兲⫽关cos共k} n ⫾_L兲⫺i⌺ n ⫾_{共k兲sin共k} n ⫾_L兲兴⫺1_{, 共41兲} ⌺n⫾共k兲⫽ 1 2

冉

k_n⫾ k ⫹ k kn⫾

冊

, 共42兲 ⌬n⫾共k兲⫽ 1 2

冉

k_n⫾ k ⫺ k k_n⫾

冊

, 共43兲 ␶n

⬘

⫾_共k,k b兲⫽

冋

cos共kn⫾L兲⫺i kb k ⌺n ⫾_{共k兲sin共k} n ⫾_L兲

册

⫺1_, 共44兲 ␶n

⬙

⫾_共k,k b兲⫽

冋

cos共kn⫾L兲⫺i k k_b⌺n⫾共k兲sin共kn⫾L兲

册

⫺1 , 共45兲 ␶ ˜ n ⫾_共k,k

b兲⫽关cos共kn⫾L兲⫺i⌺˜n⫾共k,kb兲sin共kn⫾L兲兴⫺1, 共46兲

␶ ¯ n ⫾_共k,k b兲⫽

冋

cos共kn⫾L兲⫺i k⫹kb 2k_b ⌺n⫾共k兲sin共kn⫾L兲

册

⫺1 , 共47兲 ⌺˜n⫾共k,kb兲⫽

冉

k_n⫾ k⫹kb⫹ k_b k⫹kb k kn⫾

冊

, 共48兲

k_nc共L兲⫽i„k⫹i cot共kn ⫺_L/2兲k n ⫺_…„k b⫹i cot共kn⫹L/2兲kn⫹… cot共k_n⫺L/2兲k_n⫺⫺cot共k_n⫹L/2兲k_n⫹ , 共49兲 k_nt共L兲⫽i„k⫺i tan共kn

⫺_L/2兲k n ⫺_…„k b⫺i tan共kn⫹L/2兲kn⫹… tan共k_n⫹L/2兲k_n⫹⫺tan共k_n⫺L/2兲k_n⫺ . 共50兲 At resonance,␦⫽0, ␪n⫽␲/4, kb⫽k, ␶n⫾(k)⫽␶n

⬘

⫾(k,kb) ⫽␶

⬙

n⫾(k,kb)⫽˜␶⫾n(k,kb)⫽¯␶n⫾(k,kb), and the reflection and transmission coefficients reduce to the well-known results 共see Ref. 关2兴兲 ␶na_⫽1 2共␶n ⫹_⫹␶n⫺_{兲, 共51a兲} ␳n a_⫽1 2共␳n ⫹_⫹␳n⫺_{兲, 共51b兲} and

␶nb⫹1⫽ 1 2共␶n ⫹_⫺␶n⫺_{兲, 共52a兲} ␳n⫹1 b _⫽1 2共␳n⫹⫺␳n⫺兲. 共52b兲

III. INDUCED EMISSION PROBABILITY

The induced emission probability of a photon inside the cavity is given by Pem共n兲⫽Rn⫹1 b _⫹T n⫹1 b . 共53兲

According to Eqs.共15兲, this probability may be written as

Pem共n兲⫽

再

k_b k 关兩␳n⫹1 b _兩2_⫹兩␶n ⫹1 b _兩2_{兴 if} k ␬⬎

冑

␦ g , 0 otherwise. 共54兲

We distinguish three regimes determined by the incident kinetic energy of the atom compared with the internal energy Vn⫹ 共see Fig. 2兲: the hot atom regime 共when kⰇ␬n

冑

tan␪n and kb is approximated to k), the intermediate regime (k ⬇␬n

冑

tan␪n), and the cold atom regime (kⰆ␬n

冑

tan␪n). In comparison with the resonant case, the detuning defines an additional parameter that fixes the working regime of the system.

A. Hot atom regime

In the hot atom regime, the kinetic energy is much higher than the energies V_n⫾ and the atoms are always transmitted through the cavity. For the mesa mode, the atomic momen-tum inside the cavity is given by

បkn⫹⯝បk

冉

1⫺ ␬n 2 2k2tan␪n

冊

, 共55a兲 បkn⫺⯝បk

冉

1⫹ ␬n 2 2k2cot␪n

冊

. 共55b兲 After the atom-field interaction, the global state of the system reduces to 兩␺共t兲

典

⫽

冕

dz␺共z,t兲共cos␪_ne⫺i(␬n 2 L/2k)tan␪_n兩z,⫹,n

_典

⫺sin␪nei(␬n 2_L/2k)cot␪ n兩z,⫺,n

典

₎ 共56兲 with

␺共z,t兲⫽eikz_e⫺i(បk2/2m)t_{. 共57兲}

The induced emission probability is thus given by

Pem共n兲⫽円

具

z,b,n⫹1兩␺共t兲

典

円2 ⫽sin 2_共2␪ n兲 4 兩e ⫺i(␬n 2 L/2k)tan␪_n ⫺ei(␬_n2L/2k)cot␪_n兩2_{. 共58兲}

Using Eq. 共20兲 we get straightforwardly

Pem共n兲⫽

冋

1⫹

冉

␦ ⍀n

冊

2

册

⫺1 sin2

冉

␶ 2

冑

⍀n 2_⫹␦2

冊

_{, 共59兲} where␶⫽mL/បk is the classical transit time of the thermal atoms through the cavity.

Equation 共59兲 is exactly the classical expression of the induced emission probability of an atom interacting with a single mode during a time ␶. We recover the well-known Rabi oscillations in the general case where the field and the atomic frequencies are detuned by the quantity␦.

B. Intermediate regime

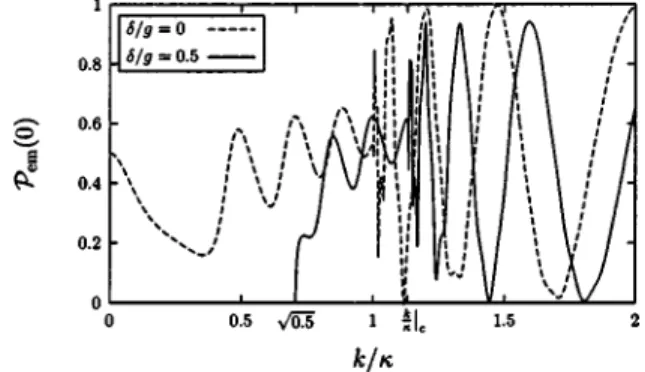
The frontier between the cold atom and the hot atom re-gime appears when the atomic kinetic energy becomes equal to the positive energy Vn⫹ inside the cavity, i.e., when the ratio k/␬n is equal to the critical value

k ␬n

冏

_c ⫽

冑

tan␪_n⫽

冉

冑

共␦/g兲 2_{⫹4共n⫹1兲⫹␦/g}

冑

共␦/g兲2⫹4共n⫹1兲⫺␦/g

冊

1/4 . 共60兲

At resonance, this frontier occurs for k/␬n⫽1. This condi-tion changes significantly when the cavity and the atomic transition are detuned. This is well illustrated in Fig. 3, which shows the induced emission probability as a function of k/␬ at resonance and for a positive value of the detuning. In the second case, the regime change occurs for a larger value of k/␬ than one. Please notice also that the induced emission probability vanishes for k/␬⬍

冑

␦/g according to Eq. 共54兲.

Equation共60兲 may be inverted to yield a critical detuning when working with a fixed value of k/␬. We get

FIG. 3. Induced emission probabilityPem(n⫽0) with respect to

␦ g

冏

_c⫽

冑

n⫹1

冋冉

k ␬n

冊

2 ⫺

冉

_␬nk

冊

⫺2

册

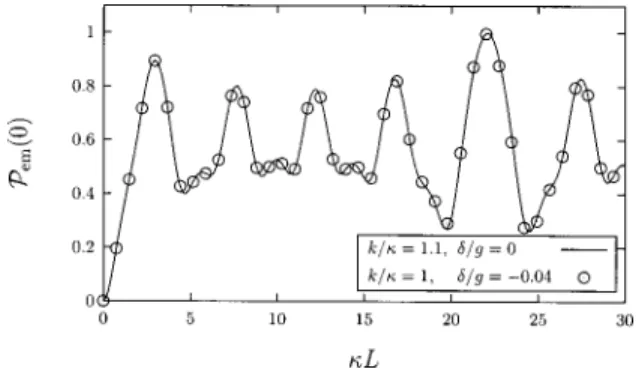
. 共61兲 Figure 4 illustrates the induced emission probability as a function of the detuning for k/␬ slightly greater than 1. At resonance, the system is on the hot atom regime side as the atomic kinetic energy is greater than the internal energy V_n⫹. When the detuning is increased, V_n⫹is increased as well and becomes greater than the kinetic energy 关see Fig. 2共a兲兴, switching the system toward the cold atom regime. This therefore could define a convenient way to switch from one regime to the other rather than by varying the incident atomic momentum.

A similar effect of the detuning is presented in Fig. 5 which presents the induced emission probability with respect to the interaction length in the intermediate regime. It ap-pears clearly there that working with a negative detuning is similar to working with hotter atoms at resonance. This re-sults merely from the level of V_n⫹compared to the incident

kinetic energy, which is identical in both cases considered in Fig. 5.

From all these situations, we conclude that a detuning variation has an identical effect as a change of the kinetic energy of the incoming atoms, confirming that the only im-portant parameter of the system in the intermediate regime is the actual value of the V_n⫹ energy in comparison with the kinetic energy ប2k2/2m.

C. Cold atom regime

In the cold atom regime (k/␬nⰆ

冑

tan␪n), the induced emission probability exhibits a completely different behav-ior. We have in this regime for兩␦兩/⍀nⰆ1, exp(␬nL)Ⰷ1, and ␬nLⰆ(␬n/k)2,

Pem共n兲⫽

B共L兲

2

1⫹关共cot␪n兲/2兴sin共2␬n

冑

cot␪nL兲 1⫹共␬n/2k兲2 cot␪nsin2共␬n

冑

cot␪nL兲

, 共62兲 with B共L兲⫽kb k 1 兩共cos2_␪ n兲共k⫺kb兲/kn c_{共L兲⫺1兩}2_兩共cos2_␪ n兲共k⫺kb兲/kn t_{共L兲⫺1兩}2. 共63兲

At resonance, this expression simplifies to

Pem共n兲⫽ 1 2 1⫹ 1 2 sin共2␬nL兲 1⫹共␬n/2k兲2 sin2共␬nL兲 共64兲 and the results of Meyer et al.关2兴 are well recovered. Figure 6 illustrates the induced emission probability 共62兲 with re-spect to the interaction length ␬L for various values of the detuning. The curves present a series of peaks where the induced emission probability is optimum. The detuning af-fects the peak position, amplitude, and width. Similarly to the resonant case, the curves still look like the Airy function of classical optics 关1⫹F sin2(⌬/2)兴⫺1 with finesse F and total phase difference⌬, even if the structure of Eq. 共62兲 has

become complicated with the factorB(L). In fact, this equa-tion is extremely well fitted in its domain of validity by the function Pem共n兲⫽ 2kb/k 共1⫹kb/k兲2 1⫹12 sin共2␬n

冑

cot␪nL兲 1⫹关␬n/共kb⫹k兲兴2 sin2共␬n

冑

cot␪nL兲 . 共65兲 1. Peak position

The induced emission probability is optimum when

␬n

冑

cot␪nL⫽m␲ 共m a positive integer兲. 共66兲

FIG. 4. Induced emission probabilityPem(n⫽0) with respect to

␦/g in the intermediate regime (k/␬⫽1.01). The interaction length was fixed to␬L⫽100.

FIG. 5. Induced emission probabilityPem(n⫽0) with respect to

the interaction length␬L in the intermediate regime. Comparison of a detuning variation with a change of the atomic kinetic energy.

This occurs when the cavity length fits a multiple of one-half the de Broglie wavelength␭_dBof the atom inside the cavity:

L⫽m␭dB

2 . 共67兲

Indeed, in the cold atom regime, only the 兩⫺,n

典

compo-nent propagates inside the cavity with the de Broglie wave-length ␭dB⫽ 2␲ k_n⫺⯝ 2␲ ␬n

冑

cot␪n. 共68兲 Inserting Eq.共68兲 into Eq. 共67兲 gives the condition 共66兲.

2. Peak amplitude

The peak amplitude of the induced emission probability

Pem(n) is given by A⬅B共L⫽m␭dB/2兲 2 ⯝ 1 2 4kb/k 共1⫹kb/k兲2 . 共69兲

We illustrate this amplitude in Fig. 7 as a function of the detuning␦. In contrast to the hot atom regime关see Eq. 共59兲兴, the curves present a strong asymmetry with respect to the sign of the detuning. This results from the potential stepប␦ 共see Sec. II兲 experienced by the atoms when they emit a photon. For cold atoms whose energy is similar to or less

than the step height, the sign of the step is a crucial param-eter. According to Eq.共54兲, the induced emission probability drops down very rapidly to zero for positive detunings, in contrast to what happens for negative detunings.

It is also interesting to note that the peak amplitude共69兲 is equal to the amplitude at resonance (1/2) times the factor (4kb/k)/(1⫹kb/k)2 that corresponds exactly to the trans-mission factor of a particle of momentum បk through a po-tential stepប␦. This is an additional argument to say that the use of a detuning adds a potential step effect for atoms emit-ting a photon inside the cavity共see Fig. 1兲.

3. Peak width

The peak width is determined by the finesse 关␬n/(kb ⫹k)兴2_{. Positive detunings increase the finesse (k}

b⬍k) while negative ones decrease it (kb⬎k).

4. Large detunings

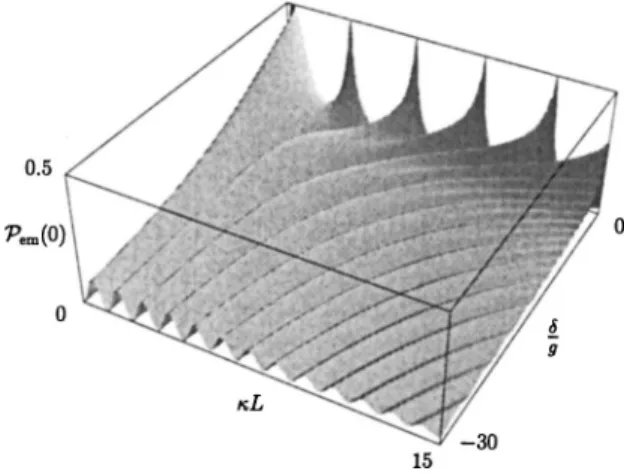
For large detunings, Eq. 共62兲 is no longer valid and the induced emission probability must be computed using the general relation共54兲. We present in Fig. 8 Pem(0) as a func-tion of the detuning and the interacfunc-tion length␬L. The varia-tion of the resonance posivaria-tions with respect to the detuning is very clear in this figure. It is interesting to note that one resonance out of two disappears when increasing the detun-ing toward negative values. Also, the induced emission prob-ability does not decrease monotonically with the detuning 共especially for small interaction lengths兲. This effect is strictly limited to the cold atom regime as for hot atoms the Rabi oscillation amplitudes always decrease when larger and larger detunings are used 关see Eq. 共59兲兴.

The use of large negative detunings in the cold atom re-gime is not limitless. As ⫺␦ increases, the internal energy V_n⫹ decreases关see Fig. 2共b兲兴 and may finally become lower than the incident kinetic energy. To keep the system in the cold atom regime, we must have for k/␬nⰆ1 关see Eq. 共61兲兴

⫺␦_g⬍

冑

n⫹1

冉

␬n k

冊

2

. 共70兲

FIG. 6. Induced emission probabilityPem(n⫽0) with respect to

the interaction length ␬L in the cold atom regime (k/␬⫽0.1) and for various values of the detuning.

FIG. 7. AmplitudeA of the resonances with respect to␦/g for two values of k/␬ in the cold atom regime.

FIG. 8. Induced emission probabilityPem(n⫽0) with respect to the interaction length␬L and␦/g共for k/␬⫽0.1).

This condition is well respected in Fig. 8 as the limiting lower value of ␦/g to keep the system in the cold atom regime is⫺100 for k/␬⫽0.1.

The use of large positive detunings in the cold atom re-gime is not possible as the induced emission probability van-ishes for ␦ g⭓

冉

k ␬

冊

2 . 共71兲 IV. SUMMARY

In this paper we have presented the quantum theory of the mazer in the nonresonant case. Interesting effects have been pointed out. In particular, we have shown that the cavity may slow down or speed up the atoms according to the sign of the detuning and that the induced emission process may be com-pletely blocked by use of a positive detuning. We have also demonstrated that the detuning adds a potential step effect not present at resonance. This defines a well-controlled

cool-ing mechanism for positive detuncool-ings. In the special case of the mesa mode function, generalized expressions for the re-flection and transmission coefficients have been obtained. The properties of the induced emission probability in the presence of a detuning have been discussed. In the cold atom regime, we have obtained a simplified expression for this probability and have been able to describe the detuning ef-fects on the resonance amplitude, width, and position. In contrast to the hot atom regime, we have shown that the mazer properties are not symmetric with respect to the sign of the detuning. In the intermediate regime, the use of detun-ing could be a convenient way to switch from the hot atom regime to the cold atom one.

ACKNOWLEDGMENTS

This work has been supported by the Belgian Institut In-teruniversitaire des Sciences Nucle´aires共IISN兲. T.B. wants to thank H. Walther and E. Solano for their hospitality at Max-Planck-Institut fu¨r Quantenoptik, Garching 共Germany兲.

关1兴 M.O. Scully, G.M. Meyer, and H. Walther, Phys. Rev. Lett. 76, 4144共1996兲.

关2兴 G.M. Meyer, M.O. Scully, and H. Walther, Phys. Rev. A 56, 4142共1997兲.

关3兴 M. Lo¨ffler, G.M. Meyer, M. Schro¨der, M.O. Scully, and H. Walther, Phys. Rev. A 56, 4153共1997兲.

关4兴 M. Schro¨der, K. Vogel, W.P. Schleich, M.O. Scully, and H. Walther, Phys. Rev. A 56, 4164共1997兲.

关5兴 J.C. Retamal, E. Solano, and N. Zagury, Opt. Commun. 154, 28共1998兲.

关6兴 T. Bastin and E. Solano, Comput. Phys. Commun. 124, 197 共2000兲.

关7兴 M. Lo¨ffler, G.M. Meyer, and H. Walther, Europhys. Lett. 41, 593共1998兲.

关8兴 Z.-M. Zhang, Z.-Y. Lu, and L.-S. He, Phys. Rev. A 59, 808 共1999兲.

关9兴 Z.-M. Zhang and L.-S. He, Opt. Commun. 157, 77 共1998兲. 关10兴 Z.-M. Zhang, S.-W. Xie, Y.-L. Chen, Y.-X. Xia, and S.-K.

Zhou, Phys. Rev. A 60, 3321共1999兲.

关11兴 Si-de Du, Lu-wei Zhou, Shang-qing Gong, Zhi-zhan Xu, and Jing Lu, J. Phys. B 32, 5645共1999兲.

关12兴 R. Arun, G.S. Agarwal, M.O. Scully, and H. Walther, Phys. Rev. A 62, 023809共2000兲.

关13兴 R. Arun and G.S. Agarwal, Phys. Rev. A 66, 043812 共2002兲. 关14兴 G.S. Agarwal and R. Arun, Phys. Rev. Lett. 84, 5098 共2000兲. 关15兴 S. Haroche, M. Brune, and J.M. Raimond, Europhys. Lett. 14,