ETUDE ET MODELISATION DE CAPTEURS EN CND PAR COURANTS DE FOUCAULT : APPLICATION A LA DETECTION DES FISSURES

(1)

Mémoire présenté en vue de l‟obtention

Du diplôme de

Magister

Option

Electricité industrielle

ETUDE ET MODELISATION DE CAPTEURS EN

CND PAR COURANTS DE FOUCAULT :

APPLICATION A LA DETECTION DES FISSURES.

Présenté par :

Ala-Eddine LAKHDARI

Soutenu publiquement le ………

/2011

Devant le jury composé de :

Salah Eddine ZOUZOU Professeur Président Université de Biskra Ahmed CHERIET MCA Directeur de mémoire Université de Biskra Souri Mohamed MIMOUNE Professeur Examinateur Université de Biskra Rabia MEHASNI MCA Examinateur Université de Constantine

تٛبؼشنا تٛطازمًٚذنا تٚزئاشجنا تٚرًٕٓجنا

République Algérienne Démocratique et Populaire

ًٙهؼنا ثحبنا ٔ ٙناؼنا ىٛهؼتنا ةراسٔ

Ministère de l‟enseignement supérieur et de la recherche scientifique

Université Mohamed Khider – Biskra Faculté des Sciences et de la Technologie Département : Génie Electrique

Ref :………

ةزكسب زضٛخ ذًحي تؼياج

اٛجٕنُٕكتنا ٔ وٕهؼنا تٛهك

مسق

:

ةيئابرهكلا ةسدنهلا

عجرملا

:

………

(2)

Remerciements

Ce travail a été réalisé au sein du Laboratoire de Génie Electrique de Biskra (LGEB), département de génie électrique, Faculté des Sciences et de la Technologie, Université de Biskra.

Je voudrais tout d‟abord exprimer ma profonde gratitude à mon directeur de mémoire Monsieur Ahmed CHERIET, Maître de Conférences classe A à l‟Université de Biskra, pour la confiance qu‟il m‟a accordée en acceptant de diriger mes recherches. Il m‟a appris la méthode des volumes finis et plusieurs choses pendant la réalisation de ce travail.

Je tiens à adresser mes plus sincères remerciements aux membres du jury :

Je remercie Monsieur Salah Eddine ZOUZOU, Professeur, directeur du laboratoire LGEB, qui m‟a fait l‟honneur de présider le jury de ma soutenance.

Monsieur Souri Mohamed MIMOUNE, Professeur à l‟Université de Biskra, pour avoir accepté de juger ma thèse.

Monsieur Rabia MEHASNI, Maître de Conférences classe A à l‟Université de Constantine, pour avoir accepté d‟être membre dans mon jury.

Mes remerciements vont aussi à tous les membres des laboratoires LGEB et LMSE. Egalement à l‟ensemble du personnel du département de génie électrique de l'université de Biskra en particulier Madame M. SAADI, secrétaire du laboratoire LGEB, pour son aide.

Enfin, je tiens également à remercier toute personne ayant participé de prés ou de loin à la réalisation de ce travail.

(3)

Dédicaces

A mes parents, A ma sœur

A ma famille, A mes amis

(4)

Table de matières

Liste des figures viii

Liste des tableaux xi

Introduction générale 2

Chapitre I : Concepts généraux sur les techniques de contrôle non destructif

I.1. Introduction 7

I.2. Généralités sur le contrôle non destructif 7

I.2.1. Principe 7

I.2.2. Les différents défauts détectés en CND 8

I.2.2.1. Les défauts surfaciques 8

I.2.3. Procédure de CND 9

I.3. Les techniques de contrôle non destructif 9

I.3.1. Examen visuel 9

I.3.2. Ressuage 11

I.3.3. Essais ultrasonores 11

I.3.4. Contrôle par Laser 12

I.3.5. Radiographie 13

I.3.6. Magnétoscopie 14

I.3.7. Courants de Foucault 15

I.3.8. Thermographie 16

I.3.9. Thermo-inductive 18

I.4. Conclusion 19

Chapitre II : Les capteurs inductifs

II.1. Introduction 22

II.2. Les courants de Foucault 22

II.3. Principe des capteurs inductifs 23

II.4. Les formes d‟enroulements des capteurs inductifs 23

II.5. Différents types des capteurs inductifs 24

II.5.1. Capteur absolu 24

II.5.2. Capteur double 24

II.5.3. Capteur différentiel 26

II.5.4. Capteur multiple 26

(5)

II.7.2. Deuxième disposition : capteurs internes 29

II.7.3. Troisième disposition : capteurs ponctuels 29

II.8. Modes d‟excitation 30

II.9. Densité du courant et profondeur de pénétration dans la cible 30 II.9.1. Propagation du champ magnétique dans un milieu conducteur 30

II.9.2. Densité du courant 34

II.9.3. Profondeur de pénétration 35

II.10. Impédance du capteur 35

II.10.1. Impédance normalisée 35

II.10.2. Impédance généralisée 37

II.11. Principaux paramètres influant le contrôle 38

II.12. Conclusion 39

Chapitre III : Modélisation du problème électromagnétique

III.1. Introduction 41

III.2. Equations de maxwell et lois de comportement 41

III.3. Conditions de transmission et conditions aux limites 42

III.3.1. Conditions de transmission 42

III.3.2. Conditions aux limites 43

III.3.3. Diagramme de Tonti 43

III.4. Formulation électromagnétique 44

III.4.1. Modèle magnétodynamique 44

III.4.2. Formulation de la magnétodynamique 44

III.4.3. Formulation en potentiel vecteur magnétique 45

III.4.4. Formulation en potentiels A-V 46

III.5. Méthodes numériques de discrétisation 47

III.5.1. Méthode des différences finis (MDF) 47

III.5.2. Méthode des éléments finis (MEF) 48

III.5.3. Méthode des intégrales de frontières (MIF) 48

III.5.4. Méthode des volumes finis (MVF) 48

III.6. Mise en œuvre de la méthode des volumes finis 49

III.6.1. Modèle 2D axisymétrique 50

III.6.2. Equation magnétodynamique 50

III.6.2.1. Intégration du premier terme 51

III.6.2.2. Intégration du deuxième terme 52

III.6.2.3. Intégration du troisième terme 53

(6)

III.6.2.5. Construction du système algébrique 53

III.6.3. Modèle tridimensionnel 53

III.6.4. Equation magnétodynamique 54

III.6.4.1. Intégration du terme 



A



55

III.6.4.2. Intégration de 



. A



57

III.6.4.3. Intégration de 



Av



57

III.6.4.4. Intégration du terme source 58

III.6.4.5. Intégration de la deuxième équation du système 58 III.7. Résolution numérique des systèmes d‟équations algébriques 59

III.7.1. Méthodes directes 59

III.7.2. Méthodes itératives 60

III.8. Conclusion 60

Chapitre IV : Applications et validations

IV.1. Introduction 62

IV.2. Première application : validation du code de calcul 63

IV.2.1. Description du problème 63

IV.2.2. Résultats 63

IV.2.2.1. Effet de la fréquence 63

IV.2.2.2. Effet du lift-off 65

IV.2.2.3. Effet de la profondeur du défaut 66

IV.2.2.4. Effet de la conductivité 68

IV.3. Deuxième application : estimation de la position d‟un défaut 69

IV.3.1. Description du problème 70

IV.4. Troisième application : test expérimental au laboratoire LGEB 71

IV.4.1. Description du problème expérimental 72

IV.5. Quatrième application : modélisation d‟un capteur différentiel 74

IV.5.1. Description du problème test 74

IV.6. Cinquième application : le problème JSAEM#6 78

IV.6.1. Description du problème JSAEM#6 78

IV.7. Sixième application : modélisation d‟un capteur matriciel 85

(7)

IV.7.2.1. Mode d‟excitation un/un 86

IV.7.2.2. Mode d‟excitation série 89

IV.7.2.3. Mode d‟excitation parallèle 90

IV.8. Conclusion 94

Conclusion générale 96

Communications internationales liées à ce travail 98

(8)

LISTE DES FIGURES

Fig. I.1. Schéma synoptique d‟un système de CND. 9

Fig. I.2. Inspection par ressuage. 10

Fig. I.3. Théorie de l‟opération Impact-Echo. 11

Fig. I.4. Inspection par radiographie. 14

Fig. I.5. Inspection par magnétoscopie. 15

Fig. I.6. Inspection par Courants de Foucault. 16

Fig. I.7. Inspection par thermographie. 17

Fig. I.8. Distributions du champ magnétique et température. 18

Fig. I.9. Inspection par thermo-inductive. 19

Fig. II.1. Jean Bernard Léon Foucault. 22

Fig. II.2. Principe des capteurs inductifs. 23

Fig. II.3. Bobine cylindrique. 23

Fig. II.4. Bobine plate. 24

Fig. II.5. Le capteur absolu. 24

Fig. II.6. Visualisation d'un défaut issu d'un capteur absolue. 25

Fig. II.7. Le capteur double. 25

Fig. II.8. Le capteur différentiel. 26

Fig. II.9. Visualisation d'un défaut issu avec une sonde différentielle. 27

Fig. II.10. Le capteur matriciel. 28

Fig. II.11. Les différentes structures de circuit magnétique. 28

Fig. II.12. Capteur encerclant. 29

Fig. II.13. Capteur interne. 29

Fig. II.14. Capteur ponctuel 29

Fig. II.15. James Clark Maxwell (1831-1879) 31

Fig. II.16. Induction de courant de Foucault dans une interface plane 33 Fig. II.17. Répartition des courants de Foucault sous une surface plane. 35 Fig. II.18. Influence de la conductivité (ζ) ou du lift-off sur le diagramme d‟impédance

normalisée

37

Fig. II.19. Géométrie de la pièce à contrôler. 38

Fig. III.1. Domaine d‟étude 41

Fig. III.2. Interface entre deux milieux. 43

Fig. III.3. Diagramme de Tonti appliqué à l‟électromagnétisme. 43

Fig. III.4. Schématisation d‟un plan de symétrie. 45

(9)

ix

Fig. III.7. Volume élémentaire Dp. 51

Fig. III.8. Approximation linéaire du potentiel à travers la facette e. 52

Fig. III.9. Modèle tridimensionnel. 54

Fig. III.10. Volume élémentaire Dp. 54

Fig. III.11. Représentation des nœuds fictifs. 56

Fig. IV.1. Organigramme de l‟algorithme de base des codes de calcul 62

Fig. IV.2. Description du problème 63

Fig. IV.3. Variation de l‟impédance en fonction de la position du capteur pour les fréquences : 50, 100, 500kHz.

64

Fig. IV.4. Variation de la réactance en fonction de la position du capteur pour les fréquences : 50, 100, 500kHz.

64

Fig. IV.5. Variation de la résistance en fonction de la position du capteur pour les fréquences : 50, 100, 500kHz.

65 Fig. IV.6. Variation de l‟impédance en fonction de la position du capteur pour

différentes valeurs de lift-off : 0.2, 0.51, 1mm.

65

Fig. IV.7. Variation de la réactance en fonction de la position du capteur pour différentes valeurs de lift-off : 0.2, 0.51, 1mm.

66

Fig. IV.8. Variation de la résistance en fonction de la position du capteur pour différentes valeurs de lift-off : 0.2, 0.51, 1mm.

66 Fig. IV.9. La variation de l‟impédance en fonction de la position du capteur pour

différentes valeurs de la profondeur de défaut: 38%, 58%, 75%.

67

Fig. IV.10. Variation de la réactance en fonction de la position du capteur pour différentes valeurs de la profondeur de défaut: 38%, 58%, 75%.

67

Fig. IV.11. Variation de la résistance en fonction de la position du capteur pour différentes valeurs de la profondeur de défaut: 38%, 58%, 75%.

68

Fig. IV.12. Variation de l‟impédance en fonction de la position du capteur pour différentes matières de fabrication: Inconel-600, Aluminium, Cuivre.

68

Fig. IV.13. Variation de la réactance en fonction de la position du capteur pour différentes matières de fabrication: Inconel-600, Aluminium, Cuivre.

69

Fig. IV.14. Variation de la résistance en fonction de la position du capteur pour différentes matières de fabrication: Inconel-600, Aluminium, Cuivre.

69

Fig. IV.15. Description du problème. 70

Fig. IV.16. Distribution de la densité des courants induits dans le tube. 70

Fig. IV.17. Description du problème expérimental 72

Fig. IV.18. Description de l‟essai expérimental. 72

Fig. IV.19. Variation de l‟impédance, la réactance et la résistance en fonction de la position du capteur pour la fréquence 10kHz.

(10)

Fig. IV.20. Variation de l‟impédance, la réactance et la résistance en fonction de la position du capteur pour la fréquence 100kHz.

73

Fig. IV.21. Description du problème. 74

Fig. IV.22. Variation de l‟impédance (ΔZ) en fonction de la position du capteur pour différentes profondeurs de la fissure : (a) 38%, (b) 58%, (c) 75%.

76 Fig. IV.23. Variation de la résistance (ΔR) et la réactance (ΔX) en fonction de la

position du capteur pour les différentes profondeurs de la fissure : (a) 38%, (b) 58%, (c) 75%.

77

Fig. IV.24. Signatures de la fissure pour les différentes profondeurs de la fissure : (a) 38%, (b) 58%, (c) 75%.

78

Fig. IV.25. Description du problème JSAEM#6 79

Fig. IV.26. Maillage 3D du problème JSAEM#6, Nt = 26908 79

Fig. IV.27. Densité des courants induits dans la plaque. 80

Fig. IV.28. Distribution des courants induits dans la plaque. 80 Fig. IV.29. Colormap 3D des potentiels A, v et des courants Jind : plaque saine 81

Fig. IV.30. Colormap 3D des potentiels A, v et des courants Jind: plaque fissurée 82

Fig. IV.31. Distribution des vecteurs de l‟induction B en 3D 83 Fig. IV.32. Variation de la résistance en la présence de la fissure, lift-off = 0.5mm. 83 Fig. IV.33. Variation de la réactance en la présence de la fissure, lift-off = 0.5mm. 83 Fig. IV.34. Variation de la résistance en la présence de la fissure, lift-off = 1mm. 84 Fig. IV.35. Variation de la réactance en la présence de la fissure, lift-off = 1mm. 84

Fig. IV.36. Représentation du dispositif de test. 85

Fig. IV.37. Variation de l‟impédance (ΔZ), la résistance (ΔR) et la réactance (ΔX) pour le lift-off=0.5mm.

87

Fig. IV.38. Variation de l‟impédance (ΔZ), la résistance (ΔR) et la réactance (ΔX) pour le lift-off =1mm.

88

Fig. IV.39. Densité des courants induits dans la plaque. 89

Fig. IV.40. Distribution des courants induits dans la plaque. 89 Fig. IV.41. Distribution des vecteurs de l‟induction magnétique en 3D 91 Fig. IV.42. Variation de l‟impédance (ΔZ), la résistance (ΔR) et la réactance (ΔX) pour

le lift-off=0.5mm.

90

Fig. IV.43. Variation de l‟impédance (ΔZ), la résistance (ΔR) et la réactance (ΔX) pour le lift-off=1mm.

(11)

xi LISTE DES TABLEAUX

Tab. IV.1. Sommaire de résultats. 71

Tab. IV.2. Dimensions du problème test (en mm). 75

Tab. IV.3. Résultats de calcul et mesure. 84

Tab. IV.4. Dimensions du problème (en mm). 85

Tab. IV.5. Résultats du code de calcul Lift-off =0.5mm. 86 Tab. IV.6. Les résultats du code de calcul Lift-off =1mm. 86 Tab. IV.7. Résultats de code de calcul en alimentation série. 89 Tab. IV.8. Résultats du code de calcul Lift-off =0.5mm. 90

(12)

(13)

Introduction générale

2 Introduction générale

Relativement aux dangers provenant par la fissuration des structures métalliques: tôles, tubes,….etc, dans le secteur industriel (aviation, automobile, centrale nucléaire), souvent un contrôle de qualité est exigé. Au niveau de la production, il faut dimensionner les pièces au plus juste tout en garantissant leurs disponibilités et leurs performances. Durant l‟exploitation d‟un produit industriel, son maintien en état de marche dans de bonnes conditions de sécurité nécessite une bonne connaissance de l‟évolution des pièces qui le constitue. Cette connaissance implique en particulier de réaliser des contrôles ne portant pas atteinte à l‟intégrité des pièces et en entravant le moins possible la disponibilité du produit. Ceci justifie l‟importance croissante que prend le contrôle non destructif (CND).

Les méthodes de CND sont utilisées soit pour évaluer des grandeurs caractéristiques du produit (épaisseur, conductivité, …etc.), soit pour déceler la présence de défauts et les caractériser. Parmi les méthodes les plus utilisées, on peut citer les ultrasons, les méthodes utilisant des rayonnements ionisants (radioscopie) et les méthodes électromagnétiques (magnétoscopie, courants de Foucault). Le choix d‟une méthode dépend d‟un grand nombre de facteurs tels que la nature des matériaux constituant les pièces à contrôler, la nature de l‟information recherchée (défaut débouchant ou enfoui), les conditions de mise en œuvre, ….etc.

Les méthodes électromagnétiques sont fréquemment utilisées pour le contrôle des pièces électriquement conductrices et/ou magnétiques. Par exemple, le contrôle de pièces de fonderie (industrie automobile, industrie pétrolière) peut se faire par magnétoscopie. Les tubes (nucléaire, industrie pétrolière) peuvent être testés par les courants de Foucault (CF).

Le contrôle non destructif par courants de Foucault (CND-CF) est une méthode à la fois simple à mettre en œuvre, il est facile de créer des courants de Foucault dans un milieu conducteur à l‟aide d‟une sonde, et complexe. En effet, pour un contrôle donné, comment peut-on créer une bonne répartition des courants de Foucault permettant d‟avoir un „signal de défaut‟ aussi important que possible? Il est nécessaire avant toute chose d‟avoir une connaissance suffisamment complète du phénomène physique. Les courants de Foucault n‟étant pas directement accessibles par la mesure, ils ne peuvent être observés que par l‟intermédiaire de mesures sur d‟autres grandeurs sur lesquelles ils agissent.

Dans ce contexte, les outils de simulation permettent d‟étudier les interactions sonde-pièce jouent un rôle croissant pour concevoir les systèmes de contrôle et démontrer leurs performances. La modélisation électromagnétique permet de simuler l‟interaction sonde-pièce et de définir une structure adaptée de la sonde. Ainsi il est possible de prévoir les conséquences de différents choix (configuration géométrique, choix des matériaux) tout en limitant le nombre de prototype à réaliser. Dans le domaine du CND-CF, la modélisation est ainsi devenue, grâce aux performances du matériel informatique, une actrice importante dans la conception de sondes.

(14)

La modélisation d‟une configuration réelle de CND-CF ne peut généralement pas être obtenue analytiquement et elle fait appel à des méthodes numériques à savoir la méthode des volumes finis (MVF). Cette méthode s‟est imposée ces dernières années, comme un outil numérique efficace pour le traitement des problèmes électrotechniques.

La simulation numérique par les volumes finis d‟un problème de CND-CF nécessite souvent un maillage adéquat. Un tel maillage doit d‟une part bien décrire la géométrie du domaine d‟étude et d‟autre part être bien adapté aux phénomènes physiques qu‟il doit décrire (variation du champ au voisinage du défaut, épaisseur de peau, ….etc.).

Au cours de la réalisation de ce travail, nous avons développé deux solveurs volumes finis pour la résolution des problèmes de CND-CF : le solveur 2D axisymétrique (MVF2D-axi) et le solveur tridimensionnel (MVF3D). Pour la validation différents types de problèmes ont été considérés, comme première application un dispositif constitué d‟un tube métallique contrôlé par un capteur absolu. Dans la deuxième application, on cherche à estimer la position par rapport à la surface d‟un défaut enfoui. Dans la troisième application, on reporte les mesures expérimentales d‟un problème réalisé au sein du laboratoire LGEB ainsi que les résultats numériques obtenus par le solveur MVF2D-axi. La quatrième application concerne la modélisation d‟un capteur différentiel. La cinquième application est consacrée à l‟étude du problème de Workshop : JSAEM#6, il est constitué d‟un capteur ponctuel placé au dessus d‟une plaque métallique (pièce à contrôler). Le capteur matriciel qui est très répandu en termes de temps d‟inspection a constitué le sujet de la sixième et dernière application.

Ce mémoire est ainsi organisé comme suit :

Le premier chapitre présente la définition, le but du contrôle non destructif (CND), les différents types de défauts détectés en CND, le principe de détection d‟un éventuel défaut ainsi que les bases physiques qui gouvernent les procédés et leurs performances. Egalement, sont exposées les différentes techniques de contrôle non destructif les plus en plus utilisées dans le secteur industriel.

Le second chapitre est consacré à donner quelques notions sur les courants de Foucault et le principe du capteur inductif. Ensuite on passera en revue les différents types de capteurs à courants de Foucault, différentes formes géométriques des circuits magnétiques, modes d‟excitation et on terminera par les principaux paramètres influant le contrôle.

Le troisième chapitre rapporte les principales méthodes numériques de discrétisation, la modélisation des problèmes CND-CF dans le cas 2D axisymétrique et dans le cas tridimensionnel. Dans ce travail, la méthode des volumes finis à été choisie comme méthode de discrétisation afin de transformer les équations aux dérivées partielles en équations algébriques.

(15)

4 Dans le but de tester et valider les codes de calcul développé sous Matlab, le quatrième et dernier chapitre est consacré à la modélisation d‟un certain nombre de problèmes : des applications pour valider la détectabilité des défauts débouchants, une application concerne l‟estimation de la position d‟un défaut enfoui, un test expérimental et un problème de Workshop. Dans l‟ensemble des applications traitées, les capteurs considérés sont : capteur absolu, capteur différentiel, capteur ponctuel et le capteur matriciel. Cependant, la prise en compte du déplacement des capteurs est réalisée par affectation des propriétés physiques.

(16)

CHPITRE I Concepts généraux sur les techniques de Contrôle Non Destructif

Chapitre I

Concepts généraux sur les techniques

de contrôle non destructif

(17)

7 I.1. Introduction

Le Contrôle Non Destructif (CND) est un ensemble de méthodes qui permettent de caractériser l'état d'intégrité de structures ou de matériaux, sans les dégrader, soit au cours de la production, soit en cours d'utilisation, soit dans la phase de maintenance. Les termes « Essais Non Destructifs » (END) ou « Examens Non Destructifs » évoquent aussi le diagnostic que le médecin formule lors de l‟examen de son patient. Le même principe appliqué aux pièces industrielles consiste à mettre en œuvre des méthodes d‟investigation pour apprécier sans destruction leur état de santé et formuler un avis sur leur aptitude à remplir la fonction à laquelle elles sont destinées.

Considérée sous cet aspect d‟aptitude au bon fonctionnement, la définition de CND suppose une bonne connaissance de tous les phénomènes mis en jeu, en particulier de la nocivité des défauts, de leur évolution dans le temps, des lois générales de la mécanique de la rupture et, dans la pratique, les spécialistes en contrôle non destructif sont plutôt confrontés à des problèmes d‟interprétation de résultats de contrôle par rapport à des critères établis en liaison avec le concepteur de la pièce.

Une définition des contrôles non destructifs plus proche de la réalité industrielle consiste donc à dire qu‟il s‟agit de « qualifier, sans nécessairement quantifier, l‟état d‟un produit, sans altération de ses caractéristiques par rapport à des normes de recette ». L‟exécution de cette tache demande une bonne connaissance des méthodes d‟investigation mises en œuvre, de leurs limites et surtout une adéquation parfaite entre le pouvoir de détection de chacune d‟elle et les critères appliqués pour la mise en œuvre [1, 2, 3].

I.2. Généralités sur le contrôle non destructif

I.2.1. Principe

L‟ensemble des techniques et procédés de CND aptes à fournir des informations sur la santé d‟une pièce ou d‟une structure sans qu‟il en résulte des altérations préjudiciables à leur utilisation ultérieure. Le terme de santé, s‟il souligne une certaine parenté avec le domaine des examens d‟aide au diagnostic médical, comme la radiologie ou l‟échographie, délimite bien l‟objectif d‟elles qui est la mise en évidence de toutes les défectuosités susceptibles d‟altérer la disponibilité, la sécurité d‟emploi et/ou, plus généralement, la conformité d‟un produit à l‟usage auquel il est destiné.

Généralement en peut distinguer les étapes suivantes, quelle que soit la technique d‟inspection employée :

 Mise en œuvre d‟un processus physique énergétique ;

 Modulation ou altération de ce processus par les défectuosités ;

(18)

 Traitement des signaux et interprétation de l‟information délivrée.

I.2.2. Les différents défauts détectés en CND

Un défaut (défectuosité) détecter dans une pièce, c‟est physiquement, mettre en évidence une hétérogénéité de matière, une variation locale de propriété physique ou chimique préjudiciable au bon emploi de celle-ci. Cela dit, on a l‟habitude de classer les défauts en deux grandes catégories liées à leur emplacement : les défauts de surface, les défauts internes.

I.2.2.1. Les défauts surfaciques

Ces défauts sont accessibles à l‟observateur directement mais pas toujours visibles à l‟œil nu, à cet effet on peut les classés en deux types distincts :

 Les défauts ponctuels

Correspond aux défauts les plus nocifs sur le plan technologique, puisqu‟il s‟agit des criques, piqûres, fissures, craquelures, généralement aptes à provoquer à terme la rupture de la pièce, en initiant par exemple des fissures de fatigue. Dans les pièces métalliques, l‟épaisseur de ces fissures est souvent infime (de l‟ordre de quelques μm) et elles peuvent être nocives dès que leur profondeur dépasse quelques dixièmes de millimètre, ce qui implique l‟emploi pour leur détection des méthodes sensibles et non destructives, telles que le ressuage, la magnétoscopie, les courants de Foucault et les ultrasons.

 Les défauts d‟aspect

C‟est à dire à des plages dans lesquelles une variation des paramètres géométriques ou physiques (rugosité, surépaisseur, taches diverses) attire le regard et rend le produit inutilisable. Ici, le contrôle visuel est possible, mais on cherche souvent à le remplacer par des contrôles optiques automatiques.

I.2.2.2. Les défauts internes

Sont des hétérogénéités de natures, de formes, de dimensions extrêmement variées, localisées dans le volume du corps à contrôler. Leur nomenclature est très étoffée et spécifique à chaque branche d‟activité technologique et industrielle. Dans les industries des métaux, il s‟agira de criques internes, de porosités, de soufflures, d‟inclusions diverses susceptibles d‟affecter la santé des pièces moulées, forgées, laminées, soudées. Dans d‟autres cas, il s‟agira simplement de la présence d‟un corps étranger au sein d‟une enceinte ou d‟un produit emballé. Ici le contrôle visuel est généralement exclu et l‟on utilisera donc l‟un ou l‟autre des grands procédés du CND que sont la radiographie, le sondage ultrasonore ou encore des techniques mieux adaptées à certains cas comme l‟émission acoustique, l‟holographie, l‟imagerie infrarouge et la neutronographie.

(19)

9 I.2.3. Procédure de CND

L‟opération de contrôle non destructif d‟un objet ne se borne généralement pas à la détection d‟éventuels défauts. En effet, même si le choix du procédé, de la méthode et du matériel a été effectué au préalable, il faut envisager toute une procédure ayant les objectifs suivants : fiabilité de l‟examen, reproductibilité, localisation des défauts, identification, caractérisation de ceux-ci, en particulier par leur taille, classement, présentation visuelle, décision concernant l‟affectation de l‟objet, enfin archivage des résultats et des conditions d‟examen.

Ce sont des opérations d‟étalonnage, de calibrage, de balayage de la sonde, de traitement des données qui permettent d‟atteindre ces objectifs désormais dans des bonnes conditions, grâce à l‟apport intensif de l‟informatique en temps réel, on peut représenter la mise en œuvre d'un système CND suivant le synoptique de la figure I.1.

Fig. I.1. Schéma synoptique d‟un système de CND

La cible se caractérise par un ensemble de paramètres que l'on va chercher à estimer afin de former un diagnostic d'intégrité. La mise en œuvre d'un système CND adéquat va permettre de produire un certain nombre de signaux qui sont fonction des paramètres recherchés. Une étape « d'inversion », plus ou moins compliquée, est bien souvent nécessaire afin de retrouver les paramètres initiaux de la pièce [1, 3, 4, 12].

I.3. Les techniques de contrôle non destructif

Il existe plusieurs techniques de CND, peuvent être classées comme suit : I.3.1. Examen visuel

L‟inspection visuelle est la plus ancienne procédure de contrôle, continu à développer dans une société américaine d‟évaluation des méthodes de contrôle non destructif (ASNT). Cette procédure d‟évaluation est la plus simple et générale. L‟examen visuel nécessite un bon éclairage localisé sur les régions suspectes. Les résultats prospères ont dépendu de la compétence de l‟opérateur, le bon nettoyage, illumination adéquate de la zone inspecté et la qualité de l'instrument optique. Ces facteurs sont encore importants aujourd'hui, mais le matériel est devenu beaucoup plus sophistiqué. Habituellement, l'inspection visuelle ne peut pas être utilisée pour vérifier des résultats de test, ni ce peut être utilisé pour remplacer d‟autres méthodes de CND. Cependant, quand l‟examen visuel direct ne peut pas être fait, les instruments optiques

Pièce à contrôler (Cible) Système CND Instrumentation (Inversion) Paramètres estimés de la cible Signaux liés aux paramètres Paramètres de la cible

(20)

sophistiqués peuvent être utilisés pour fournir une inspection éloignée de régions critiques [1, 6, 8, 12].

 Avantages

- Examen simple, rapide et pas coûteux; - Souplesse d‟inspection.

 Inconvénients

- Détection limitée aux défauts superficiels; - La surface doit être propre;

- Pas d‟interruption des parcours optiques entre l‟œil et la pièce examinée.

c- Le révélateur extrait le pénétrant retenu par les fissures

d- Observation et interprétation finale

b- Nettoyage de l‟excédent de pénétrant par lavage

(21)

11 I.3.2. Ressuage

La méthode « huile et poussière de craie », autrefois utilisée par les industries ferroviaires dans les années 1920. Le contrôle par liquide de pénétration (ressuage) a été ranimé en 1941 par Robert et Joseph Switzer. Le ressuage est un moyen de recherche des défauts superficiels qui consiste l‟amélioration de l‟inspection visuelle de défectuosité. Il consiste à l‟aspiration du pénétrant par la couche poudreuse du révélateur, le mécanisme de révélation des défauts par ressuage correspond aux quatre phases illustrées sur la figure I.2 : application du pénétrant suivie d‟un temps d‟imprégnation, élimination de l‟excès du pénétrant sur la surface de la pièce, ressuage du pénétrant par disposition d‟une couche de « révélateur » sur la surface. L‟image des défauts apparaîtra à l‟observateur dans la mesure où l‟étalement du pénétrant sur le révélateur conduit à une nette variation de couleur ou de luminance [1, 6, 8, 10, 12].

 Avantages

- Facilité de mise en œuvre et relativement sensible aux fissures débouchants ; - Appliqué sur les matériaux diélectriques et non ferromagnétique.

 Inconvénients

- Limite de l‟application sur les matériaux non poreux ;

- L‟interprétation des résultats est subjective: Il est impossible de déterminer les dimensions exactes des défauts ;

- Danger des solvants toxiques, corrosifs et inflammable.

I.3.3. Essais ultrasonores

Fig. I.3. Théorie de l‟opération Impact-Echo.

Les ultrasons sont des vibrations mécaniques prenant naissance et se propageant dans tout support matériel présentant une certaine élasticité. Les ultrasons correspondent à des fréquences

(22)

oscillatoires supérieures à la limite d‟audibilité humaine et s‟étendant dans une large gamme allant de 15kHz à plus de 100MHz. L‟ultrason est basé sur la transmission, la réflexion, et l'absorption d'une onde ultrasonore, qui se propage dans la pièce à contrôler (figure I.3). Le train d'onde émis se réfléchit dans le fond de la pièce et sur les défauts puis revient vers le transducteur qui joue souvent le rôle d‟un émetteur/récepteur. L'interprétation des signaux permet de positionner le défaut [1, 3, 6, 8, 11, 12].

 Avantages

- Grand pouvoir de pénétration (plusieurs mètres dans l'acier forge).

- Haute sensibilité de détection de défauts, notamment pour la recherche des défauts plans (dépend de la fréquence de l'onde ultrasonore);

- Détection, localisation et dimensionnement des défauts; - Inspection et détection en temps réel.

 Inconvénients

- Sensible à la nature et à l'orientation des défauts;

- Technique souvent très coûteuse (investissement, temps de contrôle) ; - Inspection limitée par la complexité de la forme de la pièce contrôlée.

I.3.4. Contrôle par Laser

La méthode de contrôle par laser est parmi les méthodes optiques les plus répandues en contrôle non destructif. Comme elle est aussi sans contact, les objets irréguliers et les surfaces non planes peuvent être inspectés sans problèmes d'usure. Le mot laser est un acronyme pour amplification légère de la radiation de l'émission stimulée. Cette lumière est très intense, essentiellement monochromatique (longueur d'onde unique), plan polarisé (unidirectionnel) et très stable. Les méthodes de contrôle non destructif par laser sont populaires dans les industries aéronautique et automobile [3, 6].

 Avantages

- Inspection sans contact, ne nécessite pas la préparation de surface de la pièce à contrôler ; - Pas de consommables : liquide de pénétration, matériaux de marquage,…etc. ;

- Avec les capteurs électro-optiques comme les caméras CCD, des mesures en temps réel sont possibles.

 Inconvénients

- Considérations de sécurité particulières doivent être prises en compte ; - Une composante de chargement est nécessaire pour voir les résultats ; - Les résultats dépendent de la composante de cisaillement ;

(23)

13 I.3.5. Radiographie

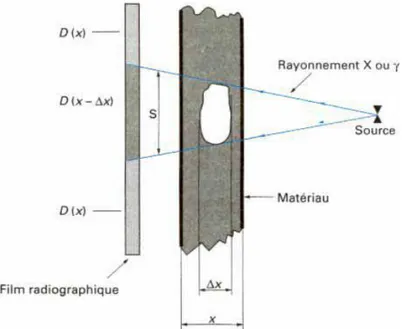
L‟examen d‟un objet par radiographie consiste à le faire traverser par un rayonnement électromagnétique (rayons X ou γ) de très courte longueur d‟onde comprises entre environ 0,1pm et 1000pm, et à recueillir les modulations d‟intensité du faisceau sous forme d‟une image sur un récepteur approprié, un film dans la plupart des cas, comme l‟illustre la figure I.4. On caractérise couramment ces rayonnements par l‟énergie unitaire, cette dernière requise en contrôle non destructif se situe dans une gamme allant de 50keV à 20meV. L‟interaction entre les rayons X ou γ et la matière implique les phénomènes suivants :

- un effet photoélectrique, correspondant à un transfert complet d‟énergie entre le photon incident et un électron, conduisant à son absorption totale et éventuellement à une réémission de fluorescence X. Cet effet est d‟autant plus grand que l‟énergie des photons est basse.

- l‟effet Compton, correspondant à un transfert partiel d‟énergie du photon vers un électron ; les photons sont déviés, alors que les électrons activés provoquent une émission secondaire ; cette diffusion Compton devient prépondérante, vers 1meV, vis-à-vis de l‟effet photoélectrique et constitue le phénomène prédominant en radiographie industrielle ;

- la formation de paires électron-position par annihilation des photons, avec émission de rayonnement secondaire hétérogène ; ce phénomène à fondamentalement un seuil énergétique à 1,02meV et n‟intéresse donc que les hautes énergies.

Ces trois phénomènes d‟interaction expliquent d‟une part l‟absorption des rayons X et γ par la matière, mais aussi un phénomène de diffusion dû aux réémissions d‟ondes de plus basse énergie que l‟onde incidente. Ce dernier phénomène est très gênant en radiographie, alors que l‟on met en œuvre le premier pour détecter et visualiser les défauts.

Dans la pratique, le choix entre radiographie X ou gammagraphie résulte de multiples considérations liées aux avantages et inconvénients de chacune de ces techniques, comme par exemple : taille et coût modeste des sources γ, forte pénétration de ces rayonnements mais durée d‟exposition beaucoup plus longue qu‟en radiographie X qui elle, par contre, nécessite la présence d‟une source électrique mais offre l‟avantage de pouvoir choisir plus aisément les paramètres de contrôle [1, 3, 4, 6].

 Avantages

- Contrôle des objets de forme compliquée ;

- Facile à Transporté (générateurs de rayons X de faibles énergies, appareils de radioactive portatifs);

- Apprécier la nature et la taille des défauts.

 Inconvénients

(24)

- Mise en en œuvre des dispositifs et procédures de protection du personnel; - Cette technique est extrêmement coûteuse et impose des conditions de sécurité ; - Le risque de ne pas détecter les fissures se présentant selon l‟axe du faisceau.

Fig. I.4. Inspection par radiographie.

I.3.6. Magnétoscopie

Le contrôle par magnétoscopie [1, 5, 6, 8, 12] fait appel aux propriétés magnétiques du matériau inspecté. L‟effet de dispersion du flux de fuite peut être mis en évidence en aspergeant la surface contrôlée d'une liqueur magnétique constituée de très fines particules ferromagnétiques et d'un liquide porteur (poudre de fer ou de magnétite colorée). Les particules noires ou fluorescentes viennent s'agglomérer sur le champ de fuite, à l'endroit du défaut, le rendant ainsi parfaitement visible, comme l‟illustre la figure I.5.

 Avantages

- Simple, peu coûteux et rapide ;

- Détection des défauts débouchant et sous-jacents.

 Inconvénients

- Applicable seulement aux matériaux ferromagnétiques ; - Aimantation dépend de la perméabilité de la pièce examinée ;

- La sensibilité de détection des défauts dépend en effet de la nature, de la direction et de l‟intensité de la magnétisation de la pièce.

(25)

15 Fig. I.5. Inspection par magnétoscopie.

I.3.7. Courants de Foucault

Les courants de Foucault ce sont des courants induits développés en circuit fermé à l‟intérieur d‟un objet conducteur placé dans un champ magnétique variable dans le temps. L‟examen par les courants de Foucault est basé sur le fait que si une bobine est alimentée par un courant variable et apportée à proximité d'une cible conductrice, génère de tels courants induits qui, créant eux-mêmes un flux magnétique qui s‟oppose au flux générateur, modifient ainsi l‟impédance de cette bobine. C‟est l‟analyse de cette variation d‟impédance qui fournira les indications exploitables pour un contrôle ; en effet, le trajet, la répartition et l‟intensité des courants de Foucault dépendent des caractéristiques physiques et géométriques du corps considéré, ainsi bien entendu que des conditions d‟excitation (paramètres électriques et géométriques du bobinage).

On conçoit dès lors qu‟un défaut, constituant une discontinuité électrique venant perturber la circulation des courants de Foucault, puisse engendrer une variation d‟impédance décelable au niveau de la bobine d‟excitation [1, 3, 4, 6, 8, 12]. La figure I.6 représente le procédé de l‟inspection par courants de Foucault.

 Avantages

- Simple, peu coûteux et rapide;

- Grande sensibilité de détection des défauts (dimensionnelles, structurales...) ; - Evaluer le dimensionnement et la profondeur d‟un défaut ;

- Pas des conditions de sécurité ni pour l'opérateur ni pour l'environnement ; - Inspection sans contact ;

Magnétite colorée Lignes de champ

magnétique

(26)

- Efficacité de la technique malgré la complexité des phénomènes électromagnétiques mis en œuvre ;

- Automatisation possible pour des pièces de géométrie constante (tubes, barres, rubans et câbles).

Bobine

Les lignes du champ magnétique généré

Les lignes du champ magnétique des courants induits Les courants

induits

Pièce conductrice

Fig. I.6. Inspection par Courants de Foucault.

 Inconvénients

- La profondeur d‟inspection est dépend de la fréquence d‟excitation ; - La détection du défaut se fait d‟une manière locale ;

- Inspection limitée aux matériaux électriquement conducteurs ;

- La position du capteur par rapport au spécimen peut influencer l‟efficacité de détection des défauts ;

- La compétence et la formation sont exigées pour le personnel d‟inspection ;

I.3.8. Thermographie

Cette technique consiste à chauffer la surface du matériau inspecté par apport d‟énergie (mécanique, air chaud, lampes flash) et à mesurer l‟élévation de température résultante avec une caméra infrarouge. L‟inspection en thermographie infrarouge peut se faire selon deux approches : la thermographie active et passive. Dans les deux cas, l‟investigation consiste à détecter la présence d‟un gradient de température qui révèle la présence d‟un défaut, gradient qui peut-être provoqué soit par une hausse ou une baisse de température. En thermographie active, le processus de détection nécessite l‟apport d‟une stimulation thermique extérieure afin de provoquer l‟apparition d‟un gradient. Par opposition, la thermographie passive n‟utilise pas de

(27)

17 naturellement. L‟approche active comporte principalement trois volets : la stimulation thermique du spécimen, l‟acquisition temporelle de la réponse thermique et l‟analyse numérique de la réponse (figure I.7). Les techniques d‟inspection par thermographie infrarouge ont été développées et continuent d‟être améliorées dans le domaine de la thermographie active. Les trois principales technique sont la thermographie pulsée (TP), elle consiste à générer une impulsion thermique de courte durée. La thermographie modulée (TM) en régime permanent thermique, la température de la surface varie périodiquement avec un module et un déphasage distinct entre les zones saines et les zones défectueuses et la thermographie de phase pulsée (TPP), combinaison entre les deux précédentes technique [4, 6, 8].

Fig. I.7. Inspection par thermographie.

 Avantages

- Méthode relativement rapide et sans contact ;

- Toute l‟épaisseur de la pièce est généralement contrôlée ;

- Les cavités (champs de bulles d‟air, fissures, délaminages, …) sont bien détectées ; - La sensibilité à la détection des défauts de faibles dimensions ;

- L‟archivage des résultats est garanti à l‟aide de la caméra infrarouge.

 Inconvénients

- Des difficultés de mesure liées aux effets perturbateurs ;

- Des difficultés de localisation de la profondeur des défauts, du fait que l‟image obtenue donne une projection de ces derniers sur le plan de la pièce testée ;

- L‟interprétation des mesures pas toujours facile, surtout pour identifier la nature des défauts ; Excitation thermique (Lampe, …) Caméra infrarouge Résultats Traitement d‟image Bruit de mesure La pièce

(28)

- La phase d‟interprétation des résultats présente des restrictions pour une automatisation totale de la technique.

I.3.9. Thermo-inductive

Ce mode d‟examen consiste, à chauffer la zone d‟une pièce électriquement conductrice inspectée par induction magnétique. En cas de présence d‟un défaut, l‟anomalie dans la distribution de la densité de courants induits, crée une concentration de la densité de puissance autour du défaut qui se traduit par des surchauffes locales. L‟inhomogénéité de la distribution de la température se propage à la surface du matériau, et peut être détectée par une caméra infrarouge (figure I.8). Donc un défaut sera révélé par la combinaison des phénomènes électromagnétique et thermique d‟une façon complémentaire.

Fig. I.8. Distributions du champ magnétique et température.

L‟intérêt de cette méthode est d‟augmenter la probabilité de détection des défauts de surface et d‟améliorer l‟interprétation des données par une corrélation des résultats obtenus avec les deux méthodes du CND : par courant de Foucault et par thermographie infrarouge. Elle présente l‟avantage de crée une perturbation supplémentaire due à la concentration des courants induits autour du défaut, où une pièce de forme d‟une plaque a été inspectée (figure I.9). La présence du défaut perturbe les lignes de courants induits et crée des surchauffes supplémentaires qui s‟ajoutent au retour de l‟onde thermique à la surface après la stimulation thermique. Cela engendre une élévation de température à la surface au-dessus du défaut. La technique thermo-inductive permet également de contrôler facilement la puissance induite, de chauffer à la surface ou au cœur et de s‟adapter aux différentes géométries des pièces inspectées et des défauts rencontrés [6, 8]. a) Distribution du champ magnétique b) Distribution du champ de température et la température de la surface de la plaque

(29)

19 Fig. I.9. Inspection par thermo-inductive.

 Avantages

- Méthode relativement rapide et sans contact ;

- La technique est globale et elle permet l‟inspection de l‟ensemble de la pièce à la fois ; - Toute l‟épaisseur de la pièce est généralement contrôlée ;

- Grande sensibilité de détection des défauts ;

- L‟automatisation est possible pour des pièces de géométries constantes.

 Inconvénients

- La technique s‟applique seulement pour les matériaux électriquement conducteurs ; - Sensible au chauffage non uniforme ;

- L‟interprétation des mesures n‟est pas toujours facile, surtout pour identifier la nature des défauts.

I.4. Conclusion

Dans ce chapitre nous avons rappelé brièvement la définition et le but du contrôle non destructif (CND), les différents types de défauts détectés en CND, le principe de détection d‟un éventuel défaut et les bases physiques qui gouvernent les procédés de contrôle. Nous avons ensuite décrit les principes des principales techniques de contrôle non destructif les plus utilisées dans le secteur industriel à savoir : l‟examen visuel, le ressuage, les essais ultrasonores, le contrôle par laser, la radiographie, le contrôle par magnétoscopie, la technique des courants de Foucault, la thermographie et enfin le procédé thermo-inductive. Pour chaque technique d‟inspection nous avons évoqué les avantages et les inconvénients. C‟est l‟examen par les courants de Foucault qui

Caméra infrarouge L‟inducteur Résultats Générateur d‟induction La pièce Traitement d‟image

(30)

constitue le sujet de ce travail. Le choix d‟un tel contrôle est justifié par sa simplicité, réalisation pratique non coûteuse. Dans le deuxième chapitre, nous rappelons les notions de base sur les capteurs inductifs utilisés dans le contrôle non destructif par courants de Foucault.

(31)

Chapitre II

(32)

CHPITRE II Les capteurs inductifs

II.1. Introduction

L‟examen non destructif par capteurs inductifs est un procédé relativement répandu dans le secteur industriel. Les capteurs à courants de Foucault sont utilisés depuis plus d'un siècle pour le contrôle des pièces conductrices notamment métalliques. De nos jours, la théorie des capteurs à courants de Foucault est déjà largement développée. Ils trouvent leurs applications dans divers domaines industriels qui vont de la mesure des propriétés de la matière, des mesures dimensionnelles jusqu'à la détection de défauts dans les pièces mécaniques. Dans ce chapitre, on essayera de donner quelques notions sur les courants de Foucault et le principe des capteurs inductifs. Ensuite on passera en revue sur les différents types de capteurs à courants de Foucault, les différentes formes géométries des circuits magnétiques, les modes d‟excitation et on terminera par les principaux paramètres influant l‟inspection.

II.2. Les courants de Foucault

Un champ magnétique variable dans le temps et passant à travers un contour conducteur fermé donne naissance à une force électromotrice qui joue le rôle d‟un générateur de tension qui engendre un courant dans ce contour. Ce courant apparaît aussi dans les corps conducteurs (acier, cuivre, aluminium, …etc.) en présence d‟un champ magnétique variable. Ces courants se referment dans les circuits situés dans des plans perpendiculaires au champ magnétique. De tels courants sont appelés courants de Foucault (courants induits).

Ces courants créent, à leur tour, leurs propres champs

magnétiques et peuvent avoir une action démagnétisante sur le champ principal (initial) d‟une part ; d‟autre part ces courants induits dans les corps métalliques entraînent un excès de consommation d‟énergie électrique et réduisent le rendement des systèmes électromagnétiques. Ces pertes sont appelées pertes par courants de Foucault. Cependant, on peut les utiliser pour mettre en action certains mécanismes pour obtenir un régime de fonctionnement souhaité. Les courants induits sont très utilisés dans les fours à induction, les magnétomètres, les compteurs d‟énergie électrique, le freinage et le diagnostique des objets métalliques (contrôle non destructif par courants de Foucault) [1, 13, 14, 16].

Fig. II.1. Jean Bernard Léon Foucault

(33)

23 II.3. Principe des capteurs inductifs

Un capteur inductif est constitué d‟une bobine parcourue par un courant variable dans le temps, génère des courants induits dans les objets métalliques apportés à proximité de ce capteur. Ces courants créant eux-mêmes un flux magnétique qui s‟oppose au flux générateur modifient ainsi l‟impédance du capteur. C‟est l‟analyse de cette variation d‟impédance qui fournira les indications exploitables pour le contrôle. En effet, le trajet, la répartition et l‟intensité des courants de Foucault dépendent des caractéristiques physiques et géométriques des objets considérés, et bien entendu des conditions d‟excitation (paramètres électriques et géométriques du bobinage). On conçoit dès lors qu‟un défaut, constituant une discontinuité électrique venant perturber la circulation des courants induits, puisse engendrer une variation d‟impédance décelable au niveau de la bobine d‟excitation, comme l‟illustre la figure II.2 [1, 4, 5, 9].

Fig. II.2. Principe des capteurs inductifs.

II.4. Les formes d’enroulements des capteurs inductifs

Selon la nature du produit à contrôler, il existe deux façons de mettre en œuvre le bobinage des capteurs inductifs [5, 9, 7].

- Bobine cylindrique (peut être utilisée, avec ou sans noyau) :

(34)

- Bobine plate (spirale) :

Fig. II.4. Bobine plate.

II.5. Différents types des capteurs inductifs

Il existe un grand nombre de façons pour mettre en œuvre le bobinage afin de réaliser un contrôle par courants de Foucault. Nous indiquons ici les configurations de base des capteurs.

II.5.1. Capteur absolu

C‟est un capteur à double fonction, il est constitué d‟une seule bobine émettrice-réceptrice qui crée le flux alternatif grâce au courant qui la parcourt et subit des variations d‟impédance que l‟on peut détecter en mesurant très finement sa signal de sortie (figure II.5) [1, 5, 8, 18]. La figure II.6 montre les signaux issus d‟un capteur absolu.

Fig. II.5. Le capteur absolu.

II.5.2. Capteur double

C‟est un capteur à fonctions séparées, il est constitué de deux bobines une excitatrice pour créer le flux et l‟autre réceptrice pour le recueillir. Ces deux bobines sont moulées dans un même boîtier pour éviter toute modification fortuite de leur mutuelle. Ce type de capteur est très utilisé pour les contrôles à basses fréquences (f < 1kHz) [1, 5, 8, 18, 19, 21]. Comme dans le cas du capteur absolu, la figure II.6 illustre les signaux de sortie d‟un capteur double.

La cible

(35)

25 a. signal de sortie.

b. Variation de la réactance et résistance en fonction du temps.

c. signature de signale de sortie.

Fig. II.6. Visualisation d'un défaut issu d‟un capteur absolue.

Fig. II.7. Le capteur double. Réactance

Résistance

La cible

(36)

II.5.3. Capteur différentiel

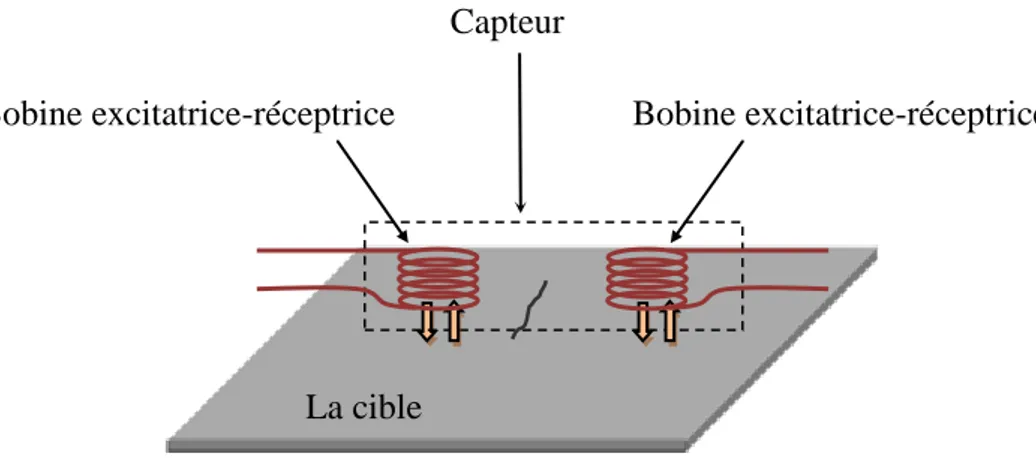
Un capteur en mode différentiel est une sonde destinée à accéder aux seules variations locales des caractéristiques du produit examiné, par différence permanente de deux mesures simultanées en deux zones voisines. Le capteur peut être constitué de deux enroulements identiques dont on mesure l‟écart de l‟impédance (figure II.8). Cette sonde est particulièrement utilisée pour détecter des discontinuités lors de son déplacement le long d‟une pièce en s‟affranchissant des perturbations induites telle que les variations de la distance sonde-pièce (lift-off) [1, 5, 8, 17, 20].

Fig. II.8. Le capteur différentiel.

II.5.4. Capteur multiple

Le capteur multiple (capteur matriciel) peut être réalisé par assemblage d‟un ensemble de bobines identiques qui fonctionnent d‟une manière autonome (figure II.10). La constitution d'un capteur matriciel est nécessaire pour répondre à certains critères. Dans le cas d‟un contrôle effectué selon deux axes, la procédure d'inspection avec un capteur unique peut s'avérer trop longue. Pour remédier ce problème, il est très intéressant d‟associer en ligne plusieurs capteurs élémentaires fonctionnent en même temps. En multiplexant les informations issues de chacun d'eux, il est possible d'accéder plus rapidement aux propriétés de la cible. L'association en ligne de plusieurs capteurs judicieusement espacés en fonction de la taille des défauts à détecter permet de recueillir des signaux suffisamment riches en information [4, 5, 9, 21, 22, 23, 24].

II.6. Différentes formes géométriques du circuit magnétique

Les lignes de champ qu'elles émettent les capteurs inductifs s'épanouissent largement. Afin de limiter les zones d'interaction de la sonde, on couple généralement celle-ci avec un circuit

La cible

Bobine excitatrice-réceptrice Bobine excitatrice-réceptrice Capteur

(37)

27 basse fréquence ou en ferrite pour les fréquences les plus élevées. Son rôle est de canaliser les lignes de champ magnétique vers la zone qu‟on veut l‟inspecter [5, 9].

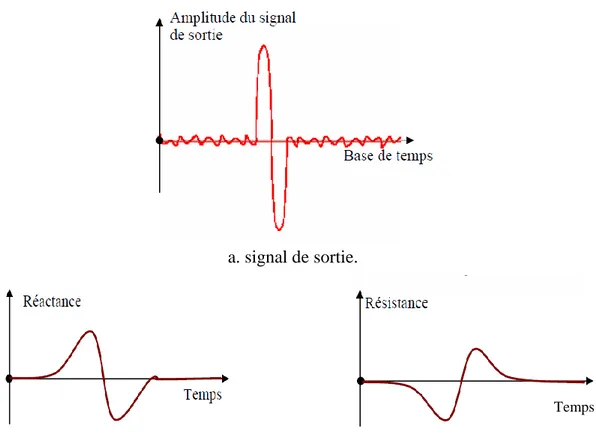
a. signal de sortie.

b. Variation de la réactance et résistance en fonction du temps.

c. signature de signal de sortie.

Fig. II.9. Visualisation d'un défaut avec une sonde différentielle. Temps

Réactance

(38)

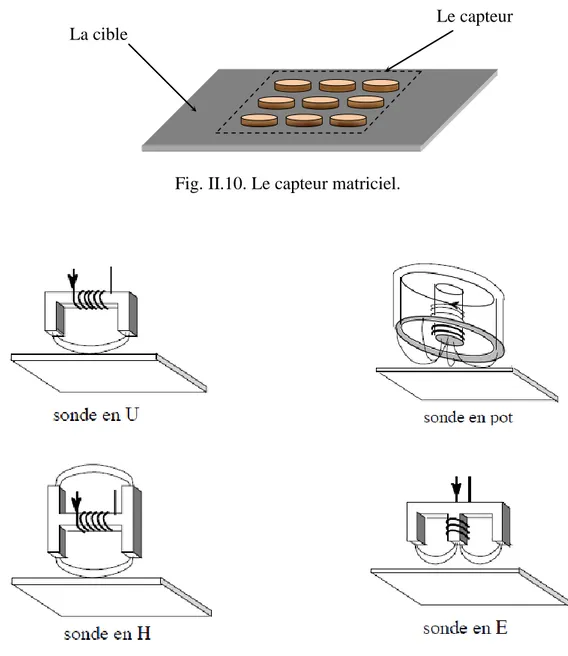
Fig. II.10. Le capteur matriciel.

Fig. II.11. Les différentes structures du circuit magnétique.

II.7. Disposition des capteurs

En pratique, on trouve essentiellement trois dispositions.

II.7.1. Première disposition : capteurs encerclant

Cette disposition est destinée au contrôle au défilé des produits longs de forme simple et de diamètre modeste tels que les fils, barres et tubes (figure II.12). Les bobines sont immobilisées et protégées dans une pièce moulée dont l‟alésage doit être de diamètre très peu supérieur à celui du produit, afin d‟obtenir un coefficient de remplissage le plus voisin possible de l‟unité. Cette condition est nécessaire pour avoir une bonne sensibilité de détection sans avoir à utiliser un taux d‟amplification trop fort apportant une dégradation du rapport signal/bruit.

La cible

Le capteur multiple

(39)

29 Fig. II.12. Capteur encerclant.

II.7.2. Deuxième disposition : capteurs internes

Ce capteur est consacré pour le contrôle des tubes par l‟intérieur, pour lesquels les bobines sont aussi moulées de façon concentrique à l‟axe du produit (figure II.13). Ce type de capteur est principalement utilisé pour le contrôle des multiples tubes de petit diamètre qui constituent les échangeurs thermiques ou les générateurs de vapeur dans l‟industrie nucléaire.

Fig. II.13. Capteur interne.

II.7.3. Troisième disposition : capteurs ponctuels

Cette disposition est adaptée aux explorations ponctuelles en contrôle manuel ou au balayage de grandes surfaces en contrôle automatique (figure II.14). Les sondes utilisées comportent un ou plusieurs bobinages moulés sont généralement dotées d‟un noyau de ferrite très perméable aux faibles champs alternatifs dont son rôle consiste à permettre d‟éloigner les enroulements de la surface à contrôler, tout en gardant une bonne sensibilité de détection [1, 5, 9].

Fig. II.14. Capteur ponctuel.

La cible Le capteur

(40)

II.8. Modes d’excitation

L‟extraction de l‟information sur la pièce à contrôler est liée au mode d‟excitation du capteur. On peut distinguer trois modes d‟excitation : excitation mono-fréquence, excitation multifréquences et l‟excitation pulsée.

Dans l‟excitation mono-fréquence, le choix de la fréquence dépend essentiellement de l‟application visée et de la sensibilité aux paramètres recherchés. Elle devra cependant se situer dans une gamme raisonnable. En effet, pour une fréquence trop basse, l‟amplitude des courants de Foucault sera faible. Une fréquence trop élevée fait apparaître des phénomènes capacitifs parasites, engendrés notamment par les capacités inter-spires de la sonde. Celles-ci provoquent des résonances et tendent à court-circuiter le circuit inductif [5, 8].

Le contrôle par courants de Foucault multifréquences est très utilisé pour l‟inversion des données fournies par la sonde en vue de déterminer des paramètres du matériau en regard. Selon les applications considérées, ces paramètres peuvent être de différentes natures :

- Distance sonde-cible (lift-off).

- Conductivité électrique de la cible (σ). - Perméabilité magnétique de la cible (μ). - Défauts dans le matériau.

- Epaisseur du matériau à contrôler.

Dans un problème d‟inversion quand il s‟agit d‟identifier n paramètres de la cible, il est nécessaire de disposer d‟au moins n observations de la sonde.

L‟inspection avec excitation pulsée a été mise en place dans les années cinquante pour une application d‟évaluation d‟épaisseur de revêtement métallique, puis elle a été appliquée à la détection de défauts profonds. Dans ce type de contrôle, c‟est l‟évolution temporelle des signaux qui est utilisée. Sur le principe, une telle méthode est plus riche en informations qu‟un contrôle par courants de Foucault sinusoïdal mono ou multifréquences. Cependant, l‟excitation pulsée nécessite une instrumentation particulière : générateur d‟impulsions à fort courant, système d‟acquisition performant puisque les signaux à mesurer étant rapides et souvent de faibles amplitude [5, 8, 9, 25, 26].

II.9. Densité du courant et profondeur de pénétration dans la cible

II.9.1. Propagation du champ magnétique dans un milieu conducteur

L‟ensemble des phénomènes électromagnétiques est régi par les équations de Maxwell. Celles-ci constituent un système d‟équations aux dérivées partielles qui lient les phénomènes magnétiques aux phénomènes électriques [8, 16, 27, 28].

(41)

31 Ces équations sont les suivantes :

D J

H

rot  t (théorème d‟Ampère-Maxwell) (II.1)

Β E

rot t (loi de Faraday) (II.2)

0

divB (loi de conservation) (II.3)

ρ



D

div (théorème de Gauss) (II.4)

Dans ces équations, ∂t symbolise la dérivée par rapport au temps, ρ représente la densité

volumique de charges électriques (C. m-3). E est le champ électrique (V. m-1), H est le champ magnétique (A. m-1). D est l‟induction électrique (C. m-2), B est l‟induction magnétique (Wb. m

-2

ou T) et J représente la densité du courant de conduction (A. m-2). A ces quatre équations, on ajoute les équations des milieux :

J = ζE (II.5)

B = μH (II.6)

D = εE (II.7)

Où μ, ε et ζ représentent respectivement la perméabilité magnétique (H. m-1

), la permittivité électrique (F. m-1) et la conductivité électrique (S. m-1 ).

On se placera dans l‟hypothèse de l‟électrotechnique et on considère des fréquences inférieures à quelques MHz [8, 28], on peut négliger le terme des courants de déplacement (tD) dans (II.1) soit : J H rot  (II.8) On a : B

rot  rot H (II.9)

 J (II.10)

 E _(II.11)

B rot

rot   rot E (II.12)

J.C. Maxwell 1831-1879

Fig. II.15. James Clark Maxwell (1831-1879)

(42)

Donc

L‟analyse vectorielle nous donne :

On combine les équations (II.3, II.13 et II.14), on obtient :

Si le champ magnétique est fonction sinusoïdale du temps :

tel que

B0 est l‟induction magnétique à l‟instant initial (t = 0) ;

ω est la pulsation de l‟induction magnétique. θ est l‟angle de déphasage.

Posant k , on obtient l‟équation générale de la propagation d‟un champ sinusoïdal dans un milieu conducteur :

Pour chaque géométrie particulière (forme de la pièce, forme de la bobine inductrice) on obtient le champ d‟induction magnétique, en développant cette équation et en l‟intégrant compte tenu des conditions aux limites [4, 18].

 Cas particulier : matériau plan

Considérons un matériau ayant une face plane (X,Y) et occupant tout le demi-espace défini par 0

Z  (figure II.16). Le matériau est excité par une nappe de courant sinusoïdal de pulsation ω, plane, uniforme et infinie, contenue dans un plan Π parallèle à la face.

B rot

rot   _tB (II.13)

B rot

rot grad (div B)B (II.14)

B   tB (II.15) B B₀ ej(t) (II.16) 0 j    B B (II.17) 0 k j 2   B B (II.18)

(43)

33 Fig. II.16. Courants de Foucault dans une interface plane.

Une telle nappe de courant crée un champ B perpendiculaire au plan (X,Z), parallèle au plan (X,Y) et garde une valeur constante dans le plan Π. Ce champ est donc fonction de Z et de t. L‟équation de propagation (II.18) s‟écrit alors :

L‟équation caractéristique de l‟équation différentielle (II.19) est :

Alors :

Pour un matériau s'étendant jusqu'à l'infini le long de L'axe Z,le champ B tend vers 0, soit :

D‟où :

C2 représente donc le champ magnétique dans la surface Z=0. On pose :

0 B k j B 2 2 z    (II.19) 2 k j 1 j k r 0 k j r2 2    (  ) (II.20) z 2 k j 1 2 z 2 k j 1 1e C e C B ) ( ) (     (II.21)  _ C e C e 0 1 2 (II.22) C1=0 et z 2 k j 1 2 e C B ) (   (II.23) C2= B0 e jωt (II.24)