Direct Simulation Monte-Carlo predictions of coarse elastic particle statistics in fully developed turbulent channel flows: Comparison with deterministic discrete particle simulation results and moment closure assumptions

O

pen

A

rchive

T

OULOUSE

A

rchive

O

uverte (

OATAO

)

OATAO is an open access repository that collects the work of Toulouse researchers and

makes it freely available over the web where possible.

This is an author-deposited version published in :

http://oatao.univ-toulouse.fr/

Eprints ID : 22827

To link to this article : DOI:

10.10.1016/j.ijmultiphaseflow.2018.06.005

URL

http://dx.doi.org/10.1016/j.ijmultiphaseflow.2018.06.005

To cite this version : Fédé, Pascal and Simonin, Olivier : Direct

Simulation Monte-Carlo predictions of coarse elastic particle statistics in

fully developed turbulent channel flows: Comparison with deterministic

discrete particle simulation results and moment closure assumptions

(2018), International Journal of Multiphase Flow, vol. 108, pp.25-41

Any correspondance concerning this service should be sent to the repository

administrator:

staff-oatao@listes-diff.inp-toulouse.fr

Direct

Simulation

Monte-Carlo

predictions

of

coarse

elastic

particle

statistics

in

fully

developed

turbulent

channel

flows:

Comparison

with

deterministic

discrete

particle

simulation

results

and

moment

closure

assumptions

Pascal Fede

∗

_{, Olivier Simonin}

Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, Toulouse, France

Keywords:

DSMC

Gas-particle vertical flow Second-order moment method

a

b

s

t

r

a

c

t

Thepaperpresentsnumericalsimulationsofparticle-ladenfullydevelopedturbulentchannelflows per-formedinastochasticLagrangianframework.Theparticleinertiaislargeinordertoneglecttheeffect oftheturbulentgasmotionontheparticledispersion.Incontrasttheinter-particlecollisionsare impor-tantandaccountedforbyusingDirectSimulationMonte-Carlo(DSMC)method.Thecomparisonofthe Monte-CarloresultswiththoseobtainedbyDiscreteParticleSimulation(DPS)showsthatthestochastic collisionsalgorithmisabletopredictaccuratelytheparticlestatistics (numberdensity, meanvelocity, second-andthird-ordervelocitymoments)inthecoreflow.More,thepaperanalysesthenumber sec-tionsneeded foraccuratepredictions.Intheverynear-wallregion,theMonte-Carlo simulationfails to accountforthewallsheltereffectduetothewall-normalunbalancedinter-particlecollisionsinfluence inducedbythepresence ofthewall.Then,the papershows thatDSMCpermits toassess theclosure approximationsrequiredinmoment approach. Inparticular, theDSMC resultsare comparedwiththe correspondingmomentclosureassumptionsforthethird-ordercorrelationsofparticlevelocity,the cor-relationsbetweenthedragforceandthevelocityandtheinter-particlecollisionterms.Itisshownthat attheoppositeofthestandardDSMC,themomentapproachcanpredictthewallsheltereffect.Finally, amodelforthemeantransverseforceisproposedfortakingintoaccountwallsheltereffectinDSMC.

1. Introduction

Particle-laden flows are found in a large spectrum of practi-cal applications ranging from geophysical flows (sediment trans-port,pyroclastic flow,volcanoashes dispersion...)toindustrial ap-plications (solid or liquid fuel combustor, catalytic reactor, spray tower, solid handling,...) and passing through medical applica-tions (room disinfection, medicament aerosol inhalation,...). In isothermal particle-laden flows, many complex phenomena take place,suchasturbulentdispersion,inter-particlecollisions,particle bouncingwithsmoothorroughwalls,orturbulencemodulationby theparticleswhoneedtobeaccuratelymodelled.

Because of the discrete nature of the particles, the numeri-cal simulation of the particle motion is widely performed in a Lagrangian framework by DiscreteParticle Simulation (DPS).That approach can be either coupled with Direct Numerical

Simula-∗ _{Corresponding author.}

E-mail address: pascal.fede@imft.fr (P. Fede).

tion (DPS/DNS),LargeEddySimulation(DPS/LES)orReynolds Av-eraged Navier–Stokes approach (DPS/RANS) (Sommerfeld, 2001; Riberetal.,2009;BalachandarandEaton,2010;Fox,2012; Capece-latro and Desjardins,2013). When the collisions are treated in a deterministicmanner,DPS/DNScanbeconsideredasfull determin-istic numerical simulationapproach because no stochastic model for both particleturbulent dispersion and inter-particle collisions are needed. In contrast, for DPS/LES and DPS/RANS, a stochastic dispersion model is neededto account forthe subgrid (LES), or thefluctuating(RANS),fluidvelocityalongtheparticletrajectories. Inpracticalapplications,duetothehugenumberofrealparticles, thecomputationofallindividualparticletrajectoriesisnot possi-blebutthisdifficultycanbeovertakenintheframeofLagrangian statisticalapproachesleading toreplacetherealparticlesbya re-ducednumberofparcelsrepresentingseveralrealparticles.

StochasticLagrangianalgorithms werefirstderivedforthe col-lisions ofmoleculesinrarefiedgases(Bird,1969;Babovsky,1986). In the framework of DPS/RANS approach these algorithms were used for taking into account the inter-particle collisions in gas-particle turbulentflows (O’Rourke,1981; Tanaka andTsuji,1991).

However,severalstudieshaveshownsomeproblemsrelatedtothe effectoftheturbulenceonthecollidingparticles(Berlemontetal., 1995;Sommerfeld,2001;Berlemontetal.,2001;Wangetal.,2009; Pawaretal.,2014;Fedeetal.,2015;Heetal.,2015;Tsirkunovand Romanyuk,2016).

In the present paper, Monte-Carlo algorithm is used to ac-count fortheinter-particlecollisions inavertical turbulent chan-nelflows.ThentheDSMCmethodisassessedbycomparisonwith statistics from DPS where the fluid flow is steady and imposed (SakizandSimonin,1998;1999b;1999a). Insuchacase, the par-ticleinertiaissufficientlylargesothattheeffectoftheturbulence ontheparticlemotioncanbeneglected.More,thesolidmass load-ing issmallinordertoneglecttheturbulencemodulationbythe presence oftheparticles. Hence,theproposedsimulationmethod is developedinthe frameofDPS/RANS approachwhere thefluid velocity isknownandpredictedbythestandardk−

ε

model.The particlesdynamiciscontrolledbythecompetitionbetweenthe en-trainment bythemeanfluidflowandtheinter-particlecollisions. In Section4,the resultsgivenbythestochastic algorithmare as-sessed by comparison with the deterministic DPS predictions. A very goodagreement isfoundbetweenboth simulationmethods, exceptintheverynear-wallregionwherethedeterministic simu-lationsexhibit a“wall sheltereffect” thatcannotbeaccountedfor byusingthestandardDSMCmethod.

Following Fede et al. (2015), DSMC methods are Lagrangian stochastic methods developed for the numerical solution of the Euleriankinetic equation governingtheparticlevelocity Probabil-ity Density Function (Reeks, 1991) orthe particle-fluid joint PDF (Simonin,1996).Anothermethodtocomputetheparticlestatistics consistsin thenumericalsolutionofgoverning equationsderived fromthePDFkineticequationforseverallow-orderparticle veloc-itymoments(numberdensity,meanvelocity,fluctuantkinetic en-ergy, ...)Suchanapproach,commonlycalledEulerianapproachor moment method,leads to solvea set ofEuleriantransport equa-tions andneeds to develop additionalclosuremodelling assump-tions for the gas-particle and particle-particle interaction terms and for the high-order velocity moment representing the kinetic dispersion (transport by the particlevelocity fluctuations). Inthe present study,DSMCresultsareusedtoanalysetheclosure mod-elsforthedrag,theturbulentdispersionandthecollisionsderived intheframeofsecondordermomentmethods.

After the introduction, the paper gives the configuration and detailstheinvestigatedcases.Thethirdsectionisdedicatedtothe statistical approaches for turbulent gas–solid flows. The focus is made on the DSMC algorithm for taking into account the inter-particlecollisions.TheDSMCresultsareanalysedinthefourth sec-tionbycomparisonwithdeterministicsimulations.Theanalysisof second ordermomentclosures fromDSMCresultsisgiveninthe fifth section.Amodelfortakingintoaccountthe“wallshelter ef-fect” inDSMCisproposed.Thepaperendsbyconcludingremarks.

2. Configurationoverview

2.1. Fluidflow

The flow configuration is a fully developed vertical gas–solid turbulent channel flow (SakizandSimonin, 1998;1999a; 1999b). AsshownbyFig.1,thecomputationaldomainisarectangularbox withperiodicboundaryconditionsinthestreamwiseandspanwise directions.

Accordingtothelargeparticleinertiaandtothelowsolidmass loading,theparticleinteraction withthefluid turbulenceandthe modificationofthemeanfluidflowbytheparticles(two-way cou-pling) wereneglected.Therefore,inthiswork,thefluidvelocityis agivenmeanfieldtakenfromk−

ǫ

modelpredictionsoffully

de-Fig. 1. Flow configuration with L x = 240 mm, L y = 40 mm, and L z = 32 mm.

Table 1

Particle material properties. The mean solid volume volume fraction is computed as αp =

Npπd3p / 6 /V with N p the total number of tracked particles in DPS and V the volume of the compu- tational domain. dp µm ρp [kg/m 3 ] αp Np 200 1038 5 × 10 −4 _{31,0 0 0} 406 1038 1 . 2 × 10 −3 _{90 0 0} 406 1038 4 × 10 −3 29,600 406 1038 10−2 73,800 1500 1032 4 . 1 × 10 −3 ₆₀₀ 1500 1032 1 . 4 × 10 −2 _{20 0 0} 1500 1032 4 . 1 × 10 −2 _{60 0 0}

velopedturbulentchannelsingle-phaseflow.Thematerial proper-tiesofthefluidare

ρ

f =1.205kg/m3an

ν

f=1.515× 10−5m2/s.

2.2.Particlemotion

The particles are assumed spherical with a diameter dp and

with a large particle-to-fluid density ratio (see Table 1). In such aframework,onlythedragforceandthegravityareactingonthe particles motion. Introducing up, the particletranslation velocity

anduf @p, thefluid velocity seenby the particle,the particle

ve-locitymomentumequationreads

dup dt = Fd mp =− up− uf @p

τ

p +g (1)

whereFd is theinstantaneous drag force acting on a single

par-ticle,gthegravity acceleration,and

τ

p theinstantaneous particle

responsetimegivenby

τ

p= 4 3

ρ

p

ρ

g dp CD 1

|

vr

|

. (2)

InEq.(2),vr=up− uf @pistheinstantaneousgas-particlerelative

velocity,

ρ

ptheparticledensity.Thedragcoefficient,CD,isgivenin

termsofparticleReynoldsnumber(SchillerandNaumann, 1935),

CD= 24 Rep

£

₁ +0.15Re0.687 p

¤

₍₃₎

withRep=dp

|

vr

|

/

ν

g.Asthegasturbulenceandthetwo-way

cou-plingare bothneglected, theinstantaneous fluidvelocity seenby theparticleisobtainedbyaninterpolationofthegivenmeanfluid velocityfieldattheparticlecentreposition:uf @p=Uf

(

xp

)

.

2.3.Inter-particleandparticle-wallcollision

In the present study the particle volume fractions are suffi-cientlylow inorderthat onlybinary collisions are takeninto

ac-Fig. 2. Effect of the number of sections used for the DSMC for a fixed number of parcels ( N par = 10 , 0 0 0 ). The left column corresponds to the case where d p = 200 µm & αp = 5 . 0 × 10 −4 and the right column to the case where d p = 406 µm & αp = 10 −2 . Top: Mean particle density number an bottom: mean vertical particle velocity.

count. Considering a collision between a particle p and a parti-cle q, the unit vector linking the centre of the p-particle to the oneoftheq-particleiskandtheinter-particlerelativevelocityis w₌uq− up.Neglectingtheinter-particlefriction,thevelocities

af-teracollisionaregivenby

u∗ p=up+ 1₊ec 2

(

w.k

)

k (4) u∗ q=uq− 1₊ec 2

(

w.k

)

k. (5)

where ec is the inter-particle restitution coefficient. The

particle-wall interactions are considered fully elastic without friction. Then the particle velocity after wall bouncing reads u∗_p=up− 2

(

up.nw

)

nw wherenwistheunitvectornormaltothewall.

3. Statisticalmodellingapproaches

3.1. Statisticaldescription

The statisticaldescriptionofthedispersedphase,composedof solid particles transportedbya turbulentfluid flow, reliesonthe analogy with the thermal motion of molecules as described by the kinetictheory ofrarefiedgases(ChapmanandCowling, 1970; Jenkins andRichman, 1985)andlaterextendedforturbulent gas-particle flows (Reeks, 1991; Simonin,2000; Zaichik et al., 2004; Reeksetal.,2016).Inthestatisticalapproach,thedispersedphase isdescribedbytheparticleProbabilityDensityFunction fp

(

cp,x; t

)

defined such that fp

(

cp,x_{; t}

)

dcpdx is the mean probable

num-ber of particles at time t with the centre of mass, xp, located

in thevolume [x,x+dx], andthe translationvelocity, up,within

[cp,cp+dcp].FromthePDF definitionthenumberdensityof

par-ticleswrites

np

(

x,t

)

= Z

Fig. 3. Effect of the number of sections used for the DSMC for a fixed number of parcels ( N par = 10 , 0 0 0 ). The left column corresponds to the case where d p = 200 µm & αp = 5 . 0 × 10 −4 and the right panel to the case where d p = 406 µm & αp = 10 −2 . Top: wall-normal component of the particle kinetic stress and bottom: inter-particle collision timescale.

themeanparticlevelocity,

Up,i

(

x,t

)

= 1

np Z

cp,ifp

(

cp,x; t

)

dcp, (7)

theparticlekineticstresstensorRp,i j=

h

u′p,iu′p, j

i

,

Rp,i j= 1

np Z

[cp,i− Up,i]× [cp, j− Up, j]fp

(

cp,x; t

)

dcp, (8)

and the third-order particle velocity correlation S_{p,i jk=}

h

u′ p,iu′p, ju′p,k

i

, Sp,i jk= 1 np Z [cp,i− Up,i] × [cp, j− Up, j] ×[cp,k− Up,k]fp

(

cp,x; t

)

dcp. (9)

The PDF of single particle velocity obeys the following Boltzmann-likekineticequation:

∂

fp

∂

t +

∂

∂

xi

£

cp,ifp

¤

+

∂

∂

cp,i

·¿

dup,i dt

|

cp

À

fp =

∂

fp

∂

t col (10)

where

_h

.

|

cp

i

is the ensemble average conditioned by the

par-ticle velocity, up=cp. The third term on the left-hand side of

Eq.(10)representstheforcesactingontheparticles,enclosingthe turbulentparticle-fluidcoupling.Astheeffectoftheturbulenceon theparticlemotionisneglected,thistermisdirectlywrittenas

∂

∂

cp,i

·¿

_du p,i dt

|

cp

À

fp =

∂

∂

cp,i

·µ

−cp,i

_τ

− Uf,i p + gi fp (11)

whereU_f,i

(

x,t

)

isthemeanfluidvelocity.InEq.(10)thetermon theright-handsiderepresentsthemodificationofthePDFby the inter-particlecollisions.

Fig. 4. Gas and particle mean vertical velocities for several particle diameters and mean solid volume fractions. The symbols are the DPS results from Sakiz and Si- monin (1998) and the solid lines ( ) are the DSMC results.

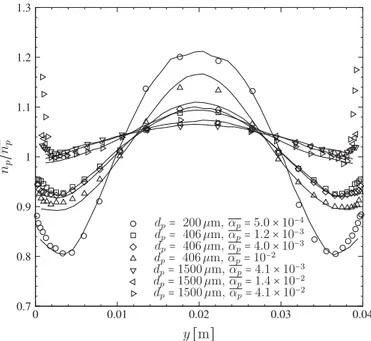
Fig. 5. Particle number density normalized by the average value over the whole domain for several particle diameters and volume fractions. The symbols are the DPS results from Sakiz and Simonin (1998) and the solid lines ( ) are the DSMC results.

3.2. Monte-Carloalgorithm

Stochastic particle methods, also called Monte-Carlo methods orDirectSimulationMonte-Carlo(DSMC),wereinitiallydeveloped forsolvingtheBoltzmannequationforrarefiedgasdynamics(Bird, 1969;Nanbu,1983;Babovsky,1986;IvanovandRogasinsky,1988; Sommerfeld,2001;Arcenetal., 2006;Fedeetal.,2015).Basically, thesemethodsapproximatethePDFas:

fp

(

cp,x; t

)

= Npar(t) X i=1 wi p

δ

£

x_{− x}i p

¤

×

δ

£

cp− uip

¤

. (12)

Fig. 6. Mean particle kinetic stress components for d p = 406 µm (top) and

dp = 1500 µm (bottom). The symbols are the DPS results from Sakiz and Si-

monin (1998) and the solid lines ( ) are the DSMC results.

Suchanapproximationcommonlyintroducestheideathatthe par-ticlesarerepresentedby“numericalparticles” or“parcels” thatare a group of wi

p of real particles located around the same space

position, and having the same velocity. An important feature of stochastic particlemethodsistheuseofafractionaltime step al-gorithm,whichconsistsinsplittingeachtimestepinthetwo fol-lowingsubsteps:

• a transport substep corresponding to the discretization ofthe free flight of parcels, i.e. the non-collisional kinetic equation. During this substep the position, velocity of each numerical particleareupdatedbysolvingtheparticlemotionequations. • a collision substep whichcorresponds to the discretizationof

the collision term. The mesh cells have to be small enough for the exact PDF to be almost uniform over them so that

Fig. 7. Third order correlations for d p = 406 µm and αp = 1 . 2 × 10 −3 . The symbols are the DPS results from Sakiz and Simonin (1998) and the solid lines ( ) are the DSMC results.

Eq.(12)couldbereplacedby:

fp

(

cp,x; t

)

= X Ci X k_∈Ind(Ci) wk p 1Ci

(

x

)

v

ol

(

C_i

)

δ

£

cp− ukp

¤

₍₁₃₎

whereCidenotesagivencellofthemeshMx,1C_i isthe

indica-torfunction ofCi (top-hatdistribution function),Ind(Ci) isthe

listofparcelslocatedincellC_iattheendofthetransportstep andvol(Ci) isthevolume ofCi.From aphysicalpoint ofview,

thisnewapproximationofthePDFmeansthat,duringthe col-lision substep, all real particles represented by a given parcel are supposed to be randomly distributed in the cell contain-ingtheparcelinsteadofbeingalllocatedatthesamepointas duringthetransportstep.Thecollisionsubstepthenconsistsin applyingaMonte-Carloalgorithmforcomputingineachcellan approximatesolutionofthespatially homogeneousBoltzmann equation:

∂

fp

∂

t

(

cp,x; t

)

=Qcoll

{

fp

}

(

cp,x; t

)

, (14)

assumingthattheinitialPDFcanbeapproximatedby(13).Itis worth noticingthattheexpressionofQcollinEq.(14)relieson

a closureassumptionforthepairPDFwhichmaybe basedon themolecularchaosassumptionforveryinertialparticleswith respecttotheturbulenttimemacroscale(Simoninetal.,2002; Fedeetal.,2015).

InDSMCmethodthewallboundaryconditionsfortheparticles arethesamethanthoseusedinDPS.

The domain is uniformly discretized in 10 to 40 Nsec vertical

sections forthe collision substep where local homogeneous ran-dom particle distribution is assumed. While computation of the particle statistics is carried out by averaging Lagrangian predic-tions on a given number of sections (Ny=40). The total

num-berof parcelsisthe sameforall casesandsetto Npar = 10,000. Figs. 2and 3 show theeffect of thesection numberNsec on the

predictions of the particle number density and of the first and second-order velocity moments. Fig. 2 shows that particle num-berdensityandmeanverticalvelocity predictionsare mesh inde-pendent froma relatively low number ofsections: Nsec = 10. In

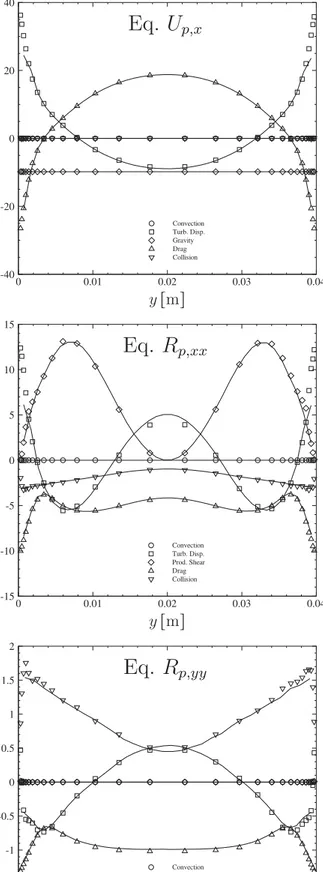
Fig. 8. Budget of moment equations for the case d p = 406 µm and αp = 1 . 2 × 10 −3 . The symbols are the DPS results from Sakiz and Simonin (1998) and the solid lines ( ) are the DSMC results.

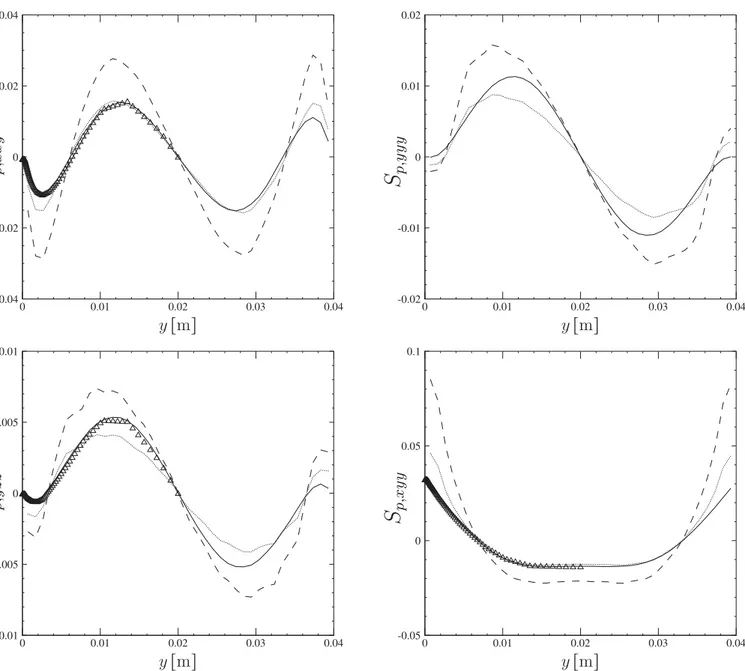
Fig. 9. Third order correlation S p,ijk for the case d p = 406 µm and αp = 1 . 2 10 −3 . The symbols are the DPS results from Sakiz and Simonin (1998) (if available), the solid lines ( ) are the DSMC results, the dashed lines ( ) the moment method modelling using Eqs. (22) and (23) and the dotted lines ( ) the moment method modelling using Eqs. (22) and (24) .

contrast,Fig.3showsthat thewallnormalparticle kineticstress,

Rp,yy,andthecollisiontimescalepredictions aremoredependent

on the number of sections. We can notice that for the smallest number of sections, Nsec = 10, the wall normal kinetic stress is slightly over-predictedfor the smallparticles, dp = 200 µm, and

under-predicted for thelarge ones, dp = 406µm.Finally, the

pre-dictionsarenearlyindependentofthemeshforNsec≥ 20,therefore thespecificvalueNsec=30isusedforthepredictionspresentedin

thepaper.

3.3. Momentapproach

FromthePDFkineticequation(Eq.(10)),itispossibletoderive thetransportequationofeachmomentofthePDF(Simonin,1996) by multiplying Eq. (10) by a polynomial function of the velocity componentsandintegratingoverallparticlevelocityexpectations. According to Sakiz and Simonin (1998), without particle deposi-tionorresuspension,forsufficientlongtime,theperiodicdiscrete particle simulation in thevertical channel leads toa fully

devel-oped particleflow withvelocity moments verifying:Up,y=0and

∂

/

∂

t≡

∂

/

∂

x≡

∂

/

∂

z≡ 0.Thenumberdensitybalanceequationwrites

∂

∂

y

(

npUp,y

)

=0. (15)

Themeanparticlevelocityequationsread

∂

Up,x

∂

t =− 1 np

∂

∂

y

(

npRp,xy

)

− g+

¿

Fd,x mp

À

+_n1 p C

(

up,x

)

, (16)

∂

Up,y

∂

t =− 1 np

∂

∂

y

(

npRp,yy

)

+

¿

Fd,y mp

À

+_n1 p C

(

up,y

)

. (17)

Astheflowisfullydeveloped,thetimederivativeinEqs.(16)and (17)is zero butit has been kept in order to clearly identify the meanvelocitycomponentwhichobeystothecorresponding equa-tion.Thefirsttermontheright-handsideisthekineticdispersion, thetwofollowingtermsarethegravityandthedragforce terms.

Fig. 10. Third order correlation S p,ijk for the case d p = 406 µm and αp = 10 −2 . The symbols are the DPS results from Sakiz and Simonin (1998) (if available), the solid lines ( ) are the DSMC results, the dashed lines ( ) the moment method modelling using Eqs. (22) and (23) and the dotted lines ( ) the moment method modelling using Eqs. (22) and (24) .

Finally,thelasttermrepresentstheeffectoftheinter-particle col-lisions.

The particle kinetic stress tensor component (or centered second-ordervelocitymoment)transportequationsarewritten

∂

Rp,xx

∂

t =− 1 np

∂

∂

y

(

npSp,xxy

)

− 2Rp,xy

∂

Up,x

∂

y +2

¿

Fd,x mp u′ p,x

À

+_n1 p C

(

u′ p,xu′p,x

)

, (18)

∂

Rp,yy

∂

t =− 1 np

∂

∂

y

(

npSp,yyy

)

+2

¿

Fd,y mp u′ p,y

À

+_n1 p C

(

u′ p,yu′p,y

)

, (19)

∂

Rp,zz

∂

t =− 1 np

∂

∂

y

(

npSp,yzz

)

+2

¿

Fd,z mp u′ p,z

À

+_n1 p C

(

u′ p,zu′p,z

)

, (20)

∂

Rp,xy

∂

t =− 1 np

∂

∂

y

(

npSp,xyy

)

− Rp,yy

∂

Up,x

∂

y +

·¿

Fd,y mp u′ p,x

À

+

¿

Fd,x mp u′ p,y

À¸

+_n1 p C

(

u′ p,xu′p,y

)

. (21)

As theflowissteady,thetimederivative inEqs.(18)–(21)iszero butit hasbeenkeptinordertoclearly identifythekinetic stress tensor component which obeys the corresponding equation. The first termon the right-hand side of Eqs. (18)–(21) is the kinetic transport (see Section 5.1). Thesecond termis theproductionby the shearofthemeanparticlevelocity. Thethirdtermrepresents theeffectofthedragforce(seeSection5.2)andthelastterm rep-resentstheeffectoftheinter-particlecollisions(seeSection5.3).

Fig. 11. A priori test of the drag term for the case d p = 406 µm and αp = 1 . 2 × 10 −3 . The symbols are the DPS results from Sakiz and Simonin (1998) , the solid lines ( ) are the DSMC results, the dashed lines ( ) the “standard” moment closure assumption of the drag ( Eqs. (26) and (27) ) and the dotted lines ( ) the extension proposed by Sakiz and Simonin (1998) including large drift effect ( Eqs. (28) and (29) ).

Fig. 12. A priori test of the drag term for the case d p = 406 µm and αp = 10 −2 . The symbols are the DPS results from Sakiz and Simonin (1998) , the solid lines ( ) are the DSMC results, the dashed lines ( ) the “standard” moment closure assumption of the drag ( Eqs. (26) and (27) ) and the dotted lines ( ) the extension proposed by Sakiz and Simonin (1998) including large drift effect ( Eqs. (28) and (29) ).

Fig. 13. Wall-normal distribution of collision time scale. The solid lines ( ) are the DSMC results, the dashed lines ( ) the moment method modelling with Eq. (30) and the dotted line ( ) with Eq. (31) .

4. DSMCresultsanddiscussion

All Monte-Carlo simulations have been made with the same numberofsectionsNsec=30ofconstantsize.Themeshfor

com-puting the statistics is also uniform with Ny=40 sections from

dp/2 to Ly− dp/2.In all cases the number of parcel is the same

Npar=10,000.Afteratransientphaseof5sthestatisticsare

com-putedduring35s.

Fig. 4 shows the mean gas and particle vertical velocities for severalmeanparticlevolumefractionsandparticlematerial prop-erties.Firstofall,itcanbeobservedthatthemeanparticlevolume fractiondoes nothaveastrongeffectontheprofilesofthemean particle velocity. At the channel centre, the mean vertical parti-cle velocity is found always smaller than the fluid velocity and, asexpectedbecauseofthe gravity,the largeristhediameterthe loweristheparticlevelocity.Closetothewallstheverticalvelocity of the particleswith dp=1500µm is always found smallerthan

the meanvertical gas velocity. In contrast, for dp=200 µm and

dp=406µm,Fig.4showsthatthemeanverticalparticlevelocity

islargerthanthefluidone.Theequilibriumbetweenthesetwo re-gionsiscontrolledbythewall-normalkineticdispersionleadingto amuchflatprofileforparticlethanforthegas.

As shownby Fig. 4,the DSMC predictions ofthe mean parti-clevelocityareinverygoodagreementwiththeDPSresults.Only slightdifferencescanbeobservedinthenear-wallregions.

The DSMC prediction of the particles number density across the channel is shownby Fig. 5. One can observed that the par-ticlenumber density profiles exhibit a maximum atthe channel centre.When approaching the wall, the particle number density decreases forreaching a minimum.Finally,for thesmaller diam-eters (dp=200 µm anddp=406 µm), the particle number den-sitycomputedfromtheDSMCresultsincreasesuptothewall.For

dp=1500µm theprofiles ofnp arefound slightlyflatter

indicat-ing a larger efficiency of the dispersion in wall-normal direction asshownby thevelocityprofiles too.Forthelarge particleswith

dp=1500µm,Fig.5showslargediscrepanciesbetweentheDSMC

andDPSparticlenumber densitypredictionsinthe near-wall re-gion.Asamatteroffact,theDPSresultsshowastrongincreaseof

Fig. 14. A priori test of the collision term in transport equation of the second order particle velocity correlation for the case of d p = 406 µm. The symbols are the DPS results from Sakiz and Simonin (1998) , the solid lines ( ) are the DSMC results, the dashed lines ( ) the moment method predictions by Eq. (32) and (30) .

Fig. 15. A priori test of collision term in U p,y moment equation for the case

dp = 406 µm, αp = 1 . 2 × 10 −3 . The symbols are the DPS results from Sakiz and Si-

monin (1998) , the solid lines ( ) the DSMC results and the dashed lines ( ) the moment method modelling with Eq. (33) . In such a case the number of sections for computing the statistics is N y = 100 .

the particlenumber densitywhen approaching thewall andthis peculiarbehaviour isnot capturedby the DSMCmethod. Follow-ingSakizandSimonin(1998),thiseffectcomesfromthefactthat the momentum transfer by inter-particle collision is unbalanced forparticlessheltered bythewall closeness.It resultsamean ef-fective forcetowards thewallleading toan increase ofthe parti-clenumberdensity.Thiseffect,calledhere“wallsheltereffect”,is foundtobeeffectiveonlywhentheparticlecentretowalldistance issmallerthan3/2dp.

The time-averaged components of the particle kinetic stress tensor components (or second order velocity correlations) mea-sured in DPSandpredicted by the stochastic Lagrangian simula-tions areshownbyFig.6.Itcanbe observedthatthepredictions

of the DSMC method are in very good agreement withthe DPS results. Fig. 6 shows that the fluctuating motion of the particles is anisotropic because of the production by the gradient of the mean particle velocity and a weak redistribution effect fromthe vertical velocity variance towardsthe horizontalones. It canalso be observedthatwhenthesolid volumefractionisincreasingthe anisotropyisdecreasing(Fig.7).

Fig.8showsacomparisonbetweentheDSMCandtheDPS re-sultsofeachtermfromthemomentequationsEqs.(16)–(21).

5. Evaluationofclosureassumptionsforsecond-ordermoment transportequation

5.1. Triplevelocitycorrelationclosuremoment

AsshownbyEqs.(18)–(21),thesecondordermomentapproach requiresclosureassumptionsforthethirdorderparticlefluctuating velocitycorrelationsSp,ijk.FollowingSimonin(1996)andSakizand

Simonin (1999b), such a closure assumption can be obtained by writingthetransport equationofthethirdordercorrelation Sp,ijk

forsteadyflowconditions.Severaladditionalassumptionsare nec-essary asthe effectof theturbulence andthe productionby the gradients of the mean particle velocity are neglected. Then, the fourth-order correlation,Qp,ijkl,isapproximatedassuminga

Gaus-sian distribution leading to write the fourth-order correlation in terms of the second-order correlations. Finally a Grad’s approxi-mation (Grad, 1949)is usedforwritingthecollisiontermsinthe equationofSp,ijk.

Hence, similarly to the model proposed (Hanjalic and Laun-der,1972)forsingle-phaseturbulentflows,thethirdorder correla-tioncanbewrittenas:

Sp,i jk=−Kp,in

∂

Rp, jk

∂

xn − Kp, jn

∂

Rp,ik

∂

xn − Kp,kn

∂

Rp,i j

∂

xn (22)

wheretheparticledispersioncoefficientreads

Kp,i j=

·

₃

τ

F f p +2₃

ξ

_τ

c c −1 Rp,i j (23)

and

ξ

c=

(

1+ec

)(

49− 33ec

)

/60isamodelconstantdepending on

Fig. 16. Particle number density normalized by the average value over the whole domain for the case d p = 1500 µm (left: αp = 1 . 4 × 10 −2 and right: αp = 4 . 1 × 10 −2 ). The symbols are the DPS results from Sakiz and Simonin (1998) , the solid lines ( ) the standard DSMC results and the dotted lines ( ) the DSMC results with the “wall force” given by Eq. (34) .

Fig. 17. Particle vertical velocity for the case d p = 1500 µm. Left: αp = 1 . 4 × 10 −2 and right: αp = 4 . 1 × 10 −2 . The symbols are the DPS results from Sakiz and Simonin (1998) , the solid lines ( ) the standard DSMC results and the dotted lines ( ) the DSMC results with the “wall force” given by Eq. (34) .

Figs. 9 and10 show thethird-order correlations, appearingin the kinetic stress transport Eqs.(18)–(21),forthe casewithdp=

406 µm.Asalreadyshown, it canbe denotedtheremarkably ac-cordancebetweentheDPSandDSMCresults.Themomentclosure assumptions ofSp,ijk usingEqs. (22)and (23)are also shownby

Figs.9and10.

Figs. 9and10showthat themomentclosureapproachallows toreproduceroughlytheshapeoftriplevelocitycorrelationradial profiles givenby DPS orDSMC andthe agreement between mo-ment closure approach and simulation results is increasing with respecttothevolumefraction.Therefore,themeasured discrepan-ciesmaybeinterpretedasanoverestimationofthedispersion coef-ficientgivenby Eq.(23).AccordingtoSakizandSimonin(1999a), this effect is due to the fact that inter-particle collision time

τ

c

isnotsufficientlysmall,comparedtothe particlerelaxationtime,

τ

F

f p,andto themean particletransit time acrossthe channel

τ

pK

(

τ

K

p =Ly/ Rp,yy, where Ly is the width of the channel)to allow

thecollisionprocesstocounterbalancenon-equilibriumeffects in-ducedby the interactionwith thefluid andby the wall confine-ment.Following Sakizand Simonin(2001),a semi-empirical cor-rectionofthedispersioncoefficientisproposedtoaccountforthe non-equilibriumeffect, Kp,i j= 1 C 3

τ

F f p +2₃

ξ

_τ

c c −1 Rp,i j (24)

Fig. 18. Particle kinetic stress tensor for the case d p = 1500 µm. Left: αp = 1 . 4 × 10 −2 and right: αp = 4 . 1 × 10 −2 . The symbols are the DPS results from Sakiz and Si-

monin (1998) , the solid lines ( ) the standard DSMC results and the dotted lines ( ) the DSMC results with the “wall force” given by Eq. (34) .

with, C₌1₊ √₃₂

π

τ

K p

·

₂

τ

F f p +

σ

_τ

cc p −1 (25)

We can notice that C is about 3 in the very dilute case (

α

p=

1.2× 10−3) andis aboutunityinthe lessdilute case(

α

p=10−2). Figs. 9 and 10 show that the model proposed by Sakiz and Si-monin (2001) improvessignificantly themoment methodclosure assumption.

5.2. Gas-particlemomentumtransferterms

Inthepresent paper,thefocusismadeonthecasewherethe gas-particleinteractions aredriven onlyby thedrag force.Except forthe Stokes’s regime,forvery smallparticulateReynolds num-bers, the drag force dependence on the gas-particle relative ve-locity is nonlinear. In 1991, Simonin (1991) proposes to approx-imate the drag force by introducing the mean particle response time

τ

F f p,definedas 1 τF f p= 18ρfνf ρpd2p

£

1₊0.15

h

Rep

i

0.687

¤

with

h

Rep

i

=

dp

­|

vr

|

2

®

/

ν

f.Themeanrelativevelocitybeinggivenby

­|

vr

|

2

®

=

Vr,mVr,m+

­

v

′_r,m

v

′_r,m

®

.Usingthisapproximation,thedragtermsin

momentumandparticlekineticstresstransportequationsread

¿

Fd,i mp

À

=−

_τ

Vr,iF f p (26)

¿

Fd,i mp u′ p, j

À

+

¿

_F d, j mp u′ p,i

À

=−2Rp,i j

τ

F f p . (27)

Later, Sakiz and Simonin (1998) proposed a model extension based on aTaylor expansion ofthe drag force nearthe averaged value

_h|

vr

|

2

i

,leadingtothedragtermmodels:

¿

Fd,i mp

À

=−

_τ

Vr,iF f p +2Vr,m

h

v

′_r,m

v

′ r,i

i

∂

8

∂

X X=h|vr|2i (28)

¿

Fd,i mp u′_{p, j}

À

+

¿

Fd, j mp u′_p,i

À

=−2

_τ

RFp,i j f p +2Vr,m

£

Vr,i

h

v

′_r,m

v

′ r, j

i

+Vr, j

h

v

′_r,m

v

′ r,i

i

¤µ ∂

8

∂

X X=h|vr|2i (29)

where the function

8

(X) is given by the drag law

8(

X

)

= −18ρ_ρfνf pd2p

·

1₊

³

dp νf

´

B

AXB/2 _{. Here for the Schiller and Nauman’s} (see Eq. (3)) correlation the model coefficients are A₌0.15 and

B₌0.687.

Figs.11and12showthedragtermsinmomentumandparticle kinetic transportequationsmeasuredincasewheredp= 406µm

and solid volume fraction is

α

p=1.2× 10−3 and

α

p=10−2. In momentum equation one can observe that, in axial direction, all model assumptionsgive nearlythe samepredictions.Inthe wall-normal direction, Eq.(17),the standard approach leads to a zero dragtermincontradictionwithDPSandDSMCresults.Incontrast, the modelextension proposed by Sakizand Simonin (1998) and computedwithDPSdataareinverygoodagreementwiththe nu-mericalsimulations.

Forthe particlekineticstress transport equations,Figs. 11and 12 show that the standard model overpredicts the drag termin the streamwisedirection. Onceagain, themodelextension taking into account large gas-particle drift clearly exhibits a better pre-dictions.TheextendedmodelisalsoinbetteragreementwithDPS andDSMCresultsfortheshearcomponentdragterm.Forthe wall-normal and spanwise directions no significant improvements are found.

5.3. Inter-particlecollisionclosuremodel

Theanalysisofinter-particlecollisiontermeffectstartswiththe inter-particle collisiontime scale

τ

c whichcharacterizesthe

colli-sion effect onanymoment. Fig.13 showsthe collision timescale measured fromDSMC. Forthe small valuesof the meanparticle volume fraction, one can observe that the collision timescale is maximum (small collision frequency) at the centre of the chan-nelanddecreasestowardsthewalls(largecollisionfrequency).For largervalue ofthemeanparticlevolumefraction,thetimescaleis foundmoreuniformacrossthechannel.

For a given particle diameter, the collision timescale depends on two parameters:the localparticleconcentration andthelocal particleagitation.AsshownbyFig.5theparticledensitynumber distributionacrossthechannelexhibitsapeakinthenear-wall re-gion andFig. 6 showslarge values of the agitation. Botheffects leads toincrease thecollisionfrequency.In contrastatthe centre of thechannel, the solidvolume fractionexhibits apeak butthe particlekineticenergyagitationissmall.Thelargevalueofthe col-lisiontimescaleinsucharegionmeansthatthecollisionfrequency ismainlycontrolledbytheparticleagitation.

In theframeworkofthe kinetictheory,itis possibletoderive ananalyticalexpressionfortheinter-particlecollisiontimescale,

1

τ

c = np

π

d2p

r

16

π

2 3q2p. (30)

For deriving Eq.(30),it hasbeen assumedthat theflow is suffi-cientlydiluted(

α

p<5%)andtheparticlesareveryinertialwith

re-specttofluidturbulence(Simoninetal.,2002)inordertoconsider that theradialdistributionfunctionisequaltounity.Fig.13 com-paresthecollisiontimescalemeasuredfromDSMCandthe predic-tiongivenbyEq.(30).Fortheparticleswiththelargestinertia,the momentclosuremodellingisinaccordancewiththeDSMCresults. Incontrast,forthesmallparticlediameters,itisobservedthatthe model overestimatesthecollisionfrequencyleading to acollision timescalesmallerthantheonemeasuredfromDSMC.

Eq.(30)isobtainedbyassuming thatthesingleparticlePDFis a Maxwellian distributionmeaningthat thefluctuatingmotionof the particles isassumedisotropic. Pialat(2007)proposed to take into account the anisotropy ofthe particle fluctuatingmotion by using an anisotropic Gaussian, or Richman, distribution. Such an approach leads to following expression ofthe inter-particle colli-siontimescale, ˜

τ

c=

τ

c 1 2√S+2 3

h

√ S₊sinh−1

(

√ S−1

)

√ S−1

i

. (31)

whereS isthecoefficientrepresentingtheanisotropy ofthe fluc-tuating particle motion. Such a coefficient is given in terms of eigenvalues oftheparticlekineticstresstensorRp,ij.Basically,S=

λ

p/

λ

q with

λ

kthe eigenvaluesofRp,ij and

λ

p>

λ

q(note thatthe

derivation

λ

qisassumedtobeadoubleeigenvalue).Asshownby

Fig.13theEq.(31)isinbetteraccordancewithDSMCresults. Following Grad(1949) andJenkinsandRichman (1985), in di-lute particulate flows andusingthe molecular chaosassumption, thecollisiontermsinparticlekineticstresstensorwrites

1 np C

(

u′_p,iu′_p,i

)

=−1− e 2 c 3

τ

c 2 3q2p

δ

i j−

σ

c

τ

c

³

Rp,i j− 2 3q2p

δ

i j

´

(32)

with

σ

c=

(

1₊ec

)(

3− ec

)

/5. Fig.14 comparesthe particlekinetic stresscollisiontermsmeasuredfromDPSandDSMCwiththe mo-ment closuremodelassumptionsgivenbyEqs.(32)and(30) pre-dictions.It can beobserved thatin thestreamwisedirection, Rxx,

the collisiontermis negativein contrastwiththecollisionterms in the wall-normal and spanwise directions. Such a behaviour is well known and represents the driving mechanism towards a Maxwellian distribution byinter-particle collision.Here the parti-clevelocityvarianceinthex-directionisredistributedtowardsthe twoothersdirectionswithoutenergydissipation.Fig.14exhibitsa very goodagreementbetweentheDPSandDSMCresultsandthe modelsgivenbyEq.(32).

FromDPSofverticalparticle-ladenchannelflows,Sakizand Si-monin(1998)measuredanaccumulationofparticlesatawall dis-tance ofthe orderofa particle diameter.Theyshowed, fromthe wall-normalmeanvelocityequationbalanceEq.(17),thatthis ac-cumulationwas duetotheemergenceofacollisiontermpushing the particles towardsthe wall andresultingfroma shelter effect

bythewall.Toaccountforsuchamechanism,theyperformedthe theoreticalcomputationofthecollisiontermbyconsideringa re-ducedspaceof integrationaccounting forthewall closeness and theyobtainedthefollowingequation,

1 np C

(

up,y

)

=− 1+ec 2 npd2p

³

2

_π

3 q2p

´

sin2

(

θ

m

)

−1+₆ecnpd3p

³

2

_π

3 q2p

´

¡

₁ − cos3

(

θ

m

)

¢

×

·

₂ np

∂

np

∂

y + 1 q2p

∂

q2_p

∂

y −1+₈ecnpd2p √

_π

h

Rp,yy− 2 3q2p

i

sin2

(

θ

m

)

¡

₁ +3cos2

(

θ

m

)

¢

. (33)

InEq.(33),

θ

mistheparameterdefiningtheshelteredspace.Ifthe

wall is located aty₌0,cos

(

θ

m

)

=max

(

−1,1/2− yp/dp

)

withyp

thedistancebetweentheparticleandthewall.

Fig. 15 shows that Eq. (33) predicts the non-zero value of the inter-particle momentum transfer in the near-wall region (yp<dp/2). It can alsobe observed that the Monte-Carlo method

predictsa zerovalue becauseitassumesthat thecollision proba-bilityisnotaffectedbythewallcloseness.Fortakingintoaccount the wall shelter, effect we basically proposed to add a force in theparticleequation leadingtoEq.(33) inthemomentapproach. However,anestimationfromDPSresultsofthethreetermonthe righthandsideofEq.(33)showsthatthefirstonedominatesthe others.Hence, introducing,nwall the wall-normal vector(oriented

towardthecoreflow)andywallthepositionofthewalls,the

addi-tional“wallforce” thatappearsnearthewallistakenintoaccount intheLagrangianframeworkas:

Fwall mp =−

|

y_{− y}wall

|

1₊ec 2 npd2p

³

2

π

3 q2p

´

sin2

₍

_θ

m

)

nwall . (34)

Figs.16–18showDSMCresultswithsucha“wallforce” forthe caseofdp= 1500 µmwherethe itisexpectedto be significant. It can be observed that the DSMC results are now in very good agreementwiththeDPSresultsevenintheverynear-wallregion. The effect ofthe “wall force” onthe vertical particle velocity and on the mean particle kinetic stress tensor components are shownbyFigs.17and(18).Fortunately,the“wallforce” hasaweak effect on those quantities and does not modify the good agree-mentsthatwereobtainedwithstandardDSMCmethod.

6. Conclusions

DirectSimulation Monte-Carlo(DSMC)ofparticles transported byafullydevelopedverticalturbulentchannelflowsarepresented. Severaldiametersandmeanparticlevolumefractionsare consid-ered.Themainresultsofthepapercanbesplitintwoparts.

First,the comparisonofthe DSMCresults withDiscrete Parti-cleSimulation(DPS) resultsshowsthe abilityoftheMonte-Carlo method to predict the particle-laden flow. The comparison be-tweenDSMCandDPSresultsismadefortheparticlenumber den-sity,themeanverticalvelocityandthesecond-andthird-order ve-locitycorrelations. Averygoodagreementisfoundexceptforthe particlenumberdensityintheverynear-wallregion.Insucha re-gion,the presenceofthe wallproduces a wall sheltereffectthat drivestheparticlestowardsthewalls. However,theapplicationof anadditionalmeanforce,derivedintheframeofthemoment ap-proach,allowedtoreproduceaccuratelytheincreaseoftheparticle concentrationintheverynear-wallregion.

Second, theDSMC results havebeenused fortesting the sec-ondordermoment assumptionforthethirdorder velocity corre-lation,forthedragterm,andforthecollisionterms.Itwasshown that,inthecaseoflargefluid-particlemeanslipvelocity,thedrag

termmodelproposedbySakizandSimonin(1998)isinverygood agreementwiththeDPSorDSMCresults.

Finally,evenissome additionalvalidationstudiesarerequired, theDSMCmethodcanbestraightforwardextendedfornon-elastic frictionalparticle-particleandparticle-wallcollisions.

Acknowledgements

TheauthorswouldliketothankDr.PhilippeVilledieufrom ON-ERAforfruitfuldiscussionsandhelpinthedevelopmentof Monte-Carloalgorithm.

The authorswouldalso liketo thankDr.MarcSakizfor theo-reticalderivationsandDPSstatistics.

References

Arcen, B. , Tanière, A. , Oesterlé, B. , 2006. On the influence of near-wall forces in par- ticle-laden channel flows. Int. J. Multiphase Flow 32 (12), 1326–1339 . Babovsky, H. , 1986. On a simulation scheme for the Boltzmann equation. Math.

Methods Appl. Sci. 8, 223–233 .

Balachandar, S., Eaton, J.K., 2010. Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42 (1), 111–133. doi: 10.1146/annurev.fluid.010908.165243 . Berlemont, A. , Achim, P. , Chang, Z. , 2001. Lagrangian approaches for particle colli-

sions: the colliding particle velocity correlation in the multiple particles track- ing method and in the stochastic approach. Phys. Fluids 13, 2946–2956 . Berlemont, A. , Simonin, O. , Sommerfeld, M. , 1995. Validation of inter-particle col-

lision models based on large eddy simulation. In: Gas-Solid Flows, 228. ASME FED, pp. 359–369 .

Bird, G.A. , 1969. Direct numerical and the Boltzmann equation. Phys. Fluids 11, 2676–2681 .

Capecelatro, J., Desjardins, O., 2013. An Euler–Lagrange strategy for simulating particle-laden flows. J. Comput. Phys. 238, 1–31. doi: 10.1016/j.jcp.2012.12.015 . Chapman, S. , Cowling, T. , 1970. The Mathematical Theory of Non-Uniform Gases.

Cambridge University Press .

Fede, P., Simonin, O., Villedieu, P., 2015. Monte-Carlo simulation of colliding particles or coalescing droplets transported by a turbulent flow in the framework of a joint fluid–particle pdf approach. Int. J. Multiphase Flow 74 (0), 165–183. doi: 10. 1016/j.ijmultiphaseflow.2015.04.006 .

Fox, R.O., 2012. Large-eddy-simulation tools for multiphase flows. Annu. Rev. Fluid Mech. 44 (1), 47–76. doi: 10.1146/annurev- fluid- 120710- 101118 .

Grad, H. , 1949. On the kinetic theory of rarefied gases. Commun. Pure Appl. Math. 2, 331–407 .

Hanjalic, K. , Launder, B. , 1972. A Reynolds stress model of turbulence and its appli- cation to thin shear flows. J. Fluid Mech. 52, 609–638 .

He, Y., Zhao, H., Wang, H., Zheng, C., 2015. Differentially weighted direct simulation Monte Carlo method for particle collision in gas–solid flows. Particuology 21, 135–145. doi: 10.1016/j.partic.2014.05.013 .

Ivanov, M. , Rogasinsky, S. , 1988. Analysis of numerical technics of the direct simula- tion Monte Carlo method in the rarefied gas dynamics. Sov. J. Num. Anal. Math. Modell. 3, 453–465 .

Jenkins, J.T. , Richman, M.W. , 1985. Grad’s 13-moments system for dense gas of in- elastic spheres. Arch. Ration. Mech. Anal. 87, 355–377 .

Nanbu, K. , 1983. Stochastic solution method of the master equation and the boltz- mann equation. J. Phys. Soc. Jpn. 52, 2654–2658 .

O’Rourke, P.J. , 1981. Collective Drop Effects in Vaporizing Sprays Ph.D. thesis . 1532-T Pawar, S., Padding, J., Deen, N., Jongsma, A., Innings, F., Kuipers, J., 2014. Lagrangian modelling of dilute granular flow - modified stochastic {DSMC} versus deter- ministic {DPM}. Chem. Eng. Sci. 105 (0), 132–142. doi: 10.1016/j.ces.2013.11.004 . Pialat, X., 2007. Développement Dune Méthode hybride Eulérienne-Lagrangienne Pour la Modélisation Numérique de la Phase Particulaire Dans les Écoulements Turbulents Gaz-particules. Ecole Nationale Supérieure de l’Aéronautique et de l’Espace Ph.D. thesis https://tel.archives-ouvertes.fr/tel-00224819v1 . Reeks, M.W. , 1991. On a kinetic equation for the transport of particles in turbulent

flows. Phys. Fluids 3 (3), 446–456 .

Reeks, M.W., Simonin, O., Fede, P., 2016. Multiphase Flow Handbook. In: Computa- tional Methods: PDF Models for Particle Transport Mixing and Collision in Tur- bulent Flows. CRC Press, pp. 79–284. doi: 10.1201/9781315371924-3 .

Riber, E., Moureau, V., Garcia, M., Poinsot, T., Simonin, O., 2009. Evaluation of nu- merical strategies for large eddy simulation of particulate two-phase recirculat- ing flows. J. Comput. Phys. 228 (2), 539–564. doi: 10.1016/j.jcp.2008.10.001 . Sakiz, M. , Simonin, O. , 1998. Continuum modelling and Lagrangian simulation of the

turbulent transport of particle kinetic stresses in a vertical gas-solid channel flow. In: Proc. 3rd International Conference on Multiphase Flows .

Sakiz, M. , Simonin, O. , 1999. Development and validation of continuum particle wall boundary conditions using Lagrangian simulation of a vertical gas-solid channel flow. In: Proc. 8th Int. Symp. on Gas-Particle Flows, ASME Fluids Engineering Division Summer Meeting, FEDSM99-7898 .

Sakiz, M. , Simonin, O. , 1999. Numerical experiments and modelling of non-equilib- rium effects in dilute granular flows. In: Gatignol, R., Lengrand, J.C. (Eds.), Rar- efied Gas Dynamics, Proc. of the 21st Int. Symp. on Rarefied Gas Dynamics, 1. Cépaduès Editions, pp. 287–294 .

Sakiz, M. , Simonin, O. , 2001. Continuum modelling and Lagrangian simulation of massive frictional colliding particles in vertical gas-solid channel flow. In: Proc. 4th International Conference on Multiphase Flows .

Schiller, L. , Naumann, A. , 1935. A drag coefficient correlation. V.D.I. Zeitung 77, 318–320 .

Simonin, O. , 1991. Prediction of the dispersed phase turbulence in particle-laden jets. In: Proc. 1st Int. Symp. Gas-Solid Flows. ASME, pp. 197–206 .

Simonin, O. , 1996. Combustion and Turbulence in Two-phase Flows. Lecture Series 1996-02. Von Karman Institute for Fluid Dynamics .

Simonin, O. , 20 0 0. Statistical and Continuum Modelling of Turbulent Reactive Par- ticulate Flows. Part 1: Theoretical Derivation of Dispersed Eulerian Modelling from Probability Density Function Kinetic Equation. Lecture Series 20 0 0-06. Von Karman Institute for Fluid Dynamics, Rhodes Saint Genèse (Belgium) . Simonin, O. , Février, P. , Laviéville, J. , 2002. On the spatial distribution of heavy par-

ticle velocities in turbulent flow: from continuous field to particulate chaos. J. Turbul. 3 (040), 1–18 .

Sommerfeld, M. , 2001. Validation of a stochastic lagrangian modelling approach for inter-particle collisions in homogeneous isotropic turbulence. Int. J. Multiphase Flow 27, 1829–1858 .

Tanaka, T. , Tsuji, Y. , 1991. Numerical simulation of gas–solid two–phase flow in a vertical pipe on the effects of interparticle collision. In: P4th Symp. on Gas-Solid Flows, 121. ASME-FED, pp. 123–128 .

Tsirkunov, Y.M., Romanyuk, D.A., 2016. Computational Fluid Dynamics / Monte Carlo Simulation of Dusty Gas Flow in a Rotor-stator Set of Airfoil Cascades. In: Ar- ray (Ed.), Progress in Propulsion Physics, 8, pp. 427–4 4 4. doi: 10.1051/eucass/ 201608427 .

Wang, S., Li, X., Lu, H., Yu, L., Ding, J., Yang, Z., 2009. DSMC prediction of granular temperatures of clusters and dispersed particles in a riser. Powder Technol. 192 (2), 225–233. doi: 10.1016/j.powtec.2009.01.008 .

Zaichik, L. , Oesterlé, B. , Alipchenkov, V. , 2004. On the probability density function model for the transport of particles in anisotropic turbulent flow. Phys. Fluids 16, 1956–1964 .