Détection et classification de différents types d'observations dans un modèle de régression linéaire

Detection et classification de differents types d'observations

dans un modele de regression lineaire

par

Genevieve Brassard Houde

memoire presente au Departement de mathematiques en

vue de l'obtention du grade de maitre es sciences (M.Sc.)

FACULTE DES SCIENCES

rf*l uNivEBsrrt ra-t a l SHERBROOKE

1*1

Library and

Archives Canada

Published Heritage

Branch

Bibliotheque et

Archives Canada

Direction du

Patrimoine de I'edition

Your file Votre reference ISBN: 978-0-494-49466-0 Our file Notre reference ISBN: 978-0-494-49466-0

NOTICE:

The author has granted a

non-exclusive license allowing Library

and Archives Canada to reproduce,

publish, archive, preserve, conserve,

communicate to the public by

telecommunication or on the Internet,

loan, distribute and sell theses

worldwide, for commercial or

non-commercial purposes, in microform,

paper, electronic and/or any other

formats.

AVIS:

L'auteur a accorde une licence non exclusive

permettant a la Bibliotheque et Archives

Canada de reproduire, publier, archiver,

sauvegarder, conserver, transmettre au public

par telecommunication ou par Plntemet, prefer,

distribuer et vendre des theses partout dans

le monde, a des fins commerciales ou autres,

sur support microforme, papier, electronique

et/ou autres formats.

The author retains copyright

ownership and moral rights in

this thesis. Neither the thesis

nor substantial extracts from it

may be printed or otherwise

reproduced without the author's

permission.

L'auteur conserve la propriete du droit d'auteur

et des droits moraux qui protege cette these.

Ni la these ni des extraits substantiels de

celle-ci ne doivent etre imprimes ou autrement

reproduits sans son autorisation.

In compliance with the Canadian

Privacy Act some supporting

forms may have been removed

from this thesis.

Conformement a la loi canadienne

sur la protection de la vie privee,

quelques formulaires secondaires

ont ete enleves de cette these.

While these forms may be included

in the document page count,

their removal does not represent

any loss of content from the

thesis.

Canada

Bien que ces formulaires

aient inclus dans la pagination,

il n'y aura aucun contenu manquant.

Le 14 Janvier 2009

lejury a accepte le memoire de Mme Genevieve Brassard Houde dans sa version finale.

Membres dujury

M. Ernest Monga

Directeur

Departement de mathematiques

M. Benoit Fraikin

Membre

M. Bernard Colin

President-rapporteur

Departement de mathematiques

SOMMAIRE

Le probleme de la detection et de la classification de differents types d'observations est important dans les modeles de regression lineaire. En effet, pour pouvoir se fier aux donnees et s'assurer que celles-ci correspondent aux modeles sous-jacents utilises lorsque nous appliquons la regression, il peut s'averer necessaire de devoir les repartir en categories. Apres avoir presente les principales methodes et techniques utilisees dans les modeles de regression lineaire, ce memoire propose des diagnostics qui permettent de determiner les differentes categories de donnees. Ces diagnostics sont particulierement utiles dans tous les domaines ou sont utilises les modeles lineaires. Ceux-ci sont utilises en physique, astronomie, biologie, chimie, medecine, geographie, sociologie, histoire, economie, linguistique, droit, etc. Finalement, ce memoire presente en detail trois exemples portant sur des donnees reelles dans les domaines suivants : l'economie, la geographie et l'astronomie. Le traitement de ces exemples est fait a l'aide du logiciel R.

R E M E R C I E M E N T S

Je tiens a remercier ici mes parents et amis qui ont toujours ete la pour me soutenir et m'encourager. Mes remerciements vont egalement a Leia et tous les autres chats que j'ai pu croiser pendant la redaction de ce memoire. En particulier, je souhaite remercier vivement Ernest Monga pour toute Faide qu'il a su m'apporter.

TABLE DES MATIERES

SOMMAIRE ii REMERCIEMENTS iii

INTRODUCTION 1 1 Analyse de regression lineaire 2

1.1 Relation entre deux variables 4 1.2 Relation deterministe 4 1.3 Relation stochastique 5 1.4 Methode des moindres carres 7

1.4.1 Historique 7 1.4.2 La methode 7 1.5 Variation expliquee et inexpliquee 10

2 Regression lineaire simple 13 2.1 Le modele de regression lineaire simple 13

2.1.1 Presupposes sur les e^ 14 2.2 Proprietes des estimateurs des moindres carres 14

2.2.1 Esperance mathematique de fix 14

2.2.2 Esperance mathematique de /?o 15

2.2.3 Variance de 4i 1 6

2.2.5 Covariance entre $i et f30 18 2.2.6 La distribution des estimateurs $o et J5\ 18

2.3 Estimation de la variance des erreurs 19 2.4 Inference sur les parametres du modele 21

2.4.1 Test sur la pente ft 21 2.4.2 Test sur Pordonnee a Forigine ft 22

2.5 Analyse de la variance 23 3 Regression lineaire multiple 25

3.1 Hyperplan de regression 25

3.2 Cas general 26 3.3 Proprietes des moindres carres 28

3.4 Presupposes du modele 30 3.5 Estimation de la variance des erreurs 32

3.6 Inference sur les parametres du modele 34

3.6.1 Tests d'hypotheses 34 3.7 Analyse de la variance 35

4 Diagnostics 38 4.1 Matrice H 38 4.2 Variance des residus 40

4.3 Analyse graphique des residus 41 4.3.1 Les residus en fonction des valeurs estimees j/; 41

4.3.2 Les residus en fonction des variables explicatives x,j 42

4.3.3 QQ-plot des residus 42

4.4 Notations 43 4.5 Detection des observations aberrantes 44

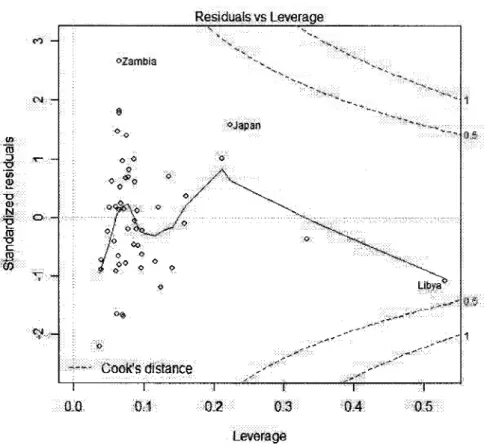
4.5.1 Studentisation des residus 44 4.6 Detection des points leviers 46

4.7 Detection des observations influentielles 47 4.7.1 Matrice des covariances COVRATIOi 47

4.7.2 Distance de Cook CD\ 49 4.7.3 Le diagnostic DFFITSi 50

4.7.4 Le diagnostic DFBETASm 50

4.8 Classification 50 4.8.1 Types d'observations 50

4.8.2 Exemple de types d'observations 52

4.8.3 Remarques 53 4.9 Suppression multiple 54

4.9.1 Le diagnostic COVRATIO 54

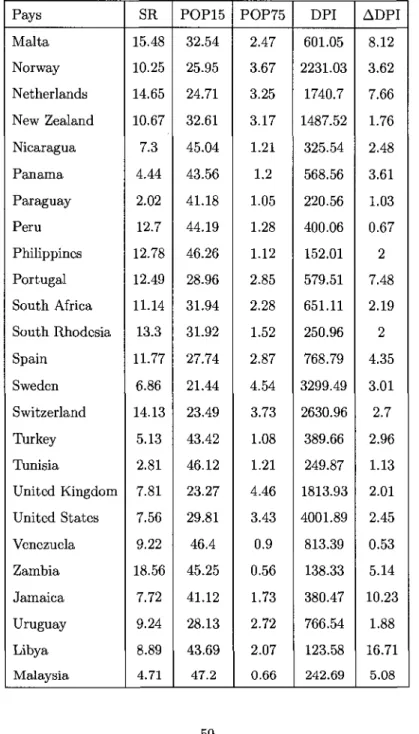
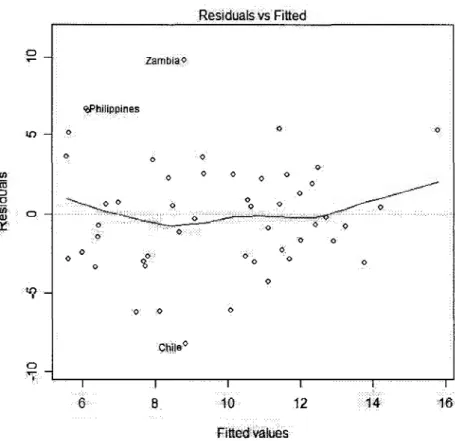
5 Exemples 56 5.1 Exemple 1-Une fonction du cycle de vie de Pepargne entre pays . . 56

5.1.1 Analyse des resultats 57 5.2 Exemple 2-Une analyse des niveaux de precipitation en Californie . 67

5.2.1 Analyse des resultats 69 5.3 Exemple 3-Une etude des quasars 77

5.3.1 Analyse des resultats 80

CONCLUSION 90 A Tableaux pour les diagnostics 91

B Exemples 94 B.l Exemple 1 94 B.2 Exemple 2 103 B.3 Exemple 3 I l l B.4 Commandes R utilisees pour l'exemple 1 116

C Statistiques 119 C.l Lois utilisees [1] 119

C.l.l Loi normale N(fj,,a2) 119

C.1.2 Loi du khi-deux x2(r) 119

C.1.3 Loi de Student t(r) 120

C.1.4 Loi de Fisher F ( n , r2) 120

C.2 Tables des lois 121 BIBLIOGRAPHIE 127

LISTE DES TABLEAUX

2.1 ANOVA pour la regression lineaire simple 24 3.1 ANOVA pour la regression lineaire multiple 37 5.1 Observations sur le cycle de vie de l'epargne entre pays(l) 58

5.2 Observations sur le cycle de vie de l'epargne entre pays(2) 59

5.3 RSTUDENT 61

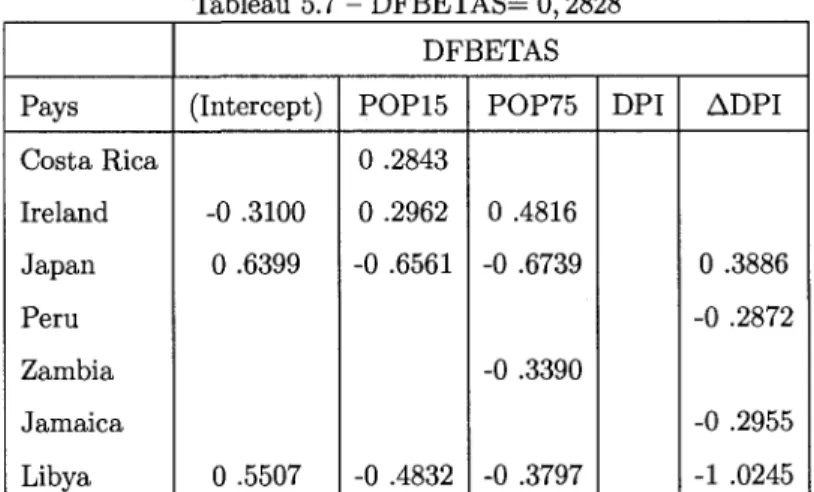
5.4 ha 62 5.5 DFFITS 63 5.6 COVRATIO 66 5.7 DFBETAS 66 5.8 Observations de stations meteorologiques en Californie(l) 68

5.9 Observations de stations meteorologiques en Californie(2) 69

5.10 RSTUDENT 71

5.11 hu 71 5.12 DFFITS 72 5.13 COVRATIO 76 5.14 DFBETAS 76 5.15 Observations sur des quasars 81

5.16 RSTUDENT 83 5.17 DFFITS 83 5.18 COVRATIO 88

5.19 DFBETAS 88 5.20 CD} 89 A.l Notations utilisees pour les diagnostics 91

A.2 Valeurs critiques pour les diagnostics 92 A.3 Type d'observation et diagnostic associe 93

B.l RSTUDENT et hti{l) 95 B.2 RSTUDENT et hu(2) 96 B.3 DFFITS et COVRATIO(l) 97 B.4 DFFITS et COVRATIO(2) 98 B.5 DFBETAS(l) 99 B.6 DFBETAS(2) 100 B.7 CD}{\) 101 B.8 CD}{2) 102 B.9 RSTUDENT et hu{l) 103 B.10 RSTUDENT et hu(2) 104 B.ll DFFITS et COVRATIO(l) 105 B.12 DFFITS et COVRATIO(2) 106 B.13 DFBETAS(l) 107 B.14 DFBETAS(2) 108 B.15 CDf{\) 109 B.16 CD}{2) 110 B. 17 RSTUDENT et hu 112 B.18 DFFITS et COVRATIO 113 B.19 DFBETAS 114 B.20 CD} 115

TABLE DES FIGURES

1.1 Exemples de nuages de points 5 4.1 Exemples d'analyse graphique des residus 42

4.2 Exemple de types d'observations 52

4.3 Masquage d'observation 54 5.1 Sommaire obtenu a l'aide de la commande summary() de R 60

5.2 Anova obtenue a l'aide de la commande anova() de R 60 5.3 Graphique des residus en fonction des valeurs estimees 62 5.4 Graphique des residus studentises internes en fonction des points leviers 63

5.5 QQ-plot des residus 64 5.6 Graphique des residus studentises internes en fonction des valeurs

estimees 65 5.7 Sommaire obtenu a l'aide de la commande summaryQ de R 70

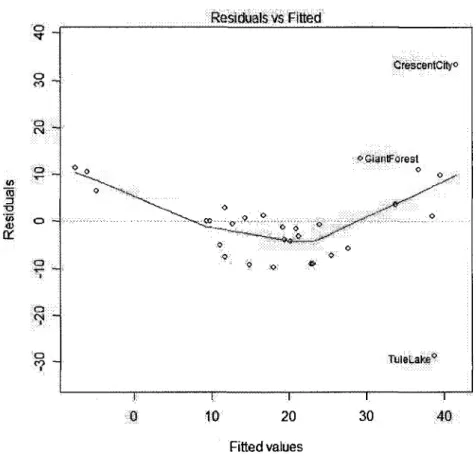
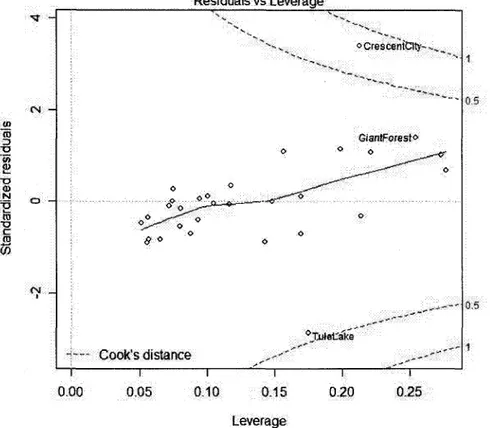
5.8 Anova obtenue a l'aide de la commande anovaQ de R 70 5.9 Graphique des residus en fonction des valeurs estimees 72 5.10 Graphique des residus studentises internes en fonction des points leviers 73

5.11 QQ-plot des residus 74 5.12 Graphique des residus studentises internes en fonction des valeurs

estimees 75 5.13 Sommaire obtenu a l'aide de la commande summary() de R 82

5.15 Graphique des residus en fonction des valeurs estimees 84 5.16 Graphique des residus studentises internes en fonction des points leviers 85

5.17 QQ-plot des residus 86 5.18 Graphique des residus studentises internes en fonction des valeurs

estimees 87 B.l lm(LifeCycleSavings) 116

B.2 summary(regLCS) 117 B.3 anova(regLCS) 118 C.l Table de la loi normale centree reduite 121

C.2 Table de la loi du Khi-Deux 122 C.3 Table de la loi de Student 123 C.4 Table de la loi de Fisher 124 C.5 Table de la loi de Fisher (Suite 1) 125

I N T R O D U C T I O N

Lorsque nous desirons utiliser un modele de regression lineaire arm d'analyser un jeu de donnees, outre 1'identification des variables dependantes et de la variable a expliquer, une question que nous avons coutume de nous poser est celle de la detection et l'identification des differents types d'observations.

Nous proposons un algorithme de detection et de classification d'observations issues d'un modele de regression lineaire. Cet algorithme utilise differents diagnostics dont certains sont connus mais que nous avons adapte a notre methodologie. Notre ob-jectif, ce faisant, est d'en faciliter l'usage aux non-inities pouvant utiliser le logiciel R qui est du domaine public.

Le premier chapitre presente la problematique de Panalyse de la regression lineaire. Dans le second chapitre nous decrivons le modele de regression lineaire simple en insistant sur les proprietes des estimateurs des moindres carres des parametres ainsi que des tests et intervalles de confiance sur les valeurs de ces parametres.

Le troisieme chapitre est consacre a la generalisation des propri6tes et tests deve-loppes dans le chapitre precedent au cas de la regression multiple.

Le quatrieme chapitre illustre les differents outils de diagnostics que nous retrouvons eparpilles dans la litterature. Nous avons Fanalyse graphique des residus, Putilisation de la matrice H, Fanalyse des residus studentises, Putilisation de la matrice des covariances et la distance de Cook pour ne citer que ceux-la. Ce chapitre se termine par une classification de types d'observations et une generalisation de la technique de suppression simple en suppression multiple.

Nous terminons par un chapitre illustratif compose de Petude detaillee de trois exemples : une fonction du cycle de vie de Pepargne entre pays; une analyse du niveau de precipitation en Californie; une etude des quasars.

CHAPITRE 1

ANALYSE DE REGRESSION LINEAIRE

I N T R O D U C T I O N ET HISTORIQUE

La regression a ete introduite pour la premiere fois par Sir Francis Galton, un homme de science britannique qui contribua de son savoir dans plusieurs domaines scientifique. Sir Francis Galton vecu de 1822 a 1911 et etait le cousin de Charles Darwin. II a etudi6 la medecine dans sa ville d'origine Birmingham, a Londres et a Cambridge. II etudia ensuite les mathematiques avec Hopkins mais devint malade pendant sa troisieme annee d'etude et ne pu finir son diplome. A la suite de la mort de son pere, il herita d'un bon montant d'argent qui lui a permis de voyager. Lorsque Galton retourna en Angleterre, il publia ses histoires de voyage en Afrique du sud tropical. La meme annee, en 1853, il fut elu fellow of the Royal Geographical Society. Apres la publication de Origin of the Species en 1859 par son cousin Charles Darwin, il s'interessa a ce domaine [2]. Dans le cadre d'une etude biologique sur l'heredite, vers 1875, il decida d'etudier le lien entre le diametre des graines de pois de senteur mere et celui de leur descendance. En faisant un graphique confrontant en abscisse le diametre des graines meres et en ordonnees le diametre des graines issues des graines meres, il constata une tendance lineaire. Ensuite, il remarqua que la droite calculee lors de cette experience, avait une pente inferieure a celle obtenue par le rapport des ecarts-types empiriques de ces deux variables

En d'autres mots, les graines de grand diamdtre avaient tendance a donner des graines de diametre plus petit et les graines de petit diametre avaient tendance a engendrer des graines de diametre plus grand. Le diametre des graines avaient tendance a regresser vers la moyenne. Le terme regression a ete utilise a partir de ce moment pour decrire ce type d'analyse [3].

La recherche d'une relation entre deux ou plusieurs variables est un probleme im-portant en statistique. Lorsque Ton veut lier une variable Y a une variable X par une relation du type Y = f{X), on a coutume de dire que Ton fait la regression de Y en X. Ce type de relation trouve des applications dans plusieurs domaines dont la physique, l'astronomie, la biologie, la chimie, la medecine, la geographie, la sociologie, l'histoire, Peconomie, la linguistique, le droit, etc. En void quelques exemples.

Astronomie, la prevision en cosmologie : Le jour du Nouvel An de 1801, l'as-tronome italien Giuseppe Piazzi fit la decouverte de la desormais planete naine Ceres (anciennement asteroi'de). II a alors pu suivre sa trajectoire durant 40 jours. Durant cette annee, plusieurs scientifiques ont tente de predire sa trajectoire sur la base des observations de Piazzi. La plupart des predictions furent erronees et le seul calcul suffisamment precis, base sur la methode des moindres carres, qui permi a Zach, un astronome allemand, de localiser a nouveau Ceres a la fin de l'annee, fut celui de Carl Friedrich Gauss, alors age de 24 ans [4].

Chimie : Dans de nombreux cas il est souhaitable de determiner la nature de la relation pouvant exister entre certaines grandeurs observees sur des unites d'une population determinee, par exemple des eprouvettes d'acier dont on mesure la resis-tance a la traction y et la teneur en carbone x, ou bien encore le rendement y d'une reaction chimique et la temperature x. Des considerations d'ordre pratique ou theo-rique conduisent souvent a 6tudier en fait les variations de y en fonction de a; a la suite d'une experimentation portant sur des eprouvettes caracterisees par certaines valeurs de a;, la teneur en carbone, en vue de mesurer les valeurs correspondantes

de la resistance a la traction y, ou bien, dans le cas du second exemple, d'effectuer des repetitions de la reaction chimique en question a differentes temperatures pour en relever les rendements [5].

D'autres exemples sont donnes a la fin de ce memoire.

1.1 Relation entre deux variables

Considerons deux variables X et Y et cherchons a determiner la relation qui les lie. La variable X peut representer la taille d'une personne et Y son poids. Nous voulons savoir s'il y a un lien entre la taille d'un individu et son poids. Pour ce faire, prenons un echantillon de n individus, c'est-a-dire que nous mesurerons la taille et le poids de chacun des n individus (xi, y{) avec i variant de 1 a n. La methode la plus simple pour verifier la relation entre la variable X et Y est de faire un graphique ou les valeurs de chaque couple {xi,y{) sont representees sur deux axes. Un tel graphique pour lequel X{ est l'abscisse et y; est Pordonnee est appele nuage de points. Le nuage de points nous donne une bonne idee a priori sur le type de relation qui peut exister entre la variable X et la variable Y. Nous avons un exemple de nuage de points a tendance lineaire dans la figure 1.1(a) et un exemple de nuage de point a tendance parabolique dans la figure 1.1(b).

II existe deux principaux types de relation entre les variables : les relations deter-ministes et les relations stochastiques.

1.2 Relation deterministe

Une relation entre deux variables est dite deterministe si l'une des variables peut s'exprimer exactement en fonction de l'autre. Nous pouvons, par exemple, trouver la temperature en Celsius a partir de la temperature en Fahrenheit et vice-versa et ce a partir de la formule suivante : F = \C + 32. La relation qui lie les variables dans ce cas s'exprime comme suit

(a) Tendance lineaire (b) Tendance parabolique

Figure 1.1 - Exemples de nuages de points

Y = f(X)

ou / est une fonction determinee et connue.

Dans ce qui suit, nous allons utiliser des fonctions affines pour exprimer la relation entre deux variables.

f(X)=0o + l31X ou les parametre /?0 et /3j sont des nombres reels fixes.

1.3 Relation stochastique

Dans la realite, ce ne sont pas toutes les variables qui peuvent etre liees a partir d'une relation deterministe. Ce ne sont pas toutes les relations qui sont exactes. Lorsque nous essayons de trouver la relation entre la taille X et le poids Y d'un individu nous rencontrons ce probleme. Plusieurs personnes ayant la meme taille peuvent avoir des poids differents. Par contre, nous savons que la taille et le poids d'un individu devrait varier dans le meme sens en general. En effet, plus une personne

allons utiliser une relation du type

Y = (30 + f31X + e

entre X et Y, ou e est une perturbation aleatoire qui gere le fait que des individus de m6me taille peuvent avoir des poids distincts. Lorsque nous supposons que nos donnees sont liees selon la relation Y = (30 + ftX + e, nous aurons pour tout % variant d e l a n

ou £j est la valeur de e pour l'individu i et n le nombre d'individus.

Le type de relation que nous venons de decrire se nomme un modele lineaire sto-chastique ou encore un modele de regression lineaire. On dit qu'un modele du type

Y = p0 + ftX + e explique Y en fonction de X. C'est pourquoi on appelle X la variable ind6pendante ou la variable explicative, et Y la variable dependante ou la variable expliquee par le modele. Dans un probleme de regression, on considere generalement les a;* comme valeurs fixees et les j/j comme des valeurs d'une variable aleatoire, dont la composante aleatoire d'un j/j est £j.

La droite de regression est inconnue. Le probleme de l'analyse de regression consiste alors a estimer les parametres (30 et ft a partir d'un echantillon de donnees Xj,y». Les parametres fa et /?i de cette droite sont alors des estimations de /?o et ft. L'estimation de la droite de regression est donnee par

y{x) = fa + Pix.

Lorsque la valeur x coi'ncidera avec une valeur xt observee sur les donnees, nous noterons y(xi) = &. Nous avons done

Vi = A) +

PxXi-Les yi sont appeles parfois les valeurs estimees par le modele. Elle nous permettent d'estimer les quantites inobservables

par les quantites observables

e-i = Vi ~ Po ~ PiXi =

Vi-Ces quantites e* sont appelees les residus du modele.

La methode la plus largement utilisee pour estimer les parametres d'un modele lineaire est la methode des moindres carres.

1.4 Methode des moindres carres

1.4.1 Historique

En 1795, a Fage de 18 ans, Carl Friedrich Gauss developpa le principe fondamental de l'analyse des moindres carres. Cette affirmation n'est cependant pas confirme par des ecrits et se base sur la parole de Gauss et sur sa prediction de la trajectoire de Ceres. II publia ses resultats seulement en 1809 dans Theoria Motus Corporum

Coelestium in sectionibus conicis solem ambientium, un document sur la mecanique

celeste. En 1823, Gauss publia Theoria combinationis observationum erroribus

mi-nimis obnoxiae avec un supplement en 1828 qui se consacrait a la mathematique

statistique et en particulier a la methode des moindres carres [6]. Le theoreme de Gauss-Markov stipule que pour un modele lineaire dans lequel les erreurs ont une es-perance nulle, ne sont pas correlees et sont de variances egales, le meilleur estimateur sans biais (BLUE : best linear unbiased estimator) des coefficients est donne par la methode des moindres carres. Independamment, la methode des moindres carres fut formulee par le Frangais Adrien-Marie Legendre en 1805 et par PAmericain Robert Adrain en 1808.

1.4.2 La m e t h o d e

La methode des moindres carr6s consiste a minimiser le residu comme decrit dans la section 1.3. Nous cherchons done les valeurs de p0 et Pi qui minimisent l'equation

suivante

X > i = X > - / ? o - A ^ )

j = l « = 1

ou n est le nombre d'observations. Dans la suite de ce memoire nous omettrons les indices lorsque nous ecrirons le signe de la sommation. En d'autres termes nous aurons toujours

n

E =

E-Les estimateurs /30 et J3\ sont les valeurs qui minimisent la fonction objectif

* = /(A>,/?i) = J > i - A - / ? i ^ )

-Pour trouver les valeurs qui minimisent cette fonction, nous annulons les derivees partielles de z par rapport a /3Q et, ensuite, par rapport a f3\. La derivee partielle de

z par rapport a /?0 est donnee par

^ = - 2 ^ (y i- / 30- / 3 i ^ ) .

La derivee partielle de z par rapport a (3\ est donnee par

Nous obtenons le systeme d'equations

Y^Vi -P°- ^

i) = °

Yxi(Vi - Po - PiXi) = 0 .

En developpant les equations, nous obtenons les equations normales

ou x = " ^ et w = **&•.

n •* n

A partir de la deuxieme equation normale et de l'egalit6 que nous venons de d6flnir nous obtenons

ft Yl

i

Y1

~ fi°

= ^ Xi\ji - nxy + pinx2. Nous obtenons l'estimateur fa suivant :

A E xiVt ~ nxy Pi = v^ 2

=F-2_, xf — nx1 En notant que

~^2(xi - x)(yi -y) = 'YjXiyi - nxy

nous obtenons une autre formule pour jl\

Efci - *)2

En notant que

$^(w - v) = $3(*< - x) = o

nous obtenons d'autres formulations pour /3i

Pl

Efe-*)

Ete-*)

'

En resume, si Ton veut utiliser la methode des moindres carres, nous devons, pre-mierement, calculer /?x a partir de l'une des formules precedemment decrites et,

deuxiemement, calculer J30 a l'aide de J30 = y — (3\X. On verifie aisement que les valeurs de fa et (3\ obtenues satisfont les conditions de second ordre d'un minimum. Lorsque nous avons les valeurs calculees des parametres /?o et 0i nous pouvons obte-nir l'estimation de la droite de regression aussi appelee la droite des moindres carres par la formule suivante

PlX-Les valeurs estimees sont alors donnees par

Vi = A) + PiXi = y + Pi{xi - x)

et les residus par

ei = yi-yi = {Vi -y)- Pi{xi - x).

1.5 Variation expliquee et inexpliquee

La variation d'une variable est habituellement exprimee par sa variance. Dans un modele de regression lineaire nous essayons d'expliquer la variation de la variable Y en fonction de la variable X. Differentes valeurs de la variable explicative X donnent generalement lieu a differentes valeurs de la variable expliquee Y. II en resulte une variance des valeurs de Y. Cette variation est celle expliquee par le modele. II arrive que, pour une meme valeur de X, nous ayons plusieurs valeurs differentes de Y, il s'agit de la variance inexpliquee par le modele. Nous obtenons dans ce cas

Variation totale

V

Variation expliquee Variation inexpliquee par le modele

\ y par le modele / y par le modele J Nous utilisons la difference entre les observations yt et la moyenne y pour mesurer la variation de la variable Y. Pour ce faire, nous allons utiliser la decomposition suivante

(j/i ~V) = (Vi -V) + (Vi ~ Vi)

avec (j/j — y) qui represente la variation expliquee par le modele et (y, — yCj = e, qui represente la variation inexpliquee par le modele ou encore le residu du modele. La methode des moindres carres permet d'avoir la meme decomposition pour la somme des carres des differences

car

En effet

et

E&

2 =

E&^-E &

= ^ ( y + / ? i f e - « ) )

= nf + 2j/& ^2(xi -x) + fc\ Y^(xi - x]

= y-ny + 0 + J31-J31 ^ ( ^ - xf

£ ( t t - Vif = E tf -

E VM + E $

=

E*<?-E#-^ 2

De plus, nous avons aussi que

^2(Vi -V? = E $ ~

V E & + ^

= E &

~

y

+

y

= E&

~

£

-Nous obtenons ainsi

Y^^-y)

=Yy

~

y

= [E^-^

2

] + [ E ^ - E ^ ]

-Avec cette nouvelle decomposition nous obtenons la somme des carres totale,

SC

= X > - y )

la somme des carres due a la regression,

sc

= J2(m-y)

et la somme des carres des residus,

SCres = Y^iVi -

Vif-Nous obtenons la decomposition

/

Somme des carres totale

sc

\ /

Somme des carres due a la regression

bCreg

\ /

Somme des carres des residus

bCrea

\

Nous utilisons le coefficient de determination note R2 pour mesurer le pourcentage total qui est explique par le modele. Le coefficient de determination R2 peut etre obtenue a partir d'une des formules suivantes

W SCt, Variation expliquee SC Variation totale

E(vi-y)

E t e - v)

T,y?-ny

E y

-

y

Uvi-v)

p2Y.x

-nx

E y

- W'

CHAPITRE 2

REGRESSION LINEAIRE SIMPLE

Dans ce chapitre, nous verrons comment generaliser Pinference sur la droite de regression a partir de ces estimations.

2.1 Le modele de regression lineaire simple

Supposons que nous ayons un modele, pour tout i variant de 1 a n, de la forme

Vi = Po + PiXi + ct

ou les e, sont des quantites aleatoires inobservables que nous appelerons les erreurs. Decoulant de ce fait, les y\ sont des variables aleatoires et les re, sont considered comme des nombres fixes. En supposant l'esperance des e; nulle, nous obtenons que

E(yi) =f3o + PiXi + E{ei) = Po + PlXi

et que

Var(yi) = Var{/30 + faxi + e<) = Vor(ej). Lorsque nous desirons faire de Finference sur la droite de regression

et ce a partir de la droite des moindres carres

y(x) =0o + Pix,

nous devons faire des presupposes supplementaires sur les variables aleatoire e^.

2.1.1 Presupposes sur les e;

- La variance de ej est egale a une quantite a2 (inconnue) et ne depend pas de X{. Nous avons done, pour tout i variant de 1 a n, que Var{ti) = Var(yi) = a2. - Les e; sont independantes.

- Les £j sont distributes suivant une loi normale d'esperance nulle et de variance egale a a2.

En d'autres termes, les e» sont independantes et identiquement distributes suivant une loi normale d'esperance nulle et de variance egale a a2.

Avec ces presupposes, nous sommes maintenant pret a etudier les estimateurs et leurs proprietes.

2.2 Proprietes des estimateurs des moindres carres

Dans cette section nous etudions les proprietes des estimateurs des parametres du modele de regression lineaire simple Y = f30 + (3\X + e. Nous calculons l'esperance mathematique de ces estimateurs, nous montrons qu'ils sont sans biais1 pour leur

parametre et nous calculons les variances de ces estimateurs de meme que leur loi de probabilite sous les presupposes de la section 2.1.1.

2.2.1 Esperance mathematique de fii

L'estimateur des moindres carres est

^ .... S f o -x)Vi

J2(xi - V)2

comme nous l'avons vu dans la section 1.4.2. Nous avons alors

£(/?i) =E T,(xi - x)2 _ "£{Xi - x)E(Vi) J2(xi - x)2 = Z)(jc» - x)(/3p + fiiXj) J2(xi - x)2 J2(Xi - x)2 = 0 + Pi Y,(xi - X)XJ Yj{Xi - X)2 = Pi ^{Xj - xf Y,(Xi - X)2

Done E(0i) = pi et pi est un estimateur sans biais de pi.

2.2.2 Esperance mathematique de fio

L'estimateur des moindres carres est

Po = y- Pix

comme nous l'avons vu dans la section 1.4.2. En notant que E(y) =E>'Y'Vi n n ^(Po + PlXj) n npo + PiY^Xj n Pa + Pix

nous obtenons que E(0O) = E{y-0\x) = E(y)-xE0!) = E(y)-x01 = 0o + Pix - x0x = 0o.

Done E(fio) = 0O et 0o est un estimateur sans biais de 0O.

2.2.3 Variance de ft

Pour calculer la variance Var(0i) nous supposons que Var(e) = a2 et que E(e) = 0

comme dans la section 2.1.1. Nous avons alors

^

- xfVar{yi)

(Efe-*)

)

a2

^ ( X i - x )2' Nous obtenons done Var{0\) = y(x<T_-^.

2.2.4 Variance de /?o

Rappelons tout d'abord que si X et Y sont deux variables aleatoires et que a et 6 sont des constantes quelconque alors

Ainsi nous voulons calculer

Var(f30) = Var{y-plX)

= Var{y) + Var(-fax) - 2xCov{y,/31). Notons que Var{y) = Var (£*) = LX^M = ^ = ?1 \ n J nz n1 n et que _ E I U E ^ i f o j - x)Cov{yi,yj) nJ2(xi-x)2

_ E l L i f a - x)Var{yi) + E I U T,]=i,j^i(xj ~ x)Cov(yi,yj) nJ2{xi-x)2

= o.

II s'ensuit que

Var0o) = Var(y) + x2Var{fa) - 2xCov(y, ft) a2 x2a2 n

L w -

)

_ °

(E

l —

+

)

2.2.5 Covariance entre fii et /3

Nous aurons besoin pour certains calculs, concernant restimation de la variance des erreurs de determiner la quantite Cov [Pi,PoJ. Nous avons

Cow (&,#>) =C<m(fa,y-kx)

= Cov(puij)-xVar{p1)

—xa2

J2(xi-x)

'

Nous obtenons done Cov f " • ( & , & ) = Efe-*)2 •

2.2.6 La distribution des estimateurs J3Q et (3\

II reste a etablir la distribution des estimateurs /3Q et fi\. Ces distributions dependent de celle des perturbations aleatoires e. Puisque les e, sont normalement distributes d'esperance nulle et de variance egale a a2, il s'ensuit que y est distribute suivant une loi normale avec E{y) = /?o + Pix et Var(y) = a2 que l'on peut noter

y~N(p0 + prX,a2).

Puisque 0o et ft sont des combinaisons lineaires des variables yi,...,yn nous pou-vons deduire que

ft ~ N(E0i),Var0i))

ou i = 0,1.

Nous avons vu precedemment apparaitre la valeur a2 qui represente la variance des Ci. La valeur de a2 est inconnue et doit etre estimee.

2.3 Estimation de la variance des erreurs

Nous avons vu dans la section 1.4.2 que les erreurs £j pouvaient etre estimees par les residus du modele, les e, = y* — yt. Nous allons done estimer la somme des carres des erreurs a Faide de la somme des carres des residus

ou e designe la moyenne des e, qui est nulle. Au chapitre 1, nous avons vu que

E ( ^ ~ yJ

E

y

i - E $•

Nous avons done que

s(5>-&)

a

) = E ^ ) - E ^ )

= E (Varbh) + E\yi))) - E {Var{Vi) + E2(Vi)). Comme nous avons que

E(

) =£(/3

+ /W)

= /30 + XiPi = E(Vi) nous obtenons que

E

(E(w - M

) = E

^ - E

^

Sachant que

Var(yi) = Var (fa + fcxA

= Var (/30) + x2Var ( f t ) + 2XiCov0o, Pi) a2 Erf x\a2 _ 2xiXa2 n Y^ixj ~ xf J2(XJ - x)2 J2(xj - xf

J2x

E f e

-

x)

= a2{n - 2).

Nous pouvons maintenant definir un estimateur sans biais de a2 comme suit n - 2 O^res ~~ n - 2 _ ^Gtot ~ kCreg ~ n - 2 n - 2

Lorsque les perturbations aleatoires sont normalement distributes on peut montrer que ^%* est distribuee suivant une loi du khi-deux d'esperance egale a n — 2. La fonction de densite, ainsi que certaines propriety de la loi du khi-deux sont donnees en annexe C.l.

2.4 Inference sur les parametres du modele

Nous allons maintenant nous pencher sur les tests d'hypotheses sur les parametre

ft et #>.

2.4.1 Test sur la pente pi

Nous avons vu dans la section 2.2.6 que ft est distribute selon une loi normale d'esperance egale a ft et de variance egale a <p(x -xY

( a2

Pi~N[(3u- _{£ ( x i - x )2/ '} Ainsi

Mais la quantite a1 est inconnue. Dans la pratique nous estimons la variance de ft par

J2(xi-x)

'

e T = % $ - est distribute t de liberte [7]

La statistique T = ,fi est distribute selon une loi de Student t avec (n — 2) degres

s (pi)

La fonction de densite, ainsi que certaines proprietes de la loi de Student sont donntes en annexe C.l.

Dans un probleme de test d'hypotheses bilateral ou nous desirons tester l'hypothese nulle

Ho : ft = h

contre l'hypothese alternative

la regie de decision est de rejeter Ho au seuil de signification a si |ic| > i(a/2,n-2) ou

t ^~bl

est la valeur observee de T et ta est le quantile d'ordre 1 — a d'une loi de Student t avec (n — 2) degres de liberte.

2 . 4 . 2 T e s t s u r l ' o r d o n n e e a l ' o r i g i n e f30

Nous avons vu dans la section 2.2.6 que /?o est distribuee selon une loi normale d'esperance egale a /30 et de variance egale a ny^^U2

Ainsi A>-/?o

Po~N( fa,

Mais la quantite a2 est inconnue. Dans la pratique nous estimons la variance de $0 par

s2(Po)= S2T,X* nJ2(xi-x)2' > T = ^ ^ est distribuee

de liberte [7]

La statistique T = ^\^} est distribuee selon une loi de Student t avec (n — 2) degres

s(Po)

Dans un probleme de test d'hypotheses bilateral ou nous desirons tester 1'hypothese nulle

Ho : Po = bo

contre 1'hypothese alternative

Hx-.Po^ bo,

la regie de decision est de rejeter H0 au seuil de signification a si |tc| > £(a/2,n-2) ou

t Po-bo

est la valeur observee de T et ta est le quantile d'ordre 1 — a d'une loi de Student t avec (n — 2) degres de liberte.

2.5 Analyse de la variance

Nous cherchons a tester l'hypothese nulle

H0 : ft = 0 contre l'hypothese alternative

ft:A/ 0,

a l'aide des trois sommes de carres SCto4, SCres et SCres definies dans la section 1.5.

Lorsque H0 est vraie, nous pouvons montrer que l'esperance de ces sommes valent £(SCt o t) = (n - l)a2

£(SCreg) = a2 E(SGtes) = (n - 2)<72.

Dans ce cas, on en deduit les estimateurs sans biais suivant de a2 MCtot = ^

n — 1

MCreg = ^ I

MCres = - ^

n — 2

ou MC symbolise la moyenne des sommes de carres. Lorsque l'hypothese HQ est vraie

SCtot _ „;2 V SG SG 2 X\n - 1) 2 £

~ x

«

b O r e

Les quantites —ff3- et ^ p sont independantes. Ainsi, toujours lorsque H0 est vraie, nous avons la statistique

(fife)

(n-2)-<r>J

o O r e g Tl Z IVLOj-eg

bOr( 1 M C

qui suit une loi de Fisher avec 1 et (n — 2) degres de liberte. La fonction de densite, ainsi que certaines proprietes de la loi de Fisher sont donnees en annexe C I . Au niveau a on rejette Ho si Fc > Fa ou Fa est le quantile d'ordre a d'une loi de Fisher avec 1 et (n — 2) degres de liberte.

Les resultats precedents sont resumes dans le tableau 2.1.

Tableau 2.1 - ANOVA pour la regression lineaire simple Source de variation Regression Residuelle Totale Degres de liberte 1 ra-2 n - 1 Somme des carres SCeg = £ ( & - Vif

sc

= Y,{vi - mf

sc

= E(

-y

)

CHAPITRE 3

REGRESSION LINEAIRE MULTIPLE

Dans un modele de regression lineaire multiple, la droite de regression est remplacee par un hyperplan de regression. Pour estimer les parametres de cet hyperplan de regression, la methode des moindres carres est utilisee comme dans le cas de la regression lineaire simple.

3.1 Hyperplan de regression

Le principe est le meme qu'en regression lineaire simple, nous cherchons a expliquer une variable Y a l'aide d'un certain nombre de variables explicatives.

Voici la forme du modele lineaire stochastique pour decrire la relation entre la variable expliquee et les variables explicatives

Y = p

+ faXi + P

X

+ ... + ft^Vi + e.

Nous avons pour ce faire, un echantillon de n vecteurs d'observations contenant chacun p valeurs qui sont les Xij et le j/j correspondant

(^n, a; 12,..., xi(p_i), j/i), (x2i,x22, •••, x2(P-i), V2), •••, (xni,xn2,..., x„(p-i),y„) et nous obtenons, pour tout i variant de 1 a n

qui constitue le modele de regression lineaire multiple. Nous cherchons maintenant a determiner l'hyperplan

V(xi,X2, ..., Xp-i) = f30 + fiiXi + P2X2 + • • • + Pp-lXp-i

qui approche au mieux les observations de notre echantillon.

A l'aide de cet hyperplan nous obtenons les valeurs estimees par l'echantillon

Vi = A) + Pixa + P2xi2 + ... + 4 - i ^ i ( p - i )

qui nous permettent de remplacer les erreurs inobservables

£i = Vi- Po— Pi%a ~ PiXn - . . . - Pp-iXi(p-i)

par les residus observables :

&i = Vi - Po - PlXn - P2Xi2 - . . . - Pp-iXi(p-i) =Vi-Vi.

3.2 Cas general

Considerant maintenant un modele avecp—1 variables explicatives, nous cherchons a estimer les p parametres inconnus du modeles po,Pi,..-, Pv-\ par p0,$i,..., pp-i. Pour estimer ces p parametres, nous cherchons a minimiser

^2 ei = ] C (Vi ~ ^° ~ @lXil ~ @2Xi2 ~ •••- ^>-lxi(p-l))

ou encore a minimiser la fonction

z = / ( A ) , A , /?2, • • •, Pp-i) = ^2(vi-Po- P&a - PIXQ. - . . . - Pp-ix^p-!)) .

Afin de trouver les estimateurs dans ce cas, introduisons la notation matricielle. Les n equations sont alors remplacees par l'unique equation suivante

Vi

2/2

1 3?nl *^n2

Qui se traduit plus simplement par

1 xn a;i2 ••• xip-i 1 z2i ^ 2 2 • • • x2p-i 1 X31 ^ 3 2 • • • X3p-1 %nv—l Po

ft

+

ou y est un vecteur (n x 1) representant la variable expliquee, X est une matrice (n x p) representant les (p — 1) variables explicatives et contenant une colonne de 1 associe a /3Q, (3 est un vecteur ( p x l ) representant les parametres inconnus que Ton veut estimer et finalement e est un vecteur ( n x l ) representant les erreurs.

Nous cherchons done a estimer le vecteur f3 par un estimateur (3. La methode des moindres carres, dans ce cas, consiste a minimiser

(y-X(3)T(y-Xp)

En utilisant le fait que /3TXTy est un scalaire nous obtenons le developpement suivant

(y - XP)T(y - XP) = yTy - PTXTy - yTXp + PTXTXp = yTy-2XTyPT + pXTXp.

Suite a ce developpement nous obtenons la derivee partielle de eTe par rapport a P

qui est donne par

-2XTy + 2XTXP.

L'estimateur P que nous cherchons est done la valeur qui annule la derivee partielle

En developpant l'expression precedente nous obtenons

(XTX)P = XTy. L'estimateur des moindres carres obtenu est alors

0=(XTX)-1XTy

lorsque (XTX)~1 existe. Le vecteur des valeurs estimees est y = X(3. Comme pour la regression lineaire simple, la valeur (3 obtenue verifie les conditions de second ordre d'un minimum.

3.3 Proprieties des moindres carres

Comme vu a la section 1.5, nous avons la propriete suivante

en utilisant la methode des moindres carres. Posons e = y — y d'ou e, = y\ — jji pour tout i variant de 1 a n.

La meme propriete sous forme matricielle est

A T A T A A T v y=y y=yy puisque fy =(XP)TX/3

= p

x

xp

= (Xpfy

= y v

et que

eTe ={y- yf{y - y)

= (yT - yT)(y - v)

= yTy - vTy - yTy + yTy

= y y-y

v-Ainsi, nous obtenons une nouvelle formule pour la somme des carres des residus

Lorsque nous considerons un modele possedant une constante /?o, il est possible de montrer que l'une des equations obtenue est egale a

Po = v hxi h%i ••• 4 I ^ P I

-Dans ce cas, l'hyperplan obtenu par la methode des moindres carres contient le point (xi,x2,...,xp-i,y).

En considerant le developpement suivant

E Vi

]C \P°

@

@

+ • • • +

= n$

+ $i ^2 xn + (3

^2

n + • • • + 4 - i E

%i(p— 1)

= n(y- P\X\ - fax?, - . . . - J3p-ixp-i\ + ftnxi + /32nz2 + • • • + Pp-inXp-i

= ny

nous remarquons que la somme des residus est toujours nulle

-En considerant le developpement

E ( » - y)

= E y

i -

& E &

v

= Y,yi-

yJ2

y

= E &

~~

y

+

y

= E&

£

B f t - ^+B* -

M

= [ E £

-

A + [E»? - E y

]

nous obtenons la decomposition suivante de la somme des carres des residus

Efo - ^)

= E & -£)

+E(w - »)

-En d'autres termes

A l'aide des sommes precedentes, nous pouvons definir le coefficient de determination de la meme fagon que dans le cas de la regression simple :

2 __ P^reg SCtot

Le coefficient de determination nous indique le pourcentage de la variation de la variable Y qui est expliquee par le modele.

3.4 Presupposes du modele

Avant de pouvoir faire de l'inference sur les parametres obtenus a l'aide de la me-thode des moindres carres, nous devons definir quelques presupposes. Nous suppo-serons que nos donnees s'expriment a l'aide d'une formule du type suivant

ou e suit une loi multinormale avec E(e) = 0 et Cov(e) = a2In {In est la matrice identite de dimension n et a2 est une constante inconnue).

Sous forme matricielle ce presuppose s'exprime comme suit

Efa)

Var(ei) Cov(eue2) ••• Cov{euen) Cov(e2,el) Var(e2) ••• Cov(e2,e„)

a2 0 0 a1

0 0

Cov(en,ei) Cov(en,e2) ••• Var{e„)

A partir des presupposes decrits, nous pouvons montrer que les estimateurs des moindres carres sont sans biais

E(p) =E((XTX)-'XTy) = (XTX)-'XTE(y) = (XTX)-1XTX/3 = /?.

De plus, la matrice de variance-covariance des estimateurs defmie par Cov{/3) = Var0o) CovfaA) Cov0upo) Var(&) Cov0o,Pp-i) CowG9i,4-i)

CouiPp-upo) Covip^ufa) ••• Var(/?p_i)

est donnee par

Cov(/3) = Cov ((XTX)-1XTy)

= (XTX)-1XTCav(y) {{XTX)-lXTf = a2(XTX)-1XTX(XTX)~1

= a2(XTX)-K

Puisque le vecteur aleatoire /? est obtenu a partir du vecteur aleatoire multinormal

y par multiplication par une matrice, nous pouvons deduire que

0 ~ N

(E0),Cov0))

ou Np designe une loi normale p-dimensionnelle.

3.5 Estimation de la variance des erreurs

Comme en regression simple, nous allons estimer la variance a2 des erreurs a l'aide de la somme des carres des residus

Le vecteur y suit une loi multinormale avec

ou encore pour tout i variant d e l a n

La matrice de variance-covariance des valeurs estimees definie par

Var(yi) Cov(yi,y2) ••• Cov{yuyn) r, ,,s Cov(y2,yi) Var{y2) ••• Cov(y2,y„)

Cow(j/n,i/i) Cov{yn,y2) ••• Var(yn) est donnee par

Cov{y) =Cov{Xp)

= Cov (X(XTX)-1XTy)

= X(XTXr1XTCov(y) (X(XTX)-1XTf = a2X(XTX)-1XTX(XTX)-1XT

= a2X(XTX)~1XT Ainsi, les variances des y, sont des multiples de a2. Ces multiples se trouvent sur la diagonale de la matrice

H = X(XTX)~1XT. Nous avons que

E(J2(m-m?) -Efcti-Zti)

et ainsi,

E

Q>>

-

ytf)

=

E

^) - E

^

= na2 - a2Tr(H).

Comme la trace d'une matrice est un operateur commutatif, nous obtenons que

Tr(H) =Tr(X{XTX)-lXT) = Tr ({XTX)~lXTX) = Tr(Ip).

Comme la matrice Ip est la matrice identite de dimension p, sa trace vaut p. Sachant que

E(^{y

-y

f)={n-

y

2 _ Z-^iVi ~ Vi) _ SCres _ SCtot — SCreg

n—p n—p n—p

est un estimateur sans biais de a2

Lorsque les perturbations aleatoires sont normalement distributes on peut montrer que ^ p - est distribute suivant une loi du khi-deux d'esperance egale a (n—p).

3.6 Inference sur les parametres du modele

Nous allons maintenant nous pencher sur les tests d'hypotheses concernant les pa-rametres du modele.

3.6.1 Tests d'hypotheses

Nous avons vu dans la section 3.4 que J3 est distribute suivant une loi normale avec

E0) = (3et Covp) = a2{XTX)-1

Mais la quantite a2 est inconnue. Dans la pratique nous estimons la variance des j3j par les s2($j) qui se trouve sur la diagonale de la matrice s2($)

2 / v T y \ - l

s2(/3) = s\XTX)

ou s2 designe l'estimateur de la variance trouve a la section 3.5.

La statistique de liberte [7]

La statistique T = Kitl est distribute selon une loi de Student t avec (n—p) degres

T=%-Ji~t(n-p).

Dans un probleme de test d'hypotheses bilateral ou nous desirons tester Fhypothese nulle

Ho : ^ = bi

contre l'hypothese alternative

Hi : % + ^

la regie de decision est de rejetter HQ au seuil de signification a si \tc\ > t(a/2,n-p) ou

t -h~

*

(4)

est la valeur observee de T et ta est le quantile d'ordre 1 — a d'une loi de Student t avec (n — p) degres de liberte.

3.7 Analyse de la variance

Nous cherchons a tester l'hypothese :

H0 : /?i = /?2 = • • • = Pp-i = 0

contre l'hypothese alternative

a l'aide des trois sommes de carres SCtot, SCreg et SCres definies dans la section 3.3.

Si yt = /30 + €j ou encore lorsque H0 est vraie, nous pouvons montrer que l'esperance de ces sommes valent

£(SCt o t) = ( n - l ) a2

£(SCreg) = ( p - l ) < r2

£(SCres) = {n-p)a2

Dans ce cas, on en deduit les estimateurs sans biais suivant de a2 SCtot MCtot MC MC, reg n - 1 o Ore s n — p

Ainsi, toujours lorsque H0 est vraie, nous avons la statistique

/ SCreg A

{{p-iy^J SCreg n-p MCreg

(

n—p-cr2 J SCres p - 1 MCr,

qui suit une loi de Fisher avec (p— 1) et (n—p) degres de liberte(Pour une explication de la loi de Fisher voir la section C.l.

Au niveau a on rejette -Ho si Fc > Fa ou Fa est le quantile d'ordre a d'une loi de Fisher avec (p — 1) et (n — p) degres de liberte.

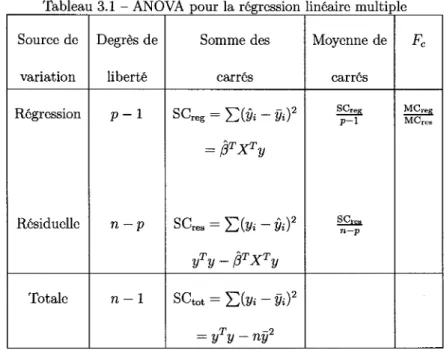
Tableau 3.1 - ANOVA pour la regression lineaire multiple Source de variation Regression Residuelle Totale Degres de liberte P - 1 n—p n - 1 Somme des carres

SCreg = Z)(& - Vif

= PTXTy

SCres = Y.{Vi - Vif

yTy-pTXTy sct o t = E(2/i-l/i)2 = yTy - ny1 Moyenne de carres SCreg P - l oOres n—p Fc MCr e (5 MCre,

C H A P I T R E 4

DIAGNOSTICS

« All models are wrong but some are useful» -George E.P. Box

Apres avoir bati un modele de regression lineaire, nous avons coutume d'etudier les donnees afin de voir comment elles influencent le modele. Pour ce faire, nous presenterons plusieurs outils pour poser des diagnostics sur les types de donnees rencontrees dans notre analyse. En analysant les donnees nous cherchons a verifier si les hypotheses du modele sont justes. Nous voulons aussi verifier si le modele ajuste bien les donnees et est representatif de la population etudiee. Ensuite nous presenterons une classification des types de donnees issus des diagnostics utilises.

4.1 Matrice H

La matrice H est definie comme suit

H = X(XTX)-1XT Les elements de la diagonale de la matrice H sont definies par

hu = Xi{XTX)~lxJ ou Xi est la ieme ligne de la matrice X.

La matrice H, pour hat matrix en anglais, est appelee ainsi car elle permet par simple multiplication de passer du vecteur y au vecteur y, autrement dit d'ajouter un chapeau (hat) a y

V = Hy.

Les proprietes de la matrice H sont enumerees ainsi

1. La matrice H est une matrice carree, idempotente et symetrique. 2. Tous les elements de la matrice H sont compris entre —1 et 1. 3. Les elements de sa diagonale sont compris entre 0 et 1. 4. La somme des elements de sa diagonale est egale a p. La propriete 1 est montree de la fagon suivante

H2 =HH = X(XTX)-lXTX(XTX)-1XT = X(XTX)-1XT et HT =(X{XTXYlXTf

= {x

)

(x

xy

x

Nous avons aussi les identites suivantes

EX = X(XTX)'1XTX = X

(/„ - H)X = x - x(x

xy

x

x = o

Lorsque nous observons les elements de la diagonale de la matrice H nous conside-rons comme une observation suspecte une valeur de ha depassant un certain seuil que nous jugeons suffisant. Dans notre cas nous dirons qu'une observation est sus-pecte si ha> 2E. La justification du choix de cette valeur se retrouve dans la section 4.6.

4.2 Variance des residus

Nous avons vu precedemment, dans la section 1.3, que le residu est defini par e =

y — y. Pour faciliter les calculs relatifs aux residus nous presentons la decomposition

suivante

e =y-y

= y-Hy = (In ~ H)y.

Designons par Hw la matrice des variances et covariances d'un vecteur w que nous avons precedemment note Cov(w).

Nous avons alors la matrice des variances et covariances des residus Se = S(/„-if)!/

= {In-H)Vy(In-H)T

= a2(In-H-H + H)

= a2 (In - H),

puisque Ev = Ee = E2.

La variance du residu i est donne par

La covariance entre le residu i et le residu j est estimee par

Cov(ei,ej) = —a2hij Ainsi, l'estimation de la variance du residu i est

s2(e;) = 52(1 - ha)

et l'estimation de la covariance entre le residu i et le residu j est

ou nous avons l'estimateur habituel de la variance des erreurs a2 qui est n — p

4.3 Analyse graphique des residus

L'analyse graphique des residus est une methode simple permettant de detecter des valeurs aberrantes. A l'aide de ces graphiques, nous pouvons voir d'un seul coup d'oeil les valeurs qui se detachent du lot. Void trois methodes graphiques parmi celles les plus utilisees

- Le graphique des residus en fonction des valeurs estimees y,.

- Le graphique des residus en fonction des donnees relatives aux variables

explica-tives Xij.

- Le QQ-plot des residus.

4.3.1 Les residus en fonction des valeurs estimees fa

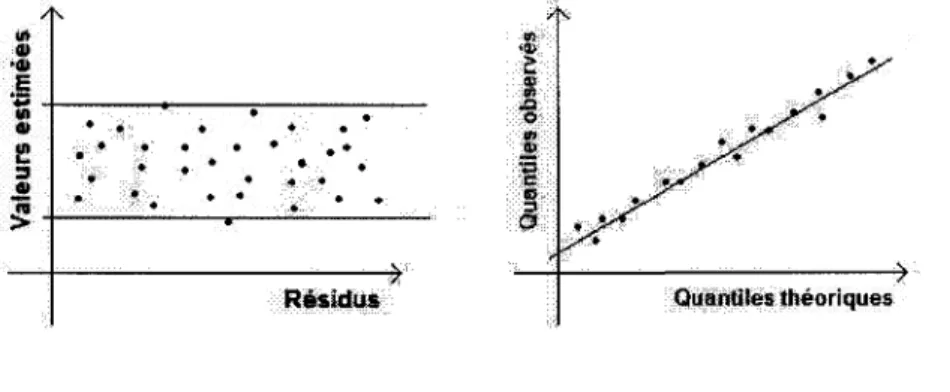
Ce graphique est habituellement le plus utilise pour verifier la validite du modele. Lorsque le modele est correct, les valeurs des residus sont reparties selon une bande horizontale et ce de fagon quasi uniforme comme dans la figure 4.1(a).

4.3.2 Les residus en fonction des variables explicatives Xij

Pour chaque variable explicative nous construisons un graphique confrontant les residus en fonction de cette variable. Lorsque le modele est correct, les valeurs des r6sidus sont reparties selon une bande horizontale et ce de fagon quasi uniforme comme dans la figure 4.1(a).

4.3.3 QQ-plot des residus

Avec ce graphique nous voulons verifier la normalite des erreurs. Pour ce faire nous allons trier les residus en ordre croissant en nommant le plus petit residu e,\ le second e2 et ainsi de suite jusqu'au nl6me residu qui se nommera en. Ensuite nous assignerons a chaque r6sidu un quantile de la loi normale centree reduite, e, est associe au , ',-quantile g, de la loi normale. Si les erreurs sont normalement distributes nous devrions obtenir une droite d'equation e< = <& comme dans la figure 4.1(b).

Les methodes graphiques sont moins rigoureuses que les methodes statistiques usuelles et ainsi le jugement de l'uniformite des donnees ne se calcule pas de maniere precise. Nous devrions ainsi utiliser des methodes complementaires pour confirmer que nos observations suspectes trouvees a l'aide de ces graphiques le sont vraiment.

Residus Quantiles theoriques

(a) Rfisidus en fonctions des valeurs estimees (b) QQ-plot

Avant de continuer Fanalyse de nos donnees voici un rappel de la structure du modele et la presentation de la notation utilisee pour le reste du document.

4.4 Notations

Nous avons le modele lineaire suivant

Sous forme matricielle nous avons que

2/i 2/2 2/3 Vn 1 XU Xn • • • Xip-i 1 X2i X22 ••• X2p-l 1 X3i X32 • • • 2 J3 p- l

ft

ft

ft-1

+

Chaque observation est associee a une ligne de la matrice X et a sa composante correspondante dans le vecteur y. Nous recherchons les observations qui ont une grande influence sur les diverses valeurs calculees en comparaison avec le reste des observations. La methode la plus evidente consiste a comparer les valeurs obtenues a Faide de toutes les observations a celles obtenues en supprimant une observation. Voici maintenant la notation adoptee pour la suppression de l'observation i

- La ligne i de la matrice X est represents par Xj = (xti,..., xip).

- La matrice X a laquelle nous avons supprime la ligne i est representee par X^). - Le vecteur des valeurs estimees base sur n — 1 observations est note y^. - L'estimateur de /? base sur n observations est note J3 = (XTX)~1XTy - L'estimateur de (3 base sur n — 1 observations est note /3^).

- Le residu sans l'observation i est note e^ = y\ — Xi(3(i).

- L'estimateur de la variance de Ferreur base sur n observations est note s2 =

n~p

- L'estimateur de la variance de Ferreur base sur n — 1 observations est note s%y

La matrice des covariances d'un vecteur Y = (Yi,..., Yp-i)T est deflnie par

= E[(Y-E(Y))(Y-E(Y)f]

[7]-4.5 Detection des observations aberrantes

Nous appelons une observation aberrante celle qui a un residu en valeur absolue plus eleve que les autres. En anglais une observation aberrante est appelee outlier. Le residu, e, = j/j — &, peut nous aider a detecter des observations aberrantes, mais parfois des observations ayant un grand impact n'auront pas un grand residu. Ce qui nous amene a developper de nouveaux diagnostics qui utilises conjointement avec les methodes graphiques de la section 4.3 nous permettrons de detecter plus efncacement les observations aberrantes.

4.5.1 Studentisation des residus

Residus studentises internes

Nous avons vu a la section 4.2 que l'estimation de la variance des erreurs est s2(e;) =

s2(l — ha) ou nous avons l'estimateur habituel de la variance des erreurs a2 qui est „2 _ T,(Vi - Vif

n — p

Les erreurs ei sont normalement distributes avec une cspcrance nullc ct une variance

nulle et de variance egale a 1, ainsi nous divisons e; par la racine carree de sa variance et nous obtenons

y/a2(l - ha)

Nous avons vu a la section 3.5 que ^ p = ("-w3 e st distribute suivant une loi du

khi-deux d'esperance egale a (n — p), ainsi nous obtenons

De plus nous pouvons montrer que les statistiques U et Z sont independantes. Posons la statistique

T _ Z _ y/o*(l-hu) _ y/<72(l-hu) _ ei

yw.

qui est distribuee suivant une loi de Student avec (n — p) degres de liberte, selon la definition d'une loi de Student que Ton retrouve dans la section C.l.

Ainsi nous definissons le residu studentise interne comme suit

e*i — . ~ Student(n — p) s • VI - ha

Le residu studentise interne e* est nomme standardized residual en anglais et son abbreviation est RSTANDARD. Pour 95% des residus studentises, nous avons, si le modele est correct que |ej| < i(o,o25;n-p) ou i(o,025;n-p) e st le 0,975-quantile d'une

loi de Student avec (n — p) degres de liberte.

Une observation i est consideree comme aberrante si |e*| > i(o,o25;n-p) [3]. Residus studentises externes

Le residu studentise externe s'obtient de la meme facon que le residu studentise interne, sauf qu'il est calcule en considerant n — 1 observations.

Nous avons ici une version du residu studentise qui prend en compte la suppression de l'observation i

, _ e( i )

et qui est distribute suivant une loi de Student avec (n—p—l) degres de liberte. Le r6sidu studentise externe ejL est nomme studentized residual en anglais et son abbreviation est RSTUDENT.

Pour 95% des residus studentises, nous avons, si le modele est correct que |e/U| < ^(o,025;n-p-i) ou i(o,o25;n-p-i) est le 0,975-quantile d'une loi de Student avec (n—p—l) degres de liberte.

e(i) >

£(0,025;n-p-l)-Une observation i est consideree comme aberrante si

Nous pouvons faire des graphiques des residus studentises par rapport aux diffe-rentes valeurs comme montres dans la section 4.3 [3], [8].

4.6 Detection des points leviers

Nous observons les elements de la diagonale de la matrice H, les ha, pour detecter les points leviers. En anglais, le point levier est appele leverage point. Ce diagnostic est base sur un resultat d'analyse de regression lineaire qui dit que la valeur predite de la ieme observation, &, peut s'ecrire comme une combinaison lineaire des n valeurs observees j / i , . . . , y„ comme suit

Vi = hiyx + h2y2 + ••• + hnyn,

pour tout i variant de 1 a n.En particulier, le coefficient hi mesure Finfluence de la valeur observee yt sur sa propre valeur predite &. La valeur d'un point levier est proportionnelle a l'influence qu'il a sur sa propre valeur predite [9]. La valeur du point levier d'une observation est habituellement comparee avec la moyenne des points leviers h = £. Ainsi une observation i est consideree comme un point levier

4.7 Detection des observations influentielles

Un diagnostic d'observations influentielles est un nombre qui mesure a quel point une observation a de Finfluence sur l'analyse de la regression. Nous cherchons, ainsi, a detecter des observations qui ont une influence plus grande que les autres sur les differentes valeurs calculees.

4.7.1 Matrice des covariances COVRATIOi

Nous cherchons a comparer la matrice des covariance englobant toutes les observa-tions a la matrice de covariance obtenue avec une observation supprime.

La matrice des covariances des coefficients estimes incluant toutes les observations est donnee par

La matrice des covariances obtenue avec une observation supprimee est donnee par

s

/3

= Ax^Xa)}'

-La methode la plus simple pour comparer ces deux matrices consiste a faire le ratio de leurs determinant detix'i''x]-i • Puisque les deux matrices different seulement par l'inclusion d'une observation, des valeurs du ratio s'approchant de un nous indiquent que les deux matrices sont semblables. La methode que nous venons de decrire ne prend pas en consideration que Pestime de a2 change aussi lors de la suppression d'une observation. Nous pouvons inclure le nouvel estime de a2 en consideration en comparant les deux matrices s2[XTX]~1 et s^JX^Jfy)]- 1 dans le

ratio de determinants suivant

COVRATIOi

det | sff

det(s2[XTX}-1) En tenant compte du fait que

et que

(n-p- l ) ^ ) = (n - p)s

(1 - ha) TTTPI. Ce qui implique que

2 _ ( n - p ) a

*(0 - " ~ s -_{( n - p - 1 ) ( n - p - l ) ( l - / i « ) '}

Par ailleurs pour une matrice A inversible nous avons det{A~l) = [det(A)]-\ et ainsi nous obtenons

detfa^]-

) =[det(X£

X

)y

1

~ {l-hii)det(XTX)'

Sachant que si nous avons une matrice A de dimension n x n e t une constante a quelconque alors det [aA] = andet [A] il vient que

det I s2

:O[*M*(«P

f»

(1 - M