Conception d'un système à initiative partagée humain-ordinateur pour l'optimisation des systèmes linéaires

CONCEPTION D’UN SYSTÈME À INITIATIVE PARTAGÉE

HUMAIN-ORDINATEUR POUR L’OPTIMISATION DES

SYSTÈMES LINÉAIRES

Mémoire

Simon Hamel

Maitrise en génie mécanique

Maître ès sciences (M.Sc.)

Québec, Canada

iii

Résumé

Les problèmes de planification dans les entreprises du secteur manufacturier sont très complexes. Pour prendre de bonnes décisions, le décideur doit utiliser des systèmes d’aides à la décision exploitant des modèles d’optimisation mathématiques. Malheureusement, les systèmes d’aide à la décision conventionnels sont souvent inadaptés et incompatibles avec les besoins des décideurs.

Dans le cadre de ce mémoire, nous proposons un système interactif qui permet au décideur d’adapter les solutions proposées en fonction de ses préférences. Nous exploitons une approche interactive inspirée des systèmes multi-agents (l'un des agents est humain et l'autre est l'ordinateur). Dans la littérature, ces systèmes sont appelés systèmes à initiative

partagée (en anglais : mixed-initiative system, ou MIS).

Nous analysons et proposons différentes approches qui permettent au décideur d'interagir avec le modèle mathématique et de choisir sa solution.

Pour tester et évaluer la faisabilité de ces méthodes, nous avons utilisé un cas industriel réel. Il s’agit d’un problème de planification collaborative des ventes, de la production et de la distribution dans l’industrie des produits forestiers.

v

Table des matières

RÉSUMÉ... III LISTE DES FIGURES ... VII REMERCIEMENTS ... IX AVANT-PROPOS ... XI

1 INTRODUCTION ... 1

2 CONCEPTS PRÉLIMINAIRES ... 5

2.1 RÉSEAUX DE CRÉATION DE VALEUR ... 5

2.2 OPTIMISATION ... 8

2.2.1 Combinaison linéaire, combinaison affine, convexité et espace convexe ... 11

2.3 UTILISATION DE SOLVEURS DANS UN CONTEXTE D’AIDE À LA DÉCISION ... 14

2.4 SYSTÈMES À INITIATIVE PARTAGÉE (SIP) ... 16

3 SYSTÈME À INITIATIVE PARTAGÉE PROPOSÉ POUR L’OPTIMISATION LINÉAIRE ... 21

3.1 INTERFACE UTILISATEUR PROPOSÉE ... 22

3.1.1 Affichage de la zone d’optimalité d’une variable ... 23

3.1.2 Navigation dans l’espace des solutions optimales ... 24

3.2 CALCUL DES ZONES D’OPTIMALITÉ DES VARIABLES ... 25

3.3 CALCUL D’UNE NOUVELLE SOLUTION OPTIMALE SUITE À L’INTERVENTION DE L’UTILISATEUR ... 25

3.3.1 Exemple d’une interface à trois variables ... 27

3.3.2 Présentation des méthodes utilisées pour générer les combinaisons convexes ... 29

4 ÉVALUATION DU SYSTÈME PROPOSÉ ... 39

4.1 DESCRIPTION DU CAS INDUSTRIEL ... 39

4.1.1 Production ... 39 4.1.2 Ventes ... 41 4.1.3 Distribution ... 41 4.2 EXPÉRIMENTATIONS ... 42 4.2.1 Protocole ... 43 4.2.2 Résultats et discussion ... 46 5 CONCLUSION ... 51 RÉFÉRENCES ... 53

ANNEXE 1: MODÈLE MATHÉMATIQUE LINÉAIRE UTILISÉ POUR L’ÉTUDE DE CAS ... 57

vii

Liste des figures

Figure 1: Exemple de plan optimal jugé inadéquat par le décideur. ... 2

Figure 2: Réseau logistique de la compagnie [Brousseau 2010]. ... 7

Figure 3: Exemple de problème d'optimisation linéaire. ... 9

Figure 4: Exemple d’une face orthogonale au gradient de la fonction objectif. ... 11

Figure 5: L'approche classique ... 15

Figure 6: Approche proposée. ... 21

Figure 7: Quantité de bois transportée par train ou par camion en PMP à différent point de vente pour une période d’un an. ... 23

Figure 8: Solution optimale avec les zones d'optimalités des variables. ... 24

Figure 9: Espace des solutions optimales versus espace des solutions accessibles. ... 27

Figure 10: Solutions optimales des variables x1, x2, x3 et les poids α1, α2, α3... 28

Figure 11: Les solutions disponibles lorsqu’on change la valeur de la variable x2 pour une interface à deux variables. ... 33

Figure 12: Saut (problème de stabilité) occasionné par le déplacement de la variable à partir d’une solution initiale ( , ) pour une interface à 2 variables. ... 34

Figure 13: La nouvelle solution est calculée à partir d'une droite reliant la solution courante et la solution maximale ou minimale de la variable active. On constate qu’il n’y a pas de saut lors du déplacement de la variable active. ... 35

Figure 14: Dans cet exemple, on diminue la valeur de la variable et ensuite on diminue la valeur de la variable . ... 36

Figure 15: Temps de réponse des méthodes en fonction du nombre de variables pour un petit, un moyen et un grand déplacement. ... 47

Figure 16: La distance euclidienne entre la solution originale et la solution calculée pour un petit, moyen et grand déplacement en fonction du nombre de variables affichées. ... 50

ix

Remerciements

Je tiens à remercier mon directeur de recherche, Jonathan Gaudreault, ainsi que mon codirecteur Claude-Guy Quimper qui ont tous les deux fortement contribué à l’élaboration de ce mémoire.

Merci également à toute l’équipe du Consortium de recherche FORAC, en particulier à Mathieu Bouchard et Philippe Marier qui ont collaboré à ce projet.

xi

Avant-propos

Ce travail de maîtrise a été entrepris dans le but de voir comment il était possible de s’inspirer des méthodes interactives d’aide à la décision utilisées en intelligence artificielle (systèmes à initiative partagée) et de les adapter au contexte de l’optimisation linéaire continue.

Ce mémoire décrit l’approche proposée et l’évaluation qui en a été faite. Elle a été appliquée à un problème d’optimisation d’un réseau de création de valeur dans l’industrie des produits forestiers. Les données ont été fournies par un partenaire du Consortium de recherche FORAC.

Les résultats ont été publiés dans un article de conférence (avec comité de lecture) présenté en annexe (Human-Machine Interaction for Real-time Linear Optimization, IEEE

International Conference on Systems, Man and Cybernetics, Séoul, Corée, 14-17 octobre 2012). Je suis le premier auteur de cet article, pour lequel j’ai aussi réalisé toutes les

expérimentations. Les coauteurs sont mes directeurs et les professionnels de recherche Philippe Marier (auteur du modèle mathématique linéaire - présenté en annexe - qui a été intégré à mon système d’optimisation) et Mathieu Bouchard (qui m’a conseillé sur différents aspects liés à l’optimisation et a proposé l’une des quatre méthodes évaluées).

1

1 Introduction

En industrie, les problèmes de planification (e. g. planification des ventes, de la production et de la distribution) sont généralement résolus en adoptant l’une des deux approches suivantes : soit on confie la planification à un expert, soit elle est réalisée de manière automatisée.

Avec la première approche (1), le plan est basé sur le jugement, l’expertise, l’expérience et l’intuition de l’expert. Celui-ci a la responsabilité de planifier les opérations et les activités de l’entreprise. La solution (i. e. le plan) ne sera probablement pas optimale, car aucun outil d’optimisation et modèle mathématique n’est utilisé. Par contre, cette approche a l’avantage de tenir compte de certains facteurs informels qui ne peuvent être modélisés mathématiquement.

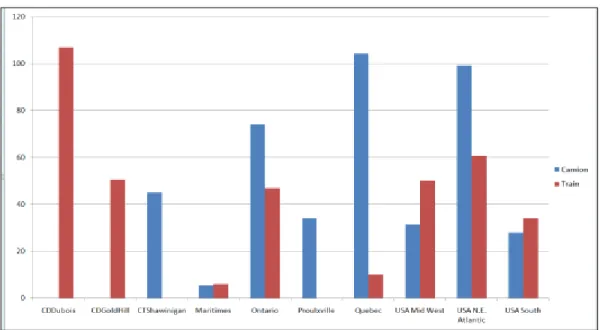
La seconde approche (2) consiste à utiliser un modèle mathématique et un algorithme qui cherche à maximiser une fonction objectif (e. g. le profit). Cette approche a le désavantage de ne pas tenir compte de certains facteurs informels qui peuvent difficilement être modélisés mathématiquement. La Figure 1 montre un exemple de solution pour un problème de transport. Le graphique affiche la quantité de produits fabriqués et transportés par train ou par camion vers différents marchés. En visualisant cette solution, le décideur pourrait avoir la perception que le marché des maritimes est sous-représenté et qu’à coût de distribution égal, il faudrait y être plus présent pour des raisons stratégiques. Or, cette information n’était pas connue/modélisée a priori dans le modèle mathématique soutenant l’optimisation. C’est seulement en visualisant la solution que le décideur prend conscience de cet état de fait.

2

Figure 1: Exemple de plan optimal jugé inadéquat par le décideur.

Les deux approches précédentes ont des lacunes. Idéalement, il faudrait les combiner afin d’obtenir une solution qui soit à la fois optimale et qui tient compte des facteurs informels difficilement modélisables

Ce projet de maîtrise a donc pour but de concevoir et développer une méthode interactive et conviviale qui donnera plus de choix et de flexibilités au gestionnaire dans ses prises de décisions. Cette interface permettra au décideur de naviguer dans un espace de solutions optimales1 de façon interactive avec un minimum d’effort et d’expertise. Cette approche aura donc l’avantage de tenir compte de l’intuition et de l’expérience du décideur.

Le reste du mémoire est organisé de la manière suivante. Le chapitre 2 présente des notions préliminaires concernant les problèmes d’optimisation qui nous intéressent (réseaux de création de valeur), l’optimisation et les systèmes à initiative

1 _{Il y a souvent plusieurs solutions mathématiquement équivalentes, alors que les algorithmes}

3 partagée (SIP). Le chapitre 3 présente un nouveau type de SIP destiné à être utilisé pour les problèmes linéaires continus. Quatre approches/méthodes seront proposées. Ces méthodes permettront de générer des solutions alternatives adaptées aux besoins du décideur avec un temps de réponse acceptable. Le chapitre 4 contient des expérimentations comparant la performance des méthodes. Le tout est suivi d’une conclusion présentée au chapitre 5.

5

2 Concepts préliminaires

Ce chapitre permet au lecteur de se familiariser avec les chaines logistiques (réseaux de création de valeurs), l’optimisation, la modélisation, et les systèmes à initiatives partagée. Ces notions sont essentielles à la compréhension du reste du mémoire.

2.1 Réseaux de création de valeur

Le problème industriel à l’origine de ce projet concerne la planification

collaborative des ventes et de la production (PCVP) ou, en anglais, Sales and Operations Planning (S&OP) [Márcio et al, 2012].

Il s’agit d’un problème important pour la gestion efficace des chaînes

logistiques. Une chaîne logistique (également appelée réseau de création de valeur)

est constituée d’unités de production, de réseaux de transport (train, camion), d’unités d’entreposage et de sites de distributions. La figure 2 présente un exemple de réseau de création de valeur. Ce réseau est composé d’une source d’approvisionnement de bois (la forêt), de trois complexes à sciage, de plusieurs zones d'entreposages, d’un centre de transbordement et de deux centres de distribution. La cour de transbordement est un centre de connexion intermodale qui sert à alimenter deux centres de distributions aux États-Unis.

La planification collaborative des ventes et de la production se définit comme un processus qui intègre l’ensemble des plans d’affaire de l’entreprise [Gips 2002; Hardison et Bettini 2002; Pomerleau 2004]. Ce processus permet de synchroniser les décisions prises aux ventes, à la distribution et à la production de façon à maximiser les profits. Autrement dit, ce processus permet aux décideurs des ventes et des opérations d’établir un plan commun qui répond mieux aux besoins de la

6

compagnie. Cette synchronisation des ventes et de la production permet d’augmenter les profits globaux de l’entreprise. Les décisions devant être prises simultanément sont les suivantes :

- déterminer comment, en quelle quantité et à quel moment (période) les produits seront fabriqués et quelles ressources seront utilisées;

- déterminer comment, en quelle quantité et combien de temps (périodes) entreposer les ressources et les produits;

- déterminer comment, en quelle quantité et à quel client les produits seront distribués.

7 Figure 2: Réseau logistique de la compagnie [Brousseau 2010].

Sc ia ge s Sc ia ge s Sc ia ge s B ill es & t ig es B ill es & t ig es B ill es & t ig es R éc ep ti o n Sc ia ge Sé ch ag e Ex p éd it io n St -R o ch T ra ns po rt c am io n T ra ns po rt tr ai n D éc is io n T ra ns fo rm at io n/ M an ut en tio n C lie nt /F ou rn is se ur B oi s d’ oe uv re 20 09 K ru g er – R és ea u lo g is ti q u e R éc ep ti o n Sc ia ge Sé ch ag e R ab o ta ge Ex p éd it io n P ar en t R éc ep ti o n Sc ia ge Sé ch ag e R ab o ta ge Ex p éd it io n P ro ul xv ill e C lie nt s U S A L ég en d e: F lu x de m at ér ia ux – ti ré F lu x d’ in fo rm at io n F lu x de m at ér ia ux – p ou ss é In ve nt ai re C lie nt s C an ad a R éc ep ti o n E xp éd iti on C T S ha w in ig an © K ru ge r & C on so rt iu m d e re ch er ch e F O R A C , 2 00 9 C D D u B oi s C D G ol d H ill / N C C en tr e de d is tr ib ut io n C D CT C or po ra tif P la n de p ro du ct io n et be so in s en tr an sp or t B es oi ns e n pr od ui ts C om m an de s fe rm es P la n de r éc ol te R ab o ta ge C om m an de s pr év is io nn el le s C ap ac ité to ta le : 2 m ill io ns d e pm p F ou rn is se ur F or êt B es oi n de tr an sp or t B es oi ns M P 60 % É pi ne tte 35 % P in g ris 5% S ap in C en tr e de tr an sb or de m en t T ra ns bo rd em en t

8

2.2 Optimisation

Tel qu’expliqué en introduction, un plan intégré des ventes et de la production peut être créé manuellement ou à l’aide d’algorithmes d’optimisation. Pour utiliser un algorithme d’optimisation, il faut avant tout modéliser le problème sous forme mathématique.

Un problème d’optimisation a pour but de maximiser ou de minimiser certains objectifs. On pourrait par exemple chercher à minimiser les coûts de transport du bois provenant de nos ressources forestières, ou encore maximiser la productivité d’une papetière. Le problème d’optimisation sera modélisé mathématiquement à l’aide de variables, de contraintes et d’une fonction objectif.

Les variables représentent les décisions à prendre. Elles peuvent prendre différentes valeurs possibles parmi un ensemble qu’on appelle le domaine de la variable. Par exemple, une variable (Qabt) pourrait représenter la quantité de bois a (en tonne) entreposée à l’usine b pour la période t, c’est-à-dire Qabt.

La solution à un problème est définie par l’ensemble des valeurs que nous affecterons à chacune des variables.

Les contraintes permettent de modéliser le problème sous forme d’équations. Elles sont en quelque sorte les règles à suivre et à respecter afin qu’une solution soit

réalisable. Ce sont elles qui déterminent les limitations et les dépendances entre les

variables. Par exemple, pour indiquer que l’inventaire (P) des produits a et b à l’usine c est une quantité positive qui ne doit jamais dépasser 5000 unités, nous écrivons les trois contraintes suivantes :

Pac + Pbc ≤ 5000 Pac ≥ 0 Pbc ≥ 0 (1)

Dans un problème d’optimisation, on doit également spécifier une fonction objectif. La fonction objectif prend en entrée une solution et retourne une valeur

9 (ex: le profit associé à la solution). Généralement, on cherchera à maximiser (ou minimiser) la valeur de la fonction objectif. Le but de l’optimisation est donc de chercher la ou les solutions qui maximisent la fonction objectif tout en respectant chacune des contraintes du problème d’optimisation. On parlera alors de solution

optimale.

À titre d’exemple, le problème d’optimisation de la Figure 3 montre une fonction objectif qui retourne la somme de six variables. On cherche à maximiser cette somme tout en respectant certaines contraintes.

Figure 3: Exemple de problème d'optimisation linéaire.

Dans un problème linéaire, les contraintes sont exprimées sous forme d'équations ou d'inéquations linéaires. Les problèmes linéaires peuvent s’écrire sous cette forme plus compacte:

Max z = ct x

Sujet à

Ax ≤ b

10

Où c et x sont des vecteurs de taille n, ct est la transposé du vecteur c. b est un vecteur de taille m et A une matrice de taille m x n. n est le nombre de variables et

m est le nombre de contraintes. L’exemple présenté à la Figure 3 montre l’exemple

d’un problème linéaire constitué de n = 6 variables, m = 3 contraintes et d’une fonction objectif z.

Pour un programme linéaire constitué d’un ensemble d’inégalités linéaires (les contraintes), l’espace des solutions réalisables est l’intérieur d’un polytope qui a autant de dimensions qu’il y a de variables dans le problème linéaire. Pour un problème d’optimisation linéaire, la solution optimale est obligatoirement sur un sommet s’il existe une seule solution optimale. Il peut aussi y avoir plusieurs solutions qui maximisent (ou minimisent) la fonction objectif. Dans ce cas, cet ensemble de solutions sera alors délimité par une des faces du polytope. Dans le cas d’un problème linéaire à n dimensions, cette face est elle-même un polytope de dimension n-1. Cette face est orthogonale au gradient de la fonction objectif.

La Figure 4 montre l’exemple d’un polytope à deux dimensions (programme linéaire à 2 variables). Dans cet exemple fictif, la fonction objectif est orthogonale à la contrainte x + y ≤ 10. Ce segment de droite borné par les contraintes – x+ y≤3 et x – y ≤5 représente un polytope de dimension 1. Toutes solutions sur ce segment de droite sont des solutions optimales, le gradient étant le vecteur [1, 1].

11 Figure 4: Exemple d’une face orthogonale au gradient de la fonction objectif.

Un problème linéaire peut être facilement2 résolu/optimisé à l’aide d’un logiciel appelé solveur. Les solveurs tels que IBM ILOG CPLEX peuvent résoudre un problème linéaire constitué de plusieurs centaines de milliers de contraintes et de plusieurs centaines de milliers de variables en l’espace de quelques minutes grâce à des algorithmes d’optimisation bien connus tel que l’algorithme du Simplex [Hillier et Lieberman 2005].

2.2.1 Combinaison linéaire, combinaison affine, convexité et espace

convexe

À partir de deux solutions d’un programme linéaire, il est possible d’en construire une troisième. Afin d’arriver à ce résultat (voir théorème 1 plus loin), nous présentons et définissons différents types de combinaisons linéaires.

2

Pour peu que l’on n’exige pas qu’une ou des variables prennent obligatoirement des valeurs entières. Ces problèmes linéaires avec nombres entiers ne sont pas traités ici.

12

Soit un problème linéaire constitué de n variables. Un vecteur de dimension n représente les valeurs assignées aux n variables du modèle. Ce vecteur représente donc un point dans un espace à n dimensions qui constitue une solution au problème.

Soit x et y deux vecteurs de n dimensions appartenant à l’espace des solutions du problème. Soit également deux scalaires α et β. Nous avons alors les définitions qui suivent.

Une combinaison linéaire de deux vecteurs est la somme pondérée des deux vecteurs :

Z = αx + βy (3)

Une combinaison linéaire affine, c’est une combinaison linéaire dont la somme des poids est égale à 1.

α + β =1 (4)

Z = αx + (1 – α) y (5)

Tous les points appartenant à la droite (3) sont des combinaisons affines des points x et y.

Une combinaison linéaire est dite convexe si elle est affine et si les poids sont tous positifs ou nuls. C’est-à-dire:

Z = αx + (1 – α) y tel que α Є [0, 1] (6)

Un espace S est dit convexe si toute combinaison convexe de deux points de cet espace appartient aussi à cet espace.

Finalement, la combinaison convexe de deux solutions optimales d’un problème linaire est également une solution optimale. Il s’agit d’un résultat bien

13 connu dans la littérature sur la programmation linéaire [Papadimitriou et Steiglitz 1998] démontré par le théorème 1 :

Théorème 1: La combinaison convexe de deux solutions optimales d’un problème linéaire est également une solution optimale.

Soit l’espace S tel queS





Maximiser ctx

Sujet à Ax ≤ b

x ≥ 0 (7)

Considérons également deux solutions optimales x et y appartenant à S (x S et

y S ), tel que d = ctx = cty. Considérons également la combinaison linéaire affine z

= αx + (1 – α) y

Nous pouvons démontrer que cette combinaison linéaire affine appartient aussi à S, donc qu’il s’agit d’une solution réalisable et quelle est optimale :

A(αx + (1 – α)y) = αAx + (1-α)Ay

≤ αb + (1-α)b = b ₍₈₎ et αx + (1 – α)y ≥ 0 + (1 – α) y ≥ 0 (9) et

14

ct z = ct (αx + (1 – α) y)

= αctx + (1 – α) ct y (10)

= αd + (1 – α) d

= d (11)

Ce théorème est valide peu importe la dimension du vecteur x. Il est donc valide pour des problèmes linéaires à n variables.

2.3 Utilisation de solveurs dans un contexte d’aide à la

décision

L’optimisation des chaînes logistiques est un exemple typique de problèmes pouvant être résolus à l’aide d’un solveur. Ce sont des problèmes d’optimisation qui peuvent contenir plusieurs millions de variables et de contraintes. Les possibilités ou les combinaisons sont alors, excessivement élevées. Malgré son expérience, son jugement et son intuition, l’humain est incapable de résoudre ce type de problème de façon optimale. L’utilisation d’un solveur devient alors un atout majeur dans de telles situations.

Il y a néanmoins un problème avec cette approche de résolution. Les solveurs ne retournent qu’une seule solution. Habituellement, l’algorithme d’optimisation utilisé par le solveur (e.g. méthode du simplex) retourne la première solution optimale trouvée qui respecte les contraintes, alors qu’en réalité, il peut exister des milliers de solutions optimales alternatives. Qui plus est, le décideur peut avoir une certaine marge de tolérance en ce qui concerne l’optimalité de la solution. Il peut exister des solutions quasi-optimales qui conviennent mieux au besoin de l’entreprise.

15 Par ailleurs, souvent, la solution optimale retournée à l’aide d’un solveur et d’un modèle mathématique sera inadéquate du point de vue du décideur, car le problème linéaire ne tient pas compte de certains paramètres informels et souvent non modélisables connus uniquement par l’humain. Assez souvent, de nouvelles contraintes ne sont « découvertes » par le décideur que lorsqu’il visualise une solution qui ne les respecte pas.

Lorsque la solution proposée ne convient pas au décideur, celui-ci peut obtenir une nouvelle solution en utilisant ce que nous appelons l’approche classique (voir Figure 5). Cette approche consiste à modifier le modèle mathématique, obtenir une nouvelle solution, analyser les résultats et réitérer jusqu’à ce que la solution soit acceptable. Préparer le modèle mathématique Obtenir/ Calculer une solution Analyser la solution Solution satisfaisante ? Non Oui

Ajouter/modifier les contraintes de façon à satisfaire les préférences utilisateur.

Figure 5: L'approche classique

Il s’agit souvent d’un processus lourd et complexe qui nécessité une expertise que le décideur possède rarement. De plus, cette itération peut être excessivement frustrante car lorsque la valeur d’une variable ne lui convient pas, le décideur ne sait pas si la variable est obligée de conserver cette valeur pour que la solution reste optimale ou s’il est possible de modifier sa valeur puis d’obtenir une autre solution optimale avec cette valeur. Il doit procéder par essai-erreur.

16

2.4 Systèmes à initiative partagée (SIP)

Un système à initiative partagée est un solveur qui résout des problèmes en combinant la puissance et l’exactitude de l’ordinateur à l’intuition de l’humain. C’est un système hybride qui exploite les points forts de l’humain et les points forts de la machine lors d’une recherche de solution [Hearst 1999]. Ces systèmes ont surtout été utilisés pour les problèmes d’optimisation discrets (variables non continues) très difficiles à résoudre. En principe, cette synergie humain-machine permet d’obtenir de meilleurs résultats qu’il serait possible d’obtenir en utilisant les capacités de la machine seule ou celle de l’humain seul [Fleming 2004].

L’humain a une connaissance implicite du problème qui ne peut pas toujours être formalisé. Cette connaissance implicite du problème permet de guider la « machine » dans la bonne direction et ainsi améliorer de beaucoup la performance des algorithmes de recherche [Klau et al., 2010]. De plus, l’humain prend souvent conscience de contraintes ou de situations inattendues à la toute dernière minute ou encore au fur et à mesure que le problème se résout. Selon le contexte, on trouve donc deux grands avantages à ces approches:

- Les algorithmes de recherches pourront converger plus rapidement vers une solution optimale car ils sont guidés par l’humain [Klau et al., 2010];

- La solution pourra être mieux acceptée en industrie, car elle tient compte des contraintes et des objectifs informels de la compagnie ou du décideur.

Par ailleurs, on constate que la recherche sur les systèmes à initiative partagée (SIP) se fait principalement sur des problèmes d’optimisations combinatoires discrets. Voici quelques exemples d’approches proposées dans la littérature:

[Fleming 2004] a proposé un système d’interaction humain-machine qui utilise un modèle pour déterminer le niveau d’interactivité qui doit se faire entre l’agent humain et l’agent machine. Ce modèle de connaissances contient de l’information

17 sur les connaissances, les habilités et les préférences de l’utilisateur. Grâce à ce modèle, il est possible de déterminer le niveau adéquat de sollicitation ou d’interactivité humain-machine de façon à exploiter au maximum les forces de chacun. Un spécialiste ayant une forte expertise sur le sujet sera plus sollicité qu’un novice.

[Klau et al. 2010] ont proposé une technique de recherche guidée par l’utilisateur (Human-Guided Search). Cette technique permet de modifier ou de construire interactivement la solution. Les solutions proposées sont adaptées selon les besoins de l’utilisateur à l’aide d’un processus interactif et itératif. L’humain guide les algorithmes de recherche en modifiant les solutions, en ajoutant des contraintes pour limiter l’espace de recherche. Les résultats obtenus montrent que cette technique améliore la performance des algorithmes de recherche (temps d’exécution et pertinence des résultats obtenus). Huit applications utilisant un modèle d’optimisation combinatoire discret ont été développées et testées avec cette technique de recherche.

[Kun et Havens 2005] ont développé un système de planification des cours pour les étudiants universitaires. Le système de planification retourne l'ensemble des cours que l'étudiant doit faire à chaque semestre pour obtenir son baccalauréat. Ce système interactif humain-machine est modélisé grâce à un problème de satisfaction de contraintes. Deux catégories de contraintes sont données au modèle. La première catégorie est les contraintes associées à la réglementation de l'université, telles que les exigences, les prérequis, les équivalences, la disponibilité de chacun des cours, les cours obligatoires pour compléter le baccalauréat, etc. La deuxième catégorie contient les contraintes qui modélisent les préférences de l'étudiant. Les variables sont discrètes et sont associées à un ensemble de cours disponibles pour un semestre donné. Cet ensemble doit obligatoirement respecter les contraintes de la première catégorie. La solution est obtenue en deux étapes. Une solution initiale satisfaisant les contraintes associées à la réglementation de

18

l'université est générée. Ensuite, un algorithme de recherche interactif est appliqué à cette solution. Durant cette étape, l'étudiant peut modifier les cours proposés de la solution initiale grâce à une interface graphique. Cet algorithme de recherche utilise les contraintes des deux catégories. Dans cette approche, l'agent système génère la solution finale et s'assure que les contraintes universitaires sont respectées. L'agent humain joue un rôle secondaire en faisant quelques modifications à la solution générée. Les résultats de l’expérimentation montrent que cette interaction humain-machine permet d’obtenir de meilleurs résultats qu’un système sans interaction.

[Ai-Chang et al. 2004, Bresina et al 2006, Bresina et al. 2007] discutent d’un système de planification des tâches et des activités pour les missions dans l’espace. Ce système de planification appelé MAPGEN permet d’effectuer la gestion des astromobiles. Chaque jour, les opérateurs utilisent ce système pour préparer un plan d’activité pour les astromobiles. Un éditeur de contraintes permet aux opérateurs de visualiser le plan et aussi d’éditer, d’ajouter et de modifier les activités et les tâches qui devront être exécutées par les astromobiles le jour suivant. MAPGEN utilise le modèle de planification par contraintes EUROPA pour valider les activités et générer le plan. L’interaction humain-machine est donc contrôlée par l’utilisateur, mais la solution finale doit respecter les contraintes du modèle. Autrement dit, l’utilisateur joue un rôle principal dans ce système. L’interaction humain-machine du système MAPGEN permet d’obtenir d’excellents résultats pour les activités et les opérations effectuées lors des missions dans l’espace.

[Guiost et al. 2004] proposent un système de contrôle du trafic aérien servant à gérer plus efficacement les situations de risques de collision entre les avions. Une interface graphique commune permet au contrôleur d'afficher les conflits et déléguer certaines décisions stratégiques aux autres contrôleurs et aussi à la machine (le système de contrôle). Pour un conflit potentiel, on dispose d'information sur les avions concernés, la distance entre les avions et l'ordre qui devra être envoyé (ou qui a été envoyé) aux avions par le contrôleur ou par le

19 système. Lorsqu'une décision stratégique (un risque de collision) est déléguée au système, une solution est calculée et proposée. Dans la plupart des cas, la solution proposée consistera à corriger la trajectoire d’un des deux avions (son cap, sa vitesse et son altitude). Si la solution proposée est acceptée, le contrôleur peut déléguer l'exécution de la solution au système ou à un autre contrôleur. Les ordres sont alors envoyés aux avions concernés. Le contrôleur a toujours le dernier mot. Le système propose des solutions, mais joue un rôle secondaire. Les résultats démontrent que le système de contrôle procure des avantages notables pour la gestion du trafic.

Finalement, [Lenor et al 2000, Linegang et al 2003] proposent des interfaces humain-machine utilisées à des fins militaires. Il s’agit de systèmes interactifs permettant de trouver le chemin le plus court (minimiser la distance) pour déplacer des troupes à un point de rendez-vous dans un environnement donné. L’interface utilisateur (MokSAF) utilise un système d’intelligence artificiel lié à un système d’information géographique (GIS) pour la planification et l’optimisation des chemins. Pour obtenir un chemin optimal, l’utilisateur doit indiquer le point d’origine et le point de destination ainsi que la composition et les caractéristiques du peloton (unité militaire). Deux systèmes interactifs humain-machines et un système naïf (the Naïve RPA) ont été considérés et testés. Dans le premier cas (the Autonomous RPA), le système propose un chemin en tenant compte du terrain, des troupes à déplacer et des contraintes décrivant des situations intangibles (social ou situationnelle). Dans le deuxième cas (the Cooperative RPA), l’utilisateur propose une route et travaille conjointement avec le système pour obtenir un chemin optimal. En ce qui concerne le système naïf (the Naïve RPA), l’utilisateur trace un chemin et le système le valide. Les résultats démontrent que le système autonome et le système coopératif donnent de meilleurs résultats que le système naïf. Le système autonome et le système coopératif donnent des résultats passablement similaires. Par contre, il y a une préférence pour le système coopératif à cause de

20

l’interaction humain-machine qui donne plus de flexibilité dans les décisions (contraintes intangibles mieux respectées, par exemple).

En pratique, les systèmes à initiative partagée ne sont pas utilisés dans les secteurs industriels tels que la gestion des chaînes logistiques. Ceci est probablement dû au fait que dans beaucoup de ces situations, les problèmes peuvent être facilement modélisés grâce à des modèles mathématiques linéaires pour lesquels de très bons algorithmes existent. Les méthodes SIP pour les problèmes combinatoires ne s’y adaptent pas facilement.

21

3 Système à initiative partagée proposé pour

l’optimisation linéaire

Un bon système à initiative partagé pour les problèmes d’optimisation linéaires (tel que notre problème d’optimisation d’une chaîne logistique) devrait en tout temps permettre au décideur de savoir s’il est possible de modifier la valeur d’une variable tout en conservant l’optimalité de la solution. L’utilisateur devrait pouvoir interagir avec le système en temps réel. L’utilisateur devrait être capable d’ajuster (augmenter ou diminuer) la variable selon ses besoins et le système devrait réagir en réajustant les autres variables de façon à ce que l’optimalité de la solution soit conservée. De plus, le temps de réaction du système devrait être pratiquement instantané, car l’interaction humaine machine se fait en temps réel.

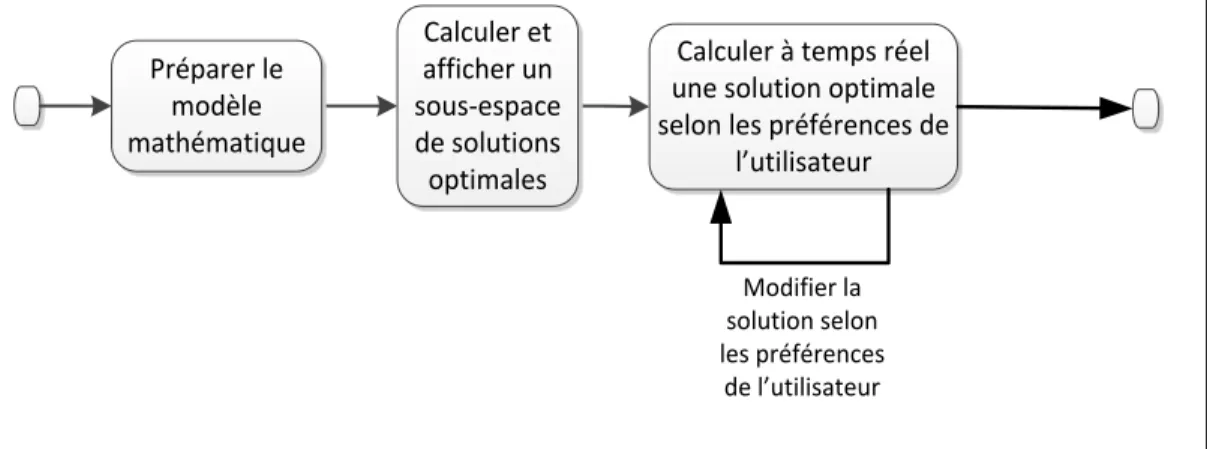
C’est ce que nous proposons dans ce chapitre : une approche coopérative (voir Figure 6) où le rôle du décideur ne consistera pas uniquement à analyser les résultats. Le choix de la solution se fait de façon dynamique et coopérative par l’ordinateur et l’humain. Préparer le modèle mathématique Calculer et afficher un sous-espace de solutions optimales

Calculer à temps réel une solution optimale selon les préférences de

l’utilisateur

Modifier la solution selon les préférences

de l’utilisateur

22

Cette approche permettra au décideur de naviguer dans un espace de solutions optimales de façon interactive en temps réel et de choisir la solution souhaitée avec un minimum d’effort et d’expertise.

Il s’agit d’une approche inspirée des systèmes multi agents (l'un des agents est humain et l'autre est l'ordinateur). Le rôle du décideur ne consistera pas uniquement à analyser les résultats, la construction de la solution se fera de façon dynamique et coopérative entre la machine et le décideur.

Les prochaines sous-sections expliquent comment ces activités sont supportées par le logiciel proposé : l’interface utilisateur proposée (3.1), comment est établi un espace de solutions optimales (3.2) et finalement comment le système calcule une nouvelle solution lorsqu’une variable est modifiée par l’utilisateur (3.3).

3.1 Interface utilisateur proposée

Prenons le cas d’un décideur d’une chaîne logistique en foresterie. Celui-ci veut transporter des produits par train ou par camion dans certaines régions du Canada. L’utilisateur doit être capable de visualiser, analyser, sélectionner et réajuster un sous-ensemble des variables3 du problème linéaire. L’affichage des solutions se fait à l’aide de graphiques. Le décideur peut utiliser autant de graphiques que désiré afin d’analyser une solution. Chaque graphique permet de visualiser un aspect différent de la solution. Les graphiques sont donc contextuels et dépendent de ce qui doit être analysé. Ainsi, chaque graphique comporte un nombre limité de variables présélectionnées par le décideur, selon un format défini. La Figure 7 donne l’exemple d’un graphique pour un sous ensemble de variables d’une solution proposée au décideur.

3 En pratique pour un modèle mathématique pouvant contenir plusieurs milliers de variables de décisions, le décideur s’intéressera à seulement quelques variables. .

23 Figure 7: Quantité de bois transportée par train ou par camion en PMP à différent point de vente pour une période d’un an.

3.1.1 Affichage de la zone d’optimalité d’une variable

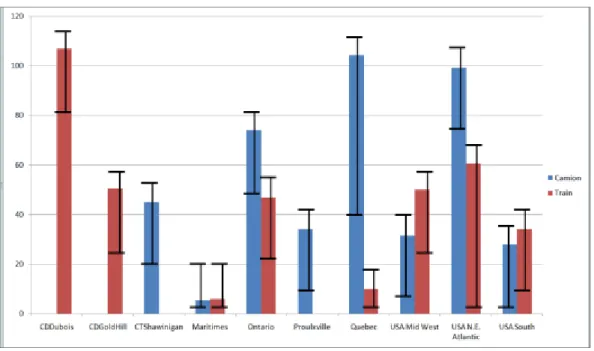
Pour rendre le système interactif, il faut que le décideur puisse visualiser et choisir les solutions optimales à partir d’un espace de solutions optimales. Pour chaque variable, nous proposons donc d’afficher (en plus de la valeur choisie par le solveur), les valeurs minimum et maximum que peuvent prendre cette variable dans l’espace des solutions optimales. Sur la Figure 8, on voit que même si le solveur a retourné une solution telle que la première variable prend une valeur égale à 107, il existerait d’autres solutions optimales pour toute valeur de la variable comprise entre 90 et 120. Ces valeurs minimales et maximales définissent la zone

d’optimalité d’une variable. Tant et aussi longtemps que la valeur de la variable est

dans cette zone, il est donc possible d’obtenir une solution appartenant à la zone d’optimalité.

24

Figure 8: Solution optimale avec les zones d'optimalités des variables.

3.1.2 Navigation dans l’espace des solutions optimales

Le décideur doit être en mesure de choisir sa solution optimale en réajustant les variables du graphique à l’intérieur des zones d’optimalité. Il pourra le faire en déplaçant à l’aide de la souris le haut du rectangle correspondant à la valeur de la variable, à l’intérieur de la zone d’optimalité.

Cependant, pour tout changement à l’une des variables, le système doit être en mesure de recalculer en temps réel de nouvelles valeurs pour les autres variables (c’est-à-dire trouver une nouvelle solution optimale). Cela doit pouvoir être fait en temps réel afin de conserver le concept d’interactivité.

25

3.2 Calcul des zones d’optimalité des variables

Voici comment on procède pour obtenir les zones d’optimalités des variables. À l’aide d’un solveur et du problème linéaire P, nous obtenons une première solution optimale maximisant, par exemple, le profit. Nous ajoutons ensuite une contrainte au problème P qui force le profit à être égal à cette valeur. En ajoutant cette contrainte au problème P, nous obtenons un nouveau problème P’ dont l’espace des solutions est égal à l’espace des solutions optimales de P. Finalement, pour chaque variable affichée , nous calculons la solution de P’ qui maximise la valeur de la variable et la solution qui minimise la valeur de la variable. Ces 2n recherches peuvent être fait en parallèle sur un système multiprocesseurs.

Pour exemple, considérons le problème linéaire à deux variables suivant:

3.3 Calcul d’une nouvelle solution optimale suite à

l’intervention de l’utilisateur

Le décideur peut changer la valeur de la variable à l’intérieur de la zone d’optimalité en augmentant ou en diminuant la hauteur de la colonne du graphique Nous avons la garantie que s’il modifie la valeur de la variable à l’intérieur de la zone d’optimalité, il existe une solution optimale satisfaisant cette nouvelle contrainte (i.e. il existe des valeurs pour les autres variables telles que nous obtiendrons une nouvelle solution optimale). Le défi est de trouver cette solution. Normalement, ceci nécessiterait une complète réoptimisation du problème linéaire complet. Nous savons cependant, en vertu du théorème 1 (chapitre 2), qu’il est possible d’obtenir une nouvelle solution optimale en effectuant une combinaison

26

convexe d’autres solutions optimales (en l’occurrence, les solutions minimisant/maximisant chaque variable du graphique). Grâce à cette technique de calcul, il est possible d’obtenir une solution optimale en temps réel et rafraîchir instantanément les graphiques. Le décideur peut donc naviguer dans un espace de solutions optimales en modifiant les valeurs des variables jusqu’à ce que la solution lui convienne.

Il y a néanmoins un inconvénient à cette technique. L’espace des solutions accessibles (l’espace contenant les solutions pouvant être obtenu grâce à une combinaison convexe de solutions pré-calculées) est un sous-ensemble de la zone d’optimalité du problème linéaire. La plupart du temps, il ne sera pas possible d’obtenir toutes les solutions optimales du problème linéaire à partir de nos combinaisons convexes.

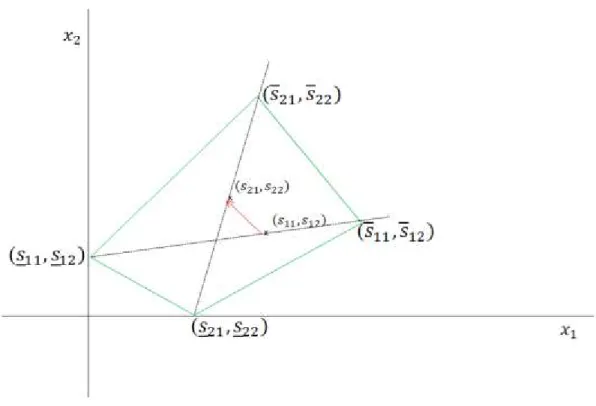
La Figure 9 démontre bien cette idée. La zone délimitée par une ellipse représente l’espace des solutions optimales. Pour tout point (solution), la valeur sur l’axe des abscisses représente la valeur de la variable x1 dans cette solution, et la valeur sur l’axe des ordonnés la valeur de la variable x2. Les quatre points identifiés par des coordonnées montrent les valeurs prises par les variables lorsqu’on minimise (x) ou maximise (x) individuellement la valeur de chaque variable sous contrainte d’optimalité du problème original. Le losange vert (reliant ces quatre sommets) représente la région accessible grâce à la combinaison convexe de quatre solutions optimales pour des vecteurs de solutions à deux dimensions. Il s’agit d’un sous-ensemble de l’ellipse.

27 Figure 9: Espace des solutions optimales versus espace des solutions accessibles.

3.3.1 Exemple d’une interface à trois variables

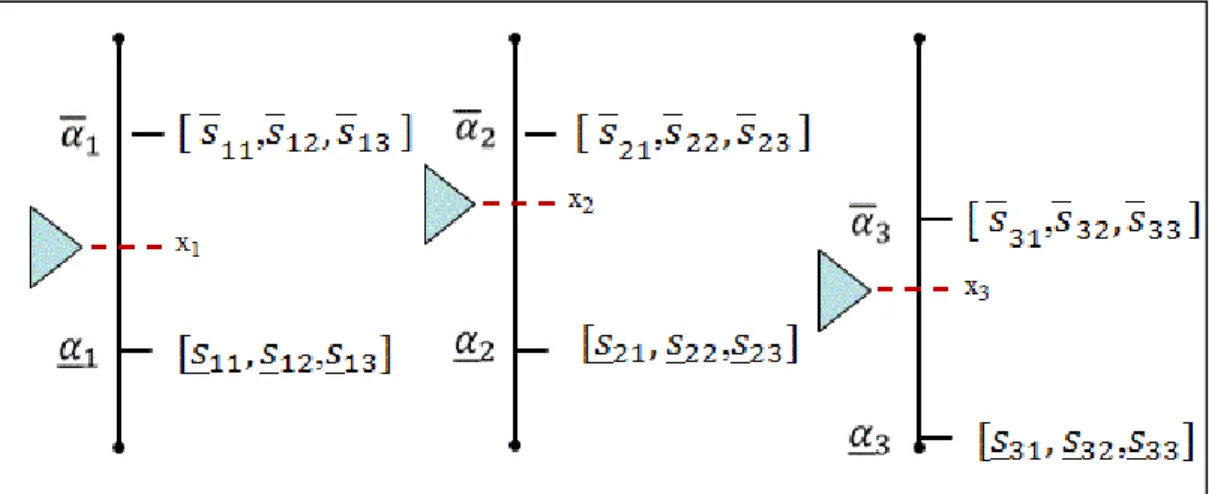
Afin de mieux faire comprendre de quelle façon les nouvelles solutions optimales sont calculées, voici l’exemple d’une interface utilisateur affichant trois variables x1, x2 et x3 (Figure 10). Dans les faits, le problème a peut-être plus de trois variables, mais on suppose que l’utilisateur s’intéresse à seulement trois d’entre elles et que seules celles-ci sont représentées sur graphique affiché à l’utilisateur.

28

Figure 10: Solutions optimales des variables x1, x2, x3 et les poids α1, α2, α3.

Six poids αi sont utilisés pour obtenir une solution à partir d’une combinaison convexe des solutions maximisant et minimisant les trois variables (on pose un poids αi = 0 pour toutes les variables du problème linéaire qui ne sont pas représentées sur le graphique). Pour une interface à 3 variables, nous avons donc les équations suivantes permettant d’obtenir la nouvelle valeur des trois variables à partir de la combinaison convexe:

x1= + + + + + (12)

x2 = + + + + + (13) x3 = + + + + + (14)

+ + + + + = 1 (15)

Une question demeure cependant. Comment déterminer ces poids? La section suivante y répond.

29

3.3.2 Présentation des méthodes utilisées pour générer les

combinaisons convexes

Nous proposons quatre méthodes permettant de recalculer dynamiquement de nouvelles solutions optimales en effectuant des combinaisons convexes des 2n solutions pré-calculées lors de l’initialisation de l’interface-utilisateur.

Les quatre approches proposées sont les suivantes : minimisation de la distance euclidienne (MDE); minimisation de la distance maximale (MDM); heuristique bipolaire (BP), heuristique triangulaire (TRI).

Ces méthodes seront évaluées au chapitre 4 par rapport à deux critères principaux : (1) la rapidité avec laquelle elles permettent de générer des solutions, et (2) la stabilité des solutions générées. Le critère de stabilité vise à s’assurer que le logiciel ne s’éloigne pas de la solution originale lorsque l’utilisateur demande un changement. Ce critère est très important pour la raison suivante. Après que l’utilisateur ait positionné une variable à une certaine valeur, il faut qu’elle se modifie le moins possible suite au déplacement subséquent d’autres variables. Autrement le décideur ne sera jamais capable de converger vers la solution désirée.

Avec les méthodes MDE et MDM, on génère une solution en utilisant les solutions maximales et minimales de toutes les variables affichées sur l’interface graphique. On le fait en résolvant un problème d’optimisation où on cherche à minimiser les écarts de déplacement de toutes les variables du graphique.

Les méthodes BIP et TRI génèrent des solutions en effectuant des combinaisons convexes des solutions maximales et minimales de la variable active (et de la solution courante pour la méthode TRI). Ces deux approches ne nécessitent pas l’utilisation du solveur. Ce sont donc les approches qui devraient donner les meilleurs résultats de rapidité, au détriment de la stabilité.

30

3.3.2.1 Minimiser la distance euclidienne (MDE)

Avec cette méthode, on recherche la combinaison convexe qui minimise la distance euclidienne entre la solution trouvée ( ) par rapport à la solution originale (x).

Soit S la matrice des 2m solutions : où est la solution qui maximise la variable et

[ ] est la solution qui minimise la variable . La solution que nous cherchons est une combinaison convexe des colonnes de la matrice S. Nous cherchons un vecteur α tel que la solution recherchée sera égale à , ∑

=1 et . Nous voulons aussi que la valeur de la variable active soit égale à v, la valeur choisit par le décideur.

La solution est obtenue en optimisant le modèle quadratique suivant :

(16)

où est un vecteur qui contient des valeurs nulles à l’exception de la valeur à la position i, qui est égale à 1. ⃗ est un vecteur dont les valeurs sont égales à 1 et ⃗ est un vecteur nul.

3.3.2.2 Minimiser la distance maximale (MDM)

Cette approche utilise une fonction objectif linéaire pour obtenir une solution. C’est en quelque sorte une approximation de l’approche euclidienne. Elle sera donc plus rapide comparativement à l’approche euclidienne qui utilise une fonction objectif quadratique.

31 Au lieu de chercher à minimiser la distance Euclidienne entre la solution recherchée et la solution initiale, cette approche cherche à minimiser la plus grande distance entre la nouvelle valeur des variables et leurs valeurs originales. Elle minimise la fonction objectif | | où est la valeur initiale et est la valeur finale de la variable.

Comme pour l’approche précédente, nous cherchons un vecteur α tel que est la combinaison convexe des 2m solutions des variables du graphique ( ∑

). Il faut néanmoins ajouter deux contraintes pour forcer la variable d’écart g du programme linéaire à une valeur supérieure ou égale à| |. Ces deux contraintes permettent d’indiquer que l’on veut minimiser le plus grand des écarts.

Voici le programme linéaire :

(17)

Où g est la variable d’écart.

Ce programme peut être résolu par la méthode du simplex qui est plus performante que la méthode du point intérieur utilisée pour les problèmes semi-définis (notre problème quadratique pour MDE).

La faiblesse de cette approche, c’est que la fonction objectif minimise la distance du plus grand des écarts, mais ne minimise pas la distance des autres variables. La solution obtenue ne devrait pas donner une aussi bonne stabilité que l’approche MDE.

32

Par exemple, prenons le cas d’une solution dont toutes les variables sont augmentées d’une distance d. Prenons aussi le cas d’une solution x dont seule la variable est augmentée d’une distance d. La valeur de la fonction objectif des deux solutions est identique du point de vue de MDM, pourtant x a une meilleure stabilité que .

3.3.2.3 Une heuristique bipolaire (HB)

Cette troisième approche met l’accent sur le temps de réponse. En fait, parmi les quatre approches proposées, l’approche bipolaire est possiblement et probablement la plus performante. Contrairement à l’approche MDE et l’approche MDM, l’approche bipolaire n’a pas besoin d’un solveur pour le calcul d’une solution. La solution est obtenue en effectuant une combinaison convexe des solutions maximales et minimales de la variable active.

Considérons le cas où le décideur veut déplacer la variable à la valeur v. Le calcul de la solution se fait grâce à l’équation: où . Le poids est égal à tel que et sont les i-èmes composantes des solutions qui maximisent et qui minimisent .

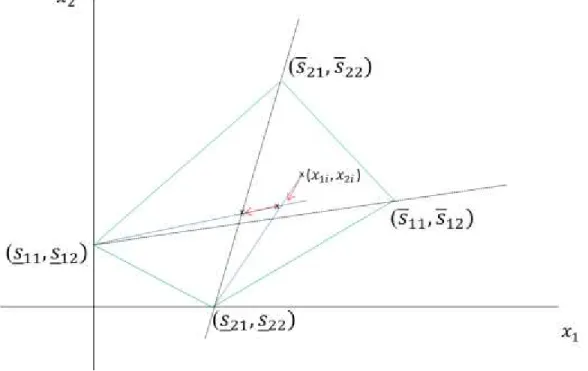
Cette approche utilise uniquement les solutions extrêmes de la variable active (la solution maximale et la solution minimale). Les solutions optimales accessibles proposées se limitent donc à une droite qui relie le vecteur de solution et le vecteur de solution (voir Figure 11).

33 Figure 11: Les solutions disponibles lorsqu’on change la valeur de la variable x2 pour une

interface à deux variables.

La zone d’optimalité accessible étant très limitée, cela occasionne un problème de stabilité. Entre autres, l’apparition de sauts (changement brusque de la valeur de plusieurs variables en même temps) occasionnés lorsqu’on passe d’une variable à l’autre.

La Figure 12 illustre un saut occasionné par le changement de variable active pour un système à deux variables. Les solutions disponibles se limitent aux deux droites indiquées en pointillé. Les solutions accessibles lorsque l’on bouge la variable sont sur le segment de droite entre les points ( , ) et ( , ) alors que les solutions accessibles lorsque l’on bouge la variable sont sur le segment de droite entre les points ( , ) et ( , ).

34

Dans ce système, la solution initiale était à la position ( , ). L’utilisateur a décidé de bouger la variable . Cela a occasionné un saut à cause de la distance qui sépare les segments de droite et .

Figure 12: Saut (problème de stabilité) occasionné par le déplacement de la variable à partir d’une solution initiale ( , ) pour une interface à 2 variables.

3.3.2.4 Une heuristique triangulaire (TRI)

Pour pallier le problème de stabilité de l’approche bipolaire, il est possible d’utiliser une approche dite « triangulaire »4.

Cette approche calcule la solution alternative en effectuant une combinaison convexe de la solution courante avec une solution extrême (maximisant ou minimisant la variable courante). La méthode commence par déterminer si (la

4

Cette approche est une idée de Mathieu Bouchard, professionnel de recherche au Consortium FORAC. Il a eu cette idée après avoir vu la méthode bipolaire à l’œuvre.

35 variable courante) est augmentée (v> ) ou si elle est diminuée (v <xi). Dans le premier cas, on fait une combinaison convexe entre la solution extrême maximale et la solution courante x. Dans le second cas, on la fait entre la solution extrême minimale et la solution courante (voir Figure 13).

Formellement, si on augmente la variable:

tel que

(18)

Si on diminue la variable :

tel que

(19)

Figure 13: La nouvelle solution est calculée à partir d'une droite reliant la solution

courante et la solution maximale ou minimale de la variable active. On constate qu’il n’y a pas de saut lors du déplacement de la variable active.

36

Contrairement à la méthode bipolaire, toute la zone d’optimalité bornée par les solutions extrêmes est accessible (la même zone que pour les méthodes MDM et MDE est donc accessible). De plus, le déplacement entre les solutions est continu et n’occasionne pas de sauts lorsque l’utilisateur décide de changer de variable courante.

Dans l’exemple de la Figure 14, l’utilisateur commence par diminuer la valeur de la variable , ensuite il diminue la valeur de la variable . On constate que cette approche permet de parcourir toute la zone réalisable et optimale bornée par les solutions maximales et minimales des variables affichées.

Figure 14: Dans cet exemple, on diminue la valeur de la variable et ensuite on diminue la valeur de la variable .

37 L’accessibilité de la totalité de la zone peut être démontrée ainsi:

Soit la solution finale appartenant à la zone ( ). Soit S la matrice des solutions[ ]. Alors, il existe nécessairement un vecteur non négatif α tel que la somme des composantes du vecteur est égale à 1 et tel que = Sα.

Nous démontrons par induction à l’aide des composantes non-nulles de α que n’importe quel appartenant à la zone d’optimalité est atteignable grâce à une séquence de mouvements triangulaires.

Supposons qu’il n’existe qu’une seule composante non nulle dans α. Cette composante est égale à 1 et nous avons : = ou = , où i est la position de la variable dans le vecteur. Si on augmente la valeur de xi à son maximum ou son minimum, alors la nouvelle solution devient égale à .

Supposons que nous pouvons obtenir toutes les solutions x grâce à des combinaisons convexes de x = Sα avec k>0 composants non nul dans α. Nous démontrons alors qu’il est aussi possible d’obtenir toutes les solutions = Sβ avec

k + 1 composantes non nuls dans β.

Soit j l’index des composants non nul dans β. Nous construisons le vecteur α suivant :

{

(20)

La solution = Sα est possible puisqu’il y’a k composantes non nulles. Par ailleurs, soit { } la solution obtenue grâce aux composantes .

38

Il est possible d’obtenir la solution à partir de la solution x en utilisant l’heuristique triangulaire :

( ) (21)

Cette relation est obtenue lorsque le décideur déplace la solution x à la solution .

39

4 Évaluation du système proposé

L’évaluation des méthodes proposées au chapitre précédent a été réalisée en collaboration avec un partenaire industriel. Celui-ci veut implanter au sein de sa compagnie un processus qui intègre la planification collaborative des ventes et de la production (PCVP). La section 4.1 décrit ce cas industriel (le modèle mathématique linéaire correspondant à ce cas est présenté en annexe). L’évaluation de la méthode proposée est ensuite réalisée (sections 4.2 et suivantes).

4.1 Description du cas industriel

Dans le cadre de ce processus, un programme linéaire contenant plus de 200 000 variables et plus de 100 000 contraintes modélisant le réseau logistique de la compagnie a été développé antérieurement (voir le modèle mathématique en annexe). Ce modèle linéaire génère un plan tactique d’opération. Ce plan tactique est divisé en 52 périodes d’une semaine. Ce plan tactique donne les décisions tactiques d’opérations par période pour la production, la distribution et les ventes. L’objectif est de déterminer le plan de production, vente et distribution optimal (maximiser les revenus moins les coûts) en exploitant au mieux les fluctuations saisonnières des prix et en ajustant la production en conséquence. Le modèle est présenté en annexe mais nous présentons ici une description générale du problème.

4.1.1

roduction

La production de bois dans une scierie se fait en trois étapes : le sciage, le séchage et le rabotage.

Le sciage permet de transformer un produit en plusieurs produits différents. Cette étape consiste à couper le produit entrant (une bille de bois) en plusieurs

40

morceaux selon un certain mode d’opération. Le mode d’opération dépend du type de panier de produits désiré.

Le séchage permet de retirer l’humidité du bois. Un bois correctement séché aura moins tendance à se déformer durant son temps de vie. Le séchage est fait en utilisant de grands séchoirs. Le processus de séchage peut durer plusieurs jours (deux à cinq jours). La durée dépend de différents facteurs tels que l’essence de bois, la dimension et le taux d’humidité du bois. Le bois peut-être séché à l’extérieur (processus de séchage à air) avant le séchage dans les séchoirs. Ce processus de pré-séchage peut durer entre deux et 18 semaines. Le séchage à air réduit le temps de séchage dans les séchoirs et peut aussi améliorer la qualité du produit fini. La réduction du temps de séchage dans les séchoirs dépend alors du temps de séchage à l’air et aussi, évidemment, de la période de l’année qui fera fluctuer le taux d’humidité et la température moyenne à l’extérieur.

Le rabotage améliore le fini du bois et permet d’obtenir la dimension exacte recherchée. Étant donné que les caractéristiques du bois et les défauts sont différents d’un produit à l’autre, il est impossible de prédire avec exactitude le produit résultant du rabotage. Tout comme pour le sciage, le rabotage produit simultanément plusieurs produits à la fois pour un même intrant donné (généralement une vingtaine de produits). La technique ou recette de rabotage utilisée permet un certain contrôle sur les proportions des différents produits en sortie. Des données statistiques sont utilisées pour estimer les produits résultants en fonction du produit entrant. Le rabotage est optionnel. Selon le cas, le produit peut être vendu non raboté.

Un plan tactique d’opération permet de déterminer pour chaque scierie du réseau logistique et pour chaque semaine, la recette ou le panier de produits à produite au sciage, le volume de produit à sécher air libre et la durée du séchage, le

41 volume de produit à sécher dans les séchoirs, le volume de produit à raboter et la recette de rabotage à utiliser.

4.1.2 Ventes

Les prix des produits forestiers de nos industries nord-américaines fluctuent selon les saisons. Cette fluctuation affecte nécessairement les ventes et le rendement global de l’industrie. Le modèle tient compte de cette fluctuation saisonnière et propose à l’avance la production et l’entreposage de produits qui seront vendus lorsque le prix de vente sera plus élevé. De plus, à l’étape du rabotage, le processus suggère la technique idéale en tenant compte de la fluctuation des prix de vente et des capacités de vente du produit par marché. Ce processus tient non seulement compte de la variation des prix par période, mais aussi de la capacité de vente de chacun des marchés.

L’utilisateur du modèle peut, par ailleurs, limiter le pourcentage de production selon le marché concerné.

4.1.3 Distribution

Le réseau logistique de notre partenaire industriel est constitué de trois scieries situées dans la province de Québec et trois centres de distribution. L’un étant situé au Québec et les deux autres dans l’est des États-Unis.

La distribution et le transport des produits aux différents marchés des ventes ne se font pas obligatoirement via les centres de distribution, bien que ce soit souvent la solution la plus économique. Les scieries peuvent transporter les produits directement aux marchés.

Le transport des produits se fait aussi entre les scieries, très souvent parce que l’usine d’origine n’est pas équipée pour faire l’étape du rabotage. Le transport et la distribution peuvent se faire par train ou par camion.

42

En conclusion, la planification tactique d’un tel réseau logistique doit tenir compte de la capacité de production des usines, de la fluctuation des prix, des marchés de ventes et des coûts de transport. Obtenir une solution optimale n’est donc pas une tâche facile. Pour un problème aussi complexe, dépendamment de la capacité de l’ordinateur utilisé, un solveur tel que CPLEX peut prendre jusqu’à 45 minutes pour trouver une solution optimale maximisant les profits.

4.2 Expérimentations

Nous proposons deux métriques pour comparer les méthodes introduites au chapitre 3. La rapidité est le délai de réponse (en millisecondes) lors du déplacement de la variable active. Il s’agit du temps mis par le système pour recalculer une nouvelle solution. La stabilité est la propriété de calculer une solution la plus près de la solution originale. Une méthode stable déplace peu les variables autres que la variable active.

Les critères ou protocoles que nous utiliserons pour évaluer le SIP seront :

- La rapidité. Avec cette métrique nous chercherons à vérifier les

points suivants :

o Les délais ou les temps de réponse lors du déplacement de la variable active sont-ils acceptables;

o Quelles sont les approches les plus intéressantes (leurs points forts et leurs faiblesses).

- La stabilité. Avec cette métrique nous chercherons à vérifier les

points suivants :

o Minimiser les sauts (les sauts des curseurs donnent une mauvaise impression);

43 o Minimiser la distance de déplacement de l’ensemble des variables affichées (idéalement on voudrait que les variables ne bougent pas lorsque la variable active est déplacée).

La stabilité est calculée en utilisant la distance euclidienne entre la nouvelle solution et la solution initiale :

stabilité = ∑ (22)

est la valeur de la variable i de la solution finale

est la valeur de la variable i de la solution initiale

4.2.1 Protocole

Le but de cette expérimentation est d’évaluer le comportement de l’interface en termes de stabilité et de rapidité pour chacune des approches expliquées à la section 3.3.2.

L’expérimentation est faite sur les variables affichées seulement. Elle ne prend pas en considération les autres variables du modèle mathématique. Autrement dit, on veut minimiser le déplacement des variables utilisées par le graphique et on veut maximiser le temps de réponse sans tenir compte du comportement des variables non affichées5.

Les tests du cas industriel sont faits sur des graphiques comportant 1, 10, 20, 30, 40 et 52 variables de décisions. Les tests consistent à déplacer les variables en

5

Rappelons que lors du calcul d’une nouvelle solution, les méthodes que nous avons proposé calculent de nouvelles valeurs pour toutes les variables du problème original, mais on cherche seulement à minimiser les perturbations pour les variables affichées à l’écran.

44

suivant un ordre ou une séquence d’exécution prédéfinie. Cette séquence d’exécution est choisie en fonction de l’ordre d’affichage des variables sur le graphique. On commence par augmenter la variable complètement à gauche sur le graphique et on termine avec celle la plus à droite.

Après chaque déplacement de variable, une solution est calculée, puis les délais de calcul et la distance de déplacements des variables sont mesurés afin de permettre les calculs de rapidité et de stabilité. Ensuite on réinitialise la solution affichée afin de conserver une uniformité dans l’évaluation des approches (le prochain déplacement se fera à partir de la solution originale et non pas la solution modifiée). Cela permet d’uniformiser les tests. Par défaut, nous avons choisi la solution optimale moyenne comme solution de départ, après chaque déplacement. Cette solution est calculée en faisant une combinaison convexe des solutions extrêmes avec un poids de (α = 1/(2n)). Cette solution « moyenne » est approximativement au centre de chaque zone d’optimalité des variables affichées. En choisissant cette solution de départ, il devient alors possible de faire des déplacements dans le sous-ensemble des solutions optimales sans toucher les frontières et les solutions extrêmes.

Les tests sont effectués pour de petits déplacements (environs 7% de la région optimale de la variable) de la variable de décision, de moyens déplacements (45%) et de grands déplacements (75%).

Voici l’algorithme de test :

Algorithme: Cas industriel (Solution initiale, La grandeur du déplacement)

ENTRÉE: S = Solution initiale, N = La longueur du déplacement SORTIE: Le résultat de l’expérimentation